Label-free probe of HIV-1 TAT peptide binding to mimetic membranes

Significance

The TAT protein is important in the progression of AIDS. Studies show that a small highly charged region of the protein, the TAT peptide, enables the protein to penetrate cells. We have developed a laser method, which differs from traditional methods and, being sensitive to surface charge, enables us to probe mechanisms of binding and penetration of artificial membranes. Using this method, which does not require a label for detection, we measured the electric potential, the strength of TAT binding to artificial membranes, and the maximum number of TATs that bind to a given liposome. This special property to transport molecules across membranes, which could not penetrate otherwise, has delivery applications for molecules of biomedical importance.

Abstract

The transacting activator of transduction (TAT) protein plays a key role in the progression of AIDS. Studies have shown that a +8 charged sequence of amino acids in the protein, called the TAT peptide, enables the TAT protein to penetrate cell membranes. To probe mechanisms of binding and translocation of the TAT peptide into the cell, investigators have used phospholipid liposomes as cell membrane mimics. We have used the method of surface potential sensitive second harmonic generation (SHG), which is a label-free and interface-selective method, to study the binding of TAT to anionic 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-1′-rac-glycerol (POPG) and neutral 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) liposomes. It is the SHG sensitivity to the electrostatic field generated by a charged interface that enabled us to obtain the interfacial electrostatic potential. SHG together with the Poisson–Boltzmann equation yielded the dependence of the surface potential on the density of adsorbed TAT. We obtained the dissociation constants K_d for TAT binding to POPC and POPG liposomes and the maximum number of TATs that can bind to a given liposome surface. For POPC K_d was found to be 7.5 ± 2 μM, and for POPG K_d was 29.0 ± 4.0 μM. As TAT was added to the liposome solution the POPC surface potential changed from 0 mV to +37 mV, and for POPG it changed from −57 mV to −37 mV. A numerical calculation of K_d, which included all terms obtained from application of the Poisson–Boltzmann equation to the TAT liposome SHG data, was shown to be in good agreement with an approximated solution.

The HIV type 1 (HIV-1) transacting activator of transduction (TAT) is an important regulatory protein for viral gene expression (1–3). It has been established that the TAT protein has a key role in the progression of AIDS and is a potential target for anti-HIV vaccines (4). For the TAT protein to carry out its biological functions, it needs to be readily imported into the cell. Studies on the cellular internalization of TAT have led to the discovery of the TAT peptide, a highly cationic 11-aa region (protein transduction domain) of the 86-aa full-length protein that is responsible for the TAT protein translocating across phospholipid membranes (5–8). The TAT peptide is a member of a class of peptides called cell-penetrating peptides (CPPs) that have generated great interest for drug delivery applications (ref. 9 and references therein). The exact mechanism by which the TAT peptide enters cells is not fully understood, but it is likely to involve a combination of energy-independent penetration and endocytosis pathways (8, 10). The first step in the process is high-affinity binding of the peptide to phospholipids and other components on the cell surface such as proteins and glycosaminoglycans (1, 9).

The binding of the TAT peptide to liposomes has been investigated using a variety of techniques, each of which has its own advantages and limitations. Among the techniques are isothermal titration calorimetry (9, 11), fluorescence spectroscopy (12, 13), FRET (12, 14), single-molecule fluorescence microscopy (15, 16), and solid-state NMR (17). Second harmonic generation (SHG), as an interface-selective technique (18–24), does not require a label, and because SHG is sensitive to the interface potential, it is an attractive method to selectively probe the binding of the highly charged (+8) TAT peptide to liposome surfaces. Although coherent SHG is forbidden in centrosymmetric and isotropic bulk media for reasons of symmetry, it can be generated by a centrosymmetric structure, e.g., a sphere, provided that the object is centrosymmetric over roughly the length scale of the optical coherence, which is a function of the particle size, the wavelength of the incident light, and the refractive indexes at ω and 2ω (25–30). As a second-order nonlinear optical technique SHG has symmetry restrictions such that coherent SHG is not generated by the randomly oriented molecules in the bulk liquid, but can be generated coherently by the much smaller population of oriented interfacial species bound to a particle or planar surfaces. As a consequence the SHG signal from the interface is not overwhelmed by SHG from the much larger populations in the bulk media (25–28).

The total second harmonic electric field, E_2ω, originating from a charged interface in contact with water can be expressed as (31–33)

$$E_{2\omega }\propto {\displaystyle \sum _i{\chi }_{c,i}^{\left(2\right)}}{E}_{\omega }{E}_{\omega }+{\displaystyle \sum _j{\chi }_{\mathrm{inc},j}^{\left(2\right)}{E}_{\omega }{E}_{\omega }}+{\chi }_{{\mathrm{H}}_2\mathrm{O}}^{\left(3\right)}{E}_{\omega }{E}_{\omega }\mathrm{\Phi },$$ [1]

where ${\chi }_{c,i}^{\left(2\right)}$ represents the second-order susceptibility of the species i present at the interface; ${\chi }_{\mathrm{inc},j}^{\left(2\right)}$ represents the incoherent contribution of the second-order susceptibility, arising from density and orientational fluctuations of the species j present in solution, often referred to as hyper-Rayleigh scattering; ${\chi }_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\left(3\right)}$ is the third-order susceptibility originating chiefly from the polarization of the bulk water molecules polarized by the charged interface; Φ is the potential at the interface that is created by the surface charge; and E_ω is the electric field of the incident light at the fundamental frequency ω. The second-order susceptibility, ${\chi }_{c,i}^{\left(2\right)}$, can be written as the product of the number of molecules, N, at the surface and the orientational ensemble average of the hyperpolarizability α_i⁽²⁾ of surface species i, yielding ${\chi }_{c,i}^{\left(2\right)}=N\langle {\alpha }_i^{\left(2\right)}\rangle$ (18). The bracket $\langle \rangle$ indicates an orientational average over the interfacial molecules. The third term in Eq. 1 depicts a third-order process by which a second harmonic field is generated by a charged interface. This term is the focus of our work. The SHG signal is dependent on the surface potential created by the electrostatic field of the surface charges, often called the χ⁽³⁾ contribution to the SHG signal. The χ⁽³⁾ method has been used to extract the surface charge density of charged planar surfaces and microparticle surfaces, e.g., liposomes, polymer beads, and oil droplets in water (21, 25, 34–39).

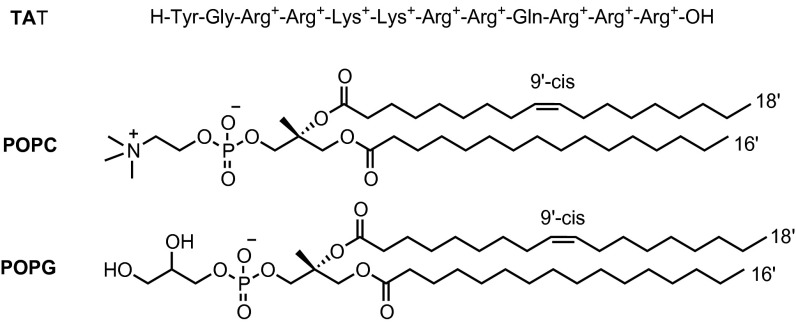
In this work, the χ⁽³⁾ SHG method is used to explore a biomedically relevant process. The binding of the highly cationic HIV-1 TAT peptide to liposome membranes changes the surface potential, thereby enabling the use of the χ⁽³⁾ method to study the binding process in a label-free manner. Two kinds of liposomes, neutral 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and anionic 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-1′-rac-glycerol (POPG), were investigated. The chemical structures of TAT, POPC, and POPG lipids are shown in Scheme 1.

Scheme 1.

Chemical structures of HIV-1 TAT (47–57) peptide and the POPC and POPG lipids.

Results and Discussion

Adsorption of the TAT Peptide to the Neutral POPC Liposome.

As there is no significant population of electrolytes in the solution containing POPC liposomes before the addition of TAT, we note that it is the hydrolysis of the TAT peptide yielding the +8 charged TAT and the accompanying hydroxide ions that together serve as the electrolytes. We thus have the interesting situation where TAT functions as both an electrolyte and an adsorbate to the POPC liposomes, both of which affect the interface potential.

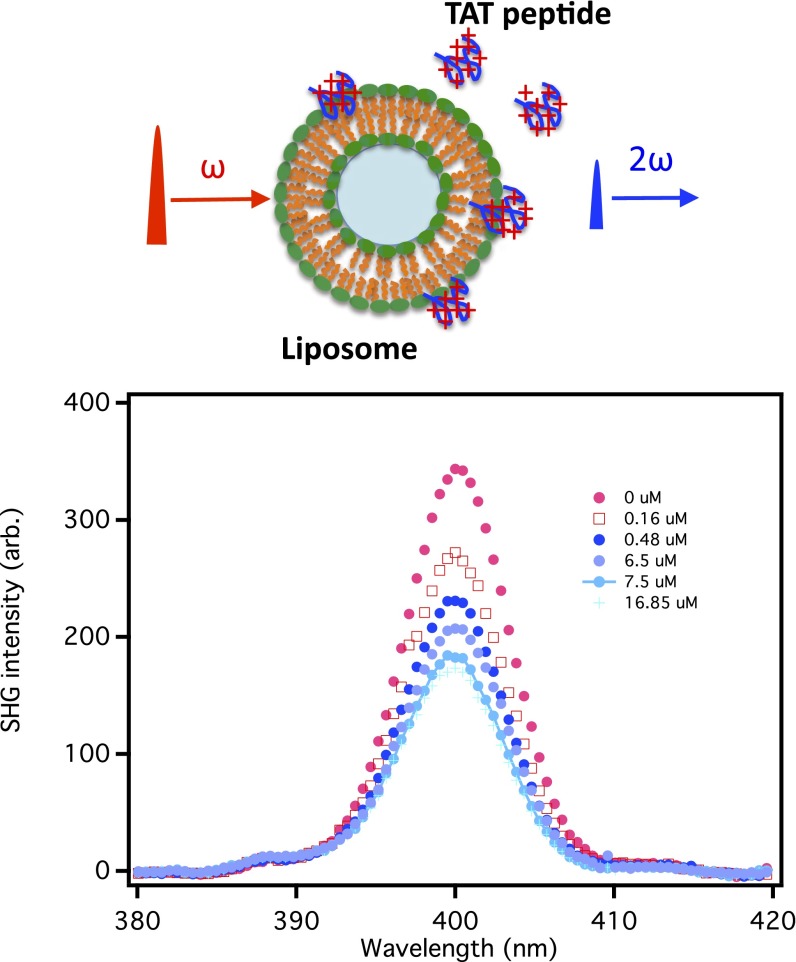
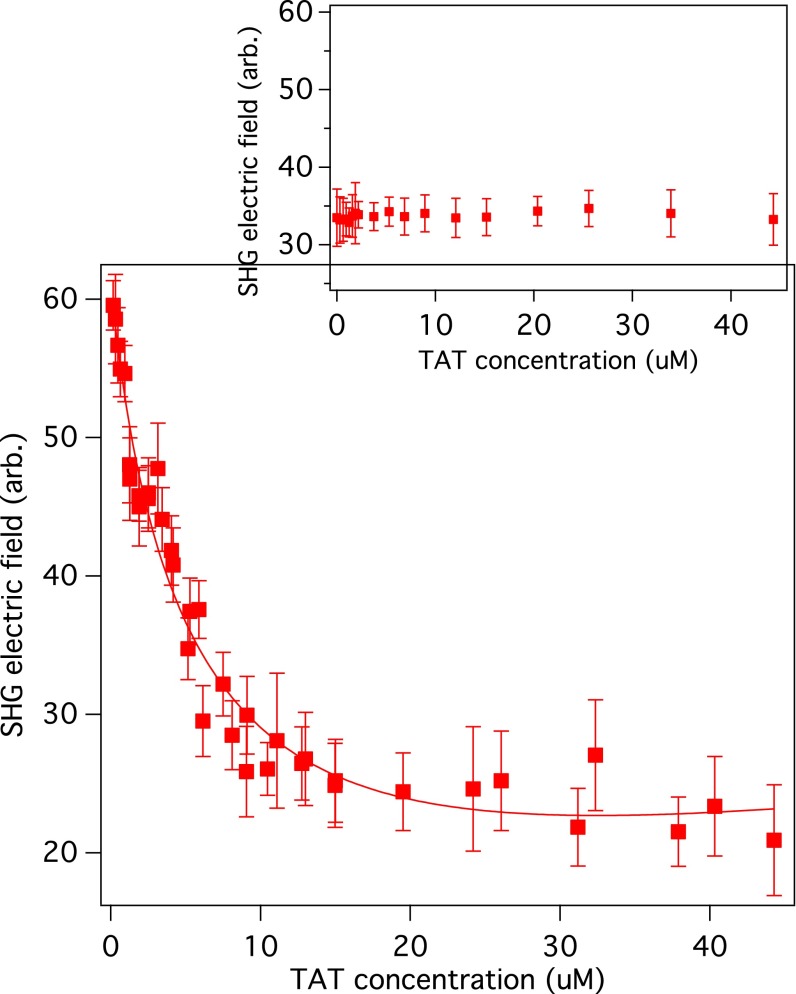
The SHG intensity profiles of POPC liposomes were taken at various concentrations of the TAT peptides as shown in Fig. 1. The SHG signal in the absence of TAT is due to hyper-Rayleigh scattering and also the χ⁽²⁾ of the species at the liposome/water interface. The SHG intensity decreases significantly as the concentration of the TAT peptide is increased from 0.0 μM to 17 μM. Fig. 2 shows the SHG electric field as a function of TAT peptide concentration for liposomes consisting of the neutral phospholipid POPC. The SHG electric field decreases with increasing TAT peptide concentration, reaching a plateau above 35 μM. The decrease in the SHG signal indicates that χ⁽²⁾ and χ⁽³⁾ in Eq. 1 have opposite signs, inferred from the fact that the surface potential Φ becomes increasingly more positive as the TAT bulk concentration is increased. A control experiment in which there were peptides but no liposomes is shown in Fig. 2, Inset. As shown in Figs. 2 and 3, the SHG electric field generated without TAT is approximately three times larger for POPG liposomes than for the POPC liposomes. This can be attributed to the fact that the surface potential of POPG liposomes has an intrinsic χ⁽³⁾Φ contribution that is negative due to its initial surface charge, which enhances the SHG signal. On the other hand, the POPC is neutral in the absence of TAT and therefore there is initially no χ⁽³⁾Φ contribution to the SHG signal. To relate the dependence of the SH signal to the binding of the +8 charged TAT requires an expression that connects the surface potential to the adsorption of TAT. This can be done using the Poisson–Boltzmann equation. The application of the Poisson–Boltzmann equation to a model of a charged interface that has been used frequently is the Gouy–Chapman model in which the surface has a fixed charge and there is an oppositely charged diffuse layer of ions that compensates the surface charge. The Gouy–Chapman model is not applicable to our systems because the model requires the surface charge to be fixed, which is not the case in our experiments; i.e., the surface charge changes as the positively charged TAT peptide is adsorbed to the neutral and charged liposome surfaces. In addition, the Gouy–Chapman model specifies that the electrolyte be a symmetric one, (+z, −z) whereas in our work the TAT yields an asymmetric electrolyte (+8, −1). This asymmetry can be removed if a significantly higher concentration of a symmetric electrolyte is added to the solution. In our investigation of the TAT peptide binding to a liposome we obtained a solution of the Poisson–Boltzmann equation that expresses the relation of the surface potential to the surface charge density and the bulk concentrations of electrolytes. The solution of the Poisson–Boltzmann equation for the TAT–POPC system was calculated with no approximations and also for comparison calculated with an approximation that simplifies the expression for the interface potential. The “approximate” solution of the Poisson–Boltzmann equation is given by Eq. 2 (a detailed derivation can be found in SI Text):

$$\mathrm{\Phi }=\frac{kT}{e}\ln (\frac{{\sigma }^2}{16\epsilon C_{0}kT}+\frac{9}{8})=\frac{kT}{e}\ln \left(\frac{{\left(8eN/4\pi R^2\right)}^2}{16\epsilon C_{0}kT}+\frac{9}{8}\right).$$ [2]

C₀ is the bulk concentration of TAT before any adsorption and σ is the TAT surface charge density of a POPC liposome, which is given by $\sigma =8eN/4\pi R^2$, where R is the radius of the liposome and N gives the number of TAT peptides bound to a liposome. Including possible depletion of the bulk TAT population due to adsorption by the liposome surface yields a modified Langmuir equation given by ref. 40,

$$N=\frac{\left(N_{\max }+C_0/d+55.5K_{\mathrm{d}}/d\right)-\sqrt{{\left(N_{\max }+C_0/d+55.5K_{\mathrm{d}}/d\right)}^2-4N_{\max }{C}_0/d}}{2},$$ [3]

where K_d is the dissociation constant (moles per liter), 55.5 is the number of moles of water in 1 L, d is the liposome number per unit volume, and N_max is the maximum number of TATs that can bind to a POPC liposome. The SHG electric field is given by

$$E_{2\omega }\propto A+B\ln \left(\frac{{\left(8eN/4\pi R^2\right)}^2}{16\epsilon C_{0}kT}+\frac{9}{8}\right),$$ [4]

Where A and B were found to be of opposite sign based on the observed decrease in SHG signal as the peptide concentration was increased. The constant A contains the χ⁽²⁾ contribution, B contains the χ⁽³⁾ contribution, and both have local optical field corrections. The fitting of the SHG data for POPC shown in Fig. 2 using Eq. 4 yields a dissociation constant K_d of 32.0 ± 5.6 μM and the maximum number N_max of bound TATs per liposome was found to be 117 ± 10.

Fig. 1.

SHG intensity profile spectra of POPC liposomes taken at different concentrations of the TAT peptide. nset shows the schematic representation of the SHG experiments.

Fig. 2.

SHG electric field is shown as a function of HIV-1 TAT peptide concentration in a solution of POPC liposomes. The solid line is a fit to Eq. 4, which was obtained from a solution of the Poisson–Boltzmann equation (SI Text). The fitting yielded a dissociation constant K_d of 32.0 ± 5.6 μM. Inset shows a control experiment without liposomes.

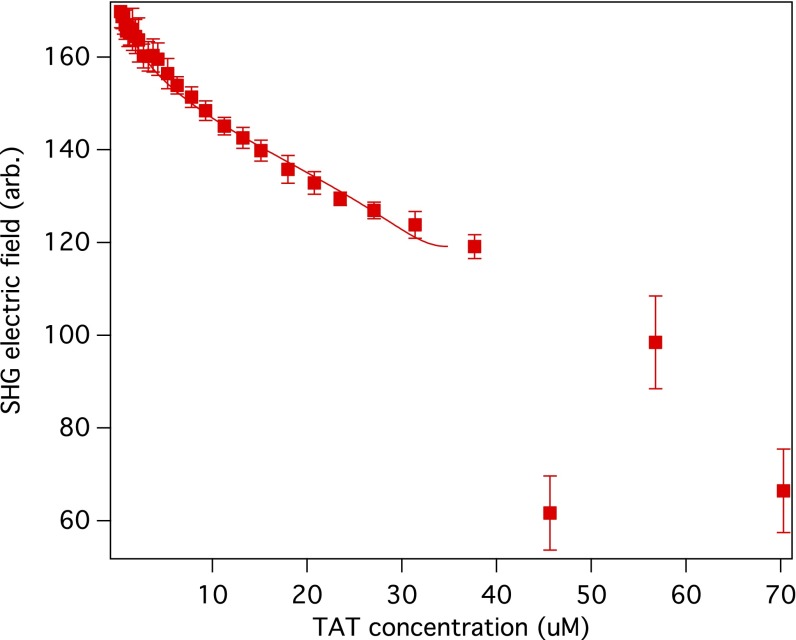
Fig. 3.

SHG electric field is shown as a function of HIV-1 TAT peptide concentration for negatively charged POPG liposomes. The solid line is a fit to Eq. 6. The fitting yielded a dissociation constant K_d of 7.5 ± 2.0 μM. Above 37 μM, the liposomes aggregate and the solution becomes cloudy.

Adsorption of the TAT Peptide to the Negatively Charged POPG Liposome.

Unlike POPC, there is a surface charge on the POPG liposomes before the addition of the TAT peptide to the solution. Thus, the analysis of TAT binding differs from the analysis for the POPC liposomes. Upon solving the Poisson–Boltzmann equation for the TAT–liposome system without approximations, and also for comparison with approximations is given in SI Text, we obtained an expression for the surface potential of the negatively charged POPG liposomes as a function of the bulk TAT concentration,

$$\mathrm{\Phi }=-\frac{kT}{8e}\ln \left(\frac{{\sigma }^2}{2\epsilon C_{0}kT}+\frac{C_{{\mathrm{Na}}^{+}}}{C_0}+9\right),$$ [5]

where C₀ is the bulk concentration of TAT before any adsorption, and $C_{{\mathrm{Na}}^{+}}$ is the concentration of Na⁺ in the solution. Before adding TAT peptides, the concentration of electrolyte is 200 μM due to the release of one Na⁺ for each of the POPG lipids that compose the POPG liposomes. The maximum concentration of TAT is less than 50 μM, which is small compared with the sodium ion concentration. The positively charged TAT peptides bind to the negatively charged POPG liposomes and reduce their negative charge. The surface charge density can be written as $\sigma ={\sigma }_0-8e{N}^{\prime }/4\pi R^2=8e{N}_{\max }/4\pi R^2-8e{N}^{\prime }/4\pi R^2$, where σ₀ is surface charge density of POPG liposomes (coulombs per square meter) before TAT adsorption, N_max is the maximum number of TATs that can bind to a POPG liposome, N′ is the number of TATs adsorbed to a POPG liposome at a given bulk concentration of TAT and includes possible depletion of TAT in the bulk solution, and R is the radius of the liposome (41). The SHG electric field is given by

$$E_{2\omega }\propto A^{\prime }+B^{\prime }\ln \left(\frac{{\left(8e{N}_{\max }/4\pi R^2-8e{N}^{\prime }/4\pi R^2\right)}^2}{2\epsilon C_{0}kT}+\frac{C_{{\mathrm{Na}}^{+}}}{C_0}+9\right),$$ [6]

where A′ and B′ were found to be of opposite sign based on the observed decrease in SHG signal as the peptide concentration was increased. The constant A′ contains the χ⁽²⁾, B′ contains χ⁽³⁾, and both have local optical field corrections. From the fit of the SHG data, shown in Fig. 3, the dissociation constant K_d and the maximum number of TATs that bind to a POPG liposome, N_max, were found to be 7.5 ± 2.0 μM and 4.6 × 10³ ± 0.5 × 10³, respectively. The increasing neutralization of POPG as TAT is added to the solution results in aggregation of the liposomes, which can be seen visually when the TAT concentration exceeds ∼40 μM. We attribute the fluctuations in the SHG signal to the aggregation of the POPG liposomes, which occurs as the repulsive interactions between liposomes decrease, due to TAT being adsorbed to the POPG surface.

It is seen that the TAT peptide binds more strongly to POPG than to POPC and that is attributed to the attractive electrostatic interactions between the oppositely charged TAT and POPG. With respect to the role of the conformation of the TAT peptide on the binding process we note that studies have shown that the secondary structure of the TAT peptide is a random coil when free in solution and when bound to a liposome (15). If the structures of the giant unilameller vesicle (GUV) liposomes used in previous studies are similar to those of the large unilamellar vesicle (LUV) liposomes used in our studies, we suggest that a conformational change of the TAT peptide does not play a significant role in the binding process. Although attractive electrostatic interactions are absent for the POPC liposomes, which in fact become increasingly repulsive as the number of bound TATs increases, we still find from the free energies of adsorption that there is strong binding of the TAT peptides to the POPC liposomes, ΔG° = −8.5 ± 1.1 kcal/mol for POPC and ΔG° = −9.4 ± 2.2 kcal/mol for POPG. Recognizing that the zwitterionic POPC head group is significantly hydrated (42, 43) suggests that a possible mechanism for binding is the dehydration of POPC. This process could contribute to the binding of TAT peptide to the liposome, driven by an increase in entropy as the water molecules are displaced by the TAT peptides, i.e., the classical hydrophobic effect (43).

Several groups have studied the binding of HIV-1 TAT peptide to liposomes, using different techniques (11, 12, 14, 16). Fluorescence spectroscopy has been used to study a fluorescent analog of TAT peptide (tryptophan-substituted) binding to 30-nm liposomes in buffer solution (12). Two apparent dissociation constants were observed for 30-nm egg PC liposomes: K_d1 = 2.6 ± 0.6 μM (24% of the extent of binding) and K_d2 = 610 ± 150 μM (76% of binding). The authors suggested that hydrophobic forces are responsible for K_d1 and electrostatic forces are responsible for K_d2. In our experiments we found that the fit to the SHG data was not improved with two K_d dissociation constants. Isothermal calorimetry has been used also to measure TAT peptide binding to liposomes (11). In that study a single dissociation constant K_d = 15.4 μM, for 100-nm liposomes containing 75%POPC/25% POPG, was obtained (11). At the same composition of liposomes, we obtained from our SHG studies a binding dissociation constant of 24.7 ± 0.2 μM. The difference in our findings although not very large could be due to their using the Gouy–Chapman model, which requires that the surface electric charge remains constant. This is not the case for TAT binding to POPC and POPG because the surface charge changes as the +8 TAT binds to the liposomes. We note that the SHG method, unlike the other methods, yields information not only about the strength of TAT binding but also about the maximum number, N_max, of TATs that can bind to the liposome surface, i.e., the assembly properties of TAT on the liposome surface.

To determine, without approximations, the dissociation constants and the N_max values for the binding of TAT to the POPC and POPG liposomes, we performed numerical calculations that included all terms in our derived expressions, i.e., no approximations in the application of the Poisson–Boltzmann equation. The K_d values obtained for POPC are 29.0 ± 4.0 μM for the numerical calculation and 32.0 ± 5.6 μM for the approximated calculation. The values for the POPG liposomes are 8.0 ± 1.4 μM for the numerical calculation and 7.5 ± 2.0 μM for the approximated calculation. For the POPC liposome we obtain an N_max value of 117 ± 13, using the “approximate expression,” and from the numerical calculation an N_max value of 98 ± 13. For the POPG liposome the approximate expression yields an N_max value of 4.6 × 10³ ± 0.5 × 10³ and from the numerical calculation an N_max value of 5.1 × 10³. Although the numerical calculations are the best that can be obtained using the Poisson–Boltzmann equation and the modified Langmuir model for adsorption, the approximate solution provides a physical picture of the dependence of the surface potential on the surface charge density, the total peptide concentration, the electrolyte concentration, the temperature, and the dielectric constant of the bulk solution.

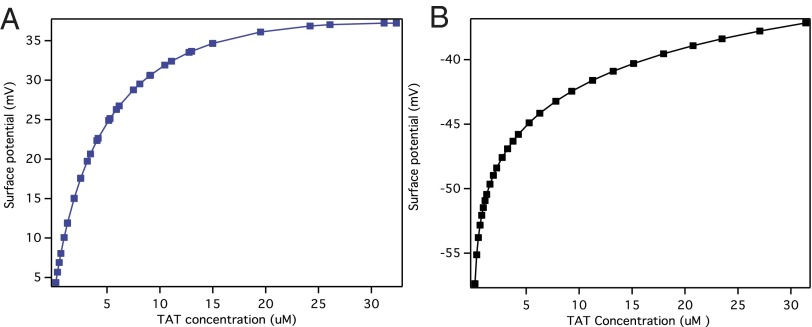
It is noted that the interfacial electrostatic potential plays a key role in determining chemical equilibrium at interfaces, the interfacial pH, and in general the interfacial population of charged species. Fig. 4 shows the calculated surface potential as a function of added TAT concentrations for POPC (Fig. 4A) and POPG (Fig. 4B) liposomes. The surface potentials obtained change from 0 mV to +37 mV for POPC and from −57 mV to −37 mV for POPG, as the TAT peptide was added.

Fig. 4.

The calculated surface potentials vs. added TAT concentrations for POPC (A) and POPG (B).

Conclusions

A new way has been developed to measure the dissociation constant of the HIV-1 TAT peptide–liposome complex. This investigation yields the value of the electrostatic surface potential as the +8 charge TAT binds to the liposome surface. Furthermore, we obtained the maximum number of TATs that can bind to the membrane mimetic neutral (POPC) and charged (POPG) liposome surfaces. The method used here is the “label-free” χ⁽³⁾ SHG method. It is the sensitivity of the SHG signal to the surface electric potential that is central to the studies reported here. Using the Poisson–Boltzmann equation and a modified Langmuir model, we have related the SHG electric field to the dissociation constants and the surface electrostatic potential. The unique characteristics of SHG make it a promising approach to explore DNA, peptides, proteins, and drugs at biomembrane surfaces.

Materials and Methods

HIV-1 TAT peptide (H-YGRKKRRQRRR-OH) was obtained from Sigma-Aldrich. The TAT peptide has a charge of +8 in solution at pH 6. The lipids POPC and POPG were obtained in 1-mL aliquots, at 10 mg/mL in chloroform solution, from Avanti Polar Lipids.

Large unilamellar vesicles (LUVs) were prepared using the extrusion method with the Mini-Extruder (Avanti Polar Lipids) (25). Five milliliters of either POPC or POPG lipids at 2 mg/mL in chloroform was dried under a stream of nitrogen. The leftover dry thin film was hydrated with a 100-mM sucrose solution, followed by vigorous vortexing for 10 min. After five freeze–thaw cycles, the lipid suspension was then extruded through a polycarbonate membrane with a pore diameter of 200 nm (Avanti Polar Lipids). Using dynamic light scattering (Zetasizer Nano-ZS; Malvern Instruments), the diameters of the POPC and POPG liposomes were found to be ∼120 nm. The final concentration of liposomes used was 5 × 10¹¹/mL. HIV-1 TAT peptide was dissolved in 100 mM sucrose to maintain a constant osmotic pressure across the lipid bilayer when the peptide was added to the liposome solution.

The SHG measurements were carried out in a forward scattering geometry setup. Briefly, a Ti:Sapphire oscillator (Maitai; Spectra-physics) yielded 80-fs pulses at 800 nm at a repetition rate of 80 MHz, with an energy of 10 nJ per pulse. After passing through a half-wave plate and a polarizer, the light was gently focused into the sample in a 5-mm cuvette. The SHG photons generated from the sample were collected by lenses and focused into the monochromator. A CCD detector was used to record the SHG signal. A typical exposure time for each SHG intensity profile spectrum was 5 s. At each concentration, 60 SHG intensity profile spectra were taken for averaging. SHG signals were obtained by integrating an intensity profile after subtraction of a background intensity and correction of linear scattering by the liposomes at 800 nm and 400 nm.