Plasmonic nanoparticle scattering for color holograms

Significance

In this work, we demonstrate a multicolor hologram based on plasmonic scattering of nanoparticles that is capable of encoding more information than the spatial bandwidth dictates. This device is designed based on the fundamental concept of diffraction produced by the scattering of arrays of nanoparticles. Hence, when multiple arrays of plasmonic nanoparticles are multiplexed without coupling, they carry independent information such as polarization and wavelength to the far field. The device shown is unique because, to our knowledge, this is the first multichannel diffractive element produced from a single thin film that simultaneously controls two wavelengths in-plane and within subwavelength distances. These results will lead to a new range of applications in diffractive optics, information storage, and 3D displays.

Abstract

This work presents an original approach to create holograms based on the optical scattering of plasmonic nanoparticles. By analogy to the diffraction produced by the scattering of atoms in X-ray crystallography, we show that plasmonic nanoparticles can produce a wave-front reconstruction when they are sampled on a diffractive plane. By applying this method, all of the scattering characteristics of the nanoparticles are transferred to the reconstructed field. Hence, we demonstrate that a narrow-band reconstruction can be achieved for direct white light illumination on an array of plasmonic nanoparticles. Furthermore, multicolor capabilities are shown with minimal cross-talk by multiplexing different plasmonic nanoparticles at subwavelength distances. The holograms were fabricated from a single subwavelength thin film of silver and demonstrate that the total amount of binary information stored in the plane can exceed the limits of diffraction and that this wavelength modulation can be detected optically in the far field.

Metallic nanoparticles have been used for centuries to create vibrant colors in works of art. The Lycurgus cup (fourth century), for example, uses metallic nanoparticles to produce a dichroic effect. The nanoparticles are positioned randomly, and the optical characteristics can be approximated using its effective refractive index. Their spectra response depends on the size, shape, and material of the nanoparticles (1). This phenomenon is analogous to the electronic resonance of an antenna in the visible region of the electromagnetic spectrum. In photonics, behavior of this kind is attributed to the interaction of the electric component of light and free electron oscillations in the materials, commonly referred to as surface plasmon resonance (SPR). Although this phenomenon has always fascinated scientists, only over recent years has it been possible to accurately manipulate these structures on the nanoscale due to improved fabrication techniques. In this work, we show a novel approach to produce narrow-band diffraction and holography based on plasmonic enhanced optical scattering of nanostructures. The diffraction produced by the scattering of atoms has been widely studied in X-ray crystallography. We apply a similar concept with 2D arrays of scattering nanoparticles to produce diffraction for visible light. Furthermore, we designed and fabricated a direct-beam hologram that produces a narrow-band image when directly observed in reflection. We also achieved colorful holography by placing two independent plasmonic nanostructures in a subwavelength distance to diffract two colors simultaneously. In contrast with dielectric multiplexing of nansutructures, we show that metallic nanoparticles can be uncoupled because of their plasmonic properties. This feature allows them to carry independent wavelength information without cross-talk.

In the traditional concept of holography, the fringes that produce diffraction are larger than half the wavelength. For instance, according to Bragg's law, a grating of pitch d diffracts light at angles θ_m satisfying the equation dsin(θ_m) = mλ (m = 1,2,3...). It can be observed that any wavelength smaller than d will be diffracted. A similar effect is achieved when any structure is placed periodically on a plane. When white light illuminates a 2D periodic array, different wavelengths are diffracted at different angles, creating a dispersive effect in the far field (2). This effect is an intrinsic limitation for producing multicolor diffractive devices on surfaces. In holography, it is possible to mimic an object reconstruction by replacing the parallax of one dimension with the dispersive effect, producing the so-called “rainbow hologram” (3). To date, there has not been a methodology to produce multicolor holography from a single diffraction plane. Even with multiple holograms illuminated using monochromatic sources (such as lasers or light filtering), the spatial multiplexing required to form the reconstruction is nontrivial. Multiple set ups for nondirect white-light beaming have been suggested but they have been impractical because of their narrow field of view, aligning complexity and the many other limitations of all of the optical devices involved (4–6). Here we use narrow-band scattering points to produce two simultaneous independent color holograms in plane. Interestingly, in contrast with the traditional concept of optical information storage, we prove that multiple wavelength binary information can be stored in distances less than λ/2. Our scheme in achieving multicolor holography paves the way toward robust color holographic displays.

In classical holography, the dispersion constraint has been overcome by using a 3D structure rather than single diffraction planes. With 3D structures, such as Lippmann holograms (7) or photonic crystals (8), it is possible to store the wave-front information with a corresponding band gap associated to specific wavelengths. The Lippmann approach has been the only successful multicolor holography technique for direct illumination, but the nanoengineering of its 3D fringe structure has not been possible with a different method other than by using laser interference on photosensitive materials (7). A critical factor of the traditional concept of holography is that the amount of information stored is band limited to the wavelength (9). This limitation means that without the information of the evanescent wave in the near field, it is not possible to retrieve optical information for features with dimensions below λ/(2n) where n is the refractive index of the medium. This is equivalent to the Abbe resolution limit in optical microscopy or the storage capacity for optical memory devices. Holography in the subwavelength domain has been somewhat limited to the treatment of nanostructures with effective medium theory (EMT), for either dielectrics (10, 11) or metals with the concept of metamaterials (8, 12) [or metasurfaces (13, 14), a 2D extension of a bulk metamaterial (15–17)], such that the effect of each diffractive unit (sometimes quoted as pixel) is analyzed with the properties of the effective medium or average permittivity of the whole pixel. EMT is often applied to materials whose permittivity changes spatially in dimensions much smaller than the wavelength. The application of EMT allows creation of different diffractive pixels with an effective response. This methodology simplifies the far-field modeling of large areas that in practice cannot be computed with the complete solution of Maxwell's equations. The situation becomes complex for functional surfaces where the wavelength approaches the period of the array producing higher-order Floquet-Bloch modes (15, 18, 19). In this case, describing the entire surface with an effective index of refraction is no longer valid. In contrast to the idea of metamaterial or metasurface, for our approach, the scattering of each nanoparticle is considered independently as an emission point, which is sampled on a diffractive plane. Even if the nanostructure is in the subwavelength domain, it is assumed as a single scattering point. Furthermore, there is not an intrinsic pixel shape associated with the emission point. The envelope and all of the characteristics of the far field can be extracted directly from the behavior of the scattering points (20). These scattering points are assumed to be spherical waves with the origin at the lattices of the crystal. The validation and generalization of this concept is known as the Floquet-Bloch theorem, and it has been widely applied in X-ray crystallography, where the diffraction is produced by the elastic scattering of atoms in periodical arrays (21). Hence, the far field of a crystal is the reciprocal lattice (or the Fourier transform) of the direct lattice vector. In this analogy, the Mie scattering of nanoparticles can be assumed to be the source of spherical waves in a 2D diffractive array. A 2D array of nanoparticles cannot produce a band gap for a ray with normal incidence. Therefore, if the scattering of nanoparticles is expected to scatter equally at all wavelengths, the result would be a color dispersion as predicted by Bragg's law. However, if the scattering cross section of the plasmonic nanoparticle is wavelength dependent, then the diffraction observed will also carry that dependence. This nonuniform scattering cross section of plasmonic nanoparticles along the spectrum dramatically alters the dispersion predicted by Bragg's law. The advantage of this perspective is that multiple arrays of nanostructures can be engineered and multiplexed in subwavelength distances. Recent work has shown that a hologram is capable of storing binary information of two transverse polarizations simultaneously within distances of ∼λ/2 (22). Additionally, the scattering occurs in 360°, and therefore, the field of view is not limited like in traditional holography.

To achieve a narrow-band hologram, the scattering properties of the nanoparticle should be optimized. By means of the numerical solution of Maxwell equations or with the Mie-Lorenz spheroid approximation, it is possible to estimate the scattering spectrum of a nanoparticle. In addition to the theoretical estimations, we developed a series of experiments to measure the far-field emission of the nanoparticles. For this experiment, we concentrated in the first harmonic corresponding to the half-wave dipolar resonance of the particle. It is important to consider that the size of the nanoparticle is not necessarily half the wavelength as expected in radio-antennas. In general, a reduction in size takes place in metallic nanoantennas for the visible regime. When the skin depth is comparable to the wavelength, radiation penetrates the metal and induces oscillations of the free-electron gas. Following a literature review (23, 24), numerical solutions, and fabrication capabilities, we decided to use the scattering from spheroidal Ag nanoparticles. The anisotropy of the nanoparticles can be advantageous if the scattering bandwidth is reduced. Nanoparticles with a width of 60 nm, height of 50 nm, and length ranging from 60 to 165 nm were fabricated (see Methods). A square lattice arrangement was used to allow the generation of different diffraction spots carrying the far-field emission characteristics of the nanoparticles. Consequently, when a white light source is used to illuminate, the color dispersion observed in the far field produces an image with a narrow spectral response, which is in contrast to nonresonant diffractive structures. Fig. 1A shows the narrow-band dispersive effect produced by two different plasmonic Ag nanoparticles captured in reflection. The left image corresponds to the far-field scattering of a nanoparticle with the localized surface plasmon resonance (LSPR) operating in the blue. In this case, the nanoparticle is circularly symmetric and therefore polarization insensitive. The right image shows the diffraction from an elliptical nanoparticle with two resonances in the visible regime (blue and red) when the light is polarized in the direction of the long axis. In this case, the nanoparticle is asymmetrical and therefore polarization sensitive. Fig. 1B shows the spectral emissions of multiple grids of nanoparticles with similar height and width but different varying lengths. For all cases, the polarization of incident light is oriented in the direction of the long axis. It is observed that the peak corresponding to the half-wave dipolar resonance crosses the complete visible spectra when the length of the nanoparticle ranges between 60 and 165 nm; the peak wavelengths shown here are in agreement with simulations and other work (22, 25). In addition to the first harmonic, a second peak appears in the blue for the longer nanostructures. This phenomena has been previously reported and attributed to substrate interactions with Ag nanoparticles (26). Notice that the scattering properties observed in this experiment corresponds to a superposition of the back scattering and forward scattering that is reflected back from the Si substrate with a given phase delay. The half-wave dipolar resonances peaks are plotted in Fig. 1C and compared with the simulation scattering peaks. The simulations were performed using the boundary element method (BEM) (27) with different nanorods embedded in a homogeneous dielectric with an index of refraction of 1.1 (considering an effective permittivity of air and the SiO₂ substrate) (28). Simulation results isotropically record the nanorod scattering; yet in reality, a fraction of this power will be observed due to the device operating in reflection. In the ideal case, we require an anisotropic nanostructure that maximizes radiation scattering yet minimizes absorption.

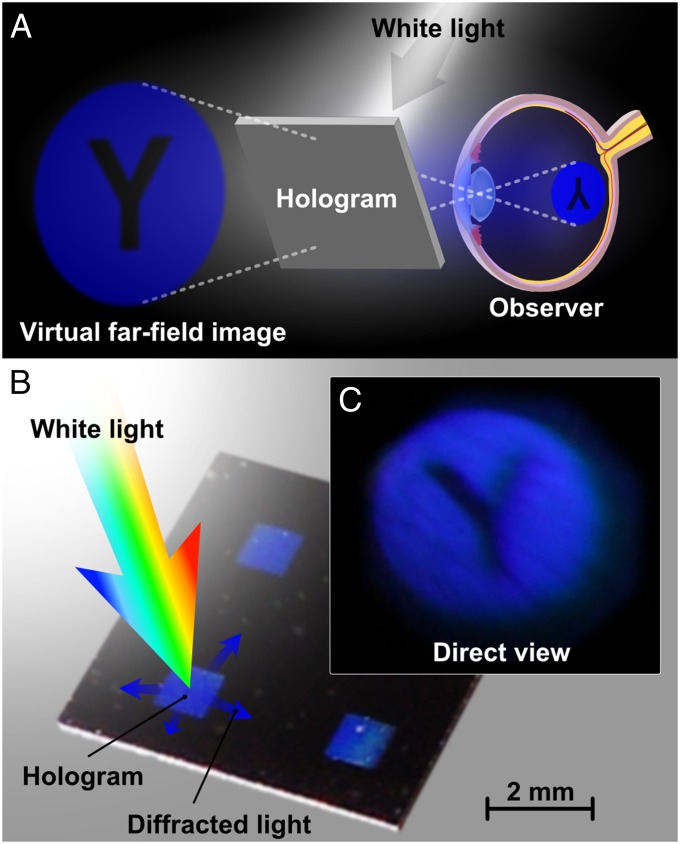
Fig. 1.

Spectral characteristics of the scattering of silver nanoparticles. (A) Projected white light diffraction pattern produced by square grids of nanoparticles of 1-µm pitch. The diffracted light carries the scattering spectrum of the nanoparticle. (B) Measurement of the far-field spectra of nanoparticles of 60 nm in width, 50 nm high, and of multiple lengths. (C) Experimental and simulated plot of the half-wave dipolar resonance peak along the visible spectra.

The color scattering of the localized plasmon resonance supported by the silver nanoparticle can be used to generate narrow-band holography when illuminated by white light. To prove this, we fabricated a direct-view scattering hologram for white light to reconstruct the letter Y inscribed on a blue circle. The procedure to achieve this consisted of sampling such nanospheres over an intensity binary hologram as described in the literature (20). To maximize the field of view and fill factor, a square grid of particles with a pitch of 390 nm was used in the sampling process. A total of ∼3.2 × 10⁶ nanospheres of 60 nm diameter were lithographically patterned in a single silver thin film. Fig. 2A shows a diagram of the wave-front reconstruction when the hologram is illuminated with a white light source. If the lens of the eye is located properly and focused to the infinity, it is possible to reconstruct a virtual blue image in the retina. Fig. 2 B and C shows the fabricated sample with three holograms under sunlight and a picture of the observed direct-view reconstruction. In this case, the camera is placed close to the sample and focused to the infinity, and the image is captured in reflection. Although the green and red colors have almost vanished, the width of the spectral emission still produces a blurry effect at the edges of the reconstructed image.

Fig. 2.

Narrow-band hologram produced with the scattering of plasmonic nanoparticles when it is illuminated by a white light source. (A) Diagram of the reconstruction of a direct-viewed hologram when it is illuminated with a broad band source. (B) Experimental holograms showing a characteristic blue scattering. (C) Real reconstruction captured with a camera placed in front of the hologram and focused to infinity.

We further demonstrate multicolor holograms by spatially multiplexing two different nanoparticles with different spectral emissions on a SiO₂ substrate. Design parameters were established to reduce the cross-talk between nanoparticles. For instance, when they are placed off-axis, their coupling is minimized (22). Also the dipolar interaction is sufficiently dampened when their separation distance is 3× their radii (29). In our case, the blue and red colors come from the scattering of 60-nm-diameter nanospheres and nanorods of 60 nm diameter and 165 nm length, respectively. To balance the intensity emission of both colors, the nanospheres are placed in pairs. The design of each hologram consists of sampling the nanoparticles with a square lattice as if they were independent. The two nanoparticles are multiplexed in a subwavelength distance (Fig. 3A). One complexity is that the nanorod showed a secondary peak in the blue region, and as a consequence, the nanosphere produces a single color hologram, and the nanorod produces a red and a blue hologram (similar to Fig. 1A). However, there is a simple way to remove the blue diffraction effect carried by the nanorod. By using a pair of nanospheres in the position of the missing nanorod, the blue diffraction is completely altered, whereas the red diffraction remains unchanged. This effect is better understood by observing the behavior of the nanoparticles at the diffraction plane. Fig. 3C shows the four possible arrangements of nanoparticles placed on a single diffractive unit and their normalized scattering intensity extracted from the BEM simulation (27) (the diffractive unit is used in this context to refer to the minimal subsection of the hologram in contrast to the pixel that describes an effective medium). The nanoparticles located on the left side of each diffractive unit show the blue color information, whereas the nanoparticles located on the right side show the red color information. It can be observed that in the case of 650-nm illumination, all of the nanospheres become virtually invisible, and just the nanorods on the right side of the diffractive unit scatter. The case of 405-nm illumination is less obvious because the effect is a mixture of two holograms. The first is created by the nanospheres on the left side of the diffractive unit and contains the relevant information. In addition, the nanorod and nanospheres on the right side of the diffractive unit always scatter, creating a secondary white hologram. However, this secondary hologram on the right side does not contain information and just acts as a mirror. In practical terms, each half in this arrangement carries independent holographic information either for blue or for red. Other possible combinations of different types and shapes of nanoparticles can be engineered according to the features required by the hologram.

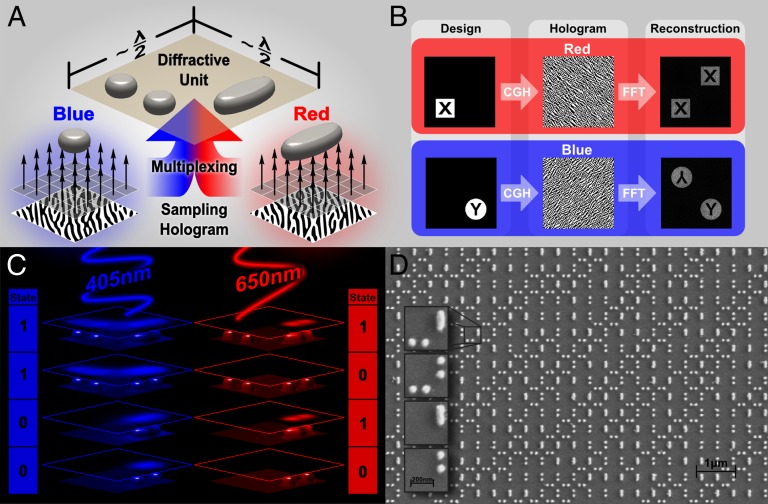
Fig. 3.

Nanoparticle multiplexing for multicolor holograms. (A) Process to design a multicolor hologram through different types of nanoparticles. Two independent holograms are sampled with square grids of nanoparticles and finally multiplexed. (B) Retrieved holograms and corresponding simulated reconstructions for the red and blue colors. (C) BEM simulation of the scattering for the four possible configurations of a diffractive unit with 405- and 650-nm light polarized in the direction of the nanorod axis. The field intensity is normalized and plotted at the nanoparticle boundaries and on a surface 150 nm above the substrate. (D) SEM image of the fabricated scattering hologram containing the two types of nanoparticles at the surface.

To fabricate a multicolor scattering hologram, we designed two independent images. For blue, we used the same Y image inscribed on a circle and for red an additional X image inscribed on a square (Fig. 3B). The two intensity holograms that reconstruct the images in the far field were retrieved independently. Then, two square lattices with a pitch of 390 nm for both types of nanoparticles were sampled and multiplexed following the methodology explained above. The final multicolor hologram was fabricated on the surface of a 200-nm SiO₂ capping layer on a Si wafer and patterned in a single Ag layer of 50 nm thickness. The final multicolor scattering hologram contained ∼12.8 × 10⁶ blue nanospheres and ∼3.2 × 10⁶ red nanorods over an area of 1 mm². Fig. 3C shows a section of the hologram containing both types of nanoparticles. The multiplexed nanospheres and nanorods produce a complex interleaving profile along the surface. However, it is possible to identify the four types of diffractive units in different locations of the hologram.

In our hologram configuration, the Si surface acts as a mirror. Therefore, the light that is not scattered by the particles is reflected back to the zeroth order. Fig. 4A shows the projection of the hologram on a diffusive sphere observed in reflection. Two laser diodes (405 and 650 nm) were combined with a beam splitter and illuminated at normal incidence to the hologram. The use of monochromatic light source eliminated the blurry effect produced by the dispersion. The polarizations of both lasers were oriented in the direction of the nanorod axis. It can be observed that the X and Y letters have similar size in the design, but the far-field projections cover different angles. Also, a conjugated image appears because of the binary nature of the hologram (30). The width and height of the first order reconstructed image corresponds to an angle of 62.6° for 405 nm and 112.8° for 650 nm, but the diagonal corresponds to 94.5° for 405 nm and 180° for 650 nm (the diagonal for red is not covered over the whole surface of the cap). The size mismatch for different colors is intrinsic to the far-field hologram but can be easily compensated from the design with an image transformation. Another feature that should not be confused with the image size is the envelope of the projection. The origin of the envelope of a traditional hologram is given by the shape of the diffractive unit. For instance, in a far-field computer generated hologram (CGH) produced with square pixels, the reconstruction is projected over a sinc function. However, in a scattering hologram, the emission points are much smaller than the wavelength; thus, the envelope of the projected field does not match with a traditional square pixel of a CGH. The intensity is near uniform over 180° of the cap because the emission is highly omni-directional. It can be seen in Fig. 4A that even the second order of the blue image is as bright as the first order. Therefore, the envelope is not linked to the pixel shape but to the emission characteristics of the nanoparticle. The cross-talk was extracted with the ratio of intensities for the X and Y in both colors. In this case, the cross-talk observed is ∼6%, and therefore, a dim X can be observed for 405 nm and a Y for 650 nm. Fig. 4B shows the far-field projection designed with two independent color images overlapping on top of each other: one containing a crest for the nanorod and the other a text for the nanospheres. The back-scattered measured light in the far field is ∼3% for each wavelength. Other estimations based on simulations and the literature (22, 28) suggest that the total scattered light in this type of arrangement is about 17% of the incident light for the resonant wavelength. These estimations mean that the scattering cross section of these nanoparticles produce an enhancement of about five times the geometrical cross section.

Fig. 4.

Far-field of multicolor scattering holograms observed in reflection. (A) A design of an X for 650 nm and a Y for 405 nm shows the wide-field of view of the reconstruction with a minimal cross-talk of about 6%. (B) Two color reconstructions containing an overlapped crest and a text.

In conclusion, we demonstrated that the scattering of metallic nanoparticles can be used to create color holograms. More importantly, the wavelength characteristics of the diffraction can be manipulated based on the plasmonic scattering properties of the nanoparticles. With the nanoengineering of resonant structures with conductive behavior and their appropriate distribution, a narrow-band wave-front reconstruction can be achieved for direct white-light beaming. In addition, we showed that two different types of plasmonic nanoparticles can be multiplexed in subwavelength distances, increasing the bandwidth information limits. With this process, it is possible to create multiwavelength holograms and any other type of diffractive element using a single subwavelength film of metal.

Methods

The holograms were fabricated over a 200-nm silicon dioxide capping layer on top of a silicon wafer. The substrate was spin-coated with high-resolution positive poly(methyl methacrylate) 950K resist, and electron beam lithography was used to define the nanoparticle structures. After exposure, the samples were developed in a methyl isobutyl ketone:isopropyl alcohol solution with a 1:3 composition. Finally, 50 nm of silver was thermally evaporated, and after a lift-off process in acetone, the residual metal was removed, exposing the nanoparticles on top of the SiO₂ surface.