Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Aug 7;136(35):12489–12497. doi: 10.1021/ja507382j

Rapid Proton-Detected NMR Assignment for Proteins with Fast Magic Angle Spinning

Emeline Barbet-Massin †, Andrew J Pell †, Joren S Retel ‡, Loren B Andreas †,§, Kristaps Jaudzems ∥, W Trent Franks ‡, Andrew J Nieuwkoop ‡, Matthias Hiller ‡, Victoria Higman ‡, Paul Guerry †, Andrea Bertarello †, Michael J Knight †, Michele Felletti †, Tanguy Le Marchand †, Svetlana Kotelovica ⊥, Inara Akopjana ⊥, Kaspars Tars ⊥, Monica Stoppini #, Vittorio Bellotti #,∇, Martino Bolognesi ○, Stefano Ricagno ○, James J Chou ◆, Robert G Griffin §, Hartmut Oschkinat ‡, Anne Lesage †, Lyndon Emsley †, Torsten Herrmann †, Guido Pintacuda †,*
PMCID: PMC4156866  PMID: 25102442

Abstract

graphic file with name ja-2014-07382j_0006.jpg

Using a set of six 1H-detected triple-resonance NMR experiments, we establish a method for sequence-specific backbone resonance assignment of magic angle spinning (MAS) nuclear magnetic resonance (NMR) spectra of 5–30 kDa proteins. The approach relies on perdeuteration, amide 2H/1H exchange, high magnetic fields, and high-spinning frequencies (ωr/2π ≥ 60 kHz) and yields high-quality NMR data, enabling the use of automated analysis. The method is validated with five examples of proteins in different condensed states, including two microcrystalline proteins, a sedimented virus capsid, and two membrane-embedded systems. In comparison to contemporary 13C/15N-based methods, this approach facilitates and accelerates the MAS NMR assignment process, shortening the spectral acquisition times and enabling the use of unsupervised state-of-the-art computational data analysis protocols originally developed for solution NMR.

Introduction

In the last 15 years, magic angle spinning (MAS) NMR emerged as a generally applicable structural biology technique, complementing liquid-state NMR, X-ray crystallography, and electron microscopy. Following seminal work on microcrystalline proteins,1,2 examples demonstrating the utility of MAS include studies of prion fibrils,3,4 polydisperse full-size heat shock complexes,5 intact viral capsids,6 membrane-bound drug targets,7,8 and bacterial virulence factors9,10 at an atomic level. Approaches for sample preparation, sequence-specific resonance assignment, and collection of conformational restraints have been designed to calculate three-dimensional structures and to determine their dynamics. However, these procedures are still far from routine, and therefore, the development of a robust, rapid, and general protocol is needed for MAS NMR to become a widespread, universal tool in structural biology, for the novice as well as the expert. In particular, sequence-specific resonance assignment of MAS spectra remains the prerequisite for site-specific studies that yield internuclear distances, torsion angles, and molecular structures.

Currently, MAS NMR assignment procedures are primarily based on double- and triple-resonance spectra, making use of correlations between 13C and 15N signals.11,12 These procedures usually require large amounts (∼1 mg/kDa) of 13C/15N labeled samples, long data acquisition times, and expert manual analysis of the spectra. This is in contrast to the standard solution NMR acquisition and analysis protocols, where established triple-resonance pulse schemes correlating backbone and side chain 1H, 13C, and 15N resonances are used for sequential assignment.13 These heteronuclear approaches have been used in thousands of solution NMR studies, and in general, they provide high-quality data that allow the use of modern, error-tolerant computational algorithms and protocols for efficient and objective data analysis with minimal human intervention.14,15

Due to its high gyromagnetic ratio and natural abundance, 1H is the optimal choice for detection in solution. In solids, however, these same properties are responsible for a network of strong homonuclear 1H dipolar couplings that dramatically lower the resolution. To observe high-resolution 1H signals in solids, the homogeneous broadening characteristic of this network16 needs to be overcome, by dilution of the proton content in the sample17,18 and/or by fast sample spinning19,20 in conjunction with high magnetic fields.

In proteins, proton dilution can be controlled easily by expression in perdeuterated media followed by reintroduction of protons at exchangeable sites. Resolved spectra were demonstrated on a deuterated protein sample with full protonation of the amide sites at the MAS rate of 20 kHz,21 and a further improvement in resolution was achieved by Reif’s and Rienstra’s groups, respectively, by lowering the levels of amide protonation (typically 10–40%)22−25 or by increasing the MAS rates up to 40 kHz,26 a spinning regime where well-resolved spectra can be obtained even in fully protonated small proteins.27 Under these conditions, 1H detection can be combined with assignment protocols based on dipolar-assisted 15N/13C and 13C/13C correlations.28,29 More recently, we have shown that high-quality proton-detected cross-polarization-based 15N–1H correlations (“CP-HSQC”) that maintain simultaneously high sensitivity and high resolution can be obtained at spinning frequencies ωr/2π ≥ 60 kHz for fully back-protonated, deuterated samples.30,31 In this spinning regime, long 13C and 15N coherence lifetimes are observed with application of low power 1H decoupling,32−34 and scalar coupling interactions become viable for efficient homonuclear 13C transfer, similar to solution NMR. This has opened the way to new, expeditious backbone resonance assignment strategies for significantly larger proteins and to the rapid detection of structurally relevant parameters.35−37

Here we show that in this regime, sensitive high resolution solution-NMR-like 15N–1H protein fingerprint spectra can be recorded on a wide variety of proteins and sample preparations. This leads to well-dispersed signals in an optimized suite of 3D spectra for rapid de novo assignment of medium-sized microcrystalline proteins, sedimented particles, and membrane-integrated systems. Notably, the NMR spectra are of sufficient quality for performing automated and robust sequence-specific backbone resonance assignment using a modern computational data analysis program.38

Experimental Section

Sample Preparation

All [100%1HN,2H,13C,15N]-labeled samples were expressed in deuterated minimal media, and all refolding and reconstitution steps were performed in buffers containing 100% H2O, to obtain samples that are fully protonated in the exchangeable sites. Samples were concentrated and packed into the NMR rotor, by using microcrystallization protocols,12,39 sedimentation,40−43 or detergent dialysis into phospholipid membranes.44,45 Details on each sample preparation are provided in the Supporting Information (SI).

NMR Data Acquisition

All spectra were recorded on Bruker Avance III 800 or 1000 spectrometers operating at Larmor frequencies of 800 or 1000 MHz for 1H, at 60 kHz MAS using triple-resonance HCN 1.3 mm probes. The temperature of the sample was regulated using a VT gas flow in the range of 230–243 K, in order to achieve an estimated sample temperature of 300 K.

In the 2D CP-HSQC spectra (Figure 1), the nonselective 90° pulses were set to 2.5 μs at 100 kHz rf-field amplitude (1H), 5.0 μs at 50 kHz rf-field amplitude (15N), and 3.12 μs at 80 kHz rf-field amplitude (13C). 1H–15N forward cross-polarization (CP) was achieved using a contact time of 1.5 ms, during which the 1H rf-field amplitude was ramped linearly from 12 to 30 kHz, and the 15N rf-field amplitude was held constant at 38 kHz. The 15N–1H back CP was achieved using a contact time of 0.4 ms, during which the 1H rf-field amplitude was ramped linearly from 29 to 11 kHz, and the 15N rf-field amplitude was held constant at 39 kHz. The swept-low-power TPPM sequence47 or the WALTZ-16 sequence48 were found to be equally effective for 1H-heteronuclear decoupling during t1, while WALTZ-16 was used for 13C and 15N decoupling during 1H acquisition. Swept-low-power TPPM was applied with a two-pulse phase difference of 41°, a pulse length that was linearly ramped from 40 to 26.67 μs in steps of −1.33 μs, and an rf-field amplitude of 13.7 kHz. WALTZ-16 was applied at 10 kHz rf-field amplitude. The MISSISSIPPI pulse sequence46 was used without homospoil gradients to suppress the water signal, with a 19 kHz irradiation for 100–300 ms. All the spectra were acquired and processed using the States-TPPI procedure.49 CP-HSQCs were acquired with between 8 and 16 scans, with 160–400 increments in the indirect 15N dimension, giving total experimental times of between 25 min and 1.5 h (see Table S1 in the SI).

Figure 1.

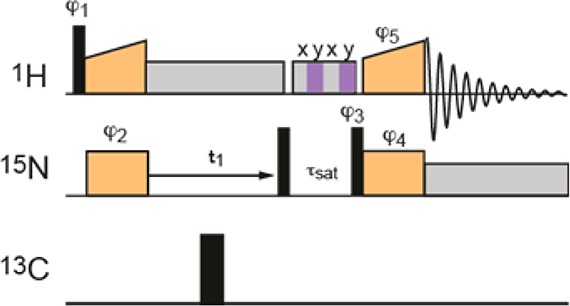
Figure 1

Open in a new tab

Pulse sequence for the 1H-detected 15N–1H 2D correlation (“CP-HSQC”). Narrow and broad black rectangles indicate π/2 and π-pulses, respectively. Orange boxes indicate cross-polarization, and gray boxes indicate heteronuclear decoupling. The MISSISSIPPI sequence46 is indicated by the striped box. All pulses are of phases 0, unless indicated differently. φ1 = 1 3, φ2 = 1, φ3 = 0 0 2 2, φ4 = 1, φ5 = {1}*4 {3}*4, φrec = 1 3 3 1 3 1 1 3.

For the six 3D experiments of Figure 3, the experimental parameters were as described for the CP-HSQC. In addition, the initial CP sequence from H to CA/CO had contact times between 3 and 5 ms, with the rf amplitude on 1H ramped linearly from 70 to 100 kHz (1 GHz) or from 90 to 100 kHz (800 MHz spectrometer) and a constant-amplitude 13C spin lock of either 40 kHz (ZQ CP) or 15–20 kHz (DQ CP).50 Both the CO–N and CA—N CP steps had a contact time between 8 and 15 ms with a constant-amplitude spin lock of about 35 kHz on 13C and a tangent-modulated amplitude spin lock of mean rf-field amplitude of about 25 kHz on 15N. The scalar CO–CA coherence transfer of the (H)CO(CA)NH experiment31 comprised two spin echoes with half-echo delays τ of duration 4.7 and 4.0 ms for the CO and CA sides of the transfer, respectively. Gaussian-cascade Q3 frequency-selective refocusing pulses51 were used during the second spin echo: the CO-selective pulse was of length 350 μs and rf-field peak amplitude 10 kHz, and the CA-selective pulse was of length 600 μs and rf-field peak amplitude 5.75 kHz. The (H)(CO)CA(CO)NH experiment52 comprised two spin echoes for the out-and-back CO–CA scalar transfer, of which the half-echo was 4.7 ms. Both the (H)(CA)CB(CA)NH52 and (H)(CA)CB(CACO)NH experiments used two spin echoes for the out-and-back CA—CB transfer, with Q3 refocusing pulse selective for the entire 13C aliphatic region of length 150 μs, rf-field peak amplitude 20 kHz, and half-echo delays of 7.2 ms. In the (H)(CA)CB(CACO)NH experiment, the second scalar transfer from CA to CO was performed using the same parameters as for the (H)(CO)CA(CO)NH sequence. All spectra were acquired and processed using the States-TPPI method49 in the indirect dimensions to obtain pure-phase line shapes and frequency discrimination. Codes and reference parameter sets for Bruker Avance III spectrometers are available on http://perso.ens-lyon.fr/guido.pintacuda/NMR.

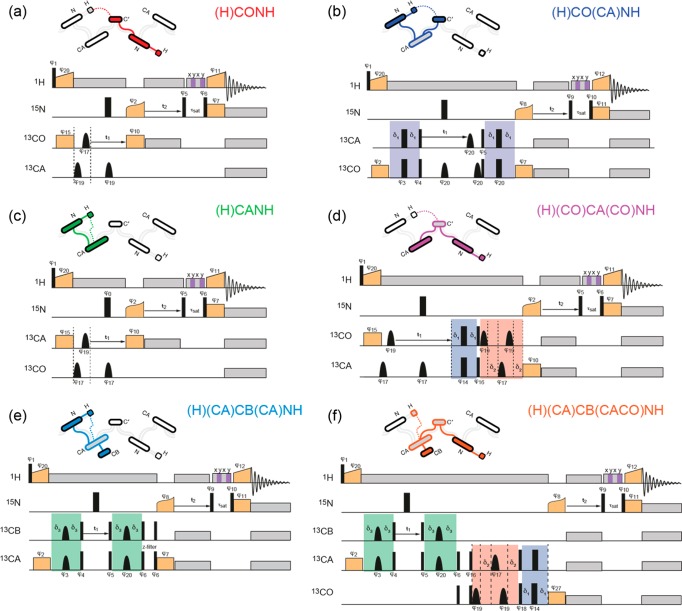
Figure 3.

Figure 3

Open in a new tab

Pulse sequences for the six 1H-detected 13C–15N–1H 3D correlation experiments, with an illustration of the coherence transfers and spins involved: (a) inter-residue (H)CONH experiment (COi-1NiHi), (b) intraresidue (H)CO(CA)NH experiment (COiNiHi), (c) intraresidue (H)CANH experiment (CAiNiHi), (d) inter-residue (H)(CO)CA(CO)NH experiment (CAi-1NiHi), (e) intraresidue (H)(CA)CB(CA)NH experiment (CBiNiHi), and (f) inter-residue (H)(CA)CB(CACO)NH experiment (CBi-1NiHi). Narrow and broad black rectangles indicate π/2 and π pulses, respectively, and bell shapes represent selective inversion pulses. Orange boxes indicate cross-polarization, and gray boxes indicate heteronuclear decoupling. The MISSISSIPPI sequence is indicated by the striped box. Spin-echoes involved in the transfer between CO and CA are highlighted in blue and red, when the coherence is present on the CO and CA, respectively, and spin-echoes involved in transfer between CA and CB are highlighted in green. All pulses are of phases 0, unless indicated differently. (a and c) φ1 = 0 2, φ20 = 1, φ2 = 1, φ6 = 0 0 2 2, φ12 = 1, φ7 = 1, φ11 = {1}*4 {3}*4, φrec = 1 3 3 1 3 1 1 3; (b) φ1 = 0 2, φ20 = 1, φ2 = 1, φ6 = 0 0 2 2, φ12 = 1, φ7 = 1, φ11 = 1, φ14 = {0}*4 {1}*4, φ17 = {0}*8 {1}*8, φrec = 3 1 1 3 1 3 3 1 1 3 3 1 3 1 1 3; (d and e) φ1 = 1 3, φ2 = 1 1 3 3, φ4 = 1, φ5 = 1, φ7 = {1}*4 {3}*4, φ8 = {0}*8 {2}*8, φ9 = 3, φ10 = 1, φrec = 0 2 2 0 2 0 0 2 2 0 0 2 0 2 2 0; (f) φ1 = 1 3, φ2 = 1 1 3 3, φ4 = 1, φ5 = 1, φ6 = {0}*16 {2}*16, φ9 = 3, φ10 = 1, φ14 = {0}*8 {1}*8, φ16 = 3, φ17 = {0}*4 {1}*4, φrec = 0 2 2 0 2 0 0 2 2 0 0 2 0 2 2 0 2 0 0 2 0 2 2 0 0 2 2 0 2 0 0 2. Specific CP to or from 13C may require a frequency shift, and in this case, the phases of rf during the two 13C CP periods are aligned respectively at the end and at the beginning of the contact time. In the diagrams, filled circles denote spins for which the frequency of evolution is measured. Solid lines represent transfers between bonded nuclei and dashed lines between nonbonded nuclei.

Computational Protocol for Automated Resonance Assignment

An improved version of MATCH38 was used to automatically obtain sequence-specific backbone assignment of the different protein data sets. MATCH employs local optimization for tracing partial sequence-specific assignments within a global, population-based search environment, where the simultaneous application of local and global optimization heuristics guarantees high efficiency and robustness of the results.38 An identical calculation protocol was applied to all protein data sets. MATCH used as input the amino acid sequence of the protein, a statistical analysis of chemical shift values of proteins contained in the BioMagResBank, and the experimental input data of the six solid-state triple-resonance NMR experiments in the form of frequency coordinates of the manually identified NMR signals. First, the input listings of the NMR signals were automatically consolidated and transformed into a set of spin systems, containing all available intra- and inter-residual chemical shifts for a given unassigned protein residue. The inevitable presence of spectral artifacts and spectral overlap in the experimental data induce ambiguity and uncertainties into the sequential as well as the sequence-specific information. In order to deal with such ambiguities, MATCH accounts for the fact that each spin system may exist in multiple states; i.e., a spin system is allowed to be degenerate. For this process of spin system assembly, large proton and nitrogen chemical shift matching tolerances of 0.05 and 0.5 ppm were used, respectively. Second, sequential connectivity of spin systems was then simultaneously established by MATCH via the three intra- and inter-residual CA, CB, and CO resonances using a carbon chemical shift matching tolerance of 0.5 ppm. After these two initialization steps of the algorithm, the genetic optimization process of MATCH was started in order to find the best possible solution to the assignment problem. For each protein data set, 10 independent optimization runs were performed, and sequence-specific resonance assignments which occur in more than 50% of the optimization runs were accepted as being correct and yielded the final list of assigned resonance frequencies. The overall calculation time was in all cases below 5 min on a single CPU of a contemporary Mac desktop equipped with a dual-core Intel Core i5 processor. The new version of MATCH is available free-of-charge for the academic community as a submodule of the UNIO application suite. Download information is available under http://perso.ens-lyon.fr/torsten.herrmann/Software.

Results and Discussion

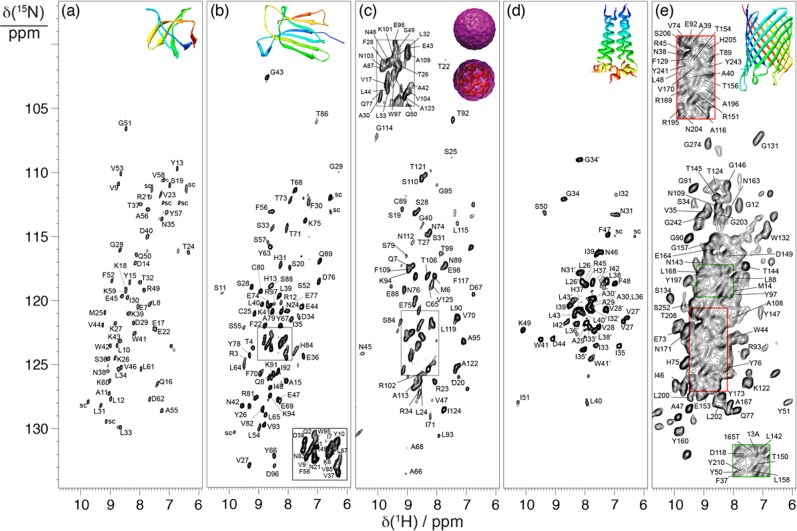
Figure 2 shows the CP-HSQC of five different proteins acquired at 1 GHz 1H Larmor frequency with ωr/2π = 60 kHz. Figure 2a,b corresponds to microcrystalline proteins, namely, the α-spectrin (SH3) domain53 and β2-microglobulin, the light chain of the class I major histocompatibility complex (β2m),54 Figure 2c to the sedimented viral nucleocapsid of Acinetobacter phage 205 (AP205),55 and Figure 2d,e to α-helical and β-barrel membrane proteins, respectively, the conductance domain from influenza A M256 and the outer membrane protein G (OmpG) from Gram-negative bacteria.57 These spectra can be acquired with adequate signal-to-noise in 5–30 min using only 2–3 mg of sample. The spectra in Figure 2a–d exhibit 1H line widths (FWHM) of approximately 50–100 Hz and 15N line widths of 20–60 Hz.

Figure 2.

Figure 2

Open in a new tab

15N–1H correlation spectra recorded on a 1 GHz spectrometer under 60 kHz MAS for [U-HN,2H,13C,15N]-labeled (a) microcrystalline SH3, (b) microcrystalline β2m, and (c) sedimented nucleocapsids of AP205, (d) M2 channel, and (e) OmpG.

These CP-HSQC spectra serve as an efficient module to build 3D triple-resonance correlation experiments. Simple 3D spectra correlating 1H, 15N, and the neighboring 13CO/13CA, such as (H)CONH and (H)CANH (parts a and c of Figure 3, respectively), can be built with two heteronuclear 1H/13C and 15N/13C cross-polarization steps followed by the 15N/1H transfer from the CP-HSQC.26

More complex experiments can be obtained by the addition of homonuclear carbon–carbon J-based coherence transfer blocks, enabled by the long 13C coherence lifetimes obtainable at 60 kHz MAS. One, two (out-and-back), or three carbon–carbon transfers result in the (H)CO(CA)NH (Figure 3b),31 (H)(CO)CA(CO)NH and (H)(CA)CB(CA)NH (Figure 3d and e),52 and (H)(CA)CB(CACO)NH experiments (Figure 3f), respectively. This latter is a newly designed pulse sequence and is crucial for the exploitation of the CB shifts in the backbone resonance assignment (see below).

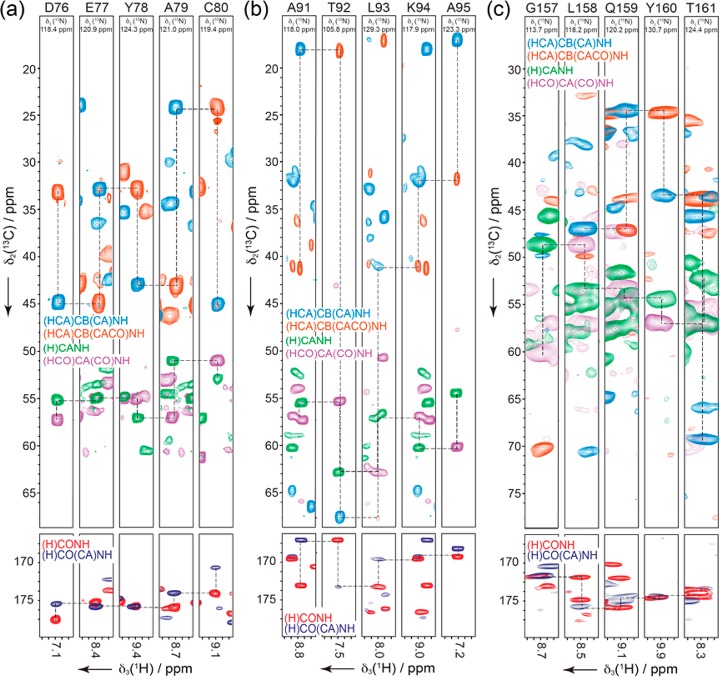
Figure 4a–c illustrates sequence-specific resonance assignments obtained by joint analysis of the set of six spectra. Simultaneous matching of three independent 13C (CO, CA, and CB) chemical shifts that are correlated with 1H and 15N nuclei from adjacent residues yields a high level of redundancy for establishing sequential connectivity. This is realized stepwise: first, CA and CB chemical shifts of each spin system allow for a rough classification of the residue type, and second, a robust sequential matching of spin systems is established. Fragments of three and more sequentially connected spin systems can then usually be unambiguously matched to the protein sequence. Following cross-peak selection, these steps may be quickly performed interactively by an experienced spectroscopist or by application of computational backbone assignment algorithms. This latter possibility is an attractive feature that is essential to accelerate the data analysis and to render the procedure more impartial. For each protein automatically investigated by MATCH, we first interactively generated peak lists of NMR resonance signals from the six NMR experiments and subjected them together with the protein sequence to a modified version of the program UNIO-MATCH.38 Contrary to contemporary computer-aided protocols tailored for the analysis of 13C-detected MAS NMR data, this routine benefits from direct application of road-proven protocols developed for solution NMR.58−61 In particular, MATCH is able to directly make use of the individual input peak lists, in contrast to many automated backbone resonance assignment routines that require (tedious and subjective) manual assembly of the spin systems, and is robust with respect to the inclusion of erroneous, artifactual NMR signals that might be present in the input peak lists. The new version of UNIO-MATCH used here automatically performs spin system assembly and residue typing and exploits a memetic optimization algorithm to find the optimal solution for sequence-specific resonance assignment.

Figure 4.

Figure 4

Open in a new tab

Strip plots of both inter- and intraresidue CB, CA, and CO resonances for NH pairs in β2m (a), AP205 (b), and OmpG (c).

Here we report the backbone resonance assignments of the five proteins (see SI for chemical shift lists). Resonance assignments were automatically obtained and validated interactively for all data sets, except for OmpG. OmpG presented an extremely challenging data analysis task that turned out to be most reliably done by interactive analysis.

For the crystalline proteins, 52 and 75 backbone amide cross-peaks were automatically assigned for the SH3 domain (62 residues) and β2m (99 residues), respectively. For both proteins, this corresponds to 100% of the observed backbone HN–N resonances in the 2D CP-HSQC (Figure 2a,b), where prolines and flexible or disordered parts such as N- and C-terminal tails are absent. Both proteins show long transverse coherence lifetimes (∼20 and 45 ms, respectively for 13CA and 13CO); hence, efficient magnetization transfers are guaranteed also in the experiments with multiple 13C homonuclear coherence transfers, allowing all six data sets to be recorded in 1.5 (SH3) and 2.5 (β2m) days (see Table 1).

Table 1. Experimental Performance of the Assignment Strategy for the Five Proteinsa.

  SH3 β2m AP205 M2 OmpG
residues (prolines) 62 (2) 99 (5) 130 (8) 2 × 43 (1) 281 (8)
CP-HSQC
S/N/√t 32.3 31.2 14.8 17.6 45.0
experimental time for (S/N)i > 4 1.6 min 3.2 min 25 min 3.2 min 16 min
actual experimental time 1 h 1 h 1 h, 30 min 1 h 25 min
scans per increment 8 8 16 8 8
NiHi peaks 52 75 95 44 –
(H)CANH
sensitivity wrt HSQC (first FID) 0.32 0.24 0.20 0.32 0.31
experimental time for (S/N)i > 4 30 min 2 h 21 h, 30 min 1 h, 10 min 6 h, 30 min
actual experimental time 1 h, 15 min 6 h, 25 min 11 h 1 h, 30 min 1 d, 21 h, 30 min
scans per increment 2 4 16 2 64
CAiNiHi peaks 52 75 94 44 251
(H)(CO)CA(CO)NH
sensitivity wrt HSQC (first FID) 0.19 0.13 0.16 0.09 0.11
experimental time for (S/N)i > 4 1 h, 25 min 6 h, 30 min 1 d, 9 h 15 h 2 d, 1 h
actual experimental time 2 h, 30 min 13 h 22 h 2 d 2 d, 1 h
scans per increment 4 8 32 64 128
CAi-1NiHi peaks 50 71 83 43 167
(H)(CA)CB(CA)NH
sensitivity wrt HSQC (first FID) 0.16 0.11 0.14 0.06 0.07
experimental time for (S/N)i > 4 2 h 9 h, 10 min 1 d, 21 h 1 d, 9 h 1 d, 6 h*
actual experimental time 7 h, 30 min 12 h, 30 min 22 h 2 d 1 d, 40 min
scans per increment 4 8 32 64 64
CBiNiHi peaks 51 72 71 42 128
(H)(CA)CB(CACO)NH
sensitivity wrt HSQC (first FID) 0.13 0.07 0.08 0.03 0.03
experimental time for (S/N)i > 4 3 h 22 h, 30 min 5 d, 18 h 5 d, 13 h 6 d, 21 h*
actual experimental time 15 h 1 d, 1 h 2 d, 16 h 7 d, 10 h 4 d, 6 h, 25 min
scans per increment 8 16 96 232 128
CBi-1NiHi peaks 49 62 61 30 106
(H)CONH
sensitivity wrt HSQC (first FID) 0.35 0.30 0.24 0.25 0.29
experimental time for (S/N)i > 4 25 min 1 h, 20 min 14 h, 50 min 2 h 7 h
actual experimental time 1 h 1 h, 45 min 6 h 3 h 1 d, 6 h
scans per increment 2 4 8 4 32
COi-1NiHi peaks 52 71 92 44 185
(H)CO(CA)NH
sensitivity wrt HSQC (first FID) 0.12 0.08 0.11 0.08 0.05
experimental time for (S/N)i > 4 3 h, 30 min 17 h, 30 min 2 d, 23 h 19 h 2 d, 12 h*
actual experimental time 8 h 14 h 1 d, 12 h 2 d, 2 h 2 d, 15 h, 45 min
scans per increment 16 32 48 64 64
COiNiHi peaks 50 75 69 40 89
           
assigned residues 52 75 94 44 112
Open in a new tab
a
The table reports the sensitivity (S/N/√t) of the CP-HSQC, calculated on the integral of the first increment, acquired for 20 ms, after 20 Hz of exponential apodization (120 Hz in the case of OmpG), as well as the estimated experimental times necessary to achieve a S/N per peak [(S/N)p] > 4. The corresponding number of scans (ns) per increment necessary was calculated according to the following relation62
graphic file with name ja-2014-07382j_m001.jpg
assuming a T2*(N) of 6.3 ms and 48 (ni) increments (t1max acquisition of a maximum of 5 ms) in the 15N (t1) indirect dimension, and t is the time required by a single scan. For each of the six 3D experiments, the relative sensitivity (rel sens) with respect to the CP-HSQC was calculated on the integral of the first increment, and the estimated number of scans ns per increment necessary to achieve a (S/N)p > 4 was calculated according to the relation:
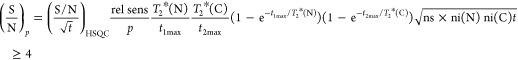graphic file with name ja-2014-07382j_m002.jpg
assuming a T2* of 6.3 ms and 48 increments (t1max and t2max acquisitions of a maximum of 5 ms) for each 15N (t1) and 13C (t2) indirect dimension. t is the time required by a single scan, and p denotes the number of peaks, taken equal to the number of observed signals in the most sensitive and dispersed among the triple-correlation experiments, (H)CANH. (*) Experimental time necessary to achieve an average sensitivity per signal (S/N)p > 2.

For sedimented AP205, in which a homodimer of 2 × 130 residues assembles into an icosahedral particle of about 2.5 MDa,55 the CP-HSQC spectrum shown in Figure 2c features a quality comparable to that of the two model microcrystalline samples. The six spectra were recorded in about 1 week, and backbone assignment was automatically determined for 94 residues (corresponding to all backbone resonances observed in the CP-HSQC and to 72% of the protein sequence).

Resonances from the N-terminus are not observed, and additional residues are likely to be absent due to incomplete unfolding during reprotonation.

Membrane-embedded systems are a challenging class of samples due to intrinsic heterogeneity, lipid dynamics, and limited protein content. The conductance domain M2 is a 5 kDa single pass transmembrane protein that assembles as a 20 kDa tetramer with a 10 kDa asymmetric dimer.56 Although half of the sample mass consists of lipids, there is still excellent sensitivity in the spectrum of Figure 2d (obtained in 30 min), and the line widths (100 Hz for 1H) are comparable to those of the crystalline models. For OmpG, several approaches to perform sequential assignments in lipid bilayers have been applied, including sparse and specific labeling and utilizing 13C-detected experiments;44 however, at 280 residues, this system remains a considerable challenge. The CP-HSQC spectrum of OmpG shown in Figure 2e displays excellent sensitivity characteristic of the 1H-detected approach, as seen for the previous examples, despite the generally larger line widths (130–180 Hz). In these membrane protein cases, bulk 13C coherence lifetimes of about 15–20 ms for both 13CA and 13CO result in some reduction of transfer efficiency (see Table 1). Nevertheless, the approach described above remains successful for the automatic assignment of M2 and of a considerable portions of OmpG by expert manual analysis, after acquisition of each set of six spectra in 14 days. In the case of M2, all 44 observed residues were assigned by MATCH constituting the transmembrane and amphipathic helices in the asymmetric dimer (26–51 and 26′–43′). As for OmpG, expert manual analysis yielded 40% overall assignment, corresponding to residues concentrated in the β-barrel; in the intracellular turns T1, T4, and T5; and in the extracellular loop L4, where crucial peaks for establishing inter-residue connectivities are most often missing.

A significant improvement in 13C transverse relaxation was observed when increasing the MAS rates from 40 to 60 kHz. For the two microcrystalline proteins, about 30–50% longer bulk transverse coherence lifetimes were measured for 13CA (15 vs 20 ms) and 13CO (30 vs 45 ms), and a similar improvement was measured in the case of M2 (15–18 ms for 13CA and 10–15 ms for 13CO). Longer coherence lifetimes lead to improved transfer efficiencies (see, for example, Figure S1 in the SI), so we expect the assignment strategy described above to perform better at even higher MAS frequencies.

Conclusions

Our results from this diverse and challenging set of proteins demonstrate the excellent performance of the proposed standard suite of triple-resonance experiments for studies of proteins of different condensed states and show that modern, error-tolerant computational algorithms can be applied for the efficient and robust NMR data analysis. For microcrystalline and sedimented proteins, we find that the efficiencies of these experiments as compared to the basic 1H-detected CP-HSQC experiment range from 0.5 for the (H)CONH and (H)CANH to 0.1 for the (H)(CA)CB(CACO)NH, while these efficiencies range from 0.32 to 0.03 for the membrane proteins. Acquisition times range from 36 h (SH3) to 2 weeks (M2 and OmpG) for the set of six spectra. The incorporation of an additional CB dimension accelerates and strengthens the reliability of backbone sequential assignment, and notably, triply redundant sequential chemical shift matching between intra- and inter-reside CA, CB, and CO resonances is the crucial component for the robustness of the procedure, using interactive or unsupervised methods alike. In the future, improved sensitivity, resolution, and coherence lifetimes are possible, for example, with the advent of probes with higher spinning frequencies, cryoprobes, or other advances, which will further improve the performance of the standard protocol proposed.

In conclusion, we were able to adapt and extend an experimental and computational protocol that is used extensively for solution protein NMR to address complex MAS spectra. In so doing, we have enlarged the sample repertoire accessible for assignment in solid-state NMR spectroscopy. This is a significant step toward routine structural investigations of large, poorly soluble, and noncrystalline systems.

Acknowledgments

We thank Lénaïc Leroux for technical assistance with the NMR spectrometers. We acknowledge support from the Agence Nationale de la Recherche (ANR 10-BLAN-713-01), from Joint Research Activity and Access to Research Infrastructures, from a Marie-Curie ITN in the 7th FP of the EC (EAST-NMR no. 228461, BioNMR no. 261863, SMBP no. 211800), from the CNRS (TGIR-RMN-THC FR3050), from the Italian Ministry of Research (grant FIRB RBFR109EOS), and from NIH (grants EB-001960 and EB-002026).

Supporting Information Available

Sample preparation, curves with simulated efficiencies of the 13C–13C transfers in the different experiments, list of assigned chemical shifts, and pulse sequence code for Bruker spectrometers. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ja507382j_si_001.pdf (576.5KB, pdf)

References

  1. Castellani F.; van Rossum B.; Diehl A.; Schubert M.; Rehbein K.; Oschkinat H. Nature 2002, 420, 98–102. [DOI] [PubMed] [Google Scholar]
  2. Rienstra C. M.; Tucker-Kellogg L.; Jaroniec C. P.; Hohwy M.; Reif B.; McMahon M. T.; Tidor B.; Lozano-Perez T.; Griffin R. G. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 10260–10265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Wasmer C.; Lange A.; Van Melckebeke H.; Siemer A. B.; Riek R.; Meier B. H. Science 2008, 319, 1523–1526. [DOI] [PubMed] [Google Scholar]
  4. Lu J. X.; Qiang W.; Yau W. M.; Schwieters C. D.; Meredith S. C.; Tycko R. Cell 2013, 154, 1257–1268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Jehle S.; Rajagopal P.; Bardiaux B.; Markovic S.; Kuhne R.; Stout J. R.; Higman V. A.; Klevit R. E.; van Rossum B. J.; Oschkinat H. Nat. Struct. Mol. Biol. 2010, 17, 1037–1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Han Y.; Ahn J.; Concel J.; Byeon I. J. L.; Gronenborn A. M.; Yang J.; Polenova T. J. Am. Chem. Soc. 2010, 132, 1976–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Lange A.; Giller K.; Hornig S.; Martin-Eauclaire M. F.; Pongs O.; Becker S.; Baldus M. Nature 2006, 440, 959–962. [DOI] [PubMed] [Google Scholar]
  8. Cady S. D.; Schmidt-Rohr K.; Wang J.; Soto C. S.; DeGrado W. F.; Hong M. Nature 2010, 463, 689–692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Shahid S. A.; Bardiaux B.; Franks W. T.; Krabben L.; Habeck M.; van Rossum B. J.; Linke D. Nat. Methods 2012, 9, 1212–U1119. [DOI] [PubMed] [Google Scholar]
  10. Loquet A.; Sgourakis N. G.; Gupta R.; Giller K.; Riedel D.; Goosmann C.; Griesinger C.; Kolbe M.; Baker D.; Becker S.; Lange A. Nature 2012, 486, 276–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Rienstra C. M.; Hohwy M.; Hong M.; Griffin R. G. J. Am. Chem. Soc. 2000, 122, 10979–10990. [Google Scholar]
  12. Böckmann A.; Lange A.; Galinier A.; Luca S.; Giraud N.; Juy M.; Heise H.; Montserret R.; Penin F.; Baldus M. J. Biomol. NMR 2003, 27, 323–339. [DOI] [PubMed] [Google Scholar]
  13. Sattler M.; Schleucher J.; Griesinger C. Progr. NMR Spectrosc. 1999, 34, 93–158. [Google Scholar]
  14. Guerry P.; Herrmann T. Q. Rev. Biophys. 2011, 44, 257–309. [DOI] [PubMed] [Google Scholar]
  15. Serrano P.; Pedrini B.; Mohanty B.; Geralt M.; Herrmann T.; Wüthrich K. J. Biomol. NMR 2012, 53, 341–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Maricq M. M.; Waugh J. S. J. Chem. Phys. 1979, 70, 3300–3316. [Google Scholar]
  17. Zheng L.; Fishbein K. W.; Griffin R. G.; Herzfeld J. J. Am. Chem. Soc. 1993, 115, 6254–6261. [Google Scholar]
  18. Reif B.; Jaroniec C. P.; Rienstra C. M.; Hohwy M.; Griffin R. G. J. Magn. Reson. 2001, 151, 320–327. [DOI] [PubMed] [Google Scholar]
  19. Samoson A.; Tuherm T.; Gan Z. Solid State Nucl. Magn. Reson. 2001, 20, 130–136. [DOI] [PubMed] [Google Scholar]
  20. Kobayashi T.; Mao K.; Paluch P.; Nowak-Krol A.; Sniechowska J.; Nishiyama Y.; Gryko D. T.; Potrzebowski M. J.; Pruski M. Angew. Chem., Int. Ed. 2013, 52, 14108–14111. [DOI] [PubMed] [Google Scholar]
  21. Paulson E. K.; Morcombe C. R.; Gaponenko V.; Dancheck B.; Byrd R. A.; Zilm K. W. J. Am. Chem. Soc. 2003, 125, 15831–15836. [DOI] [PubMed] [Google Scholar]
  22. Chevelkov V.; Rehbein K.; Diehl A.; Reif B. Angew. Chem., Int. Ed. 2006, 45, 3878–3881. [DOI] [PubMed] [Google Scholar]
  23. Linser R.; Bardiaux B.; Higman V.; Fink U.; Reif B. J. Am. Chem. Soc. 2011, 133, 5905–5912. [DOI] [PubMed] [Google Scholar]
  24. Linser R.; Dasari M.; Hiller M.; Higman V.; Fink U.; del Amo J. M. L.; Markovic S.; Handel L.; Kessler B.; Schmieder P.; Oesterhelt D.; Oschkinat H.; Reif B. Angew. Chem., Int. Ed. 2011, 50, 4508–4512. [DOI] [PubMed] [Google Scholar]
  25. Akbey U.; Lange S.; Franks W. T.; Linser R.; Rehbein K.; Diehl A.; van Rossum B. J.; Reif B.; Oschkinat H. J. Biomol. NMR 2012, 46, 67–73. [DOI] [PubMed] [Google Scholar]
  26. Zhou D. H.; Shea J. J.; Nieuwkoop A. J.; Franks W. T.; Wylie B. J.; Mullen C.; Sandoz D.; Rienstra C. M. Angew. Chem., Int. Ed. 2007, 46, 8380–8383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhou D. H.; Shah G.; Cormos M.; Mullen C.; Sandoz D.; Rienstra C. M. J. Am. Chem. Soc. 2007, 129, 11791–11801. [DOI] [PubMed] [Google Scholar]
  28. Ward M. E.; Shi L.; Lake E.; Krishnamurthy S.; Hutchins H.; Brown L. S.; Ladizhansky V. J. Am. Chem. Soc. 2011, 133, 17434–17443. [DOI] [PubMed] [Google Scholar]
  29. Zhou D. H.; Nieuwkoop A. J.; Berthold D. A.; Comellas G.; Sperling L. J.; Tang M.; Shah G. J.; Brea E. J.; Lemkau L. R.; Rienstra C. M. J. Biomol. NMR 2012, 54, 291–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lewandowski J. R.; Dumez J. N.; Akbey U.; Lange S.; Emsley L.; Oschkinat H. J. Chem. Phys. Lett. 2011, 2, 2205–2211. [Google Scholar]
  31. Knight M. J.; Webber A. L.; Pell A. J.; Guerry P.; Barbet-Massin E.; Bertini I.; Felli I. C.; Gonnelli L.; Pierattelli R.; Emsley L.; Lesage A.; Herrmann T.; Pintacuda G. Angew. Chem., Int. Ed. 2011, 50, 11697–11701. [DOI] [PubMed] [Google Scholar]
  32. Laage S.; Sachleben J. R.; Steuernagel S.; Pierattelli R.; Pintacuda G.; Emsley L. J. Magn. Reson. 2009, 196, 133–141. [DOI] [PubMed] [Google Scholar]
  33. Wickramasinghe N. P.; Parthasarathy S.; Jones C. R.; Bhardwaj C.; Long F.; Kotecha M.; Mehboob S.; Fung L. W. M.; Past J.; Samoson A.; Ishii Y. Nat. Methods 2009, 6, 215–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lewandowski J. R.; De Paëpe G.; Eddy M. T.; Struppe J.; Maas W.; Griffin R. G. J. Phys. Chem. B 2009, 113, 9062–9069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Knight M. J.; Pell A. J.; Bertini I.; Felli I. C.; Gonnelli L.; Pierattelli R.; Herrmann T.; Emsley L.; Pintacuda G. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 11095–11100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Marchetti A.; Jehle S.; Felletti M.; Knight M. J.; Wang Y.; Xu Z. Q.; Park A. Y.; Otting G.; Lesage A.; Emsley L.; Dixon N. E.; Pintacuda G. Angew. Chem., Int. Ed. 2012, 51, 10756–10759. [DOI] [PubMed] [Google Scholar]
  37. Knight M. J.; Felli I. C.; Pierattelli R.; Bertini I.; Emsley L.; Herrmann T.; Pintacuda G. J. Am. Chem. Soc. 2012, 134, 14730–14733. [DOI] [PubMed] [Google Scholar]
  38. Volk J.; Herrmann T.; Wuthrich K. J. Biomol. NMR 2008, 41, 127–138. [DOI] [PubMed] [Google Scholar]
  39. Martin R. W.; Zilm K. W. J. Magn. Reson. 2003, 165, 162–174. [DOI] [PubMed] [Google Scholar]
  40. Mainz A.; Jehle S.; van Rossum B. J.; Oschkinat H.; Reif B. J. Am. Chem. Soc. 2009, 131, 15968–15969. [DOI] [PubMed] [Google Scholar]
  41. Bertini I.; Luchinat C.; Parigi G.; Ravera E.; Reif B.; Turano P. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 10396–10399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Gardiennet C.; Schutz A. K.; Hunkeler A.; Kunert B.; Terradot L.; Bockmann A.; Meier B. H. Angew. Chem., Int. Ed. 2012, 51, 7855–7858. [DOI] [PubMed] [Google Scholar]
  43. Gelis I.; Vitzthum V.; Dhimole N.; Caporini M. A.; Schedlbauer A.; Carnevale D.; Connell S. R.; Fucini P.; Bodenhausen G. J. Biomol. NMR 2013, 56, 85–93. [DOI] [PubMed] [Google Scholar]
  44. Hiller M.; Krabben L.; Vinothkumar K. R.; Castellani F.; van Rossum B. J.; Kuhlbrandt W.; Oschkinat H. ChemBioChem. 2005, 6, 1679–1684. [DOI] [PubMed] [Google Scholar]
  45. Andreas L. B.; Eddy M. T.; Pielak R. M.; Chou J.; Griffin R. G. J. Am. Chem. Soc. 2010, 132, 10958–10960. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Zhou D. H.; Rienstra C. M. J. Magn. Reson. 2008, 192, 167–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Lewandowski J. R.; Sein J.; Blackledge M.; Emsley L. J. Am. Chem. Soc. 2010, 132, 1246–1248. [DOI] [PubMed] [Google Scholar]
  48. Shaka A. J.; Keeler J.; Frenkiel T.; Freeman R. J. Magn. Reson. 1983, 52, 335–338. [Google Scholar]
  49. Marion D.; Ikura M.; Tschudin R.; Bax A. J. Magn. Reson. 1989, 85, 393–399. [Google Scholar]
  50. Laage S.; Marchetti A.; Sein J.; Pierattelli R.; Sass H. J.; Grzesiek S.; Lesage A.; Pintacuda G.; Emsley L. J. Am. Chem. Soc. 2008, 130, 17216–17217. [DOI] [PubMed] [Google Scholar]
  51. Emsley L.; Bodenhausen G. Chem. Phys. lett. 1990, 165, 469–476. [Google Scholar]
  52. Barbet-Massin E.; Pell A. J.; Jaudzems K.; Franks W. T.; Retel J. S.; Kotelovica S.; Akopjana I.; Tars K.; Emsley L.; Oschkinat H.; Lesage A.; Pintacuda G. J. Biomol. NMR 2013, 56, 379–386. [DOI] [PubMed] [Google Scholar]
  53. Pawson T.; Schlessinger J. Curr. Biol. 1993, 3, 434–442. [DOI] [PubMed] [Google Scholar]
  54. Bjorkman P. J.; Saper M. A.; Samraoui B.; Bennett W. S.; Strominger J. L.; Wiley D. C. Nature 1987, 329, 506–512. [DOI] [PubMed] [Google Scholar]
  55. Klovins J.; Overbeek G. P.; van den Worm S. H. E.; Ackermann H. W.; van Duin J. J. Gen. Virol. 2002, 83, 1523–1533. [DOI] [PubMed] [Google Scholar]
  56. Holsinger L. J.; Nichani D.; Pinto L. H.; Lamb R. A. J. Virol. 1994, 68, 1551–1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Fajardo D. A.; Cheung J.; Ito C.; Sugawara E.; Nikaido H.; Misra R. J. Bacteriol. 1998, 180, 4452–4459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Hu K. N.; Qiang W.; Tycko R. J. Biomol. NMR 2011, 50, 267–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Schmidt E.; Gath J.; Habenstein B.; Ravotti F.; Szekely K.; Huber M.; Buchner L.; Bockmann A.; Meier B. H.; Guntert P. J. Biomol. NMR 2013, 56, 243–254. [DOI] [PubMed] [Google Scholar]
  60. Nielsen J. T.; Kulminskaya N.; Bjerring M.; Nielsen N. C. J. Biomol. NMR 2014, 59, 119–134. [DOI] [PubMed] [Google Scholar]
  61. Moseley H. B.; Sperling L. J.; Rienstra C. M. J. Biomol. NMR 2010, 48, 123–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Ernst R. R.; Bodenhausen G.; Wokaun A.. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clarendon: Oxford, UK, 1987. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja507382j_si_001.pdf (576.5KB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES