A simple acquisition strategy to avoid off-resonance blurring in spiral imaging with redundant spiral-in/out k-space trajectories

Abstract

Purpose

The major hurdle to widespread adoption of spiral trajectories has been their poor off-resonance performance. Here we present a self-correcting spiral k-space trajectory that avoids much of the well-known spiral blurring during data acquisition.

Theory and Methods

In comparison with a traditional spiral-out trajectory, the spiral-in/out trajectory has improved off-resonance performance. By combining two spiral-in/out acquisitions, one rotated 180° in k-space compared to the other, multi-shot spiral-in/out artifacts are eliminated. A phantom was scanned with the center frequency manually tuned 20, 40, 80, and 160 Hz off-resonance with both a spiral-out gradient echo sequence and the redundant spiral-in/out sequence. The phantom was also imaged in an oblique orientation in order to demonstrate improved concomitant gradient field performance of the sequence, and was additionally incorporated into a spiral turbo spin echo sequence for brain imaging.

Results

Phantom studies with manually-tuned off-resonance agree well with theoretical calculations, showing that moderate off-resonance is well-corrected by this acquisition scheme. Blur due to concomitant fields is reduced, and good results are obtained in vivo.

Conclusion

The redundant spiral-in/out trajectory results in less image blur for a given readout length than a traditional spiral-out scan, reducing the need for complex off-resonance correction algorithms.

Introduction

Spiral k-space trajectories have many advantages over traditional rectilinear acquisitions, including better acquisition efficiency, less stringent hardware requirements, and natural resilience to flow and motion (1). The major hurdle to wide-spread adoption of spiral trajectories has been their poor off-resonance performance (2). The blurring and distortion in spiral images in the presence of system non-idealities led to the two-pronged strategy of mitigation and correction in spiral imaging. First, splitting the acquisition into multiple short interleaves minimizes artifacts by ensuring that an undue amount of undesirable phase does not accrue in a single readout. Secondly, much effort has been expended to correct for off-resonance effects in image reconstruction algorithms. These techniques vary in complexity and computational cost, from a relatively simple center frequency correction and first-order trajectory warping method based on a least-squares fit to an acquired field-map (3), to time- (4, 5), frequency- (6, 7), and polynomial-approximation approaches (8), to automatic (9, 10) and semi-automatic (11) methods which demodulate the image at multiple frequencies in order to build a composite image free of blurring. Many of these algorithms have become large, requiring several seconds to reconstruct a single image.

Main field inhomogeneity is the primary source of off-resonance in MRI. However, off-resonance may be caused by other system imperfections besides B₀ inhomogeneity. Particularly at lower field strengths and for off-center slices, concomitant fields generated by normal gradient operation can cause noticeable blur in spiral images. With some exceptions (12–14), the blur due to concomitant fields is largely ignored in the spiral literature, as it requires a more complex model to appropriately address deblurring.

The most commonly encountered spiral trajectories are “spiral-out”. That is, the trajectory begins at the origin of k-space and moves outward along a spiral. Another option is the spiral-in/out trajectory, which was first proposed for efficient sampling of spin-echoes for abdominal imaging (15) and has recently been shown to improve SNR and image quality for real-time spiral bSSFP cardiac imaging due to its natural ability to center TE within TR (16). Its major use, however, is in fMRI (17–19), where its SNR, speed, and resistance to flow artifacts make it an attractive alternative to rectilinear EPI methods.

For spiral imaging, the amount of undesired phase accrued between when the center of k-space is sampled and when the edge of k-space is sampled determines the severity of the well-known spiral blur. Given a desired resolution, spiral-out and spiral-in/out trajectories require readout lengths of nearly the same duration (within a few percent due to differing amounts of time spent near the center of k-space where the k-space velocity is small). For a given readout length then, a spiral-in/out trajectory requires about half as long to move from the edge of k-space to the center compared to a spiral-out trajectory, and therefore accrues about half of the undesirable phase.

In this work, we take a closer look at spiral-in/out trajectories to address one method by which blurring due to off-resonance can be avoided through their use. The specific origin of off-resonance (B₀ or concomitant fields) is unimportant, and it will be shown that using a redundant spiral-in/out sampling scheme naturally removes the most severe off-resonance image artifacts during image acquisition, allowing for fast and simple correction methods in the image reconstruction step.

Theory

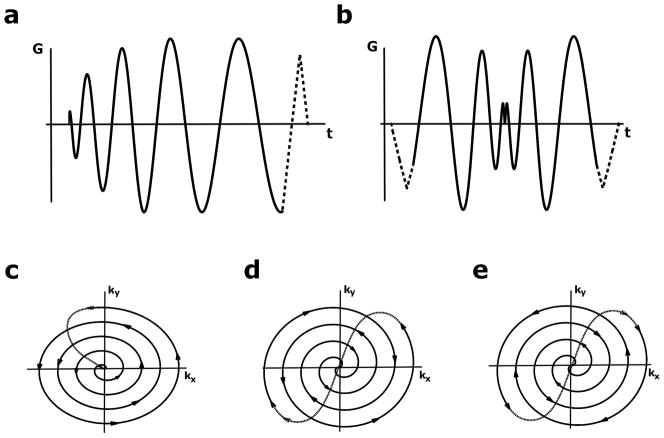
Figure 1 shows the readout gradients and trajectories for spiral-out and spiral-in/out imaging. Conceptually, spiral-in/out trajectories can be implemented in two ways. In the first method, termed here the “non-redundant” scheme, each spiral-out arm fills in the conjugate k-space location of the spiral-in arm, requiring the same number of interleaves as a spiral-out trajectory for equal k-space coverage (Fig. 1d).

Figure 1.

Spiral gradients and trajectories. a) Spiral-out read gradient (solid) with rewinding lobe (dashed). b) Spiral-in/out read gradient with prewinding and rewinding lobes. c,d) k-space trajectories for the gradients in (a,b), respectively. Arrows indicate direction of travel in k-space. e) k-space trajectory for second spiral-in/out trajectory, rotated 180° from the trajectory in (d). The redundant spiral-in/out scheme averages data acquired with trajectories (d) and (e).

The second method, which we call the “redundant” scheme, acquires each interleaf twice, once in each direction through k-space (i.e., the redundant scheme consists of acquiring two non-redundant trajectories with the second acquisition rotated 180° in k-space). Thus, the redundant scheme requires twice the number of excitations as its non-redundant counterpart. Despite this prolongation of scan time, this is a far more robust acquisition scheme, as each location in k-space is sampled twice: once with a spiral-in arm and once with a spiral-out arm. The data is then averaged, either before or after gridding the data onto a Cartesian matrix. In this way, amplitude and phase mismatches between the data acquired with spiral-in and spiral-out arms of the trajectory are averaged out. A simple illustration of the k-space weighting functions that occur when each of these trajectories are used is provided in the Supplemental Materials.

Redundant trajectory response to system non-idealities: B₀ off-resonance

Ignoring relaxation and including B₀ inhomogeneity, the classic demodulated signal equation in MRI is

$$s(t)=\int m(\mathit{r})e^{-j2\pi k(t)\mathit{r}}{e}^{-j\omega (\mathit{r})\tau (t)}d\mathit{r},$$ [1]

where m(r) is the signal, k(t) the k-space trajectory, and ω(r) the off-resonance. In this subsection, the off-resonance phase-accrual time parameter τ(t) = t because phase accrues proportionally to time for B₀ off-resonance. Phase accrual due to concomitant fields will be addressed in the next subsection, where τ(t) is more complex.

It can be shown (Appendix A, Supplemental Material) that the signal resulting from averaging the data from a redundant spiral-in/out trajectory is

$$s(t)=\int m(\mathit{r})e^{-j2\pi k(t)\mathit{r}}[cos\omega (\mathit{r})t]d\mathit{r}.$$ [2]

For small-to-moderate off-resonance values, Eq. 2 shows that the signal experiences a relatively benign cosine amplitude modulation rather than the more serious phase modulation that arises with spiral-out trajectories in the presence of off-resonance. Point-spread-functions (PSFs) for a spiral-out, non-redundant in/out, and redundant in/out trajectories with and without off-resonance were simulated and show that the PSF is sharper in the presence of off-resonance when the redundant trajectory is used (Supplemental Material). However, the modulation transfer function (MTF) provides a more intuitive grasp of the situation in this case. Figure 2a shows simulated normalized MTFs for various amounts of phase accumulated by the end of the readout for the redundant spiral-in/out trajectory (corresponding to the off-resonance-time product in Eq. 2). There are two regimes under which the shape of the MTF may fall. In the first, the number of accumulated cycles is small, either because there is not much off-resonance present, or because the readout length is short. In this regime, the cosine modulation never reaches its first zero point during the readout, so the signal experiences a windowing function that only slightly attenuates high-frequency components. In the second regime, when the value of the off-resonance-time product is high, the cosine modulation will begin nulling important frequencies as a function of k-space radius, resulting in image artifacts. This figure indicates the redundant spiral-in/out method will work well as long as the number of cycles of phase accumulated during the readout remains less than 0.5. This amount of off-resonance is easily achieved during normal operation of clinical-strength scanners, so we anticipate first-order correction should be performed on the data/trajectories prior to gridding in order to quickly correct gross off-resonance.

Figure 2.

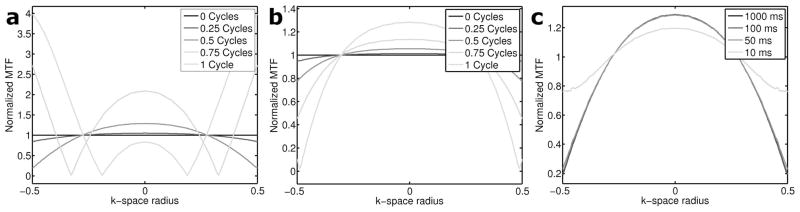
Normalized MTFs of spiral in/out trajectories. MTFs are normalized to on-resonance (0 cycles) case. a) Center-frequency offset. Until ~0.5 cycles of phase are accrued, the cosine function never reaches its first zero, resulting in a relatively benign amplitude modulation in k-space; however, important frequencies are lost as the amount of off-resonance increases. b) Off-resonance due to concomitant fields. MTFs for off-resonance due to concomitant fields shows good performance can be expected up to about 1 cycle of accrued phase. c) The effect of decay during the readout. Differing amounts of T₂ decay are simulated with 0.5 cycles of off-resonance phase accrual. Severe shaping of the MTF is only seen when the T₂ time constant approaches the readout length (10 ms).

Concomitant gradient effects

When phase accrual is due to concomitant field effects, it can be shown that ω_c(r) is a complex function of the imaging gradients and spatial coordinates of the slice, the actual form of which is unimportant for this case. As mentioned previously, in this case the phase-accrual time function takes a more complex form. Specifically,

$$\tau (t)=\frac{1}{g_m^2}{\int }_0^t[G_x^2(t^{\prime })+G_y^2(t^{\prime })]d{t}^{\prime },$$ [3]

where $g_m^2$ is the maximum gradient strength reached during the scan, and G_x(t′) and G_y(t′) are the spiral gradients on the two in-plane axes (9). Because this time function depends on the gradients squared and because the spiral-in/out gradients are symmetric, τ(−t) = −τ(t), and the signal in the presence of concomitant gradient effects is

$$s(t)=\int m(\mathit{r})e^{-j2\pi k(t)\mathit{r}}[cos{\omega }_c(\mathit{r})\tau (t)]d\mathit{r}.$$ [4]

The typical phase-accrual time function for spirals is, overall, less steep than the linear function that governs B₀ off-resonance. Thus, the redundant in/out scheme is actually more robust to phase errors caused by concomitant fields than it is to those caused by B₀ inhomogeneity and will perform well up to about 1 cycle of accrued phase (Fig. 2b).

Relaxation

In non-redundant multi-shot spiral-in/out scanning, T₂^* relaxation during the readout results in stronger signal at one side of the periphery of k-space than the other, the result of which is artifacts that look strikingly similar to those caused by off-resonance. Adding a T₂^* decay term to Eq. 1 and assuming that the readout time is short compared to T₂^* (Supplemental Material, Appendix B), the following expression for the signal in the presence of both off-resonance and T₂^* decay can be shown to be

$$s(t)=\int m(\mathit{r})e^{-j2\pi k(t)\mathit{r}}[cos\omega (\mathit{r})t]d\mathit{r}+j\int m(\mathit{r})e^{-j2\pi k(t)\mathit{r}}\frac{t}{{T_2}^{\ast }(\mathit{r})}[sin\omega (\mathit{r})t]d\mathit{r}.$$ [5]

This signal is complex, with a real part corresponding to the previously described cosine-modulated signal equation and an imaginary part that varies in amplitude with time. This is potentially worrisome, since phase cancellation is required to remove off-resonance effects. However, first note that that time has been defined to run from −T/2 to T/2 for spiral-in/out trajectories and that at t = 0, the imaginary component in Eq. 5 becomes zero. It follows that, at the center of k-space where the majority of the image energy resides, there is little impact from the imaginary component of Eq. 5. Second, the ratio of t/T₂^*(r) that controls the amplitude of the imaginary component will always be small as long as T₂^* is larger than t_max.

If there is no off-resonance (or that off-resonance is corrected somehow), then ω(r) = 0, and the averaging operation in redundant sampling works to remove T₂^*-induced artifacts. In truth, even if the linear approximation utilized in the derivation were relaxed, as would be necessary for a short T₂^* species, then there will be a symmetric emphasis on the outer regions of k-space, the result of which is more benign than the asymmetric T₂^* weighting that occurs for non-redundant spiral-in/out trajectories.

In simulations, the combination of T₂^* and off-resonance is not too different from either case alone. Figure 2c shows the performance of the redundant method in the presence of both inhomogeneity and T₂^* relaxation in terms of the MTF. As expected, strong shaping of the MTF only occurs for T₂^* on the order of readout length (10 ms). However, even at this short T₂^*, there is little degradation of the PSF (not shown). The imaginary term in Eq. 5, and thus potentially damaging phase due to T₂^* relaxation, is negligible.

Although the redundant spiral-in/out trajectory works for both gradient-echo and spin-echo imaging, spin-echoes (and spin-echo trains) provide a natural setting in which to apply them. Since the TE of spin-echo scans is generally longer, the spiral-in portion of the trajectory can be inserted with little or no increase in minimum TE. Second, the in/out trajectory aligns the gradient echo generated by the spiral gradients with the spin echo formed by the RF pulses at the center of the gradient waveform, resulting in higher signal when the center of k-space is sampled.

One attractive application for the redundant spiral-in/out trajectory is in a slab-selective version of the 3D spiral TSE sequence (20). In 3D TSE sequences with slab-selective excitation pulses and nonselective refocusing pulses, spurious FID artifacts arising from imperfect refocusing pulses are removed via an RF chopping technique, in which two averages are acquired with alternating refocusing pulse phase (2). In the spiral TSE sequence, then, multiple averages are already being performed and since the origins of the spurious FID artifacts and the spiral-in/out artifacts are different, the second, redundant acquisition can be performed with the RF-chopped acquisition to acquire a fully redundant trajectory with no increase in scan time. For further discussion, see Supplemental Materials online.

Methods

A resolution phantom was scanned on a 1.5 T Siemens Avanto scanner with a GRE sequence using a spiral-out trajectory and a redundant spiral-in/out trajectory. Acquisition parameters were: number of interleaves 14, spiral duration 10 ms, in-plane FOV 300 mm, slice thickness 5 mm. To examine off-resonance performance, the sequences were run once with a good shim applied, and again with the receive frequency manually tuned 20, 40, 80, and 160 Hz off-resonance (corresponding to 0, 0.2, 0.4, 0.8, and 1.6 cycles of off-resonance accumulated at the end of the readout). All images were acquired in the transverse plane, and were gridded and Fourier-transform-reconstructed with no off-resonance correction algorithm applied. The gridding operation automatically sums the data at the proper k-space locations, given the redundant trajectories.

To investigate concomitant field performance, the resolution phantom was imaged again using both trajectories with 14 interleaves, spiral duration 6.4 ms, in-plane FOV 300 mm, and slice thickness 3 mm in a double-oblique orientation ((C→S −41.8°)→ −27.8°) near the magnet isocenter (X −9.8 mm, Y −39.6 mm, Z −21.7 mm), then moved 50 mm along the z-axis (X −9.8 mm, Y −39.6 mm, Z −71.7 mm) and imaged again to ensure significant concomitant fields.

A comparison between the effectiveness of the redundant spiral-in/out trajectory in reducing blurring versus two post-processing techniques was performed by manually setting the second-order shim of the system such that a strong non-linear variation in B₀ existed across the FOV in one direction. This ensures the simple, linear-correction method will fail and represents a situation in which more advanced off-resonance correction algorithms are necessary. The same imaging parameters used in the previous experiment were used, except that the phantom was set up in the coronal orientation so that Z² shim could be manually detuned by +140 μT/m². The data was reconstructed first with no off-resonance correction applied; second, with a linear correction; and finally with a semi-automatic method that has been reported previously (13). For spiral-in/out data, the off-resonance correction was applied to each component image prior to combining the data in image space. The reconstruction time for each method was recorded.

To test the redundant in/out trajectory in vivo, a slab-selective version of the variable-flip-angle 3D spiral TSE (spiral SPACE) sequence was used on a normal volunteer for T₂-weighted brain imaging. Scan parameters were as follows: TR/TE 3000/200, spiral duration 6.4 ms, in-plane FOV 250 mm, number of slices = 64, slice thickness 1.0 mm. Forty-nine interleaves were used for both spiral-out and spiral-in/out acquisitions. For spiral-in/out, the second, redundant interleaf scan was combined with the chopped scan so that the total acquisition time for both sequence variations was identical. No off-resonance correction algorithm was applied in reconstruction in order to better exhibit the improved off-resonance performance of the redundant in/out sequence.

Results

The redundant spiral-in/out trajectory shows excellent robustness for off-resonance values ranging up to 0.5 cycles (Fig. 3a). Above this value, blurring appears and is comparable to a spiral-out scan performed with half the amount of off-resonance applied; consistent with the results predicted by Fig. 2. Figure 3b compares the spiral-out and spiral-in/out trajectories for double-oblique imaging planes near the magnet isocenter and off-center. The spiral-in/out trajectory results in images largely free from blurring due to concomitant fields.

Figure 3.

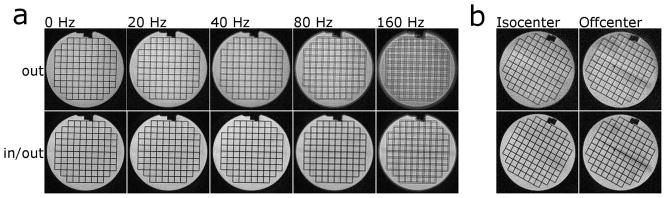
Trajectory performance in a phantom. a) Phantom images at various amounts of off-resonance. Images were acquired with a 10 ms readout, resulting in cycles of phase accumulated at the end of the readout: 0 Hz = 0 cycles, 20 Hz = 0.2 cycles, 40 Hz = 0.4 cycles, 80 Hz = 0.8 cycles, 160 Hz = 1.6 cycles. b) Trajectory performance in the presence of concomitant fields. Note blurring near the top of the phantom due to concomitant fields in the spiral-out, offcenter image, and the absence of this blurring in the in/out image. Across the entire figure, top row: spiral-out, bottom row: spiral-in/out. No off-resonance correction was applied in any reconstruction.

In the presence of non-linear B₀ variation, an uncorrected redundant in/out trajectory natively performs better than an uncorrected spiral-out acquisition (Fig. 4a vs. 4d). Applying a linear correction to the data/trajectories during reconstruction cannot fully correct the spiral-out image because the underlying field is non-linear (Fig. 4b vs. 4a). With only a linear correction, the redundant in/out trajectory can correct the residual blurring (Fig. 4e), whereas the spiral-out data requires more advanced reconstruction algorithms, such as a semi-automatic correction (Fig. 4c), to correct for the non-linear field. The reconstruction times for each off-resonance correction method was nearly identical when applied to spiral-out and spiral-in/out data and was as follows. No correction: 0.14 sec; Linear correction: 0.26 sec; Semi-automatic: 9.7 sec.

Figure 4.

Post-processing techniques applied to remove blurring due to off-resonance in spiral-out (a–c) and redundant spiral-in/out (d–f) acquisitions. A highly non-linear field was applied in the left-right direction with intentionally poor shimming. a) No correction; spiral-out. b) Linear correction; spiral-out. c) Semi-automatic correction; spiral-out. d) No correction; redundant spiral-in/out. e) Linear correction; redundant spiral-in/out. f) Semi-automatic correction; redundant spiral-in/out.

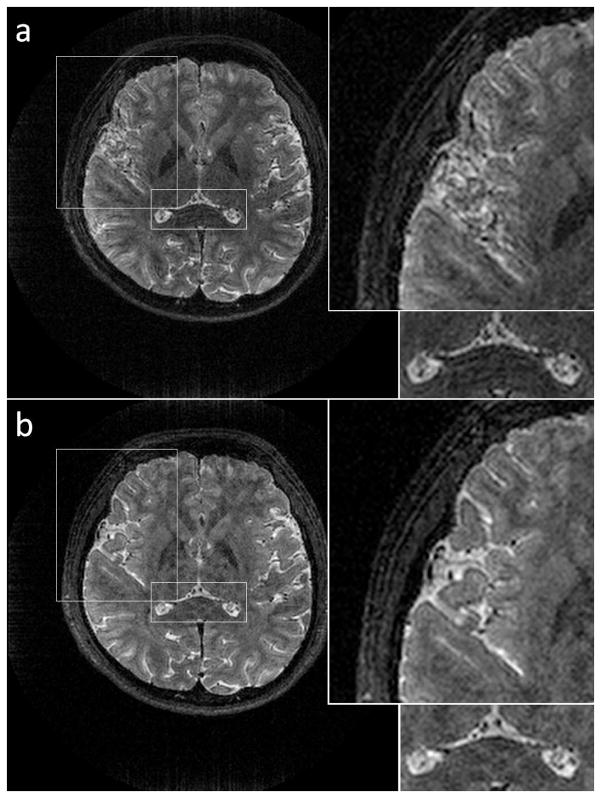
One slice from a 3D stack-of-spirals TSE in vivo dataset acquired with both spiral trajectories is shown in Fig. 5. Overall, the images acquired with the spiral-in/out trajectory are sharper due to the much improved off-resonance performance. An additional figure showing the trajectories’ performance for non-contrast MRA is available in the Supplemental Materials.

Figure 5.

Comparison of spiral-out and redundant spiral-in/out in a volunteer with no off-resonance correction applied to either dataset. One slice is shown from a slab-selective 3D stack-of-spirals trajectory. a) Spiral-out. Significant blurring is observed in areas with poor B₀ homogeneity (insets). b) Spiral-in/out. Excellent off-resonance performance is obtained with no increase in scan time.

Discussion and Conclusion

Although all of the data presented here was acquired with a single receive channel, we anticipate this technique will perform well in parallel imaging implementations, allowing fast reconstructions to take place at scan time. One major hurdle to the wide-spread adoption of non-Cartesian parallel reconstructions is their complexity due to the fact that they must address the off-resonance issue in addition to removing non-Cartesian aliasing artifacts.

For small values of off-resonance, the k-space signal in redundant sampling experiences a cosine amplitude window, which is a different (and more benign) mechanism for resolution loss compared to the PSF broadening observed in spiral-out scanning. As in regular spiral imaging, this slight blurring will be space-variant depending on local off-resonance values. For larger off-resonance values (or for long readout lengths), the cosine modulation will begin nulling important frequencies in k-space as a function of k-space radius, resulting in more severe image artifacts. Therefore, we anticipate the use of this trajectory not as a complete replacement for post-processing methods, but rather as an adjunct to these methods where appropriate. The use of the redundant in/out trajectory allows a greater margin of error for post-processing methods, resulting in better image quality and/or facilitating the use of less robust (but potentially simpler and faster) off-resonance correction algorithms, as demonstrated in Figure 4.

The robustness of this method with regards to concomitant fields is potentially very important. Most current off-resonance correction methods do not incorporate concomitant gradient correction, and we believe that this is essential for off-isocenter scans.

Spirals are mostly leveraged either for their data acquisition efficiency (speed), their robustness to motion, or their short TEs. A few general comments in regards to spiral-in/out trajectories should be made. The data acquisition efficiency and motion characteristics of in/out trajectories are very comparable to spiral-out scanning. However, the time required to spiral-in with these trajectories precludes short-TE acquisitions. For all experiments in this work, the TEs of the spiral-out and spiral-in/out scans were identical, resulting in longer TEs than might normally be used with spiral scanning, and imparting T₂^*-weighting to the resulting images. Additionally, spiral-in/out imaging has other issues that spiral-out scanning does not, such as eddy currents causing trajectory warping leading to inconsistencies at the center of k-space.

The fact that the redundant spiral-in/out trajectory necessarily requires twice the number of interleaves as a spiral-out trajectory to achieve a similar resolution cannot be overlooked. We have shown that for slab-selective 3D spiral TSE imaging, at least, the redundant acquisition may be combined with the RF-chopped second average for no penalty in scan time. For other cases where spiral trajectories are regularly used with multiple averages and long TEs (e.g. fMRI, ASL), or for time-resolved sequences, the redundant acquisition can be interleaved with the base acquisition in time and neighboring redundant in/out data can be combined with a “view-sharing” approach. In this way, overall scan time is not affected (although temporal resolution is). Recently, Jung, et al (21) reported an interleaved, high-resolution in/out trajectory for fMRI and showed that substantial improvement is obtained by combining sequential frames of redundant in/out data along with a conjugate phase reconstruction. Here, we have shown this technique to have utility for other types of spiral imaging and have explored the limits of the approach.

The redundant spiral-in/out trajectory is an attractive acquisition-based method to naturally mitigate blur due to off-resonance in spiral scanning. The technique produces excellent image quality with the simplest of post-acquisition correction methods, allowing simple, fast reconstructions.