Abstract.
We present an application of spatial frequency-domain imaging (SFDI) to the wide-field imaging of drug delivery to brain tissue. Measurements were compared with values obtained by a previously validated variation of diffuse reflectance spectroscopy, the method of optical pharmacokinetics (OP). We demonstrate a cross-correlation between the two methods for absorption extraction and drug concentration determination in both experimental tissue phantoms and freshly extracted rodent brain tissue. These methods were first used to assess intra-arterial (IA) delivery of cationic liposomes to brain tissue in Sprague Dawley rats under transient cerebral hypoperfusion. Results were found to be in agreement with previously published experimental data and pharmacokinetic models of IA drug delivery. We then applied the same scheme to evaluate IA mitoxantrone delivery to glioma-bearing rats. Good correlation was seen between OP and SFDI determined concentrations taken from normal and tumor averaged sites. This study shows the feasibility of mapping drug/tracer distributions and encourages the use of SFDI for spatial imaging of tissues for drug/tracer-tagged carrier deposition and pharmacokinetic studies.
Keywords: hyperspectral imaging, diffuse reflectance, spectroscopy, spatial frequency domain, drug delivery, mitoxantrone
1. Introduction
In cancer treatment, the outcome is often dependent on the effective tissue concentrations of anticancer drugs. Local tissue drug concentrations are an important parameter to assess effective drug delivery and treatment response. Plasma concentrations themselves are often inadequate to describe tissue drug delivery.1,2 The ability to determine site-specific tissue drug concentrations is especially important in complex organs, such as brain tissue, where diffusion is limited due to the structurally complex matrix of the underlying tissue. Chemical extraction (CE) and analytic methods, such as high-performance liquid chromatography methods, are tissue destructive, do not provide time histories, and lack spatial resolution due to homogenization.3,4
Previous camera-based methods of spatial quantitation of optical properties have employed Monte Carlo simulations to estimate an average differential path length for a specific imaging configuration for changes in tissue hemoglobin concentration.5,6 However, these estimates sometimes rely on the assumed baseline optical properties of the tissue sample. Relative variations in absorption at discrete wavelengths are then translated to tissue oxygenation changes by a modified Beer’s law model. Furthermore, this approach also poses limitations in accuracy, given that a single estimate for path length is used to generalize photon migration within the entire camera field of view (FOV).
Diffuse reflectance spectroscopy (DRS), particularly the method called optical pharmacokinetics (OP), has been shown to yield promising correlation with CE methods for drug concentration determination in tissue without the aforementioned drawbacks.7,8 Raster scanning of the optical probe head, previously used for diagnostic applications, can generate optical absorption maps that can be converted into chromophore concentrations for compounds with suitable absorption spectra.9 The time of measurement will be a function of the density of spatial sampling, speed of the stepping mechanism, and integration time of the spectrometer, while accurate, simpler methods that do not require mechanical scanning may be more universally adaptable. In addition, spatial resolution may be limited by the 1.7- to 2-mm source–detector separation required for utilization of the technique.
A relatively recent modality, spatial frequency domain imaging (SFDI), is capable of wide-field visualization of optical properties by solving light transport derived from periodic photon density waves.10,11 In recent studies, the method has been used to construct chromophore maps of tissue water content and hemoglobin oxygen saturation in vivo and ex vivo.12,13 In this report, we show the feasibility of applying SFDI to determine brain tissue uptake of tracer-tagged cationic nanoparticles in Sprague Dawley rats. We then extend the method to map out intra-arterial (IA) delivery of the chemotherapeutic drug, mitoxantrone, in glioma-bearing rat brain tissue. To the best of our knowledge, this is the first instance where SFDI has been used to quantify drug delivery. We then compare measured concentrations to values obtained by the OP method. A strong cross-correlation was observed between the two methods, and results were in good agreement with previous studies and pharmacokinetic modeling.14–16 These results support the application of SFDI for ex vivo and potentially in vivo pharmacokinetic studies.
2. Materials and Methods
2.1. Spatial Frequency Domain Imaging System
The system employs a 12-bit hyperspectral line-scan camera (Resonon Inc., Bozeman, Montana) mounted onto a motorized stage [Fig. 1(a)]. The camera permits wavelength discrimination of reflectance at visible and near-infrared wavelengths (400 to 900 nm) at a spectral resolution of 2 nm. Spectral calibration of the camera was done by the manufacturer prior to this study. A grid-based procedure similar to the one described in Ref. 17 was used for spatial calibration of the system.
Fig. 1.
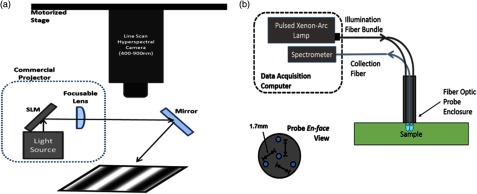
Schematic representation of system configurations for site-specific light absorption quantification methods. (a) shows the setup for hyperspectral spatial frequency-domain imaging (SFDI). (b) shows the setup for the optical pharmacokinetics (OP) method. The fiber optic probe maintains specified source–detector separation for the OP method.
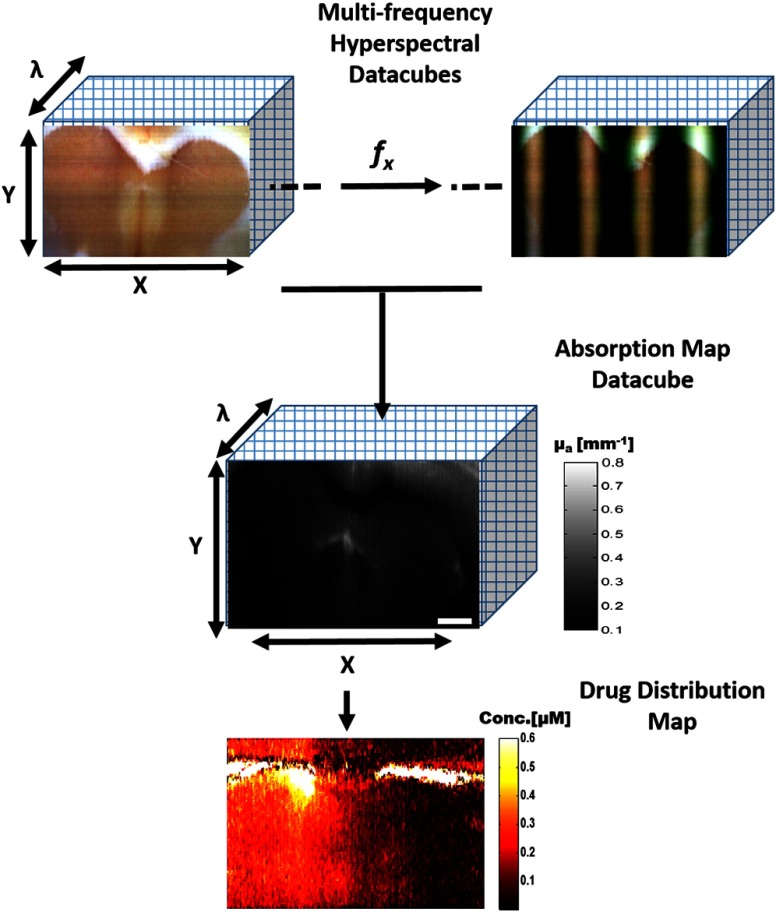
A structured illumination scheme used was based on the one described in Ref. 10. Eight-bit sinusoidal images were created in MATLAB® (Mathworks, Natick, Massachusetts), loaded into a single PowerPoint presentation (Microsoft Inc., Seattle, Washington), and then fed into a digital projector (Epson, Long Beach, California). This allowed for generated periodic illumination patterns to be imaged onto the tissue samples. The sinusoidal images were corrected according to the projector response function using a similar method as described by Lin et al.18 A custom program written in Python synchronized image acquisition along with presentation slide rotation by employing Active Python and the Windows COM API (Microsoft Inc.). Each scan produced a data-cube, which comprised a reflectance image for 240 wavelengths between 400 and 900 nm (Fig. 2). Voxels were binned by a factor of two to improve signal quality. After binning, the final resolution was 240 by 320 pixels over an FOV, with a 120 wavelength spectral profile at each spatial location. For this study, a 2 to 3 mm or less pixel size was needed for comparison to OP measurements. Spectral data were curtailed at and due to the limited light output by the commercial projector system. The total time for data acquisition was per frame, which included switching of the illumination pattern and motorized scanning and repositioning of the hyperspectral line-scan camera. Unless otherwise stated, all SFDI data in this report were captured using four illumination spatial frequencies, , 0.095, 0.158, and . Each frequency was imaged at three phases, separated by in order to apply the conventional demodulation scheme. Spatial frequencies were calculated beforehand by taking the spatial Fourier transform along the axis of modulation on a reflectance standard.11 The shifted, multifrequency data were used to calculate the dc and ac components of diffuse reflectance for each pixel in the image using
| (1) |
where is the demodulated image at a spatial illumination frequency . The parameters , , and represent the acquired single frequency image when the sinusoidal illumination is shifted by 0, , and , respectively.10,11,19 The dc image, , was calculated at with the following expression:
| (2) |
Fig. 2.
Hyperspectral SFDI acquisition and data processing flow chart. Data are captured at a minimum of two spatial illumination frequencies, three phases each, for all wavelengths in parallel. Further processing yields an absorption spectrum at each spatial location that is then used to compute a drug concentration map.
Demodulated images were simultaneously calibrated and converted into diffuse reflectance by applying a simple three-step procedure.10 A phantom with known optical properties was first imaged to derive . A forward model was then used to calculate the absolute diffuse reflectance, , based on the known optical properties of the phantom. The calibration factor was taken as the ratio of the system measured, , to the forward model predicted values, . This calibration factor was applied to all data used in this study and accounted for the system response of the imaging system as well. A least-squares regression was used to fit calibrated multifrequency diffuse reflectance data with a forward model for each pixel in the image, using absorption () and reduced scattering () coefficients as fitting parameters.
The above calculation was performed at each voxel in the hyperspectral data-cube to generate a wavelength-dependent absorption and reduced scattering spectra for each spatial location. Chromophore concentrations were extracted from the recovered absorption spectra by applying a multiparametric, least-squares minimization routine to the relationship described below.
| (3) |
where and are the molar concentration and extinction spectrum of chromophore , respectively.19 Assuming that the optical tracer/drug, oxygenated hemoglobin (HbO), and deoxygenated hemoglobin (HbR) are the dominant chromophores, Eq. (3) can be written as
| (4) |
2.2. Diffuse Reflectance Spectroscopy
A schematic diagram of the OP system is shown in Fig. 1(b). Broadband light from a pulsed xenon-arc lamp is delivered onto the sample via three radially separated illumination fibers. Backscattered light is collected and routed to a spectrometer by a fiber placed at the center of the fiber optic probe. The distance between each of the three illumination fibers and the collecting fiber was fixed at 1.7 mm. This geometric configuration permitted application of the OP method for average absorption coefficient extraction of the volume of the sampled region ( diameter to 3 mm depth).
A detailed description of the OP method has been provided elsewhere and is only briefly described here.7,20 It was demonstrated that for this source–detector separation (), the path length of collected photons is relatively insensitive to scattering changes within the range relevant for biological tissues.21 The change in absorption from two OP measurements can be related by
| (5) |
where and are the diffuse reflectance spectra of the sample taken after and before administration of an optical tracer, respectively, or at two different tissue locations (to establish the difference in concentration between locations). is a second-order polynomial that accounts for baseline shifts induced by changes in scattering parameters between measurements and is the change in absorption with respect to the reference spectra.7,20 , , and are path length fitting coefficients based on the probe fiber geometry. Establishment of these parameters is determined from analysis of spectra taken from turbid phantoms with known absorption properties. Combining Eqs. (4) and (5) yields the equation
| (6) |
In our study, the above equation was used to determine the difference in drug concentration between two diffuse reflectance measurements. It is important to note that if the reference measurement contains no drug, the change in concentration is essentially equal to the absolute drug concentration. This, however, is not valid in the case of hemoglobin concerning biological tissues, where it is difficult to obtain a reference spectrum without hemoglobin. Ideally, the optical tracer is chosen such that its distinguishing spectral features are sufficiently separated from those of the strong hemoglobin absorption bands, i.e., with a peak .
2.3. Tissue Phantom Experiments
To experimentally validate both methods of absorption quantification, a cross-correlation study was performed in tissue phantoms. As a source of scattering, Intralipid 20% (Sigma-Aldrich, St. Louis, Missouri) was diluted to 1% in deionized water. Evans Blue (EB) dye (Sigma-Aldrich) was used as an absorber. The extinction spectrum of EB between 400 and 900 nm was measured by spectrophotometry (Epoch, Biotek, Winooski, Vermont) [Fig. 3(a)]. Five aliquots of EB were then added to the 1% Intralipid prep, with SFDI and DRS measurements taken prior to each addition. The calculated EB concentrations in 1% Intralipid ranged from 0 to . OP measurements obtained from a separate phantom containing only 1% Intralipid was used as a reference spectrum. The total volume of EB addition did not exceed 0.2% of the total volume of Intralipid; therefore, changes in the reduced scattering coefficient were not expected. Reduced scattering spectra were compared with an empirical model for Intralipid reduced scattering.22
Fig. 3.
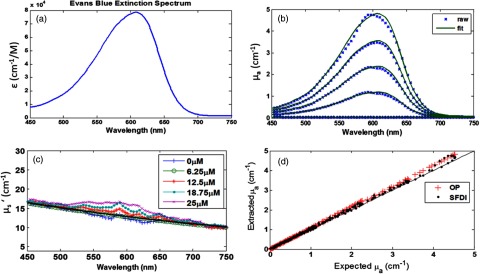
Cross-validation results from tissue phantom experiments. (a) shows the extinction spectrum recovered of Evans Blue (EB) dye (450 to 750 nm). (b) shows hyperspectral SFDI absorption spectra from absorption titration study and fitting of the overdetermined dataset for EB concentration measurement. EB concentrations were 25, 18.75, 12.5, 6.5, and from top to bottom. (c) shows reduced scattering spectra obtained over the absorption titration study. (d) shows a scatter plot of SFDI and OP measured absorption over expected values for all wavelengths.
2.4. Liposome Preparation
Cationic liposomes were prepared with 50% dioleoyltrimethylammonium-propane content and loaded with tracer dye, . The tracer dye was selected to have an absorption spectrum distinct from hemoglobin and permitted indirect tracking of the liposomal particles by measurement of absorption. A more detailed description of the liposomal preparation has been described in previous works.15,23
2.5. Animal Preparation
After approval by the Columbia University Institutional Animal Care and Use Committee, Sprague Dawley rats were sedated under 2.0% isoflurane and mounted onto a stereotactic frame. In the first group, three rats underwent tail vein cannulation for intravenous propofol. A tracheostomy was performed to allow for mechanical ventilation. The right internal carotid artery was isolated and cannulated by an experienced animal surgeon to permit IA injections. Carotid isolation was verified by the retinal discoloration test.24 Systemic blood flow was monitored by laser Doppler probe placed on the perfused hind paw (PeriFlux System 5000, Perimed, Sweden). All physiological data were routed to a single data acquisition unit (Powerlab, AD Instruments Inc., Colorado Springs, Colorado) and recorded in real time at 100 Hz.
In a separate group of six animals, the scalp was retracted and a burr hole was made 3 mm lateral and 2 mm posterior to the bregma. A Hamilton syringe was used to inject of C6 glioma cells 3 mm into the right cerebral cortex over 10 mins. Bone wax was used to seal the skull opening and the tissue was irrigated with hydrogen peroxide before closure to prevent extracranial extension of the tumors. Ten days after inoculation, animals were subject to the same preparatory procedures as the first group.
Animals in the first group received IA administration of cationic liposomes under two different cerebral blood flow conditions: normal and reduced. They were sacrificed 5 min after treatment and the brain extracted for optical assessment of liposomal uptake.
In the group of six tumor-bearing animals, chemotherapeutic drug mitoxantrone (Sigma Aldrich) was administered IA under transient cerebral hypoperfusion (TCH).23,25,26 All animals were treated on day 10 after C6 tumor cell inoculation and received the same dose of 1 ml of of mitoxantrone (or 0.97 mM). After treatment, animals were allowed to recover from anesthesia to assess immediate safety. They were then sacrificed 4 h after treatment and brains were extracted for evaluation of brain tumor uptake of mitoxantrone by optical measurements. Brain tissue sections were cryopreserved for histological verification of tumor extent with hematoxylin and eosin. Adjacent cryosections were imaged under confocal microscopy (640 nm excitation, collection) for mitoxantrone fluorescence distributions using a commercial system (Nikon A1R, Melville, New York).
2.6. Postmortem Tissue Assessment
Five-millimeter-thick coronal sections of the extracted brain were made from the parietal lobe site of injection. OP measurements were taken from the brain ipsilateral and contralateral cerebral hemispheres and the difference in drug concentration was measured by fitting data to Eq. (4).
In the tumor-bearing group, coronal sections of the extracted brain were made with care taken to bisect the tumor mass. OP measurements were taken from brain tumor tissue on the ipsilateral side and corresponding contralateral normal tissue. Optical contact of the probe tip with the tissue surface was optimized by lightly irrigating the tissue surface with saline before measurements. In order to recover an approximation of absolute mitoxantrone concentration, measurements obtained from an untreated animal were used for the OP reference spectra. The differences in HbO, HbR, and mitoxantrone concentrations between the untreated and treated tissue measurements were calculated by employing a Levenberg-Marquardt routine to fit the acquired spectra to Eq. (4).
All slices were then imaged bilaterally with SFDI to include the sites of OP measurement in the same image. Multifrequency data were reduced to absorption maps for each wavelength channel in the hyperspectral data-cube. The result generated an absorption spectrum for each spatial location. A custom program was written in MATLAB® to process SFDI tissue data. The algorithm first generated an 8-bit RGB image of the brain tissue section by using the dc reflectance images at 459, 552, and 640 nm [Fig. 4(c)]. This true-color representation of the tissue slice was used to outline regions of interest (ROIs). After ROIs that correlated with the OP measurement sites were selected, all absorption spectra were averaged for each spatial location within the enclosed region. The difference in absorption between the two regions was then fitted to Eq. (3) using a Levenberg-Marquardt routine, keeping chromophore concentrations as free parameters. OP and SFDI measurement sites and regions sampled were comparable across the animals.
Fig. 4.
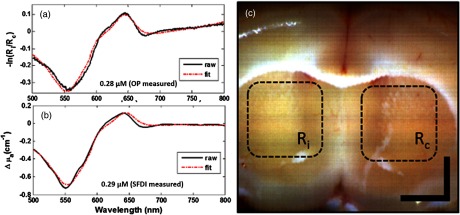
Fitting results for HbO, HbR, and for site-specific measurements on postmortem brain section. (a) shows fitting results to chromophore concentration difference by the OP method using the contralateral region as the reference. (b) shows fitting results for SFDI measured for recovery of the chromophore concentration difference across the two hemispheres. The extracted concentrations for each method is displayed on their respective graph. (c) shows the true-color image generated from the dc image at 459, 552, and 640 nm. and are the regions of interest that correspond to the sites of direct OP measurement for the ipsilateral and contralateral hemispheres, respectively. Bar is 2 mm.
Absolute concentration maps of mitoxantrone deposition were constructed by applying the spectral fitting routine to each pixel in the hyperspectral data-cube. A median filter was then translated across the image to eliminate salt and pepper noise and improve image quality.
3. Results and Discussion
3.1. Tissue Phantom Studies
OP and hyperspectral SFDI measurements were made in titrations of EB dye (0 to ) in 1% Intralipid. For OP measurements, twelve spectra were averaged from each of the titration concentrations. For SFDI, all pixel values in the absorption maps were averaged for each wavelength in the datacube to produce a mean spectral profile for each phantom. Concentrations were extracted from OP data using the model described in Eq. (4) with hemoglobin parameters set to zero and the extinction spectrum of EB used for the drug. Measurement of 1% intralipid, prior to the addition of any dye, was used as the reference for all subsequent OP measurements in the titration study. Thus, if we assume the absorption of 1% Intralipid to be negligible compared to the range of values considered, then we can equate the relative absorption derived in Eq. (4) to an approximately equal absolute .
SFDI-derived absorption values show good agreement with OP values for the absorption range used in this study (Fig. 3). However, at higher phantom EB concentrations, the SFDI-extracted reduced scattering spectrum begins to experience a slight overestimation associated with regions of high absorption. We attribute this phenomenon to the fact that, at this point, we approach the limits of validity for application of the diffusion theory-based model. In addition, the spatial frequencies used in this study were selected to bias sensitivity to absorption effects. These problems could be averted in future experiments by using a precalculated, Monte Carlo-based look-up table for inversion of diffuse reflectance to accommodate a lower albedo.
3.2. Liposomal Concentration Determination with Optical Tracer
Diffuse reflectance spectra from postmortem rat brain tissue sections were analyzed using the OP method to determine the bilateral concentration difference, [Fig. 4(a)]. For SFDI calculations, ROIs were first selected from the true-color image that corresponded to the OP measurement sites and the absorption spectrum of all enclosed spatial locations were averaged for each hemisphere. The difference in averaged absorption was processed to obtain the SFDI measured across the hemispheres. Figure 4(b) shows an example of the model fitting to the hyperspectral absorption data. Optimization was terminated when parameters converged under a specified threshold and values were 0.8 or better. Unaccounted for chromophores were not expected to produce significant effects on extracted concentration values due to low residuals. These results were compared for animals that received IA-TCH administration and the animal that was treated IA under normal blood flow. In the first animal that received IA-TCH liposomes, the OP and SFDI measured values were 0.28 and , respectively. SFDI measurement from the second IA-TCH liposome-treated animal was , while the OP measured . The animal that received IA liposomes under normal flow conditions yielded an OP measured value of , while the SFDI measured . Discrepancies between the two measurements can primarily be attributed to differences in the effective volumes sampled. In IA drug delivery, drug distribution homogeneity may not be guaranteed. Since the effective volume sampled may differ between the two methods, the determined concentration differences will be a function of evenness of drug deposition throughout the tissue depth. Therefore, the recovered concentrations were not entirely expected to exhibit a consistent relationship. Monte Carlo simulations reveal that at the source–detector separation used for OP measurements, of collected photons have a maximum depth of into the tissue.7 For SFDI, areas of low absorptions are not likely to satisfy the semi-infinite criteria assumed in the derivation of the forward model at the dc frequency. Nevertheless, calculations for effective penetration depth ranged between 1 and 4 mm for the spatial frequencies and optical properties (largely visible region) observed in this study.10 Concurrently, error contributions due to the 5 mm tissue thickness were not expected to play a significant role in absorption recovery; however, this was not thoroughly investigated. Other sources could include, but are not limited to, errors in ROI selection, specular reflectance, and system noise. It should be noted that while the number of animals studied were small, the intent was not to demonstrate statistical data between methods of drug administration but to show that the optical methods correlate under varying conditions.
Drug deposition determination was performed by applying the multiparametric, spectral fit across each pixel in the hyperspectral data-cube. The resulting concentration values revealed high preferential uptake in the infused hemisphere for the reduced-flow animals as compared to the animal that was treated under normal blood flow conditions. These preliminary findings agree with experimental data obtained from previous studies along with pharmacokinetic models for regional drug delivery, which empirically link a reduction in blood flow to increased local concentrations.14,23
3.3. Evaluation of Mitoxantrone Delivery to Brain Tumor
In the group of six glioma-bearing rats, animals were treated with the chemotherapeutic drug, mitoxantrone, under the IA-TCH protocol 10 days after C6 cell inoculation. Animals were sacrificed 4 h after treatment for optical assessment of mitoxantrone uptake on fresh postmortem tissue sections. In this group, reflectance spectra obtained from an untreated animal was used as the reference for the OP method. SFDI images were taken immediately after and average mitoxantrone concentrations were computed for sites similar to OP sampling regions. Measured concentrations were significantly greater in the tumor tissue than the contralateral normal brain tissue for both systems (). Moreover, the values determined by both methods showed good correlation as shown in Fig. 5. Drug concentrations were determined at each spatial location in the SFDI data set for a representative animal and compared reasonably to fluorescence maps obtained from confocal microscopy (Fig. 6).
Fig. 5.
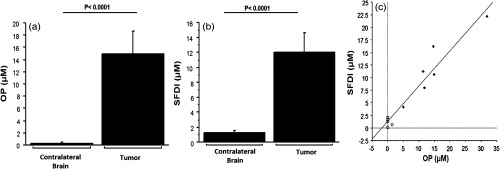
Uptake of mitoxantrone as determined by OP (a) and SFDI (b) in six treated, tumor-bearing Sprague Dawley rat postmortem brain specimens 4 h after drug injection. Together, SFDI measurements were linearly related to concentrations measured by OP (c, , ). A better correlation was seen with higher values in the tumor groups (solid circles, tumor) than with low concentrations in healthy tissue in the opposite cerebral hemisphere (open circles, contralateral brain).
Fig. 6.
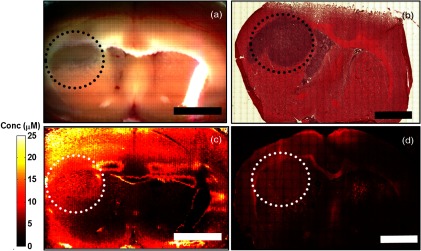
Mitoxantrone distribution map. (a) shows the composed RGB image generated from 640, 550, and 450 nm reflectance images. (b) shows tumor tissue verification with hematoxylin and eosin staining. (c) shows the spatial mitoxantrone deposition measured by hyperspectral spatial frequency domain imaging. (d) depicts a stitched, composite image of mitoxantrone fluorescence measured by confocal microscopy. Dotted circle delineates tumor area. Bar is 3 mm.
Future treatments of brain diseases are likely to rely on macromolecules or complex delivery platforms, such as liposomes and other nanoparticles. Many of these macromolecules will be guided by cell targeting molecules, such as monoclonal antibodies and cell-penetrating peptides. Optical tracers can be tagged to a variety of these transport platforms to facilitate investigation of particle pharmacokinetics. In addition, their drug cargos, such as chemotherapeutic compounds like doxorubicin or mitoxantrone, can exhibit spectral properties that can be directly interrogated by optical means.7 Visualization of uptake distribution of free, or carrier-conjugated drug formulations is especially important for studies in treating tumor-bearing animals, where highly resolved spatial imaging could help to better understand drug pharmacokinetics and dynamics at the tissue level. The feasibility of molecular diffusion and drug uptake monitoring based on scattering signatures has been previously demonstrated using optical coherence tomography.27 The tagging of drugs to contrast agents with scattering signatures, such as gold nanorods, could potentially open applications for scattering-based drug delivery monitoring with SFDI. In addition, the tagging of drugs to contrast agents with scattering signatures, such as gold nanorods, could potentially open applications for scattering-based drug delivery monitoring.
The application of the OP method for noninvasive pharmacokinetic measurements in vivo has been long used by our group to investigate IA drug delivery.20,23,28,29 SFDI measurements could be introduced through a cranial window for the in vivo spatial mapping of brain pharmacokinetics. Data from spatially resolved pharmacokinetics could be used to develop multicompartment models for plasma and tissue concentrations in larger animal models where space is more appropriate for the limited resolution of the concentration maps. However, lengthy data acquisition times have been the primary hurdle in the application of SFDI for in vivo pharmacokinetics. The development of snapshot methods for SFDI can considerably reduce data acquisition times.13,30 Also, faster data acquisition can be facilitated by identification of optimal wavelengths that strongly influence the fitting routine and can reduce the number of required acquisition wavelengths.19 While the use of hyperspectral data may improve the accuracy of the method by facilitating an overdetermined set for the fitting routine, it may be unnecessary for chromophores with stable spectra. However, certain compounds (e.g., doxorubicin, mitoxantrone, and indocyanine green) experience subtle shifts in spectra due to binding effects.7 This extra compartmental information can only be appreciated with higher spectral resolution () data sets, such as those proposed in this study.
Potential human applications could include monitoring the effects of topical drugs, toxicity of chemotherapy to peripheral compartments (i.e., skin), or during intraoperative chemotherapy where the skull is partially removed. However, this application is currently limited to drugs with dominant absorption features in the near-infrared (NIR). The development and tagging of a stable, human-safe NIR dye could expand the list of suitable compounds for imaging. To the best of our knowledge, no other imaging method has been used for imaging drug delivery. However, similar techniques have been used to quantify multispectral images for relative changes in hemoglobin. Generally, a model for average path length is derived from Monte Carlo simulations specific to the imaging system geometry and assumed baseline optical properties.5,6 Thus, the ability of SFDI to simultaneously discern absorption and scattering parameters spatially, without path length approximation, could make it a more reliable estimate for wide-field chromophore concentration monitoring. Changes in hemoglobin have been used to serve as a marker for monitoring chemotherapy response.31 Because the technique also considers hemoglobin contributions, it does not compromise the ability to quantify oxy- and deoxyhemoglobin concentrations and, thus, could be used for both drug tracking and therapy response.
4. Conclusion
In conclusion, we present the first use of SFDI for the measurement drug/tracer uptake in postmortem tissue samples. Spatial mapping of drug/tracer deposition was accomplished by employing a hyperspectral camera-based SFDI system to produce an overdetermined data set for least-squares minimization routines. We demonstrate the feasibility of the technique by a correlation to drug/tracer measurements obtained by the OP method taken from the same sampling locations. Furthermore, we show the application of the technique for quantification of brain tumor drug deposition following chemotherapeutic treatment. The reported results are promising for the application of SFDI for chromophore-tagged carrier pharmacokinetic studies.
Acknowledgments
The authors would like to thank Mei Wang for help with the experimental animal model and Robert and Ninfa Straubinger for assistance in liposomal preparation. This work was supported in part by National Cancer Institute grants RO1-CA-127500 and RO1-CA-138643 (S. J.).
Biographies
Rajinder P. Singh-Moon received his BS in electrical engineering from New York University in 2012. He is currently an MS/PhD candidate at Columbia University’s School of Engineering and Applied Sciences under Christine P. Hendon. Prior to graduate studies, he conducted research at Columbia University Medical Center under the guidance of Dr. Shailendra Joshi and collaborators Irving J. Bigio, and Darren Roblyer.
Darren M. Roblyer is an assistant professor in the Department of Biomedical Engineering at Boston University. After receiving a BS in biomedical engineering from Johns Hopkins University in 2004, he received his PhD in 2009 from the Bioengineering Department at Rice University under Rebecca Richards-Kortum. Prior to starting his faculty position, he was a Department of Defense postdoctoral fellow at the Beckman Laser Institute at the University of California, Irvine, studying under Bruce Tromberg.
Irving J. Bigio received his PhD in physics from the University of Michigan in 1974. From then until 2000 he was a scientific staff member at Los Alamos National Laboratory, including leadership of the Laser Science and Applications Group (1988 to 1994). Since 2001, he has been a professor at Boston University, with appointments in biomedical engineering, electrical and computer engineering, physics, and medicine (gastroenterology). He is a fellow of the SPIE, OSA, and the American Institute of Medical and Biological Engineering.
Shailendra Joshi does research focused on improving drug formulations and delivery methods for intra-arterial administration using optical pharmacokinetic and imaging methods.
References
- 1.Brunner M., Langer O., “Microdialysis versus other techniques for the clinical assessment of in vivo tissue drug distribution,” AAPS J. 8(2), E263–E271 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Eichler H. G., Muller M., “Drug distribution. The forgotten relative in clinical pharmacokinetics,” Clin. Pharmacokinet. 34(2), 95–99 (1998). 10.2165/00003088-199834020-00001 [DOI] [PubMed] [Google Scholar]
- 3.Alhareth K., et al. , “HPLC quantification of doxorubicin in plasma and tissues of rats treated with doxorubicin loaded poly(alkylcyanoacrylate) nanoparticles,” J. Chromatogr. B Analyt. Technol. Biomed. Life Sci. 887–888, 128–132 (2012). 10.1016/j.jchromb.2012.01.025 [DOI] [PubMed] [Google Scholar]
- 4.Groll A. H., et al. , “Compartmental pharmacokinetics and tissue distribution of multilamellar liposomal nystatin in rabbits,” Antimicrob. Agents Chemother. 44(4), 950–957 (2000). 10.1128/AAC.44.4.950-957.2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bouchard M. B., et al. , “Ultra-fast multispectral optical imaging of cortical oxygenation, blood flow, and intracellular calcium dynamics,” Opt. Express 17(18), 15670–15678 (2009). 10.1364/OE.17.015670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dunn A. K., et al. , “Spatial extent of oxygen metabolism and hemodynamic changes during functional activation of the rat somatosensory cortex,” NeuroImage 27(2), 279–290 (2005). 10.1016/j.neuroimage.2005.04.024 [DOI] [PubMed] [Google Scholar]
- 7.Mourant J. R., et al. , “Non-invasive measurement of chemotherapy drug concentrations in tissue: preliminary demonstrations of in vivo measurements,” Phys. Med. Biol. 44(5), 1397–1417 (1999). 10.1088/0031-9155/44/5/322 [DOI] [PubMed] [Google Scholar]
- 8.Austwick M. R., et al. , “Optical measurement of photosensitizer concentration in vivo,” J. Innov. Opt. Health Sci. 4(2), 97–111 (2011). 10.1142/S1793545811001460 [DOI] [Google Scholar]
- 9.Keshtgar M. R., et al. , “Optical scanning for rapid intraoperative diagnosis of sentinel node metastases in breast cancer,” Br. J. Surg. 97(8), 1232–1239 (2010). 10.1002/bjs.7095 [DOI] [PubMed] [Google Scholar]
- 10.Cuccia D. J., et al. , “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cuccia D. J., et al. , “Modulated imaging: quantitative analysis and tomography of turbid media in the spatial-frequency domain,” Opt. Lett. 30(11), 1354–1356 (2005). 10.1364/OL.30.001354 [DOI] [PubMed] [Google Scholar]
- 12.Laughney A. M., et al. , “Spectral discrimination of breast pathologies in situ using spatial frequency domain imaging,” Breast Cancer Res. 15(4), R61 (2013). 10.1186/bcr3455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weber J. R., et al. , “Multispectral imaging of tissue absorption and scattering using spatial frequency domain imaging and a computed-tomography imaging spectrometer,” J. Biomed. Opt. 16(1), 011015 (2011). 10.1117/1.3528628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dedrick R. L., “Arterial drug infusion: pharmacokinetic problems and pitfalls,” J. Natl. Cancer Inst. 80(2), 84–89 (1988). 10.1093/jnci/80.2.84 [DOI] [PubMed] [Google Scholar]
- 15.Singh-Moon R., et al. , “Surface charge of liposomes: not blood-brain barrier disruption determines uptake of after intra-arterial delivery,” J. Neurosurg. Anesthesiol. 25(4), 489–490 (2013). [Google Scholar]
- 16.Singh-Moon R., et al. , “The effectiveness of transient cerebral hypoperfusion assisted intra-arterial delivery of cationic liposomes,” J. Neurosurg. Anesthesiol. 25(4), 488–489 (2013). [Google Scholar]
- 17.Qin J., Lu R., “Hyperspectral diffuse reflectance imaging for rapid, noncontact measurement of the optical properties of turbid materials,” Appl. Opt. 45(32), 8366–8373 (2006). 10.1364/AO.45.008366 [DOI] [PubMed] [Google Scholar]
- 18.Lin A. J., et al. , “Visible spatial frequency domain imaging with a digital light microprojector,” J. Biomed. Opt. 18(9), 096007 (2013). 10.1117/1.JBO.18.9.096007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mazhar A., et al. , “Wavelength optimization for rapid chromophore mapping using spatial frequency domain imaging,” J. Biomed. Opt. 15(6), 061716 (2010). 10.1117/1.3523373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reif R., et al. , “Optical method for real-time monitoring of drug concentrations facilitates the development of novel methods for drug delivery to brain tissue,” J. Biomed. Opt. 12(3), 034036 (2007). 10.1117/1.2744025 [DOI] [PubMed] [Google Scholar]
- 21.Mourant J. R., et al. , “Measuring absorption coefficients in small volumes of highly scattering media: source-detector separations for which path lengths do not depend on scattering properties,” Appl. Opt. 36(22), 5655–5661 (1997). 10.1364/AO.36.005655 [DOI] [PubMed] [Google Scholar]
- 22.van Staveren H. J., et al. , “Light scattering in Intralipid-10% in the wavelength range of 400–1100 nm,” Appl. Opt. 30(31), 4507–4514 (1991). 10.1364/AO.30.004507 [DOI] [PubMed] [Google Scholar]
- 23.Joshi S., et al. , “Transient cerebral hypoperfusion assisted intraarterial cationic liposome delivery to brain tissue,” J. Neuro-oncol. 118(1), 73–82 (2014). 10.1007/s11060-014-1421-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Joshi S., Wang M., Hartl R., “Retinal discoloration test,” J. Cereb. Blood Flow Metab. 24(3), 305–308 (2004). 10.1097/01.WCB.0000107731.66603.18 [DOI] [PubMed] [Google Scholar]
- 25.Joshi S., et al. , “Transient cerebral hypoperfusion enhances intraarterial carmustine deposition into brain tissue,” J. Neuro-oncol. 86(2), 123–132 (2008). 10.1007/s11060-007-9450-z [DOI] [PubMed] [Google Scholar]
- 26.Wang M., Etu J., Joshi S., “Enhanced disruption of the blood brain barrier by intracarotid mannitol injection during transient cerebral hypoperfusion in rabbits,” J. Neurosurg. Anesthesiol. 19(4), 249–256 (2007). 10.1097/ANA.0b013e3181453851 [DOI] [PubMed] [Google Scholar]
- 27.Larin K. V., et al. , “Optical clearing for OCT image enhancement and in-depth monitoring of molecular diffusion,” IEEE J. Select. Tops. Quant. Electr. 18(3), 1244–1259 (2012). 10.1109/JSTQE.2011.2181991 [DOI] [Google Scholar]
- 28.Joshi S., et al. , “Inconsistent blood brain barrier disruption by intraarterial mannitol in rabbits: implications for chemotherapy,” J. Neuro-oncol. 104(1), 11–19 (2011). 10.1007/s11060-010-0466-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Joshi S., et al. , “Intra-arterial mitoxantrone delivery in rabbits: an optical pharmacokinetic study,” Neurosurgery 69(3), 706–712; discussion 712 (2011). 10.1227/NEU.0b013e3182181b67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vervandier J., Gioux S., “Single snapshot imaging of optical properties,” Biomed. Opt. Express 4(12), 2938–2944 (2013). 10.1364/BOE.4.002938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cerussi A., et al. , “Predicting response to breast cancer neoadjuvant chemotherapy using diffuse optical spectroscopy,” Proc. Natl. Acad. Sci. U S A 104(10), 4014–4019 (2007). 10.1073/pnas.0611058104 [DOI] [PMC free article] [PubMed] [Google Scholar]