Abstract
The Mantel and Knox space–time clustering statistics are popular tools to establish transmissibility of a disease and detect outbreaks. The most commonly used null distributional approximations may provide poor fits, and researchers often resort to direct sampling from the permutation distribution. However, the exact first four moments for these statistics are available, and Pearson distributional approximations are often effective. Thus, our first goals are to clarify the literature and make these tools more widely available. In addition, by rewriting terms in the statistics, we obtain the exact first four permutation moments for the most commonly used quadratic form statistics, which need not be positive definite. The extension of this work to quadratic forms greatly expands the utility of density approximations for these problems, including for high-dimensional applications, where the statistics must be extreme in order to exceed stringent testing thresholds. We demonstrate the methods using examples from the investigation of disease transmission in cattle, the association of a gene expression pathway with breast cancer survival, regional genetic association with cystic fibrosis lung disease and hypothesis testing for smoothed local linear regression. © The Authors. Stat published by John Wiley & Sons Ltd.
Keywords: exact testing, resampling, statistical computing
1. Introduction
(Mantel 1967) proposed an approach to detect clustering of location of events in space versus time of occurrence, by regressing a function of geographic distance on a function of distance in time. The prototypical application is to evaluate the evidence for communicable disease transmission, in contrast to sporadic occurrences that show no clustering. The approach has proven to be hugely popular, with 5200+ citations in the Science Citation Index as of 2013, with approximately 450 citations in each of recent years. Briefly, we let li and ti represent the geographic location (space) and time of occurrence for the ith location–time sample, i = 1, …, n. For samples i and j, we denote measures of location and time distances as cij = f(li,lj), dij = g(ti,tj), and these elements populate the matrices C and D, respectively. For a final “regression” statistic
| 1 |
high values are evidence of location–time clustering, and the author considered the power of various choices of f and g. He also noted that the Knox statistic, which records whether two locations or time points are less distant than predefined thresholds, is a special case. In addition, the paper solved for the mean and variance of S under permutation of sample labels for the location and time points. This permutation is equivalent to simultaneous permutation of rows and columns of one of the matrices C or D.
Much of Mantel's (1967) and subsequent work is concerned with finding powerful choices of f and g, but here, we assume that the statistic has been chosen, and our goal is to provide accurate testing. For numerous datasets, a normal approximation to S is inadequate, because of strong dependencies among the matrix elements. For the Knox statistic, p-values based on Poisson approximations (Knox, 1964) or a normal approximation (David & Barton, 1966) have been used. The improvements to Mantel and Knox tests for space–time interaction were proposed in several papers (Kulldorff & Hjalmars, 1999; Diggle et al., 1995; Jacquez, 1996; Baker, 1996) by not requiring as strong assumptions on the spatial and temporal scales of clustering. But in general, direct sampling from the permutation distribution had often been thought to be necessary, as enumeration of the n! outcomes is of course infeasible for most datasets. An alternative approach is to use moment-based density approximations, but the skewness and kurtosis are important for tail accuracy. (Siemiatycki 1978) provided the first four moments of S under permutation, for the most commonly encountered situation that C and D are symmetric with zero diagonals. The author described graphical patterns to aid in computing expectations of product terms, for example, in cijcklcmncst, there are 23 distinct patterns of equality/inequality for the eight subscripts. In addition, moments of S were expressed in linear combinations of products of terms of varying order from C and D—the terms for the fourth moment involve nearly 150 non-zero coefficients. Although the bookkeeping is tedious, these operations reduce the complexity from a naive O(n8) to O(n3). With this reduction, density approximations become feasible for computing p-values, with reasonable accuracy even for stringent testing thresholds.
The space–time clustering statistic can easily be seen to resemble a quadratic form yTAy, where y is an n × 1 vector with elements yi, and A is a symmetric n × n matrix with elements aij. This can be seen by rewriting 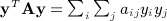 , which is similar to 1, with aij and yiyj serving the roles of cij and dij. However, a key difference lies in the diagonals, that is, that aii and
, which is similar to 1, with aij and yiyj serving the roles of cij and dij. However, a key difference lies in the diagonals, that is, that aii and 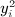 are not generally zero. Quadratic forms have been used for location–time clustering (Tango, 1984), but we are not aware that a direct equivalence has been described between the Mantel statistic and a quadratic form over permutations, and for the latter, to our knowledge, only the first two exact moments have been reported (Commenges, 2003). Quadratic forms arise in a number of disciplines, including epidemiology, genomic, economics, and other areas. The computation of exact moments enables robust analysis, while avoiding the additional computational cost of direct permutation.
are not generally zero. Quadratic forms have been used for location–time clustering (Tango, 1984), but we are not aware that a direct equivalence has been described between the Mantel statistic and a quadratic form over permutations, and for the latter, to our knowledge, only the first two exact moments have been reported (Commenges, 2003). Quadratic forms arise in a number of disciplines, including epidemiology, genomic, economics, and other areas. The computation of exact moments enables robust analysis, while avoiding the additional computational cost of direct permutation.
Despite the popularity of the Knox–Mantel and related location–time clustering statistics, software has not been available to compute the four moments or subsequently obtain approximation p-values, despite a number of packages devoted to location–time surveillance (Robertson & Nelson, 2010). Similarly, quadratic forms are increasingly used, for example, in genomics problems (Tong et al. 2010). However, standard results for normal quadratic forms may not apply, such as for binary disease traits. The application of quadratic forms to non-normal data is often justified by appealing to asymptotics (Wu et al. 2011), but the use of exact methods may be preferred.
We have developed R code to compute the first four exact moments for the location–time statistic and for centered quadratic forms and to compute approximations to the exact permutation p-values using Pearson density approximations. We believe that the software and methods are useful additions to the statistician's toolkit.
2. Methods
2.1. The location–time statistic S
For symmetric C and D (with zero diagonals), we have implemented the Siemiatycki moment computation. The permutation approach involves simultaneous permutation of rows and columns of one of the matrices (say D), which is equivalent to permutation of the location versus time observations (Mantel, 1967). We use π = 1, …, n! as a subscript to represent a permutation of the n objects, with reordered indexes π[1], …, π[n]. A random permutation is denoted as Π, and our task is to compute the first four moments of 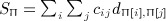 . The key computations are shown in the Appendix, expressed in matrix form to exploit linear algebra routines in R. Approximate p-values are obtained by matching the exact moments to the Pearson family of distributions using the PearsonDS package, which automatically chooses the best-fitting type within the Pearson family.
. The key computations are shown in the Appendix, expressed in matrix form to exploit linear algebra routines in R. Approximate p-values are obtained by matching the exact moments to the Pearson family of distributions using the PearsonDS package, which automatically chooses the best-fitting type within the Pearson family.
2.2. Equivalence of the quadratic form statistic S
Here, the statistic is S = yTAy, for symmetric A with corresponding permutation random variable 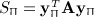 . In many useful applications, A is centered, that is, the rows and columns sum to a constant μ. Here, we will assume μ = 0, essentially without loss of generality, as non-zero μ values will offset SΠ by a constant μyTy. Standard normal-theory results typically assume that A is positive definite, and the assumption is necessary for standard χ2 distributional approximations. However, relaxing this assumption would considerably increase the variety of problems for which accurate p-values can be obtained. For example, in a genomic context, (Zhou & Wright 2013) provided motivation for useful quadratic forms with eigenvalues summing to zero. (Kuonen 1999) summarized a number of previous studies of quadratic form approximations, including those that are not positive definite, and described saddlepoint approximations applicable to normally distributed y only.
. In many useful applications, A is centered, that is, the rows and columns sum to a constant μ. Here, we will assume μ = 0, essentially without loss of generality, as non-zero μ values will offset SΠ by a constant μyTy. Standard normal-theory results typically assume that A is positive definite, and the assumption is necessary for standard χ2 distributional approximations. However, relaxing this assumption would considerably increase the variety of problems for which accurate p-values can be obtained. For example, in a genomic context, (Zhou & Wright 2013) provided motivation for useful quadratic forms with eigenvalues summing to zero. (Kuonen 1999) summarized a number of previous studies of quadratic form approximations, including those that are not positive definite, and described saddlepoint approximations applicable to normally distributed y only.
The moments computed by Siemiatycki were considerably simplified by assuming zero diagonals for C and D. Here, we describe a simple construction to map the quadratic form to the Mantel statistic. First, we define C = A − diag(A), that is, cij = aij for i ≠ j and zero otherwise. Then we define D as the matrix with entries 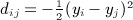 , and by this definition, each dii = 0. Our claim is that, for any π,
, and by this definition, each dii = 0. Our claim is that, for any π, 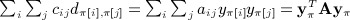 .
.
Proof
By the constraint, 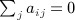 , and therefore for any fixed π, we have
, and therefore for any fixed π, we have 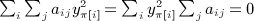 , and by the same reasoning,
, and by the same reasoning, 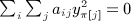 . We have
. We have
because each dπ[i],π[i] = 0. Expanding the right-hand side gives
for which the last two entries are zero. Thus, 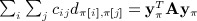 .
.
As with the location–time statistic, we use Pearson family approximations to compute p-values. Because of the row/column constraint, several moment terms can be further simplified to lower order O(n2) (Appendix), which may be useful in applications for very large n.
2.3. Permutation versus normal quadratic forms
Our motivation here is to perform approximations to exact inference, and our procedures only need the exchangeability assumption on the observed y, applying equally well to discrete or continuous data. For normal quadratic forms, where the elements of y are drawn randomly iid from a normal density, the null distribution may be computed as a weighted sum of independent 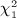 random variables, using the methods of (Imhof 1961) or the saddlepoint approximation of (Kuonen 1999), for example, as implemented in the survey package in R. A common technique used in genomics and other disciplines is to perform robust analysis by transforming data to be discrete-normal using rank-based inverse normal transformations. For example, if r(yi) is the rank of the ith observation, the transformed value is
random variables, using the methods of (Imhof 1961) or the saddlepoint approximation of (Kuonen 1999), for example, as implemented in the survey package in R. A common technique used in genomics and other disciplines is to perform robust analysis by transforming data to be discrete-normal using rank-based inverse normal transformations. For example, if r(yi) is the rank of the ith observation, the transformed value is 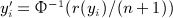 . The use of normal scores in genetics was discussed and extensively critiqued by Beasley et al. (2009). An underlying theme in the application of normal scores appears to be a presumption that permutation of the scores is nearly equivalent to unconditional normal random sampling. For individual association tests, this assumption may be reasonable. For example, the permutation variance of the Pearson correlation coefficient between fixed vectors x and y is 1/(n − 1), which is identical to the variance if y is randomly drawn as iid normal. However, permutation of y inherently creates negative correlation among the sampled elements. This dependence, which is slight for individual elements of y and decreases with n, remains highly consequential for S, because there are n2 correlation terms among the elements. This effect of with-replacement sampling is especially strong if the eigenvalues of A do not contain a few dominant values (Zhou & Wright, 2013).
. The use of normal scores in genetics was discussed and extensively critiqued by Beasley et al. (2009). An underlying theme in the application of normal scores appears to be a presumption that permutation of the scores is nearly equivalent to unconditional normal random sampling. For individual association tests, this assumption may be reasonable. For example, the permutation variance of the Pearson correlation coefficient between fixed vectors x and y is 1/(n − 1), which is identical to the variance if y is randomly drawn as iid normal. However, permutation of y inherently creates negative correlation among the sampled elements. This dependence, which is slight for individual elements of y and decreases with n, remains highly consequential for S, because there are n2 correlation terms among the elements. This effect of with-replacement sampling is especially strong if the eigenvalues of A do not contain a few dominant values (Zhou & Wright, 2013).
The permutation dependency phenomenon is illustrated in four panels in Supplementary Figure 1. For each panel, a single initial m × n matrix X was generated with elements drawn iid N(0,1) and row-centered, where m = {10,1000}and n = {50,500}. Then we let A = XTX and compare the distribution of the unconditional normal quadratic form with that of permutation of normal scores. The figure illustrates that the variability under permutation is markedly less than for unconditional sampling, except when n > > m. Thus, even if an investigator transforms y to normal scores, the normal quadratic form null distribution cannot be used for permutation testing, and the methods described here remain relevant.
Figure 1.
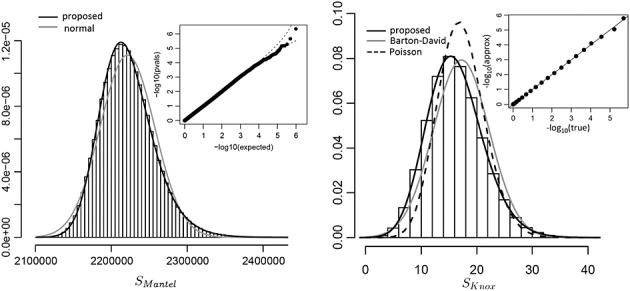
Performance of the proposed approach for space–time clustering analysis of the cattle data. The left panel shows a histogram of SMantel and a q–q plot of observed approximating p-values versus expected for 106 permutations.The right panel shows the analogous results for SKnox for 106 permutations, along with density fits based on the Barton–David and Poisson approximations, as well as our proposed density fit. The inset shows the true permutation p-values for all possible outcomes, compared to that of the approximation.
2.4. Example datasets
We illustrate our methods for four published examples, and for each of the first three examples, we use two different S statistics. The statistics are the same as proposed by the original authors or are otherwise well motivated within the context of the problem. For each example and choice of statistic, the analyst need only find C and D, or y and A, as appropriate to the problem. We note that these examples are useful not only for the observed statistics and p-values but also for the adequacy of the fit for the entire permutation distribution, and thus, the examples effectively illustrate the performance of our approximation in a variety of settings.
Example 1
In White et al. (1989), space–time clustering was used to investigate the evidence of transmissibility of dysentery in cattle for 37 outbreaks in farms in rural New York. Both the Mantel and Knox statistics were used, which we will denote SMantel and SKnox. Following the authors’ implementation of the Mantel statistic, for f, we calculated the straight-line distance in kilometres between locations, and for g, we used the unsigned difference in days between outbreaks. The resulting matrices C and D were then used to calculate SMantel.
The Knox statistic is the number of outbreak pairs that are close in space and time. Thresholds for defining closeness are required, and we used the thresholds of 5.5 km and 30 days chosen in White et al. (1989). In other words, cij = 1 for f(li,lj) < 5.5 km, and 0 otherwise. Similarly, for the Knox statistic, dij is an indicator for g(ti,tj) less than 30 days, and cii = dii = 0. The resulting matrices C and D were then used to calculate SKnox (which is twice the statistic proposed by (Kulldorff and Hjalmars 1999)). Although our moment calculations are exact, for an observed statistic s, density approximations to p-values tend to be closer to the mid p-value 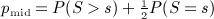 than to the p-value P(S ≥ s). For most of the examples in this paper, the difference between the two is trivial and need not be considered. However, for this example, SKnox statistic can assume only the 25 even values 0, 2, …, 48, and so we apply a continuity correction, by using the Pearson density approximation for s − 1 instead of s.
than to the p-value P(S ≥ s). For most of the examples in this paper, the difference between the two is trivial and need not be considered. However, for this example, SKnox statistic can assume only the 25 even values 0, 2, …, 48, and so we apply a continuity correction, by using the Pearson density approximation for s − 1 instead of s.
Example 2
For pathway analysis of genetic expression data, the data are typically divided into Xpath, which represents the mpath × n matrix of expression of mpath genes belonging to a pathway, and Xcomp is the remaining mcomp × n complementary matrix of genes not in the pathway. We assume that both matrices are row centered and scaled. Expressions of genes are then compared to a clinical or experimental outcome y, either by examining the association of y to only genes within the pathway (known as self-contained testing) or by contrasting the association with genes in the pathway versus that in the complement (competitive testing). (Zhou & Wright 2013) proposed corresponding quadratic form statistics 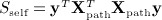 , and
, and 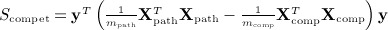 , for which they obtained p-values using a weighted beta density approximation. However, for that approximation, only the first two moments are exact. Scompet has eigenvalues summing to zero, and for some, datasets can have a negative skew, making χ2 density approximations ineffective. We use the breast cancer data of Miller et al. (2005), for which the pathway GO:0000184: “nuclear-transcribed mRNA catabolic process” (44 genes, n = 236 samples) was used in (Zhou & Wright 2013) for an example in tests of association with survival. Here, y is the vector of martingale residuals for survival time, X is gene expression data, and both have been preresidualized for p53 mutation status.
, for which they obtained p-values using a weighted beta density approximation. However, for that approximation, only the first two moments are exact. Scompet has eigenvalues summing to zero, and for some, datasets can have a negative skew, making χ2 density approximations ineffective. We use the breast cancer data of Miller et al. (2005), for which the pathway GO:0000184: “nuclear-transcribed mRNA catabolic process” (44 genes, n = 236 samples) was used in (Zhou & Wright 2013) for an example in tests of association with survival. Here, y is the vector of martingale residuals for survival time, X is gene expression data, and both have been preresidualized for p53 mutation status.
Example 3
Wright et al. (2011) described a genome-wide association analysis for lung function among 1978 cystic fibrosis (CF) patients, identifying the interval between the genes EHF and APIP on chromosome 11 as of interest. For an interval consisting of several genetics markers, we use an approach to perform regional genetic analysis, rather than testing individual markers. The approach compares similarities in the lung function phenotype between all pairs of individuals with a correlation-based measure in regional genotypes. The result (which we call Sassoc1) is similar in spirit to a Mantel statistic, except that the individual elements represent similarity rather than distance. Specifically, we let yj denote the phenotype for the jth individual, and the subsequent description is simplified by assuming y has been centered and scaled so that 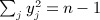 . We use dij = yiyj for i ≠ j and dii = 0, following suggestions that the product yiyj should be powerful in performing tests of phenotypic versus genotypic relatedness (Elston et al. 2000). For m genetic markers in a region, with genotypes measured on the n individuals, we have an m × n genotype matrix G, which has been centered and column scaled. For i ≠ j, we use cij = corr(g.i,g.j), where g.i is the ith column of G, and “corr” is the Pearson correlation.
. We use dij = yiyj for i ≠ j and dii = 0, following suggestions that the product yiyj should be powerful in performing tests of phenotypic versus genotypic relatedness (Elston et al. 2000). For m genetic markers in a region, with genotypes measured on the n individuals, we have an m × n genotype matrix G, which has been centered and column scaled. For i ≠ j, we use cij = corr(g.i,g.j), where g.i is the ith column of G, and “corr” is the Pearson correlation.
A closely related quadratic form statistic (Sassoc2) is the sum of squared score statistics across the markers, which is similar to Sassoc1 but with slightly different genotype scaling, and with non-zero diagonals for the corresponding matrices. We use X to denote the matrix of genotypes, which have been row centered and scaled so that 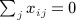 and
and 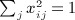 . A single score statistic for the ith marker is
. A single score statistic for the ith marker is 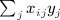 , and
, and 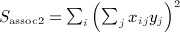 , which can be shown to be Sassoc2 = yTAy, where A = XTX.
, which can be shown to be Sassoc2 = yTAy, where A = XTX.
Example 4
(Bowman & Azzalini 1997, pp. 86–90) described a dataset resulting from sampling aquatic life in a coral reef, with 42 observations of catch score, summarized as a log weight across numerous species, versus depth. The dataset has been used by these authors and others to demonstrate local linear regression, using a normal smoothing kernel. A standard test statistic for local linear regression can be expressed as a quadratic form, as follows. The derivation applies to the Nadaraya–Watson estimator (Nadaraya, 1964; Watson, 1964)
with kernel function wh, for the regression model E(Y
i | xi) = m(xi). The fitted values 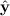 can obtained using a smoothing matrix M (which depends on h) such that
can obtained using a smoothing matrix M (which depends on h) such that 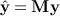 . As shown in (Bowman & Azzalini 1997), an F-like statistic can be obtained using the ratio
. As shown in (Bowman & Azzalini 1997), an F-like statistic can be obtained using the ratio
with U = I − 1n × n/n − (I − M)T(I − M) and V = (I − M)T(I − M). The p-value is P(F > Fobs), which can be rewritten as P(yT(U − FobsV)y > 0, and so we use, finally, A = (U − FobsV) in the quadratic form. It is easy to show that A is symmetric with row/column sums of zero.
(Bowman & Azzalini 1997) obtained p-values using moments from a normal quadratic form and a scaled chi-square density approximation, while acknowledging that the data included some non-normal features, such as truncation. They describe permutation analysis as an alternative approach, which they did not pursue further. For the same normal quadratic form, (Kuonen 1999) reported p-values using a saddlepoint approximation. Here, we report p-values based for direct permutation and compare to results from our moment-based density approximation.
3. Results
Example 1
Figure 1 (left panel) shows a histogram of the SMantel statistic, overlaid with the normal density approximation. Although the normal approximation is based on exact moments, the presence of skew in the data creates a poor tail fit. In contrast, the approximation from our proposed method, which uses four moments and a Pearson type IV fit, is highly accurate. An observed versus expected q–q plot for p-values from our proposed procedure, applied to 106 permutations, shows that the p-values are nearly uniform. The actual data show only marginal evidence of location–time clustering, with true p = 0.0703, with the density approximation of p = 0.0699. The results are similar for SKnox (right panel). The proposed approximation (type IV) is accurate, while the two competing approximations in common use, based on (David & Barton 1966), and a Poisson approximation are observably less accurate. For the actual data, SKnox has a permutation-based p = 0.0681 and approximating p = 0.0696. Note that the tail probabilities do not degrade in accuracy, as shown by a comparison of true versus approximating p-values for the entire range of possible outcomes (inset of Figure 1, right panel).
Example 2
Figure 2 shows histograms and q–q plots for Sself and Scompet for the Miller breast cancer data for pathway GO:0000184. Here, again the fits (type VI for Sself and type IV for Scompet) are accurate, with a slight conservativeness of the approximating p-values in the extreme right tail for Scompet. For the observed data and Sself, the permutation based p = 0.080 and Pearson distributional approximation p = 0.081. For Scompet, the respective values are p = 0.822 and p = 0.817.
Figure 2.
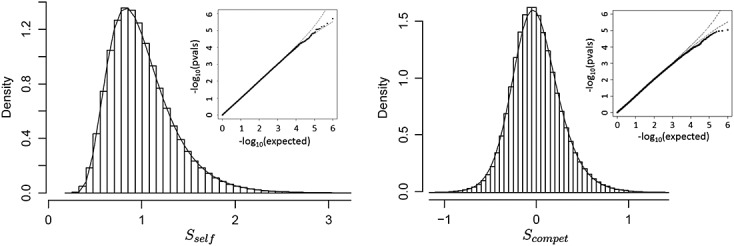
Example 2. Results for Sself (left panel) and Scompet (right panel) for the Miller breast cancer data, pathway GO:0000184 ( n = 236, 44 genes in pathway).
Example 3
Figure 3 shows − log10(p) for Sassoc1 and Sassoc2 for the CF data, where each statistic is plotted for the middle single-nucleotide polymorphism (SNP) in each 21-SNP window. q–q plots, produced for the interval showing the greatest evidence in the original data rs, again support the accuracy of the approximating p-values (type VI for all windows). The most highly significant region is in the interval between EHF and APIP, which is also supported by the single-SNP analysis. However, the evidence is much stronger for Sassoc1 and Sassoc2 than for single-SNP analysis and certainly significant in a genome-wide scan accounting for ∼ 570,000 SNPs. We attribute the greater evidence from these statistics to the potential presence of multiple causal SNPs in the region, as proposed by Wright et al. (2011) in their analyses, because the moving window can capture the combined evidence from multiple SNPs. In fact, the relative genome-wide evidence may be even stronger for the regional methods, as they tend to have higher serial correlation than for individual SNPs and thus incur a smaller multiple-testing penalty. The use of Sassoc1 and Sassoc2 in this context is very similar to using sequence kernel association test (Wu et al. 2011), which is designed for regional analysis and rare-variant testing of genetic association. However, these methods were formally designed for normal or binary phenotypes, and our use of exact moments adds considerable flexibility in handling the actual phenotype distribution.
Figure 3.
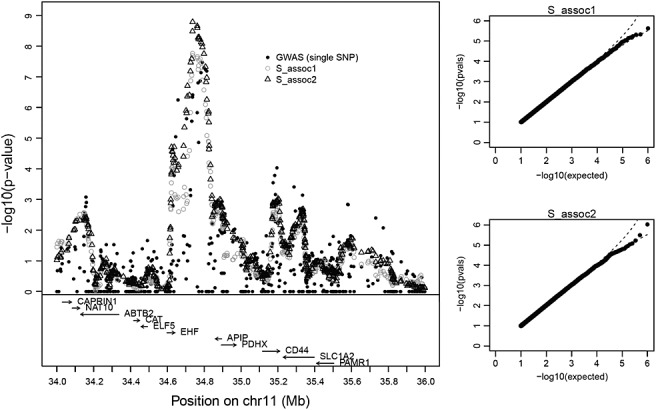
The left panel shows − log10 p-values for Sassoc1 and Sassoc2 for the CF dataset. Each p-value is computed for a moving window of ± 10 SNPs around the center SNP. The two q–q plots for a fixed interval show that the proposed approximating p-values are approximately uniform under 106 permutations.
Example 4
Figure 4 (left panel) plots the coral reef data, along with the smoothed local linear regression fit and confidence band from the R sm package, for a kernel smoothing bandwidth of h=5, produced by the sm package in R. The fitted values at the extremes are clearly outside the reference band for the no-effect model. A “significance trace” (middle panel) shows p-values as a function of h, and for which the permutation-based p-values (dots) and type IV approximation (line) are nearly indistinguishable. The permutation-based p-values are generally lower than those obtained from the normal quadratic form, which were obtained for these data in (Kuonen 1999). For example, for h=5, the permutation-based p = 0.058 but is 0.063 for the normal quadratic form.
Figure 4.
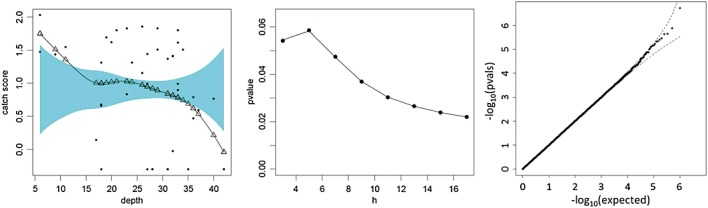
The application of the quadratic form approximation to the test statistics for local linear regression. Left panel: fitted curve and no-effected reference band. The triangles denote the fitted values for observed depth, obtained from the smoothing matrix as My. Middle panel: significance trace showing permutation p-values (dots) and the proposed approximation (line) as a function of h. Right panel: q–q plot for approximating p-values under permutation for h = 5.
4 Discussion
For standard space–time clustering statistics, our contribution has been to provide software for the moments and approximate p-values. Quadratic forms are used in a wide variety of settings, and the use of exact permutation moments has been often overlooked as an alternative to direct permutation. One setting where these approaches may be useful is SNP association pathway analysis, where the effect of sets of SNPs is aggregated and where direct permutation has been considered cumbersome, leading to alternative resampling proposals (Schaid et al. 2012). The use of our Scompet statistic, applied to genome-wide SNP association data, would enable true competitive testing for association pathway analysis. Such competitive testing had been viewed as infeasible, as a naive approach involves performing a full genome scan for each permutation.
Another point of consideration is whether direct sampling from the permutation distribution might be still preferable, as it provides an unbiased estimate of the permutation p-value. In high-throughput settings, however, extreme thresholds may be required to declare significance, and here, our approximation may be especially useful. In (Zhou & Wright 2013), even the use of adaptive permutation (performing only as many permutations as necessary for high relative accuracy) was ∼ 250 times slower than the use of a moment-based analytic approximation. For the genome-scan setting of Example 3, p-values on the order of 10− 8 are necessary in order to declare significance. Moreover, the EHF/APIP region for the CF example was initially identified using screening of individual SNPs, and so the investigator might compute the quadratic form p-value only in regions identified as of potential interest, avoiding the computational burden of genome-wide scans using the quadratic form statistic.
Acknowledgments
Supported in part by R01MH101819, P42ES005948, NSFC 71171105, and R01HL068890. We gratefully acknowledge the CF patients, the Cystic Fibrosis Foundation, the UNC Genetic Modifier Study, and the Canadian Consortium for Cystic Fibrosis Genetic Studies, funded in part by Cystic Fibrosis Canada and by Genome Canada through the Ontario Genomics Institute per research agreement 2004-OGI-3-05 (to P. R. D.), with the Ontario Research Fund—Research Excellence Program.
Appendix
We repeat here the notation from (Siemiatycki 1978), modified to accord with our notation. The patterns of equivalence in the subscripts in cijcklcmncst, for example, are represented in 23 graphical patterns in Appendix A of (Siemiatycki 1978). We have r as the order of the moment, q(r) as the number of patterns associated with the rth moment, α(r) as the pattern under consideration, 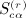 as the sums derived from matrix C,
as the sums derived from matrix C, 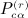 as the total of the products
as the total of the products 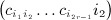 under conditions of pattern α,
under conditions of pattern α, 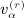 as the number of distinct subscripts in pattern α,
as the number of distinct subscripts in pattern α, 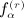 as the number of structurally equivalent forms of the αth pattern for the rth moment, and n as the sample size. All of the terms involving matrix D have analogous counterparts for D. We have q(1) = 1, q(2) = 3, q(3) = 8, q(1) = 23, and α(r); and
as the number of structurally equivalent forms of the αth pattern for the rth moment, and n as the sample size. All of the terms involving matrix D have analogous counterparts for D. We have q(1) = 1, q(2) = 3, q(3) = 8, q(1) = 23, and α(r); and 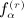 are shown in Appendix A of (Siemiatycki 1978). The terms in
are shown in Appendix A of (Siemiatycki 1978). The terms in 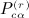 are described subsequently. We have, finally,
are described subsequently. We have, finally, 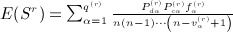 . All of the (central) moments follow from these non-central moments. Appendix B in (Siemiatycki 1978) provides algebraic sums
. All of the (central) moments follow from these non-central moments. Appendix B in (Siemiatycki 1978) provides algebraic sums 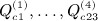 (using S instead of Q in the original reference), which are the building blocks for the
(using S instead of Q in the original reference), which are the building blocks for the 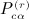 terms. Most of the terms are O(n2) or less, but several of the terms are O(n3). Later, we describe how the terms reduce to O(n2) for the quadratic form when A is centered and A = XTX for m × n matrix X. Here, we consider m to be fixed and n increasing, so O(mn2) = O(n2).
terms. Most of the terms are O(n2) or less, but several of the terms are O(n3). Later, we describe how the terms reduce to O(n2) for the quadratic form when A is centered and A = XTX for m × n matrix X. Here, we consider m to be fixed and n increasing, so O(mn2) = O(n2).
Many of the Siemiatycki Appendix B terms sum over i and j only for the matrices, and so are O(n2). The row sums of A are zero, and C = A − diag(A), so 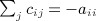 . Thus, the term
. Thus, the term
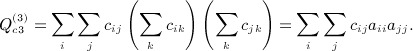 |
Other terms of this type are  ,
,  ,
, 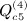 ,
, 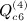 ,
, 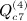 ,
, 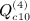 , and
, and 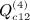 . The term
. The term 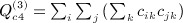 is not as obvious, but the term in parentheses can be reduced. The matrix with elements
is not as obvious, but the term in parentheses can be reduced. The matrix with elements 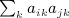 , which is ATA, can be rewritten (XTX)TXTX = XTXXTX. Computing G = XT(XXT) can be performed as O(m2n), and so the final GX is O(mn2). Then expressing the desired result in terms of C instead of A is an O(n) operation. This argument applies to
, which is ATA, can be rewritten (XTX)TXTX = XTXXTX. Computing G = XT(XXT) can be performed as O(m2n), and so the final GX is O(mn2). Then expressing the desired result in terms of C instead of A is an O(n) operation. This argument applies to 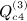 ,
, 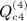 ,
, 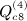 , and
, and 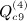 . In some applications, the eigenvalues of C or of CTC may be available from parametric analysis of the data, and for this term, the following result may also be useful.
. In some applications, the eigenvalues of C or of CTC may be available from parametric analysis of the data, and for this term, the following result may also be useful. 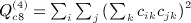 has an additional simplification in terms of eigenvalues of A. Let 1i denote the 1 × n matrix of all zeros except the ith element, which is one. We have
has an additional simplification in terms of eigenvalues of A. Let 1i denote the 1 × n matrix of all zeros except the ith element, which is one. We have
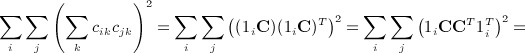 |
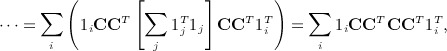 |
noting that 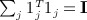 . Obtaining the singular value decomposition of W = CCT = UΛV
. Obtaining the singular value decomposition of W = CCT = UΛV
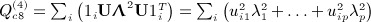 , where p = min(m,n − 1), and noting that
, where p = min(m,n − 1), and noting that 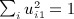 , we have
, we have 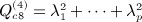 . Obtaining the singular value decomposition is O(mn2).
. Obtaining the singular value decomposition is O(mn2).
Supporting Information
Additional supporting information may be found in the online version of this article at the publisher's web site.
Supporting info item
References
- Baker RD. Testing for space–time clusters of unknown size. Journal of Applied Statistics. 1996;23(5):543–554. [Google Scholar]
- Beasley TM, Erickson S. Allison DB. Rank-based inverse normal transformations are increasingly used, but are they merited? Behavior Genetics. 2009;39(5):580–595. doi: 10.1007/s10519-009-9281-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman AW. Azzalini A. Applied Smoothing Techniques for Data Analysis. London: Oxford University Press; 1997. Oxford statistical science series. [Google Scholar]
- Commenges D. Transformations which preserve exchangeability and application to permutation tests. Journal of Nonparametric Statistics. 2003;15(2):171–185. [Google Scholar]
- David FN. Barton DE. Two space–time interaction tests for epidemicity. British Journal of Preventive and Social Medicine. 1966;20(1):44–48. [Google Scholar]
- Diggle PJ, Chetwynd AG, Haggkvist R. Morris S. Second order analysis of space–time clustering. Statistical Methods in Medical Research. 1995;4:124–136. doi: 10.1177/096228029500400203. [DOI] [PubMed] [Google Scholar]
- Elston RC, Buxbaum S, Jacobs KB. Olson JM. Haseman and Elston revisited. Genetic Epidemiology. 2000;19(1):1–17. doi: 10.1002/1098-2272(200007)19:1<1::AID-GEPI1>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Imhof JP. Computing the distribution of quadratic forms in normal variables. Biometrika. 1961;48(3/4):419–426. [Google Scholar]
- Jacquez GM. A k nearest neighbour test for space–time interaction. Statistics in Medicine. 1996;15(17–18):1935–1949. doi: 10.1002/(sici)1097-0258(19960930)15:18<1935::aid-sim406>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- Knox G. The detection of space–time interactions. Applied Statistics. 1964;13(1):25–29. [Google Scholar]
- Kulldorff M. Hjalmars U. The Knox method and other tests for space–time interaction. Biometrics. 1999;55(2):544–552. doi: 10.1111/j.0006-341x.1999.00544.x. [DOI] [PubMed] [Google Scholar]
- Kuonen D. Saddlepoint approximations for distributions of quadratic forms in normal variables. Biometrika. 1999;86:929–935. [Google Scholar]
- Mantel N. The detection of disease clustering and a generalized regression approach. Cancer Research. 1967;27(2):209–220. [PubMed] [Google Scholar]
- Miller LD, Smeds J, George J, Vega V, Vergara L, Ploner A, Pawitan Y, Hall P, Klaar S, Liu E. Bergh J. An expression signature for p53 status in human breast cancer predicts mutation status, transcriptional effects, and patient survival. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(38):13550–13555. doi: 10.1073/pnas.0506230102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadaraya EA. On estimating regression. Teoriya Veroyatnostei i ee Primeneniya. 1964;9(1):186–190. [Google Scholar]
- Robertson C. Nelson AT. Review of software for space–time disease surveillance. International Journal of Health Geographics. 2010;9(16) doi: 10.1186/1476-072X-9-16. DOI: 10.1186/1476-072X-9-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ, Sinnwell JP, Jenkins GD, McDonnell SK, Ingle JN, Kubo M, Goss PE, Costantino JP, Wickerham DL. Weinshilboum RM. Using the gene ontology to scan multilevel gene sets for associations in genome wide association studies. Genetic Epidemiology. 2012;36(1):3–16. doi: 10.1002/gepi.20632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siemiatycki J. Mantel's space–time clustering statistic: computing higher moments and a comparison of various data transforms. Journal of Statistical Computation and Simulation. 1978;7(1):13–31. [Google Scholar]
- Tango T. The detection of disease clustering in time. Biometrics. 1984;40(1):15–26. [PubMed] [Google Scholar]
- Tong L, Yang J. Cooper RS. Efficient calculation of P-value and power for quadratic form statistics in multilocus association testing. Annals of Human Genetics. 2010;74(3):275–285. doi: 10.1111/j.1469-1809.2010.00574.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson GS. Smooth regression analysis. Sankhya: The Indian Journal of Statistics, Series A. 1964;26(4):359–372. [Google Scholar]
- White ME, Schukken YH. Tanksley B. Space–time clustering of, and risk factors for, farmer-diagnosed winter dysentery in dairy cattle. Canadian Veterinary Journal. 1989;30(12):948–951. [PMC free article] [PubMed] [Google Scholar]
- Wright FA, Strug LJ, Doshi VK, Commander CW, Blackman SM, Sun L, Berthiaume Y, Cutler D, Cojocaru A, Collaco JM, Corey M, Dorfman R, Goddard K, Green D, Kent JW, Lange MM, Lee S, Li W, Luo J, Mayhew G. Naughton KM. Genome-wide association and linkage identify modifier loci of lung disease severity in cystic fibrosis at 11p13 and 20q13.2. Nature Genetics. 2011;43(6):539–546. doi: 10.1038/ng.838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu MC, Lee S, Cai T, Li Y, Boehnke M. Lin X. Rare variant association testing for sequencing data with the sequence kernel association test (SKAT) The American Journal of Human Genetics. 2011;89(1):82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou YH. Wright FA. Empirical pathway analysis, without permutation. Biostatistics. 2013;14(3):573–585. doi: 10.1093/biostatistics/kxt004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting info item


