Prediction of transplant-free survival in idiopathic pulmonary fibrosis patients using joint models for event times and mixed multivariate longitudinal data

SUMMARY

We implement a joint model for mixed multivariate longitudinal measurements, applied to the prediction of time until lung transplant or death in idiopathic pulmonary fibrosis. Specifically, we formulate a unified Bayesian joint model for the mixed longitudinal responses and time-to-event outcomes. For the longitudinal model of continuous and binary responses, we investigate multivariate generalized linear mixed models using shared random effects. Longitudinal and time-to-event data are assumed to be independent conditional on available covariates and shared parameters. A Markov chain Monte Carlo (MCMC) algorithm, implemented in OpenBUGS, is used for parameter estimation. To illustrate practical considerations in choosing a final model, we fit 37 different candidate models using all possible combinations of random effects and employ a Deviance Information Criterion (DIC) to select a best fitting model. We demonstrate the prediction of future event probabilities within a fixed time interval for patients utilizing baseline data, post-baseline longitudinal responses, and the time-to-event outcome. The performance of our joint model is also evaluated in simulation studies.

1. Introduction

While longitudinal data from biomarkers or intermediate clinical assessments are often collected in Phase II and III clinical trials, the primary clinical trial outcome typically consists of time until the occurrence of a specified event, e.g., time to onset of illness or death. An example from the field of chronic lung disease research is the study of transplant-free survival in idiopathic pulmonary fibrosis (IPF). IPF is a chronic, progressive lung disease characterized by fibrosis of unknown etiology [24]. Here, our primary concern is the prediction of failure times by modeling the relationship between longitudinally measured indicators of pulmonary function and time to either lung transplant or death. Specifically, we utilize longitudinally assessed forced vital capacity (FVC), a continuous measure of pulmonary function, as a predictor of event times. We also utilize a second, binary, disease progression indicator defined as a decline of 5% or more in FVC from baseline FVC. Since these measures are potentially conjointly informative of time to lung transplant or death, it would be desirable to implement a modeling approach that allows prediction of event times using two or more longitudinal responses simultaneously.

Several approaches have been developed for handling multivariate longitudinal outcomes [4,20,16,23,29]. For example, some approaches factorize the joint distribution as the product of the marginal distribution of one variable times the conditional distribution of the second variable given the first [3,11]. Other approaches use random effects to model relationships between outcomes [8,13]. To date, however, most researchers have implemented joint models in which a univariate continuous longitudinal response is related to the time-to-event outcome [7,14,15,27]. In this paper, we develop a joint model for mixed continuous and binary longitudinal responses and a time-to-event outcome. For longitudinal responses we investigate mixed models with shared random effects. To build a joint model with a time-to-event outcome, we assume shared parameters exist between the longitudinal mixed models and the time-to-event outcome. The longitudinal responses and the time-to-event outcome are assumed to be independent conditional on the shared parameters and measured covariates.

We apply the proposed joint model to the dynamic prediction of mortality occurring within a fixed time for a subject still at risk just before time t [30]. A number of authors have proposed the prediction of future event probabilities for subjects based on the joint modeling of longitudinal measurements, time-to-event outcomes, and other covariates [9,25]. Fieuws et al. [9] investigated predicting renal graft failure using multiple longitudinal outcomes of biochemical and physiological markers utilizing a multivariate mixed model [22] and a pattern-mixture approach [19]. Rizopoulos [25] provided individualized prediction models of survival in AIDS patients who also had longitudinal CD4 cell count measurements. Our prediction approach is most closely related to that of Rizopoulos [25]. However, as is outlined in Section 2, we use a fully parametric model and a Bayesian approach similar to that of Guo and Carlin [14].

The remainder of the paper is organized as follows. In Section 2, we present our joint model assuming shared random effects for the longitudinal outcomes. In Section 3, we describe parameter estimation approach and model selection methods. In Section 4, we illustrate the dynamic prediction of event probabilities within a fixed time window. Section 5 presents simulation studies using the proposed model, whereas Section 6 applies the joint models to prediction of failure times in idiopathic pulmonary fibrosis data. Section 7 concludes with a brief discussion.

2. Joint modeling approach

2.1 Notation and definitions

For brevity, we focus the development of the model on the case of bivariate longitudinal responses, one continuous and normally distributed and the other binary. The generalization to higher dimensions and other members of the exponential family of distributions is conceptually straightforward (see Discussion). For subject i, i = 1,···, n, let y_1ij and y_2ij denote the j^th outcome at time point t_ij consisting of continuous and binary components, respectively. Further, let ${\mathit{y}}_i={({\mathit{y}}_{1i}^{\top },{\mathit{y}}_{2i}^{\top })}^{\top }$ denote the bivariate longitudinal outcome vector for subject i, where y_hi = (y_hi1,···, y_hij)^⊤, h = 1,2, j = 1,···, n_hi is an n_hi-dimensional column vector giving the h^th longitudinal outcomes for subject i. For the longitudinal bivariate response vector, y_i, with different data types, we assume a generalized linear mixed effects model

$$E({\mathit{y}}_{hi}\mid {\mathit{b}}_{hi})=g_h({\mathbf{X}}_{hi}{\mathit{\beta }}_h+{\mathbf{Z}}_{hi}{\mathit{b}}_{hi}),h=1,2$$ (1)

where g_h(·) denotes known bijective link functions that differ across data types, X_hi and β_h denote an n_hi × p_h design matrix of covariate values and a p_h-dimensional vector of fixed effects, respectively, and Z_hi and b_hi denote n_hi × q₁ design matrix of covariates and a q_h-dimensional vector of normally distributed random effects with zero mean and covariance matrix as described below. We assume that the elements of y_hi are independent conditional on b_hi [10,12].

Here, we choose the identity link for the continuous response and the logit link for the binary response. Thus the generalized linear mixed effects model (1) can be written in the form

$$E({\mathit{y}}_{1i}\mid {\mathbf{b}}_{1i})={\mathit{X}}_{1i}{\mathit{\beta }}_1+{\mathit{Z}}_{1i}{\mathbf{b}}_{1i}$$ (2a)

$$\text{logit}(Pr({\mathit{y}}_{2i}=1)\mid {\mathbf{b}}_{2i})={\mathit{X}}_{2i}{\mathit{\beta }}_2+{\mathit{Z}}_{2i}{\mathbf{b}}_{2i}.$$ (2b)

We assume that b_1i follows a normal distribution with a mean vector of zeros and variance-covariance matrix, Σ, and that b_2i is proportional to b_1i, i.e., b_2i = A₀b_1i, where A₀ is a diagonal matrix of unknown constants. A joint model with this assumption is termed a shared random effects joint model. We briefly outline another alternative, also implemented in our code, in the Discussion section.

2.2 Joint model of multivariate longitudinal outcomes and a time-to-event outcome

Let T_i denote the true event time for subject i, C_i be the censoring time, and δ_i = I(T_i ≤ C_i) be the event indicator. Let $T_i^{\ast }=min(T_i,C_i)$ be the observed event time for subject i. We assume that censoring is non-informative [6]. A proportional hazards model is given by

$${\lambda }_i(t\mid {\mathit{x}}_{3i},U_{3i})={\lambda }_0(t)exp\{{\mathit{x}}_{3i}^{\top }{\mathit{\beta }}_3+U_{3i}\},$$ (3)

where x_3i is a p₃-dimensional vector of covariates with regression coefficients β₃, and λ₀(t) is the baseline hazard function, which can be assumed to be of a parametric form or left unspecified. To express the effects of longitudinal outcomes on the time-to-event outcome, the shared parameters, U_3i, are associated with the random effects of longitudinal outcomes b_1i and b_2i. The joint model connects the longitudinal response submodels (2a,b) and the event time outcome submodel (3)

$$U_{3i}={\mathit{a}}_1^{\top }{\mathit{b}}_{1i}+{\mathit{a}}_2^{\top }{\mathit{b}}_{2i}+b_{3i},$$ (4)

where $\mathit{a}={({\mathit{a}}_1^{\top },{\mathit{a}}_2^{\top })}^{\top }$ is a set of unknown constants and b_3i is a normally distributed frailty term with mean zero and variance ${\sigma }_3^2$, independent of the ${\mathit{b}}_i={({\mathit{b}}_{1i}^{\top },{\mathit{b}}_{2i}^{\top })}^{\top }$. The hazard function of the time-to-event depends on the longitudinal outcomes through the shared b_1i and b_2i. Thus, the parameter a quantifies the degree of association explained by the random effects in (2a,b). In terms of a shared random effects joint model, Eq. (4) can be reduced in the form

$$U_{3i}={\mathit{a}}_1^{\top }{\mathit{b}}_{1i}+b_{3i}.$$

The components of x₁, x₂, and x₃ may or may not all be the same, allowing the longitudinal continuous and binary responses, and the time-to-event outcome to depend on different and/or overlapping covariate information.

3. Estimation and model selection

3.1 Parameter estimation

We assume that the longitudinal responses vectors y_i and the time-to-event outcome T are independent conditional on covariates X, Z, and the random effects vector, b. The observed data for the i^th subject, with n_i repeated measurements, for the h^th response are denoted by

$$\{y_{hi}(t_{ij}),X(t_{ij}),Z(t_{ij}),T_i^{\ast },{\delta }_i;h=1,2,i=1,\cdots ,n,j=1,\cdots ,n_{hi}\}.$$

Based on a full conditional independence assumption, we can express the joint distribution of the observed data for the i^th subject as

$$f({\mathit{y}}_i,T_i^{\ast },{\delta }_i\mid {\mathit{b}}_i;\mathit{\theta })=f({\mathit{y}}_{1i}\mid {\mathit{b}}_{1i};{\mathit{\beta }}_1,{\sigma }_{{\epsilon }_1}^2)f({\mathit{y}}_{2i}\mid {\mathit{b}}_{2i};{\mathit{\beta }}_2)f(T_i^{\ast },{\delta }_i\mid {\mathit{b}}_i;{\mathit{\beta }}_3,\mathit{a},{\sigma }_3^2)$$

where θ denotes the complete parameter vector and f(·) denotes a generic probability density function. Thus, the log-likelihood for the observed data is given by

$$\begin{array}{l}\sum _{i=1}^{n}log{\int }_{{\mathit{b}}_i}\prod _{j=1}^{n_{1i}}\left[\frac{1}{\sqrt{2\pi {\sigma }_{{\epsilon }_1}^2}}exp\left\{-\frac{1}{2{\sigma }_{{\epsilon }_1}^2}{(y_{1ij}-{\mathit{x}}_{1ij}{\mathit{\beta }}_1-{\mathit{z}}_{1ij}{\mathit{b}}_{1i})}^2\right\}\right]\\ \times \prod _{j=1}^{n_{2i}}\left[{\left\{\frac{1}{1+exp(-{\mathit{x}}_{2ij}{\mathit{\beta }}_2-{\mathit{z}}_{2ij}{\mathit{b}}_{2i})}\right\}}^{y_{2ij}}{\left\{\frac{exp(-{\mathit{x}}_{2ij}{\mathit{\beta }}_2-{\mathit{z}}_{2ij}{\mathit{b}}_{2i})}{1+exp(-{\mathit{x}}_{2ij}{\mathit{\beta }}_2-{\mathit{z}}_{2ij}{\mathit{b}}_{2i})}\right\}}^{1-y_{2ij}}\right]\\ \times {[{\lambda }_0(T_i^{\ast })exp\{{\mathit{x}}_{3i}^{\top }{\mathit{\beta }}_3+U_i\}]}^{{\delta }_i}exp\{-{\int }_0^{T_i^{\ast }}{\lambda }_0(s)exp\{{\mathit{x}}_{3i}^{\top }{\mathit{\beta }}_3+U_i\}ds\}\\ \times f({\mathit{b}}_i\mid \mathit{\sum })d{\mathit{b}}_i\end{array}$$

where x_hij and z_hij are j^th row of matrices x_hi and z_hi, respectively, and f(b_i|Σ) is the multivariate normal density function of b_i conditional on the covariance parameter matrix, Σ.

We implement a Bayesian approach for parameter inferences, using a Gibbs sampling algorithm. The algorithm was programmed using the R interface, rbugs, which accesses the software ‘OpenBUGS’ [21]. We implement the Gibbs sampler using weakly informative priors for all parameters. Fixed effects are normal with large variance components. Error variances and random effect covariances are distributed as inverse gamma and inverse Wishart distributions, respectively [2]. Code used in the analyses is available from the first author upon request.

3.2 Model selection criteria

Spiegelhalter et al. [28] proposed the Deviance Information Criterion (DIC) for model selection. The DIC is a generalization of the Akaike Information Criterion (AIC) [1] for hierarchical models based on the deviance of the posterior distribution. For parameter vector θ and observed data vector, y, let D(θ) be the deviance, D(θ) = −2 log f(y|θ) + 2 log h(y), where f(y|θ) is the likelihood function and h(y) is a standardizing function of the data alone [2]. We define D(θ) to be $D(\mathbf{\theta })=-2{\sum }_{i=1}^{n}logf({\mathbf{y}}_i,T_i^{\ast },{\delta }_i;\mathbf{\theta })$ in our joint model, $\overline{D(\mathit{\theta })}=E_{\theta \mid y}[D(\mathbf{\theta })]$ to denote the posterior expected deviance and θ̄ = E_θ|y[θ] to denote the mean of the posterior distribution of the parameters. The effective number of parameters, p_D, which can capture the complexity of a model is $p_D=\overline{D(\mathbf{\theta })}-D(\overline{\mathit{\theta }})$. Then, the DIC is defined as $\mathit{DIC}=D(\overline{\mathit{\theta }})+2p_D=\overline{D(\mathbf{\theta })}+p_D$. Smaller values of the DIC indicate better fitting models. As with the AIC, differences of the DIC between models are a tool used for model selection. Differences of 3 to 5 are considered meaningful. In this paper, we use the DIC for model selection.

4. Dynamic prediction of event probabilities

We compute dynamic probabilities of an event occurring within a fixed window as proposed by van Houwelingen and Putter [30]. Specifically, we considered the conditional survival function of time v ≥ t given survival to time t:

$$S(v\mid t)=P(T>v\mid T\ge t,\mathit{y},\mathit{X},\mathit{Z},\mathit{b};\mathit{\theta },v\ge t)=\frac{S(v\mid \mathit{y},\mathit{X},\mathit{Z},\mathit{b};\mathit{\theta },v\ge t)}{S(t\mid \mathit{y},\mathit{X},\mathit{Z},\mathit{b};\mathit{\theta })}.$$ (5)

Equation (5) can also be expressed using a hazard function as

$$\begin{array}{l}S(v\mid t)=exp[-\{\mathrm{\Lambda }(v\mid \mathit{y},\mathit{X},\mathit{Z},\mathit{b};\mathit{\theta })-\mathrm{\Lambda }(t\mid \mathit{y},\mathit{X},\mathit{Z},\mathit{b};\mathit{\theta })\}]\\ =exp\left(-{\int }_t^v\lambda (s\mid \mathit{y},\mathit{X},\mathit{Z},\mathit{b};\mathit{\theta })ds\right)\end{array}$$ (6)

where Λ(·) denotes the cumulative hazard function and λ(·) denotes the instantaneous hazard function. Equation (6) implies that only the hazard on the interval [t, v] is necessary to predict the probability of event up to time v for a subject at risk just before time t. Let v = t + w be a fixed window of width w. We can relate the survival function to the cumulative distribution function as follows:

$$F_w(t)=1-S(t+w\mid t).$$

F_w(t) is evaluated at all-time points t where the estimates change value. The variance of this function is based on the Nelson-Aalen estimate of that cumulative hazard that is given as

$${se}^2[ln\{{\widehat{F}}_w(t)\}]=\sum _{\begin{array}{c}t\le t_i\le t+w\\ t_i\in \mathfrak{D}\end{array}}\frac{1}{R{(t_i)}^2}$$

where 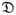denotes the set of event times and R(t) denotes the size of the risk set, i.e., the number of subjects with no event and still being followed just before time t.

5. Simulation Studies

We conducted simulation studies to investigate the performance of the proposed joint models with the longitudinal continuous and binary outcomes and the time-to-event outcome. The simulated longitudinal data consisted of a quantitative outcome and a dichotomous outcome with seven repeated measurements at fixed times 0, 0.5, 1, 1.5, 2, 2.5, and 3 years. We considered three sample sizes, N=100, N = 200 and N = 500 subjects. Both longitudinal outcomes depended on the same fixed covariates: a continuous variable (x₁) sampled from the normal distribution, x₁ ~ N(0, 5²), a dichotomous variable (x₂) sampled from the Bernoulli distribution with probability 0.5, x₂ ~ Bernoulli(0.5), and time (t), t = {0, 0.5, 1, 1.5, 2, 2.5, 3}, were included as fixed covariates. Subject-specific random intercepts and slopes were assumed. For the longitudinal continuous outcome, the measurement error term was normally distributed with mean zero and variance, ${\sigma }_{{\epsilon }_1}^2=1$. The continuous longitudinal outcome was generated from the model

$$y_1(t)={\beta }_{11}+{\beta }_{12}{x}_1+{\beta }_{13}{x}_2+{\beta }_{14}t+b_{10}+b_{11}t+{\epsilon }_1(t)$$

The binary longitudinal outcome was generated from the model

$$\text{logit}(Pr(y_2(t)=1))={\beta }_{21}+{\beta }_{22}{x}_1+{\beta }_{23}{x}_2+{\beta }_{24}t+{\alpha }_1{b}_{10}+{\alpha }_2{b}_{11}t$$

and the random effects were assumed to have distribution

$$\left(\begin{array}{c}{b}_{10}\\ b_{11}\end{array}\right)~\mathrm{N}\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left[\begin{array}{cc}{\sigma }_{b_{10}}^2& {\rho }_{12}{\sigma }_{b_{10}}{\sigma }_{b_{11}}\\ & {\sigma }_{b_{11}}^2\end{array}\right]\right).$$

The time-to-event outcome was generated from an exponential distribution, T ~ exp(μ₃), where μ₃ = exp(β₃₁ + β₃₂x₂ + α₃b₁₀ + α₄b₁₁ + b₃) and $b_3~N\left(0,{\sigma }_{b_3}^2\right)$ with ${\sigma }_{b_3}^2=0.25$. A non-informative censoring time C was generated from a uniform distribution on [0.2, 2] which resulted in roughly 35% censoring on average. For each simulation study, 200 replications were performed. In each analysis, a total of 15,000 MCMC iterations were used, discarding the first 5,000 iterations as a burn-in.

Table 1 shows the results of the simulation studies, including true parameter values, bias (defined as the true parameter minus the mean estimated parameter), standard errors of the parameter estimates (SE), mean squared error (MSE), and the coverage probability of the estimated 95% credibility intervals (CP). With a few exceptions, most parameters in the joint models show acceptably low levels of bias and good coverage probabilities. For N=100, the biases of variance and covariance of random effects are relatively higher than for larger sample sizes, and it might create very low coverage probabilities. For N=200, CP averages close to 95% for all parameters. Most parameters have very small biases, with the exception of somewhat higher biases in the α parameters. However, biases in α are fairly small as a proportion of the size of the parameter, and decrease with larger sample sizes suggesting that a bias of the links between the longitudinal and time-to-event processes are strongly related to the number of events in the survival outcome. In general, as expected, larger sample sizes (N=500) show better results as indicated by the smaller bias, SE, MSE, and less variable CP that average very close to the nominal 95% level.

Table 1.

Simulation results

Parameter	True	N = 100				N = 200				N = 500
		Bias	SE	MSE	CP	Bias	SE	MSE	CP	Bias	SE	MSE	CP
β11	5.0	−0.002	0.104	0.024	0.930	−0.015	0.078	0.014	0.915	0.003	0.051	0.005	0.935
β12	0.8	−0.005	0.138	0.047	0.920	0.008	0.107	0.029	0.880	−0.010	0.071	0.010	0.955
β13	−0.2	0.000	0.012	0.000	0.925	0.001	0.009	0.000	0.925	0.000	0.006	0.000	0.950
β14	−0.2	−0.004	0.056	0.007	0.930	−0.005	0.044	0.004	0.910	−0.004	0.028	0.002	0.945
β21	0.3	0.018	0.223	0.109	0.940	−0.009	0.164	0.054	0.945	−0.003	0.103	0.022	0.960
β22	0.3	−0.016	0.266	0.163	0.920	0.013	0.198	0.084	0.930	0.001	0.125	0.029	0.965
β23	−0.2	−0.005	0.028	0.002	0.965	−0.001	0.020	0.001	0.970	−0.001	0.012	0.000	0.940
β24	−0.25	−0.013	0.114	0.028	0.930	−0.015	0.083	0.015	0.920	−0.004	0.052	0.006	0.925
β31	0.2	−0.023	0.345	0.266	0.930	−0.074	0.266	0.156	0.940	−0.021	0.171	0.059	0.950
β32	1.0	0.003	0.419	0.398	0.945	0.031	0.307	0.216	0.915	−0.002	0.194	0.072	0.985
α1	1.6	0.224	0.536	0.632	0.945	0.280	0.331	0.296	0.890	0.147	0.198	0.098	0.870
α2	1.2	0.154	0.244	0.147	0.935	0.040	0.161	0.055	0.935	−0.012	0.100	0.022	0.930
α3	2.0	0.181	0.891	1.308	0.975	0.164	0.585	0.595	0.980	0.052	0.344	0.211	0.995
α4	3.5	0.369	0.647	0.836	0.975	0.153	0.457	0.379	0.985	0.087	0.291	0.158	0.960
${\sigma }_{{\epsilon }_1}^2$	1.0	0.029	0.061	0.008	0.925	0.023	0.043	0.004	0.940	0.008	0.027	0.001	0.975
${\sigma }_{b_3}^2$	0.25	0.005	0.058	0.003	1.000	0.001	0.055	0.003	1.000	−0.011	0.049	0.003	1.000
${\sigma }_{b_{10}}^2$	0.2	−0.073	0.020	0.006	0.010	−0.024	0.026	0.002	0.865	0.019	0.026	0.001	0.955
${\sigma }_{b_{11}}^2$	0.25	−0.081	0.022	0.007	0.080	−0.016	0.025	0.001	0.895	0.013	0.021	0.001	0.950
ρ12	0.5	−0.220	0.088	0.060	0.165	−0.027	0.067	0.007	0.995	0.043	0.052	0.006	0.945

6. Application to mortality in idiopathic pulmonary fibrosis outcomes study

6.1 Data description and Preliminary Analyses

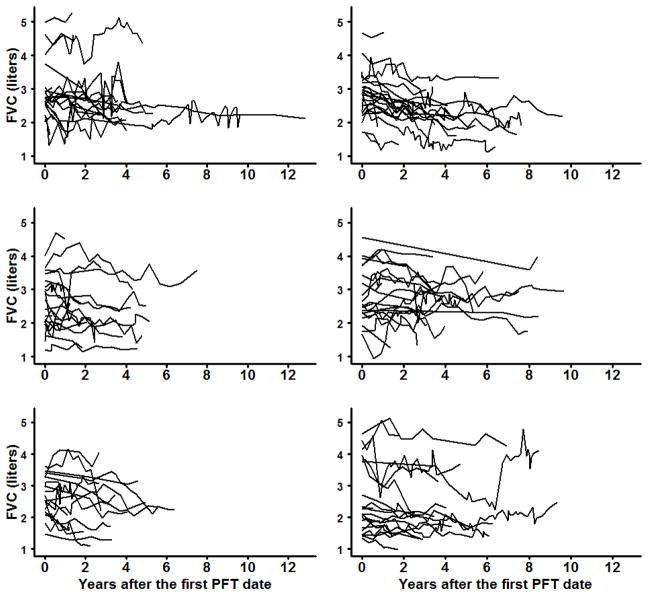
Idiopathic pulmonary fibrosis (IPF) is a chronic, progressive lung disease characterized by fibrosis of unknown etiology [24]. Our primary concern is prediction of failure times, defined as time to either lung transplant or death, utilizing longitudinally measured forced vital capacity (FVC), a continuous measure of pulmonary function. Individual profiles for the pulmonary function assessed by FVC are shown in Figure 1, with subjects randomly apportioned to six subplots in order to more clearly depict these trajectories. An additional disease progression indicator, defined as a decline of 5% or more in FVC from the baseline FVC measurement, is also used as a (binary) longitudinal response. Baseline covariates also considered for inclusion in the models were: age centered at time of diagnosis, baseline FVC, smoking, gender, and time in years.

Figure 1.

Subject-specific trajectories of FVC measurements. (PFT: pulmonary function tests)

Of the 125 patients considered in the study, 64 (51.2%) patients died or had lung transplants. Patient characteristics are summarized in Table 3. This dataset was comprised of irregular follow-up times across patients, but generally patients were followed every 3–4 months according to standard of care. The time origin for each patient was the baseline assessment of pulmonary function, performed upon evaluation at the Simmons Center for Interstitial Lung Disease (ILD). The FVC of each patient was repeatedly measured about 11 times on average, up to 43 times. Follow-up information for the study was reported through December 31, 2011. The average follow-up time was 3.7 years among all patients and 4.1 years among patients who did not die nor received a lung transplant. All IPF patients were evaluated at the University of Pittsburgh Medical Center and clinical data were obtained from the Simmons Center for ILD.

Table 3.

Bayesian Model Selection of shared random effects joint model

Model	U1(t)	U2(t)	U3	DICy1	DICy2	DICT	D̄	pD	DICtotal
	no random effects
1	0	0	0	1795	1715	356.2	3856	11.02	3867
2	0	0	b3	1795	1715	354.3	3842	23.11	3865
	random intercepts
3	b10	0	0	763.8	1715	356.1	2719	115.7	2835
4	b10	0	b3	763.9	1715	354.5	2706	127.9	2833
5	b10	0	α3b10	763.6	1715	357.3	2720	116.3	2836
6	b10	0	α3b10 + b3	763.6	1715	355.2	2706	128.2	2834
7	b10	α1b10	0	719.5	1189	356.2	2143	122.5	2265
8	b10	α1b10	b3	718.8	1189	354.5	2128	134.3	2263
9	b10	α1b10	α3b10	719.4	1189	357.8	2143	122.9	2266
10	b10	α1b10	α3b10 + b3	718.8	1189	355.3	2128	134.7	2263
	random intercepts and random slopes
11	b10 + b11t	0	0	241.8	1715	356.2	2113	200.4	2313
12	b10 + b11t	0	b3	241.9	1715	354.2	2099	212.5	2311
13	b10 + b11t	0	α3b10	241.7	1715	355.2	2111	200.8	2312
14	b10 + b11t	0	α4b11	241.9	1715	350.4	2104	203.1	2307
15	b10 + b11t	0	α3b10 + b3	241.9	1715	353.0	2098	212.2	2310
16	b10 + b11t	0	α4b11 + b3	241.0	1715	351.5	2095	212.1	2307
17	b10 + b11t	0	α3b10 + α4b11	242.3	1715	351.1	2106	202.1	2308
18	b10 + b11t	0	α3(b10 + b11)	238.9	1715	352.7	2106	200.7	2307
19	b10 + b11t	0	α3b10 + α4b11 + b3	238.9	1715	349.7	2092	211.4	2304
20	b10 + b11t	α1b10	0	374.3	1227	355.9	1742	215.1	1957
21	b10 + b11t	α1b10	b3	373.7	1227	354.6	1728	227.3	1955
22	b10 + b11t	α1b10	α3b10	374.4	1226	357.5	1743	215.8	1958
23	b10 + b11t	α1b10	α4b11	372.6	1226	346.6	1727	217.7	1945
24	b10 + b11t	α1b10	α3b10 + b3	375.0	1228	355.1	1729	228.6	1958
25	b10 + b11t	α1b10	α4b11 + b3	372.6	1227	348.0	1719	228.6	1947
26	b10 + b11t	α1b10	α3b10 + α4b11	372.8	1225	347.0	1726	218.9	1945
27	b10 + b11t	α1b10	α3(b10 + b11)	373.8	1227	356.2	1741	216.2	1957
28	b10 + b11t	α1b10	α3b10 + α4b11 + b3	373.6	1226	348.9	1719	229.4	1949
29	b10 + b11t	α1b10 + α2b11t	0	167.2	923.2	356.1	1235	211.6	1447
30	b10 + b11t	α1b10 + α2b11t	b3	167.0	923.2	354.4	1221	223.9	1445
31	b10 + b11t	α1b10 + α2b11t	α3b10	168.6	922.4	356.3	1235	211.9	1447
32	b10 + b11t	α1b10 + α2b11t	α4b11	164.1	923.0	352.9	1229	210.6	1440
33	b10 + b11t	α1b10 + α2b11t	α3b10 + b3	166.0	923.1	353.4	1218	224.0	1442
34	b10 + b11t	α1b10 + α2b11t	α4b11 + b3	167.2	924.0	351.8	1219	224.3	1443
35	b10 + b11t	α1b10 + α2b11t	α3b10 + α4b11	166.2	923.8	352.8	1230	212.7	1443
36	b10 + b11t	α1b10 + α2b11t	α3(b10 + b11)	165.3	922.5	354.8	1232	211.0	1443
37	b10 + b11t	α1b10 + α2b11t	α3b10 + α4b11 + b3	167.6	924.3	351.0	1218	224.5	1443

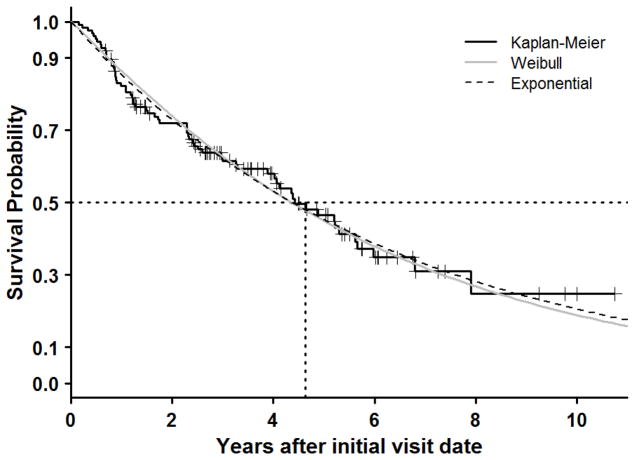
Fitted survival curves of the Weibull model and exponential model are shown in Figure 2. The survival curves of the Weibull model and exponential both show a good fit to the marginal survival function. Because the Weibull and exponential models are almost identical we used the more parsimonious exponential model. The estimated median transplant-free survival time from the initial visit date was 4.4 years.

Figure 2.

The Kaplan-Meier plot of transplant-free survival (black solid curve); Weibull survival curve (grey solid curve) and exponential survival curve (black broken curve).

6.2 Joint model

As before, let y_1ij be the continuous longitudinal outcome indicating FVC measurements, y_2ij be the binary longitudinal outcome indicating disease progression indicator, and T_i be the transplant-free survival time. More specifically, the model is given by

$$\begin{array}{l}{y}_{1ij}={\mu }_{1i}(t_{ij})+U_{1i}(t_{ij})+{\epsilon }_{1ij}\\ ={\beta }_{11}+{\beta }_{12}{\text{BaselineFVC}}_i+{\beta }_{13}{\text{Time}}_{ij}+b_{10i}+b_{11i}{\text{Time}}_{ij}+{\epsilon }_1(t),\\ \left(\begin{array}{c}{b}_{10i}\\ b_{11i}\end{array}\right)~\mathrm{N}\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left[\begin{array}{cc}{\sigma }_{b_{10}}^2& {\rho }_{b_1}{\sigma }_{b_{10}}{\sigma }_{b_{11}}\\ {\rho }_{b_1}{\sigma }_{b_{10}}{\sigma }_{b_{11}}& {\sigma }_{b_{11}}^2\end{array}\right]\right),{\epsilon }_{1ij}~N\left(0,{\sigma }_{{\epsilon }_1}^2\right)\\ \text{logit}\left(Pr(y_{2ij}=1)\right)={\mu }_{2i}(t_{ij})+U_{2i}(t_{ij})\\ ={\beta }_{21}+{\beta }_{22}{\text{Age}}_i+{\beta }_{23}{\text{Time}}_{ij}+{\alpha }_1{b}_{10i}+{\alpha }_2{b}_{11i}{\text{Time}}_{ij},\\ T_i~\text{Exponential}({\mu }_3),\\ log({\mu }_{3i})={\mathbf{x}}_{3i}^T{\mathit{\beta }}_3+U_{3i}={\beta }_{31}+{\beta }_{32}{\text{Gender}}_i+{\beta }_{33}{\text{Smoking}}_i+{\beta }_{34}{\text{BaselineFVC}}_i+{\alpha }_3{b}_{10i}+{\alpha }_4{b}_{11i}+b_{3i}.\end{array}$$

Under the shared random effects joint model, the random effects terms of the three submodels are defined as follows:

• U_1i(t_ij) = b_10i + b_11it_ij

• U_2i(t_ij) = α₁b_10i + α₂b_11it_ij

• U_3i = α₃b_10i + α₄b_11i + b_3i

The association between longitudinal responses and time-to-event outcome is explained by the parameter α = (α₁, α₂, α₃, α₄). For the continuous longitudinal response, we included the covariates of baseline FVC and time in years. For the binary longitudinal response, age and time in years were found to be significant covariates. Gender, smoking, and baseline FVC were significant in the model for transplant-free survival.

Non-informative priors were used for all parameters. For the coefficients of the fixed effects β₁, β₂, and β₃, we assume a multivariate normal distribution with mean zero and variance-covariance matrices 100I₃, 100I₃, and 100I₄, respectively, where I_k indicates an identity matrix with dimension k. We assumed that the association coefficient, α, had a normal distribution with mean zero and variance equal to 100. A total of 15,000 MCMC iterations were used discarding the first 5,000 iterations for the burn-in period.

6.3 Results

We considered all possible combinations of random effects resulting in 37 assessed models. Table 3 summarizes DICs for each submodel, the posterior expected deviance, D̄, the effective number of parameters, p_D, and total DIC scores (DIC_total) for each joint model. Note that DIC_y1, DIC_y2, and DIC_T denote DIC from the longitudinal continuous outcome, the longitudinal binary outcome, and the time-to-event outcome submodels, respectively. These scores show relative contributions of each component to the overall model DIC. DIC_total, was used to choose the “best” model.

Joint models with both subject-specific random intercepts and slopes in both the longitudinal continuous outcome submodel and binary outcome submodel (Models 29–37) have the smallest DICs, and hence the smallest DIC_total compared with other joint models with random effect structures. In the time-to-event submodel, adding a frailty term leads to only a very slight decrease in DIC_T. Model 32 with the smallest DIC_total was selected as our best model. Under Model 32, the longitudinal binary outcome shares the subject-specific random intercept and slope of the longitudinal continuous outcome and the time-to-event outcome is related to the subject-specific random slope of the longitudinal continuous outcome.

In Table 4, the posterior estimates for Model 32 parameters along with their standard errors and 95% credibility intervals are presented. For longitudinal continuous FVC, both the baseline FVC and time are statistically significant. Hence, patients with high values of baseline FVC have high FVC measurements and FVC measurements tend to decrease as time progresses. For the longitudinal binary outcome, there is a significant time effect. For the time-to-event outcome, male smokers with lower baseline FVC have a higher risk of death or transplant. The association parameter, α₄ indicates that there is a nearly significant negative association between the subject-specific random slopes of FVC measurements and the hazard of the transplant-free survival outcome.

Table 4.

Posterior estimates for Model 32

Parameter	Posterior Mean	Std. Error	95% CI
Longitudinal continuous submodel
Intercept (β11)	0.167	0.048	(0.072, 0.263)
BaselineFVC (β12)	0.933	0.014	(0.906, 0.961)
Time (β13)	−0.094	0.016	(−0.122, −0.061)
${\sigma }_{b_{10}}^2$	0.081	0.008	(0.066, 0.098)
${\sigma }_{b_{11}}^2$	0.068	0.007	(0.056, 0.084)
ρb1	−0.068	0.069	(−0.200, 0.067)
${\sigma }_{\epsilon }^2$	0.060	0.002	(0.055, 0.064)
Longitudinal binary submodel
Intercept (β21)	−1.424	0.325	(−2.043, −0.796)
Age (β22)	−0.015	0.014	(−0.044, 0.012)
Time (β23)	1.019	0.180	(0.6513, 1.341)
α1	−10.67	0.835	(−12.38, −9.145)
α2	−10.31	0.727	(−11.82, −8.961)
Time-to-event submodel
Intercept (β31)	−1.967	0.530	(−3.003, −0.939)
Male (β32)	0.903	0.360	(0.214, 1.648)
Smoking (β33)	0.719	0.341	(0.087, 1.422)
BaselineFVC (β34)	−0.405	0.203	(−0.807, −0.013)
α4	−1.613	0.810	(−3.201, −0.025)

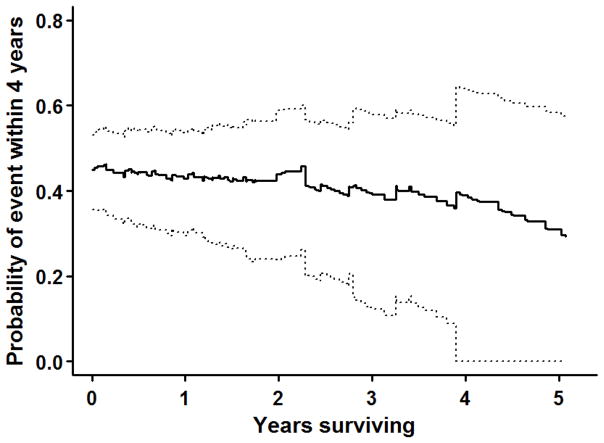
Figure 3 shows the predicted four-year-ahead failure probabilities for the IPF data set along with 95% confidence intervals, obtained from the best-fitting Model 32. In general, the probability of event within the next four years decreases slowly, with a deceleration apparent if the patient survives longer than two years, so that at baseline subjects have ~45% chance of failure in four years, whereas if a patient does not experience failure by year five, the probability of a failure in the next four years decreases to ~35%. As time progresses, confidence intervals become wider because of the sparsity of the data.

Figure 3.

Probability of transplant or death within the next four years using shared random effects joint model 32: Point estimates (solid curve) and 95 % confidence intervals (dotted curves).

7. Discussion

In this paper, we have developed a joint model for multivariate longitudinal continuous and binary responses and a time-to-event outcome, applying this model to the prediction of failure times from idiopathic pulmonary fibrosis. This general approach was introduced in Rizopoulos and Ghosh [26] who used natural splines to model three mixed longitudinal processes (two continuous and one binary) as predictors of a time-to-event outcome. In our case, we used parametric models for the longitudinal processes as the number of longitudinal observations per individual was relatively small and hence parametric random effect models were more tractable. Simulation studies indicate good performance for our models.

Our joint model was developed utilizing a unified Bayesian framework, including model fitting, parameter inferences, computation of dynamic prediction probabilities with posterior credible intervals, and a DIC model selection criterion that parses out the contributions of the joint sub-models to the overall fit. Results from the best fitting model indicate that the two longitudinal responses jointly contribute nearly significantly to prediction of failure times in IPF as indicated by the value of the shared parameter, α₄, and its 95% credibility interval (Table 4). Our approach for choosing prior distributions followed that of Guo and Carlin [14], which is quite general and easier to implement than that used by Rizopoulos and Ghosh [26].

In our present investigation, we utilized shared random effects to characterize the relationship between the longitudinal continuous and binary outcomes. A disadvantage of the shared random effects joint model is that the structure of the random effects for both the longitudinal outcomes is limited. Nevertheless, shared parameter random effects models do gain efficiency by using a smaller number of random effects parameters compared to other joint model formulations.

A practical purpose our investigation was to illustrate the utility of joint models for computing dynamic predictions of the probabilities of events occurring within a fixed window of time. Given a subject is at risk just before time t, the probability of an event occurring within the next fixed window of time is predicted using the survival function obtained from our proposed joint models. By predicting the probability of event within a fixed window of time we can easily visualize conditional probabilities of events. Plots such as these can be an effective means for presenting dynamic risk of failure times to clinician researchers. Finally, we have implemented our shared random effects joint models in an R interface using OpenBugs, available from the first author upon request.

Finally, in related work, we have implemented a correlated random effects joint model [5] which we plan to investigate further. As part of this future investigation, we wish to extend models proposed by Lee and Nelder [17,18] that expand the correlated random effects models by introducing a general method called maximum h-likelihood estimation. In the correlated random effects model, the relationship between the continuous and binary outcomes can be investigated through correlations among the random effects b_1i and b_2i.

Table 2.

Patient characteristics of Idiopathic Pulmonary Fibrosis (IPF) outcome data

	N(=125)	%
Gender
Male	84	67.2
Female	41	32.8
Race
White	122	97.6
Black	1	0.8
American Indian	1	0.8
Oriental	1	0.8
Smoking
Ever	88	70.4
Never	37	29.6
Diagnosis made
Clinically	63	50.4
Historically	62	49.6
Transplant
Yes	23	18.4
No	102	81.6
	Mean	SD
Age (year)
Overall	65.2	9.34
Male	65.7	9.00
Female	64.2	10.04
Follow-up (year)
All patients	3.7	2.32
Alive and not transplanted	4.1	2.35
Baseline PFTs
FVC	2.7	0.85
FEV1	2.2	0.65
DLCO	12.7	4.36

Definition of abbreviations: PFT = pulmonary function tests; FVC = forced vital capacity; FEV1 = forced expiratory volume in 1 second; DLCO = diffusing capacity of carbon monoxide.