Leaf mass per area is independent of vein length per area: avoiding pitfalls when modelling phenotypic integration (reply to ⁾

Highlight text

In a previous paper we clarified the roles of veins in determining leaf function. Here we contribute further data and address the concerns of Blonder et al. (2014), and provide guidance for phenotypic modelling.

Abstract

It has been recently proposed that leaf vein length per area (VLA) is the major determinant of leaf mass per area (LMA), and would thereby determine other traits of the leaf economic spectrum (LES), such as photosynthetic rate per mass (A _mass), nitrogen concentration per mass (N _mass) and leaf lifespan (LL). In a previous paper we argued that this ‘vein origin’ hypothesis was supported only by a mathematical model with predestined outcomes, and that we found no support for the ‘vein origin’ hypothesis in our analyses of compiled data. In contrast to the ‘vein origin’ hypothesis, empirical evidence indicated that VLA and LMA are independent mechanistically, and VLA (among other vein traits) contributes to a higher photosynthetic rate per area (A _area), which scales up to driving a higher A _mass, all independently of LMA, N _mass and LL. In their reply to our paper, Blonder et al. (2014) raised questions about our analysis of their model, but did not address our main point, that the data did not support their hypothesis. In this paper we provide further analysis of an extended data set, which again robustly demonstrates the mechanistic independence of LMA from VLA, and thus does not support the ‘vein origin’ hypothesis. We also address the four specific points raised by Blonder et al. (2014) regarding our analyses. We additionally show how this debate provides critical guidance for improved modelling of LES traits and other networks of phenotypic traits that determine plant performance under contrasting environments.

Introduction

Leaf economic spectrum (LES) relationships are a topic of fundamental interest. Fast-growing, resource-acquisitive species tend to have low leaf dry mass per area (LMA, which is equal to leaf thickness × leaf dry mass density), and high light-saturated rates of photosynthesis per mass (A _mass), high nitrogen concentration per mass (N _mass), and high respiration rate per mass (R _mass), but shorter leaf lifespan (LL) relative to slow-growing, resource-conservative species (Small, 1972; Lambers and Poorter, 1992; Reich et al., 1997; Wright et al., 2004; Wright et al., 2005; Donovan et al., 2011; Heberling and Fridley, 2012; Edwards et al., 2014; Reich, 2014). Blonder et al. (2011, 2013) proposed as the ‘origin’ of the LES that the leaf vein length per leaf area (VLA, also known as ‘vein density’) determines LMA, and thereby drives LES relationships both across diverse species as well as within species (the ‘vein origin’ hypothesis). Sack et al. (2013) argued that the simple mathematical model used by Blonder et al. to support their hypothesis was a circular argument leading to predestined outcomes. In our comprehensive analysis of previously published data for vein and LES traits, we found that VLA and LMA were mechanistically independent and uncorrelated in comparisons across large species sets, and that VLA influenced A _mass independently of LMA, N _mass, and LL.

In a reply, Blonder et al. (2014) questioned some of our findings, i.e. that (1) their model was circular, (2) VLA and interveinal distance were manipulated unrealistically in their modelling, (3) their equations were not sensitive to vein traits, and (4) the published data did not support their assumptions and predicted correlations. In this paper we summarize the lack of support for the ‘vein origin’ hypothesis based on logic and data, and address the concerns raised by Blonder et al. Finally, we show how this debate provides useful guidance for future modelling of phenotypic integration.

LMA is independent of VLA, and vein traits influence the LES independently of LMA

A one-trait-drives-all hypothesis, such as that VLA would determine LES traits and their inter-relationships, would be very appealing due to its simplicity, but attributing all that variation to one trait is an extraordinary proposition. This hypothesis was derived by Blonder et al. (2011) on the expectation that VLA and its negative correlate, interveinal distance (IVD), would determine LMA and leaf thickness (LT). A high VLA was hypothesized to drive a high LMA by contributing to the mass of the leaf, and a high IVD simultaneously to drive a high LT for optimal water flow, and thereby also drive a high LMA. These ideas are not mechanistically realistic because the leaf minor veins which determine VLA account for <5% of leaf volume and mass, and the relationship between IVD and LT is not fixed but highly variable across species (Sack et al., 2013).

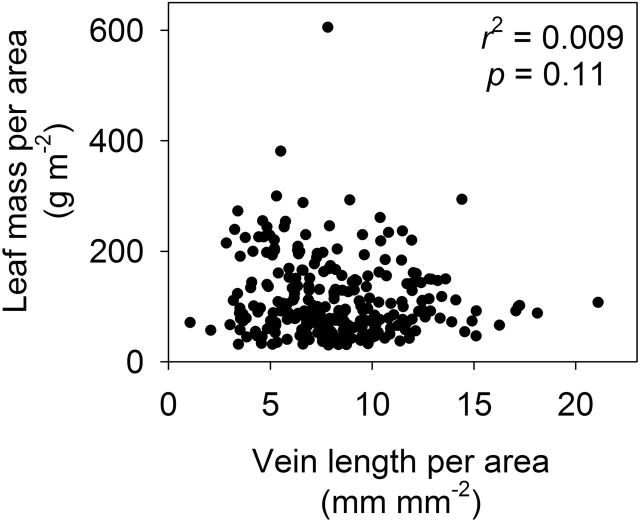
An extraordinary claim, such as the one-trait-drives-all ‘vein origin’ hypothesis, should require extraordinary evidence (Sagan, 1980). Instead, we found no empirical support. The clearest evidence against the ‘vein origin’ hypothesis is that LMA is independent of VLA across dicotyledons in a wide range of data sets, including within lineages of closely related species, and in a compiled database for 196 phylogenetically diverse species (Fig. 3A; Sack et al. 2013). The same is true after adding data that became recently available (total n = 275 species in 68 plant families; Fig. 1). Even within families, the data show that VLA and LMA are mechanistically independent. Among the nine families represented in our database by six or more species, VLA and LMA were correlated weakly within only Sapindaceae (log-transformed data; R ² = 0.16; P < 0.05; n = 34), probably due to both variables being selected for greater values in species adapted to higher irradiance (i.e. a case of ‘concerted covergence’; Sack et al. 2013); for the other families no correlation was found (Campanulaceae, Fabaceae, Fagaceae, Myrtaceae, Plantaginaceae, Proteaceae, Rosaceae, and Violaceae; R ² < 0.001–0.40; P = 0.18–0.97; n = 6–52).

Fig. 1.

The independence of leaf mass per area (LMA) from vein length per leaf area (VLA) across phylogenetically diverse angiosperms. This is a replot of graph 3A of Sack et al. (2013), with additional data for 87 species of dicotyledons, for a total of 275 dicotyledonous species in 68 plant families. Additional data: six Hawaiian lobeliads, 29 Bolivian rainforest trees, and 52 species of Australian Proteaceae (data of Brodribb et al., 2013; Jordan et al., 2013; unpubl. data of L Sack, L Markesteijn, L Poorter, C Scoffoni, TJ Givnish, J Kunkle, R Montgomery, and M Rawls).

A further, direct way to test the ‘vein origin’ hypothesis is by partial correlation analysis. Here one can determine whether the correlations among A _mass, LMA, and N _mass are reduced or lost when VLA is partialed out—i.e. when the relationships are considered at a given VLA—as would be expected if VLA were the determinant of the relationships. However, when we applied that analysis to either the data set of Blonder et al. (2011) for 24 angiosperm species, or to the data set for the 114 angiosperm species in 48 families for which these traits were available in our compiled database of Sack et al. (2013), we found the opposite. In both data sets the inter-relationships among A _mass, LMA, and N _mass remained significant (|r| = 0.49–0.78; P < 0.05) after accounting for VLA and indeed, the partial correlation coefficients did not differ from the raw correlation coefficients (paired t-test; P = 0.75–1.0; analyses applied for each data set with or without log-transformation of the data). These analyses demonstrate that VLA does not drive the LES trait relationships in the way that Blonder et al. proposed. Other leaf traits beyond vein traits play a well-known role in determining LMA and the LES relationships (see final section).

The ‘vein origin’ hypothesis is also not supported by a wider view of the plant kingdom that includes lineages in which leaves do not have minor veins. LES relationships are found in needle-leafed conifers, which only possess a single central vein (Reich et al., 1998; Wright et al., 2004); in ferns, which possess systems of few vein orders, and generally lack angiosperm-like minor veins (Karst and Lechowicz, 2007); in cycads, including species that lack any veins in their lamina other than the central midrib (Y. Zhang, K. Cao & L. Sack, unpubl. data); and even mosses, which lack any veins at all in their ‘leaves’ (Waite and Sack, 2010). Minor veins cannot be driving LES trait relationships in these lineages.

We thus concluded that the ‘vein origin’ hypothesis was not supported by critical evaluation of its assumptions or by the available data. Rather, we are of the opinion that in angiosperms vein traits influence LES traits and plant function in a different way—a higher VLA (among other vein traits) enables a higher photosynthetic rate per area (A _area), which scales up to driving a higher A _mass and relative growth rate, independently of LMA, N _mass, and LL (Sack et al., 2013).

Answering point 1: did the model predictions arise from circularity?

Blonder et al. (2011) argued for their ‘vein origin’ hypothesis based on a simple mathematical model, which we found to be circular, because its outcome was predetermined by inputs of other non-vein traits that drive the leaf economic spectrum traits (Sack et al. 2013). In their reply, Blonder et al. (2014) denied that their model was based on traits other than vein traits. Here, by stripping away the redundancies and revealing its core, we provide a new clarification of how their model predicts LMA and other LES variables from LT—a well-understood relationship, given that LMA = LT × leaf density (Witkowski and Lamont, 1991; Niinemets, 1999; Roderick et al., 1999b ).

Blonder et al. (2011) proposed that the LES traits LMA, N _mass, A _mass, and LL are determined by four equations (eqns 4–7; Blonder et al., 2011; see also Appendix 1) that require inputs of LT, other LES traits, and constant values for many other traits that are highly variable across species in reality. Two vein traits are also inputted, VLA and IVD. However, these vein traits either cancel out if the equations are re-written more simply, or have negligible effect on the predictions because they are multiplied by very small numbers in the equations (see eqns 4a, 6a, and 7a; Appendix 1). For clarity, we have re-drawn Fig. 1 of Blonder et al. (2014), without the constants, and using our symbols, after correction of inaccuracies in their depictions of their Eqns 4–7 (Fig. 2 of this paper).

Fig. 2.

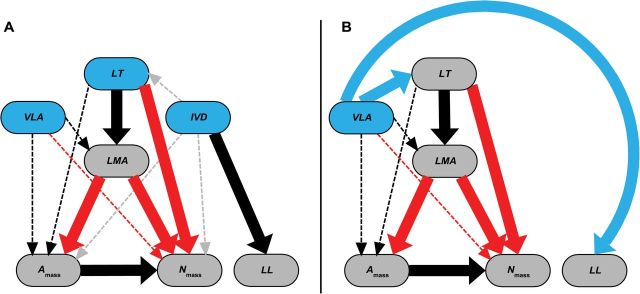
The structure of the ‘vein origin’ model of Blonder et al. (2011), based on eqns 4–7 (see Appendix 1), redrawn to highlight the influences of given variables (leaf mass per area, LMA; photosynthetic rate per mass, A _mass; leaf nitrogen per mass, N _mass; and leaf lifespan, LL; leaf thickness, LT; vein length per area, VLA; interveinal distance, IVD). This schema shows only the measured traits; other variables that were treated as constants are not included. Raw input traits are depicted in blue ovals; output traits are depicted in grey ovals (these are used as inputs for estimating other traits). The two panels show the contrasting implementation of equations for (A) prediction of leaf economics spectrum (LES) traits, and (B) for simulation of LES relationships. Black arrows represent positive influence according to eqns 4–7, red arrows negative influence. The thick arrows indicate the important drivers, and the thin dashed arrows represent negligible effects, according to sensitivity analyses (Table 2) and randomization analyses (Sack et al. 2013); the grey dotted arrows linking IVD to most variables represent drivers apparent in the equations that cancel out when the equations were rewritten as eqns 4a, 5a and 7a. When the model was implemented for prediction (A), LT, VLA, and IVD were inputted, and the estimates of LES traits were driven by measurements of LT, which resulted in weak relationships among the estimated LES variables and weak correlations between estimated and observed values for LES traits, independently of vein trait inputs, which have negligible effects in these equations. When the model was implemented for simulation (B), VLA was used to directly determine LT and LL, not reflecting a real mechanism, indicated by blue arrows. Thus, the input of VLA drove all output traits in the simulation, forcing the predetermined outcome in which VLA appears to drive LES trait relationships.

They implemented these equations in two ways (LES trait prediction and LES relationship simulation; Fig. 2A and 2B in this paper). For LES trait prediction (Fig. 2A in this paper) they applied the four equations to data for 24 species, and found weak correlations between predicted and observed LES trait values (R ² = 0.10–0.35; Fig. S3 in Blonder et al. 2011). Our sensitivity analyses demonstrated that this weak predictive power was caused by the use of LT and LES traits as inputs in eqns 4, 6, and 7, with negligible influence of vein traits per se (see ‘Addressing point 3’, below). Randomizing the VLA had no impact on the predictions of LES traits using these equations (Sack et al., 2013).

The second modelling approach they used was LES relationship simulation (Fig. 3 in both Blonder et al., 2011 and Blonder et al., 2014). Here, realistic data for VLA were inputted into the equations, which apparently drove LES relationships among the output variables LMA, N _mass, A _mass, and LL. However, if they had run simulations using their model just as described above for prediction, they would have found a negligible sensitivity to VLA. For their simulations, they used a different equation (eqn 4b or 4c, Appendix 1) in which VLA was used to directly determine LT, by assuming a constant ratio of IVD to LT (where the ratio of IVD to LT was defined as ‘k _o’ and made equal to 1), and a constant leaf tissue mass density for all species. Then, Blonder et al. used this simulated LT to directly determine LMA and the other LES variables (Fig. 2B in this paper). Thus, they ‘wrote in’ a direct dependency of LT, LMA, and the other LES traits on VLA (eqns 4b and 4c, Appendix 1). The predicted LES relationships fall in the centre of the global data set for LES traits because the constants in the equations were chosen for that purpose. Of course, one might consider this as simply a theoretical exercise to represent scaling up a scenario where VLA truly did drive LT and LMA perfectly, according to those assumptions. However, this does not reflect reality: IVD (or VLA) and LT are only correlated in some species sets and decoupled in others, and weakly correlated across diverse species (Table 3 of Sack et al., 2013), and hence k _o is not optimized at a single value but varies widely across angiosperm species (with values varying more than 10-fold, ranging from 0.85 to 9.9 across 85 angiosperm species; Zwieniecki and Boyce, 2014). Even within families, VLA and LT are not generally tightly optimized; VLA and LT were negatively correlated in only two of the six families in our database represented by six or more species, Proteaceae and Violaceae (log-transformed data; R ² = 0.42–0.59; P <0.05; n = 46 and 8, respectively); the other four families showed no significant relationships (Campanulaceae, Fabaceae, Plantaginaceae, and Sapindaceae; R ² = 0.002–0.26; P = 0.30–0.80; n = 6–31). Blonder et al. (2014) have recognized that the linkage of IVD (or VLA) with LT can be weak, but did not address the implications of this for their model. Additionally, leaf tissue mass density is not constant as they assumed, but highly variable across species (Witkowski and Lamont, 1991; Niinemets, 1999), and for most groups of species is a more important determinant of LMA and the other variables of the LES than leaf thickness (Poorter et al. 2009). Consequently, as shown above, LMA is independent of VLA across diverse species (Fig. 1).

Attempting to demonstrate that VLA drives the LES by generating values for LT and LMA directly as a function of VLA, and then using these values to generate other LES traits, and then showing the resulting variables to be inter-related, without a realistic basis, is arguing in a circle, also known as ‘begging the question’. Such an argument implicitly asserts in one of the premises of an argument what is desired as the outcome, and is not valid evidence in support of a hypothesis (Damer, 2001). Any other variable (e.g. sunlight or herbivory) could be written in this way as a driver for LT and LMA in eqn 4, and by this circularity would have been ‘supported’ as the origin of the LES. Such modelling proves only its predetermined conclusion.

The same issues exist in the extended model of Blonder et al. (2013), which additionally includes flexible, unspecified parameters, and thus cannot be tested against data (Appendix 3 of Sack et al., 2013).

Answering point 2: did the model treat IVD and VLA as correlated or uncorrelated?

It is a well-known fact that IVD and VLA are inversely related by geometry, as first shown by Jane Philpott (1953) and reviewed in Sack et al. (2013). Blonder et al. (2014) agreed with us, but disputed our statement that they had ever considered them to be independent. However, in deriving their equations they had considered IVD and VLA to be independent enough that they could both be positively correlated with LMA and LL (their eqns 4–7; Fig. 1 of Sack et al. 2013 and of Blonder et al. 2014). Further, in their predictive modelling, Blonder et al. (2011) used these variables as independent inputs (eqns 4–7), contrary to what they depicted in their Fig. 1. On the other hand, in their simulation modelling, as discussed in ‘Answering Point 1’, they did indeed consider these traits as perfectly correlated, and translated VLA into IVD and then into LT values (eqns 4b and 4c). Thus, they treated the IVD and VLA as independent or non-independent as a matter of convenience—whichever led to a desired outcome. We advocate that models based on leaf vein traits incorporate the intrinsic correlations for VLA and IVD at each step, rather than treating them as fully independent or perfectly correlated depending on context.

Answering point 3: what do the sensitivity and randomization analyses show?

Blonder et al. (2014) questioned whether our sensitivity analysis was mathematically correct and relevant. In our paper we compared the raw partial derivatives for their eqns 4–7, which tests the numerical impact of shifts in the input variables, at their actual values, units, and scales, on the output variable. That type of sensitivity analysis is well established in mathematical modelling (e.g. Hamby, 1994; Fasso and Perri, 2002). The analysis showed that the LES traits had the dominant influence on the outputs of eqns 4, 5, and 7, with a negligible role for VLA. Blonder et al. (2014) suggested that it would be better to use a ‘relative’ partial derivative sensitivity analysis, which tests the sensitivity of the output variable to a given proportional change in given input variables (Hamby, 1994; Fasso and Perri, 2002). That analysis actually results in the same conclusion: the equations are insensitive to vein traits (Table 1). In the example they presented, they estimated for their Eqn 4a that the sensitivity of LMA to a 10% shift in VLA was a third of its sensitivity to a 10% shift in LT, and they considered these influences to be ‘nearly equivalent’. However, using a more accurate across-species mean LT of 300 µm rather than their 100 µm (Poorter et al. 2009), the sensitivity of LMA to a 10% shift in VLA was a tenth of that for a 10% shift in LT (Table 1). This extremely low sensitivity to VLA in eqn 4a was due to its multiplication by the square of a small number, i.e. the inputted radius of a minor vein (r _v) of 20 µm reported from a previous study of wheat leaves (Altus et al., 1985) and assumed by Blonder et al. to be constant across all species, and independent of VLA. Those assumptions are not valid, as recent work has shown that across dicotyledonous species, leaves with higher VLA tend to have narrower minor veins (Feild and Brodribb, 2013): across 111 species, r _v scaled with VLA ^–0.6. If that scaling relationship is inserted into eqn 4a to increase its accuracy, the left-hand term containing VLA becomes even more negligible (with VLA now raised to a –0.2 power), and the equation becomes altogether insensitive to VLA. In plain terms, the mass and volume of the minor veins is very small, due to their having such narrow diameters—and if the fact that the diameter is indeed negatively related to VLA is taken on board, the contribution of the veins to leaf volume and mass becomes even more negligible. The equations for N _mass and A _mass (eqns 5 and 7) likewise show them to be determined by LT and LMA and negligibly affected by VLA (Table 1). All these analyses prove that their equations have outputs negligibly driven by vein traits, and determine LES traits from LT and other LES traits.

Table 1.

Results of a ‘relative’ partial derivative sensitivity analysis of eqns 4, 5, and 7 of Blonder et al. (2011)

		Sensitivitya to input variable (i.e. shift in output variable due to a 10% shift in input variable)
Output variable	Eqn	VLA	LT	LMA	A mass
LMA (g m–2)	4	0.880	9.00 b
A mass (nmol g–1 s–1)	5	0.249	0.213	–37.5 b
N mass (%)	7	–0.00120	–0.0287 b	–0.0273 b	0.115 b

^a Sensitivity = the partial derivative of the output variable with respect to each input variable (∂y/∂x) × a mean value for the input variable × 10%. This gives the influence on the output variable (in the given units) of a 10% shift in the input variable. ^b Values in bold italics are those which have >10 x the influence on the output variable than VLA. Mean trait values used: VLA, 10mm mm^–2; LT, 300 µm; LMA, 110g m^–2; light-saturated A _mass, 115 nmol g^–1 s^–1; foliar N _mass, 2% (based on the database of Sack et al., 2013). For partial derivative formulae, see Appendix 2 of Sack et al. (2013).

The same result was found in a randomization analysis: eqns 4, 6, and 7 produced the same predicted values for LMA, N _mass, and A _mass from the data set of Blonder et al. even when the VLA values were randomized (Fig. 6 in Sack et al., 2013). In an effort to challenge this demonstration, Blonder et al. (2014) claimed to have repeated our analysis but found a different result (their Fig. 4 and attached R script). That analysis, however, did not use their eqns 4–7 as given, or as used for their original prediction. Rather, they used eqn 4b, in which VLA acts as a direct proxy for LT, and then randomized VLA, thus effectively randomizing LT; this obviously has a major impact on predictions of LMA and other LES traits. As we showed, when simply applying eqns 4, 5, and 7 without such manipulation, and randomizing VLA in a real or realistic data set, one finds negligible influence of VLA on LES trait estimation. We conclude that it is critical to conduct detailed sensitivity analyses and/or appropriately designed randomization analyses to fully understand a model prior to its publication.

Answering point 4: what do the data show?

Our examination of vein trait correlations was based on 14 studies and in considering all traits, included data for over 350 species from 88 families. It is the most systematic and comprehensive database to date and did not support the assumptions or predictions of the ‘vein origin’ hypothesis, as summarized in Table 3 and Figs 1 and 3 of Sack et al. (2013). Rather than confront this fact, Blonder et al. (2014) have instead claimed that all the data supported their hypothesis, and six times misreported our findings and those from other published papers. These statements are listed and corrected in Table 2. We contend that data must be respected as the only means to support or (in this case) to falsify a hypothesis such as the ‘vein origin’ hypothesis.

Table 2.

Misreporting of data by Blonder et al. (2014) to claim support for their ‘vein origin’ hypothesis

Topic	Reporting by Blonder et al. (2014)	Actual finding or statement in Sack et al. (2013) or other literature
Correlation of LMA and VLA	‘Our model proposes that VLA should be correlated with LMA. In the data cited by Sack et al. ... three of three data sets support the LMA– VLA linkage [their Table 3.2]’	Table 3, row 2 reported that only one data set of six tested for LMA vs VLA showed the positive correlation predicted by Blonder et al. (2011). As stated in the text that single data set was for species of Acer adapted across a light gradient, and thus the trend was probably due to co-selection of both traits during adaptation to contrasting irradiances. Fig. 3a of Sack et al. (2012) showed LMA and VLA are independent when data are compiled across many species; see Fig. 1 of this paper for the updated version, now for 276 species in 68 plant families. Table 3, row 2 of Sack et al. (2012) also reported that neither of two data sets showed the positive correlation of LMA vs IVD predicted by Blonder et al. (2011).
Correlation of N mass and VLA	‘Our model proposes that VLA should be correlated with … N mass. and no data are presented for the N mass–VLA linkage except our 2011 results, which support predictions.’	Such a direct relationship was not proposed by Blonder et al. (2011); they hypothesized that N mass was determined by eqn 7, which in fact predicts a negligible, but negative influence of VLA (Table 2 of this paper). The VLA–N mass relationship was not significant across species- means in Blonder et al. (2011) (r = 0.27; P = 0.20). That relationship was also not supported in our compiled database (n = 162 species for this test; r = 0.08; P = 0.32).
Correlation of LL and VLA	‘Our model proposes that VLA should be correlated with LL. In the data cited by Sack et al. … three of three data sets support the LL–VLA linkage [their Table 3.4]’	Blonder et al. (2011) predicted that LL would be correlated with VLA due to their shared positive relationship with LMA. Table 3, row 4 of Sack et al. (2012) showed that in three of three data sets LL tended to be weakly correlated negatively with VLA across species, but in all three of three data sets this trend was not driven by the mechanism they proposed, since it occurs independently of LMA (i.e. the trend exists even when LMA is partialled out). As also described in Table 3, row 4 of Sack et al. (2012), this trend probably arises due to co-selection of both traits during adaptation to contrasting environments. In the one data set tested, the trend disappeared for Helianthus when mean annual precipitation was partialled out.
Correlation of A mass with VLA	‘Our model proposes that VLA should be correlated with A mass … In the data cited by Sack et al. … one of one data set supports the A mass–VLA linkage [their Fig. 8]’	Such a direct relationship was not proposed by Blonder et al., 2011; they hypothesized that A mass was determined by Eqn 6, which was negligibly sensitive to VLA (Table 2 of this paper). The VLA–A mass relationship was not significant across species- means in Blonder et al. (2011) (r = 0.34; P = 0.13). This relationship was shown for the first time to our knowledge in a large compiled data set for 119 species by Sack et al. (2012). Contrary to the vein origin hypothesis, this relationship arose independently of LMA, because VLA drove A area (Fig. 8 of Sack et al., 2012).
Contribution of minor veins to leaf volume	‘the volume contribution of minor veins does play an important role in high-VLA leaves (Feild and Brodribb, 2013)’	Feild and Brodribb (2013) showed that in high VLA leaves, the minor vein diameter was lower and thus the minor vein volume per leaf area (= VLA × π × minor vein radius2) was lower: ‘Many of the most densely veined angiosperm leaves known bound the lower limits of leaf cost, with low leaf mass per area’.
Overall support for their model	‘Sack et al. (2013) examined the theoretical basis and empirical evidence for the Blonder et al. (2011) venation model and found limited support.’ ‘Sack et al. (2013) … feel that empirical support for the proposed correlations is weak.’ ‘At this point, multiple lines of evidence at both the intra- and interspecific scale are consistent with the main predictions of the Blonder et al. models.’	We found no support at all for the ‘vein origin’ hypothesis and clearly stated this in the Abstract and throughout the 2013 paper.

Outlook: the need for mechanistic and fallacy-free models for phenotypic integration

This debate highlights important principles for modelling of traits in integrated phenotypes.

First, a more sophisticated approach than applying correlative models to simple leaf traits in an attempt to elucidate the LES as Blonder et al. (2014) recommend, is to develop an explanatory model based on the underlying traits known to be important. Anatomical and compositional determinants have been described for LMA (e.g. Garnier and Laurent, 1994; Pyankov et al., 1999; Roderick et al., 1999a ; Poorter et al., 2009; John et al., 2013; Villar et al., 2013), for N _mass (e.g. Villar et al., 2006; Funk et al., 2013), and for rates of photosynthesis (e.g. Terashima et al., 2011; Tosens et al., 2012; Tomás et al., 2013) and respiration (Buckley and Adams, 2011; Tcherkez et al., 2012), and leaf lifespan (Onoda et al. 2011). These direct determinants should form the basis for a mechanistic model of the LES. The influence of other plant traits that also influence the LES should be considered, such as branching architecture and growth form, which can influence LL and its relationship with LMA (Funk and Cornwell, 2013; Edwards et al., 2014).

Indeed, we advocate considering the wider set of traits that influence a given function, rather than excluding them or treating them as constants. The ‘flux-traits’ hypothesis we presented for the influence of vein traits on plant function was synthesized from the literature and makes testable predictions for a much larger set of leaf traits, and their influence on whole plant function; parts of this framework have been applied mathematically in several previous studies (e.g. McKown et al., 2010; Osborne and Sack, 2012; Flexas et al., 2013). Blonder et al. (2014) claimed that this framework is ‘overly parameter rich’, but we presented a network of traits known to be involved, and it was not exhaustive. We acknowledge a role for simplified models. However, ignoring information of leaf anatomy and function in favour of a model at odds with what is known, as they did, is unlikely to move forward our understanding of plant function or ecological processes.

Likewise, mechanistic models for the underlying basis and function of traits should be based on the state of the art understanding of processes. Blonder et al. (2011) developed their equations (particularly those for N _mass and A _mass) using incorrect assumptions on the physics and biology of gas exchange and the hydraulics of water transport. For example, they assumed that the leaf hydraulic conductance is negligible rather than strongly limiting to transpiration rate and A _area (Sack and Holbrook, 2006; Brodribb et al., 2007; Brodribb et al., 2010), that N _mass is causally determined by A _mass rather than the other way around (Fig. 2), that minor veins contribute strongly to leaf volume and mass, and many more. They assigned constant values to traits that vary enormously across species, such as vein diameters, mass density of lamina, and stomatal density. Such an approach is risky as it can lead to a ‘house of cards’ situation where the model can lose both mechanistic realism and predictiveness. Our ‘flux-traits’ hypothesis for the influence of vein traits on plant function is explicitly mechanistic, supported, and testable by measurements of anatomy and physiological processes.

It is also important for modelling to be conducted at the right scale. Thus, contrary to what Blonder et al. have argued, emerging understanding of the genetic basis of vein traits in Arabidopsis does not automatically support the ‘vein origin’ hypothesis, which made no predictions for any genetic linkages. Recent studies have indicated correlations across genotypes of vein traits with mesophyll and epidermal cell size, lamina thickness, and other traits, all of which should be associated with LES traits, according to their common genetic and developmental basis (Perez-Perez et al., 2011; Sack and Scoffoni, 2013). At a higher scale, studies of the linkage of venation traits with plant performance, species-distributions, community assembly, and their relationships to climate benefit from data sets of simpler traits such as VLA and LMA for many species (Sack & Scoffoni, 2013). For maximum progress, such studies should be informed by sound knowledge and fallacy-free models for trait-based mechanisms; e.g. the ‘flux-traits’ hypothesis predicts that these traits will have mechanistically independent impacts on whole plant relative growth rate (Sack et al., 2013).

Finally, we advocate that in mathematical modelling the desired output variable is in no way inputted or ‘written in’ to the model. This can be avoided by conducting sensitivity analyses to identify the major drivers of the output variables.

Developing new models with improved realism will lead to increased predictive power, especially if these avoid a single-trait focus, take on board known underlying variables and mechanisms, consider traits at the right scale, avoid circularity, and apply sensitivity analyses. Models of such quality are increasingly essential for understanding phenotypic structure/function trait networks, discoveries of the underlying basis for key physiological rates, and for predicting plant performance and larger scale ecological patterns under contrasting environments.

Funding

This work was supported by National Science Foundation Grant 1147292.

Appendix 1. Equations presented by Blonder et al. (2011) as their ‘vein origin’ hypothesis, and used for predictive and simulation modelling

The equations are presented using symbols as in Table 1 of Sack et al. (2013) with equation numbers as presented in that paper and Blonder et al. (2011).

Prediction of LMA

$$LMA=\pi r_v^{2}VLA\left({\rho }_v-{\rho }_L\right)+\frac{2{\rho }_{L}IVD}{k_o}$$ (4)

where r _v, ρ_v, and ρ_L are respectively the vein bundle radius, the mass density of veins, and the mass density of lamina; k _o is the ratio of interveinal distance to half the leaf thickness: k _o = IVD / (0.5 × LT), where LT is leaf thickness. Eqn 4 can be rewritten as

$$LMA=\pi r_v^{2}VLA\left({\rho }_v-{\rho }_L\right)+(LT\times {\rho }_L)$$ (4a)

This is the equation that Blonder et al. (2011) used to predict LMA values from observed data for VLA and LT. This was not necessarily clear, because they stated that they used measured IVD values and measured k _o values in eqn 4; the IVD thus cancelled out and effectively eqn 4a was used. Sensitivity analyses showed that, of its inputs that are not constants, this equation is driven by LT, rather than VLA, because the constants in the left-hand term render the influence of VLA very small (Table 1).

For their simulation modelling, Blonder et al. modified their approach. They replaced IVD in the right-hand term of eqn 4 with VLA, by estimating IVD as 1/VLA or 2/VLA (their reticulate and non-reticulate network simulations, respectively). This allowed input of VLA into the right-hand term of eqn 4, to which the equation is sensitive. Additionally, they fixed k _o as a constant value of 1, although this is an unrealistic assumption (see main text), and forces VLA to drive LMA in this equation. Thus, according to this formulation,

$$LMA=\pi r_v^{2}VLA\left({\rho }_v-{\rho }_L\right)+\frac{2\times {\rho }_L}{VLA}$$ (4b)

or,

$$LMA=\pi r_v^{2}VLA\left({\rho }_v-{\rho }_L\right)+\frac{4\times {\rho }_L}{VLA}$$ (4c)

Thus, through this manipulation, 1/VLA or 2/VLA was inserted into the right-hand term of eqn 4, such that it acts as a direct proxy for LT in eqn 4a, and thus drives LMA.

Prediction of LL

$$LL=k_{\text{1}}IVD$$ (5)

where k ₁ was set to a constant value chosen to allow predictions of realistic LL values.

Prediction of A_mass

$$A_{\text{mass}}=\frac{c_o\left(1-h\right)WUE}{\pi r_v^{2}VLA\left({\rho }_v-{\rho }_L\right)+\frac{2{\rho }_{L}IVD}{k_o}}\frac{1}{\frac{1}{\frac{\pi D\times VLA}{2log\frac{IVD}{k_o{r}_v}}}+\frac{1}{D\frac{a_s{n}_s}{t_s+\sqrt{a_s/\pi }}}}$$ (6)

where c _o, h, WUE, D, a _s, n _s, and t _s are respectively the saturation vapour concentration of water in air, relative humidity, water use efficiency, the diffusion constant of water in air, stomatal pore area, stomatal density, and stomatal pore thickness.

Eqn 6 can be rewritten as

$$A_{\text{mass}}=\frac{WUE}{LMA}\frac{c_o\left(1-h\right)}{\frac{1}{\frac{\pi D\times VLA}{2log\frac{0.5LT}{r_v}}}+\frac{1}{D\frac{a_s{n}_s}{t_s+\sqrt{a_s/\pi }}}}$$ (6a)

This is the equation that Blonder et al. (2011) used to predict A _mass values from observed data for VLA, LMA, and LT. This was not necessarily clear, because they stated that they used measured IVD values and measured k _o values in eqn 6; the IVD thus cancelled out and effectively eqn 6a was used. Sensitivity analyses showed that, of its inputs that are not constants, this equation is driven by LMA, rather than VLA, because constants in the equation render the influence of VLA very small (Table 1).

For their simulation modelling, Blonder et al. modified their approach. They replaced IVD in eqn 6 with VLA, by estimating IVD as 1/VLA or 2/VLA (their reticulate and non-reticulate network simulations, respectively). This allowed an additional direct input of VLA into equation 6. Additionally, they fixed k _o as a constant value of 1, although this is an unrealistic assumption (see main text). In simulations, A _mass was driven by LMA which in turn was driven by LT, which was defined as a direct proxy of VLA (see above).

Prediction of N_mass

$$N_{\text{mass}}=k_2{A}_{\text{mass}}+\frac{k_3}{k_0}\frac{2\times IVD-k_0\pi r_v^2\times VLA}{LMA}$$ (7)

For r _v, ρ^v, ρ_L, a _s, n _s, and t _s, Blonder et al. used constants based on the literature, though values in fact vary widely among species. The k ₂ and k ₃ were set to constant values chosen to allow predictions of realistic N _mass values.

Eqn 7 can be rewritten as

$$N_{\text{mass}}=k_2{A}_{\text{mass}}+\frac{k_3(LT-\pi r_v^2\times VLA)}{LMA}$$ (7a)

This is the equation that Blonder et al. (2011) used to predict N _mass values from observed data for VLA, LMA, LT, and A _mass. This was not necessarily clear, because they stated that they used measured IVD values and measured k _o values in eqn 7; the IVD thus cancelled out and effectively eqn 7a was used. Sensitivity analyses showed that, of its inputs that are not constants, this equation is driven by A _mass, rather than VLA, because constants in the equation render the influence of the other variables very small (Table 1).

For their simulation modelling, Blonder et al. modified their approach. They replaced IVD in eqn 7 with VLA, by estimating IVD as 1/VLA or 2/VLA (their reticulate and non-reticulate network simulations, respectively). This allowed an additional direct input of VLA into eqn 7. Additionally, they fixed k _o as a constant value of 1, although this is an unrealistic assumption (see main text). In simulations, N _mass was driven by A _mass which in turn was driven by LMA, which was in turn driven by LT, which was defined as a direct proxy of VLA (see above).