Abstract
Population genetic differentiation will be influenced by the demographic history of populations, opportunities for migration among neighboring demes and founder effects associated with repeated extinction and recolonization. In natural populations, these factors are expected to interact with each other and their magnitudes will vary depending on the spatial distribution and age structure of local demes. Although each of these effects has been individually identified as important in structuring genetic variance, their relative magnitude is seldom estimated in nature. We conducted a population genetic analysis in a metapopulation of the angiosperm, Silene latifolia, from which we had more than 20 years of data on the spatial distribution, demographic history, and extinction and colonization of demes. We used hierarchical Bayesian methods to disentangle which features of the populations contributed to among population variation in allele frequencies, including the magnitude and direction of their effects. We show that population age, long-term size and degree of connectivity all combine to affect the distribution of genetic variance; small, recently-founded, isolated populations contributed most to increase F ST in the metapopulation. However, the effects of population size and population age are best understood as being modulated through the effects of connectivity to other extant populations, i.e. F ST diminishes as populations age, but at a rate that depends how isolated the population is. These spatial and temporal correlates of population structure give insight into how migration, founder effect and within-deme genetic drift have combined to enhance and restrict genetic divergence in a natural metapopulation.
Introduction
Sewall Wright [1] introduced the study of geographic population structure and its genetic consequences with the Island Model. In the Island Model, populations are assumed to be stable and interconnected by migration, with population differentiation (F ST) at neutral loci generated by drift and diminished by gene flow among populations. When the simplifying assumptions of the island model are violated, a number of additional factors are necessary to understand population genetic differentiation [2], [3]. In metapopulations, where demes experience extinction and recolonization, there are broad conditions under which the founder effect can be a powerful structuring mechanism [4], and population differentiation can occur despite high levels of gene flow. The importance of founder effects depends on several parameters including migration, extinction and colonization rates, the number of founding propagules, as well as the fraction of demes from which the colonists originate [2], [3].
Empirical evidence that founder effects can drive population differentiation has been gathered from age-structured populations. For example, elevated population structure among newly established demes in metapopulations is consistent with founder effects generating increased population structure, with subsequent gene flow reducing genetic differentiation among populations as they age [5]–[9]. Although these classic studies demonstrate that metapopulation processes (extinction and recolonization) can influence genetic differentiation, it is important to estimate their importance relative to other structuring mechanisms such as local adaptation, which will also contributed to increased population genetic structure [10], [11].
Recent advances in evaluating the causes and consequences of population structure have benefitted from the development of a Bayesian model-based approach known as the F-model [12]–[17]. This approach has an advantage over previous methods in that rather than estimating “global” values of genetic differentiation, it takes into account the biological reality that local populations differ in their effective sizes and migration rates and, therefore, their degree of differentiation from other populations [12]. Foll and Gaggiotti [18] introduced a hierarchical formulation of the F-model that uses population-specific measurements to obtain priors for F ST, then estimates the proportional contribution of population-specific variables generating among population variance in allele frequencies.
We used the hierarchical Bayesian approach of Foll and Gaggiotti [18] to understand variation the causes F ST in a well studied plant metapopulation. Our objective was to estimate how population structure results from equilibrium process such as those in the island model (e.g. drift, migration) versus non-equilibrium factors that operate in metapopulations (e.g. extinction and recolonization with founder effects). To accomplish this, we applied the F-model formulation to a long-term data set of the plant, Silene latifolia, where the size and spatial distribution of demes was known, and could be combined with information about their demographic history and age structure. We used fine-scale sampling, microsatellite genotyping, and the application of an F-model based approach to explore the spatial and temporal features of populations that affect their contributions to the observed distribution of F ST, including simultaneous estimates of the magnitude and direction of these effects.
Materials and Methods
Study Organism
Silene latifolia Poir. ( = S. alba, Caryophyllaceae) is a short-lived perennial plant that is broadly used as a model system for studying sex determination, sex chromosome evolution, host-pathogen dynamics, biological invasions, organelle evolution, sexual dimorphism, sex ratio evolution, and evolution in structured populations [19].
We studied a S. latifolia metapopulation located in Giles and Craig Counties, Virginia, USA (Figure 1). This region has been the subject of a 20+ year study of population dynamics and genetic structure in more than 800 populations [5], [20]–[25]. An annual census of an approximately 25×25-km area adjacent to Mountain Lake Biological Station has been conducted since 1988, recording the location and sex of S. latifolia individuals along ∼150 km of predominantly roadside habitat. The structure of the data and how it was collected is reported in Antonovics et al. [20]. Briefly, the roadside habitat is divided up into ∼40 m grid units which we classify as populations. Previous studies have indicated that the utilized grid system may encompass one or two genetic neighborhoods on average [26], [27], levels of extinction and colonization scale consistently with grid segment size [20], [28], and that dispersal distances are such that populations separated by 20 meters were almost panmictic, while populations separated by 80 meters were nearly isolated [24]. Dispersal of pollen is insect mediated, primarily noctuid moths, and seed dispersal is passive and happens at a much smaller scale [22]. Much longer distance dispersal is likely mediated by human activity [29], with road grading and mowing as possible mechanisms [24]. Which units are occupied and the number of plants in each occupied population are recorded annually. Important phase transitions, such as extinction and colonization events, are confirmed with a second census during the same season. Time since colonization (or population age) is based on the year plants were first observed in a given grid unit. We identified extinction as the disappearance of plants from a grid unit for a single year. A previous study has indicated that seeds can remain viable in the soil for approximately four years, raising the possibility of a seed bank [30]. For our purposes, we treat the recolonization of a population by propagules in the seed bank as roughly equivalent as recolonization by propagules from a nearby site. The census data provide the demographic data, spatial relationships among populations, and extinction/recolonization dynamics used in this study (Table 1).
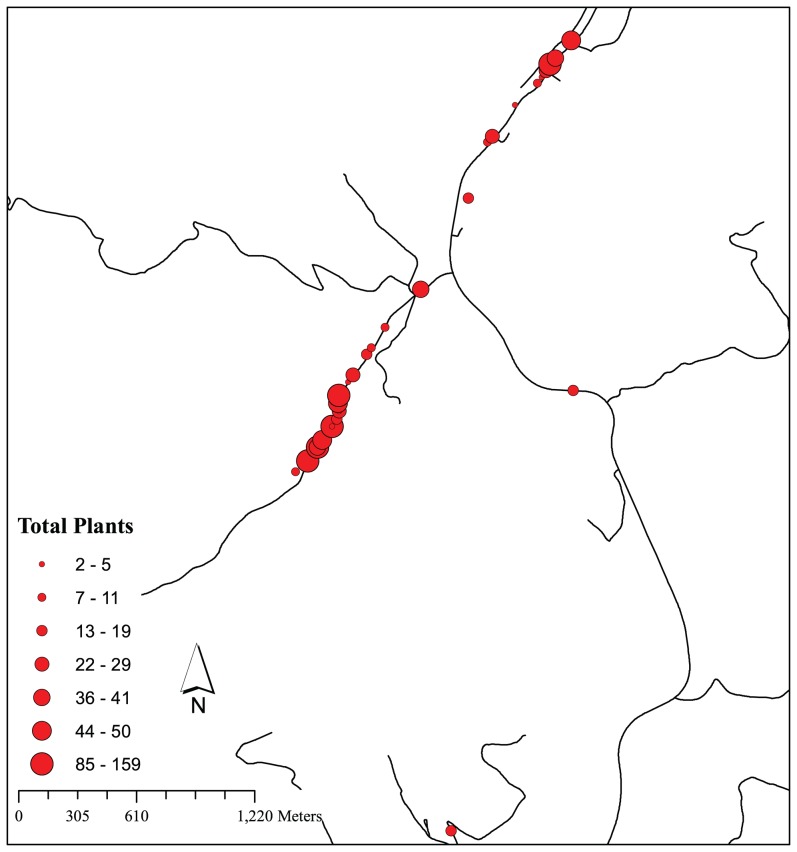
Figure 1. Map of the focal populations of the S. latifolia metapopulation located in Giles and Craig County, VA, USA sampled in the presented analysis.
Circles represent individual populations, where the size of the circle indicates the total number of plants located within our grid. Black lines represent both the assumed grid of population arrangement and small country roads. Due to the topology of the focal area (mountain, valley systems), it was assumed that pollinators move along the linear grid, rather than crossing over ridges.
Table 1. S. latifolia populations used in the genetic analysis.
| F ST Statistics | Factors | |||||||
| Population ID | Sample Size | Mean | Mode | 95% HPDI | Age | Population Size |
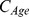
|
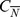
|
| Population 1 | 24 | 0.183 | 0.174 | [0.128; 0.248] | 21 | 22.038 | 2.15 | 44.543 |
| Population 2 | 12 | 0.2 | 0.188 | [0.111; 0.302] | 3 | 1.246 | 0.143 | 1.246 |
| Population 3 | 7 | 0.108 | 0.096 | [0.041; 0.186] | 3 | 4.485 | 0.51 | 9.304 |
| Population 4 | 5 | 0.177 | 0.147 | [0.0719; 0.296] | 1 | 4.82 | 0.228 | 9.675 |
| Population 5 | 19 | 0.064 | 0.058 | [0.0298; 0.1] | 21 | 13.477 | 6.192 | 54.116 |
| Population 6 | 50 | 0.046 | 0.043 | [0.0272; 0.0665] | 21 | 9.023 | 4.37 | 18.625 |
| Population 7 | 22 | 0.056 | 0.051 | [0.0247; 0.0886] | 18 | 5.956 | 5.308 | 23.917 |
| Population 8 | 24 | 0.048 | 0.045 | [0.0244; 0.0744] | 21 | 10.309 | 5.218 | 21.658 |
| Population 9 | 39 | 0.041 | 0.039 | [0.0242; 0.06] | 20 | 9.389 | 6.54 | 38.816 |
| Population 10 | 21 | 0.044 | 0.039 | [0.0197; 0.0718] | 12 | 3.774 | 3.924 | 15.602 |
| Population 11 | 18 | 0.043 | 0.038 | [0.0199; 0.0715] | 21 | 8.873 | 6.098 | 27.936 |
| Population 12 | 47 | 0.048 | 0.045 | [0.028; 0.0713] | 18 | 1.733 | 5.362 | 7.004 |
| Population 13 | 8 | 0.071 | 0.054 | [0.014; 0.142] | 21 | 7.827 | 6.256 | 31.624 |
| Population 14 | 20 | 0.064 | 0.059 | [0.0287; 0.105] | 17 | 4.16 | 3.808 | 9.361 |
| Population 15 | 44 | 0.024 | 0.022 | [0.011; 0.0376] | 10 | 6.521 | 1.663 | 8.719 |
| Population 16 | 11 | 0.156 | 0.139 | [0.0743; 0.248] | 21 | 5.255 | 4.213 | 13.407 |
| Population 17 | 8 | 0.099 | 0.088 | [0.037; 0.165] | 12 | 2.051 | 2.627 | 6.986 |
| Population 18 | 19 | 0.139 | 0.129 | [0.0784; 0.209] | 4 | 3.84 | 0.876 | 13.077 |
| Population 19 | 10 | 0.179 | 0.166 | [0.0888; 0.275] | 3 | 1.503 | 0.474 | 3.963 |
| Population 20 | 16 | 0.106 | 0.098 | [0.0533; 0.163] | 1 | 1.392 | 0.139 | 3.147 |
| Population 21 | 10 | 0.166 | 0.15 | [0.0809; 0.269] | 1 | 1.507 | 0.055 | 1.543 |
| Population 22 | 6 | 0.155 | 0.137 | [0.0669; 0.252] | 12 | 5.771 | 1.175 | 11.573 |
| Population 23 | 36 | 0.11 | 0.106 | [0.0724; 0.151] | 11 | 1.807 | 1.077 | 3.622 |
| Population 24 | 27 | 0.156 | 0.148 | [0.0962; 0.223] | 3 | 2.345 | 0.19 | 2.408 |
| Population 25 | 8 | 0.218 | 0.205 | [0.119; 0.334] | 1 | 1.486 | 0.066 | 1.506 |
| Population 26 | 21 | 0.116 | 0.107 | [0.0619; 0.173] | 20 | 4.22 | 1.343 | 5.159 |
| Population 27 | 8 | 0.124 | 0.111 | [0.0572; 0.2] | 21 | 7.679 | 2.696 | 15.767 |
| Population 28 | 4 | 0.075 | 0.066 | [0.0205; 0.139] | 21 | 17.038 | 2.358 | 21.839 |
| Population 29 | 15 | 0.124 | 0.113 | [0.0649; 0.188] | 21 | 19.11 | 2.283 | 21.082 |
| Population 30 | 44 | 0.113 | 0.107 | [0.0718; 0.161] | 21 | 45.22 | 2.335 | 51.538 |
| Population 31 | 24 | 0.143 | 0.133 | [0.0885; 0.209] | 4 | 1.535 | 0.614 | 3.454 |
| Population 32 | 29 | 0.136 | 0.129 | [0.0818; 0.193] | 21 | 26.265 | 2.568 | 39.887 |
| Population 33 | 44 | 0.104 | 0.101 | [0.0677; 0.143] | 1 | 1.161 | 0.128 | 2.166 |
Population ID = census ID of individual populations, Mean, Mode, and 95% HPDI of the RJ-MCMC derived posterior model estimates, Age = number of continuously occupied years of individual populations, Population Size = harmonic mean population size of each sampled population, 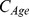 = composite character composed of the sum distance between a focal population to all other extant populations and a focal populations age, and
= composite character composed of the sum distance between a focal population to all other extant populations and a focal populations age, and 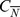 = composite character composed of the sum distance between a focal population to all other extant populations and a focal population's size.
= composite character composed of the sum distance between a focal population to all other extant populations and a focal population's size.
Spatiotemporal Data
We estimated characteristics of populations that are thought to significantly influence the magnitude of genetic differentiation among demes in a metapopulation, including population size, population connectivity (a characteristic that will influence gene flow between populations), and population age (a factor that estimates the when founder effects occurred and opportunities for subsequent migration).
Given our incomplete knowledge of the contribution and life-span of an individual population's seed bank, we estimated harmonic mean population size (hereafter population size) based upon the number of plants (both flowering and vegetative) occupying a given grid-unit throughout the time of the annual census as:
Population size estimates derive from the occupancy of a given site throughout the full census period. Detailed surveys on a subset of the metapopulation have been conducted to estimate the extent that our non-invasive census protocol sacrifices precision and accuracy. In the survey, we carefully searched the vegetation and when plants were found, the shoots were carefully traced down to the ground to distinguish individuals that were rooted close together. Non-flowering plants were also counted. Population sizes in the detailed survey were highly correlated with population size from the metapopulation census as assessed with a Pearson Product Moment Correlation (0.74, P<0.001). Population size in the metapopulation census (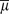 = 14.32) is lower than in the detailed survey (
= 14.32) is lower than in the detailed survey (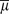 = 36.91) because clustered plants many be counted as single individuals in the annual census. The census, therefore, accurately measures relative population sizes, but likely underestimates absolute size.
= 36.91) because clustered plants many be counted as single individuals in the annual census. The census, therefore, accurately measures relative population sizes, but likely underestimates absolute size.
To estimate population age, we assumed sites unoccupied for a single year went extinct, and that plants occupying that site in the future were classified as colonizations. This reflects the conservative assumption that recolonization from neighboring sites and recolonization from the seed bank involve similar bottlenecks of genetic diversity; if this assumption were violated, and new colonization from a seed bank did not involve the same degree of bottleneck, this would tend to obscure any differences we observed between younger and older populations. Following extinction and re-colonization, age is calculated as the number of years a site has been occupied up until the time of collection. Given this operational definition of population age, individual sites could vary in age from one to 21 years (the extent of the demographic census started in 1988). Populations in the age class of 21 years might reasonably be considered as a heterogeneous grouping of extant populations given that some populations may actually be older than the extent of the current long-term census.
There are a number of methods described in the literature that have been used to estimate population connectivity. The majority of ecological studies have used a nearest neighbor/patch approach, or distance to multiple neighbors within a limited neighborhood of a focal patch (or buffer) [31]. However, these measures have been shown to be poor predictors of ecologically important metapopulation dynamics such as colonization potential. To measure population connectivity, we generated two composite variables, each of which includes a negative exponential dispersal kernel and accounts for distance to all other potential extant populations for gene flow [32]. Each variable has the following structure:
where 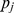 is in
is in 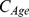 the proportion of the censuses for which a given site was occupied (1/21 – 1) or in
the proportion of the censuses for which a given site was occupied (1/21 – 1) or in 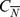 , the population size over the life span of the population, of some population j;
, the population size over the life span of the population, of some population j;  is a parameter scaling the effect of distance on dispersal, and
is a parameter scaling the effect of distance on dispersal, and 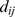 is the road network based distance between a target population i and source population j
[31], [32]. Pair-wise distances were calculated using a network constructed based upon the public roadway system, using ArcGIS (ESRI) Network Analyst tool. Given the mountain-valley geographic topology of the area, this network-based approach is more appropriate than standard Euclidean distances.
is the road network based distance between a target population i and source population j
[31], [32]. Pair-wise distances were calculated using a network constructed based upon the public roadway system, using ArcGIS (ESRI) Network Analyst tool. Given the mountain-valley geographic topology of the area, this network-based approach is more appropriate than standard Euclidean distances. 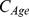 or
or 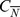 are indicative of a population's probability of receiving migrants, whether through seeds or pollen, though these are modulated by the opportunity for gene flow over-time or through apparency to pollinators, respectively.
are indicative of a population's probability of receiving migrants, whether through seeds or pollen, though these are modulated by the opportunity for gene flow over-time or through apparency to pollinators, respectively.
Sampling
We focused on one of the nine metapopulation sections, which are classified with an ad hoc partitioning of the mountain-valley system topology of the area, and is consistent with the expectation that each are mostly genetically isolated [27]. We sampled plants from 33 spatially distinct populations during peak flowering in the summer of 2008. Sites occupied by < 4 plants were excluded since we could not reliably estimate gene frequencies in our estimation of F ST. S. latifolia is identified as in introduced weed in the study area, and does not require specific permits to collect tissue samples. We collected leaf tissue from every plant in the population, or up to 50 individuals in the larger populations, and stored the leaves with silica gel (Sigma, USA).
Genomic DNA was extracted and amplified following established microsatellite techniques for S. latifolia [33]. We genotyped each plant at 8 microsatellite loci. Microsatellites were derived from multiple sources [34]–[36]. PCR amplification was conducted using previously published methods [37]. Briefly, PCR products were amplified with the forward primer end-labeled with a fluorescent dye, either 5(or 6)-FAM, NED, TAMRA, JOE, or VIC. Three to four PCR products of different loci were then pooled together and added to a loading buffer containing formamide and GENESCAN 400HD ROX size standard (Applied Biosystems, USA). Following five minutes of denaturing at 95°C, fluorescently labeled fragments were separated on an Applied Biosystems 3130 sequencer and analyzed with GENEMAPPER v3.0 software (Applied Biosystems, USA). Allele binning was accomplished using the software TANDEM [38].
Statistical Methods
Overall, the data involved 730 plants each with a multi-locus genotype derived from eight microsatellite markers. The plants were associated with one of 33 populations that had size, age and connectivity data collected from the long-term demographic dataset.
We used the program GenoDive [39] to estimate global summary statistics of population structure for our molecular markers, including observed (H
O) and expected (H
E) heterozygosity, F
ST, and Jost's D
[40]. We used the the analytical software R [41] and the package hierfstat v. 0.04-10 [42] to calculate rarefied allelic richness. We used the hierarchical Bayesian method of Foll and Gaggiotti [18], implemented in the program GESTE v. 2, to evaluate the effect of spatial and temporal characteristics of populations on the magnitude of genetic differentiation among populations. The method implemented in GESTE estimates F
ST values for each sampled population using the approach first proposed by [14] and relates them to environmental factors using a generalized linear model framework [43]. Specifically, 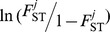 is related to models of the form
is related to models of the form 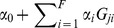 , where
, where 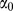 is a constant,
is a constant, 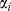 is a regression coefficient of the effect of factor
is a regression coefficient of the effect of factor 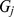 from some pop j affecting the response variable, in this case individual population F
ST values. We considered four factors, thus generating 16 alternative regression models The simplest null model included only a constant term, whereas the most complex model included a constant and all four factors. Because the two connectivity variables,
from some pop j affecting the response variable, in this case individual population F
ST values. We considered four factors, thus generating 16 alternative regression models The simplest null model included only a constant term, whereas the most complex model included a constant and all four factors. Because the two connectivity variables, 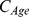 and
and 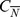 , were found to be significantly correlated with a Pearson product-moment correlation coefficient of 0.6141 (95% confidence interval (CI) 0.3432–0.797; P = 0.0001), we additionally ran GESTE excluding one or the other connectivity measure. GESTE does not allow for testing a full model that would include all four pairwise interactions. The method provides posterior probabilities for the alternative models using a RJ-MCMC approach [18]. Under this framework, the model with the highest posterior probability is the one that best explains the data [18], [43]. We followed the method of Gaggiotti et al.
[43], using 10 pilot runs of 1000 iterations to obtain parameters of the proposal distributions used by the MCMC, followed by an additional burn-in of 5×106 iterations and a thinning interval of 50, with a final iteration sample size of 60,000 on which the model fit probability was based. Convergence was assessed visually using the Plot GESTE.exe function included in the GESTE v.2 distribution. Using this method, we identified the model that best explained the observed genetic structuring. The magnitude and direction of a spatiotemporal character on genetic structuring was inferred from estimates of the regression coefficients from the model with the highest posterior probability.
, were found to be significantly correlated with a Pearson product-moment correlation coefficient of 0.6141 (95% confidence interval (CI) 0.3432–0.797; P = 0.0001), we additionally ran GESTE excluding one or the other connectivity measure. GESTE does not allow for testing a full model that would include all four pairwise interactions. The method provides posterior probabilities for the alternative models using a RJ-MCMC approach [18]. Under this framework, the model with the highest posterior probability is the one that best explains the data [18], [43]. We followed the method of Gaggiotti et al.
[43], using 10 pilot runs of 1000 iterations to obtain parameters of the proposal distributions used by the MCMC, followed by an additional burn-in of 5×106 iterations and a thinning interval of 50, with a final iteration sample size of 60,000 on which the model fit probability was based. Convergence was assessed visually using the Plot GESTE.exe function included in the GESTE v.2 distribution. Using this method, we identified the model that best explained the observed genetic structuring. The magnitude and direction of a spatiotemporal character on genetic structuring was inferred from estimates of the regression coefficients from the model with the highest posterior probability.
Results
Global summary statistics (Table 2) revealed a high degree of population structure, with an overall F ST = 0.103, and a range among markers of 0.055 to 0.231. This was similar to previous estimates in this metapopulation using allozymes [0.134, 21]. The observed levels of population genetic structure are also consistent with other published datasets on plant metapopulations using microsatellite markers, including other Silene species. Previous research has shown that the sub-structuring of alleles is not the consequence of PCR artifacts such as null alleles [34]–[36]. We estimated a significantly negative Pearson product-moment correlation coefficient between the genetic diversity of individual populations and that population's contribution to F ST (r = −0.3601, 95% CI −0.6260, −0.0191; P = 0.0396; Table S1). D had a mean of 0.131, and a range of 0.047–0.337.
Table 2. Global estimates of genetic diversity and variation in allele frequencies.
| Locus | N | Ho | H s | D | FST |
| slat_18 1 | 10 | 0.338 | 0.592 | 0.158 | 0.09 |
| slat_32 1 | 9 | 0.303 | 0.673 | 0.337 | 0.135 |
| slat_33 1 | 3 | 0.07 | 0.13 | 0.051 | 0.231 |
| slat_48 1 | 2 | 0.078 | 0.202 | 0.047 | 0.143 |
| slat_72 1 | 12 | 0.325 | 0.593 | 0.103 | 0.055 |
| slat_85 1 | 16 | 0.324 | 0.538 | 0.178 | 0.125 |
| SL_82 | 43 | 0.693 | 0.819 | 0.245 | 0.051 |
| SV_11 3 | 11 | 0.305 | 0.573 | 0.19 | 0.122 |
| Overall | 13.25 | 0.304 | 0.515 | 0.131 | 0.103 |
Variables are the number of alleles (N), observed heterozygosity (HO), Expected heterozygosity (HS), Jost's D (D) and global variation in allele frequencies (F ST). Overall, populations showed a high degree of substructure, as has been observed in other Silene metapopulations. Population structure was high for each marker. Our lowest F ST corresponded to the only marker composed of a dinucleotide repeat. 1 [34], 2 [35], 3 [36].
The magnitude and direction of the effect of each of the spatiotemporal characters on genetic differentiation was inferred from the estimates of the regression coefficients for the most probable model. The four parameters affected genetic differentiation in directions that were consistent with both theoretical expectations concerning the role of spatial-temporal dynamics affecting the distribution of F
ST across a metapopulation [8], as well previous research on the system (Table 3, 4; Fig. S1–S3). For example, recent founder effects and small population size enhanced F
ST, as was previously described theoretically by Whitlock [8], and has been shown empirically in a number of other systems across a broad range of taxa known to occur as a metapopulations [6], [9]
[5], [6], [9], including the focal plant metapopulation. However, the parameters of population age and population size were not individually components of models with the highest posterior probabilities. Instead, a composite parameter that combined population age and the degree of connectivity, 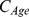 , provided the highest posterior probability (0.752) model (Table 3, 4; Fig. S2), consistent previous studies by Moilanen and Nieminen [31] for predicting extinction and colonization processes. To identify which population-level character contributed the most to global F
ST, we summed the posterior probabilities of models that included individual factors. Among these, population age (
, provided the highest posterior probability (0.752) model (Table 3, 4; Fig. S2), consistent previous studies by Moilanen and Nieminen [31] for predicting extinction and colonization processes. To identify which population-level character contributed the most to global F
ST, we summed the posterior probabilities of models that included individual factors. Among these, population age (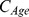 , with a posterior probability of 0.994), emerged as the one factor that had an overwhelming effect on a population's contribution to the global value of F
ST (Table 3). The 14 other models attained <0.1 posterior model probability.
, with a posterior probability of 0.994), emerged as the one factor that had an overwhelming effect on a population's contribution to the global value of F
ST (Table 3). The 14 other models attained <0.1 posterior model probability.
Table 3. Sum of posterior probabilities of models that include a given factor.
| Factor | Sum of the posterior probabilities |
| Population Age | 0.0935 |
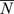
|
0.0541 |
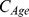
|
0.994 |
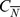
|
0.124 |
Bold value indicates factor with highest score.
Table 4. Posterior probabilities of all 16 models.
| Model | Pr | Factors included |
| 5 | 0.75 |
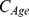
|
| 13 | 0.10 |
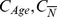
|
| 6 | 0.08 |
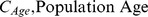
|
| 7 | 0.04 |
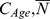
|
| 15 | 0.01 |
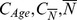
|
| 14 | 0.01 |
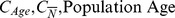
|
| 1 | 0.00 |
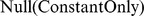
|
| 8 | 0.00 |
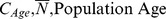
|
| 16 | 0.00 |
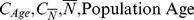
|
| 2 | 0.00 |
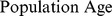
|
| 9 | 0.00 |
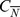
|
| 3 | 0.00 |
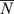
|
| 10 | 0.00 |
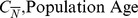
|
| 4 | 0.00 |
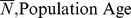
|
| 11 | 0.00 |
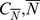
|
| 12 | 0.00 |
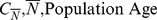
|
Our most probable model (bolded) included the composite variable of population age and population connectivity. The second most probable model includes composite variables of population age and connectivity, and population size and connectivity.
Comparison of the GESTE derived estimates of individual factors contribution to variation in F
ST across individual models, i.e. all models including a given factor, showed that population age was the most important determinant of population genetic structure, followed by population size, and that each of these were influenced by the degree of connectivity. GESTE analyses run excluding population size, 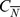 , resulted in the
, resulted in the 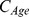 factor remaining the dominant factor increasing F
ST (Table S2.a). The reverse analysis, which excluded
factor remaining the dominant factor increasing F
ST (Table S2.a). The reverse analysis, which excluded 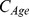 and included
and included 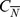 , resulted in a model with a low posterior probability (Table S2.b)
, resulted in a model with a low posterior probability (Table S2.b)
Posterior estimates of the regression parameters of the model that only included Constant + 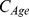 were significantly negative (
were significantly negative (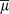 = −0.439, mode = −0.447, 95% HPDI [−0.680; −0.200]), indicating that the initial increase in F
ST resulting from founder effects is reduced over time, presumably by subsequent migration (Table 5; Fig. S3). Posterior estimates of the regression parameters of the next best model indicated a consistent effect of population age,
= −0.439, mode = −0.447, 95% HPDI [−0.680; −0.200]), indicating that the initial increase in F
ST resulting from founder effects is reduced over time, presumably by subsequent migration (Table 5; Fig. S3). Posterior estimates of the regression parameters of the next best model indicated a consistent effect of population age, 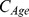 (
(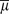 = −0.575, mode = −0.600, 95% HPDI [−0.857; −0.265]), and a positive effect of populations size,
= −0.575, mode = −0.600, 95% HPDI [−0.857; −0.265]), and a positive effect of populations size, 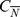 (
(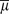 = 0.207, mode = 0.201, 95% HPDI [−0.079; 0.472]) indicating that younger and smaller populations contributed proportionately greater to the overall magnitude of genetic differentiation, and that proportional effects were modulated through population connectivity. Regression parameters for models excluding one or the other connectivity factor were of similar direction and magnitude (Table S3a, S3b).
= 0.207, mode = 0.201, 95% HPDI [−0.079; 0.472]) indicating that younger and smaller populations contributed proportionately greater to the overall magnitude of genetic differentiation, and that proportional effects were modulated through population connectivity. Regression parameters for models excluding one or the other connectivity factor were of similar direction and magnitude (Table S3a, S3b).
Table 5. Posterior estimates of regression parameters for the model with the highest posterior probability.
| Regression coefficient | Factor | Mean | Mode | 95% HPDI |
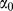
|
Constant | −2.26 | −2.25 | [−2.50; −2.00] |
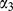
|
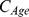
|
−0.435 | −0.445 | [−0.687; −0.193] |
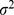
|
- | 0.369 | 0.316 | [0.168; 0.617] |
Parameter estimates are consistent with theoretical expectations (e.g. older and larger populations contribute proportionately less to the global F ST).
Discussion
In the present study, we simultaneously identified several important spatiotemporal parameters that contributed to population genetic differentiation. While previous research on other plant metapopulations has shown that founder effects contribute to population differentiation [5]–[7], [21], [22], [44]–[46], none of these previous studies have been capable of quantifying the relative magnitudes of these effects.
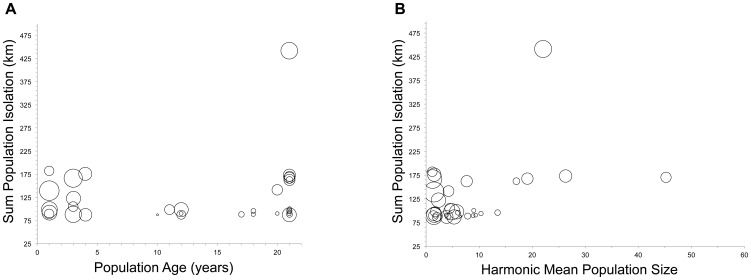
In the Silene latifolia metapopulation, population size, degree of connectivity and population age were each important determinants of population structure, but composite characters (so-called connectivity scores; [31]) were most important. This implicates the extinction and recolonization of demes, followed by subsequent opportunities for gene flow as a population ages, as the most important driving force in the genetic differentiation among populations in this system. This point is particularly clear when observing Population 1 which is part of the oldest age class but also maintains one of the higher F ST values due to isolation (Figure 2; upper right quadrant). The genetic consequences of founder effects and within-population genetic drift, as modulated by long-term population size, were influenced by the degree of population connectivity and hence the opportunities for gene flow.
Figure 2. The effect of population age, connectivity, and population size on F ST.
Individual population F ST is represented by the size of the circle, where larger circles represent larger F ST. (A) Simultaneous effect of population connectivity and population age effects on FST, and (B) of population connectivity and population size on F ST.
The S. latifolia metapopulation is neither a true Island Model, nor an idealized metapopulation [47]; populations are characterized by frequent colonizations and extinctions, on the order of 5-20% per year [20], [27], [48], [49], but populations vary in size, dispersal is limited, and within population dynamics are important relative to the time scale of the study. Colonizations are likely to be source-size and distance dependent, as is typical in other metapopulation systems [50]–[52], though this point has not been explicitly tested. Our findings support the general notion that founder effects during colonization can enhance genetic differentiation among populations [5], but we additionally show that the magnitude of these effects are large (Figure 2) relative to the structuring mechanism assumed in most models, i.e. genetic drift among extant demes as described by Wright's Island Model [1].
It is a nearly universal observation that a given species range will be composed of populations that are patchily distributed in space. There are clear similarities in the extinction/colonization and incidence parameters in Silene versus other model systems; e.g. the Glanville fritillary (Melitea cinxia) metapopulation in Finland [53]. Spatial patterns of colonization and extinction responded similarly to scaling in regional studies of sunflowers in the mid-west (Helianthus annuus; [27])(Helianthus annuus; [28]). Metapopulation dynamics have also been documented in the fresh water crustacean Daphnia longispina and D. magna (Cladocera), where the founding of new populations by single or few individuals was followed by predominantly clonal reproduction. This lead to an initially large increase in F ST in newly founded populations followed by the gradual dissolution of variation in allele frequencies through limited gene flow [9]. While the direct quantitative values will obviously vary from system to system, one might expect that non-equilibrium dynamics that result from the extinction and recolonization of local demes would be most important in systems like these, where there is a high turnover of demes. On the other hand, drift can be expected to be a less powerful structuring mechanism when demes are larger and more permanent. For example, Cosentino [32] show that connectivity and wetland area were the most important factors driving variation in allele frequencies amongst populations of the tiger salamander Ambystoma tigrinum.
The observed global F ST in the present study was lower than has been previously reported. Specifically, McCauley [21], [44] reported mean estimates F ST = 0.134 in seven allozyme markers. Previous research has suggested that the F ST of microsatellite markers will be smaller than for allozymes due to the higher heterozygosity of microsatellite markers and the inverse relationship of F ST and marker heterozygosity [54]. In addition, the estimated F ST in the present study is likely an underestimate due to our sampling scheme, which include almost all individuals rather than a small sample. Specifically, Whitlock [8] describes the sampling scheme used on a metapopulation of the forked fungus beetle (Bolitotherus cornutus) as encompassing almost the entirety of the population. In such cases Whitlock [8] suggests the use of a hypergeometric sampling correction to account for the sampling error normally assumed by a binomial sampling error. Recently Wood et al. [55] describe a more recent analysis of the same focal Bolitotherus cornutus metapopulation, though not exactly the same section as Whitlock [8]. Wood et al. [55] report much lower values of F ST values for microsatellite markers, which might be similarly affected by the issues described by Edelaar et al. [54] wherein markers showing larger numbers of alleles, e.g. microsatellites, will show a general trend towards smaller values of F ST compared to markers that have fewer alleles (allozymes), but also because a multinomial-hypergeometric correction was not included for the estimation of F ST.
Theoretical explorations of metapopulation dynamics have shown that spatiotemporal characters should have direct effects on each other, and we found empirical evidence for this. For example, we found a significant positive pairwise correlation (Pearson Product Moment Correlation = 0.478, P<0.01) between population size and population age; older populations also tended to be larger. Thus, while we show that both of these effects are potentially important in generating genetic divergence, our ability to fully disentangle the effects of age and population size is limited. Neither population size nor age was significantly correlated with population connectivity (P>0.05).
While the present approach provides insights into the biology of the Silene metapopulation, additional insights would be gained from sampling populations over time. Lamy et al. [56], longitudinally sampled populations of the freshwater snail, Drepanotrema depressissimum, to show that demographic survey-derived assessments of extinction were incorrect; rather than a true metapopulation, they detected persistent demes with genetic diversity driven by different population sizes and rates of immigration. Similarly, Robinson et al. [57] applied a novel use of approximate Bayesian computation (ABC; [58]) to genetic data from a Daphnia magna metapopulation described by Haag et al. [9]. They concluded that some populations act as persistent sources, similar to a continent-island model.
Discernment of presence/absence of extant populations within a census is highly efficient in S. latifolia (see above). However, previous research has also suggested the presence of a seed bank [30], though allele frequencies observed in the seed bank are highly consistent with above ground cohorts [30]. We believe our ad hoc measure of population extinction is consistent with the theoretical expectations of the effect of founder effects on the distribution of variation in allele frequencies [8]. Temporally spaced samples as in Lamy et al. [56] could more conclusively confirm this particular hypothesis, as well analyses such as the one presented by Robinson et al. [57]. Further investigations such as those carried out by Lamy et al. [59] and Fréville et al. [60], where the expectation of a seed bank/resting form is assumed as part of larger model of demographic dynamics, will allow for a better understanding misidentification of extinctions would effect our inference of metapopulation dynamics.
Thus far, we have focused on evolutionary processes that are driven by non-selective, drift related processes. However, previous studies have indicated the potential for metapopulation structure to have a significant outcome on selective dynamics and vice versa [61]. Since we derived our molecular markers from non-coding regions, they were assumed to be neutral and to be unlinked to functionally important genomic regions [34]–[36]. Although our panel of markers does not exhibit discontinuities in their distribution characteristic of outliers, given our limited panel size and the complexity of detecting outliers in hierarchically structured populations [62], we have only limited power to test this assumption.
Natural selection could have a powerful effect on population structure, even when the alleles under selection are not closely linked to marker loci. Studies in this S. latifolia metapopulation have confirmed that population genetic structure, where individuals in closer proximity tend to be more related than expected from chance, can have a significant negative average effect on individual fitness through the expression of deleterious recessive alleles [25]. Because inbreeding depression will reduce average fitness and therefore population size, drift processes could be enhanced through selective reductions in population size. Because many of the young, recently colonized populations will experience inbreeding depression, gene flow from other populations may be enhanced beyond neutral expectations due to heterosis [63], [64]. This initial enhancement in gene flow could, combined with stochastic dynamics associated with non-equilibrium metapopulation conditions, enhance the observed reductions in population specific F ST over time. Thus, our analyses are unable to disentangle neutral and the selective effects of spatiotemporal metapopulation structure in generating variation in allele frequencies among populations.
The present study demonstrates that the appropriate combination of long term ecological data and population genetic analyses may be a powerful tool for studying the mechanisms that generate population structure. Spatiotemporal characters of populations have long been hypothesized to have significant effects in generating population genetic differentiation, and its selective consequences. This fact seems to be particularly true in the S. latifolia metapopulation, where population connectivity, age and population size all combine to drive population genetic differentiation.
Supporting Information
Posterior 95% HPDI estimates of individual population's F -model based estimate of F ST.
(TIFF)
Posterior model probabilities for GESTE run including all four factors.
(TIFF)
Plots of the GESTE estimated ln(
F
ST/1-
F
ST) against (A) population age, (B) Population Size, (C)
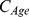 , and (D)
, and (D)
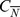 . Each cross represents a single population.
. Each cross represents a single population.
(TIFF)
Population genetic summaries of rarified allelic richness (Ar) and genetic diversity ( HS ).
(DOC)
Posterior probabilities models excluding one or the other connectivity score. Our most probable model (bolded) a) included the composite variable 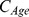 when the composite variable of
when the composite variable of  was excluded, while b) the exclusion of the
was excluded, while b) the exclusion of the 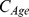 resulted in the null model having the highest posterior probability.
resulted in the null model having the highest posterior probability.
(DOC)
Posterior estimates of regression parameters for the model with the highest posterior probability when either (a)
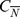 or (b)
or (b)
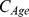 variable is excluded from the model comparisons.
variable is excluded from the model comparisons.
(DOC)
Acknowledgments
Comments from members of the Taylor lab, as well as two anonymous reviewers, improved the manuscript substantially. We would also like to thank the Mountain Lake Biological Station for logistical support. Genotype and demographic data are archived at Dryad (doi:10.5061/dryad.5n2s7).
Funding Statement
This work was funded by the National Science Foundation (NSF), DEB #0919335 (http://www.nsf.gov/) to Douglas R. Taylor and Janis Antonovics. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Wright S (1931) Evolution in mendelian populations. Genetics 16: 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Wade MJ, McCauley DE (1988) Extinction and recolonization: their effects on the genetic differentiation of local populations. Evolution 42: 995–1005. [DOI] [PubMed] [Google Scholar]
- 3. Whitlock MC, McCauley DE (1990) Some population genetic consequences of colony formation and extinction: genetic correlations within founding groups. Evolution 44: 1717–1724. [DOI] [PubMed] [Google Scholar]
- 4. Slatkin M (1977) Gene flow and genetic drift in a species subject to frequent local extinctions. Theoretical Population Biology 12: 253–262. [DOI] [PubMed] [Google Scholar]
- 5. McCauley DE, Raveill J, Antonovics J (1995) Local founding events as determinants of genetic structure in a plant metapopulation. Heredity 75: 630–636. [Google Scholar]
- 6. Giles B, Goudet J (1997) Genetic differentiation in Silene dioica metapopulations: estimation of spatiotemporal effects in a successional plant species. American Naturalist 149: 507–526. [Google Scholar]
- 7. Ingvarsson PK, Giles BE (1999) Kin-structured colonization and small-scale genetic differentiation in Silene dioica . Evolution 53: 605–611. [DOI] [PubMed] [Google Scholar]
- 8. Whitlock MC (1992) Nonequilibrium population-structure in forked fungus beetles - extinction, colonization, and the genetic variance among populations. American Naturalist 139: 952–970. [Google Scholar]
- 9. Haag CR, Riek M, Hottinger JW, Pajunen VI, Ebert D (2005) Genetic diversity and genetic differentiation in Daphnia metapopulations with subpopulations of known age. Genetics 170: 1809–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Gaggiotti OE, Brooks SP, Amos W, Harwood J (2004) Combining demographic, environmental and genetic data to test hypotheses about colonization events in metapopulations. Molecular Ecology 13: 811–825. [DOI] [PubMed] [Google Scholar]
- 11. Pannell JR, Fields PD (2014) Evolution in subdivided plant populations: concepts, recent advances and future directions. New Phytologist 201: 417–432. [DOI] [PubMed] [Google Scholar]
- 12. Gaggiotti OE, Foll M (2010) Quantifying population structure using the F-model. Molecular Ecology Resources 10: 821–830. [DOI] [PubMed] [Google Scholar]
- 13. Falush D, Stephens M, Pritchard J (2003) Inference of population structure using multilocus genotype data linked loci and correlated allele frequencies. Genetics 164: 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Balding DJ, Nichols RA (1995) A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica 96: 3–12. [DOI] [PubMed] [Google Scholar]
- 15. Karhunen M, Ovaskainen O (2012) Estimating population-level coancestry coefficients by an admixture F model. Genetics 192: 609–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nicholson G, Smith A, Jónsson F, Gústafsson Ó, Stefánsson K, et al.. (2002) Assessing Population Differentiation and Isolation from Single-Nucleotide Polymorphism Data. Journal of the Royal Statistical Society Series B (Statistical Methodology). pp. 695–715.
- 17.Bhatia G, Patterson NJ, Sankararaman S, Price AL (2013) Estimating and interpreting Fst: the impact of rare variants. Genome Research. [DOI] [PMC free article] [PubMed]
- 18. Foll M, Gaggiotti OE (2006) Identifying the environmental factors that determine the genetic structure of populations. Genetics 174: 875–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bernasconi G, Antonovics J, Biere A, Charlesworth D, Delph LF, et al. (2009) Silene as a model system in ecology and evolution. Heredity 103: 5–14. [DOI] [PubMed] [Google Scholar]
- 20.Antonovics J, Thrall P, Jarosz A, Stratton D (1994) Ecological genetics of metapopulations: the Silene-Ustilago plant-pathogen system. In: Real L, editor. Ecological genetics: Princeton University Press, NJ. pp. 146–170.
- 21. McCauley DE (1994) Contrasting the distribution of chloroplast DNA and allozyme polymorphism among local populations of Silene alba: implications for studies of gene flow in plants. Proceedings of the National Academy of Sciences of the United States of America 91: 8127–8131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. McCauley DE (1997) The relative contributions of seed and pollen movement to the local genetic structure of Silene alba . Journal of Heredity 88: 257–263. [Google Scholar]
- 23. Richards CM, Emery SN, Mccauley DE (2003) Genetic and demographic dynamics of small populations of Silene latifolia. Heredity 90: 181–186. [DOI] [PubMed] [Google Scholar]
- 24. Richards CM, Church S, McCauley D (1999) The Influence of Population Size and Isolation on Gene Flow by Pollen in Silene alba . Evolution 53: 63–73. [DOI] [PubMed] [Google Scholar]
- 25. Richards CM (2000) Inbreeding depression and genetic rescue in a plant metapopulation. American Naturalist 155: 383–394. [DOI] [PubMed] [Google Scholar]
- 26. Alexander HM (1990) Epidemiology of anther-smut infection of Silene alba caused by Ustilago violacea: patterns of spore deposition and disease incidence. Journal of Ecology 78: 166–179. [Google Scholar]
- 27.Antonovics J (2004) Long term study of a plant-pathogen metapopulation. In: Hanski I, Gaggiotti O, editors. Ecology, genetics and evolution of metapopulations: Academic Press. pp. 471–488.
- 28. Moody-Weis J, Antonovics J, Alexander H, Pilson D (2008) Predicting local colonization and extinction dynamics from coarser-scale surveys. Ecography 31: 61. [Google Scholar]
- 29. Barluenga M, Austerlitz F, Elzinga JA, Teixeira S, Goudet J, et al. (2011) Fine-scale spatial genetic structure and gene dispersal in Silene latifolia . Heredity 106: 13–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Peroni PA, Armstrong RT (2001) Density, Dispersion and Population Genetics of a Silene latifolia Seed Bank from Southwestern Virginia. Journal of the Torrey Botanical Society 128: 400–406. [Google Scholar]
- 31. Moilanen A, Nieminen M (2002) Simple connectivity measures in spatial ecology. Ecology 83: 1131–1145. [Google Scholar]
- 32. Cosentino BJ, Phillips CA, Schooley RL, Lowe WH, Douglas MR (2012) Linking extinction–colonization dynamics to genetic structure in a salamander metapopulation. Proceedings of the Royal Society B: Biological Sciences 279: 1575–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Jolivet C, Bernasconi G (2007) Molecular and quantitative genetic differentiation in European populations of Silene latifolia (Caryophyllaceae). Annals of Botany 100: 119–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Abdoullaye D, Acevedo I, Adebayo AA, Behrmann-Godel J, Benjamin RC, et al. (2010) Permanent genetic rsources added to Molecular Ecology resources database 1 August 2009-30 September 2009. Molecular Ecology Resources 10: 232–236. [DOI] [PubMed] [Google Scholar]
- 35. Teixeira S, Bernasconi G (2007) High prevalence of multiple paternity within fruits in natural populations of Silene latifolia, as revealed by microsatellite DNA analysis. Molecular Ecology 16: 4370–4379. [DOI] [PubMed] [Google Scholar]
- 36. Juillet N, Freymond H, Degen L, Goudet J (2003) Isolation and characterization of highly polymorphic microsatellite loci in the bladder campion, Silene vulgaris (Caryophyllaceae). Molecular Ecology Resources 3: 358–359. [Google Scholar]
- 37. Keller SR, Gilbert KJ, Fields PD, Taylor DR (2012) Bayesian inference of a complex invasion history revealed by nuclear and chloroplast genetic diversity in the colonizing plant, Silene latifolia . Molecular Ecology 21: 4721–4734. [DOI] [PubMed] [Google Scholar]
- 38. Matschiner M, Salzburger W (2009) TANDEM: integrating automated allele binning into genetics and genomics workflows. Bioinformatics 25: 1982–1983. [DOI] [PubMed] [Google Scholar]
- 39. Meirmans PG, Van Tienderen PH (2004) GENOTYPE and GENODIVE: two programs for the analysis of genetic diversity of asexual organisms. Molecular Ecology Notes 4: 792–794. [Google Scholar]
- 40. Jost L (2008) G ST and its relatives do not measure differentiation. Molecular Ecology 17: 4015–4026. [DOI] [PubMed] [Google Scholar]
- 41.R Development Core Team (2011) R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing.
- 42. Goudet J (2005) HIERFSTAT, a package for R to compute and test hierarchical F-statistics. Molecular Ecology Notes 5: 184–186. [Google Scholar]
- 43. Gaggiotti OE, Bekkevold D, Jørgensen HBH, Foll M, Carvalho GR, et al. (2009) Disentangling the effects of evolutionary, demographic, and environmental factors influencing genetic structure of natural populations: Atlantic Herring as a case study. Evolution 63: 2939–2951. [DOI] [PubMed] [Google Scholar]
- 44. McCauley DE (1995) The use of chloroplast DNA polymorphism in studies of gene flow in plants. Trends in Ecology & Evolution 10: 198–202. [DOI] [PubMed] [Google Scholar]
- 45. McCauley DE, Stevens J, Peroni P, Raveill J (1996) The spatial distribution of chloroplast DNA and allozyme polymorphisms within a population of Silene alba (Caryophyllaceae). American Journal of Botany 83: 727–731. [Google Scholar]
- 46. Giles B, Lundqvist E, Goudet J (1998) Restricted gene flow and subpopulation differentiation in Silene dioica . Heredity 80: 715–723. [Google Scholar]
- 47. Levins R (1969) Some demographic and genetic consequences of environmental heterogeneity for biological control. Bulletin of the Entomological Society of America 15: 237–240. [Google Scholar]
- 48.Antonovics J, Thrall P, Jarosz A (1998) Genetics and the spatial ecology of species interactions: the Silene-Ustilago system. In: Tilman D, Kareiva P, editors. Spatial ecology: the role of space in population dynamics and interspecific interactions: Princeton University Press. pp. 158–180.
- 49. Thrall PH, Antonovics J (1995) Theoretical and Empirical Studies of Metapopulations - Population and Genetic Dynamics of the Silene-Ustilago System. Canadian Journal of Botany-Revue Canadienne De Botanique 73: S1249–S1258. [Google Scholar]
- 50.Hanski I, Simberloff D (1997) The metapopulation approach, its history, conceptual domain and application to conservation. In: Hanski I, Gilpin M, editors. Metapopulation Biology: Ecology, Genetics and Evolution: San Diego Academic Press. pp. 5–26.
- 51.Hanski I, Gaggiotti O (2004) Metapopulation biology: past, present and future. In: Hanski I, Gaggiotti O, editors. Metapopulation Ecology, Genetics and Evolution: San Diego Academic Press. pp. 3–22.
- 52. Alexander HM, Foster BL, Ballantyne F, Collins CD, Antonovics J, et al. (2012) Metapopulations and metacommunities: combining spatial and temporal perspectives in plant ecology. Journal of Ecology 100: 88–103. [Google Scholar]
- 53.Hanski I (2001) Spatially realistic models of metapopulation dynamics and their implications for ecological, genetic and evolutionary processes. In: Silvertown J, Antonovics J, editors. Integrating ecology and evolution in a spatial context: Blackwell Science, Oxford. pp. 139–156.
- 54. Edelaar P, Burraco P, Gomez-Mestre I (2011) Comparisons between Q ST and F ST-how wrong have we been? Molecular Ecology 20: 4830–4839. [DOI] [PubMed] [Google Scholar]
- 55. Wood CW, Donald HM, Formica VA, Brodie ED (2013) Surprisingly little population genetic structure in a fungus-associated beetle despite its exploitation of multiple hosts. Ecology and Evolution 3: 1484–1494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Lamy T, Pointier JP, Jarne P, David P (2012) Testing metapopulation dynamics using genetic, demographic and ecological data. Molecular Ecology 21: 1394–1410. [DOI] [PubMed] [Google Scholar]
- 57. Robinson JD, Hall DW, Wares JP (2013) Approximate Bayesian estimation of extinction rate in the Finnish Daphnia magna metapopulation. Molecular Ecology 22: 2627–2639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Beaumont MA (2010) Approximate Bayesian Computation in Evolution and Ecology. Annual Review of Ecology, Evolution, and Systematics 41: 379–406. [Google Scholar]
- 59. Lamy T, Gimenez O, Pointier J-P, Jarne P, David P (2013) Metapopulation Dynamics of Species with Cryptic Life Stages. The American Naturalist 181: 479–491. [DOI] [PubMed] [Google Scholar]
- 60. Fréville H, Choquet R, Pradel R, Cheptou P-O (2013) Inferring seed bank from hidden Markov models: new insights into metapopulation dynamics in plants. Journal of Ecology 101: 1572–1580. [Google Scholar]
- 61. Whitlock MC (2002) Selection, load and inbreeding depression in a large metapopulation. Genetics 160: 1191–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Narum SR, Hess JE (2011) Comparison of F ST outlier tests for SNP loci under selection. Molecular Ecology Resources 11: 184–194. [DOI] [PubMed] [Google Scholar]
- 63. Ingvarsson PK, Whitlock MC (2000) Heterosis increases the effective migration rate. Proceedings of the Royal Society of London Series B-Biological Sciences 267: 1321–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Whitlock MC, Ingvarsson PK, Hatfield T (2000) Local drift load and the heterosis of interconnected populations. Heredity 84: 452–457. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Posterior 95% HPDI estimates of individual population's F -model based estimate of F ST.
(TIFF)
Posterior model probabilities for GESTE run including all four factors.
(TIFF)
Plots of the GESTE estimated ln(
F
ST/1-
F
ST) against (A) population age, (B) Population Size, (C)
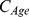 , and (D)
, and (D)
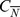 . Each cross represents a single population.
. Each cross represents a single population.
(TIFF)
Population genetic summaries of rarified allelic richness (Ar) and genetic diversity ( HS ).
(DOC)
Posterior probabilities models excluding one or the other connectivity score. Our most probable model (bolded) a) included the composite variable 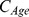 when the composite variable of
when the composite variable of  was excluded, while b) the exclusion of the
was excluded, while b) the exclusion of the 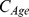 resulted in the null model having the highest posterior probability.
resulted in the null model having the highest posterior probability.
(DOC)
Posterior estimates of regression parameters for the model with the highest posterior probability when either (a)
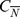 or (b)
or (b)
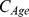 variable is excluded from the model comparisons.
variable is excluded from the model comparisons.
(DOC)