Cortical surface shift estimation using stereovision and optical flow motion tracking via projection image registration

Abstract

Stereovision is an important intraoperative imaging technique that captures the exposed parenchymal surface noninvasively during open cranial surgery. Estimating cortical surface shift efficiently and accurately is critical to compensate for brain deformation in the operating room (OR). In this study, we present an automatic and robust registration technique based on optical flow (OF) motion tracking to compensate for cortical surface displacement throughout surgery. Stereo images of the cortical surface were acquired at multiple time points after dural opening to reconstruct three-dimensional (3D) texture intensity-encoded cortical surfaces. A local coordinate system was established with its z-axis parallel to the average surface normal direction of the reconstructed cortical surface immediately after dural opening in order to produce two-dimensional (2D) projection images. A dense displacement field between the two projection images was determined directly from OF motion tracking without the need for feature identification or tracking. The starting and end points of the displacement vectors on the two cortical surfaces were then obtained following spatial mapping inversion to produce the full 3D displacement of the exposed cortical surface. We evaluated the technique with images obtained from digital phantoms and 18 surgical cases – 10 of which involved independent measurements of feature locations acquired with a tracked stylus for accuracy comparisons, and 8 others of which 4 involved stereo image acquisitions at three or more time points during surgery to illustrate utility throughout a procedure. Results from the digital phantom images were very accurate (0.05 pixels). In the 10 surgical cases with independently digitized point locations, the average agreement between feature coordinates derived from the cortical surface reconstructions was 1.7–2.1 mm relative to those determined with the tracked stylus probe. The agreement in feature displacement tracking was also comparable to tracked probe data (difference in displacement magnitude was <1 mm on average). The average magnitude of cortical surface displacement was 7.9 ± 5.7 mm (range 0.3–24.4 mm) in all patient cases with the displacement components along gravity being 5.2 ± 6.0 mm relative to the lateral movement of 2.4 ± 1.6 mm. Thus, our technique appears to be sufficiently accurate and computationally efficiency (typically ~15 s), for applications in the OR.

1. Introduction

Modern neuronavigational systems depend on co-registered preoperative magnetic resonance (pMR) images to provide image-guidance in open cranial procedures. Using skull-implanted or skin-affixed fiducial markers, accurate registration between the patient and pMR can be established at the start of surgery (Maurer et al., 1997). However, maintaining the same level of registration accuracy (e.g., <2 mm) is challenging once surgery begins because brain shift invalidates the initial registration. Intraoperative brain shift can be significant (e.g., magnitude can reach 20 mm or more at the cortical surface (Hill et al., 1998; Roberts et al., 1998)), dynamic (deformation is more significant as surgery progresses (Nabavi et al., 2001)), complex (brain motion does not necessarily correlate with gravity and the magnitude of movement is greater in the hemisphere ipsi-lateral to the craniotomy (Hartkens et al., 2003)), and seemingly unpredictable. As a result, brain shift is generally regarded as the single most important factor that degrades registration accuracy, making its compensation especially important.

Intraoperative imaging has been employed to compensate for brain shift during surgery. Both intraoperative MR (iMR; (e.g., Wirtz et al., 1997; Hall et al., 2000; Ferrant et al., 2002)) and ultrasound (iUS; (e.g., Comeau et al., 2000; Bonsanto et al., 2001; Bucholz et al., 2001)) sample the region of interest (e.g., tumor) when deep in the brain. Although iMR provides unparalleled soft tissue contrast, its substantial capital cost, intrusion to neurosurgical workflow in the OR, and relatively long image acquisition time are practical barriers to its gaining wider acceptance. IUS image noise, artifacts, and limited feature localization accuracy make delineation of anatomical structures more difficult; thus it is often co-registered with pMR to enhance image interpretation.

Stereovision (Sun et al., 2005; Paul et al., 2005, 2009; DeLorenzo et al., 2010) and laser range scanning (Miga et al., 2003; Ding et al., 2011) capture 3D geometry and texture intensity of the exposed cortical surface, and have become important tools for brain shift compensation. With intraoperative stereovision (iSV), reconstructed cortical surfaces are registered either with pMR (Sun et al., 2005; DeLorenzo et al., 2006), or with each other when acquired at two temporally distinct surgical stages (Paul et al., 2009). Because reconstructed stereo surfaces offer both 3D geometry and texture information, either can be employed for registration. However, rigid registrations that depend solely on geometry (e.g., iterative closest point, ICP (Besl and McKay, 1992)) may not accurately capture surface deformation especially when significant lateral shift occurs (Fan et al., 2012; Paul et al., 2009). In this case, incorporating texture intensity will likely improve registration accuracy. For example, Paul et al. (2009) used a cost function that incorporates both intensity and geometrical distance between two reconstructed surfaces and tracked landmarks (i.e., bifurcation locations of major vessels) to derive surface displacement. Clinical results demonstrated a significant improvement in registration accuracy relative to ICP (misalignment of 2.2 ± 0.2 mm with the approach as compared to 5.8 ± 0.9 mm using ICP; the initial alignment was 6.2 ± 2.1 mm).

Similarly, Miga et al. (2003) incorporated both geometry and intensity information to register texture-encoded point clouds from laser range scanning (LRS) with pMR using mutual information. They demonstrated that performance was comparable (and in many cases, superior) to point-based or ICP algorithms. Their method was subsequently extended to serial datasets and nonrigid registration was employed to extract sparse displacement data (Sinha et al., 2005) for modeling purposes (Dumpuri et al., 2007). The study by Sinha et al. (2005) illustrates a shift-tracking concept in which point correspondence is achieved via a 2D nonrigid image registration applied to the serial LRS texture data while the 3D spatial positions of the tracked points are found through texture mapping between the LRS point clouds and the corresponding texture images before and after deformation. This approach simplifies the correspondence process significantly because it reduces the 3D nonrigid point correspondence problem into a much easier 2D image registration, and minimizes the loss of information acquired by the LRS. However, because positioning of the LRS device and acquisition of intraoperative data required on the order of 1 min, only temporally sparse measurements would most likely be available in a given case, and computing intermediate updates could become challenging in some cases (Kumar et al., 2013). More recently, Ding et al. (2011) used intensity-encoded point clouds to reconstruct 3D surfaces where the corresponding 2D images were registered with video frames acquired through the surgical microscope to track segmented vessels in order to determine 3D displacements. Results from three patient cases suggested high accuracy in vessel tracking and registration (~3 pixels).

The published studies to date with iSV and LRS demonstrate that video images can compensate for cortical surface shift during surgery. However, the need for vessel segmentation (Paul et al., 2009; Ding et al., 2011) to aid registration makes these techniques less attractive in the OR, especially when the segmentation involves user interventions (Ding et al., 2009). Further, lens distortion contributes to displacement errors in the physical space because video images are used directly for registration. More importantly, video images from the surgical microscope depend on acquisition settings (e.g., image magnification, lens focal length, and orientation with respect to the patient) that are frequently altered by the surgeon to obtain an optimal view; and therefore, require additional processing (e.g., spatial transformation) prior to registration in order to derive cortical surface displacement. These considerations pose challenges for existing methods to be fully functional in the OR as part of standard operating procedures.

We recently applied an optical flow (OF) motion-tracking algorithm to a sequence of rectified (left) camera images (which effectively corrected for lens distortion) acquired after dural opening to derive dense displacements on the cortical surface for estimation of in-plane principal strains. The resulting dynamic deformation correlated with synchronized blood pressure pulsation and mechanical ventilation over time, demonstrating the sensitivity and fidelity of the technique (Ji et al., 2011). In this paper, we extend the method to register nonrigidly a pair of reconstructed cortical surfaces acquired at temporally distinct surgical stages in order to derive cortical surface displacements for brain shift compensation. Unlike in Ji et al. (2011), rectified images acquired at different time points during surgery are not used for OF motion-tracking directly because the images are not necessarily acquired in the same coordinate system due to changes in settings of the operating microscope’s field-of-view and/or orientation with respect to the patient. Instead, reconstructed cortical surfaces at two time points are projected into a local coordinate system in order to generate 2D images for OF motion-tracking because the algorithm operates directly on 2D images instead of intensity-encoded 3D surfaces. This approach is clinically appealing because displacements are found from reconstructed surfaces in the same coordinate system (i.e., either in pMR image space or in physical space), and thus, do not require any additional image processing to compensate for camera lens distortion or for changes in microscope acquisition settings and/or orientation. Compensation for changes in microscope acquisition settings is accomplished by mapping the acquired images into the equivalent data recorded in a calibrated baseline setting through a pre-computed deformation field (i.e., to warp the new images as if they were acquired at the calibrated baseline camera settings; Ji et al., 2014).

Conceptually, the cortical surface registration algorithm presented here is similar to the one described in Sinha et al. (2005) except that (1) we extend the technique to incorporate high-resolution stereo-image data (instead of LRS information), (2) perform OF motion-tracking to obtain 2D image nonrigid registration directly (instead of a two-step approach that locally refines an initial registration obtained from a multi-scale, multi-resolution mutual-information-based registration) and (3) evaluate the robustness and accuracy of the approach in eighteen (18) patient cases undergoing open-cranial neurosurgery (instead of in physical phantoms and 1 clinical case). Although a more recent study by the same research group also applied the method to 10 clinical patient cases (Ding et al., 2009), semi-automatic segmentation of vessels was necessary. In contrast, the technique developed in this paper is fully automatic with no need for segmentation; therefore, it significantly improves the clinical utility of the tracking concept. The clinical cases presented in our study include ten (10) surgeries prospectively evaluated during which point-based measurements of surgical surface features were acquired via a tracked probe and their coordinates were compared to their corresponding 3D iSV reconstructed locations. In addition, eight (8) cases were retrospectively evaluated (no probe data available), four (4) of which had images acquired at multiple time points during surgery to assess the feasibility of using the technique later in surgery (i.e., when more substantive tissue resection has occurred and toward the end of resection). These clinical evaluations extend those presented in Sinha et al. (2005) and Ding et al. (2009) significantly, and establish the robustness of the technique for estimating 3D cortical surface shift though 2D nonrigid registration via OF-motion tracking of serial iSV image acquisitions.

2. Methods

2.1. Stereovision hardware

Stereovision is part of our integrated, model-based neurosurgical guidance system (Ji et al., 2010), and consists of two compact C-mount cameras (Flea2 model FL2G-50S5C-C, dimension of 29 × 29 × 30 cm³; Point Grey Research Inc.; Richmond, BC, Canada) rigidly attached through a binocular port on a commercial surgical microscope (OPMI^® Pentero™, Carl Zeiss, Inc., Oberkochen, Germany; Fig. 1). The cameras have a maximum pixel resolution of 2448 × 2048 but were operated at a resolution of 1024 × 768 with a maximum recording rate of 30 fps (frames per second) due to hardware limitations. Camera image acquisitions are externally triggered through a digital I/O port to ensure that each pair of stereo images are acquired at the same time (typical stereovision acquisitions range from 4 to 10 fps for patient cases). In order to record the position and orientation of the stereo cameras, an infrared light emitting sensor is rigidly attached to the surgical microscope, which is tracked by the Medtronic StealthStation^® navigational system (Medtronic Navigation; Louisville, CO).

Fig. 1.

Illustration of typical setup in the OR (left) consisting of the computer-controlled data acquisition system, the Medtronic StealthStation^®, and the Zeiss Pentero™ surgical microscope. Magnified view (inset) on the right shows the active tracker and stereovision cameras.

2.2. Surface reconstruction from stereovision images

Techniques for stereo image calibration and reconstruction based on a pinhole camera model and radial lens distortion correction can be found, e.g., in Sun et al. (2005), and are briefly outlined here for completeness. A 3D point in world space (X, Y, Z) is transformed into the camera image coordinates (x, y) using a perspective projection matrix:

$$\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)=\left(\begin{array}{cccc}{\alpha }_x& 0& C_x& 0\\ 0& {\alpha }_y& C_y& 0\\ 0& 0& 1& 0\end{array}\right)\times \mathbf{T}\times \left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right),$$ (1)

where α_x and α_y incorporate the perspective projection from camera-to-sensor coordinates and the transformation from sensor-to-image coordinates, (C_x, C_y) is the image center, and T is a rigid body transformation describing the geometrical relationship between the two cameras. A total of 11 camera parameters (6 extrinsic: 3 rotation and 3 translation; and 5 intrinsic: focal length, f, lens distortion parameter, k₁, scale factor, S_x, and image center, (C_x, C_y)) are determined through calibration using a least squares fitting approach.

Stereo image rectification is employed to establish epipolar constraints that limit the search for correspondence points along “epipolar lines” (defined as the projection of the optical ray of one camera via the center of the other camera following a pinhole model). In addition, images are rotated so that pairs of epipolar lines are collinear and parallel to image raster lines in order to facilitate stereo matching (see Fig. 2a and b for the two rectified images). An intensity-based correlation metric and a smoothness constraint are used to find the correspondence points. Each pair of correspondence points is then transformed into its respective 3D camera space using the intrinsic parameters, and transformed into a common 3D space using the extrinsic parameters. Together with their respective camera centers in the common space, two optical rays are constructed with their intersection defining the 3D location of the correspondence point pair. Fig. 2c shows an exemplary reconstructed cortical surface, and Fig. 2d shows the cross-sections on a same axial MR image from reconstructed cortical surfaces acquired at four different times during surgery.

Fig. 2.

Illustration of stereovision surface reconstruction: rectified left (a) and right (b) camera images after dural opening, allow the correspondence point search to occur along a horizontal line (i.e., epipolar line). The reconstructed 3D cortical surface is shown in pMR image space (c). Reconstructed cortical surface cross-sections on a pMR axial image are shown (d) at four distinct surgical stages (0: before dural opening; 1: after dural opening; 2: before tumor resection; and 3: after partial tumor resection).

2.3. Compensation for arbitrary camera image acquisition settings

An important element of our surface-shift tracking strategy is transformation of reconstructed cortical surfaces into a common coordinate system for subsequent nonrigid registration. Because the stereovision cameras are attached to the surgical microscope whose magnification and focal length settings are frequently altered by the surgeon to obtain an optimal view, an efficient technique to compensate for arbitrary camera image acquisition settings is essential to recover the cortical surface accurately. Existing techniques for camera calibration at an arbitrary setting either actively re-calibrate at a given setting on-demand (Figl et al., 2005) or interpolate camera parameters, for example, via bivariate fitting of explicitly modeled polynomial functions of zoom and focal length based on a dense set of pre-calibrated camera parameters (Willson, 1994; Edwards et al., 2000). Unfortunately, these approaches can be cumbersome (e.g., repeatedly imaging an instrumented calibration target in the OR) or require substantial personnel time to pre-calibrate a dense combination of calibration settings, and have not been widely used in clinical settings such as the OR.

We recently reported an efficient approach to accurately reconstruct stereo images acquired at an arbitrary magnification and focal length setting (S) from a single pre-calibration at a reference setting (S₀) without the need for camera re-calibration (Ji et al., 2014). Essentially, images acquired at S are warped into the equivalent data acquired at S₀ using pre-determined deformation fields obtained by successively imaging a simple planar phantom at different combinations of magnification and focal length. The approach treats the calibration process as a transfer function by directly modeling the relationship between input (changes in magnification and focal length) and output (image warping) instead of many intermediate camera parameters that are often nonlinearly related, co-dependent and form a jagged hyper-surface in parametric space (Willson, 1994). Sub-millimeter to millimeter accuracy has been obtained with this technique when comparing the reconstructed surfaces at arbitrary settings with their ground-truth counterparts reconstructed at the baseline setting (average of 1.05 mm and 0.59 mm along and perpendicular to the optical axis of the microscope for six phantom image pairs, respectively, and 1.26 mm and 0.71 mm for images acquired with a total of 47 arbitrary surgical microscope settings during three clinical cases along the two directions), indicating the effectiveness of the approach.

2.4. Two-frame optical flow (OF) computation

OF is widely used in computer vision to track small scale motion in time sequences of images, and is based on the principle of intensity conservation between image frames (Horn and Schunck, 1981; Lucas and Kanade, 1981). Here, the undeformed (at time t) and deformed (at time t + 1) projection images of the textured cortical surfaces were subjected to OF motion tracking using a variational model (Brox et al., 2004). Assuming the image intensity of a pixel or material point, (x, y), does not change as a result of its displacement, the gray value constancy constraint

$$I(\mathbf{p}+\mathbf{w})=I(\mathbf{p})$$ (2)

holds in which p = (x, y, t) and the underlying flow field, w(p), is given by w(p) = (u(p), v(p), 1), where u(p) and v(p) are the horizontal and vertical components of the flow field, respectively. The global deviations from the gray value constancy assumption are measured by an energy term,

$$E_{\mathit{Data}}(u,v)={\displaystyle \int \psi ({\left|I(\mathbf{p}+\mathbf{w})-I(\mathbf{p})\right|}^2)}d\mathbf{p},$$ (3)

where a robust function, $\psi (x)=\sqrt{x^2+{\epsilon }^2}$, was used to enable an L₁ minimization. The choice of ψ does not introduce any additional parameters other than a small constant, ɛ (ɛ = 0.001), for numerical purposes (Black and Anandan, 1996).

The gray-value constancy constraint only applies to a pixel locally and does not consider any interactions between neighboring pixels. Because the flow field in a natural scene is typically smooth, an additional piecewise smoothness constraint can be applied only to the spatial domain (if only two frames are available) or to the spatio-temporal domain (if multiple frames are available) to generate displacements over a sequence of images. In this study, the piecewise smoothness constraint is applied in the spatial domain because we are interested in deriving cortical surface displacements between two surgical stages, which leads to the energy term

$$E_{\mathit{Smooth}}(u,v)={\displaystyle \int \varphi ({\left|\nabla u\right|}^2+{\left|\nabla v\right|}^2)d\mathbf{p},}$$ (4)

where ϕ is a robust function chosen to be identical to ψ, ∇ is the gradient operator and ${\left|\nabla u\right|}^2=u_x^2+u_y^2$, with $u_x=\frac{\partial }{\partial x}u$, $u_y=\frac{\partial }{\partial y}u$.

Combining the gray value constancy and piecewise smoothness constraints results in an objective function in the continuous spatial domain written as

$$E(u,v)=E_{\mathit{Data}}+\alpha E_{\mathit{Smooth}},$$ (5)

where α (α > 0; was empirically chosen as 0.02 in this study) is a regularization parameter. Computing OF is then transformed into an optimization problem in which a spatially continuous flow field, described by u and v, is determined that minimizes the total energy, E. We used an iterative reweighted least squares algorithm (Meer, 2004) and a multiscale approach starting with a coarse, smoothed image set to ensure global minimization. In addition, the formulation was extended for application to a multi-channel RGB image, where a vector, I(p), accounted for image intensities in the red, green, and blue channels (Liu, 2009).

2.5. Generation of projection images and 3D displacements

Because the two-frame OF algorithm operates directly on 2D images instead of reconstructed 3D intensity-encoded surfaces, a local coordinate system to project 3D texture maps onto 2D images must be established for 3D displacement mapping. A schematic illustration of the projection process is shown in Fig. 3. First, texture-encoded cortical surfaces reconstructed from iSV at two distinct surgical stages (referred to as the “undeformed” and “deformed” surfaces, respectively) are transformed into the same pMR image space (i.e., (X, Y, Z) in Fig. 3). A local coordinate system is established with its z-axis parallel to the average nodal normal direction of the undeformed surface (i.e., (x, y, z) in Fig. 3), which allows intensity-encoded points on both surfaces to be projected onto the same xy-plane through spatial mapping, P¹(X) and P²(X), respectively, where X denotes surface points in the global coordinate system (Fig. 3 shows the spatial mapping between points P¹ and p¹ on the undeformed surface for illustration). Because both surfaces capture largely the same physical area within the craniotomy, the projection points from the two surfaces using the same local coordinate system are expected to overlap. A set of grid points from the undeformed surface are subsequently generated in the local coordinate system (0.1 mm × 0.1 mm resolution) with a bounding box determined by the corresponding projection points. The projection images of the undeformed and deformed surfaces are then generated by numerically interpolating their respective image intensities at the set of grid points, x. OF motion tracking (see Section 2.5) is launched to derive displacement vector, dx, between the two projection images at the pixel level.

Fig. 3.

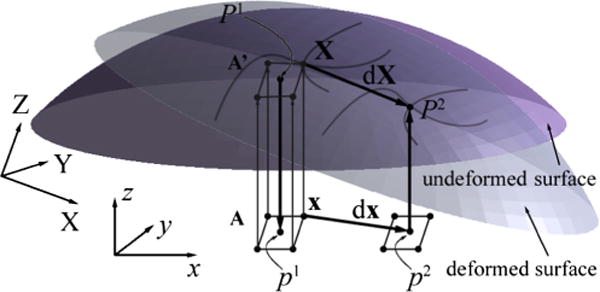
Schematic illustration of the coordinate systems and process used to derive a 3D displacement vector, dX, between two corresponding points, P¹ and P², in 3D space from 2D projection images generated from the undeformed and deformed texture surfaces. See text for details.

Once the 2D projection image displacements, dx, are found, the full 3D displacements can be determined by inverting the spatial mappings. The resulting points in 3D space expressed in the global coordinate system define the starting and end positions of the corresponding displacement vector, dX, as illustrated in Fig. 3. Alternatively, displacements at the projection points, p¹, can be numerically interpolated based on displacement values at grid points, x, and the original position and its displaced locations are mapped back to the undeformed and deformed surfaces, respectively, to compute the 3D displacement vector. Both approaches are similar in computational efficiency because they involve two separate interpolations but differ in terms of the sampling locations used to represent the 3D displacement field. We used the former approach to quantify cortical surface displacements (illustrated in Fig. 3) because it maintains a grid pattern in the starting point locations, which is computationally attractive for local smoothing to improve estimates of cortical surface strain (Ji et al., 2011). On the other hand, when displacements but not strains are desired, the need for a locally smooth (differentiable) field is reduced; hence, the 3D displacement vectors at the projection points, p¹, can be approximated by those at their closest grid positions (i.e., similarly to a closest point interpolation) to further improve computational efficiency.

2.6. Simulated phantom image

Simulated phantom images were used to evaluate the robustness and accuracy of the OF motion tracking. In order to simulate parenchymal surface deformation captured from stereovision, a left camera image from a typical patient (i.e., “undeformed” image) was selected. The exposed cortical area was manually segmented (regions within 50 pixels of the image boundaries were excluded). A synthetic radial displacement field was generated with its magnitude determined by pixel distance from the craniotomy centroid described by

$$u_x=2\sqrt{d}\frac{x-m_x}{d},\text{and}{u}_y=2\sqrt{d}\frac{y-m_y}{d},$$ (6)

where d is the distance between the pixel at (x, y) relative to the image centroid (m_x, m_y). A factor of 2 was introduced to produce a maximum displacement of approximately 37 pixels or 4 mm near the craniotomy rim (pixel resolution was 0.1 mm in both directions).

Functional mapping and interpolation generated the “deformed” image based on the simulated displacement field in Eq. (6). Assuming that image intensity, F(X), at pixel location, X (X = (x, y)), remained identical after displacing dX (dX = (u_x, u_y)), the functional mapping for the deformed image, F′(X), was numerically interpolated based on the relationship:

$$F^{\prime }(\mathbf{X}+\mathit{d}\mathbf{X})=F(\mathbf{X})\text{,}$$ (7)

the outcome of which is shown in Fig. 4.

Fig. 4.

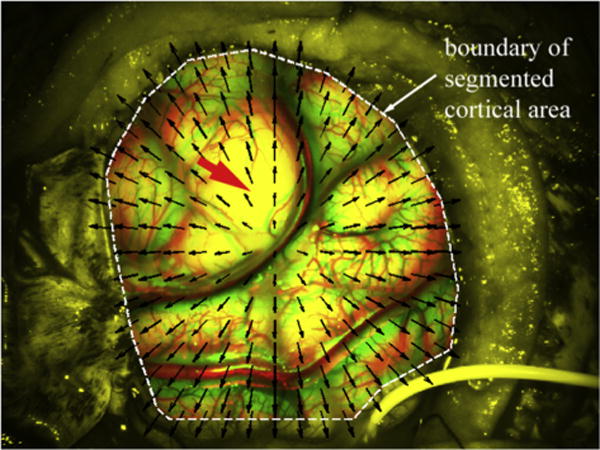
Simulated deformed image with radially outward displacements (arrows) within the craniotomy (dashed line) relative to its undeformed counterpart. Vessels in the undeformed and deformed images appear in red and green, respectively. The thick arrow indicates a “feature-less” area resulting from image saturation during acquisition. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

To test the robustness of OF, the roles of the deformed and undeformed images were interchanged, resulting in a radially-inward compression of the (new) deformed image relative to the (old) undeformed image. In this case, a material point at X + dX in the undeformed image is identical to the point located at X in the deformed image; hence, the displacement vector at X or its functional mapping, G(X), was interpolated based on the relationship

$$G(\mathbf{X}+d\mathbf{X})=-d\mathbf{X}\text{.}$$ (8)

2.7. Clinical data

A total of 18 patient cases involving tumor or abnormal brain tissue (epilepsy) resection were evaluated in this study. Ten of these involved independent measurements of feature locations acquired with a tracked stylus for accuracy comparisons, and 4 of the 8 others involved stereo image acquisitions at three or more time points during surgery to illustrate utility throughout a procedure Images were acquired and analyzed under IRB approval. Demographic information on patient age, gender, and type and location of lesion is reported in Table 1.

Table 1.

Demographic distribution of patient age, gender, and type and location of lesion. Probe tracking data were available at selected feature locations for the first 10 patient cases prospectively evaluated at relatively early stages of surgery.

Patient ID	Age/gender	Type of lesion	Location of lesion
1	58/M	Anaplastic astrocytoma	Right temporal
2	35/M	Meningioma	Right frontal
3	41/M	Oligodendroglioma	Right temporal
4	61/F	Meningioma	Right parietal
5	78/M	Metastatic neuroendocrine carcinoma	Right occipital
6	60/M	Glioblastoma multiforme	Left temporal
7	59/F	Anaplastic with mixed oligodendroglioma	Right frontal
8	46/F	Meningioma	Right parietal
9	75/M	Glioblastoma multiforme	Left frontal–temporal
10	24/F	Mixed oligoastrocytoma	Left frontal
11	56/M	Glioblastoma multiforme	Left frontal
12	61/F	Meningioma	Right parietal
13	18/M	Epilepsy	Right frontal
14	50/F	Metastasis	Right parietal
15	54/M	Glioblastoma multiforme	Left parietal
16	49/F	Glioblastoma multiforme	Right frontal
17	67/F a	Metastasis	Right frontal
18	50/F	Meningioma	Left lateral decubitus

^aA surgical case with tissue retraction.

2.7.1. Accuracy of stereovision reconstruction

For each patient, stereo images were acquired after dural opening and after initial tumor/tissue removal (for those with multiple acquisitions), as well as after more substantive tissue removal or toward the end of resection in a few cases. For cases where the digitizing stylus was used, additional image pairs were acquired at each surgical stage with the probe in view to digitize a set of feature points (e.g., vessel junctions) on the exposed cortical surface in order to evaluate the accuracy of stereovision reconstruction (the number of points typically ranged 2–5 at each stage). The corresponding feature points on the reconstructed cortical surfaces (i.e., without the probe in view) were manually identified to compute pair-wise location differences relative to their probe-determined coordinates. The resulting location differences between homologous feature points were pooled to quantify the overall accuracy of stereovision surface reconstruction at each surgical stage.

2.7.2. Measurement of cortical surface displacement

Full field cortical surface displacements between two surgical stages were obtained from the OF-based registration technique after transforming and projecting the two reconstructed texture surfaces into a common 2D coordinate system, as described in detail in Section 2.4. In order to evaluate the accuracy of the recovered displacement field, displacement vectors independently obtained with the tracked stylus probe at feature point locations common to the two surgical stages were compared. The probe-based feature point displacement vectors served as a “bronze standard” with which to assess the fidelity of the flow-based displacements (e.g., by evaluating the difference in displacement magnitude of the same feature points) because of localized errors caused by the probe tip when in contact with the cortical surface, cortical surface pulsation resulting from blood pressure and respiration (Ji et al., 2011), and the probe tracking system, itself.

Cortical surface displacements between serial surgical scenes were determined using the technique described in the previous sections. For surgeries with cortical surfaces acquired at three or more time points (patients 12, 13, 15, and 16), displacements between the first and last acquisitions were also reported. Because the recovered displacements depend on the specific surgical stage that is categorized as the “undeformed” or “deformed” state, we used an ascending numerical index to label successive iSV images acquired at different times to identify the recovered displacements when necessary (i.e., for images acquired at multiple surgical stages, “1” represents images acquired immediately after dural opening; see Fig. 2 for illustration). Displacement measurements were necessarily limited to the overlapping regions in the projection images acquired during a case. Pixels approximately 2 mm away from the boundary of overlap were also excluded through image erosion as part of the process used to define the iSV field-of-view. For all displacement mappings, the projection image obtained at an earlier (later) surgical stage was chosen as the “undeformed” (“deformed”) image.

The resulting displacements were decomposed along the gravity direction ( ${\overrightarrow{\mathbf{n}}}_{\mathit{gv}}$; obtained by subtracting the tracked locations of the digitizing probe at two vertical positions in the OR) to assess whether the bulk of cortical surface movement correlated with gravitation. Similar evaluations were performed along the average nodal normal direction obtained immediately after dural opening ( $({\overrightarrow{\mathbf{n}}}_{\mathit{nml}})$ to report the magnitude of cortical surface distention (bulging) or collapse (sagging). For both analyses, a signed displacement magnitude was reported to indicate whether the parenchyma moved along (positive) or opposing to (negative) ( ${\overrightarrow{\mathbf{n}}}_{\mathit{gv}}$ or ( ${\overrightarrow{\mathbf{n}}}_{\mathit{nml}}$. Parenchymal surface displacement magnitude in the lateral direction perpendicular to ( ${\overrightarrow{\mathbf{n}}}_{\mathit{nml}}$ was also determined along with the angle between $({\overrightarrow{\mathbf{n}}}_{\mathit{gv}}$ and $({\overrightarrow{\mathbf{n}}}_{\mathit{nml}}$. The total computational time for each pair of cortical surfaces (including generation of projection images, OF motion-tracking, and numerical interpolation to generate 3D displacements) is provided to indicate the computational overhead of the technique. All image processing and data analyses were performed on a Windows computer with two quad-cores (3.2 GHz, 126 GB RAM) using MATLAB (R2013a, The Mathworks, Natick, MA).

3. Results

3.1. Simulated phantom images

The recovered displacement field within the craniotomy from the simulated data is shown in Fig. 5a and b, together with differences relative to the ground-truth (Fig. 5c and d). The majority of pixels had a difference <0.05 pixel (Fig. 5c and d). A small area of pixels had differences in u_y exceeding 0.5 pixel (Fig. 5d), which spatially corresponded to the “feature-less” area indicated in Fig. 4. As expected, displacement estimates were relatively poor at the craniotomy boundary because no physical correspondence between the undeformed and deformed images existed for pixels in this region.

Fig. 5.

Displacement components, u_x (a) and u_y (b), recovered from OF and their corresponding difference images relative to the ground truth (c and d, respectively) for the synthetic data shown in Fig. 4. An area in which the difference magnitude was >0.5 pixel is also shown (thin line in d). The “width” of the band of pixels with relatively poor displacement accuracy near the craniotomy rim was approximately 40 pixels, similarly to the maximum displacement in this region.

Swapping the undeformed and deformed images produced the results shown in Fig. 6. Similarly to Fig. 5, the displacements of the majority of pixels within the craniotomy were recovered almost exactly (typical difference <0.05 pixels). The recovered displacements in the featureless region matched well with the ground-truth (maximum difference ~1.2 pixels; area with difference >0.5 pixels shown in Fig. 6c and d) because of the smoothness constraint applied to the displacement field. However, the rim of pixels with relatively poor displacement accuracy (Fig. 6c and d) was smaller compared to Fig. 5 because all of the displacement vector end points became visible (since they are moving into the craniotomy).

Fig. 6.

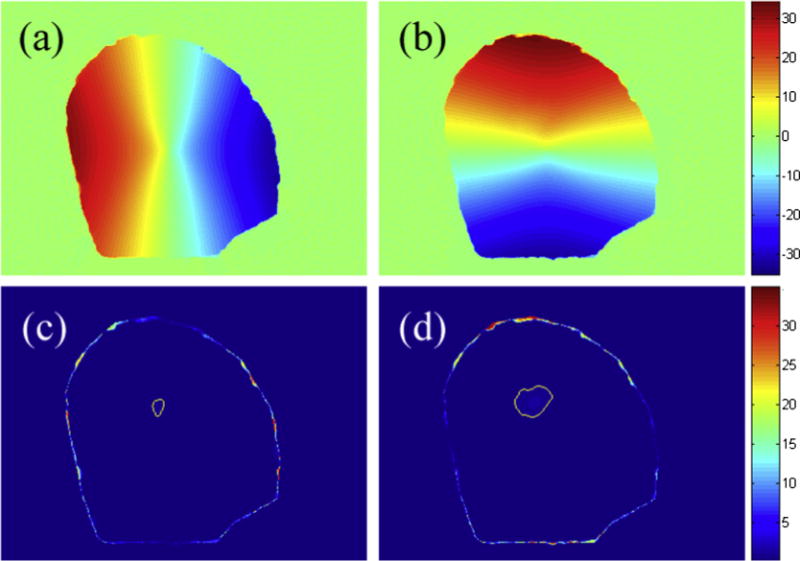
Displacement components, u_x (a) and u_y (b), recovered from OF and their corresponding difference images relative to the ground truth (c and d, respectively) after swapping the undeformed and deformed images used in Fig. 5. Areas in which the magnitude of difference was >0.5 pixel are also shown (thin lines in c and d). The typical “width” of the band of pixels with poor displacement accuracy near the boundary was 3 pixels.

3.2. Clinical patient cases

Assessment of the stereovision surface reconstruction accuracy is available from the collected data with the probe (summarized in Table 2) in which individual cortical features were tracked independently with the stylus. On average, the agreement between the reconstructed surfaced localization and the stylus probe was 1–2 mm both before dural opening and after partial tumor resection, and was also similar for the individual probe recordings used to compute cortical surface displacement at the corresponding feature point locations. Displacements of the selected feature points were obtained either by subtracting the spatial locations of the tracked probe tip between two surgical stages or by extracting values from the dense deformation field recovered from the flow-based motion compensation technique at the corresponding feature locations. The two methods reported similar displacement magnitudes (average of 7–8 mm, range ~3–18 mm). The difference in displacement magnitude was approximately 1 mm on average, suggesting that the congruence between the two displacement measures was satisfactory (Table 2).

Table 2.

Summary of the average accuracy in stereo surface reconstruction at two surgical stages as well as for specific probe-identified points used to compute surface point displacements. Flow- and probe-based point displacements are also shown together with their displacement difference magnitudes (components in parentheses along the microscope optical axis and two perpendicular directions). Except where indicated, only one pair of probe points was available on the cortical surface.

Patient ID	Accuracy (surface 1)	Accuracy (surface 2)	Accuracy (Probe 1)	Accuracy (Probe 2)	Probe-based displacement	Flow-based displacement	Disp. diff. magnitude (components)
1a	1.6 ± 0.6	1.6 ± 0.4	1.5 ± 0.5	1.0 ± 0.2	4.1 ± 0.7	4.5 ± 0.08	0.5 ± 0.2 (0.4, 0.2, 0.1)
2a	2.8 ± 2.3	2.2 ± 1.3	0.6 ± 0.9	2.1 ± 0.5	5.7 ± 0.6	5.2 ± 0.2	0.4 ± 0.3 (0.2, 0.2, 0.3)
3	1.5 ± 0.8	2.9 ± 1.7	1.4	3.6	13.6	14.3	0.8 (0.7, 0.0, 0.2)
4	1.8 ± 1.2	1.6 ± 0.6	2.2	1.9	4.2	6.9	2.7 (0.3, 2.1, 1.8)
5	1.3 ± 0.8	1.2 ± 1.1	1.6	0.6	17.8	17.8	0.1 (0.0, 0.1, 0.0)
6	1.3 ± 0.9	1.9 ± 1.6	0.7	3.7	4.6	5.5	1.0 (0.9, 0.2, 0.2)
7	1.9 ± 0.6	0.7 ± 0.3	2.7	2.6	4.5	4.6	0.1 (0.1, 0.0, 0.1)
8	0.6 ± 0.5	1.9 ± 0.9	2.9	0.9	2.8	3.1	0.3 (0.1, 0.2, 0.0)
9	2.1 ± 1.7	2.5 ± 0.9	1.7	2.8	14.9	17.8	2.8 (2.6, 0.6, 0.5)
10	1.9 ± 2.5	1.4 ± 0.5	2.2	2.5	2.5	3.5	1.0 (0.3, 0.0, 1.0)
Avg.	1.6 ± 0.6	1.8 ± 0.6	1.7 ± 0.7	2.1 ± 1.1	7.3 ± 5.4	7.9 ± 5.7	0.9 ± 0.9

^aPatients 1 and 2 had two and three pairs of probe points on cortical surface available, respectively. Data presented in mm.

For the representative case (patient 1) shown in Fig. 7, the rectified and projection left images before dural opening and after partial tumor resection were compared along with their corresponding reconstructed 3D cortical surfaces. The rectified images are not in the same physical coordinate system (e.g., due to adjustment of the microscopic view), which precluded a direct registration to obtain feature displacements. The projection images, however, were created from reconstructed cortical surfaces in a common coordinate system. Therefore, immobilized features around the craniotomy were naturally aligned, which provided a quality check on the accuracies of the tool tracking and stereovision surface reconstructions (Fig. 8a). Any misalignment between features would indicate gross feature displacements between the two surgical stages (Fig. 8b), which were corrected with the OF-based motion tracking technique (Fig. 8c). The resulting displacements in the projection images were used to recover true 3D displacement vectors through a numerical inversion scheme (Section 2.4). Fig. 9 illustrates similar results from a second patient case.

Fig. 7.

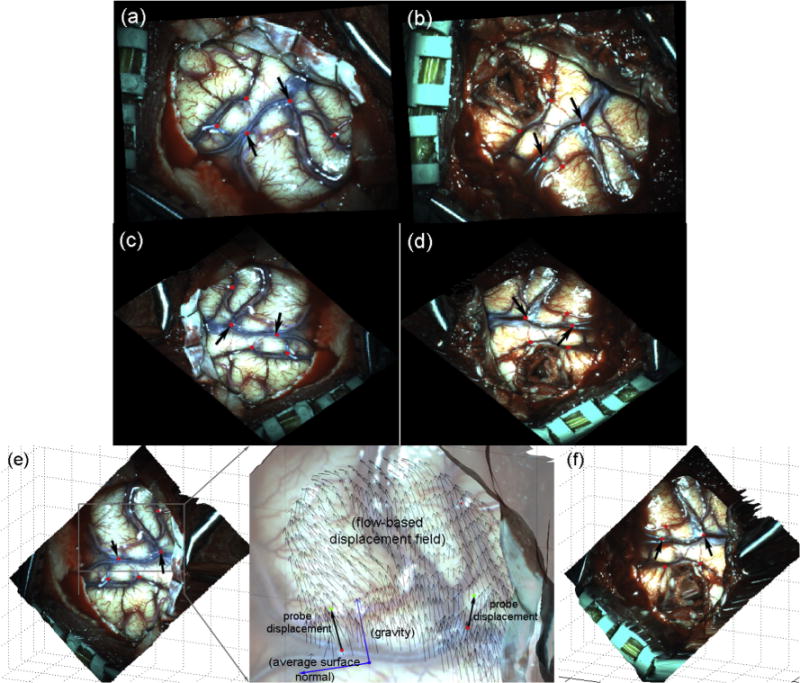
Comparison of rectified (a and b) and projection (c and d) left camera images and the corresponding reconstructed 3D surface (e and f) capturing the exposed cortical surface immediately after dural opening (a and c) and after partial tumor resection (b and d). The tracked feature points at the two surgical stages are also marked with arrows indicating two common feature points probed at these two surgical stages. The two feature point displacement vectors were obtained by subtracting the corresponding homologous point locations recorded by the probe, and are overlaid on the flow-based displacement field (magnified inset in e).

Fig. 8.

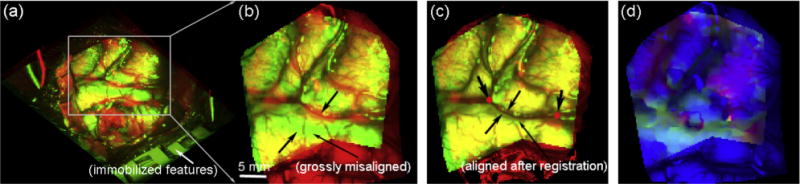
Overlays of projection images before (a and b) and after (c) OF motion compensation for patient 1. The “undeformed” and “deformed” images appear in red and green, respectively. Two common feature points identified in the two surgical stages are also shown (c). The resulting color-coded magnitudes of horizontal (red) and vertical (green) displacements are overlaid on the undeformed image (d). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 9.

Overlay of projection images before (a) and after (b) flow-based registration, along with the corresponding color-coded magnitudes of horizontal (red) and vertical (green) displacements for patient 2. The flow- and probe-based 3D displacement vectors are shown on the reconstructed surface (flow-based displacements around the boundary were excluded from analysis). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.3. Components of cortical surface displacements

For each patient, the magnitudes of the average displacement and the three components (i.e., along ( ${\overrightarrow{\mathbf{n}}}_{\mathit{gv}}$, and along and perpendicular to $({\overrightarrow{\mathbf{n}}}_{\mathit{nml}})$, the angle between $({\overrightarrow{\mathbf{n}}}_{\mathit{gv}}$ and $({\overrightarrow{\mathbf{n}}}_{\mathit{nml}}$, and the total computation times are reported in Table 3. For the four surgeries with iSV data acquired throughout the case (patients 12, 13, 15, and 16), displacement magnitudes reached 10–25 mm, which is in agreement with findings in the literature (Hill et al., 1998; Roberts et al., 1998). The average cortical surface shift was 7.9 mm based on all of the image pairs analyzed, with most of the displacement occurring along the direction of gravity (5.2 mm), whereas the lateral shift was significantly less (2.4 mm on average). The total computational costs ranged from approximately 5–28 s (14 s on average).

Table 3.

Summary of displacement magnitude (d) and components along $({\overrightarrow{\mathbf{n}}}_{\mathit{gv}}(d_{\text{gravity}})$ and $({\overrightarrow{\mathbf{n}}}_{\mathit{nml}}(d_{\text{normal}})$, parenchymal lateral shift (d_lateral), the angle between $({\overrightarrow{\mathbf{n}}}_{\mathit{gv}}$ and $({\overrightarrow{\mathbf{n}}}_{\mathit{nml}}$, as well as the corresponding total computation times. The average magnitude values of these metrics across the patient cases are also reported. Image pairs in parentheses (1st column) indicate the two acquisitions being evaluated, and the time between these image acquisitions, separation time (2nd column), is also given.

Patient ID (image pair)	Separation time (min)	D (mm)	dgravity (mm)	dnormal (mm)	dlateral (mm)	Angle (°)	Compute time (s)
1 (1 → 2)	100	4.1 ± 0.9	3.4 ± 0.8	−3.0 ± 1.1	2.0 ± 1.0	152.2	16
2 (1 → 2)	31	4.4 ± 2.2	2.3 ± 1.9	−3.3 ± 2.8	2.0 ± 1.0	116.3	12
3 (1 → 2)	150	8.4 ± 2.0	6.2 ± 1.2	−7.7 ± 1.8	3.2 ± 1.2	156.4	22
4 (1 → 2)	60	6.7 ± 1.4	3.2 ± 0.9	−6.4 ± 1.4	1.7 ± 1.1	112.0	16
5 (1 → 2)	92	15.3 ± 2.1	−3.1 ± 2.2	−15.0 ± 2.2	2.8 ± 1.0	79.86	11
6 (1 → 2)	82	6.5 ± 1.0	1.8 ± 0.7	−6.3 ± 1.1	1.1 ± 0.6	109.7	21
7 (1 → 2)	37	5.9 ± 0.8	−2.0 ± 0.8	−5.7 ± 0.9	1.3 ± 0.6	73.8	20
8 (1 → 2)	205	4.6 ± 1.9	1.6 ± 2.1	1.8 ± 2.4	3.6 ± 1.7	119.1	11
9 (1 → 2)	154	14.5 ± 2.0	13.5 ± 1.6	−13.9 ± 2.1	3.9 ± 1.4	157.7	9
10 (1 → 2)	170	3.3 ± 1.3	2.3 ± 1.3	−2.9 ± 1.4	1.2 ± 0.7	144.8	10
11 (1 → 2)	11	1.4 ± 0.3	0.05 ± 0.5	−0.4 ± 0.4	1.3 ± 0.3	101.5	11
11 (2 → 3)	14	4.6 ± 1.2	0.8 ± 0.8	−4.3 ± 1.1	1.3 ± 0.6	101.5	12
11 (3 → 4)	57	12.9 ± 1.4	4.2 ± 1.4	−12.6 ± 1.5	2.7 ± 1.2	101.5	13
11 (4 → 5)	2	8.8 ± 0.6	−4.3 ± 1.7	8.1 ± 0.4	3.5 ± 1.4	101.5	10
11 (1 → 5)	84	9.1 ± 1.0	1.5 ± 1.3	−8.9 ± 1.1	1.7 ± 0.9	101.5	15
12 (1 → 2)	5	0.3 ± 0.2	−0.005 ± 0.3	0.003 ± 0.3	0.1 ± 0.06	164.4	13
13 (1 → 2)	21	1.2 ± 0.5	0.7 ± 0.6	−0.9 ± 0.6	0.7 ± 0.3	106.5	21
13 (2 → 3)	38	6.4 ± 2.0	5.6 ± 2.2	−5.9 ± 2.1	2.5 ± 1.0	106.5	18
13 (3 → 4)	100	15.1 ± 11.7	14.0 ± 12.3	−12.7 ± 11.5	8.6 ± 5.9	106.5	20
13 (1 → 4)	159	24.4 ± 14.5	22.1 ± 13.8	−20.3 ± 11.4	4.4 ± 2.0	106.5	22
14 (1 → 2)	17	2.4 ± 0.8	N/A a	1.1 ± 0.6	2.0 ± 1.0	N/A a	13
15 (1 → 2)	25	5.9 ± 2.1	4.2 ± 1.9	−5.2 ± 2.2	2.5 ± 1.0	152.4	28
15 (2 → 3)	48	6.9 ± 2.2	6.6 ± 2.1	−6.1 ± 2.0	2.9 ± 1.4	152.4	24
15 (1 → 3)	73	10.7 ± 3.2	9.6 ± 3.0	−10.0 ± 3.5	3.3 ± 1.3	152.4	24
16 (1 → 2)	50	8.2 ± 1.1	7.9 ± 1.1	−7.9 ± 1.2	2.1 ± 1.0	167.3	11
16 (2 → 3)	74	11.7 ± 2.0	11.5 ± 2.0	−11.1 ± 2.1	3.5 ± 1.3	167.3	12
16 (1 → 3)	124	18.7 ± 2.2	18.1 ± 2.4	−18.3 ± 2.4	4.1 ± 1.8	167.3	19
17 (1 → 2)	1	1.2 ± 0.6	−0.9 ± 0.5	1.0 ± 0.8	0.4 ± 0.3	138.2	6
18 (1 → 2)	9	7.0 ± 0.9	6.2 ± 0.9	−6.8 ± 1.0	1.3 ± 0.7	156.2	5

^aData not available because $({\overrightarrow{\mathbf{n}}}_{\mathit{gv}}$ was not recorded.

The effectiveness of OF motion tracking is qualitatively evident from the four cases illustrated in Fig. 10 where composite images were generated to compare feature (mostly, blood vessels) alignment before and after deforming the initial projection image with the resulting displacement field. The corresponding displacement magnitudes in the horizontal and vertical directions are also shown. Similarly to the simulated data, features in the warped image after OF compensation aligned well with their counterparts in the deformed image in areas with distinct features. However, displacement artifacts did occur, primarily around the boundary or in areas where features in the cortical surface were degraded from tissue resection (e.g., see arrows).

Fig. 10.

Overlays of projection images before (left column) and after (middle column) OF motion compensation on the original image. The “undeformed” and “deformed” images appear in red and green, respectively. Displacement magnitudes in the horizontal and vertical directions are shown in red and green, respectively (right column). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Spatial distributions of cortical surface displacement vectors are illustrated in 3D in Fig. 11 for patient 11, whose iSV images were acquired at five time points after dural opening resulting in four measurements of displacements between consecutive image pairs. Evidently, the parenchymal surface continued to sag along the direction of gravity during the course of tumor resection, but distended after completion of tumor removal, likely due to the release of the retractor and/or tissue strain from the lesion at this point during the case.

Fig. 11.

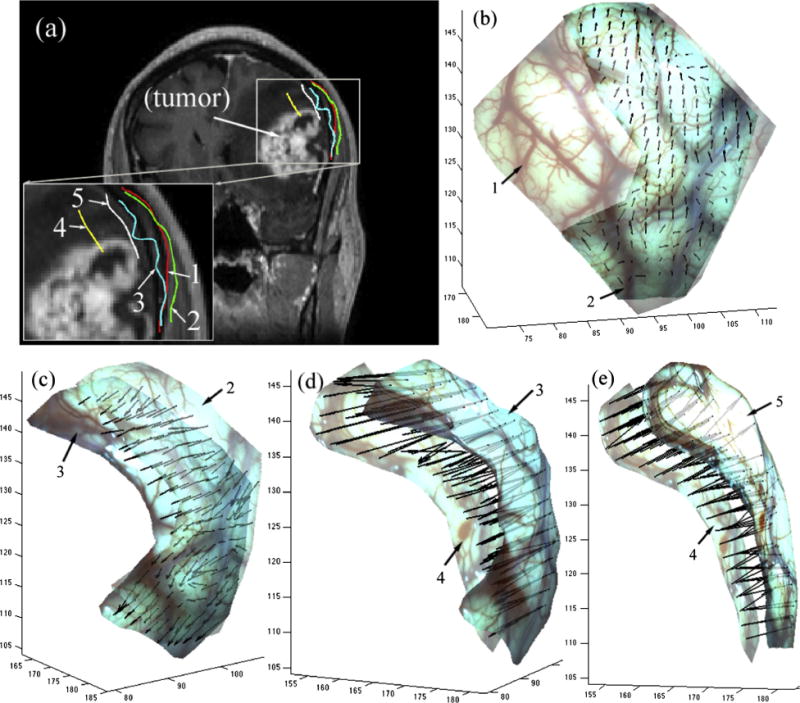
Cross-sections of cortical surfaces reconstructed from iSV at five time points during surgery on the same coronal pMR image showing the progression of the exposed cortical surface during tumor resection for patient 11 in (a). The resulting 3D displacement vectors between two consecutive surgical states are shown in b–e (1: immediately after dural opening, 2 and 3: after partial tumor resection, 4: toward the end of tumor resection with a tumor cavity, and 5: end of resection with tumor cavity filled with fluid).

Finally, Fig. 12 shows displacements recovered between the cortical surfaces captured immediately after dural opening and at an early stage of retraction in patient 17. The intersections with the sagittal pMR (Fig. 12a) suggest bulging from the retractor in place, which agrees with the 3D displacements recovered between the two cortical surfaces (Fig. 12b).

Fig. 12.

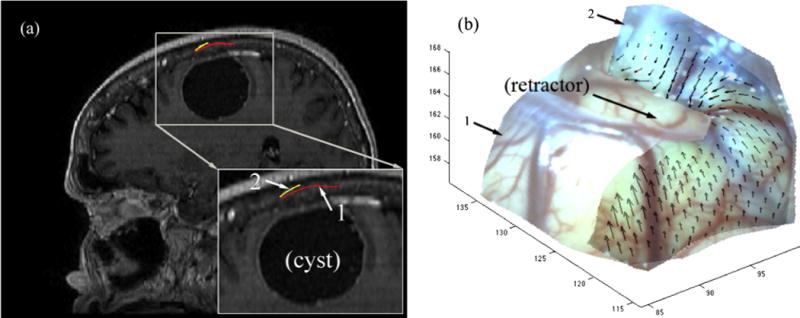
Intersections of reconstructed cortical surfaces after dural opening (1) and at an early stage of retraction (2) on a sagittal pMR image (a) for patient 17. The resulting 3D displacements between the two surfaces are shown in (b) and suggest surface bulging from the retractor in place. Arrow points to retractor location on surface 2 (no retractor was present when surface 1 was acquired).

4. Discussion and conclusion

Stereovision is an attractive intraoperative imaging technique in image-guided neurosurgery because it provides detailed, high-resolution information on the cortical surface geometry and texture intensity. In addition, stereo cameras are easily mounted to existing surgical microscopes unobtrusively and acquire images of the exposed cortical surface at any time during surgery with no intrusion to surgical workflow. The image warping approach we recently developed for efficient cortical surface reconstruction at arbitrary magnification and focal length settings of the surgical microscope (Ji et al., 2014) further facilitates the effective deployment of the intraoperative imaging technique for surface-shift tracking in the OR. As a result, frequent image sampling of the surgical scene is possible throughout the course of surgery and can be used to update pMR images for neuronavigation, through which more accurate guidance is expected in a given patient case.

In this study, we have successfully applied OF motion tracking to determine deformation of the exposed cortical surface during surgery in phantom images and 18 clinical cases with different lesions and surgical procedures (tumor/brain tissue resection and retraction). Results from the digital phantom study suggest the OF motion-tracking algorithm is very accurate (<0.05 pixels in general). Because of the confinement of the craniotomy, tissue locations around the rim became invisible when the synthetic, radially-outward displacement field was applied which led to displacement artifacts in this area. By switching the undeformed and deformed images (and thereby producing a radially inward displacement field) the end points of all of the displacement vectors were visible (i.e., inside the craniotomy boundary), and significantly reduced the area of displacement artifacts (Figs. 5 and 6).

The accuracy of the stereovision reconstruction and associated OF-based displacement maps was assessed with the “bronze standard” of stylus probe tracking of the displacements of individual features in 10 surgical cases. We found an average agreement of 1.7–2.1 mm was typical for feature movements derived from the reconstructed stereovision cortical surfaces relative to those measured with a tracked stylus probe (Table 2) – a level of accuracy in the clinical setting similar to earlier reports based on physical phantoms evaluated in a controlled environment (Sun et al., 2005). Displacement vectors at selected feature points from the flow- and probe-based measurements were similar (Figs. 6 and 8) and differed in magnitude by approximately 1 mm on average (Table 2), suggesting the agreement between the two displacement measures was excellent. Based on the OF-based displacements, the magnitude of cortical surface displacements was 7.9 ± 5.7 mm (range 0.3–24.4 mm) in the 18 cases evaluated, which is consistent with values reported in the literature (e.g., mean shift of 9.4 mm with a range from 2 to 24 mm measured from 10 patient cases in Ding et al. (2009)). In addition, average displacement components along the direction of gravity, along the average surface nodal normal at the craniotomy (obtained immediately after dural opening), and in the lateral direction were 5.2 ± 6.0, 2.9 ± 8.9 and 2.4 ± 1.6, respectively. For surgeries where cortical surfaces were visible toward or at the end of tumor resection, we found that the parenchymal surface continued to sag throughout the procedure most of the time, except in patient 11 where the parenchymal surface distended (relative to the previous stage) after completion of tumor resection, likely due to removal of the retractor and/or release of tissue strain caused by the space-occupying lesion. In addition, the accumulated displacements between successive surgical stages were consistent with those found between the first and last stage in terms of the gravitational and average surface normal directions (difference between the displacement magnitudes <2 mm for patients 11, 13, 15, and 16 in Table 3). The accumulated lateral shifts were less consistent because unlike the gravitation (or average surface normal) direction determined immediately after dural opening, the lateral direction was not necessarily unique at each surgical stage (Table 3).

Our technique for determining cortical surface shift over time is conceptually similar to the method described in Sinha et al. (2005), where 2D nonrigid image registration was performed on laser range scanner (LRS) texture images while full 3D displacements were recovered by mapping the texture image pixel coordinates into their 3D correspondence points. Because the resolution of the LRS point cloud is routinely less dense than the texture image, the resolution of the resulting 3D displacements could also be limited. In our method, the 2D images were generated by directly projecting the 3D reconstructed texture surface, in which case the resolution is maintained without loss of image information. Our technique is also analogous to approaches used in Paul et al. and Ding et al. where 3D cortical surface profiles were reconstructed at multiple points during surgery. However, our method differs significantly in the way registration is performed to obtain the deformation field. Both prior approaches require video streams to be continuously acquired to identify and track a set of features (e.g., natural landmarks in Paul et al. (2009) or vessels in Ding et al. (2011)), which demand additional image processing when sudden appearance/disappearance of blood or surgical tools occurs in the field-of-view. In Paul et al. (2009), the two cortical surfaces were registered directly by optimizing a cost function based on intensity, inter-surface distance, and sparse displacement information provided by the tracked feature points. In Ding et al. (2011), registration was conducted between 2D video images directly because a laser range scanner was used to provide 3D coordinates for pixels in the video images. Our approach does not require continuous video streams of the cortical surface, nor does it need to identify or track landmarks/features. Instead, we project reconstructed cortical surfaces obtained from two surgical scenes into a common 2D local coordinate system and perform image registration between the resulting projections. Because the projection images and their original 3D surfaces are uniquely related through numerical inversion (as long as no surface “folding” occurs), a full 3D displacement field can be recovered from the resulting 2D displacements generated through the nonrigid registration via optical flow. Unlike registering video images directly (Ding et al., 2011), the computed displacement field does not suffer from camera lens distortion because it has already been corrected during cortical surface reconstruction (Sun et al., 2005). Although rectified images prior to cortical surface reconstruction are also free of camera lens distortion, they were not selected for OF motion-tracking in this study because they are not necessarily in the same coordinate system due to changes in microscope image acquisition settings and/or orientation with respect to the patient when collected at different times during surgery. Our method using projected 2D images from reconstructed cortical surfaces does not require video streaming or feature identification, nor does it depend on image acquisition settings or orientation relative to the patient; hence, our technique is simple to implement in the OR and is independent of these types of difficult to control OR parameters.

The effectiveness of OF motion tracking for registering cortical surface projection images was also demonstrated in the study. Unlike the feature-based approaches in Paul et al. (2009) and Ding et al. (2011), the OF algorithm operates on the images automatically based on a constrained gray value constancy assumption. As shown here as well as previously (Ji et al., 2011), the OF algorithm is able to produce a dense displacement field at the pixel level with sub-pixel resolution as long as sufficient and distinct features are present in the images acquired.

The ability of our technique to estimate cortical surface shift using stereovision through projection image registration depends on the underlying OF-based nonrigid registration which is based on the principle of intensity conservation (Section 2.4). As long as physical correspondences exist between the two projection images in their overlapping region that satisfy the intensity conservation principle, the technique is expected to be successful, irrespective of how far apart the stereo image pairs were acquired in time (e.g., between 1 min to more than 3 h apart in patients 17 and 8, respectively; Table 3). However, the OF algorithm can fail or result in displacement artifacts when the gray value constancy assumption no longer holds. For example, displacement artifacts occurred when no physical correspondence existed for pixels near the craniotomy in the synthetic undeformed image when it was radially stretched outward within the craniotomy (but maintained identical image content outside this area; Fig. 5). However, after switching the undeformed and deformed images to establish the physical correspondence, displacement artifacts near the boundary were significantly reduced (Fig. 6). Displacement artifacts may also result in clinical cases when bleeding occurs or the cortical surface is altered during the surgical procedure, especially toward the end of a case (see arrow in Fig. 10). Under these conditions, green or blue channels (instead of the full RGB images) may be used for registration since the red channel is likely influenced the most when bleeding takes place. In addition, the surgeon may be able to remove the blood on the surface as much as possible before image acquisition. These regions could also be manually selected and excluded from OF motion tracking and displacement mapping because the artifacts only affect the local deformation. Alternatively, features found in the projection images (e.g., vessels) could be registered to recover the full 3D displacement through stereopsis, which would be similar to Ding et al. (2011), but without lens distortions. On the other hand, the success of OF-based image registration becomes more challenging as surgery progresses in some cases, for example, as more extensive resection occurs that would likely reduce the overlapping regions in the projection images and their concomitant physical feature correspondences.

The computational cost of our technique depends on the density of displacement field desired as well as the field of view in the projection images. In this study, we fixed the pixel resolution to 0.1 mm/pixel in the projection images, which resulted in an average of 15 s in total to compute a full 3D displacement field from a pair of cortical surfaces. In practice, the pixel resolution could be lowered, e.g., to 0.5 mm/pixel, in order to capture brain surface shift to millimeter accuracy, in which case the computational burden can be significantly reduced (e.g., less than 5 s). The computational efficiency can also be improved when only displacement but not surface strain is needed, in which case the 2D-to-3D inversion can be simplified by using a nearest neighbor (instead of a trilinear) interpolation. In addition, because the textured 3D surfaces are projected into a common 2D coordinate system, any image-based registration technique can be applied to compensate for feature misalignment from which the 2D in-plane displacements are derived. For example, mutual information-based nonrigid registration (e.g., via B-spline) could be used to register the 2D projection images. These other registration techniques may be more tolerant of surgical light saturation and lack of local correspondence than the OF-based method applied here. However, their displacement accuracy would likely be determined by the optimization of parameters such as the number of grids. Regardless, future investigation should compare the relative performances (accuracy and efficiency) of the mutual information- and flow-based nonrigid registrations to identify their relative strengths and weaknesses when applied to model-based brain shift compensation.

Ultimately, cortical surfaces reconstructed from iSV need to be registered with pMR images to determine displacement maps relative to the undeformed parenchyma for model-based brain shift compensation. Although full 3D surfaces can be reconstructed both before and after dural opening, intensity-based registration alone is not sufficient to establish the relative deformation because the two surfaces are not homologous – they differ substantially in appearance. Similarly, geometry-only registration methods (e.g., ICP) may not be able to fully capture brain surface shift especially in the lateral direction as shown in previous studies (Fan et al. 2012; Paul et al., 2009). This challenge is solved by generating an intensity-encoded cortical surface profile from pMR images within the craniotomy to highlight surface vessels which are registered with the iSV-reconstructed surface after dural opening using their projection images in a local coordinate system (Fan et al., 2012). Once the initial deformation is established between iSV and pMR, further cortical surface displacement relative to the undeformed brain becomes available, which can serve as data for brain shift compensation.

In summary, we have presented a cortical surface registration technique using iSV image pairs acquired at two time points of interest during surgery without the need for continuous video streaming or individual feature identification/tracking. Instead, cortical surfaces are registered using their projection images in a common local coordinate system with optical flow motion tracking. Using both digital phantom images and clinical patient cases, we have shown that the technique is accurate and computationally efficient and capable of generating displacement maps for model-based brain shift compensation in the OR.