Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Sep 9.
Published in final edited form as: J Biomech. 2012 Sep 8;45(15):2719–2723. doi: 10.1016/j.jbiomech.2012.08.007

The inaccuracy of surface-measured model-derived tibiofemoral kinematics

Kang Li a, Liying Zheng b, Scott Tashman b,d, Xudong Zhang b,c,d,*
PMCID: PMC4158613  NIHMSID: NIHMS401965  PMID: 22964018

Abstract

This study assessed the accuracy of surface-measured OpenSim-derived tibiofemoral kinematics in functional activities. Ten subjects with unilateral, isolated grade II PCL deficiency performed level running and stair ascent. A dynamic stereo radiography (DSX) system and a Vicon motion capture system simultaneously measured their knee or lower extremity movement. Surface marker motion data from the Vicon system were used to create subject-specific models in OpenSim and derive the tibiofemoral kinematics. The surface-measured model-derived tibiofemoral kinematics in all 6 degrees of freedom (DOFs) were then compared with those measured by the DSX as the benchmarks. The differences between surface- and DSX-measured tibiofemoral kinematics were found to be substantial: the overall mean (±SD) RMS differences during running were 9.1±3.2°, 2.0 ± 1.2°, 6.4 ± 4.5° for the flexion-extension, abduction-adduction, and internal-external rotations, and 7.1± 3.2mm, 8.8± 3.7mm, and 1.9± 1.2mm for anterior-posterior, proximal-distal, and medial-lateral translations. The differences were more pronounced in the relatively higher speed running than in stair ascent. It was also found that surface-based measures significantly underestimated the mean as well as inter-subject variability of the differences between PCL-injured and intact knees in abduction-adduction, internal-external rotation, and anterior-posterior translation.

Keywords: Surface Measurement, Dynamic X-ray, Tibiofemoral Kinematics, Plug-in Gait Model, OpenSim

1. Introduction

Biodynamic simulation is a powerful means for studying the musculoskeletal system. However, the significant time investment and technical challenges associated with developing realistic dynamic simulations have been a formidable barrier in its widespread use (Delp et al., 2007). OpenSim (Delp et al., 2007) exemplifies an integrative and effective open-source platform for creating sophisticated musculoskeletal models and simulations. Biomechanical studies are increasingly utilizing such a platform to derive joint kinematics, to estimate neuromuscular responses, and to understand the cause-effect relationships in musculoskeletal dynamics (e.g. Arnold et al., 2007; Damiano et al., 2010; Fox and Delp, 2010; Riley et al., 2010; Xiao and Higginson, 2010).

Although modeling platforms such as OpenSim provide a relatively easy path towards creating musculoskeletal simulations, the veracity of these simulations persists as an issue of concern. More specifically, surface-based marker or sensor motion data, combined with kinematic relations or constraints in the model construct, determine the underlying skeletal kinematics of most of these simulations. While the effects of soft tissue artifacts on kinematic variables directly estimated from surface-based measurement have been well recognized and characterized (Cappozzo et al., 1996; Tsai et al., 2011), the accuracy of surface-measured model-derived kinematics remains largely unknown.

This study aimed to assess the accuracy of surface-measured tibiofemoral kinematics derived using OpenSim as a convenient yet representative modeling platform, with simultaneous measurement by a dynamic radiographic system as the ‘gold standard.’

2. Methods

We used data from an experimental study of posterior cruciate ligament (PCL) injury. Ten subjects with unilateral, isolated grade II PCL injury participated in the study, which was approved by University of Pittsburgh Institutional Review Board. The mean (± standard deviation) weight, height, and BMI of the 10 subjects were 78.4 (±17.2) kg, 178.9 (±8.5) cm, and 24.3 (±3.2). The subjects' age ranged from 19 to 28 (mean: 21.7±3.6).

After informed consent was obtained, each subject underwent the experimental protocol illustrated in Fig. 1. High-resolution CT scans of the subject's knees were taken with slice spacing of 0.625 mm. Mimics software (Materialise, Belgium) was used to segment the femur and tibia from the CT scans and create 3D surface models of the bones. One slice of both hips (through the center of the femoral heads) and one slice of both ankles (through the malleoli) were also obtained to facilitate defining local coordinate systems on the femur and tibia (Tashman et al., 2004).

Fig. 1.

Fig. 1

Open in a new tab

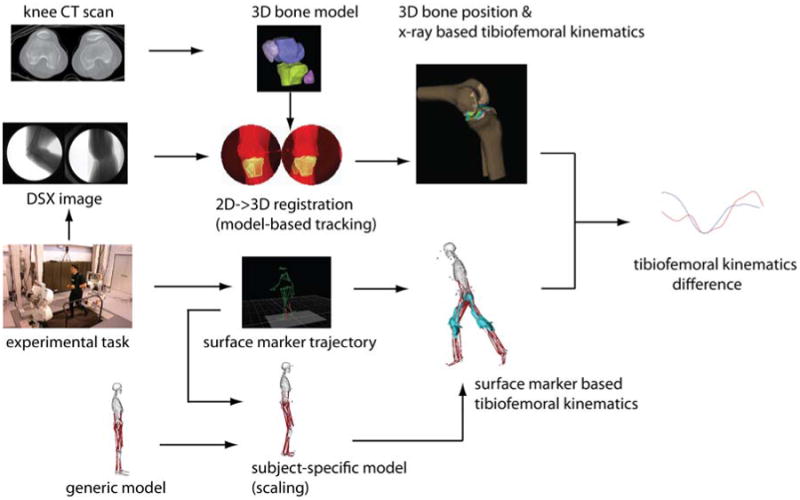
Data analysis logic diagram. CT scans of both knees were used to reconstruct 3D bone models to facilitate a model-based tracking process which determined the DSX-measured tibiofemoral kinematics. The surface-measured tibiofemoral kinematics, with a Plug-in Gait Marker Set, was derived using the inverse kinematics algorithm in OpenSim.

Each subject performed three activities: static standing, level running on a dual-belt instrumented treadmill at 2.5 m/s, and self-paced stair ascent on a custom-made three-step stairway (run: 29.21 cm; rise: 19.69 cm). A dynamic stereo radiography (DSX) system measured the subject's knee joint kinematics while a Vicon MX motion capture system (8 MXF20 cameras, Nexus software) measured the motions of spherical reflective surface markers (1-cm diameter) placed on subject's lower extremity as specified by the Vicon Plug-in Gait Marker Set (Davis et al., 1991). The sampling frequencies for both systems were set at 150Hz during running and 100Hz during stair ascent. The Vicon and DSX systems were synchronized using a precision pulse generator (Berkeley Nucleonics Corp, model 565). Before each test session, the DSX system was calibrated for correcting image distortion using a marker grid and for determining image geometry using a 3-D calibration cube (You et al., 2001).

A model-based tracking procedure (Tashman et al., 2004; You et al., 2001) determined the 3D tibial and femoral bone positions from the dynamic radiographic images with previously documented precision of ±0.2°/0.2 mm under static or low-speed conditions and ±0.9°/0.7 mm or better under dynamic conditions (Anderst et al., 2009). Tibiofemoral rotations were calculated according to the definitions by Grood and Suntay (1983); translations were defined by the motion of the tibial coordinate system origin relative to the femur origin, expressed in the femoral coordinate system (Tashman et al., 2004).

The use of OpenSim for computing tibiofemoral kinematics from measured surface marker motions required the creation of a subject-specific musculoskeletal model via scaling of a generic model (Fig. 1). The musculoskeletal model developed by Arnold et al. (2010) was chosen as the generic model, which defined the translations (anterior-posterior and proximal-distal) and rotations (internal-external and adduction-abduction) of the tibia relative to the femur as functions of the knee flexion angle, according to relationships established in the literature (Walker et al., 1988). The joint coordinate systems were chosen to be the same as those used to define the DSX-measured joint kinematics. A ‘virtual’ Plug-in Gait Marker Set was placed on the model. The scaling procedure utilized the Scale Model tool in OpenSim, which adjusted the body segment lengths of a generic model to best match the ‘virtual’ markers and the corresponding experimental surface markers captured during a standing trial. After scaling, the inverse kinematics tool embedded in OpenSim (Arnold et al., 2010; Delp et al., 2007) was used to solve for the joint angles such that the discrepancy between experimentally measured surface markers and virtual markers on the model was minimized. The surface-measured model-derived tibiofemoral kinematics were then computed from the knee flexion angle and kinematic constraints.

Data from four experimental trials by each subject were used: two trials of level running (one for the intact limb and one for the injured), and two trials of stair ascent (one for the intact limb and one for the injured). All trials were interpolated to the maximum common time window with respect to the heel strike (-0.06s to 0.1s for running and -0.04s to 0.34s for stair ascent). The root-mean-square (RMS) and maximum differences between DSX- and surface-measured kinematics in three rotational degrees of freedom (DOFs) (i.e. internal-external rotation, abduction-adduction, and flexion-extension) and three translational DOFs (medial-lateral, proximal-distal, and anterior-posterior translations) were quantified and summarized across all subjects and limbs. Paired t-tests were performed at discrete time points with 0.02-second intervals on each limb for each activity to examine whether the surface- and DSX-measured kinematics were significantly different. All the preceding data analyses were performed using MATLAB® programs (The MathWorks, Boston, MA).

3. Results

Substantial differences were observed between surface- and DSX-measured tibiofemoral kinematics during running and stair-ascent as quantified by the RMS and maximum differences (Table 1). These RMS and maximum differences were greater or comparable to the DSX-measured kinematic differences between injured and intact limbs except the flexion-extension during stair-ascent (Table 2).

Table 1. Mean (±SD) RMS and maximum differences between DSX- and surface-measured tibiofemoral kinematics across 10 subjects.

Kinematics Activities
Running Stair-Ascent
Overall Injured Intact Overall Injured Intact
Flexion- Extension (°) RMS 9.1±3.2 9.5±3.2 8.8±3.3 3.3±1.1 2.7±0.7 3.9±1.2
Max 15.8±4.8 16.3±4.6 15.4±5.1 5.9±1.1 5.6±1.0 6.4±0.8
Abduction- Adduction(°) RMS 2.0±1.2 1.5±0.7 2.4±1.5 2.5±1.7 2.3±1.8 2.8±1.6
Max 2.7 ± 1.4 2.2±0.8 3.2±1.6 3.5 ± 1.8 3.2±2.0 3.8±1.6
Internal- External Rotation(°) RMS 6.4±4.5 6.9±5.7 6.0±3.4 5.1±3.3 5.8±3.5 4.4±3.2
Max 9.0 ± 5.1 9.4±6.5 8.5±3.7 7.3 ± 4.4 8.0±5.0 6.6±4.0
Anterior- Posterior Translation (mm) RMS 7.1±3.2 6.6±2.9 7.6±3.5 6.1±2.5 6.2±2.7 5.9±2.5
Max 11.2±3.6 11.0±4.0 11.4±3.4 8.7± 3.3 9.1±3.6 8.4±3.1
Proximal-Distal Translation (mm) RMS 8.8±3.7 8.2±3.9 9.4±3.7 11.0±4.6 9.7±4.4 12.2±4.7
Max 12.3±3.8 11.8±4.1 12.8±3.7 13.0±5.0 11.9±4.5 14.2±5.4
Medial-Lateral Translation (mm) RMS 1.9±1.2 1.9±1.1 1.9±1.3 1.5±0.8 1.3±0.4 1.6±1.0
Max 3.0± 1.7 2.9±1.7 3.0±1.9 2.0± 0.9 1.9±0.5 2.1±1.2
Open in a new tab

Table 2. Mean (±SD) RMS and maximum differences of tibiofemoral kinematics between injured and intact limbs across subjects.

Kinematics Activities
Running Stair-Ascent
DSX Surface DSX Surface
Flexion- Extension (°) RMS 8.3±4.6 10.95±5.2 6.8±3.9 7.5±6.0
Max 14.4±8.0 20.5±11.2 9.9±6.0 10.4±7.8
Abduction- Adduction(°) RMS 2.0±1.0 0.5±0.2 1.5±0.7 0.2±0.2
Max 2.8±1.2 0.9±0.4 2.3±1.2 0.4±0.4
Internal-External Rotation(°) RMS 5.3±2.4 2.1±0.9 5.0±1.8 0.6±0.7
Max 7.8±2.3 3.7±1.7 7.5±2.1 1.2±1.4
Anterior- Posterior Translation (mm) RMS 5.3±4.7 2.5±1.1 3.8±5.9 0.9±1.1
Max 8.4±6.0 4.5±2.2 5.1±6.7 1.7±1.9
Proximal-Distal Translation (mm) RMS 2.4±1.9 2.2±1.2 4.9±7.2 2.4±1.8
Max 4.0±3.8 4.5±2.5 8.0±10.0 3.3±2.0
Medial-Lateral Translation (mm) RMS 1.7±1.0 0.0±0.0 1.2±0.7 0.0±0.0
Max 2.8±1.8 0.0±0.0 1.9±0.9 0.0±0.0
Open in a new tab

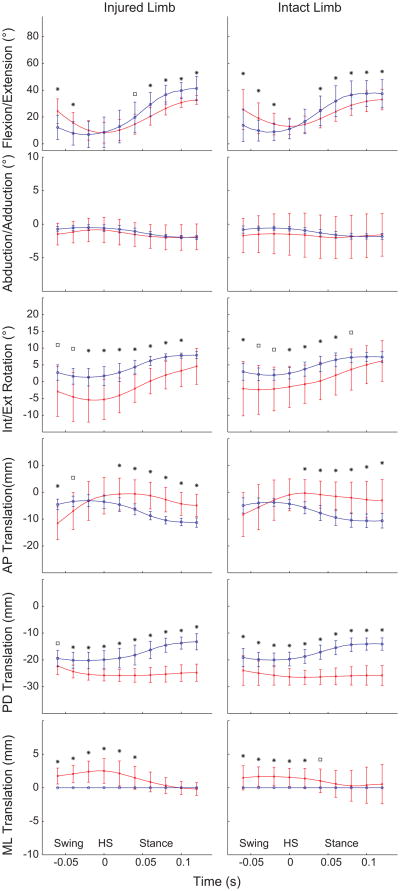
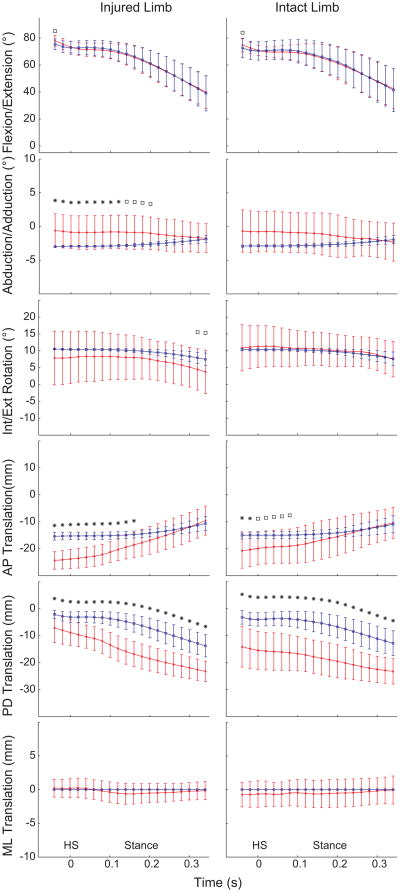
The inaccuracy of surface-measured model-derived tibiofemoral kinematics appeared to be greater during the relatively higher-speed running activity than stair ascent (Fig. 2 and 3). During the early stance phase of stair-ascent, no significant differences in flexion-extension, internal-external rotation, and medial-lateral translation were observed between DSX- and surface-measured kinematics for either injured or intact limb. Significant differences were found in anterior-posterior translation near heel-strike and proximal-distal translation for both limbs, and abduction-adduction rotation for the injured limb. The differences between DSX- and surface-based kinematics during running were more pronounced: all but abduction-adduction rotation exhibited significant differences in the stance phase and all but anterior-posterior translation and abduction-adduction rotation in the swing phase.

Fig. 2.

Fig. 2

Open in a new tab

Comparisons of DSX-measured (red line) and surface-measured model-derived (blue line) tibiofemoral kinematics of injured and intact limbs during running with 0.02 second intervals. Note that the medial-lateral translation is always zero for the surface-measured kinematics. Time 0 is set at heelstrike (HS). *P<.05. □P<.10.

Fig. 3.

Fig. 3

Open in a new tab

Comparisons of DSX-measured (red line) and surface-measured model-derived (blue line) tibiofemoral kinematics of injured and intact limbs during stair-ascent with 0.02 second intervals. Note that the medial-lateral translation is always zero for the surface-measured kinematics. Time 0 is set at heelstrike (HS). *P<.05. □P<.10.

The surface-based approach could fail to detect important kinematic changes due to injury. The surface-based model-derived measures significantly underestimated the mean as well as inter-subject variability of the differences between injured and intact knees in abduction-adduction, internal-external rotation, and anterior-posterior translation (Table 2)—three defining measures of knee joint instability.

4. Discussion

The present study assessed the accuracy of surface-measured model-derived tibiofemoral kinematics, using a common video-motion capture system and an open, increasingly popular modeling platform. While previous studies (Akbarshahi et al., 2010; Benoit et al., 2006; Cappozzo et al., 1996; Peters et al., 2010; Reinschmidt et al., 1997; Stagni et al., 2005; Tsai et al., 2009; Tsai et al., 2011) have recognized and characterized the effects of skin motion artifacts on surface-based measurement of joint kinematics, surface-measured model-derived tibiofemoral kinematics remains as an investigative niche. Definitions of functionally and clinically meaningful tibiofemoral kinematics rely on an underlying bone model, which is featured in musculoskeletal modeling software such as OpenSim. We therefore coined the term ‘surface-measured model-derived’ to distinguish this increasingly adopted approach to estimating joint kinematics either explicitly or as part of biodynamic simulation. We found that the errors in surface-based model-derived tibiofemoral kinematics to be substantial and comparable to or even greater than the differences between PCL-injured and intact knees in corresponding measures. We further demonstrated that surface-measured differences were smaller than the ‘true’ differences measured by dynamic stereo radiography, and confirmed that surface-based approach would underestimate or fail to discern subtle but important patho-mechanical responses.

The inaccuracy in surface marker-based model-derived kinematics mainly stemmed from two sources: soft tissue artifacts (STAs) and model inadequacies (Andersen et al., 2010). The former effects are activity-dependent and more pronounced in higher speed motions as shown in the current study and reported by several previous studies (Fuller et al., 1997; Peters et al., 2010; Stagni et al., 2005); the latter, which could include idealized joint geometry, improper kinematic constraints and anthropometric scaling (Lathrop et al., 2011), should have more uniform effects on different activities. We speculate, based on our data of the specific activities considered (Table 1), that STAs mainly accounted for the inaccuracy in flexion-extension whereas the effects due to OpenSim model limitations might have dominated for the other five DOFs. However, it must be acknowledged that the contributions of these two sources of error were not quantitatively ascertained in the current study.

It should also be noted that the surface-based movement measurement was made using the Plug-in Gait Marker Set, which involves a relatively small number of markers on the lower extremity. Techniques employing more markers, such as the cluster point method (Andriacchi et al., 1998), or Helen Hayes marker set (Kadaba et al., 1990), may mitigate the effect of skin motion artifacts. It would be worthwhile to assess the accuracy of those approaches using dynamic radiographic measurement of skeletal motion as the ‘benchmark.’

While dynamic stereo radiography may be considered the “gold standard” to date for measuring skeletal kinematics, it can only focus on one body joint or region for a stringently limited exposure time. Therefore, a method to integrate both surface- and X-ray based kinematics is desired such that both the holistic whole-body responses and more detailed joint mechanical responses can be examined simultaneously.

Acknowledgments

This work was supported in part by the NFL Charities and the NIH/NIAMS (5R03AR59939).

Footnotes

Conflict of Interest: None.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Akbarshahi M, Schache AG, Fernandez JW, Baker R, Banks S, Pandy MG. Noninvasive assessment of soft-tissue artifact and its effect on knee joint kinematics during functional activity. Journal of Biomechanics. 2010;43:1292–1301. doi: 10.1016/j.jbiomech.2010.01.002. [DOI] [PubMed] [Google Scholar]
  2. Andersen MS, Benoit DL, Damsgaard M, Ramsey DK, Rasmussen J. Do kinematic models reduce the effects of soft tissue artefacts in skin marker-based motion analysis? An in vivo study of knee kinematics. Journal of Biomechanics. 2010;43:268–273. doi: 10.1016/j.jbiomech.2009.08.034. [DOI] [PubMed] [Google Scholar]
  3. Anderst W, Zauel R, Bishop J, Demps E, Tashman S. Validation of three-dimensional model-based tibio-femoral tracking during running. Medical Engineering & Physics. 2009;31:10–16. doi: 10.1016/j.medengphy.2008.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andriacchi TP, Alexander EJ, Toney MK, Dyrby C, Sum J. A point cluster method for in vivo motion analysis: applied to a study of knee kinematics. Journal of Biomechanical Engineering. 1998;120:743–749. doi: 10.1115/1.2834888. [DOI] [PubMed] [Google Scholar]
  5. Arnold AS, Schwartz MH, Thelen DG, Delp SL. Contributions of muscles to terminal-swing knee motions vary with walking speed. Journal of Biomechanics. 2007;40:3660–3671. doi: 10.1016/j.jbiomech.2007.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Arnold EM, Ward SR, Lieber RL, Delp SL. A model of the lower limb for analysis of human movement. Annals Biomedical Engineering. 2010;38:269–279. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Benoit DL, Ramsey DK, Lamontagne M, Xu L, Wretenberg P, Renstrom P. Effect of skin movement artifact on knee kinematics during gait and cutting motions measured in vivo. Gait & Posture. 2006;24:152–164. doi: 10.1016/j.gaitpost.2005.04.012. [DOI] [PubMed] [Google Scholar]
  8. Cappozzo A, Catani F, Leardini A, Benedetti MG, Croce UD. Position and orientation in space of bones during movement: experimental artefacts. Clinical Biomechanics (Bristol, Avon) 1996;11:90–100. doi: 10.1016/0268-0033(95)00046-1. [DOI] [PubMed] [Google Scholar]
  9. Damiano DL, Arnold AS, Steele KM, Delp SL. Can strength training predictably improve gait kinematics? a pilot study on the effects of hip and knee extensor strengthening on lower-extremity alignment in cerebral palsy. Physical Therapy. 2010;90:269–279. doi: 10.2522/ptj.20090062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Davis R, Ounpuu S, Tyburski D, Gage J. A gait analysis data collection and reduction technique. Human Movement Science. 1991;10:575–587. [Google Scholar]
  11. Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54:1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
  12. Fox MD, Delp SL. Contributions of muscles and passive dynamics to swing initiation over a range of walking speeds. Journal of Biomechanics. 2010;43:1450–1455. doi: 10.1016/j.jbiomech.2010.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fuller J, Liu LJ, Murphy MC, Mann RW. A comparison of lower-extremity skeletal kinematics measured using skin- and pin-mounted markers. Human Movement Science. 1997;16:219–242. [Google Scholar]
  14. Grood ES, Suntay WJ. A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. Journal of Biomechanical Engineering. 1983;105:136–144. doi: 10.1115/1.3138397. [DOI] [PubMed] [Google Scholar]
  15. Kadaba MP, Ramakrishnan HK, Wootten ME. Measurement of lower extremity kinematics during level walking. J Orthop Res. 1990;8:383–392. doi: 10.1002/jor.1100080310. [DOI] [PubMed] [Google Scholar]
  16. Lathrop RL, Chaudhari AMW, Siston RA. Comparative Assessment of Bone Pose Estimation Using Point Cluster Technique and OpenSim. J Biomech Eng-T Asme. 2011;133 doi: 10.1115/1.4005409. [DOI] [PubMed] [Google Scholar]
  17. Peters A, Galna B, Sangeux M, Morris M, Baker R. Quantification of soft tissue artifact in lower limb human motion analysis: a systematic review. Gait & Posture. 2010;31:1–8. doi: 10.1016/j.gaitpost.2009.09.004. [DOI] [PubMed] [Google Scholar]
  18. Reinschmidt C, van den Bogert AJ, Nigg BM, Lundberg A, Murphy N. Effect of skin movement on the analysis of skeletal knee joint motion during running. Journal of Biomechanics. 1997;30:729–732. doi: 10.1016/s0021-9290(97)00001-8. [DOI] [PubMed] [Google Scholar]
  19. Riley PO, Franz J, Dicharry J, Kerrigan DC. Changes in hip joint muscle-tendon lengths with mode of locomotion. Gait & Posture. 2010;31:279–283. doi: 10.1016/j.gaitpost.2009.11.005. [DOI] [PubMed] [Google Scholar]
  20. Stagni R, Fantozzi S, Cappello A, Leardini A. Quantification of soft tissue artefact in motion analysis by combining 3D fluoroscopy and stereophotogrammetry: a study on two subjects. Clinical Biomechanics (Bristol, Avon) 2005;20:320–329. doi: 10.1016/j.clinbiomech.2004.11.012. [DOI] [PubMed] [Google Scholar]
  21. Tashman S, Collon D, Anderson K, Kolowich P, Anderst W. Abnormal rotational knee motion during running after anterior cruciate ligament reconstruction. American Journal of Sports Medicine. 2004;32:975–983. doi: 10.1177/0363546503261709. [DOI] [PubMed] [Google Scholar]
  22. Tsai TY, Lu TW, Kuo MY, Hsu HC. Quantification of three-dimensional movement of skin markers relative to the underlying bones during functional activities. Biomedical Engineering-Applications Basis Communication. 2009;21:223–232. [Google Scholar]
  23. Tsai TY, Lu TW, Kuo MY, Lin CC. Effects of soft tissue artifacts on the calculated kinematics and kinetics of the knee during stair-ascent. J Biomech. 2011;44:1182–1188. doi: 10.1016/j.jbiomech.2011.01.009. [DOI] [PubMed] [Google Scholar]
  24. Walker PS, Rovick JS, Robertson DD. The effects of knee brace hinge design and placement on joint mechanics. Journal of Biomechanics. 1988;21:965–974. doi: 10.1016/0021-9290(88)90135-2. [DOI] [PubMed] [Google Scholar]
  25. Xiao M, Higginson J. Sensitivity of estimated muscle force in forward simulation of normal walking. Journal of Applied Biomechanics. 2010;26:142–149. doi: 10.1123/jab.26.2.142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. You BM, Siy P, Anderst W, Tashman S. In vivo measurement of 3-D skeletal kinematics from sequences of biplane radiographs: application to knee kinematics. IEEE Trans Med Imaging. 2001;20:514–525. doi: 10.1109/42.929617. [DOI] [PubMed] [Google Scholar]

RESOURCES