Histotripsy-Induced Cavitation Cloud Initiation Thresholds in Tissues of Different Mechanical Properties

Abstract

Histotripsy is an ultrasound ablation method that depends on the initiation and maintenance of a cavitation bubble cloud to fractionate soft tissue. This paper studies how tissue properties impact the pressure threshold to initiate the cavitation bubble cloud. Our previous study showed that shock scattering off one or more initial bubbles, expanded to sufficient size in the focus, plays an important role in initiating a dense cavitation cloud. In this process, the shock scattering causes the positive pressure phase to be inverted, resulting in a scattered wave that has the opposite polarity of the incident shock. The inverted shock is superimposed on the incident negative pressure phase to form extremely high negative pressures, resulting in a dense cavitation cloud growing toward the transducer. We hypothesize that increased tissue stiffness impedes the expansion of initial bubbles, reducing the scattered tensile pressure, and thus requiring higher initial intensities for cloud initiation. To test this hypothesis, 5-cycle histotripsy pulses at pulse repetition frequencies (PRFs) of 10, 100, or 1000 Hz were applied by a 1-MHz transducer focused inside mechanically tunable tissue-mimicking agarose phantoms and various ex vivo porcine tissues covering a range of Young’s moduli. The threshold to initiate a cavitation cloud and resulting bubble expansion were recorded using acoustic backscatter detection and optical imaging. In both phantoms and ex vivo tissue, results demonstrated a higher cavitation cloud initiation threshold for tissues of higher Young’s modulus. Results also demonstrated a decrease in bubble expansion in phantoms of higher Young’s modulus. These results support our hypothesis, improve our understanding of the effect of histotripsy in tissues with different mechanical properties, and provide a rational basis to tailor acoustic parameters for fractionation of specific tissues.

I. Introduction

Histotripsy is a noninvasive tissue ablation method that controls cavitation to fractionate soft tissue through high pressure (>10 MPa), short duration (<20 μs) ultrasound pulses at low duty cycles (<1%) [1]–[4]. Histotripsy depends on the initiation and maintenance of a dense cavitation bubble cloud to produce mechanical tissue fractionation [3], [5]. With sufficiently high pressure (>10 MPa peak negative pressures) and adequate number of pulses (>500 pulses), histotripsy can completely fractionate soft tissue into a liquid-appearing homogenate, resulting in effective tissue removal [4], [6]. The histotripsy process is often self-limited at anatomical boundaries such as blood vessels, the capsule of an organ (e.g., the prostate) or fibrous structures (e.g., the collecting system in the kidney) [7], [8]. These structures have a higher Young’s modulus than surrounding tissue.

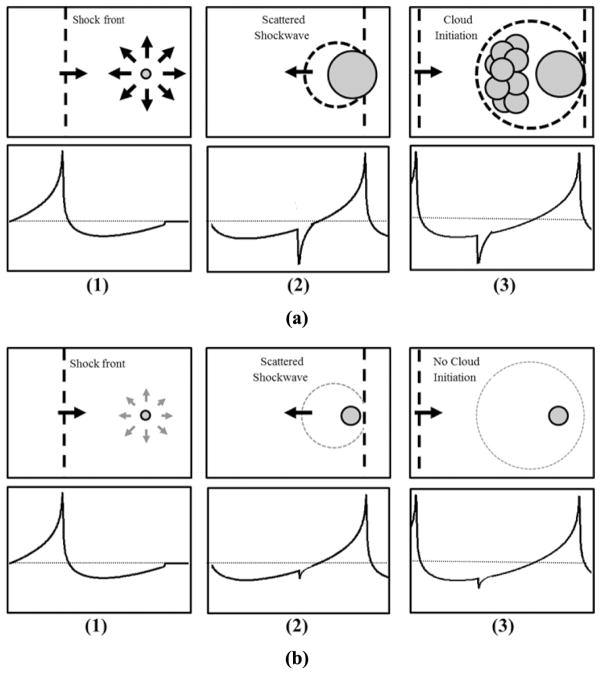
In histotripsy, the dense lesion-forming cavitation bubble cloud has a higher threshold to initiate than the thresholds for inertial cavitation of individual microbubbles reported in the literature [9]–[18]. A dense bubble cloud can be formed during one multi-cycle histotripsy pulse using shock scattering from single bubbles formed and expanded from the initial cycles of the pulse [Fig. 1(a)] [19]. In this process of cloud initiation, these initial bubbles act as a pressure release surface wherein the following positive pressure half cycles, usually very high peak pressure shock fronts, are inverted and superimposed on the incident negative pressure phase to form extremely high negative pressures that produce a dense cavitation cloud growing back toward the transducer [19]. The dense bubble clouds thus formed are necessary to achieve histotripsy tissue fractionation. The process of shock scattering initiates a histotripsy bubble cloud at negative pressure magnitudes weaker than what is required to directly generate dense bubble clouds without shock scattering [15]. Sufficient expansion of initial bubbles coupled with a shock thickness that is very small compared with the bubble diameter (~100 nm versus 100 μm) results in strong scattering of the shock and bubble cloud formation [15]. If the sparsely distributed initial bubbles are too small, they cannot effectively reflect and invert the subsequent shock front to initiate dense lesion-forming bubble clouds (Fig. 1) [15].

Fig. 1.

Schematic of bubble cloud formation by shock scattering. (1) During the initial cycles of a histotripsy pulse, individual bubbles are expanded in the focus in response to incident negative pressure. (2) The shockwaves from subsequent cycles are scattered off initially expanded bubbles, (3) which inverts the shock and constructively interferes with the negative phase of the next incident wave. (a) Previous work has demonstrated a histotripsy bubble cloud is only formed when initial bubbles expand to a large enough size for shock scattering to result in sufficiently large reflected negative pressures. (b) If expansion of initial bubbles is of insufficient size to cause significant scattering, the negative pressures produced will be insufficient to initiate a histotripsy bubble cloud.

Tissue mechanical properties have been proposed to affect cavitation threshold and bubble expansion in elastic media similar to soft tissue [20]–[25]. We hypothesize that the expansion of initial bubbles during the histotripsy pulse is impeded in tissue of increased mechanical stiffness (i.e., Young’s modulus), which reduces shock scattering and increases the pressure threshold (of incident wave) necessary to initiate a cavitation bubble cloud [Fig. 1(b)]. In this paper, we investigate the threshold to initiate a dense cavitation cloud in mechanically tunable tissue-mimicking agarose phantoms and various ex vivo porcine tissues covering a wide range of mechanical properties.

II. Materials and Methods

A. Therapeutic Ultrasound

Histotripsy pulses were generated by a 1-MHz focused ultrasonic transducer (Imasonic, Besançon, France) with an aperture of 100 mm, focal length of 90 mm, and a 50-mm-diameter concentric hole. The transducer was driven by a custom-designed class-D amplifier with appropriate electrical matching circuits built in our laboratory. Input signals were provided by a custom-built field-programmable gate array (FPGA) board (Altera Corporation, San Jose, CA) that functioned as a signal generator. Acoustic waveforms produced by the 1-MHz therapeutic transducer were obtained using a fiber optic probe hydrophone built in house [26]. Pressure wave measurements were recorded in free-field in both degassed water and degassed 1,3-butanediol (Sigma-Aldrich, St. Louis, MO) at room temperature. Measurements were made in 1,3-butanediol to prevent cavitation at the fiber tip at high pressures. Butanediol was chosen because it has almost identical acoustic impedance to water, so no correction due to mismatch was needed for the peak negative pressure measurements. The effects of attenuation were minimized by submerging the hydrophone in only a small volume of butanediol with sound propagating approximately 1 mm in butanediol. The hydrophone sensitivity in butanediol was calibrated by comparison with known measurements in water. Both fluids were used because water is needed for reference and butanediol allowed higher peak negative pressure amplitudes to be measured directly. Although the positive pressures measured in butanediol were suppressed because of the higher attenuation, the negative pressures which were used as metrics for the cavitation threshold were shown to match those measured in water. The peak negative pressures used in this work were 10 to 27.9 MPa. Positive pressures were measured up to >80 MPa, corresponding to a peak negative pressure of 15 MPa. At higher pressure, peak positive pressure could not be accurately measured because of instantaneous cavitation at the fiber tip in water and attenuation or saturation effects in butanediol. The peak positive pressures corresponding to negative pressures >15 MPa used in some of the experiments are expected to be higher than 80 MPa.

B. Tissue Phantom Preparation

Agarose phantoms were used to provide a well-controlled elastic medium for this study. Agarose phantoms of 0.3%, 1%, 2.5%, and 5% w/v were prepared by slowly mixing agarose powder (Agarose Type VII, Sigma-Aldrich) into saline solution (0.9% sodium chloride, Hospira Inc., Lake Forest, IL) heated above 70°C. The solution was stirred on a hot plate until the gel turned completely transparent. Agarose solutions were degassed under a partial vacuum of 141.34 kPa for 30 min. After removing agarose mixtures from the vacuum, the solution was poured into 15 × 5 × 5 cm rectangular polycarbonate tissue phantom holders. The tissue phantom holders were placed in a refrigerator at 4°C to allow the agarose solution to solidify before use.

C. Tissue Phantom Mechanical Properties

The mechanical properties of agarose phantoms can be varied over a physiologically relevant range by changing the agarose concentration [27]. The agarose phantoms were made following the protocol previously described by Normand et al. in which the Young’s modulus was characterized for agarose phantoms of varying concentration [27]. Agarose phantoms were selected to cover the range of mechanical stiffnesses of tissues found in the body, from non-load-bearing tissues such as lung, fat, and kidney (Young’s moduli ranging from 1 to 10 kPa) to strong load-bearing tissues such as cartilage (Young’s moduli of ~1 MPa).

D. Porcine Tissue Preparation

Fresh porcine lung, fat, kidney, liver, heart, skeletal muscle, skin, tongue, tendon, cartilage, and bone were excised and immediately placed into degassed 0.9% saline solution and stored at 4°C until experiments. Tissue samples were sectioned (minimum size of 5 cm³) and warmed to room temperature in degassed saline under a partial vacuum of 141.34 kPa for 4 h before experiments. All tissues were used within 48 h of harvesting.

E. Tissue Mechanical Properties

Tissue mechanical properties have been characterized using numerous metrics in the literature, including elastic modulus, bulk modulus, ultimate stress, and ultimate fractional strain [28]–[37]. Mechanical strength has also been shown to correlate to tissue composition, including tissue density, water content, and protein concentration [28], [38]–[41]. To compare cloud initiation threshold results with tissue stiffness, Young’s modulus values from literature were chosen as a tissue mechanical property metric for this study. Tissues investigated in this work covered the large range of Young’s moduli seen in the body from <5 kPa to >100 MPa.

F. Cavitation Cloud Initiation Detection

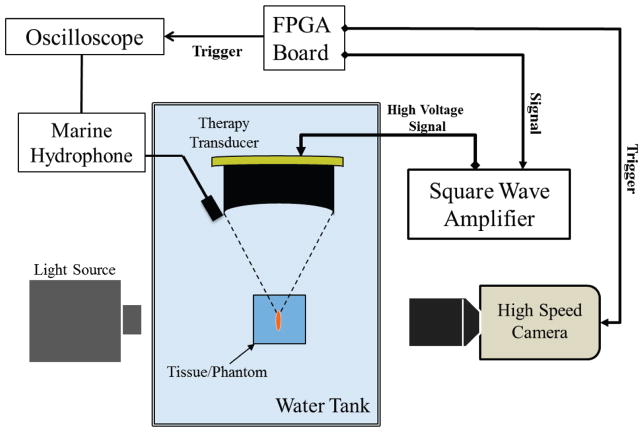
To measure the threshold to initiate a cavitation bubble cloud, histotripsy pulses were targeted inside agarose tissue phantoms or porcine tissue placed in a water tank (Fig. 2). Five cycle pulses at pulse repetition frequencies (PRFs) of 10 Hz, 100 Hz, or 1000 Hz were applied by the 1 MHz transducer. The acoustic backscatter of the therapy pulse from the bubble cloud was received by a low-frequency, unfocused marine hydrophone (H1a, Aquarian Audio Products, Anacortes, WA) with a sensitivity of −220 dB re 1 V/μPa at 100 kHz. The hydrophone was placed directly above the therapy transducer, facing the therapy focus to receive the acoustic backscatter signal at an approximately 30° angle. The significantly increased amplitude of the acoustic backscatter signal was used to detect the initiation of dense cavitation clouds. Example waveforms from the low-frequency hydrophone with and without cavitation are shown in Fig. 4. The frequency spectrum of the hydrophone signal showed local frequency peaks at 100, 300, and 500 kHz, with the largest peak at 100 kHz. Experimental results and analysis demonstrate that these low-frequency components are due to the therapy pulse envelope and system response of the low-frequency hydrophone. These low-frequency peaks change with the duration (i.e., envelope) of the therapy pulse.

Fig. 2.

Experimental setup. A 1-MHz therapy transducer focus was aligned inside samples for cavitation initiation experiments. Bubble cloud formation was monitored using a low-frequency marine hydrophone and verified with high-speed optical imaging.

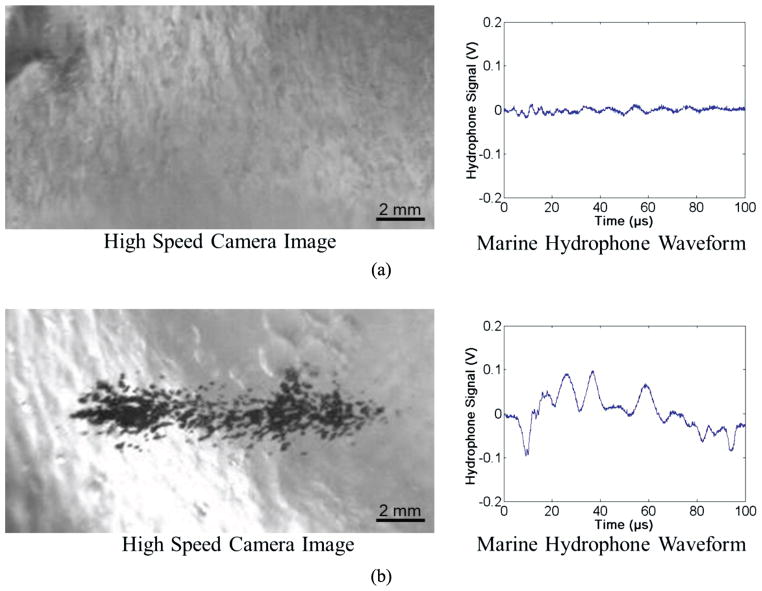
Fig. 4.

Example waveforms collected by marine hydrophone with corresponding optical images of bubble cloud. Results show a significant increase in the amplitude of the waveform collected by the marine hydrophone when a cavitation cloud has been initiated compared with uninitiated cases. Examples shown are of 2.5% agarose tissue phantoms treated at 10 Hz right below and above the cavitation cloud threshold with peak negative pressures of (a) 24.2 MPa and (b) 25.1 MPa. The threshold for cloud initiation was determined to be the lowest pressure at which a bubble cloud was initiated within ten pulses and maintained for the duration of the treatment for all six samples.

A three-step method has been developed to process the acoustic backscatter signals to detect the cavitation cloud initiation threshold. First, the energy of the acoustic backscatter signal from each pulse was calculated by integrating the square of the voltage signal received from the hydrophone. Second, the threshold for detecting cloud initiation was defined as the mean plus three standard deviations of the uninitiated acoustic backscatter energy (no cavitation cloud), which was calculated at a very low therapy pulse pressure (<5 MPa) for 30 trials of 1000 pulses each. The acoustic backscatter energy was normalized to the spatial peak pulse average intensity (I_SPPA) of the corresponding therapy pulses [11]. Third, the initiation of the bubble cloud was determined when the normalized acoustic backscatter energy exceeded the defined threshold within the first 10 histotripsy pulses and was maintained above the threshold for the duration of the 1000 pulses at a given pressure. A similar method using acoustic backscatter has previously been used to detect cavitation cloud initiation in histotripsy which correlates with tissue fractionation generation at >97% success rate [3]. Initiation within the first 10 pulses and maintenance over the 1000 pulses were chosen as part of the initiation criteria here as rapid initiation of the bubble cloud and maintenance for over 1000 pulses are needed to produce effective and efficient tissue fractionation based on previous studies. A sample size of 6 tissue phantoms or tissue samples was used for each agarose concentration and porcine tissue type. In each sample, 60 pressure levels ranging from 8 to 28 MPa were tested with 1000 pulses applied for each individual pressure. Each pressure level was tested in a different location (1 cm spacing) to avoid the influence of the previous exposure on the threshold measurement. The lowest pressure level when initiation was detected was recorded as the cloud initiation threshold in that sample.

Bubble cloud initiation detected using acoustic backscatter was verified through optical images of the bubble cloud generation in the agarose phantom using a high-speed, 1 megapixel CCD camera (Phantom V210, Vision Research) capable of a maximum frame rate of 2000 fps. The camera was focused with a macro-bellows lens (Tominon, Kyocera) and backlit by a continuous light source. The camera was triggered to record one image for each applied pulse, 10 μs after the beginning of the pulse reached the focus. The camera exposure time was 2 to 5 μs. Bubbles were indicated as black regions >5 pixels in the shadowgraphic images and a bubble cloud was considered initiated when more than 10 bubbles were visible within the image within the first 10 histotripsy pulses and throughout the remaining 1000 pulses as previously described for the backscatter detection method. The minimum resolvable diameter of a bubble was about 10 to 20 μm because of the magnification and the minimum 5 pixel area and 2 μm/pixel resolution. A sample size of 6 tissue phantoms or tissue samples (cut into sections with a minimum size of 5 cm³) was used for each agarose concentration and porcine tissue type. Cloud initiation threshold results in different tissue phantoms and porcine tissues (n = 6) were compared using a Student’s t-test. P-values < 0.05 were considered statistically significant.

G. Bubble Expansion Simulation

To investigate the effects of tissue Young’s modulus on the growth of initial bubbles, a numerical simulation based on a linear Kelvin–Voigt model was developed. We hypothesize that the first significant tension experienced by a nucleus will cause it to grow explosively, and that the behavior will be affected by the tissue elasticity. To test this hypothesis, simulations exposed a 10-nm initial bubble to a single cycle of 15 MPa peak negative pressure and 70 MPa peak positive pressure. For this proof of principle, we assume the surrounding medium to have homogeneous properties, and that the bubble contains air and remains spherical. These assumptions allow us to use a numerical model developed in-house [42] for simulating spherical bubble dynamics in a viscoelastic medium with viscous, elastic relaxation and retardation effects, including liquid compressibility and heat transfer.

Because the present focus is on growth, we neglect heat transfer and consider the simplest viscoelastic model (linear Kelvin–Voigt) that includes viscosity and elasticity [24]. In the Kelvin–Voigt model, the stress tensor τ is related to the deformation tensor γ and the rate of deformation tensor γ̇ through τ = 2Gγ + 2μγ̇, where G is the shear modulus (elasticity) and μ is the viscosity. The stress tensor is related to the bubble radius R through the Keller–Miksis equation

$$\left(1-\frac{\stackrel{.}{R}}{c}\right)R\ddot{R}+\frac{3}{2}\left(1-\frac{\stackrel{.}{R}}{3c}\right){\stackrel{.}{R}}^2=\frac{1}{\rho }\left(1+\frac{\stackrel{.}{R}}{c}+\frac{R}{c}\frac{\mathrm{d}}{\mathrm{d}t}\right)\left(p_g-\frac{2S}{R}-p_{\infty }(t)+3\underset{R}{\overset{\infty }{\int }}\frac{{\tau }_{rr}}{r}\mathrm{d}r\right),$$

which depends on the medium’s sound speed c, density ρ, and surface tension against air S. Here, p_∞(t) is the absolute forcing pressure, r is the radial coordinate, and dots over a term denote derivatives with respect to time, t. The air within the bubble is assumed to have spatially uniform pressure given by the polytropic relationship

$$p_g=p_0{\left(\frac{R_0}{R}\right)}^{3\kappa },$$

where κ = 1.4 is the ratio of specific heats for air, R₀ is the initial bubble radius, and p₀ = p_∞(0) + 2S/R₀ is the initial bubble pressure. By conservation of mass, the radial velocity of the surrounding medium is u(r, t) = R²Ṙ/r², and hence

$${\stackrel{.}{\gamma }}_{rr}=-\frac{\partial u}{\partial r}=-\frac{2R^2\stackrel{.}{R}}{r^3},{\gamma }_{rr}=-\frac{2}{3r^3}(R^3-R_0^3),$$

from which it follows that

$$3\underset{R}{\overset{\infty }{\int }}\frac{{\tau }_{rr}}{r}\mathrm{d}r=-\frac{4G}{3}\left(1-\frac{R_0^3}{R^3}\right)-\frac{4\mu \stackrel{.}{R}}{R}.$$

These substitutions allow the Keller–Miksis equation to be solved for the bubble wall acceleration R̈ and integrated in time. The properties ρ = 1060 kg/m³, c = 1430 m/s², and S = 0.056 (blood–air surface tension) were used to describe the surrounding medium. The medium’s viscosity was assumed to be that of blood (μ = 3.0 cP); the Young’s modulus (E = 3G) was varied in decades from 1 kPa to 10 MPa to match the range of tissues studied in this work. The bubble radius was graphed as a function of time over this range of Young’s moduli to provide insight into the effects of tissue elasticity on the expansion of small bubbles at the focus of histotripsy pulses.

H. Bubble Behavior

To study the effects of mechanical properties on bubble expansion and collapse, optical images of the growth and collapse of individual bubbles and the cloud were recorded by the high-speed camera. A bubble cloud was generated by 5-cycle histotripsy pulses at 25.9 MPa peak negative pressure applied by 1 MHz transducer with a PRF of 100 Hz. Because of the limited frame rate of the camera, we could not image the bubble expansion and collapse during and after a single histotripsy pulse. Therefore, a series of time-delayed images of bubble clouds generated by 200 identical pulses with delay increased 2 μs per pulse were taken to reconstruct a sequence of bubble images covering the entire period of bubble expansion and collapse. Shadowgraph images were converted from grayscale to binary by an intensity threshold determined by the background intensity using image processing software (Matlab, The MathWorks Inc., Natick, MA). The size of single bubbles visible within the bubble cloud was measured for each pulse to determine the maximum bubble expansion diameter as well as the time until bubble collapse. The time until bubble collapse measured in this work was measured as the time from the pulse arriving at the focus until a bubble was no longer visible on optical imaging using the same 5-pixel (10-μm) qualification as outlined in the previous section. A sample size of 6 tissue phantoms was used for each agarose concentration.

III. Results

A. Cavitation Cloud Initiation Threshold in Agarose Tissue Phantom

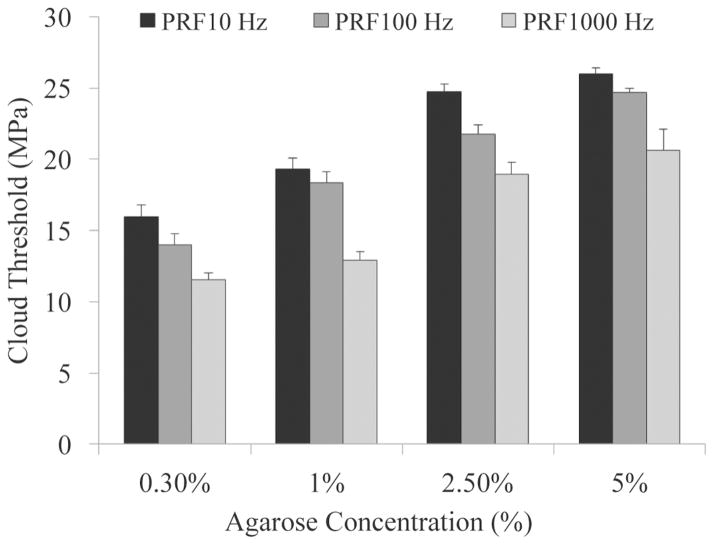
To test the effects of tissue mechanical properties on the pressure threshold required to generate a bubble cloud, histotripsy pulses (Fig. 3) were applied to the centers of mechanically tunable agarose tissue phantoms. Bubble cloud initiation results from the acoustic backscatter energy received with the low-frequency hydrophone were shown to correlate with the optical images (Fig. 4). All bubble clouds generated in this work contained 10 or more bubbles and resulted in a hydrophone signal above the defined threshold of the mean plus three standard deviations of the normalized uninitiated acoustic backscatter energy. Acoustic hydrophone measurements of histotripsy applied to tissue phantoms at different acoustic pressures demonstrated a statistically significant increase in the cavitation cloud initiation threshold with increasing agarose phantom concentration. Tissue phantoms with higher agarose concentration have a Young’s modulus (Table I) ranging from a Young’s modulus (compression) of 1.5 kPa in the 0.3% agarose phantoms to 929 kPa for the 5% agarose phantoms. Results in Fig. 5 show that the bubble cloud initiation threshold significantly increased as agarose concentration was increased from 0.3% to 1%, 2.5%, and 5%. For example, for 5-cycle pulses at a PRF of 100 Hz, the cloud initiation peak negative pressure threshold increased from 14.0 MPa to 24.7 MPa as the phantom agarose concentration was changed from 0.3% to 5%, corresponding to a change in Young’s modulus of nearly 10³. The trend of increasing cavitation cloud initiation pressure with increasing agarose concentration was seen for all PRFs tested. Additionally, cavitation cloud initiation pressure thresholds were observed to be significantly lower at higher PRF.

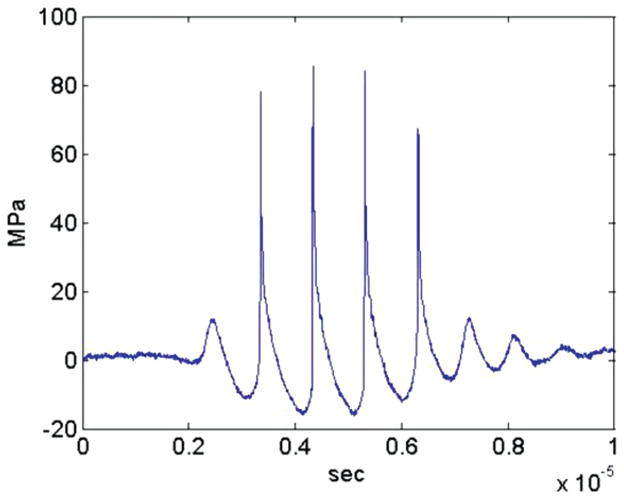
Fig. 3.

Example histotripsy pressure waveform.

TABLE I.

Cavitation Cloud Initiation Threshold in Tissue Phantoms.

Agarose (%)	Threshold (MPa) PRF 10	Threshold (MPa) PRF 100	Threshold (MPa) PRF 1000	Young’s Modulus (MPa) Compression, Tension
0.30	15.94 ± 0.88	14.00 ± 0.80	11.54 ± 0.49	0.0015, N/A
1	19.34 ± 0.77	18.34 ± 0.79	12.94 ± 0.58	0.038, N/A
2.5	24.75 ± 0.52	21.77 ± 0.65	18.98 ± 0.82	0.25, 0.44
5	25.98 ± 0.42	24.66 ± 0.33	20.65 ± 1.44	0.93, 1.34

Table shows cavitation initiation threshold for agarose phantoms treated at pulse repetition frequencies (PRFs) of 10, 100, and 1000 Hz with corresponding Young’s moduli values (tension, compression) [27].

Fig. 5.

Cavitation cloud initiation threshold in phantoms with varied agarose concentration. Threshold results show significant increase in the peak negative pressure required to initiate cavitation inside higher concentration tissue phantoms. All increases in threshold between gel concentrations were considered significant (p-values < 0.05).

B. Cavitation Cloud Initiation Threshold in Porcine Tissue

Cavitation cloud initiation threshold was investigated in ex vivo porcine tissues covering a range of different mechanical properties at PRFs of 100 and 1000 Hz (Table II). The cloud initiation thresholds for porcine skin, tongue, tendon, and cartilage (high Young’s modulus) were significantly higher than other tissues such as skeletal muscle, cardiac muscle, and liver (intermediate Young’s modulus), whereas lung, fat, and kidney (low Young’s modulus) were significantly lower. All differences in cloud initiation threshold between types of porcine tissue were significant (p < 0.05) except the differences between fat and kidney, skin and tongue, and tongue and tendon (p > 0.05). These three tissue combinations which didn’t show a significant difference in threshold had similar mechanical properties (elastic modulus). Cavitation cloud initiation was unattainable in bone for both 100 and 1000 Hz PRFs and in cartilage at 100 Hz PRF. A complete list of initiation threshold results in ex vivo porcine tissues are summarized in Table II along with the corresponding Young’s moduli. Further analysis showed a trend of increasing cavitation cloud initiation threshold with increased Young’s modulus (Fig. 6). Logarithmic regression analysis demonstrated a high correlation between the cloud initiation threshold and Young’s modulus for tissues with Young’s moduli below 0.1 MPa, with R² values of 0.85 and 0.76 at 100 Hz and 1000 Hz PRF, respectively. The cavitation cloud initiation threshold plateaued at an upper limit between 25 and 30 MPa for tissues with Young’s moduli above 0.1 MPa (cartilage and tendon), for both PRFs of 100 Hz and 1000 Hz (Fig. 6).

TABLE II.

Cavitation Cloud Initiation Threshold in Ex Vivo Porcine Tissue.

Tissue	Threshold (MPa) PRF 100	Threshold (MPa) PRF 1000	Young’s modulus (MPa)
Lung	1.578 ± 0.89	13.42 ± 1.08	0.0026
Fat	17.13 ± 1.41	13.26 ± 1.85	0.0032
Kidney	17.84 ± 1.48	14.56 ± 0.95	0.0061
Liver	19.97 ± 0.77	17.75 ± 1.07	0.0087
Heart	20.03 ± 0.36	17.06 ± 1.28	0.0042
Muscle	21.01 ± 0.48	19.12 ± 0.57	0.0062
Skin	25.10 ± 0.69	23.21 ± 1.01	0.014
Tongue	26.54 ± 0.88	24.27 ± 0.44	0.025
Tendon	26.41 ± 0.52	24.47 ± 0.49	380
Cartilage	no cloud	27.28 ± 0.85	0.90
Bone	no cloud	no cloud	18 600

Table shows cavitation initiation threshold for porcine tissue treated at pulse repetition frequencies (PRFs) of 100 and 1000 Hz with corresponding Young’s modulus (tension) values from literature [28]–[37].

Fig. 6.

The initiation threshold of cavitation clouds induced by histotripsy in ex vivo porcine tissues plotted as a function of tissue Young’s modulus.

C. Bubble Expansion Simulation

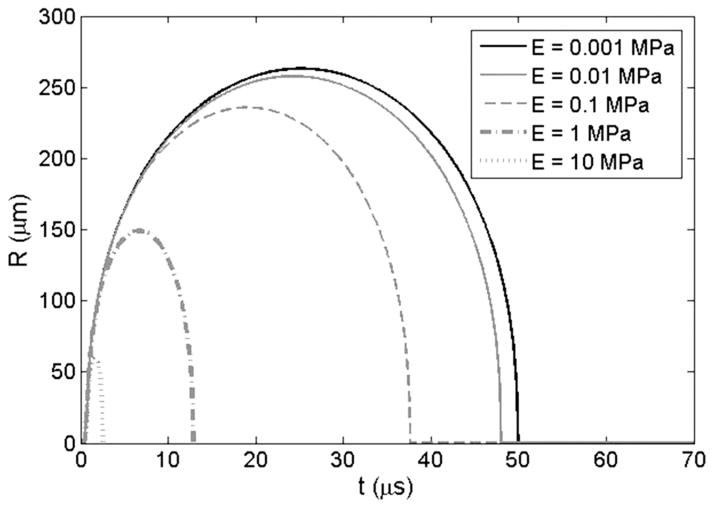
The effects of tissue Young’s modulus on the growth of initial bubbles during histotripsy was investigated using a numerical simulation based on a linear Kelvin-Voigt model. Simulation results supported the hypothesis that increases in Young’s modulus cause a reduction in bubble expansion (Fig. 7). A plot showing the history of the bubble radius for a 10 nm initial bubble subjected to the first cycle of a histotripsy pulse at a peak negative pressure of 15 MPa demonstrated a decrease in bubble expansion as Young’s moduli was varied from 1 kPa to 10 MPa. Following the passage of the pulse, the bubble rapidly expands, slows down as it reaches a maximum radius, and collapses violently. Increases in Young’s modulus were shown to inhibit bubble growth, as predicted, because this elastic property (spring-like behavior) increases the isotropic stress on the bubble as the departure from the original configuration becomes larger [43]. Results further showed that only a small reduction in bubble expansion was observed between Young’s moduli of 1 kPa to 10 kPa whereas larger decreases in bubble expansion were observed as Young’s moduli was increased to 100 kPa, 1 MPa, and 10 MPa. For instance, for a Young’s modulus of 10 kPa, the growth was reduced by about 2% compared with 1 kPa, whereas the growth was reduced by ~12% at Young’s modulus of 0.1 MPa, nearly a factor of 2 at Young’s modulus of 1 MPa, and factor of 4 at a Young’s modulus of 10 MPa. These decreases in expansion of initial bubbles have previously been shown to result in a decrease in shock scattering [15], which supports our hypothesis and helps explain why higher pressures are required for cloud initiation in tissues with higher Young’s moduli.

Fig. 7.

Simulation of initial bubble expansion in tissues of varied Young’s modulus. Plot shows the history of the bubble radius for a 10-nm initial bubble subjected to the first cycle of a histotripsy pulse at a peak negative pressure of 15 MPa with Young’s moduli varied from 1 kPa to 10 MPa.

D. Bubble Behavior

The results from the bubble behavior experiments showed a significant decrease in both maximum bubble expansion and bubble cloud collapse time in tissue phantoms of increased mechanical stiffness (Fig. 8), supporting our hypothesis and validating numerical simulation results. The maximum bubble diameter was significantly higher in the 0.3% agarose compared with the higher concentration gels, with the average maximum bubble diameter decreasing from 373.8 ± 38.2 μm for the 0.3% phantom to 268.7 ± 44.8 μm, 140.2 ± 38.2 μm, and 58.4 ± 23.4 μm for the 1%, 2.5%, and 5% phantoms, respectively. The bubble cloud collapse time followed a similar trend, with a significantly shorter bubble cloud lifespan observed in the higher concentration phantoms. The average bubble cloud collapse time decreased from 98.5 ± 12.0 μs for the 0.3% phantom to 86.5 ± 7.5 μs, 53.5 ± 2.5 μs, and 37.5 ± 5.7 μs for the 1%, 2.5%, and 5% phantoms, respectively. All differences in maximum diameter and bubble collapse time were statistically significant (p < 0.05). Control treatments in which bubble clouds generated by 200 identical pulses without the 2-μs delay increased demonstrated the average bubble size within the cloud remained consistent with no significant difference in bubble size over the course of the 200 pulses.

Fig. 8.

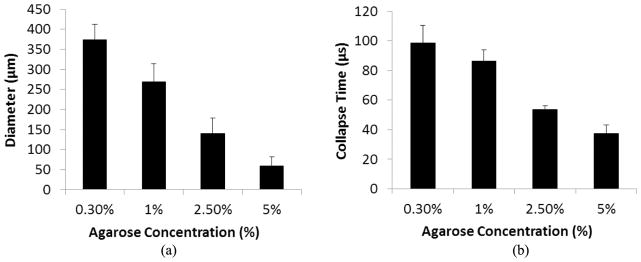
Bubble expansion in agarose tissue phantoms of varied concentration. Results show the maximum bubble expansion and the bubble collapse time for bubbles produced by histotripsy in agarose tissue phantoms. Results show a significant decrease in (a) maximum bubble expansion and (b) bubble collapse time with increasing agarose concentration. All decreases in bubble diameter and collapse time between gel concentrations were considered significant (p-values < 0.05).

IV. Discussion

In this study, the effects of tissue mechanical properties on histotripsy bubble cloud initiation threshold were studied. The results of this work support our hypothesis that increases in tissue mechanical stiffness lead to higher cloud initiation thresholds when the shock scattering mechanism is the mode of dense bubble cloud formation. This increase in initiation threshold for stronger tissues with higher Young’s moduli was demonstrated in a mechanically tunable agarose tissue phantom as well as excised porcine tissue. The mechanism responsible for this increase in cavitation cloud threshold is hypothesized to be the result of decreased bubble expansion in tissue with higher mechanical stiffness, which leads to reduced shock scattering. Results further support this hypothesis, because maximum bubble diameter was decreased in higher-agarose- concentration tissue phantoms.

The first part of this work investigated the effects of increased tissue mechanical stiffness on the pressure threshold to initiate a dense bubble cloud in histotripsy. Controlled increases in the stiffness of tissue phantoms consistently resulted in significant increases in the cavitation cloud initiation threshold. This trend of increasing threshold for tissues with higher Young’s moduli was verified in ex vivo tissue. Results demonstrated a high correlation between the cavitation initiation threshold and tissue Young’s modulus. Among the tissues tested, cavitation could not be generated in cartilage at 100 Hz PRF and bone at both 100 and 1000 Hz PRF. The finding that cloud initiation threshold is dependent on tissue properties explains previous observations in which bubble cloud initiation was difficult to achieve within certain tissues, such as cartilage and highly calcified aged plaque.

In addition to the shock scattering mechanism using multi-cycle ultrasound pulses, there is another mechanism for cloud formation using shorter pulses (≤3 cycles). In a separate study [44], histotripsy bubbles have been generated in tissue phantoms and ex vivo tissues using a single 1- to 2-cycle pulse when the peak negative pressure exceeds a distinct threshold that seems to be intrinsic to the media, which is referred to as the intrinsic threshold of the tissue. The intrinsic threshold is at the peak negative pressure of ~26 to 30 MPa in soft tissue containing mostly water and appears to be independent of tissue type with the exception of fat. With the extremely short pulse, bubble cloud initiation depends solely on the negative pressure, without contribution from shock scattering, resulting in bubble cloud formation matching the region of the focal region above the intrinsic threshold of ~26 to 30 MPa. This intrinsic threshold range is close to the peak negative pressure thresholds in tissues with high Young’s moduli (tongue, tendon, cartilage) observed in this work (25 to 28 MPa) as well in the higher concentration 5% agarose tissue phantoms. This suggests that bubble cloud formation in tissues with higher Young’s moduli was primarily driven by the negative pressure of the incident wave while the contributions of shock scattering were significantly decreased in tissues with higher Young’s moduli, probably because of suppressed bubble expansion, which was also observed. This finding further explains why the trend of increasing threshold with increasing Young’s modulus was only observed to hold up to approximately 0.1 MPa. When the Young’s modulus reached 0.1 MPa, the threshold saturated to near the intrinsic threshold for cloud initiation, and further increases in Young’s modulus did not further increase the pressure threshold.

To initiate the dense lesion-forming bubble cloud observed in histotripsy using the shock scattering mechanism, single bubbles must expand during the initial cycles of the pulse in order for the shockwave to be effectively scattered. If these initial bubbles do not expand to sufficient size, a dense bubble cloud will not be initiated using shockwave scatter from these bubbles. For example, a previous study using a 1-MHz therapeutic transducer demonstrated that initial bubbles must expand to >80 μm to effectively scatter the shock wave and initiate a dense bubble cloud [15]. Simulations in this previous study further showed that, using an incident wave of 20 MPa peak negative pressure and 90 MPa peak positive pressure, increasing initial bubble size from 100 μm to 200 μm resulted in a peak negative pressure increase from <30 MPa to >60 MPa. Our work shows that the expansion of initial bubbles was significantly decreased for higher Young’s moduli, which would result in decreased shock scattering. The simulation shows that a three orders of magnitude increase in the Young’s modulus (from 1 kPa to 1 MPa) results in a 2-fold decrease in the maximum radius of the initial bubble. Correspondingly, the experimental results demonstrated a factor of 2 increase was observed in the threshold with a 10³ increase in tissue Young’s modulus. These results support our hypothesis that the increases in cloud initiation threshold are a result of impeded expansion of initial bubbles resulting from increases in tissue Young’s modulus. Because the Young’s modulus provides only the simplest description of the elastic response of the material, future work will attempt to develop a full model of the shock scattering process to predict the scattered pressure field in tissues with different microstructural mechanics and viscoelastic properties to better understand the results of this study.

The numerical simulation results were further supported by experiments showing decreased bubble expansion in tissue phantoms with higher Young’s modulus. It is worth noting that the bubbles measured were within a cavitation cloud rather than the single bubbles formed during initial cycles of the pulse that were referred to in our hypothesis and modeled in the simulation. The initial bubbles were difficult to capture, especially in higher-agarose-concentration phantoms because of the precise timing and ultrafast frame rate necessary to image them. The elastic properties of the media are expected to impact the expansion of bubbles within the cloud in a similar manner to the initial single bubbles essential to shock scattering and cloud initiation, which is suggested by the similar trend seen in both simulations and experiments. As a result of impeded bubble expansion in stiffer tissues, larger negative pressures are needed to expand initial bubbles to sufficient size for shock scattering. Additionally, an increase in the positive pressure shock amplitude also probably contributes by increasing the amplitude of the reflected inverted shockwaves, which then interact with the incident negative pressure of the subsequent cycle to produce tensile pressures exceeding the intrinsic threshold of the tissue.

Understanding the dependence of bubble cloud initiation threshold on tissue mechanical properties will help guide future histotripsy treatments. For example, treatments in softer tissues such as kidney and fat can be initiated at lower acoustic pressures than those in firmer tissues such as heart and liver. Although results suggest histotripsy treatments may not be feasible in very stiff tissues such as tendon and cartilage, the observation that the cavitation cloud threshold is lower at higher PRFs may be utilized to decrease the acoustic pressure needed to initiate cavitation by increasing PRF if desired for these applications. The mechanism responsible for the decreased threshold at higher PRF is not completely understood. We hypothesize that the higher PRF pulses facilitate the growth of pre-existing nuclei in the focus to form the initial bubbles and achieve shock scattering. Future work is needed to investigate this hypothesis to determine the specific mechanism.

The suppression of bubble expansion and the decrease in the time until bubble collapse was observed in stiffer tissue phantoms. Because the energetic bubble expansion and collapse is believed to cause tissue fractionation, this reduced bubble expansion will likely also result in a decrease in the rate and extent of tissue fractionation even in cases in which a bubble cloud has been initiated. This finding further suggests that treating well above the intrinsic threshold may be necessary to achieve the bubble expansion needed for effective fractionation in stiffer tissues. Future work will investigate the bubble cloud dynamics and tissue fractionation in stiffer tissues of increasing mechanical strength with the objective of developing strategies to increase bubble expansion and fractionation efficiency in stiffer tissues when needed.

The findings in this work may guide the development of a self-limiting tissue-selective fractionation technique using histotripsy. The mechanical strength and stiffness is higher for many vital tissues, such as blood vessels and renal connecting system, in comparison to other tissues, such as liver and kidney. The differential threshold offers the ability to create a self-limiting tissue-selective ablation strategy which would spare stiffer tissues with higher mechanical strength while ablating other surrounding tissues, for example, ablating liver metastases while preserving the hepatic portal vein and artery or fractionating kidney tumors while protecting the collecting system.

V. Conclusion

In this study, the effects of tissue properties on histotripsy cavitation cloud initiation threshold were investigated. The results demonstrate a significant increase in cavitation initiation threshold for tissues of increased mechanical stiffness. Cavitation cloud initiation threshold increased in agarose tissue phantoms and porcine tissues with higher Young’s modulus. The results further suggest that these increases in cavitation cloud initiation threshold are the result of decreased bubble expansion and reduced shock scattering in stiffer tissues. This work improves our understanding of how tissue mechanical properties affect histotripsy and provide a rational basis to tailor acoustic parameters for treatment of the specific tissues of interest.

Biographies

Eli Vlaisavljevich is a graduate student in the Department of Biomedical Engineering at the University of Michigan, Ann Arbor, MI. He received a B.S. degree in biomedical engineering from Michigan Technological University in 2010, and an M.S. degree in biomedical engineering from the University of Michigan in 2013. Selected honors include a Goldwater Scholarship, a Michigan Tech Provost’s Award for Scholarship, and an NSF Graduate Research Fellowship. Eli’s research interests include focused ultrasound for noninvasive surgery, acoustic cavitation, cancer, tissue engineering, and tissue mechanics.

Adam D. Maxwell is a postdoctoral fellow in the Department of Urology at the University of Washington. He received a B.S. degree in electrical engineering from the University of Washington in 2006, an M.S. degree in electrical engineering from the University of Michigan in 2007, and a Ph.D. degree in biomedical engineering from the University of Michigan in 2012. From 2004 to 2006, he was with the Center for Industrial and Medical Ultrasound at the University of Washington, where he was engaged in research on therapeutic ultrasound and lithotripsy. His research interests include focused ultrasound therapies, medical ultrasound transducer development, acoustic cavitation, and nonlinear acoustics.

Matthew T. Warnez is pursing the B.S.E degree in engineering physics from the University of Michigan, Ann Arbor. He has held undergraduate research positions in mechanical engineering at the University of Michigan and King Abdullah University of Science and Technology. His research interests include bubble dynamics modeling and numerical algorithms. He has presented his work at the 2013 American Physics Society Division of Fluid Dynamics conference.

Eric Johnsen is an assistant professor in the Mechanical Engineering Department at the University of Michigan, where he conducts and directs research in computational fluid dynamics, with an emphasis on modeling and high-fidelity numerical simulations of complex multiscale and multi-physics problems. His research interests lie in multi-phase flows, high-speed flows and shock waves, turbulence and mixing, unsteady flows, interfacial instabilities, plasmas, and high-performance computing. Applications of his group’s work include energy, aeronautics, naval engineering, and biomedical engineering, including cavitation and wave dynamics in diagnostic and therapeutic ultrasound. He received his B.S. from the University of California, Santa Barbara, and M.S. and Ph.D. degrees from the California Institute of Technology, all in mechanical engineering; he was then a post-doctoral fellow at the Center for Turbulence research at Stanford. Selected honors include the National Science Foundation CAREER Award and Office of Naval Research Young Investigator Award.

Charles A. Cain (S’65–M’71–SM’80–F’89) was born in Tampa, FL, on March 3, 1943. He received the B.E.E. (highest honors) degree in 1965 from the University of Florida, Gainesville, FL; the M.S.E.E. degree in 1966 from the Massachusetts Institute of Technology, Cambridge, MA; and the Ph.D. degree in electrical engineering in 1972 from the University of Michigan, Ann Arbor, MI. From 1965 through 1968, he was a member of the Technical Staff at Bell Laboratories, Naperville, IL, where he worked in the electronic switching systems development area. From 1972 through 1989, he was in the Department of Electrical and Computer Engineering at the University of Illinois at Urbana-Champaign, where he was a professor of electrical engineering and bioengineering. Since 1989, he has been in the College of Engineering at the University of Michigan, Ann Arbor, as a professor of biomedical engineering and electrical engineering. He was the chair of the Biomedical Engineering Program from 1989 to 1996, the founding chair of the Biomedical Engineering Department from 1996 to 1999, and the Richard A. Auhll Professor of Engineering in 2002. He has been involved in research on the medical applications of ultrasound, particularly high-intensity ultrasound for noninvasive surgery. He was formerly an associate editor of the IEEE Transactions on Biomedical Engineering and the IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control and an editorial board member of the International Journal of Hyperthermia and Radiation Research. He is a fellow of the IEEE and the AIMBE.

Zhen Xu (S’05–M’06) is an Assistant Professor in the Department of Biomedical Engineering at the University of Michigan, Ann Arbor, MI. She received the B.S.E. (highest honors) degree in biomedical engineering from Southeast University, Nanjing, China, in 2001, and her M.S. and Ph.D. degrees from the University of Michigan in 2003 and 2005, respectively, both in biomedical engineering. Her research is focused on ultrasound therapy, particularly the applications of histotripsy for noninvasive surgeries. In 2006, she received IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society Outstanding Paper Award; the American Heart Association (AHA) Outstanding Research in Pediatric Cardiology award in 2010; and the National Institutes of Health (NIH) New Investigator Award at the First National Institute of Biomedical Imaging and Bioengineering (NIBIB) Edward C. Nagy New Investigator Symposium in 2011.