Abstract
Analysis of heart rate variability (HRV) is a promising diagnostic technique due to the noninvasive nature of the measurements involved and established correlations with disease severity, particularly in inflammation-linked disorders. However, the complexities underlying the interpretation of HRV complicate understanding the mechanisms that cause variability. Despite this, such interpretations are often found in literature. In this paper we explored mathematical modeling of the relationship between the autonomic nervous system and the heart, incorporating basic mechanisms such as perturbing mean values of oscillating autonomic activities and saturating signal transduction pathways to explore their impacts on HRV. We focused our analysis on human endotoxemia, a well-established, controlled experimental model of systemic inflammation that provokes changes in HRV representative of acute stress. By contrasting modeling results with published experimental data and analyses, we found that even a simple model linking the autonomic nervous system and the heart confound the interpretation of HRV changes in human endotoxemia. Multiple plausible alternative hypotheses, encoded in a model-based framework, equally reconciled experimental results. In total, our work illustrates how conventional assumptions about the relationships between autonomic activity and frequency-domain HRV metrics break down, even in a simple model. This underscores the need for further experimental work towards unraveling the underlying mechanisms of autonomic dysfunction and HRV changes in systemic inflammation. Understanding the extent of information encoded in HRV signals is critical in appropriately analyzing prior and future studies.
Keywords: mathematical modeling, autonomic dysfunction, human endotoxemia
Introduction
A marker of a healthy functioning autonomic nervous system (ANS) is variability in the time intervals between successive heart beats, known as heart rate variability (HRV). There are a wide range of analytical techniques to quantify HRV from heart rate (HR) measurements (Bravi et al., 2011). Power spectral analysis has traditionally been viewed as a way to quantify the states of the sympathetic and parasympathetic branches of the ANS since both branches converge at the sinoatrial (SA) node and convey oscillatory signals to the heart (Malliani et al., 1994). This type of mechanistic interpretation of HRV data, where physiological meaning is derived directly from HRV analysis, has long been a contentious issue (Eckberg, 1997); however, broad inferences about autonomic activity are still commonly made from HRV data, due in large part to the difficulty of more directly measuring autonomic activity (Scheff et al., in press). Analysis of HRV data aimed at diagnostic and prognostic applications is appealing because of the noninvasive nature of HRV assessment and the apparent correlation between HRV depression, i.e., loss of HR variability, with disease severity (Annane et al., 1999; Barnaby et al., 2002; Garrard et al., 1993; Korach et al., 2001; Piepoli et al., 1995; Tateishi et al., 2007). In particular, dysregulation of autonomic signaling is seen as a critical component in the progression of inflammation-linked disorders like sepsis (Annane et al., 1999; Schmidt et al., 2001), which has motivated research on inflammation and HRV. However, there is still a limited understanding of the precise mechanistic links between inflammation and HRV, which limits the clinical uses of HRV metrics and the potential knowledge gained from HRV analysis (Dick et al., 2012; Scheff et al., 2012a).
Due to the significant challenges remaining in understanding the underlying mechanistic basis of the inflammatory response in general, there has been extensive work on experimental models of systemic inflammation such as the human endotoxemia model (Lowry, 2005). While a number of studies have explored the effect of endotoxemia on HR and HRV as well as other metrics of autonomic function (Alvarez et al., 2007; Godin et al., 1996; Jan et al., 2010; Jan et al., 2009; Kox et al., 2011; Lehrer et al., 2010; Rassias et al., 2011; Rassias et al., 2005; Sayk et al., 2008; Scheff et al., 2011), careful experimental design and analysis is required to interpret results and coherently build a conceptual framework linking inflammation with autonomic dysfunction (Scheff et al., 2012a; Scheff et al., 2012b). It is important to extract the maximal amount of information from experiments while understanding their limitations and the scope of remaining unknowns. For instance, while changes in HRV metrics are often cited as evidence for changes in autonomic function, the underlying physiological complexity makes such conclusions difficult (Eckberg, 1997; Goldstein et al., 2011; Heathers, 2012). If alternative hypotheses can equally plausibly explain experimental observations, then further investigations are required for a more complete understanding; but if this is not appreciated, then scientific progress will be impeded. In this respect, a mathematical model can serve as a framework allowing for the rationalization of experimental results and the elucidation of deeper meaning (Ottesen, 2011).
In this manuscript, we study two models describing the relationship between the autonomic nervous system and patterns of heart beats. These models incorporate mechanisms that govern the relationship between autonomic activity and both HR and HRV, such as high frequency autonomic oscillations, binding kinetics of neurotransmitters to receptors at the SA node, changes in mean levels of autonomic activity, and inflammation-induced uncoupling between the heart and the autonomic nervous system. Frequency-domain metrics are used to quantify HRV, as these metrics are commonly used in literature and are most directly related to the autonomic oscillations included upstream in the model. We analyzed these models first to illustrate the challenges inherent in inferring autonomic function from HR and HRV data alone. We then investigated the human endotoxemia response in particular by leveraging our models to explain and rationalize experimental observations. The unintuitive relationships between autonomic signaling and HRV play a role in explaining the effect of the cholinergic anti-inflammatory pathway on the inflammatory response. Furthermore, by combining experimental data with model analysis, we concluded that significant uncertainty remains in the general function of the autonomic nervous system, even in a very controlled experimental model like human endotoxemia. Multiple plausible patterns of autonomic changes could be leading to the observed responses (increased HR, decreased HRV, uncoupling between the autonomic nervous system and the heart) and it is important to properly interpret what is learned from experiments measuring HRV.
Methods
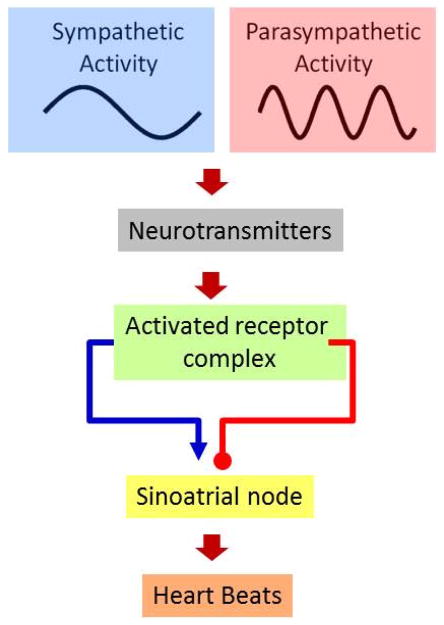
HRV arises largely due to oscillations in autonomic activity which are apparent in the power spectrum of RR intervals primarily in two frequency bands termed low frequency (LF, 0.04–0.15 Hz) and high frequency (HF, 0.15–0.4 Hz) (Task, 1996). A model to evaluate the relationship between the autonomic nervous system and the beating of the heart requires, at a minimum, four components, as shown in Figure 1: (1) a representation of sympathetic activity; (2) a representation of parasympathetic activity; (3) a combination of sympathetic and parasympathetic activities, representing autonomic modulation of the SA node; (4) a method to convert this autonomic modulation into heart beats, which can then be analyzed through the application of HRV metrics, as we have previously demonstrated (Scheff et al., 2011). Each of these four components is, in reality, made up of a multitude of complex interactions and feedback loops, such as autonomic oscillations which arise due to the baroreflex and the respiratory sinus arrhythmia. However, high-level properties of the system can be studied without exhaustively detailing these components. A simple model including these four components was earlier investigated by Brennan et al. in an attempt to gain insight into the relationship between autonomic signaling and Poincaré plots of RR intervals (Brennan et al., 2002). Chiu et al. analyzed a slightly more complex model that accounts for some of the signal transduction steps between the release of autonomic neruotransmitters and the regulation of SA node activity (Chiu and Kao, 2001; Chiu et al., 2003). The goal was to investigate the relationship between autonomic inputs, such as oscillating frequency and mean levels of autonomic outputs, and the beating of the heart. Equation 1 shows a general example of this type of model structure.
Figure 1.
Components of the models linking autonomic activity with heart beats shown in Equation 1 and Equation 2. Sympathetic and parasympathetic nerves impose oscillatory activation of the sinoatrial (SA) node, leading to variability in discrete heart beats. The frequencies of oscillations in sympathetic and parasympathetic activities are derived from the observed frequencies present in the HR power spectrum, the LF and HF bands, 0.095 Hz and 0.275 Hz respectively.
| (1a) |
| (1b) |
| (1c) |
| (1d) |
The variables nor and ach represent norepinephrine and acetylcholine, neurotransmitters released by the sympathetic and parasympathetic nerves respectively which modulate the beating of the heart. Each of these variables has a mean level mk as well as an oscillatory component with amplitude ak and frequency ωk. These sinusoids are the source of variability in the model and represent the underlying LF and HF signals apparent in HRV data. In reality, oscillations at other time scales are also present, such as circadian rhythms, but the analysis presented here focuses only on a short time scale so these much higher frequency rhythms are not included. The two autonomic variables are linearly combined to produce m(t), the autonomic modulation of the SA node. This equation also includes the parameter kicpm to account for the intrinsic cardiac pacemaker function in the absence of autonomic signaling. Sympathetic activity increases m(t) and parasympathetic activity decreases m(t). Then, Equation 1d defines an integral pulse frequency modulation (IPFM) model, which consists of the repeated integration of m(t) up to a threshold I. Whenever this threshold is reached, it represents a heartbeat. Thus, the differences between successive firings of the IPFM model constitute RR intervals. It is important to note that, while Equation 1d models the SA node as a single cell when in reality it is a cluster of cells, this assumption matches well with experimental data on the high-level function of the SA node (Dexter et al., 1989; Pyetan and Akselrod, 2003).
However, there is an obvious drawback to these kinds of linear models: they do not account for nonlinearity in the effects of autonomic activity on the heart. Although there are clearly myriad complexities of physiology not embodied by Equation 1, possibly the most significant issue is that any change in the autonomic inputs proportionally produces a change in m(t) regardless of the state of the system; for instance, repeatedly increasing nor will lead to faster and faster HRs with no upper bound. Of course, autonomic modulation of the heart does not simply linearly reflect autonomic signaling; as is typical in physiology, saturation introduces an upper bound on the response of the heart (Goldberger et al., 2001; Saul, 1990). Considering the model in Equation 1, increases in mean sympathetic activity (i.e. increases in mnor) will produce corresponding increases in HR, even going well beyond what is physiologically possible. Furthermore, oscillations in autonomic activity will always be equally transduced to the SA node, regardless of the mean levels of oscillations. Saturation of autonomic modulation of the SA node destroys the linearity that facilitates those behaviors in the model. An expanded version of Equation 1, including saturation effects, is shown in Equation 2.
| (2a) |
| (2b) |
| (2c) |
| (2d) |
| (2e) |
| (2f) |
Equation 2 is largely the same as Equation 1, except that a saturation function appears between each neurotransmitter and the SA node, representing binding of norepinephrine to adrenergic receptors (adr, Equation 2c) and acetylcholine to cholinergic receptors (cho, Equation 2d). Although autonomic neurotransmitters do act primarily through binding to receptors and a finite number of receptors does imply that saturation will occur at some point, conceptually the model structure would be the same for any type of similar saturation occurring upstream of the SA node. These saturation functions limit the range of potential HR responses to autonomic signaling.
Equation 1 contains 9 parameters and Equation 2 contains 13 parameters. Given that these parameters are generally not known and that the majority of insights derived from these theoretical models are qualitative and independent of specific parametrizations, the simulations below were performed with all parameters set to 1, with the following exceptions: the frequencies of autonomic oscillations were set to the mean values of the standard LF and HF ranges, 0.095 Hz and 0.275 Hz respectively; and the amplitudes of oscillations anor and aach were both set to 0.25, as if they were 1 then some simulations would result in m(t) becoming negative. One particularly important aspect of parametrization regards the saturation functions in Equation 2. Parameters could be chosen such that oscillations occur either in a nearly-linear range (low) or a nearly-saturated range (high). In those cases, the output of the model would be either very similar to the linear model or nearly without any variability, respectively. The parametrization described above does not fall into either of those categories and thus represents good values to study the impact of saturation functions. Further scenarios where specific parametrizations of the model may become important are discussed in more detail in subsequent sections.
Frequency domain HRV metrics were calculated by estimating the power spectrum of RR intervals with MATLAB’s fft function and finding the area under the curve over the LF (0.04–0.15 Hz) and HF (0.15–0.4 Hz) frequency bands. Because variations in HR defined by the models of Equations 1 and 2 are deterministic sinusoids, the “variability” quantified by the HRV metrics is due to these sinusoidal patterns. In reality, as in any biological system, there are also stochastic patterns in heart beats which influence HRV. Stochasticity is not included in our model because we seek to explore the theoretical relationship between autonomic oscillations and frequency domain HRV metrics, which would not be significantly altered by the presence of noise.
Results
HRV, HR, and coupling as functions of mean autonomic activity
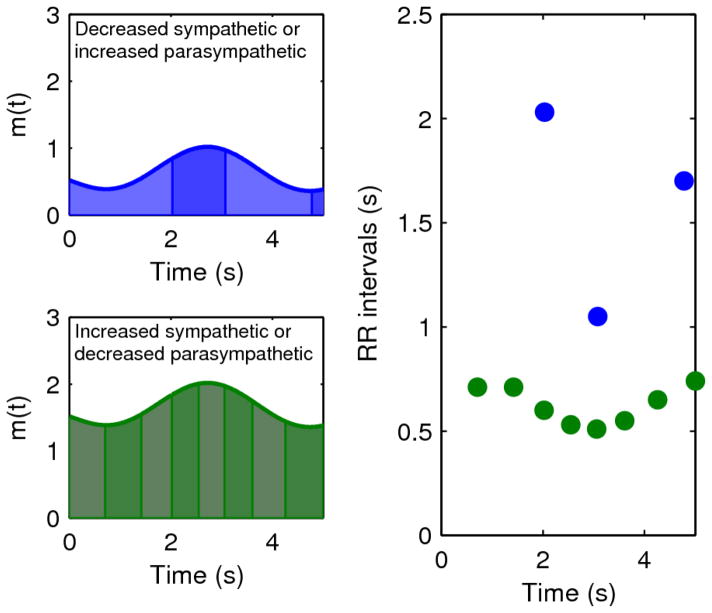
Two mechanisms built into the models in Equations 1–2 contribute to a relationship between mean levels of autonomic activity and HRV. First, there is an effect related to the magnitude of the inputs to an IPFM model, as illustrated in Figure 2. As m(t) increases and thus heart beats become faster, variability decreases because successive intervals are more similar due to their closeness relative to the frequency of oscillations in m(t). This means that perturbations that tend to increase m(t), such as increased sympathetic activity or decreased parasympathetic activity, suppress HRV while changes in the opposite direction lead to more variability. Second, the inclusion of saturation, which only appears in the nonlinear model in Equation 2, plays an important role in evaluating the relationship between mean autonomic activity and transduction of oscillatory signals through an IPFM model, as shown in Figure 3. Increased mean values of sympathetic or parasympathetic activities leads to blunted oscillations in their corresponding neurotransmitters downstream due to saturation, thus leading to lower HRV.
Figure 2.
Relationship between mean HR and HRV. Holding all parameters in Equation 1 constant except the mean sympathetic activity mnor produces the black (mnor = 0.5) and gray (mnor = 1.5) curves on the left, with the gray curve having higher values of m(t). Because sympathetic and parasympathetic are combined additively in the linear model, these are equivalent to setting mach to 1.5 and mach to 0.5, respectively. The black and gray points in the panel to the right correspond to heart beats derived by integrating under the curves to the left. Increasing the mean of m(t) produces higher HR (shorter RR intervals) as well as decreased variability, as all of the integrals (highlighted areas under the curves on the left) are over more similar time ranges.
Figure 3.
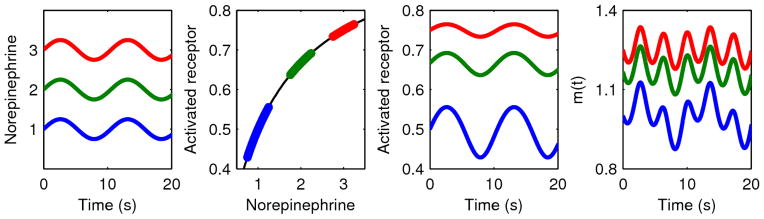
Three sinuosoids with identical amplitudes and different means representing different norepinephrine profiles (Equation 2a) pass through a saturation function representing the binding of norepinephrine to a finite number of adrenergic receptors (Equation 2c), producing significantly different oscillatory amplitudes. The higher values experience more of the saturation effect, blunting oscillations in the output. This ultimately leads to differences in the variability of autonomic stimulation of the SA node, m(t) (Equation 2e). In the linear model of Equation 1, there is no saturation function and thus the inputs and outputs would have the same amplitudes.
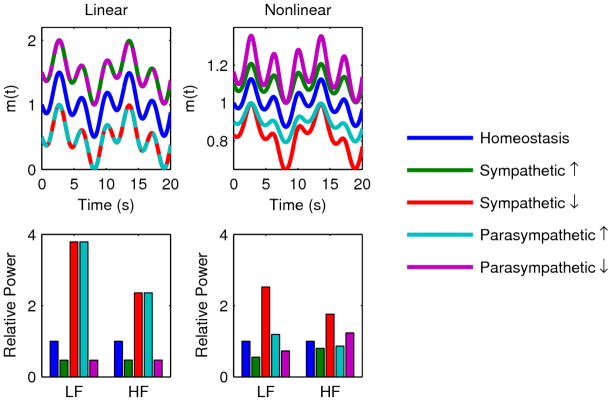
For the linear model (Equation 1), only the first mechanism (increased HR leads to decreased HRV) plays a role, and thus Table 1 and Figure 4 show a direct relationship between the mean value of m(t) and HRV. For the nonlinear model, both mechanisms are active, and under different regimes of autonomic signaling these two effects can be either cooperative or competitive, as shown in Table 1 and Figure 4. In the case of changing mean sympathetic activity, the two effects are cooperative. Increased mean sympathetic activity leads to smaller RR intervals as well as saturation-blunted amplitudes, which both decrease variability in IPFM output; the reverse is true for decreased mean sympathetic activity. However, the two effects are in opposition for parasympathetic activity. As mean parasympathetic activity increases, RR intervals grow longer and variability increases, but the saturation effect blunts parasympathetic oscillations and variability decreases. Thus, in the nonlinear model, HF power can either increase or decrease as parasympathetic activity increases, depending on which effect predominates due to the particular parametrization of the model.
Table 1.
Relationship between changes in mean autonomic activity and changes in mean HR size, LF power, and HF power. Results are shown for both the linear (Equation 1) and nonlinear (Equation 2) models (ΔHR is the same for both models). Up and down arrows represent increases and decreases. Two arrows represent a larger magnitude change, due to the cooperativity of both mechanisms for amplitude changes in the nonlinear model. A question mark represents an uncertain change, due to the two mechanisms working in opposite directions and thus leading to either and increase or decrease depending on the parametrization of the model.
| Linear model | Nonlinear model | ||||
|---|---|---|---|---|---|
| Perturbation | ΔHR | ΔLF | ΔHF | ΔLF | ΔHF |
| Increase mean sympathetic activity | ↑ | ↓ | ↓ | ↓↓ | ↓ |
| Decrease mean sympathetic activity | ↓ | ↑ | ↑ | ↑ ↑ | ↑ |
| Increase mean parasympathetic activity | ↓ | ↑ | ↑ | ↑ | ? |
| Decrease mean parasympathetic activity | ↑ | ↓ | ↓ | ↓ | ? |
Figure 4.
Relationship between changes in mean autonomic activity and changes in LF power and HF power for both the linear (Equation 1) and nonlinear (Equation 2) models. LF and HF powers were calculated as described in the Methods section for 50% increases/decreases in mean sympathetic/parasympathetic activities. In the plots, these values are all shown relative to homeostatic LF and HF powers. For the linear model, increased sympathetic activity and decreased parasympathetic activity both decrease LF and HF, while decreased sympathetic activity and increased parasympathetic activity both increase LF and HF; the magnitude of these changes in m(t) is identical, which is reflected by the overlapping dashed lines. For the nonlinear model, the same directional relationships hold of LF, although changes in sympathetic activity produce larger magnitude changes in LF. These relationships also hold for the response of LF to changes in parasympathetic activity. However, depending on the parametrization of the model, a change in parasympathetic activity can either increase or decrease HF. These differences between the two models are due to the competing effects of the two mechanisms driving changes in LF and HF as mean autonomic levels change.
Perturbations to the model leading to changes in HR are more straightforward than those leading to changes in HRV, as anything that increases m(t) will increase HR and anything that decreases m(t) will decrease HR. As is described in Table 1, HR increases in response to increased sympathetic or decreased parasympathetic activities, and HR decreases in response to decreased sympathetic or increased parasympathetic activities. Due to the additive terms representing the effect of sympathetic and parasympathetic modulation on m(t), perturbations downstream of nor and ach can also have similar effects if they lead to changes in m(t).
Additionally, we evaluated coupling between the autonomic nervous system and the heart. Table 1 and Figure 4 show that the system is highly responsive, both in terms of HR and HRV, to changes in mean autonomic activities. However, if the parameters were perturbed from their nominal values prior to an autonomic stimulus, this may no longer be the case – for instance, imagine if the response to sympathetic signaling is already saturated, then further increases in sympathetic activity will have no effect downstream. Robust interorgan coupling has been hypothesized as an important factor in disease progression (Godin and Buchman, 1996) and quantification of coupling between the heart and the autonomic nervous system has been investigated as a marker of disease severity in multiple organ dysfunction syndrome (Schmidt et al., 2004).
To quantify the state of coupling between the autonomic nervous system and the heart, we evaluated the partial derivative of m(t) as mean autonomic activities change for the nonlinear model, as shown in Equation 3.
| (3a) |
| (3b) |
When the sensitivities are near 0, then changes in mean autonomic activities will produce little change in m(t), and thus little change in either HR or HRV. So, for instance, decreasing the coefficients on the autonomic inputs into m(t) (kadr and kcho) pushes both Equations 3a3b towards 0, as does altering the parameters of the saturation functions to make saturation occur earlier.
While these results only consider the effect of changing mean sympathetic or parasympathetic activities while holding oscillatory amplitudes constant, the Appendix considers the case where mean value and amplitude are proportional.
Case study: Autonomic function in human endotoxemia
Elective administration of bacterial endotoxin (LPS) to otherwise healthy human volunteers serves as a useful model of TLR4 agonist-induced systemic inflammation, providing a reproducible experimental platform tying systemic inflammation to physiological signal generation (Lowry, 2005; Lowry, 2009). Low doses of LPS given to humans elicit neuroendocrine, hemodynamic, and leukocyte transcriptional responses that reproduce, in part, those seen after acute injury and systemic inflammation (Andreasen et al., 2008; Lowry, 2005; Lowry, 2009; Shanker et al., 2010), including a reduction in HRV. Thus, human endotoxemia experiments represent a platform for the analysis of relationships between inflammation, autonomic dysfunction, and changes in HRV (Scheff et al., 2012a).
In human endotoxemia, consistent patterns in HR and HRV have been observed across several different experiments. HR increases while metrics of HRV, including LF and HF powers, decrease (Alvarez et al., 2007; Godin et al., 1996; Jan et al., 2010; Jan et al., 2009; Kox et al., 2011; Lehrer et al., 2010; Rassias et al., 2011; Rassias et al., 2005; Sayk et al., 2008; Scheff et al., 2011). Considering the results in Table 1, this is in line with what would be expected to occur from stimuli leading to increased HR, such as increased sympathetic activity and/or decreased parasympathetic activity (Scheff et al., 2011). Another key feature observed in human endotoxemia is uncoupling between the autonomic nervous system and the heart, such that induced changes in autonomic activity during endotoxemia fail to produce corresponding changes in the output of the heart (Sayk et al., 2008).
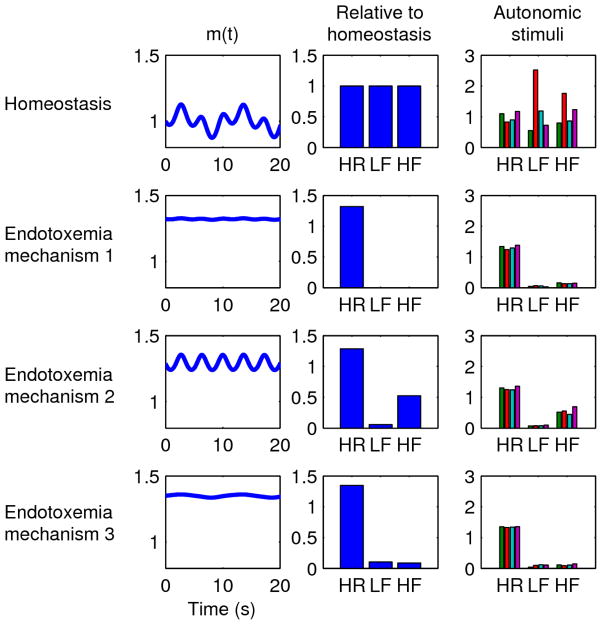
Three hypothetical scenarios for autonomic function giving rise to these observed patterns of HR, HRV, and uncoupling in human endotoxemia are shown in Figure 5, along with a homeostatic case for comparison. These scenarios represent different levels of autonomic activity (by altering mnor and mach), receptor-level regulation and coupling between the autonomic nervous system and the heart (by altering kadr and kcho), and non-autonomic influences on HR (by altering kicpm), all producing similar outputs in terms of HR and HRV:
Figure 5.
Mechanisms for HR/HRV changes in endotoxemia. Each row represents a different simulation. The m(t) column shows the autonomic modulation of the heart as defined in Equation 2e based on the oscillations shown in the first two columns. The “Relative to homeostasis” column shows how HR, LF, and HF changed relative to homeostatic values in the first row. In all cases relative to homeostasis, HR increases while LF and HF decrease; the specific magnitudes of these changes (i.e. how much HR increases, etc.) can be tuned by the parameters of the model. The “Autonomic stimuli” column shows how HR, LF, and HF respond to 4 perturbations (as in Figure 4: increased sympathetic activity 50%, decreased sympathetic activity 50%, increased parasympathetic activity 50%, and decreased parasympathetic activity 50%, respectively) to quantify the level of uncoupling between the autonomic nervous system and the heart, again shown relative to homeostatic values. Uncoupling is indicated by relative insensitivity to autonomic stimuli. First row: homeostasis. Second row: endotoxemia mechanism 1, where sympathetic and parasympathetic activities increase and saturation of receptors leads to uncoupling. Third row: endotoxemia mechanism 2, where sympathetic activity increases, parasympathetic activity decreases (or increases), and uncoupling is due to a loss of sensitivity of the heart to autonomic stimuli. Fourth row: endotoxemia mechanism 3, where autonomic activities are uncoupled from the heart due to a loss of sensitivity but non-autonomic factors still increase HR.
Homeostasis. The nominal parameter values given in the Methods section were used to create a reference simulation.
Endotoxemia mechanism 1. Sympathetic and parasympathetic activities increase (mnor = 10 and mach = 5) leading to blunted oscillations due to saturation as in Figure 3. Sympathetic activity predominates (kach,2 = 1.5) resulting in increased HR.
Endotoxemia mechanism 2. Sympathetic activity increases (mnor = 10), resulting in increased HR and decreased LF rhythms. Diminished autonomic sensitivity at the SA node (kadr = 0.5 and kcho = 0.5) further reduces both LF and HF. In this scenario, parasympathetic activity can either increase or decrease, but the results shown in Figure 5 are for decreased parasympathetic activity (mach = 0.5).
Endotoxemia mechanism 3. Autonomic activity is largely uncoupled from the SA node (kadr = 0.1 and kcho = 0.1), resulting in decreased HRV. HR increases due to non-autonomic factors (kicpm = 1.4). In this scenario, autonomic activities can change in either direction without substantially impacting the output of the heart, but the results shown in Figure 5 are for decreased sympathetic activity (mnor = 0.5) and increased parasympathetic activity (mach = 5).
Furthermore, the Appendix illustrates how, even after significantly changing the assumptions that give rise to Equation 2, these three scenarios depicted in Figure 5 continue to reproduce changes in HR, HRV, and uncoupling similar to what has been observed in human endotoxemia experiments.
Discussion
Although traditionally LF oscillations were seen as reflecting sympathetic activity and HF oscillations representing parasympathetic activity, spectral analysis truly quantifies the amplitudes of oscillations at certain frequencies, not their mean values (Akselrod, 1995; Eckberg, 1997; Saul, 1990). In other words, LF and HF powers most closely reflect anor and aach in Equations 2a–b rather than mnor and mach. This is a critical point, as LF and HF powers do not directly represent mean autonomic activities; instead they reflect the amount of oscillations on top of these mean levels. Furthermore, it is generally the mean values that are of interest, rather than the oscillatory amplitudes, but there is not a one-to-one correspondence between the amplitude of oscillations in inputs to the IPFM model and variability in generated heart beat intervals. Niklasson et al. found that HRV analysis based on RR intervals reveals a negative correlation between HR and HRV in both homeostatic experimental data as well as in a theoretical IPFM model (Niklasson et al., 1993), as is described in Figure 2. This was more thoroughly investigated by Chiu et al., revealing that autonomic perturbations that increase HR (increased sympathetic activity or decreased parasympathetic activity) tend to decrease both LF and HF powers, while perturbations that decrease HR (decreased sympathetic activity or increased parasympathetic activity) have the opposite effect (Chiu and Kao, 2001; Chiu et al., 2003). The results of Niklasson et al. and Chiu et al. roughly correspond to the results for the linear model (Equation 1) shown here in Table 1 and Figure 4. These results clearly illustrate how conventional wisdom about the physiological interpretation of frequency domain HRV metrics does not necessarily correspond with the basic mechanisms by which the ANS regulates the heart, as even under the very simplistic assumptions of the linear model, the relationship between autonomic activity and LF and HF powers is contrary to conventional wisdom.
The nonlinear model (Equation 2) is still fairly simple, yet adds complexity to the relationship between autonomic activity and HRV. Pyetan et al. studied this issue specifically for the parasympathetic branch alone (Pyetan and Akselrod, 2003; Pyetan and Akselrod, 2004; Pyetan et al., 2001) and also found complex relationships between autonomic inputs and HRV. In total, what we learn from these simple modeling studies in isolation is that changes in HRV can be difficult to interpret, as changes in even basic assumption can have significant impacts on the results (see the differences between the linear and nonlinear models in Table 1 and Figure 4). Even in a more complex physiology-based model, where factors such as baroreflex-driven rhythms and the respiratory sinus arrhythmia could give rise to oscillatory patterns in autonomic activity, the same fundamental conclusions would still hold true. This emphasizes the importance of our analysis, as if conventional interpretations of HRV break down even in the context of an idealized model, those same interpretations would likely be even more strained in a more complex system.
These challenges in interpretation are important in experimental settings such as human endotoxemia, where HRV analysis is applied in attempts to gain insight into autonomic dysfunction in systemic inflammation. For instance, consider the cholinergic anti-inflammatory pathway, a key link between the ANS and the immune system (Huston and Tracey, 2011; Pavlov et al., 2003). Parasympathetic afferent sensory fibers are activated in response to inflammation, leading to not only the central release of hormones, but also efferent parasympathetic activity which exerts an anti-inflammatory effect through acetylcholine signaling. Based on the view that HF power reflects parasympathetic activity, some have deemed it paradoxical that HF power and other correlated HRV metrics are so significantly suppressed in endotoxemia (Fairchild et al., 2011; Gholami et al., 2012). Fairchild et al. addressed this issue at least in part by identifying transient increases in HRV mediated by parasympathetic signaling in response to a variety of different bacterial infections in mice (Fairchild et al., 2011). However, this does not necessarily explain scenarios like human endotoxemia where no such transient increase in HRV is observed, and instead there is only a decrease in HRV until homeostasis is restored.
Thinking in terms of the nonlinear model presented in Equation 2 presents an alternative explanation as to the effect of the cholinergic anti-inflammatory pathway on HRV. An increase in parasympathetic signaling can lead to either increased or decreased HF power depending on the particular situation, as illustrated in Table 1 and Figure 4. Therefore, there is no theoretical disconnect between heightened parasympathetic signaling and decreased HF power and HRV in general. This is fundamentally due to HF power reflecting the oscillatory amplitude rather than the mean level of parasympathetic activity, thus making the cholinergic anti-inflammatory response only indirectly linked to HRV, such as through the model shown in Equation 2. And in reality, physiology is much more complex than Equation 2, thus presenting even more opportunities for deviation from the normally-assumed relationship between HF and parasympathetic activity. Although more complex models, such as that of Ursino and Magosso, confirmed some aspects of the traditional relationships between LF power, HF power, sympathetic activity, and parasympathetic activity, they also found several other parameters that could confound direct interpretations of these frequency domain HRV metrics (Ursino and Magosso, 2003). Additionally, they noted how saturation of signal transduction due to sigmoidal functions could also significantly interfere with interpretations of HRV, as is discussed here regarding the nonlinear model presented in Equation 2. Zenker et al. also identified this type of saturation as a potential physiologically-relevant mechanism that can drive changes in HRV (Zenker et al., 2007), such as the apparent loss of “sympathetic activity” in HRV caused by a real underlying increase in sympathetic activity, similar to the results shown in Figure 4 and Table 1.
The concept of uncoupling, the loss of interorgan communication, is also important in the context of systemic inflammation, as it has long been hypothesized to play a critical role in disease progression (Godin and Buchman, 1996) and changes in variability metrics such as HRV have been proposed as metrics for uncoupling (Godin et al., 1996; Pincus, 1994). Clinically, similar quantification of uncoupling has been shown to be a marker of disease severity in patients with multiple organ dysfunction syndrome (Schmidt et al., 2004). The most thorough investigation of the autonomic nervous system in human endotoxemia was performed by Sayk et al. through two novel experimental techniques: 1.) measuring muscle sympathetic nerve activity (MSNA) to directly quantify sympathetic activity in endotoxemia; and 2.) modulating blood pressure (BP) to quantify how BP-induced autonomic signaling is coupled to the heart in endotoxemia (Sayk et al., 2008). This produced two novel insights. They found that MSNA in the peroneal nerve is suppressed in endotoxemia, which is the opposite of what would have been expected based on changes in HR, and that the autonomic nervous system and the heart were effectively uncoupled in endotoxemia, as autonomic perturbations induced by changes in BP produced no significant effect on HR or HRV even as they significantly altered MSNA.
The fact that sympathetic output of the peroneal nerve is diminished in endotoxemia does not necessarily mean that sympathetic activity at the heart behaves similarly, as different parts of the sympathetic nervous system may respond differently. Thus, it could very well be that sympathetic activity increases (Kox et al., 2011). However, the striking uncoupling found between changes in BP and HR requires closer examination. One can imagine that saturation at some point in autonomic signaling pathways, such as defined in Equations 2c–d, could explain a kind of uncoupling in that if the system was responding to very high levels of autonomic activity, such that further changes in autonomic activity were be blunted by the time they reached the SA node and thus were not reflected in the output of the heart. For the model in Equation 2, this would only be possible to rationalize with observations of increased HR and decreased HRV in endotoxemia if mean sympathetic and parasympathetic activities were either 1.) significantly elevated in endotoxemia (e.g. by increasing mnor and mach in Equations 2a–b) or if 2.) sensitivity to autonomic signaling was significantly decreased (e.g. by increasing the parameters in the denominators of Equations 2c–d). The former is possible, particularly in light of the cholinergic anti-inflammatory response as discussed above. The latter is possible as well, as non-autonomic inflammatory mediators exert regulatory effects on the beating of the heart (Gholami et al., 2012; Takayama et al., 2005; Zorn-Pauly et al., 2007) and crosstalk between the sympathetic and parasympathetic activities can result in altered sensitivities to autonomic neurotransmitters (Pyetan and Akselrod, 2003).
Additionally it is possible that 3.) the decrease in peroneal MSNA (Sayk et al., 2008) is matched by a decrease in sympathetic activity at the heart. Experiments in rats found that endotoxemia led to increased acetylcholine concentration and decreased norepinephrine concentration in the liver, lending further support to the hypothesis that sympathetic activity is diminished in endotoxemia (Huang et al., 2010). In this hypothetical regime, uncoupling between the autonomic nervous system and the heart (Sayk et al., 2008) would mask the effects of diminished sympathetic activity on HR, and the endotoxemia-induced increase in HR could be due to non-autonomic pathways (Gholami et al., 2012; Takayama et al., 2005; Zorn-Pauly et al., 2007). In terms of Equation 2, this scenario would be equivalent to decreasing mnor to simulate decreased sympathetic activity, decreasing kicpm to simulate a non-autonomic increase in HR, and decreasing both kadr and kcho to represent uncoupling.
Distinguishing between these three mechanisms, as shown in Figure 5, requires novel experimental work to look more closely at the autonomic nervous system in human endotoxemia (Sayk et al., 2008). It is important that these issues are approached with an accurate mindset of what the analysis of heart beats can and cannot provide. Signal transduction from the autonomic nervous system to the heart is complex, nonlinear, unintuitive, and often misinterpreted. Simple mathematical models, as discussed here and elsewhere (Brennan et al., 2002; Chiu and Kao, 2001; Niklasson et al., 1993; Pyetan and Akselrod, 2003), can elucidate issues related to the interpretation of HR and HRV data. Specifically in the literature related to human endotoxemia, overzealous interpretation of HR and HRV signals is common and may be impeding more fundamental understanding of autonomic function in systemic inflammation. All three hypothetical mechanisms discussed above also allow for the possibility that autonomic modulation of the heart may be substantially different than autonomic activity elsewhere in the body, and the additional complexity in real physiological systems presents even more opportunities for other factors to influence HR and HRV. While quantification of HR and HRV can provide valuable insight into a system, the extent of this insight depends on how well the specific underlying mechanisms in a specific scenario are known, so that physiologically important signals can be accurately identified and isolated.
Conclusions
Even the simple models discussed here illustrate some of the challenges in interpreting HRV data, despite the lack of such physiological elements as crosstalk between branches of the autonomic nervous system, redundant/complementary pathways, and closed loop autonomic control, to name just a few of the simplifications made here. Incorporating these further complexities into the conceptual picture makes the relationship between HRV and autonomic signaling even less clear. The primary implication of these results is that caution must be exercised when attempting to interpret the autonomic implications of changes in HRV in systemic inflammation, and likely also in many other clinically relevant scenarios. However, in a well-characterized system where relationships between autonomic activity and HRV have been established experimentally within a specific context, changes in HF and LF powers may still be meaningful and may predictably reflect changes in autonomic signaling. Lacking that, it is difficult to draw mechanistic conclusions from HRV data, as exemplified by the competing mechanisms shown in Figure 5 that can all equally rationalize HRV changes in human endotoxemia. Proper understanding of the information content and interpretation of HRV data is important in accurately assessing experimental data; thus, these issues also influences the perceived state of knowledge about autonomic function in systemic inflammation. Therefore, it is important to keep this in mind in experimental design and interpretation as progress is made towards the goal of deciphering the function of the autonomic nervous system in systemic inflammation.
study models describing the relationship between the autonomic nervous system and patterns of HRV
incorporate high frequency autonomic oscillations and neurotransmitters kinetics
study changes in autonomic activity and inflammation-induced uncoupling of the heart
discuss the uncertainty in the mechanistic implications of HRV changes in human endotoxemia
Acknowledgments
Grants
IPA acknowledges support from NIH GM082974. SEC was supported, in part, from NIH GM34695. JDS was supported by a University and Louis Bevier Graduate Fellowship from Rutgers University.
Appendix
The analysis presented in the main text relies on a number of assumptions with regards to the analysis techniques used to investigate HRV and the structure of the models in Equations 1–2. In the results presented in this appendix, we evaluated the implications of altering or relaxing these assumptions on the conclusions drawn about the relationship between the autonomic nervous system and the heart, particularly in human endotoxemia.
Alternative method for calculating LF and HF powers
LF and HF powers are typically calculated by estimating the power spectrum of RR intervals (Task, 1996), which is what was done for the results shown in the main text. However, it is known that calculating LF and HF powers based on RR intervals introduces dependencies on mean values of autonomic inputs, as was originally discussed by Niklasson et al. (Niklasson et al., 1993). This effect contributes to the dependency of LF and HF powers on mean autonomic activities illustrated in Figure 4 and Table 1. By estimating the power spectrum based on instantaneous HR rather than RR intervals, this relationship would be expected to change (Niklasson et al., 1993) and therefore could also impact the theoretical human endotoxemia results in Figure 5.
Using HR rather than RR to calculate LF and HF powers produced results similar to the model considered by Niklasson et al. in that using HR eliminates the relationship between mean autonomic inputs and spectral powers (Niklasson et al., 1993). For the nonlinear model, LF and HF powers do continue to change as the input changes, but the pattern is different than in Figure 4; this is because these changes are all driven purely by the saturation mechanism. For instance, increased sympathetic activity leads to blunted oscillations in norepinephrine, ultimately resulting in decreased LF power.
However, when this technique is applied for the endotoxemia scenarios in Figure 5, it does not significantly impact the level of uncoupling present in the various hypothetical scenarios in.
Proportional changes in mean value and amplitude
To interpret LF and HF powers, it is often implicitly (and sometimes explicitly) assumed that the amplitude of oscillations is proportional to the mean value, even though it is not clear if such a relationship generally holds (Akselrod, 1995; Eckberg, 1997; Saul, 1990). In Equations 1–2, the opposite assumption is made: mean value and amplitude are independent.
In both the linear (Equation 1) and nonlinear (Equation 2) models in the manuscript, neurotransmitter concentrations are defined as:
| (4a) |
| (4b) |
The mean values m and the amplitudes a are independent in Equation 4. An alternative formulation is shown in Equation 5, where the amplitude is directly proportional to the mean value.
| (5a) |
| (5b) |
The effect of Equation 5 is to counter the saturation mechanism. Saturation causes high values of neurotransmitters to produce blunted oscillations downstream. However, if the amplitudes of oscillations are proportional to mean values, they oppose the saturation-induced decreases in oscillations.
Applying Equation 5 within the linear model produces larger changes in LF and HF powers due to the direct amplitude modulation, since there is no saturation to blunt this new effect. However, in the nonlinear case, since the changes in Equation 5 oppose the saturation in the nonlinear model, differences in relative powers are blunted relative to Figure 4.
As in the previous section, Equation 5 still does not substantially affect the uncoupling in the hypothetical endotoxemia scenarios in Figure 5.
Combined changes
If these two altered assumptions (different method of HRV calculation and amplitudes depending on mean values) are applied together, the responses to the hypothetical endotoxemia scenarios remain uncoupled. What this suggests is that, even with a variety of different assumptions, there are still a number of hypothetical scenarios that can equivalently capture experimental results. Furthermore, changing relatively simple assumptions in the model produced significantly different relationships between mean autonomic signaling and LF and HF powers. In total, these results serve to strengthen the conclusions of the paper with respect to the function of the autonomic nervous system in endotoxemia and the uncertainty of HR- and HRV-based insight into autonomic function.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akselrod S. Components of heart rate variability: basic studies. In: Malik M, Camm AJ, editors. Heart Rate Variability. Futura; Armonk, NY: 1995. pp. 147–63. [Google Scholar]
- Alvarez SM, Katsamanis Karavidas M, Coyle SM, Lu SE, Macor M, Oikawa LO, Lehrer PM, Calvano SE, Lowry SF. Low-dose steroid alters in vivo endotoxin-induced systemic inflammation but does not influence autonomic dysfunction. J Endotoxin Res. 2007;13:358–68. doi: 10.1177/0968051907086465. [DOI] [PubMed] [Google Scholar]
- Andreasen AS, Krabbe KS, Krogh-Madsen R, Taudorf S, Pedersen BK, Moller K. Human endotoxemia as a model of systemic inflammation. Curr Med Chem. 2008;15:1697–705. doi: 10.2174/092986708784872393. [DOI] [PubMed] [Google Scholar]
- Annane D, Trabold F, Sharshar T, Jarrin I, Blanc AS, Raphael JC, Gajdos P. Inappropriate sympathetic activation at onset of septic shock: a spectral analysis approach. Am J Respir Crit Care Med. 1999;160:458–65. doi: 10.1164/ajrccm.160.2.9810073. [DOI] [PubMed] [Google Scholar]
- Barnaby D, Ferrick K, Kaplan DT, Shah S, Bijur P, Gallagher EJ. Heart rate variability in emergency department patients with sepsis. Acad Emerg Med. 2002;9:661–70. doi: 10.1111/j.1553-2712.2002.tb02143.x. [DOI] [PubMed] [Google Scholar]
- Bravi A, Longtin A, Seely AJ. Review and classification of variability analysis techniques with clinical applications. Biomed Eng Online. 2011;10:90. doi: 10.1186/1475-925X-10-90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brennan M, Palaniswami M, Kamen P. Poincare plot interpretation using a physiological model of HRV based on a network of oscillators. Am J Physiol Heart Circ Physiol. 2002;283:H1873–86. doi: 10.1152/ajpheart.00405.2000. [DOI] [PubMed] [Google Scholar]
- Chiu HW, Kao T. A mathematical model for autonomic control of heart rate variation. IEEE Eng Med Biol Mag. 2001;20:69–76. doi: 10.1109/51.917726. [DOI] [PubMed] [Google Scholar]
- Chiu HW, Wang TH, Huang LC, Tso HW, Kao T. The influence of mean heart rate on measures of heart rate variability as markers of autonomic function: a model study. Med Eng Phys. 2003;25:475–81. doi: 10.1016/s1350-4533(03)00019-5. [DOI] [PubMed] [Google Scholar]
- Dexter F, Levy MN, Rudy Y. Mathematical model of the changes in heart rate elicited by vagal stimulation. Circ Res. 1989;65:1330–9. doi: 10.1161/01.res.65.5.1330. [DOI] [PubMed] [Google Scholar]
- Dick TE, Molkov YI, Nieman G, Hsieh YH, Jacono FJ, Doyle J, Scheff JD, Calvano SE, Androulakis IP, An G, Vodovotz Y. Linking Inflammation, Cardiorespiratory Variability, and Neural Control in Acute Inflammation via Computational Modeling. Front Physiol. 2012;3:222. doi: 10.3389/fphys.2012.00222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckberg DL. Sympathovagal balance: a critical appraisal. Circulation. 1997;96:3224–32. doi: 10.1161/01.cir.96.9.3224. [DOI] [PubMed] [Google Scholar]
- Fairchild KD, Srinivasan V, Moorman JR, Gaykema RP, Goehler LE. Pathogen-induced heart rate changes associated with cholinergic nervous system activation. Am J Physiol Regul Integr Comp Physiol. 2011;300:R330–9. doi: 10.1152/ajpregu.00487.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrard CS, Kontoyannis DA, Piepoli M. Spectral analysis of heart rate variability in the sepsis syndrome. Clin Auton Res. 1993;3:5–13. doi: 10.1007/BF01819137. [DOI] [PubMed] [Google Scholar]
- Gholami M, Mazaheri P, Mohamadi A, Dehpour T, Safari F, Hajizadeh S, Moore KP, Mani AR. Endotoxemia is associated with partial uncoupling of cardiac pacemaker from cholinergic neural control in rats. Shock. 2012;37:219–27. doi: 10.1097/SHK.0b013e318240b4be. [DOI] [PubMed] [Google Scholar]
- Godin PJ, Buchman TG. Uncoupling of biological oscillators: a complementary hypothesis concerning the pathogenesis of multiple organ dysfunction syndrome. Crit Care Med. 1996;24:1107–16. doi: 10.1097/00003246-199607000-00008. [DOI] [PubMed] [Google Scholar]
- Godin PJ, Fleisher LA, Eidsath A, Vandivier RW, Preas HL, Banks SM, Buchman TG, Suffredini AF. Experimental human endotoxemia increases cardiac regularity: results from a prospective, randomized, crossover trial. Crit Care Med. 1996;24:1117–24. doi: 10.1097/00003246-199607000-00009. [DOI] [PubMed] [Google Scholar]
- Goldberger JJ, Challapalli S, Tung R, Parker MA, Kadish AH. Relationship of heart rate variability to parasympathetic effect. Circulation. 2001;103:1977–83. doi: 10.1161/01.cir.103.15.1977. [DOI] [PubMed] [Google Scholar]
- Goldstein DS, Bentho O, Park MY, Sharabi Y. Low-frequency power of heart rate variability is not a measure of cardiac sympathetic tone but may be a measure of modulation of cardiac autonomic outflows by baroreflexes. Exp Physiol. 2011;96:1255–61. doi: 10.1113/expphysiol.2010.056259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heathers JA. Sympathovagal balance from heart rate variability: an obituary. Exp Physiol. 2012;97:556. doi: 10.1113/expphysiol.2011.063867. [DOI] [PubMed] [Google Scholar]
- Huang J, Wang Y, Jiang D, Zhou J, Huang X. The sympathetic-vagal balance against endotoxemia. J Neural Transm. 2010;117:729–35. doi: 10.1007/s00702-010-0407-6. [DOI] [PubMed] [Google Scholar]
- Huston JM, Tracey KJ. The pulse of inflammation: heart rate variability, the cholinergic anti-inflammatory pathway and implications for therapy. J Intern Med. 2011;269:45–53. doi: 10.1111/j.1365-2796.2010.02321.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan BU, Coyle SM, Macor MA, Reddell M, Calvano SE, Lowry SF. Relationship of basal heart rate variability to in vivo cytokine responses after endotoxin exposure. Shock. 2010;33:363–8. doi: 10.1097/SHK.0b013e3181b66bf4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan BU, Coyle SM, Oikawa LO, Lu SE, Calvano SE, Lehrer PM, Lowry SF. Influence of acute epinephrine infusion on endotoxin-induced parameters of heart rate variability: a randomized controlled trial. Ann Surg. 2009;249:750–6. doi: 10.1097/SLA.0b013e3181a40193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korach M, Sharshar T, Jarrin I, Fouillot JP, Raphael JC, Gajdos P, Annane D. Cardiac variability in critically ill adults: influence of sepsis. Crit Care Med. 2001;29:1380–5. doi: 10.1097/00003246-200107000-00013. [DOI] [PubMed] [Google Scholar]
- Kox M, Ramakers BP, Pompe JC, van der Hoeven JG, Hoedemaekers CW, Pickkers P. Interplay between the acute inflammatory response and heart rate variability in healthy human volunteers. Shock. 2011;36:115–20. doi: 10.1097/SHK.0b013e31821c2330. [DOI] [PubMed] [Google Scholar]
- Lehrer P, Karavidas MK, Lu SE, Coyle SM, Oikawa LO, Macor M, Calvano SE, Lowry SF. Voluntarily produced increases in heart rate variability modulate autonomic effects of endotoxin induced systemic inflammation: an exploratory study. Appl Psychophysiol Biofeedback. 2010;35:303–15. doi: 10.1007/s10484-010-9139-5. [DOI] [PubMed] [Google Scholar]
- Lowry SF. Human endotoxemia: a model for mechanistic insight and therapeutic targeting. Shock. 2005;24(Suppl 1):94–100. doi: 10.1097/01.shk.0000191340.23907.a1. [DOI] [PubMed] [Google Scholar]
- Lowry SF. The stressed host response to infection: the disruptive signals and rhythms of systemic inflammation. Surg Clin North Am. 2009;89:311–26. vii. doi: 10.1016/j.suc.2008.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malliani A, Lombardi F, Pagani M. Power spectrum analysis of heart rate variability: a tool to explore neural regulatory mechanisms. Br Heart J. 1994;71:1–2. doi: 10.1136/hrt.71.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niklasson U, Wiklund U, Bjerle P, Olofsson BO. Heart-rate variation: what are we measuring? Clin Physiol. 1993;13:71–9. doi: 10.1111/j.1475-097x.1993.tb00318.x. [DOI] [PubMed] [Google Scholar]
- Ottesen JT. The mathematical microscope – making the inaccessible accessible. In: Booβ-Bavnbek B, et al., editors. BetaSys. Vol. 2. Springer; 2011. pp. 97–118. [Google Scholar]
- Pavlov VA, Wang H, Czura CJ, Friedman SG, Tracey KJ. The cholinergic anti-inflammatory pathway: a missing link in neuroimmunomodulation. Mol Med. 2003;9:125–34. [PMC free article] [PubMed] [Google Scholar]
- Piepoli M, Garrard CS, Kontoyannis DA, Bernardi L. Autonomic control of the heart and peripheral vessels in human septic shock. Intensive Care Med. 1995;21:112–9. doi: 10.1007/BF01726532. [DOI] [PubMed] [Google Scholar]
- Pincus SM. Greater signal regularity may indicate increased system isolation. Math Biosci. 1994;122:161–81. doi: 10.1016/0025-5564(94)90056-6. [DOI] [PubMed] [Google Scholar]
- Pyetan E, Akselrod S. Do the high-frequency indexes of HRV provide a faithful assessment of cardiac vagal tone? A critical theoretical evaluation. IEEE Trans Biomed Eng. 2003;50:777–83. doi: 10.1109/TBME.2003.812158. [DOI] [PubMed] [Google Scholar]
- Pyetan E, Akselrod S. A theoretical appraisal of the dependence of respiratory sinus arrhythmia on gradual vagal blockade. Methods Inf Med. 2004;43:52–5. [PubMed] [Google Scholar]
- Pyetan E, Zoran O, Toledo E, Akselrod S. A theoretical model for the dependency of heart rate on gradual vagal blockade by atropine. Comput Cardiol. 2001;28:653–6. [Google Scholar]
- Rassias AJ, Guyre PM, Yeager MP. Hydrocortisone at stress-associated concentrations helps maintain human heart rate variability during subsequent endotoxin challenge. J Crit Care. 2011;26:636, e1–5. doi: 10.1016/j.jcrc.2011.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rassias AJ, Holzberger PT, Givan AL, Fahrner SL, Yeager MP. Decreased physiologic variability as a generalized response to human endotoxemia. Crit Care Med. 2005;33:512–9. doi: 10.1097/01.ccm.0000155908.46346.ed. [DOI] [PubMed] [Google Scholar]
- Saul JP. Beat-to-beat variations of heart rate reflect modulation of cardiac autonomic outflow. News Physiol Sci. 1990;5:32–7. [Google Scholar]
- Sayk F, Vietheer A, Schaaf B, Wellhoener P, Weitz G, Lehnert H, Dodt C. Endotoxemia causes central downregulation of sympathetic vasomotor tone in healthy humans. Am J Physiol Regul Integr Comp Physiol. 2008;295:R891–8. doi: 10.1152/ajpregu.90444.2008. [DOI] [PubMed] [Google Scholar]
- Scheff JD, Mavroudis PD, Calvano SE, Androulakis IP. Translational applications of evaluating physiologic variability in human endotoxemia. J Clin Monit Comput. 2012a doi: 10.1007/s10877-012-9418-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheff JD, Mavroudis PD, Calvano SE, Lowry SF, Androulakis IP. Modeling autonomic regulation of cardiac function and heart rate variability in human endotoxemia. Physiol Genomics. 2011;43:951–64. doi: 10.1152/physiolgenomics.00040.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheff JD, Mavroudis PD, Foteinou PT, Calvano SE, Androulakis IP. Modeling physiologic variability in human endotoxemia. Crit Rev Biomed Eng. 2012b;40:313–22. doi: 10.1615/critrevbiomedeng.v40.i4.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheff JD, Mavroudis PD, Calvano SE, Lowry SF, Androulakis IP. Autonomic dysfunction in SIRS and sepsis. In: Stevens RD, et al., editors. Brain Disorders in Critical Illness. Cambridge University Press; in press. [Google Scholar]
- Schmidt H, Muller-Werdan U, Nuding S, Hoffmann T, Francis DP, Hoyer D, Rauchhaus M, Werdan K. Impaired chemoreflex sensitivity in adult patients with multiple organ dysfunction syndrome--the potential role of disease severity. Intensive Care Med. 2004;30:665–72. doi: 10.1007/s00134-003-2131-2. [DOI] [PubMed] [Google Scholar]
- Schmidt HB, Werdan K, Muller-Werdan U. Autonomic dysfunction in the ICU patient. Curr Opin Crit Care. 2001;7:314–22. doi: 10.1097/00075198-200110000-00002. [DOI] [PubMed] [Google Scholar]
- Shanker BA, Coyle SM, Reddell MT, Choi CW, Calvano J, Macor MA, Calvano SE, Lowry SF. Modeling the human injury response. Journal of the American College of Surgeons. 2010;211:S53–S54. [Google Scholar]
- Takayama K, Yuhki K, Ono K, Fujino T, Hara A, Yamada T, Kuriyama S, Karibe H, Okada Y, Takahata O, Taniguchi T, Iijima T, Iwasaki H, Narumiya S, Ushikubi F. Thromboxane A2 and prostaglandin F2alpha mediate inflammatory tachycardia. Nat Med. 2005;11:562–6. doi: 10.1038/nm1231. [DOI] [PubMed] [Google Scholar]
- Task. Heart rate variability: standards of measurement, physiological interpretation and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation. 1996;93:1043–65. [PubMed] [Google Scholar]
- Tateishi Y, Oda S, Nakamura M, Watanabe K, Kuwaki T, Moriguchi T, Hirasawa H. Depressed heart rate variability is associated with high IL-6 blood level and decline in the blood pressure in septic patients. Shock. 2007;28:549–53. doi: 10.1097/shk.0b013e3180638d1. [DOI] [PubMed] [Google Scholar]
- Ursino M, Magosso E. Role of short-term cardiovascular regulation in heart period variability: a modeling study. Am J Physiol Heart Circ Physiol. 2003;284:H1479–93. doi: 10.1152/ajpheart.00850.2002. [DOI] [PubMed] [Google Scholar]
- Zenker S, Clermont G, Pinsky MR. Using mathematical models to improve the utility of quantitative ICU data. In: Vincent J-L, editor. Yearbook of Intensive Care and Emergency Medicine. Springer; 2007. [Google Scholar]
- Zorn-Pauly K, Pelzmann B, Lang P, Machler H, Schmidt H, Ebelt H, Werdan K, Koidl B, Muller-Werdan U. Endotoxin impairs the human pacemaker current If. Shock. 2007;28:655–661. [PubMed] [Google Scholar]