TWO APPLICATIONS OF PERMUTATION TESTS IN BIOSTASTICS

Abstract

We show two examples of how we answer biological questions by converting them into statistical hypothesis testing problems. We consider gene abundance data, and apply permutation tests. Though these tests are simple, they allow us to test biologically relevant hypotheses. Here we present the analysis of data rising from two studies on Type 1 Diabetes. In the first study [3] are interested in comparing the gut bacterial biodiversity in children at risk and not at risk of developing diabetes. In the second study, [4] compare the gut bacterial biodiversity of children in six different sites in USA and Europe. The statistical analyses presented here are parts of the “statistical methods” in two papers mentioned above. Here we offer a detailed explanation of the “Statistical Methods” addressed to readers with a statistics background.

1. Introduction

The main focus of this paper is to present in more detail the “statistical methodology” of two relevant studies [3] and [4] in Type 1 Diabetes (T1D). A deeper explanation of the data set and biological interpretation can be found there. Here we aim to explain the biological question and the structure of the data that it is analyzed there in. In [3], the researchers found that children who developed T1D later in life have a more different gut bacterial biodiversity than children who do not develop T1D. In [4],the gut diversity of individuals in different geographic locations is measured across time. The researchers are interested in testing if the gut bacteria diversity evolves similarly at these sites. In Sections 2 and 3 we present the first and second examples respectively. There is also a small discussion section at the end.

2. First example

The study of [3] is motivated by several animal studies suggesting that rats that develop T1D have a significantly different gut bacteria than rats that are resistant to the disease. They were interested in seeing if the same applies to human beings. The researchers wanted to determine whether the children in the control group have a gut bacteria population (microbiome) more similar to one another than the corresponding microbiomes of the case group.

(2.1) Data

The data come from eight Finnish children participating in the Diabetes Prediction and Prevention study [8, 5, DIPP]. For each child, three stool samples were obtained at three time points, obtaining a total of 24 separate samples. There are four cases and four controls, the cases are children that became autoimmune and developed T1D. This is a paired design, each child in the case group was matched with a child in the control group of the same age and T1D-susceptibility genotype that did not develop autoimmunity or T1D during the study. Though the matching is used in other statistical analyses in [3], in the analysis discussed here this matching is ignored.

The stool samples of the 8 individuals provide the data for this paper. High-throughput, 16S ribosomal ribonucleic acid (16S rRNA) sequencing was performed on the stool samples. 16S rRNA gene sequencing is a widely used technology that allows the classification of bacteria. The 16S rRNA is a highly conserved gene found in all bacteria that contains hypervariable regions. The nucleic acid sequence of these regions is unique to different species of bacteria and can be used to identify bacteria. The set of 16S rRNA sequences that are amplified from a sample during high-throughput sequencing are clustered into Operational Taxonomic Units (OTUs) based on sequence similarity. Different OTUs correspond to different groups of bacteria that share a certain level of 16S rRNA sequence similarity. Every OTU has a name and the data used here are counts of OTUs in each sample. Table 2.1 shows some rows of the data set corresponding to the first and third individuals at time 1. We will use the data in this table as an example below.

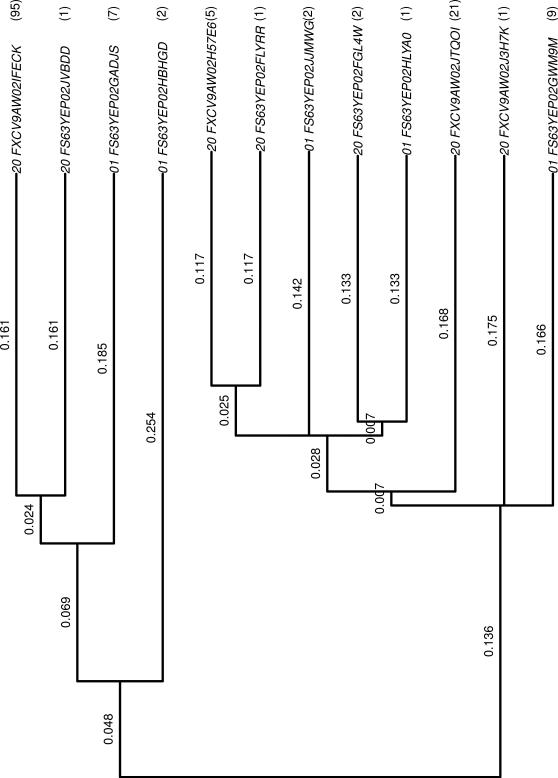
The first row of the Table 2.1 indicates that the OTU “FS63YEP02GADJS” was observed 7 times in the first individual at time point 1. Two different OTUs correspond to two different bacteria, but two OTUs may be similar. The similarity is a measure based on the sequences and it is measured in a 0-100% scale. A similarity matrix can then be built, and with it a phylogenetic tree is built. This is a weighted tree in the Theory of Graphics sense, where every leaf corresponds to an OTU. Every branch of the tree has a weight associated to it. The tree is built in such a way that the similarity between two leaves is the sum of the weight of the branches we have to pass in order to go from the leaf to the root of the smallest subtree containing both leaves. Figure 1 shows the phylogenetic tree corresponding to the OTU in Table 1. For example, the similarity between the first and third most upper leaves (labeled 20_FXCV9AW02IFECK and 01_FS63YEP02GADJS) tree is 0.161+0.024 = 0.185.

Figure 1.

Phylogenetic tree corresponding to the OTUs in Table 1. The counts are given between parentheses.

Table 1.

A subsample of the data corresponding to the first and third individuals at time 1.

First individual	Counts
First individual
01_FS63YEP02GADJS	7
01_FS63YEP02GWM9M	9
01_FS63YEP02HBHGD	2
01_FS63YEP02HLYA0	1
01_FS63YEP02JJMWG	2
Third individual
20_FS63YEP02FGL4W	2
20_FS63YEP02FLYRR	1
20_FS63YEP02JVBDD	1
20_FXCV9AW02H57E6	5
20_FXCV9AW02IFECK	95
20_FXCV9AW02J3H7K	1
20_FXCV9AW02JTQOI	21

(2.2) Statistical Analysis

In this subsection we explain how we used the Unifrac distance [6] and a permutation test inspired in the P-test of [7] to compare the gut diversity of the case and control groups. In particular, we are interested in testing if the gut microbiome of the control groups are more similar to one another than the microbiomes in the case group.

The phylogenetic tree considers the similarity between OTUs but not the OTU counts. The weighted version of the UNIFRAC distance [6] incorporates the OTU count and the OTU similarity information. Using the phylogenetic tree with the OTUs of two individuals, we can compute the weighted UNIFRAC distance between the two bacteria populations. It is defined as

$$u=\sum _{i=1}^n{b}_i\mid \frac{A_i}{A_T}-\frac{B_1}{B_T}\mid$$ (2.1)

Here, n is the total number of branches in the tree, b_i is the length of branch i, A_i and B_i are the number of descendants of branch i from communities A and B respectively, i = 1,...,n. A_T and B_T are the total number of sequences from communities A and B respectively. To adjust for different sample sizes, A_i and B_i are divided by A_T and B_T. In our toy example (See Figure 1), if A and B represent, respectively, the community coming from the first and third individuals, n = 22, A_T = 21, B_T = 126,

$$u=0.048\mid \frac{9}{21}-\frac{96}{126}\mid +0.069\mid \frac{7}{21}-\frac{96}{126}\mid +0.024\mid \frac{0}{21}-\frac{96}{126}\mid +0.161\mid \frac{0}{21}-\frac{95}{126}\mid +\cdots +0.166\mid \frac{9}{21}-\frac{0}{126}\mid =0.45$$

The more different the two populations are, the larger the unifrac distance is. [7] proposes a permutation test called “P test” to determine if two populations are significantly (i.e., statistically) different. Under the null hypothesis, i.e. under the assumption that both bacteria populations are equal, the population labels of the OTUs are exchangeable. The test consists in permuting the population labels in the phylogenetic tree, with the permuted labels, compute u_* according to (2.1). We repeat the process M times to obtain $u_{\star }^{\left(1\right)},\dots ,u_{\star }^{\left(M\right)}$. The p-value is the proportion of times that u > u_*, in math, $p\text{-value}={\Sigma }_{m=1}^{M}1(u>u_{\star }^{\left(m\right)})∕M$, where 1(A) is the indicator function of the event A. Rejecting the null hypothesis is claiming that the bacteria populations are different. In other words, the difference between the OTU counts are not due to random chance. It is worth it to mention that the Unifrac distance measures the difference in the diversity of two populations. This is, a large unifrac distance indicated that one population is more diverse than the other. Two populations can be equally diverse but completely different. This is, two samples or populations could be statistically similar even though they might not contain any common bacteria.

As mentioned earlier, [3] were interested in knowing if the controls have a more similar gut bacteria population to one another than the case individuals. To test so, in [3], we performed the following permutation test, inspired in the P-test:

1. Denote with a_i, o_j the case i and control j individuals respectively, i, j 1,2,3,4; and u(□○) the unifrac distance between the individuals □ and ○. For each one of the six possible pairs of individuals in the case group we compute the unifrac distances and sum them to obtain

   $$S_{\mathrm{a}}^{obs}=u({\mathrm{a}}_1,{\mathrm{a}}_2)+u({\mathrm{a}}_1,{\mathrm{a}}_3)+u({\mathrm{a}}_1,{\mathrm{a}}_4)+u({\mathrm{a}}_2,{\mathrm{a}}_3)+u({\mathrm{a}}_2,{\mathrm{a}}_4)+u({\mathrm{a}}_3,{\mathrm{a}}_4)$$

   Similarly, we define $S_{\mathrm{o}}^{obs}$ as the sum of the unifrac distances of each of the six possible pairs of individuals in the control group. Our test statistic is

   $$D^{obs}=S_{\mathrm{a}}^{obs}-S_{\mathrm{o}}^{obs}.$$

2. For each phylogenetic tree, we randomly permute the labels of the individuals (children) and, as we computed D^obs but now considering these permuted-label trees, we compute D*.

3. We repeat step 2 a total of M = 10⁵ times to get a sample of differences, i.e., of D*: D*₁,...,D*_M

4. We compute the p-value as the proportion of D*s greater than D^obs. In math,

   $$p-\text{value}=(1∕M)\sum _{m=1}^{M}1(D^{obs}>D_m^{\star }).$$

Since the Unifrac distance is a measurement of how far apart two microbiomes (i.e., bacteria populations) of two individuals are, a large value of D^obs would suggests that the case microbiomes are more different to one another than the control microbiomes. Equivalently, D^obs large is evidence that the control microbiomes are more similar to each other than the case microbiomes. The question becomes now what large means. If all the populations were equal, the population labels in every phylogenetic tree would be exchangeable. Following the idea of the P-test, simulated samples from the null distribution of the statistic D are obtained by permuting the population labels in every phylogenetic tree.

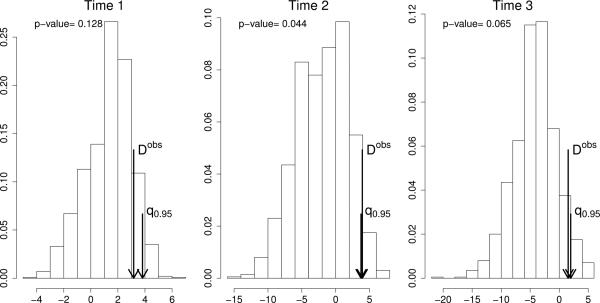
Figure 2 shows the histogram of the D*s for each time. The short and long arrows indicate the 95% quantile and D^obs respectively. The long arrow is at the right of the 0.95 quatile (short arrow) just at time 2. That is, we are able to claim that at time 2 the population of microrganisms in the control group are more similar to one another than in the case group. The data suggest that the same is true at time 1 and 3 but is not conclusive.

Figure 2.

Histogram of simulated D*s along with the 95% percentile, D^obs and p-value for each one of the times in the study. See

3. Second Example

The second example is part of the statistical analysis in the paper [4]. Inspired by the findings of [3] and others, researchers suspect that the gut microbiome has a role in the development of T1D. The composition of the gut microbiome of children in six different locations was analyzed across time. The sampling units are children genetically at high risk for T1D but currently free of islet autoantibodies or disease. The TEDDY group gathered data about the the composition of the gut microbiome of children across time in six different locations. The sampling units are children genetically at high risk for type 1 diabetes but currently free of islet autoantibodies or disease. In the current manuscript, we explain and reproduce the statistical analysis that yields them to conclude that the microbiome diversity across time differs in the six study sites.

(3.1) Data

[4] analyzed stool samples taken monthly from children starting at age four months old until they turned 19 months old. The data correspond to 90 children, 15 from each one of the six different participating sites: Finland, Germany, Sweden, Washington state, Colorado, and Georgia/Florida. As in the example in Section 2, high-throughput 16S rRNA sequencing was performed on these stool samples. The data consists of a table of genus-level OTU counts for every stool sample (not shown). Since we are interested in the bacterial diversity the biologists work with the Shannon Diversity Index [10, SDI],

$$\mathrm{SDI}=\sum _{i=1}^R{p}_i\log p_i,$$

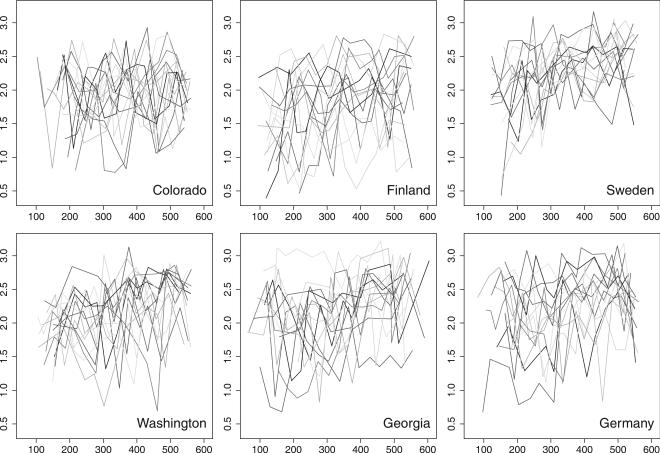
where i indexes the different OTUs in the sample, p_i is the proportion of OTUs i in the sample, and R is the total number of different OTUs in the sample. The more diverse the bacteria population is, the larger the SDI is. For our purposes the data were reduced to a sequence of SDI measurements across different time points for every child. These sequences are shown in Figure 3. Every line represents the SDI of a child across time. Visually, we cannot appreciate any clear difference among the SDI curves across the sites, except, probably, Sweden where the SDI seems to have less variance. [4] speculate that the reason for this may be that the Sweden children are the least exposed to antibiotics of all the sites in the study. Since there are few stool samples for the youngest and oldest ages, we have removed from this analysis the data corresponding to ages under 100 days and over 550 days.

Figure 3.

Shannon Diversity Index per child through time (days) in the six different study sites. Every line represents the measurement of the Shannon Diversity Index of a child across time. For visual purposes, the line joints the time/SDI points of the child it represens.

(3.2) Statistical Analysis

The aim of this statistical analysis is to test if the curves of the SDI are statistically different or not. In order to do so we need to introduce a statistical model. We consider the following mixed model

$$y_{ijk}=\mu +{\alpha }_i+{\beta }_j+\gamma t_k+{\delta }_i{t}_k+\eta t_k^2+e_{ijk},$$ (3.1)

where, y_ijk represents the k-th measurement of the SDI for child j at site i, μ is the over all mean, α_i is the fixed site effect (for estimation purposes we impose Σ_i α_i = 0), ${\beta }_j\sim N(0,{\sigma }_{child}^2)$ is the child-specific random effect, t_k is the child age in days (treated as a continuous variable standardized to have sample mean and variance equal to 0 and 1 respectively) when the k-measurement was taken, the fixed effect δ_i is the interaction coefficient between days and site (also assuming Σ_i δ_i = 0), η is also a fixed effect, and ${∊}_{ijk}\sim N(0,{\sigma }_{∊}^2)$ is a random error. In the context of the model, testing if the SDI curves are statistically significant reduces to test

$$H_0:{\alpha }_1={\alpha }_2=\cdots ={\alpha }_6=0vs{H}_1:\sum _i{\alpha }_i^2>0$$ (3.2)

Strictly speaking, in order to test if the curves are the same for all sites, we should not only test that all α_i are zero but also that all δ_is are equal to zero. Nevertheless, rejecting the null hypothesis as stated above would make us conclude not all curves are equal.

We can think of the model in (3.1) as an Analysis of covariance ANCOVA [2, See p. 62 on ] where the covariate is time (in days). Fitting the model in a statistical package is straightforward. We used the function “aov” in the lme4 R package [9] by [1]. The R code is,

> model=aov(Shannon \sim Site+Error(1/Patient)+Time+Time:Site+Time2)

where Shannon is the SDI, Site takes one of the six possible locations, Time is the standardized time in days and Time2 = Time² fits the model. An F test of (3.2) is straightforward, (R code >summary(model))

	Df	Sum Sq	Mean Sq	F value	Pr(> F)
Site	5	30.98	6.20	25.58	< 2 × 10–16
Time	1	20.42	20.42	84.29	< 2 × 10–16
Time2	1	0.00	0.00	0.01	0.9217
Site:Time	5	2.93	0.59	2.42	0.0341
Residuals	1099	266.17	0.24

As one can see Site is highly significant and we reject the null in (3.2). We notice that the site time interaction (Site : Time) is significant. One of the assumptions of ANCOVA is that the “covariate is not related with the treatment” [2, See p. 63 on ]. This is not the case if there is an interaction between Site and treatment. Additionally, the Kolmogorov-Smirnov test rejects (not shown) the normality of the residuals. The ANCOVA is known to be robust against the normality assumption of the errors as long as the symmetry of the errors follows. We test the symmetry of the residuals following [11], explained below. Let x = x₁,..., x_n denote the sample of size n from a distribution with mean μ, median ν and standard deviation σ. Let x̄, M and s denote the sample mean, median and standard deviation. They propose a Bootstrap test of symmetry consisting in

1. Define C_obs = (x̄ − M)/s, the sample version of the measure of skewness (μ – ν)/σ

2. Define the symmetrized empirical distribution F̂^s as the CDF that gives 1/(2n) to all possible values in the sample and to all points in {2M − x₁,...,2M − x_n}

3. Obtain T bootstrap samples F̂^s of size n. For each bootstrap sample x* compute its sample mean, median and standard deviation x̄*, M*, s* and obtain C* = (x̄* M*)/s*

4. The bootstrap p-value is then the proportion of |C*|s greater that C_obs|. Here |x| denotes the absolute value of x.

This test applied to the residuals (with T = 10⁶ boot strap samples in step 3) yields a boot-strap p-value of < 10⁻⁶. The residuals and then the error terms are not symmetric.

To deal with the violation of the assumptions of the ANCOVA model, we apply a permutation test. Large values of F indicate that the null hypothesis is false. We apply the following simple permutation test permuting the labels of Site.

1. Compute F_obs, the F statistic in the ANCOVA table testing for the model in (3.1) testing (3.2).

2. Permute the “Site” label, and compute the F statistic T times to obtain a sample F*⁽¹⁾,...,F*^(M)

3. The p-value of this permutation test is the percentage of F*s greater than F_obs

Applying this permutation test (with T = 10⁵) we obtain a p-value < 10⁻5. The data provide enough evidence to reject the null hypothesis in (3.2). This is, the SDI curves are not all equal in the six sites.

4. Discussion

Through this paper we have shown two examples of the application of simple permutation tests to answer relevant biological questions. These examples are the product of joint work with researchers at the University of Florida and are part of the “Statistics Methods” section of two biology papers. The main merit of these analyses is the collaboration between biologists and statisticians to formulate the biological problem in statistical terms. In the first example a permutation test allowed us to answer a relevant question without the need to depend on model assumptions. In the second example, a model is required. A standard F-test is applied to the parameters of the model. If the data followed the assumptions of this F-test (normality or at least symmetry of the random errors), the F-test would be valid. This is not the case, we obtain evidence against the symmetry of the distribution of the random errors trough a boot-strap test of symmetry applied to the residuals of the model. The F-test is not valid. Nevertheless, we are able to take advantage of this F-test by incorporating it into the scheme of a permutation test. With this we avoid more complicated models in order to get an answer to the biological question.

Appendix

The Teddy Study Group

Colorado Clinical Center

Marian Rewers, M.D., Ph.D., PI^1,4,6,10,11, Katherine Barriga¹², Kimberly Bautista¹², Judith Baxter^9,12,15, George Eisenbarth, M.D., Ph.D., Nicole Frank², Patricia Gesualdo^2,6,12,14,15, Michelle Hoffman^12,13,14, Lisa Ide, Rachel Karban12, Edwin Liu, M.D.¹³, Jill Norris, Ph.D.^2,3,12, Kathleen Waugh^6,7,12,15, Adela Samper-Imaz, Andrea Steck, M.D.3, University of Colorado, Anschutz Medical Campus, Barbara Davis Center for Childhood Diabetes.

Georgia/Florida Clinical Center

Jin-Xiong She, Ph.D.,PI^1,3,4,11,†, Desmond Schatz, M.D.*^4,5,7,8, Diane Hopkins¹², Leigh Steed^12,13,14,15, Jamie Thomas*^6,12, Katherine Silvis², Michael Haller, M.D.*¹⁴, Meena Shankar*², Melissa Gardiner, Richard McIndoe, Ph.D., Haitao Liu, M.D.^†, John Nechtman^†, Ashok Sharma, Joshua Williams, Gabriela Foghis, Stephen W. Anderson, M.D.^{^} Medical College of Georgia, Georgia Regents University, *University of Florida, †Jinfiniti Bio sciences LLC, Augusta, GA, ^Pediatric Endocrine Associates, Atlanta, GA.

Germany Clinical Center

Anette G. Ziegler M.D.,PI^1,3,4,11, Andreas Beyerlein Ph.D.², Ezio Bonifacio Ph.D.*⁵, Lydia Henneberger^2,12, Michael Hummel M.D.¹³, Sandra Hummel Ph.D.², Kristina Foterek^Υ2, Mathilde Kersting Ph.D.^Υ2, Annette Knopff⁷, Sibylle Koletzko, M.D.^¶13, Stephanie Krause, Claudia Peplow¹², Maren Pflüger Ph.D.⁶, Roswith Roth Ph.D.⁹, Julia Schenkel^2,12, Joanna Stock^9,12, Elisabeth Strauss¹², Katharina Warncke M.D.¹⁴, Christiane Winkler Ph.D.^2,12,15, Forschergruppe Diabetes e.V. at Helmholtz Zentrum München, * Center for Regenerative Therapies, TU Dresden, ¶Dr. von Hauner Children's Hospital,Department of Gastroenterology, Ludwig Maximillians University Munich, Υ Research Institute for Child Nutrition, Dortmund.

Finland Clinical Center

Olli G. Simell, M.D., Ph.D., PI^{Υ^ 1,4,11,13}, Heikki Hyöty, M.D., Ph.D.*^±6, Jorma Ilonen, M.D., Ph.D.^Υ¶3, Mikael Knip, M.D., Ph.D.*^±, Maria LŽnnrot, M.D., Ph.D.*^±6, Elina Mantymaki^{Υ^}, Juha Mykkänen, Ph.D.^{^Υ3}, Kirsti Nanto-Salonen, M.D., Ph.D.^{Υ^12}, Tiina Niininen^±*12, Mia Nyblom*^±, Anne Riikonen*^±2, Minna Romo^{Υ^}, Barbara Simell^{Υ^9,12,15}, Tuula Simell, Ph.D.^{Υ^9,12}, Ville Simell^{^Υ13}, Maija SjŽberg^{Υ^12,14}, Aino Stenius^μ□12, Jorma Toppari, M.D., Ph.D., Eeva Varjonen^{Υ^12}, Riitta Veijola, M.D., Ph.D. ^μ□¹⁴, Suvi M. Virtanen, M.D., Ph.D.*^±§2. ΥUniversity of Turku, *University of Tampere, μUniversity of Oulu, ^Turku University Hospital, ± Tampere University Hospital, □Oulu University Hospital, §National Institute University for Health and Welfare, Finland, ¶University of Kuopio.

Sweden Clinical Center

Åke Lernmark, Ph.D., PI ^{1,3,4,5,6,8,10,11,15}, Daniel Agardh, M.D., Ph.D.¹³, Carin Andrén-Aronsson^2,13, Maria Ask, Jenny Bremer, Corrado Cilio Ph.D., M.D.⁵, Emilie Ericson-Hallström², Lina Fransson, Thomas Gard, Joanna Gerardsson, Gertie Hansson^12,14, Monica Hansen, Susanne Hyberg, Fredrik Johansen, Berglind Jonasdottir M.D., Ulla-Marie Karlsson, Helena Lars-son M.D., Ph.D. ^6,14, Barbro Lernmark, Ph.D.^9,12, Maria Markan, Theodosia Massadakis, Jessica Melin¹², Maria Månsson-Martinez, Anita Nilsson, Kobra Rahmati, Falastin Salami, Monica Sedig Järvirova, Sara Sibthorpe, Birgitta Sjöberg, Ulrica Swartling, Ph.D. ^9,12, Erika Trulsson, Carina Törn, Ph.D. ^3,15, Anne Wallin, Åsa Wimar¹², Sofie Åberg. Lund University.

Washington Clinical Center

William A. Hagopian, M.D., Ph.D., PI^{1,3,4,5,6,7,11,13,14}, Xiang Yan, M.D., Michael Killian^6,7,12,13, Claire Cowen Crouch^12,14,15, Kristen M. Hay², Stephen Ayres, Carissa Adams, Brandi Bratrude, David Coughlin, Greer Fowler, Czarina Franco, Carla Hammar, Diana Heaney, Patrick Marcus, Arlene Meyer, Denise Mulenga, Elizabeth Scott, Jennifer Skidmore², Joshua Stabbert, Viktoria Stepitova, Nancy Williams. Pacific Northwest Diabetes Research Institute.

Pennsylvania Satellite Center

Dorothy Becker, M.D., Margaret Franciscus¹², MaryEllen Dalmagro-Elias², Ashi Daftary, M.D. ChildrenÕs Hospital of Pittsburgh of UPMC.

Data Coordinating Center

Jeffrey P. Krischer, Ph.D.,PI ^1,4,5,10,11, Michael Ab bondondolo, Sarah Austin, Rasheedah Brown^12,15, Brant Burkhardt, Ph.D.^5,6, Martha Butterworth², David Cuthbertson, Christopher Eberhard, Steven Fiske⁹, Veena Gowda, David Hadley, Ph.D.^3,13, Page Lane, Hye-Seung Lee, Ph.D.^3,6,13,15, Shu Liu, Xiang Liu, Ph.D.^2,12, Kristian Lynch, Ph.D.^6,9, Jamie Malloy, Cristina McCarthy^12,15, Wendy McLeod^2,5,6,13,15, Laura Smith, Ph.D.^9,12, Susan Smith^12,15, Roy Tamura, Ph.D.², Ulla Uusitalo, Ph.D.^2,15, Kendra Vehik, Ph.D. ^4,5,9,14,15, Earnest Washington, Jimin Yang, Ph.D., R.D.^2,15. University of South Florida.

Project scientist

Beena Akolkar, Ph.D.^{1,3,4,5,6,7,10,11}, National Institutes of Diabetes and Digestive and Kidney Diseases.

Other contributors

Kasia Bourcier, Ph.D.⁵, National Institutes of Allergy and Infectious Diseases. Thomas Briese, Ph.D.^6,15, Columbia University, Suzanne Bennett Johnson, Ph.D.^9,12, Florida State University, Steve Oberste, Ph.D.⁶, Centers for Disease Control and Prevention, Eric Triplett, Ph.D. ⁶, University of Florida.

Autoantibody Reference Laboratories

Liping Yu, M.D.⁵, Dongmei Miao, M.D.^{^}, Polly Bingley, M.D., FRCP*⁵, Alistair Williams*, Kyla Chandler*, Saba Rokni*, Anna Long Ph.D.*, Joanna Boldison*, Jacob Butterly*, Jessica Broadhurst*, Gabriella Carreno*, Rachel Curnock*, Peter Easton*, Ivey Geoghan*, Julia Goode*, James Pearson*, Charles Reed*, Sophie Ridewood*, Rebecca Wyatt*. ^Barbara Davis Center for Childhood Diabetes, University of Colorado Denver, *School of Clinical Sciences, University of Bristol UK.

Cortisol Laboratory

Elisabeth Aardal Eriksson, M.D., Ph.D., Ewa Lönn Karlsson. Department of Clinical Chemistry, Linköping University Hospital, Linköping, Sweden.

Dietary Biomarkers Laboratory

Iris Erlund, Ph.D.², Irma Salminen, Jouko Sundvall, Jaana Leiviskä, Mari Lehtonen, Ph.D. National Institute for Health and Welfare, Helsinki, Finland.

HbA1c Laboratory

Randie R. Little, Ph.D., Alethea L. Tennill. Diabetes Diagnostic Laboratory, Dept. of Pathology, University of Missouri School of Medicine.

HLA Reference Laboratory

Henry Erlich, Ph.D.³, Teodorica Bugawan, Maria Alejandrino. Department of Human Genetics, Roche Molecular Systems.

Metabolomics Laboratory

Oliver Fiehn, Ph.D., Bill Wikoff, Ph.D., Tobias Kind, Ph.D., Mine Palazoglu, Joyce Wong, Gert Wohlgemuth. UC Davis Metabolomics Center.

Microbiome and Viral Metagenomics Laboratory

Joseph F. Petrosino, Ph.D.⁶ Alkek Center for Metagenomics and Microbiome Research, Department of Molecular Virology and Microbiology, Baylor College of Medicine.

OGTT Laboratory

Santica M. Marcovina, Ph.D., Sc.D. Northwest Lipid Metabolism and Diabetes Research Laboratories, University of Washington.

Repository

Heather Higgins, Sandra Ke. NIDDK Biosample Repository at Fisher BioServices.

RNA Laboratory and Gene Expression Laboratory

Jin-Xiong She, Ph.D.,PI^1,3,4,11, Richard McIndoe, Ph.D., Haitao Liu, M.D., John Nechtman, Yansheng Zhao, Na Jiang, M.D. Jinfiniti Biosciences, LLC.

SNP Laboratory

Stephen S. Rich, Ph.D.3, Wei-Min Chen, Ph.D.³, Suna Onengut-Gumuscu, Ph.D.³, Emily Farber, Rebecca Roche Pickin, Ph.D., Jordan Davis, Dan Gallo. Center for Public Health Genomics, University of Virginia.

Committees

¹Ancillary Studies,²Diet, ³Genetics, ⁴Human Subjects/Publicity/Publications, ⁵Immune Markers, ⁶Infectious Agents, ⁷Laboratory Implementation, ⁸Maternal Studies, ⁹Psychosocial, ¹⁰Quality Assurance, ¹¹Steering, ¹²Study Coordinators, ¹³Celiac Disease, ¹⁴Clinical Implementation, ¹⁵Quality Assurance Subcommittee on Data Quality.