Use of Broken-Symmetry Density Functional Theory To Characterize the IspH Oxidized State: Implications for IspH Mechanism and Inhibition

Abstract

With current therapies becoming less efficacious due to increased drug resistance, new inhibitors of both bacterial and malarial targets are desperately needed. The recently discovered methylerythritol phosphate (MEP) pathway for isoprenoid synthesis provides novel targets for the development of such drugs. Particular attention has focused on the IspH protein, the final enzyme in the MEP pathway, which uses its [4Fe–4S] cluster to catalyze the formation of the isoprenoid precursors IPP and DMAPP from HMBPP. IspH catalysis is achieved via a 2e^–/2H⁺ reductive dehydroxylation of HMBPP; the mechanism by which catalysis is achieved, however, is highly controversial. The work presented herein provides the first step in assessing different routes to catalysis by using computational methods. By performing broken-symmetry density functional theory (BS–DFT) calculations that employ both the conductor-like screening solvation model (DFT/COSMO) and a finite-difference Poisson–Boltzmann self-consistent reaction field methodology (DFT/SCRF), we evaluate geometries, energies, and Mössbauer signatures of the different protonation states that may exist in the oxidized state of the IspH catalytic cycle. From DFT/SCRF computations performed on the oxidized state, we find a state where the substrate, HMBPP, coordinates the apical iron in the [4Fe–4S] cluster as an alcohol group (ROH) to be one of two, isoenergetic, lowest-energy states. In this state, the HMBPP pyrophosphate moiety and an adjacent glutamate residue (E126) are both fully deprotonated, making the active site highly anionic. Our findings that this low-energy state also matches the experimental geometry of the active site and that its computed isomer shifts agree with experiment validate the use of the DFT/SCRF method to assess relative energies along the IspH reaction pathway. Additional studies of IspH catalytic intermediates are currently being pursued.

Introduction

In 2012, the World Health Organization reported 207 million cases of malaria¹ and 8.6 million cases of tuberculosis² worldwide—problems that are further complicated by the emergence of drug-resistant pathogens.³⁻⁹ In order to address these global health problems, the development of new drugs with novel modes of action is desperately needed.

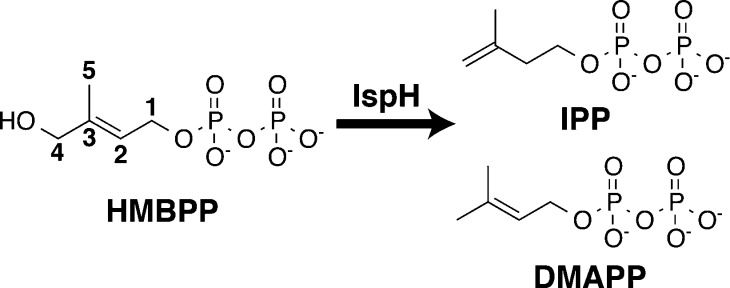
Isoprenoid biosynthesis has been determined to be an attractive enzymatic pathway for the development of novel antibacterial and antimalarial drugs.¹⁰ Isoprenoids are a class of essential biomolecules, including sterols, prenyl side chains of chlorophylls, and quinones, which are all derived from the 5-carbon precursors isopentenyl diphosphate (IPP) and dimethylallyl diphosphate (DMAPP, Figure 1).^11,12 Whereas in archaebacteria, fungi and animals, as well as in the cytosol of plants, IPP and DMAPP are synthesized through a mevalonate-dependent pathway,^12,13 Rohmer and Arigoni independently discovered an alternative, mevalonate-independent isoprenoid synthesis pathway that is specific to most pathogenic eubacteria (e.g., H. pylori and M. tuberculosis) and apicomplexan parasites (e.g., the malaria-causing parasite, P. falciparum) and also is employed in the plastids of plants.¹⁴⁻¹⁷ Because humans lack this non-mevalonate pathway, which is also referred to as the methylerythritol phosphate (MEP) pathway, the inhibition of enzymes in this pathway provides a desirable route for the development of novel antibacterials, antimalarials, and herbicides.¹⁰ To this end, fosmidomycin has recently entered the ranks of antimalarial drugs as an inhibitor of 1-deoxy-D-xylulose 5-phosphate reductoisomerase (DOXP reductase, also known as IspC) and has been shown to be effective in concert with clindamycin for treating multidrug-resistant strains of P. falciparum.¹⁸⁻²⁰

Figure 1.

IspH-catalyzed 2e^–/2H⁺ reductive dehydroxylation of HMBPP to afford DMAPP and IPP.

Recognizing the difficulties in combating rapid drug resistance and attempting to build on the success of fosmidomycin, there is considerable interest in discovering additional inhibitors for the non-mevalonate pathway. This strategy has led to multiple studies aimed at understanding the role of IspH (lytb), the final enzyme in the MEP pathway. IspH catalyzes the 2e^–/2H⁺ reductive dehydroxylation of (E)-4-hydroxy-3-methylbut-2-enyl diphosphate (HMBPP) to give the isoprenoid precursors IPP and DMAPP in a ∼5:1 ratio.²¹⁻²⁶ Only recently has IspH been structurally characterized, with a major hurdle in the process being the elucidation of the character of its central iron–sulfur cluster. Although initial electron paramagnetic resonance (EPR) spectroscopy experiments,²⁴ as well as two independently solved crystal structures,^27,28 characterized the IspH cluster composition as a [3Fe–4S] center, various spectroscopic studies using different preparation techniques have instead found IspH to be catalytically active with a [4Fe–4S]^2+/1+ cluster.^{24,25,29−31}

Notably, Groll et al. have obtained an X-ray structure of the oxidized form of IspH in complex with HMBPP in which the [4Fe–4S]²⁺ cluster is complete.³² The previously missing Fe atom, designated as Fe1 or the apical Fe, is not ligated by a Cys residue as the other three Fe atoms are but instead is ligated by the oxygen atom of the HMBPP hydroxyl group (C₄–OH). In this [4Fe–4S] IspH:HMBPP crystal structure,³² HMBPP sits in a highly polar active site and is coordinated by H41, H74, H124, S225, N227, S269, and a conserved water (W1). HMBPP is also near two residues (E126 and T167) that are proposed to participate in catalysis. Indeed, mutation of the active site E126 leads to undetectable IspH catalytic activity, implying that this residue may be responsible for transferring protons to HMBPP during catalysis.^28,29

The oxidation state of the [4Fe–4S] cluster and its coordination to HMBPP during IspH catalysis have been investigated using Mössbauer,^30,31,33 electron paramagnetic resonance (EPR),^{25,29,34−36} and electron nuclear double resonance (ENDOR) spectroscopies.^29,35−37 These studies, as well as biochemical analyses of IspH catalysis involving analogs of HMBPP^26,38−40 and ¹³C feeding experiments,⁴¹ have generated complementary data that lend support to two possible catalytic mechanisms for IspH: a Birch reduction mechanism^{22,26,31,32,40,42} and an organometallic mechanism where HMBPP forms either a ferraoxetane³⁶ or a metallacycle intermediate complex involving Fe1.^{10,29,34,35,37,41}

Proponents of the Birch reduction mechanism suggest that upon reduction of the [4Fe–4S] cluster, the reducing electron is transferred to HMBPP concurrent with cleavage of the C₄–OH bond, affording a carbon-centered radical intermediate.^{22,26,31,32,38,40,42} Subsequent addition of an electron and proton to this radical intermediate affords IPP or DMAPP. In contrast, Oldfield and co-workers have hypothesized an organometallic mechanism,²⁹ where, upon reduction of the [4Fe–4S] cluster, HMBPP forms a π-complex between its olefinic carbons (C2 and C3, Figure 1) and Fe1 by rotating about the HMBPP C₄–C₃ bond.^29,35,37,41 Following this rotation, two electrons are transferred from the [4Fe–4S] cluster to the HMBPP intermediate concurrent with the breaking of the C₄–OH bond to yield a radical anion with the [4Fe–4S] cluster in a HIPIP-like redox state.⁴³⁻⁴⁵ A subsequent proton transfer affords IPP and DMAPP, while addition of an electron to the [4Fe–4S] cluster regenerates its oxidized (resting) state.^{10,29,34,35,37,41}

Both the Birch reduction and organometallic mechanisms are highly controversial. A more thorough examination of the differences between these possible mechanisms and the data cited to support them has been the subject of several recent review articles.^10,42,46,47

Here, starting from the Grawert et al. X-ray crystal structure of the [4Fe–4S] IspH:HMBPP complex, we use density functional theory (DFT)-based computational methods to explore active-site geometries, protonation state energetics, and Mössbauer properties. Full DFT treatment is used for the [4Fe–4S] cluster, the substrate, and a number of surrounding, catalytically-important protein side chains. The remaining environment around the active site is modeled by continuum-based methods, either with the COnductor-like Screening MOdel (COSMO) or with a self-consistent reaction field (SCRF) technique that explicitly includes the protein/solvent environment, including the field produced by the permanent charges and dipoles of the protein. The protonation states considered include all possible states of the HMBPP hydroxyl, which must ultimately be cleaved, and two moieties that are candidates for involvement in acid/base catalysis: the HMBPP pyrophosphate (PP_i) and the side chain of E126. Because the [4Fe–4S] cluster is in the oxidized (2+) state, this corresponds to the Michaelis complex in either of the proposed catalytic mechanisms. The protonation states of these groups have not been established experimentally, but, clearly, they must be part of any detailed description of the mechanism. For each of the protonation states considered, we compare the computed geometry and Mössbauer properties with experimental measurements. Using these comparisons and the relative computed energetics of the protonation states, we show that the hydroxyl group of HMBPP is protonated (exists as ROH) and that E126 is deprotonated. We also demonstrate that the effects of the permanent charges of the surrounding protein environment, which are included in the SCRF model, as well as the reaction field, are crucial for the correct energetic ordering of protonation states.

Methods

Generation of an Active Site Model To Study IspH Catalysis

We constructed an active site model for DFT studies (Figure 2) using the [4Fe–4S]²⁺ IspH:HMBPP crystal structure solved to 1.7 Å resolution by Grawert et al. (PDB ID: 3KE8).³² Included in this model are the [4Fe–4S]²⁺ cluster, its coordinating thiolates (C13, C96, and C197), the substrate HMBPP, and a few key residues that may play a role in catalysis (T167, E126, H41, and H124). Furthermore, due to the large anionic characters of both the [4Fe–4S] cluster and the pyrophosphate (PP_i) tail of HMBPP, we included additional moieties to more realistically interact with these groups. With regard to the PP_i tail, we also include in the model H74, S225, S226, N227, and S269, as these five residues are ideally positioned to donate hydrogen bonds to the PP_i group. Additionally, since hydrogen bonds are known to tune the redox potentials of [4Fe–4S] complexes,⁴⁸⁻⁵¹ we include the backbone chains of A199, T200, P97, L98, G14, and V15, as well as the side chain of T200 and a crystallographic water. These groups cumulatively donate the only five hydrogen bonds to the [4Fe–4S] cluster in the [4Fe–4S] IspH:HMBPP crystal structure.³²

Figure 2.

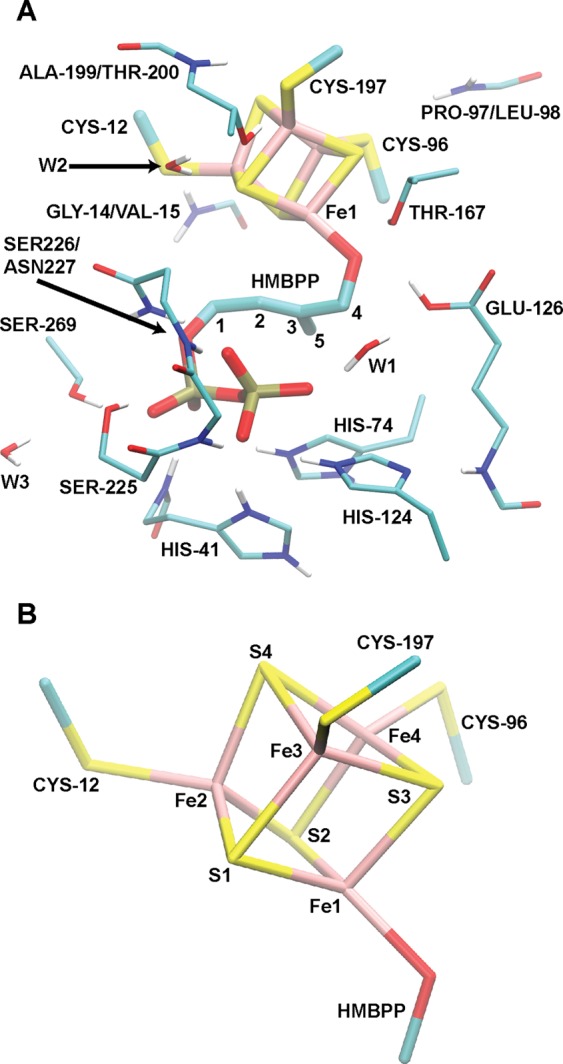
(A) Full active site model employed in the DFT/COSMO geometry optimizations and DFT/SCRF single-point energy calculations. (B) Atom labeling used in Table 1 and throughout the text.

In total, the model active site used in these studies contains 203–205 atoms, depending on the protonation state. Adopting such a large active site complex is beneficial because it reduces the dependence of computed geometries and spectroscopic data on the chosen dielectric environment⁵² and allows for a more accurate computation of relative energies in reaction pathways.⁵³ Further, the use of a large quantum cluster computation, as opposed to embedding a small quantum region within a QM/MM framework, provides a reasonable framework for describing the significant charge transfer effects found in systems with highly-charged metal centers.⁵⁴

Geometry Optimizations with Broken-Symmetry Density Functional Theory (BS–DFT)

Having chosen a model active site from the crystal structure of IspH, the input structure to be used for our BS–DFT calculations is made complete with the addition of hydrogen atoms using Schrödinger’s Maestro program.⁵⁵ Input structures varying the protonation states of the C₄–OH group of HMBPP, the PP_i moiety of HMBPP and E126 are considered in this study. It is important to note that in order to ensure the active site geometry is reasonable (given the constraints of the surrounding protein), the C_α atoms of all residues, with the exception of the thiolate residues, are constrained to their crystallographic positions.⁵⁶ In the case of the thiolates, since they are cut from the protein and capped at the C_β–C_α bond, one hydrogen atom attached to the C_β atom is constrained to lie along the C_β–C_α bond vector.

Because [4Fe–4S] clusters display a high degree of spin polarization and spin-coupling between Fe sites, which individually tend to be high spin, broken-symmetry DFT (BS–DFT) computations are utilized in this study to assess the energetics of different electronic and protonation states of the IspH active site.^57,58 BS–DFT computations are performed, as described previously, to circumvent the inability of conventional DFT methods to obtain an antiferromagnetically (AF)-coupled state. In the case of the IspH [4Fe–4S] cluster, the AF-coupled state has spins on two iron atoms aligned parallel to but opposite the spins on the other two irons.

In practice, BS–DFT solutions are obtained by first computing a ferromagnetically-coupled state, where all Fe atoms are high spin with their spins aligned (in the case of the oxidized [4Fe–4S] cluster considered in this study, S = 18/2). Following this calculation, the spin vector on two of the four Fe atoms is rotated to generate the AF-coupled, “broken-symmetry” (BS) state (S = 0). Geometry optimizations are then started from this BS state.⁵⁹

Given there are four irons that participate in the BS scheme, there exist 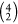ways to denote Fe–Fe pairs that spin couple. Explicitly, there are six possible states (valence isomers) that can be characterized by the net spin on a specific Fe site: ααββ, αβαβ, αββα, βααβ, βαβα, and ββαα. In the case of the ααββ state, Fe₁ and Fe₂ couple and each has an α net spin, while Fe₃ and Fe₄ couple with a β net spin. In the oxidized state investigated here, the two Fe–Fe spin-coupled pairs have identical numbers of unpaired electrons (S_α = S_β), so only three spin pairs require consideration. Our study includes geometry optimizations of the βααβ, βαβα, ααββ, and αββα states (note that the βααβ state, in principle, is identical to the αββα state). All subsequent results include only the lowest energy valence isomer. A summary of the energies for the different valence isomers considered is given in the Supporting Information (Table S1).

DFT computations are performed using the Amsterdam Density Functional (ADF) 2009 program.⁶⁰ All BS–DFT calculations use the OLYP exchange-correlation functional,^61,62 which was chosen due to its ability to generate accurate geometries, to correctly order the energies of different spin states, and to obtain accurate spectroscopic parameters for various Fe complexes.⁶³⁻⁶⁶ All geometry optimizations use the Slater-type triple-ζ plus polarization (STO-TZP) basis set⁶⁷ on all atoms with the core electrons frozen. In studies of the spin-state energies of various Fe complexes, this STO-TZP basis set is shown to facilitate rapid convergence of electronic properties, suggesting its applicability to the IspH system considered here.⁶⁸ Additionally, the numerical integration accuracy parameter,⁶⁹⁻⁷¹ which controls the number of grid points used to evaluate, e.g., the matrix elements of the XC potential, was set to 4.0 in all geometry optimizations. This value is recommended to properly balance computational efficiency and accuracy in ADF2009.⁶⁰

Solvent effects in the geometry optimizations are estimated using the COnductor-like Screening MOdel (COSMO)^72,73 with a dielectric constant (ε) of 20. This value for ε is chosen based upon the observation that various geometric and spectroscopic properties appear converged at ε = 20 in studies of active site models for ribonucleotide reductase intermediate X that are similar in size to the IspH active model constructed here.⁵² A similar COSMO model (ε = 20) was used in our DFT studies of a different [4Fe–4S] cluster enzyme, adenosine 5′-phosphosulfate (APS) reductase.⁵⁶ Following geometry optimization, a single-point energy calculation is performed using the OLYP/STO-TZP level of theory that employs full electron treatment and uses a higher value for the integration accuracy parameter than what is used in the geometry optimizations (i.e., 5.5 versus 4.0). Henceforward, the results from these single-point calculations are referred to as the DFT/COSMO result.

System Preparation for DFT/SCRF Calculations

Following geometry optimizations conducted in COSMO implicit solvent, all BS states considered in this study are subject to a single-point self-consistent reaction field (SCRF) calculation (henceforth referred to as DFT/SCRF) using the OLYP/STO-TZP basis set with frozen core electrons. In these calculations, the active site region that has been geometry optimized in COSMO (referred to as the DFT/COSMO result) is embedded within the [4Fe–4S]²⁺ IspH:HMBPP crystal structure. All atoms included in the DFT active site model are deleted from the protein region to avoid overlap between the two regions. Hydrogen atoms are then added to the protein structure in Schrödinger’s Maestro program,^55,74,75 employing the PROpKa algorithm⁷⁶⁻⁷⁹ for assigning protonation states. Following hydrogen addition, all hydrogen bonds are optimized using the IMPACT program.⁸⁰ The resulting structure is provided as input to the PDB 2PQR server for conversion to a PQR file,^81,82 which is necessary for DFT/SCRF calculations. The PQR file assigns PARSE charges and radii to the protein atoms for use in the continuum electrostatics calculations in the DFT/SCRF scheme.⁸³

Application of DFT/SCRF Calculations for a Better Description of Electrostatics

The first step in DFT/SCRF calculations is a gas-phase single-point energy calculation performed on the BS state. This calculation provides a baseline value from which the effect of stabilizing the active site complex in a protein/solvent environment can be quantified. From the gas-phase computation, point charges are obtained for the active site atoms by fitting to the DFT-derived molecular electrostatic potential (ESP) using the CHELPG algorithm⁸⁴ combined with singular value decomposition.⁸⁵ In this charge fitting, the total net charge and dipole moment vector are employed as Lagrange constraints, while the link atom (H) charges connecting the active site cluster to the protein are set to zero.

Upon deriving ESP charges for the active site cluster, a three-tiered dielectric environment is defined, whereby the values of 1, 4, and 80 are assigned to the active site quantum cluster, protein, and solvent regions, respectively. This environment gives rise to two electrostatic potentials that impinge on the quantum cluster: a reaction potential arising from the dielectric response of the environment from the cluster charges and a protein potential due to the permanent partial charges of the protein that are not included in the quantum cluster. These potentials are calculated as numerical solutions to the multidielectric Poisson equation using the MEAD (Macroscopic Electrostatics with Atomic Detail) programming suite, as implemented in the interface between ADF2012⁸⁶ and MEAD.^87,88 (We note that all calculations were performed using a development version of ADF2011, which yields identical results to SCRF calculations performed with the official release of ADF2012.) These computed protein field and reaction field potentials are subsequently added to the Coulomb interaction operator in the density functional Hamiltonian, and a single-point electronic energy calculation is again performed. This procedure of extracting ESP charges for the active site region in order to solve the Poisson equation for the protein and reaction field potentials is iterated until the sum of the electronic and protein/reaction field energies converges (ΔE between cycles <0.01 kcal mol^–1). A more detailed description of this method can be found elsewhere.⁸⁹

Calculations of Relative Energetics

Using energies obtained from either the DFT/COSMO or DFT/SCRF methods, the relative free energy of deprotonation at pH = 7, ΔG_deprot, can be obtained for a single titratable site through the application of eq 1:

1

When computing ΔG_deprot with DFT/COSMO, the total energies for the deprotonated and protonated states, E(A^–) and E(HA), respectively, are taken from the BS state energies obtained following the geometry optimization with the DFT/COSMO method. These values follow the usual ADF convention, where E(A^–) and E(HA) are “total” energies with respect to a sum of atomic fragments (spin-restricted atoms).⁷¹ Alternatively, ΔG_deprot is computed with the DFT/SCRF method using the total free energies including the protein/solvent environment interaction obtained in the SCRF procedure described previously. We approximate the difference in zero-point energy between protonated and deprotonated states, ΔZPE, as the difference in zero-point energy of the fragment that is titrated (e.g., the carboxylate of E126, the C₄–OH group of HMBPP, or the PP_i tail of HMBPP), as obtained from an OLYP frequency calculation performed on the two protonation states of that fragment. These values are computed to be −8.7, −10.4, and −8.8 kcal mol^–1 for E126, the C₄–O(H) group of HMBPP, and the PP_i moiety on HMBPP, respectively. The free energy of the titrating proton is computed using eq 2:

2

While the energy of a proton computed from a gas-phase OLYP calculation with respect to a spin-restricted hydrogen atom is found to be 291.1 kcal mol^–1, the value for E(H⁺) used in eq 2 (292.7 kcal mol^–1) is obtained upon the addition of an empirical correction term of +1.6 kcal mol^–1 to the OLYP result (see the Appendix in ref (91) for a complete derivation of this term). This ensures the computed standard hydrogen electrode matches experiment exactly.^90,91 For ΔG_sol(H⁺, 1 atm), the solvation free energy of a proton, we use the “best available” value of −264.0 kcal mol^–1, based on analysis of cluster-ion solvation data.^92,93 The translational entropy of a proton, −TΔS_gas(H⁺), is taken to be −7.76 kcal mol^–1, its value computed theoretically at 298 K and 1 atm.⁹⁴ The final term in computing the free energy of the titrating proton, 5/2 RT (1.5 kcal mol^–1), arises from the sum of the proton translational energy (3/2 RT) and the work term PV = RT.^92,94 Finally, the term ΔE_corr corrects ΔG_deprot for a neutral solvent environment (pH = 7), equal to −1.37 × 7 (−9.6 kcal mol^–1).

A more general form of eq 1 accounts for differences in free energy when any number of protons are titrated

3

where again ΔE_corr corrects for a neutral solvent environment (pH = 7), and the number of protons exerts a multiplicative effect on ΔG_ref(H⁺) and ΔE_corr. In cases where two states are tautomers (i.e., where two states have same number of protons, which themselves reside on different titratable sites), the difference in energy between states is corrected for ΔZPE for the sites that are (de)protonated.

Calculations of ⁵⁷Fe Mössbauer Isomer Shifts and Quadrupole Splittings

Multiple groups have computed ⁵⁷Fe Mössbauer isomer shifts (ISs) to help identify the oxidation state of the Fe sites considered, drawing on the property that the values of these ISs are linearly proportional to the electron density at the ⁵⁷Fe nucleus, ρ(0).^{64,66,95−99} In practice, obtaining a value for ρ(0) for a given BS state requires a single-point energy calculation that employs a basis set that includes core electrons and that uses a higher value for the integration accuracy parameter than what is used in the geometry optimizations (i.e., 5.5 versus 4.0).⁴⁶ With the hypers2003 program,¹⁰⁰ ρ(0) can then be obtained from the ADF calculation.⁶⁰

Using the linear regression given in eq 4, each ⁵⁷Fe IS can be computed given its ρ(0), using the fitting parameters A, α, and C.^66,95

4

This linear fit is dependent on the level of theory employed. As all IS computations in this report use the OLYP/STO-TZP level of theory with either the COSMO or SCRF solvation method, we apply appropriately calibrated values of α = −0.323 e^–1 a₀³ mm s^–1, C = 0.428 mm s^–1, and A = 11877 e a₀^–3.⁶⁶ We note that the DFT/COSMO and DFT/SCRF methods give nearly identical results. The similarity between these two methods is consistent with what has been observed in previous benchmark studies.⁶⁶ Consequently, we only present results obtained using the DFT/SCRF method (results from the DFT/COSMO method are given in Table S2 of the Supporting Information).

Quadrupole splittings (QSs) arise from the interaction between the ⁵⁷Fe (S = 3/2) nuclear quadrupole moment and the electric field gradient (EFG) at the nucleus. For this reason, QSs provide useful information on the oxidation state and ligand environment surrounding each ⁵⁷Fe atom. To obtain values for QSs from our DFT/COSMO and DFT/SCRF calculations, the EFG must be evaluated at the ⁵⁷Fe nucleus. Upon reordering of the components of the EFG such that |V_zz| ≥ |V_yy| ≥ |V_xx|, the asymmetry parameter η can be obtained and the QS may be computed (eqs 5 and 6) using the constants, e (the electric charge of a positron) and Q (the nuclear excited-state quadrupole moment).

5

6

Protonation Considerations for the Active Site Model

The active site of IspH contains many titratable residues, including E126 (typical pK_a ∼ 4.3), H41, H74, and H124 (typical pK_a ∼ 6.8).^101,102 Additionally, the C₄–OH group of HMBPP, if complexed strongly to Fe, can be deprotonated (typical pK_a of [Fe(OH₂)₆]³⁺ ∼ 2.4),³² and the PP_i group of HMBPP (typical pK_a values ∼0.9, 2.0, 6.7, 9.0) can likely assume different protonation states, as well.^32,103 In sum, there are 13 titratable sites, leaving 2¹³ possible protonation states to consider in order to fully characterize the system. To reduce the number of explored states, we make use of some simplifying assumptions, namely that H41 and H74 will likely assume their imidazolium form (doubly protonated) given their close proximity to the highly anionic PP_i tail of HMBPP. Similarly, we choose to fix the protonation state of H124 to be neutral (protonated at N_ε), as its N_ε is in position to donate a single hydrogen bond to the substrate, while receiving a hydrogen bond at its N_δ position from the backbone of E126 in the [4Fe–4S] IspH:HMBPP crystal structure.³² For E126, we only consider cis-protonation at its carboxylate oxygen nearer the HMBPP RO^–/ROH group and Fe1, as this site would allow for participation in an active site hydrogen bond network, as proposed by others (Figure 2).^27,29,32 With respect to the substrate, we consider protonation at the C₄–OH alkoxide group, as well as protonation of an oxygen on the terminal phosphate of the PP_i moiety. We consider only single protonation of this group due to the likelihood that the rich hydrogen bond network surrounding the PP_i group will stabilize either its −2 or −3 form. While this still leaves a considerable number of protonation states to consider (2³), evaluation of the energies of states having both E126 and the HMBPP ROH group deprotonated are found to be energetically unfavorable and, therefore, have been omitted from our discussion.

Naming Scheme for Different Protonation States under Study

To facilitate our discussion of the different active site protonation states, we utilize the naming scheme, RO^XP^YE^Z, where X, Y, and Z are assigned either a minus sign “–“ or the letter “H” to signify whether a proton resides on the C₄–OH (RO^–/ROH) group of HMBPP, the PP_i of HMBPP, or E126, respectively (Table 1). For instance, in the state RO^–P^–E^H, HMBPP has both its terminal C₄–OH group and its PP_i moiety deprotonated (giving the ligand a net charge of −4), whereas E126 is protonated. Combined with the oxidized [Fe₄S₄Cys₃]^1– cluster and two imidazoles H41 and H74 (q = +1, each), the model active site carries a total charge of −3 in this RO^–P^–E^H state (Table 1). We stress that within this naming scheme the “–” is representative of the charges of the RO^–/ROH and the E126 groups; however, it does not indicate the net charge of the PP_i group, which maintains a charge of −3 when deprotonated (P^–) and −2 when protonated (P^H).

Table 1. Description of the Nomenclature Scheme Used Throughout This Report^a.

protonation state	q	C4–O(H)	PPi	E126
RO–P–EH	–3			H
RO–PHEH	–2		H	H
ROHP–E–	–3	H
ROHPHE–	–2	H	H
ROHP–EH	–2	H		H
ROHPHEH	–1	H	H	H

^aUnless an H is listed, the moiety described by each column is assumed to be fully deprotonated. The total charge (q) of the active site quantum cluster is given for each state.

Results

Review of the Crystal Structure Solved for HMBPP-Bound [4Fe-4S] IspH

The IspH:HMBPP crystal structure referenced in this study contains a [4Fe–4S]²⁺ cluster with significant asymmetry (Table 2, with atom numbering defined in Figure 2B).³² The apical iron, Fe1, has longer Fe–S^2– bond lengths (Fe–S^2– distances of 2.34, 2.39, and 2.36 Å) than the other Fe atoms. In contrast, a second, ferric-like iron (Fe2 in Figure 2B) contains significantly shorter Fe–S^2– bonds, with Fe–S^2– distances of 2.22, 2.19, and 2.18 Å. The other two irons have intermediate bond lengths (mean Fe–S distance of 2.28 ± 0.04 Å), representative of a delocalized, mixed-valence pair (Fe^2.5+).³²

Table 2. Tabulation of Various [4Fe–4S] Cluster Distances (in Å) Obtained from Geometry Optimizations of Various Protonation Conformers of an Active Site Model of the Oxidized IspH System^a.

cluster distances	exp32	RO–P–EH	RO–PHEH	ROHP–E–	ROHPHE–	ROHP–EH	ROHPHEH
Fe1–S1	2.344	2.275	2.281	2.218	2.215	2.200	2.209
Fe1–S2	2.393	2.351	2.351	2.301	2.298	2.282	2.280
Fe1–S3	2.364	2.378	2.370	2.328	2.317	2.319	2.313
Fe2–S1	2.217	2.340	2.347	2.323	2.324	2.328	2.333
Fe2–S2	2.186	2.212	2.213	2.203	2.201	2.206	2.210
Fe2–S4	2.181	2.385	2.380	2.362	2.359	2.357	2.353
Fe3–S1	2.319	2.328	2.330	2.313	2.317	2.305	2.305
Fe3–S3	2.281	2.240	2.239	2.236	2.237	2.240	2.238
Fe3–S4	2.306	2.377	2.372	2.357	2.350	2.361	2.360
Fe4–S2	2.308	2.321	2.322	2.314	2.319	2.326	2.325
Fe4–S3	2.217	2.320	2.323	2.320	2.324	2.322	2.326
Fe4–S4	2.276	2.279	2.280	2.245	2.242	2.241	2.242
Fe2–SC12	2.283	2.305	2.303	2.263	2.258	2.256	2.257
Fe3–SC197	2.285	2.314	2.306	2.283	2.274	2.275	2.271
Fe4–SC96	2.264	2.321	2.314	2.295	2.290	2.295	2.291
Fe1–Fe2	2.792	2.815	2.822	2.692	2.674	2.681	2.692
Fe1–Fe3	2.780	2.757	2.747	2.676	2.656	2.643	2.641
Fe1–Fe4	2.820	2.752	2.728	2.672	2.658	2.645	2.631
Fe2–Fe3	2.717	2.764	2.762	2.752	2.738	2.797	2.797
Fe2–Fe4	2.694	2.767	2.770	2.729	2.723	2.729	2.730
Fe3–Fe4	2.749	2.751	2.755	2.719	2.720	2.722	2.725

^aFor comparison, the corresponding bond lengths from the IspH:HMBPP crystal structure are given.³²

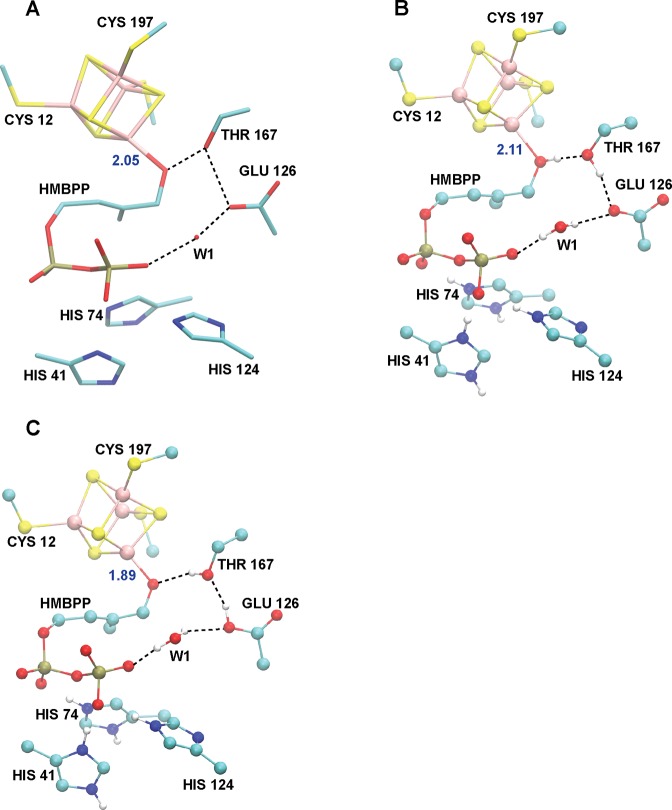
The HMBPP molecule coordinates Fe1 through its oxygen atom attached to C4 at a distance of 2.05 Å (Fe1–O_C4, Table 3), which Groll and co-workers propose to be indicative of HMBPP binding as an alkoxide (RO^–) rather than as an alcohol (ROH).³² In addition to the interaction between HMBPP and Fe1 of the [4Fe–4S] cluster, a significant hydrogen bond network further supports HMBPP within the protein active site. Indeed, several histidines and alcohol side chains forming (charged) hydrogen bonds to the PP_i tail of HMBPP are present. Further, the active site residues T167, E126, and the crystallographic water W1 link the oxygen bonded to C4 in HMBPP to its PP_i tail through a series of hydrogen bonds (Table 3, Figure 3A). This latter group of moieties has been suggested to participate in a proton relay network for catalysis.³²

Table 3. Key HMBPP Bond Lengths and Distances (in Å) between Hydrogen Bonding Atoms in the Active Site of Oxidized IspH as Computed by Geometry Optimizations of Different Protonation Conformers^a.

	exp32	RO–P–EH	RO–PHEH	ROHP–E–	ROHPHE–	ROHP–EH	ROHPHEH
HMBPP distances
Fe1–OC4	2.046	1.891	1.899	2.108	2.133	2.214	2.254
Fe1–C2	2.913	3.136	3.107	3.267	3.266	3.272	3.220
Fe1–C3	3.039	3.497	3.406	3.627	3.551	3.531	3.399
active site H-bonds
OC4–OThr	2.702	3.203	3.182	2.816	2.914	3.189	3.179
OThr–OGlu	2.761	2.628	2.639	2.770	2.771	2.661	2.667
OGlu–OW1	2.578	3.618	3.745	3.133	2.907	3.687	3.711
OW1–OPPi	2.548	2.723	2.858	2.746	3.006	2.734	2.836
RMSD		0.57	0.59	0.40	0.40	0.57	0.58

^aO_C4 refers to the oxygen attached to C4 on HMBPP, O_T167 refers to the T167 hydroxyl oxygen, O_E126 refers to the E126 carboxylate oxygen directed inward toward the active site, O_W1 is a conserved active site water, and O_PPi is the oxygen on the PP_i group that interacts with W1. For comparison, the corresponding distances from the IspH:HMBPP crystal structure are given,³² and the state computed to have the best agreement with each geometric parameter from experiment is set in bold-type font.³² The root–mean–square deviation (RMSD, given in Å) between different protonation conformers computed for oxidized IspH and the IspH:HMPP crystal structure are tabulated.

Figure 3.

(A) Crystal structure active site environment of oxidized IspH (PDB ID: 3KE8).³² (B) Optimized active site geometry for the RO^HP^–E^– state. (C) Geometry optimized active site geometry of the RO^–P^–E^H state. Active site hydrogen bond networks are indicated with dotted lines.

Different [4Fe-4S] Cluster Geometries Observed in DFT Calculations

Regardless of the protonation state of our model, none of the computed geometries for the IspH active site fully capture the asymmetry observed in the crystal structure (Table 2). More specifically, the Fe1–S^2– and Fe2–S^2– distances in our computed geometries are not uniformly elongated and shortened, respectively. Instead we observe a 4-fold compression of the oxidized [4Fe–4S] cluster, whereby the planes involving the two 2Fe–2S fragments are compressed along one direction characterized by short Fe–S^2– bonds. For instance, in the case of the lowest energy structure computed for the RO^–P^–E^H state (Table 2, Figure 3C), Fe1 has Fe–S^2– bond lengths of 2.28, 2.35, and 2.38 Å; Fe2 has Fe–S^2– bond lengths of 2.21, 2.34, and 2.39 Å; Fe3 has Fe–S^2– bond lengths of 2.24, 2.33, and 2.38 Å; and Fe4 has Fe–S^2– bond lengths of 2.28, 2.32, and 2.32 Å (Table 2). Thus, for the RO^–P^–E^H state, each iron atom has one short and two long Fe–S^2– bonds. This trend is evident for all other protonation states as well (Table 2).

Differences in the Active Site Geometries of Different HMBPP Protonation States

The geometries of the different protonation states considered can first be categorized by whether the HMBPP C₄–OH group exists as an alkoxide (RO^–) or alcohol moiety (RO^H, in our nomenclature). Two protonation states are computed for the RO^– state—specifically, the RO^–P^–E^H and RO^–P^HE^H states, which differ only by a single proton on the PP_i group. Consequently, these two RO^– states give total charges of −4 and −3 for HMBPP, respectively. These computed structures display Fe1–O distances (∼1.90 Å, Table 3) that are appreciably shorter than the Fe1–O distance observed in the IspH:HMBPP crystal structure (2.05 Å).³² While the geometries of the RO^–P^–E^H and RO^–P^HE^H states are largely similar, displaying a root-mean-square deviation (RMSD) of 0.19 Å, it is clear that protonation of the PP_i group does alter the position of the conserved active site water, W1. In turn, the oxygen–oxygen distances between E126/W1 and W1/PP_i hydrogen bond partners in the active site differ between the RO^–P^–E^H and RO^–P^HE^H states (Table 3). Both states, however, display reasonable similarity to the [4Fe–4S] IspH:HMBPP crystal structure (RMSD ∼ 0.6 Å, Table 3).³²

When HMBPP binds Fe1 via an alcohol group (as in the RO^HP^–E^–, RO^HP^–E^H, RO^HP^HE^–, and RO^HP^HE^H states), the computed Fe1–O bond lengths (ranging from 2.11 to 2.25 Å) are longer than what is observed in the [4Fe–4S] IspH:HMBPP crystal structure (2.05 Å).³² These ROH–bound states also possess shorter Fe1–S^2– bond lengths compared to those observed in the RO^––bound states; the average Fe1–S^2– bond length is 2.27 Å in the ROH states, whereas it is 2.33 Å in the RO^– states (Table 2). We note, however, that these differences in cluster geometry are restricted to Fe1 and not the other three Fe atoms. Indeed, the average Fe2–S^2–, Fe3–S^2–, and Fe4–S^2– distances in the RO^– and ROH states are similar to within 0.01 Å (Table 2).

Despite the differences in the bond distances involving Fe1, we observe strong structural similarity between the RO^– and ROH states when all other protonation states are maintained, as is the case for RO^–P^HE^–/RO^HP^HE^– and RO^–P^–E^H/RO^HP^–E^H (Table 3). This observation is further supported by measurements of RMSD between the RO^–P^HE^–/RO^HP^HE^– and RO^–P^–E^H/RO^HP^–E^H pairs, giving values of 0.05 and 0.04 Å, respectively. Similar to the RO^– states, (de)protonation of the PP_i group in the HMBPP ROH-bound states perturbs the position of W1 and its corresponding hydrogen bond interactions with PP_i and E126 (Table 3).

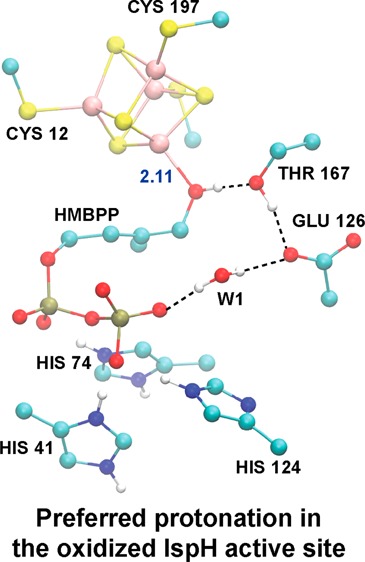
While the active site geometries following (de)protonation of the RO^–/ROH and PP_i groups show only local variation around these titratable groups, significantly larger deviations in active site structure are observed upon the (de)protonation of E126. With respect to the coordination of HMBPP to Fe1, the Fe1–OH distances are significantly shorter in E126 deprotonated states (2.11 and 2.13 Å for the RO^HP^–E^– and RO^HP^HE^– states, respectively) than in their protonated counterparts (Fe1–O distances of 2.21 and 2.25 Å for RO^HP^–E^H and RO^HP^HE^H, respectively). Aside from the HMBPP ROH group, E126 is the only titratable group whose protonation significantly alters all hydrogen bond partners in the active site (Table 3). As can be seen in Table 3, the oxygen–oxygen distances for active site hydrogen bond partners are mostly similar between the [4Fe–4S] IspH:HMBPP crystal structure and the ROH/E^– states, regardless of PP_i protonation. For instance, the distance between the C₄–OH group of HMBPP and the alcohol side chain of T167 is ∼2.8–2.9 Å in the RO^H/E^– states, ∼3.2 Å in all RO^– and RO^H/E^H states, and 2.70 Å in the crystal structure (Table 3).³²

Visually, the closer agreement between the E^– states with the crystal structure can be attributed to different orientations of the T167 and E126 side chains, as well as the position of the active site water, W1 (Figure 3B,C). When E126 is deprotonated (Figure 3B), the hydrogen bond network originates at the ROH group in HMBPP, which donates a hydrogen bond to T167, which then donates a hydrogen bond to the deprotonated E126. In contrast, the hydrogen bond network in the protonated E126 states (Figure 3C) requires that the T167 side chain accept a hydrogen bond from E126 and donate a hydrogen bond to the HMBPP RO⁻ group. To quantify these observations, we note that geometries computed with E126 deprotonated better agree with the [4Fe–4S] IspH:HMBPP crystal structure³² (RMSD = 0.40 Å, Table 3) than structures involving protonated forms of E126 (RMSD = 0.57–0.59 Å). From visualizing the superpositions of computed RO^–P^–E^H and RO^HP^–E^– geometries and the IspH:HMBPP crystal structure,³² it is clear better agreement with experiment is achieved when E126 is deprotonated (Figure S1).

Relative Energetics in the Oxidized State

For all states considered in this study, we implement two methods for computing the energetics of the system: (1) the DFT/COSMO method with ε = 20; and (2) the DFT/SCRF method, which allows the active site model described using DFT to be perturbed by the electrostatic effects of protein charges and the dielectric response of the protein and solvent regions (ε = 4 and 80, respectively). Although both methods have shown good agreement with experiment for calculated energies and reduction potentials of model systems,^51,85,104 the DFT/SCRF method has the advantage that it may provide a more realistic description of the protein and solvent environments.⁸⁹ While only the energies of the lowest-energy valence isomer for each protonation state are presented here, a summary of the relative energies for all valence isomers considered in this study is given in Table S1 of the Supporting Information.

Using the DFT/COSMO method, the RO^–P^HE^H and RO^HP^HE^H states are found to be isoenergetic and the lowest-energy oxidized states computed at pH = 7 (Table 4A, Figure 4). The RO^HP^–E^H state is 2.9 kcal mol^–1 above the energy of the RO^–P^HE^H and RO^HP^HE^H states, while the RO^–P^–E^H and RO^HP^–E^– states are the two highest-energy states computed with the DFT/COSMO energy model, at energies that are, respectively, 7.9 and 8.4 kcal mol^–1 above the RO^–P^HE^H and RO^HP^HE^H states (Figure 4). The DFT/COSMO method thus preferentially stabilizes states where either two or three of the titratable sites considered carry a proton.

Table 4. Relative Energies Computed at pH = 7 for the Different Protonation States of the Oxidized State of the IspH Active Site Cluster, Using Eq 3 with Energies Obtained from (A) the DFT/COSMO Method; (B) the Total Free Energy Stemming from the Gas-Phase Energy Plus the Reaction Field (RF) Component of the DFT/SCRF Method (i.e., the sum of E₀ and E_RF from Table 5); (C) the Full DFT/SCRF Method^a,f.

A.
	DFT/COSMO
state (charge)	ΔETot,COSMOb	nΔGref (H+)c	Σ(ZPE)id	nΔECorr,pH=7e	ΔETot,COSMO,pH=7E
RO–P–EH (−3)	3.9	22.4	–8.8	–9.6	7.9
RO–PHEH (−2)	0.0	0.0	0.0	0.0	0.0
ROHP–E– (−3)	2.6	22.4	–7.1	–9.6	8.4
ROHPHE– (−2)	3.6	0.0	1.7	0.0	5.3
ROHP–EH (−2)	1.3	0.0	1.6	0.0	2.9
ROHPHEH (−1)	2.4	–22.4	10.4	9.6	0.0

B.
	DFT/SCRF Reaction Field
state (charge)	ΔETot,RF	nΔGref (H+)	Σ(ZPE)i	nΔECorr,pH=7	ΔETot,RF,pH=7
RO–P–EH (−3)	9.5	44.9	–19.2	–19.2	16.0
RO–PHEH (−2)	–1.4	22.4	–10.4	–9.6	1.1
ROHP–E– (−3)	10.3	44.9	–17.5	–19.2	18.5
ROHPHE– (−2)	4.2	22.4	–8.7	–9.6	8.4
ROHP–EH (−2)	2.4	22.4	–8.8	–9.6	6.5
ROHPHEH (−1)	0.0	0.0	0.0	0.0	0.0

C.
	Full DFT/SCRF
state (charge)	ΔETot,SCRF	nΔGref (H+)	Σ(ZPE)i	nΔECorr,pH=7	ΔETot,SCRF,pH=7
RO–P–EH (−3)	1.7	0.0	–1.7	0.0	0.0
RO–PHEH (−2)	8.0	–22.4	7.1	9.6	2.2
ROHP–E– (−3)	0.0	0.0	0.0	0.0	0.0
ROHPHE– (−2)	10.1	–22.4	8.8	9.6	6.1
ROHP–EH (−2)	9.6	–22.4	8.7	9.6	5.5
ROHPHEH (−1)	21.5	–44.9	17.5	19.2	13.3

^aDecomposed terms used to compute relative energies with eq 3. See footnotes b–e.

^bThe total energy of the protonation state considered, as obtained from (A) DFT/COSMO, (B) the RF component of the DFT/SCRF method, or (C) the full DFT/SCRF method.

^cThe relative free energy of the titrating proton(s), taken from eq 2.

^dEnergies correcting for differences in zero-point energy between protonation states.

^eCorrection term applied to obtain relative energies at pH = 7.

^fAll energies are given in kcal mol^–1.

Figure 4.

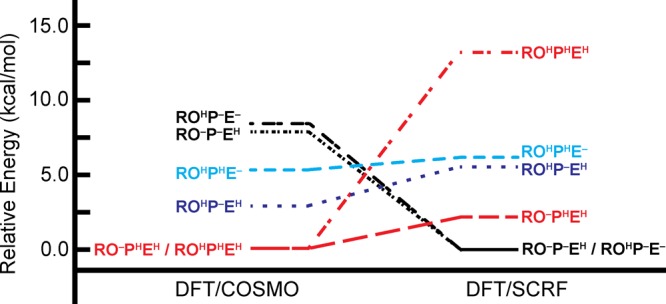
Relative energies of the different protonation conformers computed from eq 3 using (Left) DFT/COSMO and (right) DFT/SCRF.

In contrast to the DFT/COSMO results, use of the DFT/SCRF method shows the RO^–P^–E^H and RO^HP^–E^– states to be isoenergetic and lowest-energy (Table 4C, Figure 4). The RO^–P^HE^H and RO^HP^–E^H states are next lowest in energy at 2.2 and 5.5 kcal mol^–1 above the RO^–P^–E^H and RO^HP^–E^– states, while the fully protonated RO^HP^HE^H state is the highest energy state (at 13.3 kcal mol^–1 above the RO^–P^–E^H and RO^HP^–E^– states).

Rationalizing the Different Relative Energetics Obtained Using the DFT/COSMO and DFT/SCRF Methods

It is clear the relative energetics computed with DFT/COSMO and DFT/SCRF descriptions of the IspH active site model differ. While the RO^–P^HE^H and RO^HP^HE^H states, with their respective net charges (q) of −2 or −1, are preferred energetically when using the DFT/COSMO method, the DFT/SCRF method favors a highly anionic (q = −3) quantum cluster, where two of the three considered titratable sites are deprotonated (RO^–P^–E^H and RO^HP^–E^– states, Figure 4). In the gas phase, the energy of the RO^HP^HE^H state (q = −1) is 152 kcal mol^–1 lower than that of the more negatively-charged (q = −3) RO^HP^–E^– state (Table 5A,B). Solvation with either the COSMO or SCRF methods can accommodate greater charge in the quantum cluster and lessens (or even reverses) the trend in energetics obtained from gas-phase energies alone. From DFT/COSMO and DFT/SCRF computations, it is possible to isolate the energetic contributions arising from embedding the active site in an environment containing regions of different dielectric constants and, in the case of the DFT/SCRF computations, protein point charges. Understanding these energetic contributions provides insight into why certain protonation states (or, alternatively, states with specific net charges in the active site quantum cluster) are stabilized relative to others when using DFT/COSMO or DFT/SCRF methods.

Table 5. Summary of the Components of the Total Electrostatic Energy Computed by the DFT/COSMO and DFT/SCRF⁸⁹ Methods for Different Protonation States of the Oxidized IspH Active Site^j.

A.
	DFT/COSMO			DFT/SCRF
state (charge)	E0a	ESolv,COSMOb	ETot,COSMOc	E0	EStraind	EPe	ERFf	Eenv,SCRFg	ETot,RFh	ETot,SCRFi
RO–P–EH (−3)	–26445.7	–286.7	–26732.4	–26445.7	53.9	–129.9	–304.3	–380.3	–26750.0	–26826.0
RO–PHEH (−2)	–26541.2	–195.0	–26736.2	–26542.8	52.1	–110.9	–218.1	–276.9	–26760.9	–26819.7
ROHP–E– (−3)	–26440.5	–293.1	–26733.6	–26440.5	54.8	–133.3	–308.7	–387.2	–26749.2	–26827.7
ROHPHE– (−2)	–26528.4	–204.2	–26732.7	–26529.1	52.9	–115.3	–226.2	–288.5	–26755.3	–26817.6
ROHP–EH (−2)	–26537.7	–197.3	–26735.0	–26537.7	53.2	–114.2	–219.4	–280.4	–26757.1	–26818.1
ROHPHEH (−1)	–26592.2	–141.6	–26733.8	–26592.2	49.8	–96.5	–167.3	–214.0	–26759.5	–26806.2

B.
	DFT/COSMO			DFT/SCRF
state (charge)	ΔE0	ΔESolv,COSMO	ΔETot,COSMO	ΔE0	ΔEStrain	ΔEP	ΔERF	ΔEenv,SCRF	ΔETot,RF	ΔETot,SCRF
RO–P–EH (−3)	–5.2	6.4	1.3	–5.2	–0.9	3.4	4.4	6.9	–0.8	1.7
RO–PHEH (−2)	–100.7	98.1	–2.6	–102.3	–2.7	22.4	90.6	110.3	–11.7	8.0
ROHP–E– (−3)	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
ROHPHE– (−2)	–87.9	88.9	1.0	–88.6	–1.9	18.0	82.5	98.7	–6.1	10.1
ROHP–EH (−2)	–97.2	95.9	–1.3	–97.2	–1.6	19.1	89.3	106.8	–7.9	9.6
ROHPHEH (−1)	–151.7	151.5	–0.2	–151.7	–5.0	36.8	141.4	173.2	–10.3	21.5

^aThe total gas-phase electronic energy of the active site quantum cluster obtained following geometry optimization with the DFT/COSMO method.

^bThe stabilization of the quantum cluster from COSMO solvation with ε = 20 (obtained from eq 7). E_solv,COSMO contains both quantum cluster polarization, solvent interaction and electronic strain terms, analogous to those in E_env,SCRF.

^cThe total energy computed using the DFT/COSMO method (i.e., the sum of E₀ and E_Solv,COSMO) performed on the COSMO optimized geometry and used to compute relative energies in Table 4A.

^dThe energetic cost of polarizing the active site quantum cluster in response to the protein and reaction potentials in the DFT/SCRF scheme.

^eThe total protein field energy, including electronic polarization of the quantum cluster, resulting from interactions between active site and protein charges that are screened by the three dielectric media (ε = 1, 4, and 80 for the quantum cluster, protein region, and solvent, respectively).

^fThe total reaction field energy, including electronic polarization of the quantum cluster, arising from the dielectric response of the protein (ε = 4) and solvent (ε = 80) environments from the cluster charges.

^gThe total environmental (env) energy from the DFT/SCRF method (i.e., the sum of E_Strain, E_P, and E_RF).

^hThe total free energy associated with the total gas-phase electronic energy of the quantum cluster and the reaction field component of the DFT/SCRF method (i.e., the sum of E₀ and E_RF), also used to generate the relative energies given in Table 4B.

ⁱThe electrostatic free energy of a given state computed by the full DFT/SCRF method (i.e., the sum of E₀, E_Strain, E_P, and E_RF) and used to obtain the relative energies in Table 4C.

^j(A) Energies (in kcal mol^–1) are presented as total energies, and (B) relative energies (in kcal mol^–1) are given with respect to the energy of the RO^HP^–E^– state.

The stabilization of the gas-phase active site cluster by COSMO, E_Solv,COSMO, is computed as

7

where E₀ and E_Tot,COSMO are the total electronic energies of the system in the gas phase and as solvated by COSMO, respectively. The values of E_Solv,COSMO range from −142 kcal mol^–1, in the case of the RO^HP^HE^H state (q = −1), to −293 kcal mol^–1 in the case of the RO^HP^–E^– state (q = −3). Unsurprisingly, the more highly-charged states under study induce a larger reaction field and are, consequently, more stabilized by the COSMO solvation environment (ε = 20). This greater stabilization of states with q = −3 over those with q = −1 is approximately equal in magnitude (151 kcal mol^–1) to the greater gas-phase stabilization of states with q = −1 over states with q = −3. Consequently, the values of E_Tot,COSMO obtained using the DFT/COSMO method result from the cancellation of additive terms, falling into a range of relative energies that is considerably smaller than the range of the individual energetic contributions.

To better understand the differences between the DFT/COSMO and DFT/SCRF results, we now consider the latter method in a stepwise manner. First, we quantify the effects of only the reaction field energies on the relative energies of the different protonation states (Table 4B). Then, we consider the full DFT/SCRF energies, which, in addition to the reaction field, also include the effects of the protein field and electronic strain, which is the energetic cost of distorting the quantum cluster electron density in response to the protein and reaction fields (Table 4C). Similar to COSMO, the SCRF reaction field (RF) potential gives greater stabilization to the more highly-charged states. From Table 5B, it is evident the RF stabilization (ΔE_RF) of the RO^HP^–E^– state (q = −3) is 141 kcal mol^–1 greater (more negative) than that of the RO^HP^HE^H state (q = −1). Using a Hamiltonian comprising only the gas-phase energies and the RF potential, we obtain the relative energies given in Table 4B (last column), which appear similar to those computed with the DFT/COSMO method (Table 4A, last column): the RO^HP^HE^H state (q = −1) is lowest in energy, with the RO^–P^HE^H state (q = −2) only 1.1 kcal mol^–1 higher in energy.

The feature of the full SCRF treatment that reorders the energy rankings and makes the q = −3 states more favorable (Table 4C) is the protein field term, E_P. Without it, the ΔE_Tot,RF values (second column of Table 4B) of the two q = −3 states, RO^–P^–E^H and RO^HP^–E^–, are 9.5 and 10.3 kcal mol^–1, respectively, higher than that of the lowest-energy q = −1 state (RO^HP^HE^H); but as Table 5 shows, the protein field term (E_p) favors RO^–P^–E^H and RO^HP^–E^– over the RO^HP^HE^H state by 36.8 and 33.4 kcal mol^–1, respectively. This stabilization of q = −3 states by the E_P term is more than enough to change the ordering of relative energies (Table 4C). The E_strain term slightly favors the less charged states but is not large enough to change the ordering. Further, the corrections for proton free energy, ZPE, and pH are significant but do not change the ordering with respect to overall charge (Table 4C).

Calculations of Mössbauer Isomer Shifts for Comparison to Experiment

Mössbauer isomer shifts (ISs) are computed for the various protonation states considered in our oxidized IspH model (Table 6). The average IS, δ_ave, for all protonation states is computed to be ∼0.43 mm s^–1. The range of ISs present in the different states, however, differs depending on the protonation state of the HMBPP C₄–OH group. For all RO^– states, Fe1 displays an IS that is nearly indistinguishable from those of all other irons in the cluster (0.44, compared to 0.42 or 0.43 mm s^–1). In contrast, the apical Fe in ROH-bound states has an IS of 0.53–0.54 mm s^–1, which is significantly larger than those computed for the other Fe atoms (Table 6). In these states, there is also a Fe site that gives an IS that is significantly lower than the mean value (0.38–0.39 mm s^–1).

Table 6. Tabulation of Individual and Average Isomer Shifts (ISs) Computed Using the DFT/SCRF Method for Different Protonation State Conformers (Given in mm s^–1) and Compared with Experiment^33a.

	exp33	RO–P–EH	RO–PHEH	ROHP–E–	ROHPHE–	ROHP–EH	ROHPHEH
Fe1	0.64	0.44	0.45	0.54	0.53	0.53	0.54
Fe2	0.38	0.42	0.42	0.39	0.38	0.38	0.38
Fe3	0.42	0.43	0.43	0.42	0.41	0.41	0.40
Fe4	0.42	0.43	0.42	0.40	0.40	0.40	0.39
ave	0.47	0.43	0.43	0.44	0.43	0.43	0.43
MAE		0.06	0.06	0.03	0.04	0.04	0.04

^aThe error with respect to the experimental values is given as mean absolute error (MAE).

Both low-³⁰ and high-field³³ Mössbauer spectroscopic parameters are available for the [4Fe–4S]²⁺ (oxidized) IspH:HMBPP complex. Our computed isomer shifts are reasonably consistent with the experiments performed at low-field;³⁰ however, the high-field Mössbauer parameters are considered to be of superior quality.¹⁰⁵ The IS values obtained from their study display significant asymmetry, ranging from 0.38 to 0.64 mm s^–1, with the IS of 0.64 mm s^–1 attributed to the ferrous, HMBPP-bound Fe1.³³ When comparing our computed IS values to these experimental results, it is clear the asymmetric ISs computed for ROH-bound states better agree with experiment, having a mean absolute error (MAE) of 0.03–0.04 mm s^–1 (compared with 0.06 mm s^–1 for the RO^–-bound states). These MAEs for the ROH-bound states are also within the systematic error associated with computing ISs using the OLYP functional.⁶⁶ While the IS corresponding to the ferric site (Fe2 in Figure 2) in our ROH calculations matches its experimental counterpart, it is clear that the IS computed for Fe1 (with a ferrous IS of 0.53–0.54 mm s^–1) underestimates the experimental value (0.64 mm s^–1).³³

Calculations of Mössbauer Quadrupole Splittings for Comparison to Experiment

The Mössbauer quadrupole splittings (QSs) corresponding to the ISs displayed in Table 6 are given in Table 7. We note that the MAEs (relative to experiment) of the QSs computed with the DFT/COSMO and DFT/SCRF methods are almost identical (Table 7, Table S3). We observe this despite the latter approach containing a more extensive description of the surrounding electrostatics, which would be expected to affect the QS values through the values of V_zz and η (eqs 5 and 6). Here, we only discuss QSs computed using the DFT/SCRF method (results from DFT/COSMO are included as Table S3).

Table 7. Tabulation of Individual and Average Quadrupole Splittings (QSs) Computed Using the DFT/SCRF Method for Different Protonation State Conformers (Given in mm s^–1) and Compared with Experiment^33a.

	exp33	RO–P–EH	RO–PHEH	ROHP–E–	ROHPHE–	ROHP–EH	ROHPHEH
Fe1	1.22	–0.67	–0.70	0.94	0.99	1.02	1.11
Fe2	0.92	1.01	1.00	1.09	1.06	1.15	1.15
Fe3	1.33	1.11	1.11	1.13	1.15	1.24	1.25
Fe4	1.33	0.83	0.79	0.65	0.62	0.54	0.53
ave	1.21	0.91	0.91	0.96	0.96	1.00	1.02
MAE		0.34	0.34	0.33	0.32	0.33	0.31

^aThe error with respect to the experimental values is given as mean absolute error (MAE).

The average QS (QS_ave) of the RO^– states (0.91 mm s^–1) is slightly lower in magnitude than that computed for the ROH-bound states (0.96–1.02 mm s^–1). We note that the values of QS_ave obtained for all states considered are lower than experiment (1.21 mm s^–1).³³ In the case of the RO^– states, the absolute value of the QS for Fe1 is ∼0.7 mm s^–1, which is significantly lower than the experimental value of 1.22 mm s^–1.³³ In contrast, there exists good agreement between the QS computed for Fe2 in the RO^– states (1.00 mm s^–1) and the experimental value (0.92 mm s^–1). The DFT/SCRF method, however, fails to capture the elevated QSs found for the delocalized, mixed-valence pair, Fe3/Fe4 (computed to be 0.8 to 1.1 mm s^–1; experimental value is 1.33 mm s^–1).³³

All QS values computed for Fe1 in the ROH-bound states agree better with experiment than their RO^– counterparts (QS_comp = 0.94–1.11 mm s^–1; QS_exp = 1.22 mm s^–1), with the ROH/E^– states giving the best agreement with experiment (Table 7). Similar to the RO^– states, the QS values computed for Fe2 (QS = 1.06–1.15 mm s^–1) match experiment (0.92 mm s^–1) reasonably well, but those computed for Fe3/Fe4 are underestimated. In the case of Fe4, in particular, the QS computed for the ROH-bound states (0.52–0.64 mm s^–1) are much lower than the experimental value (1.33 mm s^–1).³³ In sum, the results from computation of QSs are largely inconclusive, with both RO^– and ROH states (MAEs of 0.34 and 0.31–0.33 mm s^–1, respectively) giving good agreement with the experimentally determined QSs for Fe1 and Fe2, while underestimating the QSs for Fe3 and Fe4. The MAEs computed for the QSs, however, are only slightly larger than those obtained for synthetic Fe–S complexes of known structure (MAE ∼ 0.25 mm s^–1).⁶⁶

Discussion

By performing DFT calculations on a large active site model of the oxidized form of the [4Fe–4S] cluster in IspH, we are able to characterize geometries, relative energies, and Mössbauer signatures of different protonation states. A thorough understanding of the interplay between [4Fe–4S]–HMBPP interactions and protein electrostatics in this state are of value both for understanding the unique catalytic mechanism of IspH and for assessing factors that determine how new competitive inhibitors may best interact with the IspH active site.

The geometries of the [4Fe–4S] clusters computed for the various RO^XP^YE^Z states do not fully match the asymmetry seen in the IspH:HMBPP crystal structure at 1.7 Å resolution,³² although we do observe a 4-fold compression of the cluster that is consistent with what is seen in other [4Fe–4S] protein systems.¹⁰⁶ In our calculations, a short Fe1–O bond length of 1.9 Å differentiates the RO^– states from their ROH counterparts; however, this distance is significantly shorter than what is observed in the IspH:HMBPP crystal structure (2.05 Å).³² Instead, RO^HP^YE^– states (regardless of PP_i protonation) give better agreement with the crystal structure, displaying Fe1–OH distances of 2.11–2.13 Å. These RO^HP^YE^– states also better match the hydrogen bonding network implied by the crystal structure and, consequently, display higher structural similarity to the crystal structure, as measured by RMSD (Table 3).

An analysis of the relative energies of the different protonation states in our model provides different possibilities as to which states are energetically favorable in the oxidized state, depending on the solvation method employed (Figure 4). While the DFT/COSMO method indicates the RO^–P^HE^H and RO^HP^HE^H states (q = −2 and −1, respectively) are lowest in energy, the DFT/SCRF method favors the RO^–P^–E^H and RO^HP^–E^– states (q = −3). Further, the computed Mössbauer isomer shifts show preference for HMBPP to bind Fe1 as an alcohol group rather than an alkoxide. The ROH-bound states all display asymmetric isomer shift values, similar to what is seen experimentally.^30,33 In contrast, all states where an RO^– group coordinates Fe1 display symmetric isomer shifts. This finding indicates the dominant oxidized state involves HMBPP with its C₄–OH group protonated (ROH).

The finding that RO^–- and ROH-bound states give different Mössbauer signatures follows from the different ligand environments of the apical Fe atom. The “harder” RO^– form of HMBPP binds Fe1 more tightly than the ROH form, with concomitant lengthening of the Fe1–S^2– bonds. The net effect of these RO^– geometries is an isomer shift for Fe1 that appears similar to what is observed in related [Fe₄S₄(SR)₄]^2– systems^66,107,108 and is more indicative of a valence delocalized Fe^2.5+ oxidation state. In contrast, when bound as an alcohol, the HMBPP–Fe1 distance is elongated with shortened Fe1–S^2– distances. This results in a net effect of giving Fe1 more ferrous character, as evidenced by its greater isomer shift (Table 6).

Overall, the quadrupole splittings (QSs) obtained for active site clusters containing ROH-bound HMBPP are slightly more accurate than those computed for RO^–-bound states. In both RO^–- and ROH-bound states, the QSs computed for Fe1, Fe2, and Fe3 better match experiment than for those computed for Fe4. It is worth noting that the active site cluster utilized in all calculations is constructed from the [4Fe–4S] cluster on the face containing Fe1 and Fe2, in order to properly stabilize the highly charged PP_i moiety on HMBPP. This approach largely omits the protein environment around Fe3 and Fe4, except the backbones amides of A199, T200, P97, and L98, as well as the side chain of T200, which cumulatively donate three hydrogen bonds to the S^2– atoms and thiolates bound to Fe3 and Fe4. Despite including nearby point charges in the DFT/SCRF scheme, it is possible that the electric field gradients at Fe3 and Fe4 suffer from excluding nearby protein residues from the quantum region in our computations.

We note that a previous study has also computed Mössbauer isomer shifts and quadrupole splittings for a [4Fe–4S]:HMBPP complex. Ahrens-Botzong et al. computed Mössbauer ISs and QSs for comparison with Mössbauer experiments they performed on complexes of [4Fe-4S] IspH with HMBPP and its amino and thiol analogues.³³ Their work utilized a DFT/MM approach, employing the B3LYP/LANL2DZ level of theory to describe the [4Fe–4S]²⁺ cluster, the SCH₂ groups of its coordinating cysteines, and a singly protonated (ROH) HMBPP ligand in the DFT region. Following the DFT/MM minimization of the IspH:HMBPP complex, the authors compute Mössbauer parameters at the B3LYP/CP(PPP)/TZVP level of theory (where the CP[PPP] basis set is used for Fe) using the ORCA program with the closed-shell approach. The resulting computed isomer shifts, which assumed ROH coordination to the [4Fe–4S] cluster, are found to be 0.48, 0.56, 0.30, and 0.81 mm s^–1, with corresponding QSs of −1.18, 1.30, −2.02, and −0.75 mm s^–1.³³

Our work differs from this previous work in two principal ways: (1) we utilize a large active site model to compute Mössbauer isomer shifts using BS–DFT/COSMO and BS–DFT/SCRF approaches; and (2) we do not make assumptions regarding the protonation state of HMBPP when coordinated to the [4Fe–4S] cluster. In regard to the computational approach employed, it is evident that BS–DFT approaches (both DFT/COSMO and DFT/SCRF) better predict IS (MAE with respect to experiment of 0.03 mm s^–1, compared to 0.11 mm s^–1) and QS values (MAE with respect to experiment of 0.33 mm s^–1, compared to 0.44 mm s^–1). Regardless, after our examination of different HMBPP protonation states, we similarly conclude that the ROH-bound geometries of HMBPP give better agreement with experiment, consistent with the assumption and conclusions of Ahrens-Botzong et al.³³

Both DFT/COSMO and DFT/SCRF results show ROH-bound states, whose computed Mossbauer properties are consistent with experiment, to be isoenergetic with the lowest-energy oxidized states. While the DFT/COSMO results show preference for protonation of E126 and the HMBPP PPi moiety (RO^HP^HE^H, q = −1), the RO^HP^–E^– state is preferred with the DFT/SCRF method. Since computed geometries with a protonated E126 show less similarity to the IspH:HMBPP crystal structure, we propose the preferred oxidized state for IspH to be RO^HP^–E^–. The ability of the DFT/SCRF method to select the most relevant state, as verified through comparisons with experimental results, indicates that the inclusion of both the protein and reaction field effects is critical to compute accurate energies along the IspH catalytic pathway.

Of additional interest, we find that when the IspH active site is described with the DFT/SCRF method, the different charge (protonation) states considered cluster together energetically. With q = −3, the RO^–P^–E^H and RO^HP^–E^– states are lowest in energy; however, states with q = −2 are both energetically accessible from these lowest-energy states and also possess an additional proton that can play a role in catalysis. For instance, the RO^–P^HE^H and RO^HP^–E^H states (q = −2) are 2.2 and 5.5 kcal mol^–1 above the energies of the RO^–P^–E^H and RO^HP^–E^– states (Table 4, Figure 4). Since the active site stabilizes q = −3 charge states, protonation to generate these q = −2 states may precede subsequent electron addition to reinforce a q = −3 active site, suggesting a mechanism by which protons and electrons can be shuttled into the active site for catalysis. It is worth noting the stabilization of a highly-anionic active site in DFT/SCRF computations can be attributed to their inclusion of the highly-polar IspH protein environment. Indeed, the active site quantum cluster is within 8 Å of the of 7 Arg/Lys (cationic) residues, 10 Asp/Glu (anionic) residues, and 95 crystallographic waters, which are all included as point charges in the protein region within the DFT/SCRF scheme.

In this work, we have demonstrated the ability of the DFT/SCRF method to describe protonation state changes in the IspH oxidized state, which suggests that similar efforts can be applied to reasonably characterize the later stages of IspH catalysis. Drawing from the results presented here, we will next use the RO^HP^–E^– state computed for oxidized IspH as a starting point to examine the proposed IspH catalytic mechanism. Evaluating the energetics along the IspH catalytic pathway will both increase the knowledge of how these [4Fe–4S] clusters facilitate catalysis, as well as reveal differences between the oxidized and reduced forms of IspH that may be exploited in the development of novel antibacterial and antimalarial drugs.

Supporting Information Available

A tabulation of the relative energies of different valence isomers for each protonation state considered in the broken-symmetry computations using both the DFT/COSMO and DFT/SCRF methods (Table S1); isomer shifts computed for all protonation states considered using the DFT/COSMO method (Table S2); quadrupole splittings computed for all protonation states considered using the DFT/COSMO method (Table S3); superposition of the geometry optimized RO^–P^–E^H and RO^HP^–E^– states onto the 3KE8 crystal structure³² (Figure S1); and xyz format coordinate files for the RO^–P^–E^H, RO^–P^HE^H, RO^HP^–E^–, RO^HP^HE^–, RO^HP^–E^H, and RO^HP^HE^H states (Text S1–S6, respectively). This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States