Changing concepts of working memory

Abstract

Working memory is widely considered to be limited in capacity, holding a fixed, small number of items, such as Miller's ‘magical number’ seven or Cowan's four. It has recently been proposed that working memory might better be conceptualized as a limited resource that is distributed flexibly among all items to be maintained in memory. According to this view, the quality rather than the quantity of working memory representations determines performance. Here we consider behavioral and emerging neural evidence for this proposal.

Working memory refers to the short-term storage and manipulation of sensory information lasting on the order of seconds¹. It has been associated with persistent neural activity in many brain regions² and is considered to be a core cognitive process that underpins a range of behaviors, from perception to problem solving and action control. Deficits in working memory have been reported in many brain disorders; whereas performance on working memory tasks improves with brain development from childhood to early adulthood, it declines in the elderly, and is closely related to measures of intelligence.

The classic view has been that working memory is limited in capacity, holding a fixed, small number (K) of items, such as Miller's ‘magical number’ seven³ or Cowan's four⁴. Such hypotheses have arisen from tasks such as letter recall or change detection that use a discrete or categorical stimulus set, such as a small number of easily identifiable colors^5,6. For vision, a highly influential proposal has been that items retained in working memory are held in three or four independent object ‘slots’, one for each item stored⁵. This slot conceptualization of working memory is all or none: an object either gets into a memory slot and is then remembered accurately, or it does not, in which case it is not remembered at all. This framework⁷ has had a huge influence on interpretation of neural data—imaging, monkey neurophysiology and human electrophysiology—as well as on studies of normal development and aging, the effects of training working memory, and brain disorders.

Resource models of working memory

Recent work has led to substantial advances in our understanding of the structure and organization of working memory. In particular, compelling reasons to reconsider the classic view have arisen from psychophysical studies showing that the precision of recall declines continuously as the number of items to be remembered increases (Fig. 1a–c), and increasing the salience or goal relevance of a stimulus causes it to be stored with enhanced precision, at the cost of poorer memory for other stimuli (Fig. 1d–f). Although interpretation of these results remains an active area of debate, neither of these findings would have been predicted on the basis of the original slot model⁵, in which every item is either stored with high precision or not at all (Fig. 2a).

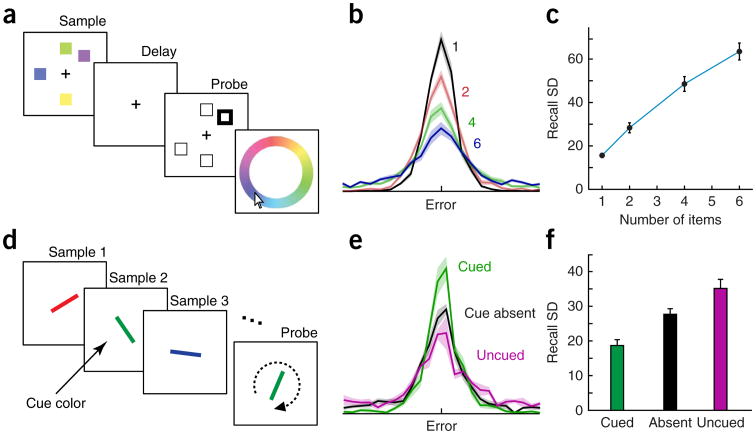
Figure 1.

Evidence from delayed estimation challenging the slot model. (a) Example of a color delayed-estimation task⁸. Observers must report the color in memory that matches a probed location by selecting from a color wheel. (b) The distribution of responses relative to the correct (target) color depends on the number of items in the sample display. (c) Recall variability as measured by the standard deviation (SD) of error increases gradually and continuously with set size. In the item-limit (slot) model, this function would be flat up to set size 4. Adapted with permission from ref. 9. (d) Example of an orientation delayed-estimation task with sequential presentation¹⁰. Observers must report the orientation in memory that matches a probed color by adjustment of the probe, using a response dial. An item of the cue color (here, green) is more likely to be probed than items of other colors, making it higher priority for accurate storage. (e,f) Response distributions and standard deviation of errors for the orientation estimation task. When an item of the cue color is present in the sequence, it is remembered with enhanced precision (lower standard deviation) compared with other items in the sequence. Comparison with trials on which the cue color is absent (no cue) shows that uncued items are recalled with lower precision when a cued item is present. Adapted with permission from ref. 10.

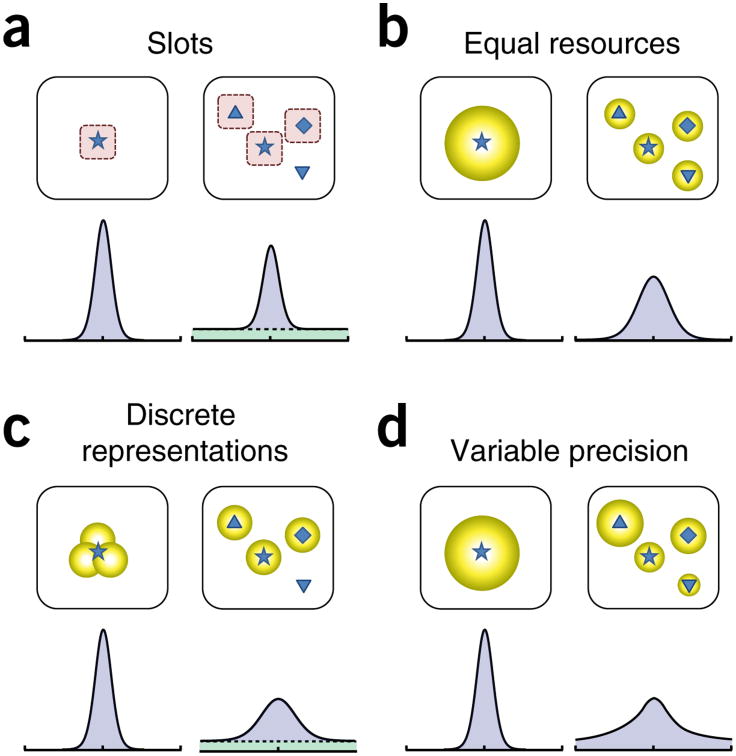
Figure 2.

Models of working memory. (a) In the slot (or item limit) model of working memory^4,5, each visual item is stored in one of a fixed number of independent memory slots (here, 3) with high resolution (left, illustrated, by narrow distribution of errors around the true feature value of a tested item). When there are more items than slots, one or more items are not stored and the slot model predicts that errors in report of a randomly chosen item will be composed of a mixture of high-precision responses (right, blue component of distribution corresponds to trials when the chosen item received a slot) and random guesses (green component corresponds to trials where it did not get a slot). (b) Resource models of working memory^8,11,17 fundamentally differ: they propose a limited supply of representational medium that is shared out between items, without a limit to the number of items that can be stored. Crucially, the precision with which an item can be recalled depends on the quantity of resource allocated to it. If resources are equally distributed between objects, error variability (width of the distribution) increases continuously with the number of items (compare distribution of error for one versus four items), with a normal distribution being commonly assumed. (c) In discrete-representation models¹⁹, the working memory medium is divided into a discrete number of quanta, similar to the slot model. However, these slots are shared out between items; in this respect, this type of model is much closer to resource models than the original slot model (a). For low set sizes (for example, one item shown at left), the quanta combine to produce a high-resolution memory of an item. However, for higher set sizes, above the number of slots available (right), all items get either one or zero quanta, predicting a mixture of low-resolution recall and random guesses. Note how this distribution differs from those in a and b. (d) Variable-precision models^15,16 propose that working memory precision varies, from trial to trial and item to item, around a mean that decreases with increasing number of items as a result of limited resources. This model predicts that recall errors will be made up of an infinite mixture of distributions (assumed normal) of different widths. Variability in precision could stem from variability in resource or from bottom-up factors.

In contrast, the results are naturally accommodated by models that consider working memory to be a limited resource, distributed flexibly between all items in a scene^8–16 (Fig. 2b–d). Crucially, although resource models consider working memory to be extremely limited, they do not invoke a fixed item limit on the number of objects that can be stored. Thus, for these models, K is not the fundamental metric with which to measure working memory. According to these views, it is not the number of items remembered, but rather the quality or precision of memory that is the key measure of working memory limits.

Resource models of working memory^8,11,17 are based on two premises. First, the internal representations (or measurements) of sensory stimuli are noisy, that is, they are corrupted by random, unpredictable fluctuations. Second, the level of this noise increases with the number of stimuli in memory. This increase is attributed to limitations in the supply of a representational medium that is distributed between items; thus, the more resource is allocated to an item, the less noise is present in its representation and the more precise the recall of that item. Resource models have strong links to other areas of neuroscience and psychology. The premise that internal representations are noisy is common to all signal detection theory and many Bayesian models of perception, whereas the increase in noise with set size is also shared with models of attention.

Just as is common in perceptual psychophysics, one way to test working memory models based on the concept of noise in memory representations is to vary stimuli on a fine scale, thereby manipulating the signal-to-noise ratio (see below). Wilken and Ma modified the method of adjustment, long employed in perceptual studies, to multiple-item working memory⁸ (Fig. 1a). In this delayed-estimation technique, both the stimulus and the response space are analog (continuous) rather than discrete. This is very different from conventional methods for probing visual or other types of working memory (for example, change detection or digit span in verbal working memory), where the stimulus or change in stimulus is held constant to obtain a discrete measure of K or span.

The delayed-estimation technique has now been used to study memory of a range of visual features, including color, orientation and motion direction^{8–10,15,16,18–21}. Rather than exhibiting the abrupt, step decline that would be expected on reaching a capacity limit of a fixed number of items⁵, in every case, recall variability has been shown to gradually and continuously increase as set size increases (Fig. 1b,c), as predicted if working memory resources are shared between items. Across a range of studies, this relationship between precision of recall and set size has been shown to follow a power law^9,11,15,17.

Although the concept of a limited working memory resource has considerable explanatory power for behavioral data (discussed below), the exact nature of the representational medium remains to be established and is an important goal for neurophysiological investigation. The majority of electrophysiological and computational studies have confined themselves to studying memory for a single object. However, understanding the neural effects of increasing set size will be crucial for determining the cognitive architecture underlying working memory and distinguishing between competing models (Fig. 2b–d). Resource models are already beginning to have an effect on systems neuroscience. Animal studies have started to measure working memory behaviorally in non-human primates using set sizes >1, with testing of resource models in mind^22–25. Looking ahead, interpretation of such neural data will crucially depend on having a sound theoretical framework for behavior. In this review, we focus on emerging data from studies that have employed simple visual memoranda, as they are the easiest to model and have been used in both human and animal studies.

Flexible resource allocation

Flexibility in memory allocation¹¹ represents a crucial distinction between competing slot and resource accounts of working memory. Rather than being limited to a fixed storage resolution, a growing body of evidence indicates that memory resources can be unevenly distributed so that prioritized items are stored with enhanced precision compared to other objects. Voluntary control over resource allocation has been demonstrated by studies in which one stimulus in a memory array is indicated as more likely to be selected for test, resulting in a robust gain in recall precision for the cued stimulus^10,18,26. Critically, this recall advantage appears to come with a corresponding cost to other stimuli in memory, which are recalled with less precision^10,11,26.

These findings are consistent with an unequally distributed, but limited, resource: when more resource is devoted to a prioritized item, less is available for other objects. Notably, these effects cannot be explained simply by biased competition for sensory processing favoring a prioritized item²⁷, for several reasons. First, equivalent findings are observed for stimuli presented one at a time in sequence¹⁰, eliminating competition in sensory input (Fig. 1d–f). Second, cues presented following prolonged examination of a stimulus array are of similar effectiveness as those presented before the array²⁶, indicating that working memory resolution can be changed after the initial encoding is complete. Finally, recall precision can be influenced by retrospective cues, presented long after the array is extinguished, that is, when there is no sensory input available²⁸.

These results indicate that the allocation of limited working memory storage can be controlled and updated with changing behavioral priorities. Similar recall advantages and costs have been observed for objects that are visually salient^11,26,29, even when test probability is equal, indicating an automatic component to memory allocation that might be linked to visual attention. Further evidence that resource is associated with allocation of visual attention has arisen from demonstration of recall advantages for targets of saccades^11,29,30 and for targets of covert shifts of attention, as inferred from micro-saccades²⁵.

In oculomotor areas, including frontal eye field (FEF) and lateral intraparietal area (LIP), neural activity is modulated by both stimulus salience and task relevance to produce retinotopic maps of stimulus priority³¹. Such priority maps have been implicated in the guidance of visual attention and eye movements, but could also be involved in determining how working memory resources are distributed between objects. When eye movement sequences are interrupted, the upcoming saccade target is held in memory with high resolution, whereas objects that had previously been the focus of attention are represented more coarsely¹¹. This allocation may reflect a dual role of working memory representations in visual exploration, whereby memory for the saccade target is compared with post-saccadic input to correct inaccurate eye movements, and a record of attended locations is maintained to inhibit re-examination of previously explored locations³².

Sources of noise

Errors in recollection of a stimulus could arise from multiple sources: noise in the initial stage of sensory processing, in storing or maintaining information in a stable state once the sensory input has been removed, or in the final stage of decoding (retrieval) and response generation. It is important to distinguish between these possibilities.

Working memory precision is inevitably limited by the precision afforded by early sensory representations, which is influenced by stimulus factors such as contrast. Moreover, encoding of sensory information is not instantaneous^26,33, so recall errors following brief exposure to multiple or complex stimuli may reflect incomplete encoding. The quality of encoding might also depend on attentional limitations^34,35 instead of, or in addition to, storage capacity limitations. Indeed, when the time available for encoding items into working memory is systematically varied, the rate at which recall precision increases over short exposures depends on the number of visual elements²⁶, consistent with a continuous parallel accumulation of sensory information into memory³⁶. However, with prolonged exposures, precision does not continue to increase, but rather approaches a maximum value that depends on the number of items stored, which is consistent with a limit on how much information can be simultaneously represented in working memory²⁶.

During the maintenance stage, additional noise might be added. Recall variability has been shown to increase with the duration of the delay period (for example, see ref. 28), which is consistent with a gradual accumulation of error resulting from noise in memory, but is difficult to explain solely in terms of noise at encoding or decoding stages. The possibility that noise in working memory recall arises predominantly at the decoding or response stage has generally received less attention. However, it is unlikely to be a major contributor in delayed-estimation tasks, as only one of the items in memory is specified for recall; thus, noise arising at this stage would not be expected to produce set size–dependent effects.

Neural data

The search for a neural basis for limits on working memory performance has primarily focused on brain areas that are active during the delay period of memory tasks. Investigations using functional magnetic resonance imaging (fMRI) have identified regions of human prefrontal and posterior parietal cortex that show elevated blood oxygen level–dependent (BOLD) signals during working memory maintenance^37–39 (Fig. 3a), whereas electroencephalography (EEG) studies have observed a sustained negativity over posterior electrodes contralateral to memorized stimuli^21,40 (the contralateral delay activity, CDA). Both BOLD and CDA signals are sensitive to the number of items in memory, displaying increasing^37,38,40 or inverted U–shaped^21,39,41 responses to increasing load.

Figure 3.

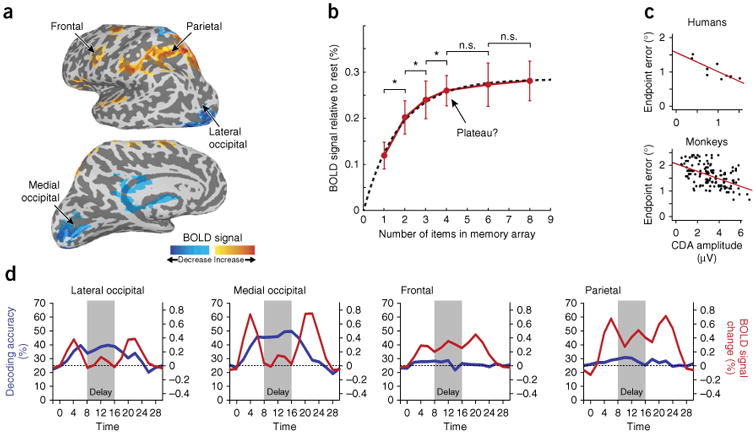
Neural correlates of storage in working memory. (a) Short-term maintenance of visual information is associated with sustained elevated BOLD signals (hot colors) in prefrontal and posterior parietal regions, whereas the signal in occipital visual cortex is the same or below that observed at rest (but see d). BOLD signals are displayed on an inflated brain surface, showing gyri in light gray and sulci in dark gray. (b) During maintenance, BOLD amplitude in posterior parietal regions varies with the number of features held in memory (data are from ref. 38). A neural capacity limit has typically been inferred by looking for increases in memory load that are not accompanied by a statistically significant (P < 0.05) increase in signal (here, above four items). However, there are many continuously increasing functions (for example, exponential saturation function, dashed line) that would be incorrectly identified as reaching a plateau by this method. (c) In both humans and monkeys, a lateralized EEG signal at posterior electrodes (the CDA) is correlated with precision of recall, as measured by the error in reproducing a single remembered stimulus location. (d) The information content of BOLD signals is dissociated from signal strength during memory maintenance. In occipital areas (left), visual parameters held in memory can be accurately decoded (blue lines) from voxels that are not consistently elevated above baseline during the delay period (red lines). Decoding from these occipital areas is more effective than from prefrontal and posterior parietal voxels (right) that show elevated delay-period responses. Adapted with permission from refs. 51 (a,d), 38 (b) and 46 (c).

Within the slot framework, an increase in neural activity with memory load has been considered to be the signature of a working memory store, based on the assumption that increasing load engages more of a store's capacity. Indeed, a number of studies^37,38,40 have reported that neural signals reach an abrupt plateau at higher memory loads, potentially corroborating the hypothesis of a maximum number of objects that can be stored⁵. However, unambiguously identifying a signal plateau in the presence of noise is not trivial, and the methods used to date have not been rigorous, either relying on appeals to subjective visual judgment or on the statistical error of accepting the null hypothesis.

It therefore remains to be established whether these neural signals reach a maximum at a particular set size and then plateau, or increase continuously toward an asymptotic limit (for example, according to a saturation function; Fig. 3b). One perspective is that increases in CDA amplitude may actually be explained by amplitude modulation asynchrony, whereby a systematic decrease in the peak, but not trough, of alpha-band oscillation can produce the appearance of a sustained negativity (the CDA) when trial averaged⁴².

At the level of individual differences, the rate at which neural signals change with load is correlated with working memory performance measures^40,43, although the common assumption that this reflects differences in signal plateau has again not been rigorously examined. Notably, both BOLD and CDA measures show effects of the complexity as well as the number of visual stimuli in the memory array^37,44, suggesting that the amplitude of neural signals may reflect both information content and object number. Consistent with this, the amplitude of the CDA is correlated with precision of recall⁴⁵, even when only a single item is held in memory⁴⁶ (Fig. 3c).

In contrast with the slot framework, resource models of working memory dictate that the same resources are engaged whether one or multiple visual items are stored. This is also true for the latest revisions of the slot model, which effectively distribute resource in discrete quanta¹⁹ (see below). Thus, increases in neural activity with load should not be considered the definitive marker of a working memory store. Nonetheless, there are several reasons why load-dependent signals might arise in a resource-based memory system. At the neuronal level, BOLD and EEG signals are believed to primarily reflect synaptic conductances, rather than spiking activity, with both excitatory and inhibitory conductances contributing to the amplitude of these signals⁴⁷. As a consequence, a working memory network whose spiking activity level is independent of memory load, for example, as a result of divisive normalization (see below), may nonetheless demonstrate increases in BOLD and EEG amplitude with load simply as a result of an increase in synaptic processing with increasing set size.

Alternatively, load-sensitive signals might not be associated with coding of object features directly, but instead with maintenance of ‘meta-information’ that is required to control resource allocation or maintain bindings between features in dimension-specific stores^48,49. Thus, if features that belong to an object need to be maintained bound veridically, increases in signal with working memory load might reflect greater demands resulting from feature binding rather than increasing number of items per se (see below).

Single-unit recordings in monkeys have identified neurons with persistent delay period activity in frontal and parietal areas, consistent with analogous regions displaying elevated BOLD signals in humans. A recent study⁴⁶ combining intracranial recording and EEG demonstrated that the magnitude of the local field potential in prefrontal areas is correlated with precision of recall, and may contribute to the CDA signal observed in humans.

In another investigation, recordings from prefrontal and posterior parietal neurons under varying working memory load revealed that the ability to decode stimulus parameters from persistent activity declined continuously with increases in memory load²². In other words, the information about a stimulus that can be extracted from delay period activity gradually decreases as the total number of stimuli in memory increases. This observation of graded degradation is consistent with division of working memory resource between items. However, memory items appear to compete for resources only with other stimuli presented in the same hemifield, suggesting a degree of hemispheric independence in monkeys that is much greater than that observed in humans⁵⁰.

Recent advances in multivariate analysis of fMRI have widened the search for working memory representations to include earlier cortical areas. Studies based on multivoxel techniques have successfully decoded simple visual features held in memory from signals in visual areas, including V1, where the BOLD signal is not globally elevated above baseline levels during working memory maintenance^51–53 (Fig. 3d). Furthermore, inter-subject differences in the information content of BOLD signals in visual cortex are correlated with the precision of an individual's recall^54,55. Atlhough the factors that determine the decodability of BOLD signals are still being explored^56,57, these results highlight the importance of looking beyond simple elevated delay activity as a unique marker of working memory representation.

Neural models

Before slot models of working memory were called into question, neural modeling studies proposed that a neural basis of slots could be found in the number of oscillatory states that can be superimposed without interference⁵⁸. These models made a connection to the binding problem, as cortical synchronization has been proposed as a mechanism for binding features of an object⁵⁹. However, they did not describe the contents of working memory, let alone contain a description of the precision of encoding. Physiological evidence supporting oscillation-based models has so far been sparse.

In the context of resource models, a possible neural basis for resource lies in the number of action potentials used to encode working memories^15,60 (Fig. 4). Cortical firing is highly variable from trial to trial⁶¹, and this variability might underlie the (encoding and maintenance) noise seen in working memory recall. A correspondence between resource and the amplitude of neural activity (gain) in a neural population representing an item is suggested by several lines of evidence. First, theoretical models of early sensory representation have proposed that neural gain is proportional to the precision of encoding of the stimulus^62,63. Second, working memory resource is often considered to be similar to attentional resource^4,34,64, and attention modulates neural gain⁶⁵. Third, there is neurophysiological evidence that firing rate decreases with increasing set size⁶⁶ and varies from trial to trial⁶⁷. Fourth, neural spiking is energetically costly and, at large set sizes, the performance benefits of investing more spikes in encoding stimuli might be outweighed by the energy spent, leading to a decrease of precision per item¹⁵.

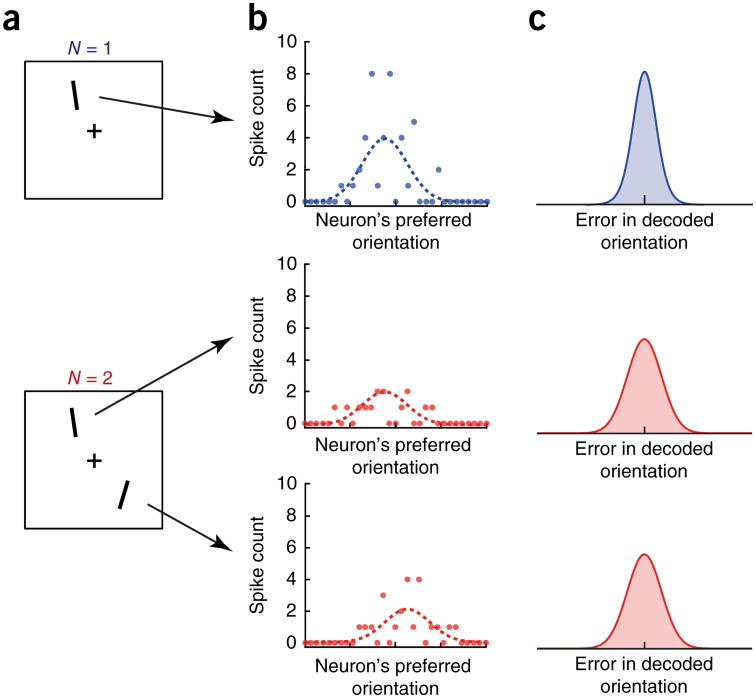
Figure 4.

Putative neural basis of set size effects in resource models of working memory. (a) Example displays for an orientation delayed-estimation task with one or two items. (b) Examples of mean firing rate (dashed lines) and activity on a single trial (points) in neural populations responding to the stimuli in a. Neurons are ordered by preferred orientation. At set size 2, gain (population amplitude) per item is reduced compared with set size 1. (c) Error distributions obtained by optimally decoding spike patterns such as those in b. Errors arise because of stochasticity in spike generation. Precision declines with decreasing gain^62,63, leading to wider distributions for more memory items. In this context, the limited resource is the gain of the population activity.

One way to realize a decrease of precision with set size arises from the relationship between precision and neural gain. It has been proposed that neural gain could be related to the number of items in memory through a mechanism of divisive normalization⁶⁰. The idea is that activity in the population encoding a particular item is divided by the grand sum of the activities of neurons in all populations encoding items. Thus, the larger the number of items, the larger this sum and the lower the gain of the population encoding each item. This is a directly testable physiological hypothesis.

A recent neural network model managed to capture a decrease of precision with set size using biologically realistic neurons⁶⁸. In this network, all items are encoded as persistent activity ‘bumps’ in a shared feature-selective population, causing working memory errors to arise from competition between and merging of these bumps. However, neurons in this simulated network had no spatial selectivity, and stimuli were therefore artificially spaced out in the feature space to be retained as distinct bumps. It remains to be seen whether the proposed mechanism can account for performance when (potentially similar) visual items are remembered in distinct spatial locations.

Making sense of memory errors

So far we have considered some key behavioral, neural and modeling data that have led to a reconceptualization of working memory. Recent studies have gone further and started to examine whether the pattern of recall errors might provide even deeper insights into the nature of working memory representations.

A crucial advantage of the delayed-estimation technique for probing working memory (Fig. 1) is that it provides the experimenter not just with an estimate of error precision, but with an entire error distribution. Theoretical models of sensory representation typically assume that errors have a normal (Gaussian) distribution, and early instantiations of resource models likewise assumed that recall errors would be normally distributed^8,17. However, recent studies have shown that errors in recall from working memory often deviate substantially from normality. Beyond changes in precision, accounting for the shape of the error distribution has become a new testing ground for comparing working memory models (Figs. 2 and 5). In addition, an important new trend is to fit models to raw, individual-trial data using maximum-likelihood estimation, instead of relying on summary statistics⁶⁹.

Figure 5.

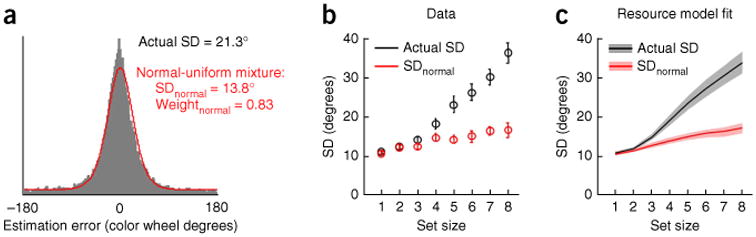
Interpreting the shape and width of working memory error distributions. (a) A crucial area of debate concerns how to model the distribution of recall errors (gray histogram, color estimation data from ref. 15, averaged over all subjects and set sizes). A popular analysis method attempts to do this with a mixture of a circular normal distribution (intended to correspond to items in memory) plus a uniform distribution (intended to correspond to items that are not stored)¹⁹. The red line depicts this fit, also averaged over all subjects and set sizes. Note that the circular standard deviation of the normal component in the mixture, SD_normal (average value given) is much lower than that of the raw data (compare actual standard deviation (actual SD) with SD_normal). The mixture does not fit human recall data well, and the interpretation of the two mixture components has therefore been called into question^15,16. (b) Actual SD and SD_normal as a function of set size. SD_normal substantially underestimates the level of noise in memory, which, if all items are stored, is simply the actual SD. An apparent plateau in SD_normal (red symbols) at higher set sizes has been used to argue for slot models^19,21, but such a plateau is not present in the raw data (black symbols). Data are from ref. 15. Error bars represent s.e.m. (c) A resource model in which all items are stored with variable precision accurately accounts for both actual SD and SD_normal. Thus, SD_normal by itself cannot serve to distinguish between slot and resource models⁶⁹. Adapted from ref. 15; shaded areas are s.e.m. of model fits.

Discrete representation

An influential study¹⁹ proposed that the shape of the error distribution in delayed estimation could be reproduced by a mixture of two classes of error: some resulting from noisy recall (with a normal distribution) and some resulting from random guessing (with a uniform distribution) (Fig. 2c). Fitting this normal + uniform mixture to the data, the authors showed that the proportion of errors accounted for by the uniform distribution (which they interpreted as guessing rate) increased with set size. The standard deviation of the normal component, denoted SD_normal, increased for the first three items, then reached a plateau (Fig. 5b)²¹, although this plateau has not always been replicated^9,11,26. To explain this, the investigators proposed that the same item could be stored in more than one slot¹⁹. When a single item is held in memory, there would then exist several independent representations of it in the brain (depicted as three overlapping quanta in Fig. 2c), which could be averaged at recall to boost precision.

While attempting to retain the terminology of the slot model, this account actually differs fundamentally from the classic slot model. Here, all the representational medium (that is, every slot) is engaged for all set sizes and shared out between items. Furthermore, the authors reported flexible allocation in response to a predictive cue, which they interpreted as some objects being allocated more slots than others¹⁹. This makes the model equivalent to a discrete or quantized resource model. The key distinction from continuous-resource models^8,11 is that it predicts a fixed upper limit on how many objects can be stored, that is, an item limit (Fig. 2b,c). The plateau in SD_normal was interpreted as indicating just such a limit on the number of items stored. However, interpretation of the parameters of the normal + uniform mixture critically depends on the validity of the mixture fit. Careful comparison with data suggests the normal + uniform mixture provides a relatively poor fit to experimental error distributions^15,16,70 and SD_normal may therefore systematically underestimate the true variability in memory (Fig. 5).

Variable precision

The most recently proposed continuous-resource model postulates that precision is itself variable across items and trials, even when set size is kept fixed^15,16 (Fig. 2d), and should therefore be modeled as being drawn from a probability distribution. In this model, the noisy memory of a stimulus would not follow a normal distribution with a fixed precision, but an infinite mixture of normal distributions of different precisions, including very low ones. Many sources could potentially contribute to variability in precision, including stimulus differences⁷¹, waxing and waning of alertness, covert attention shifts²⁵, grouping and other configural effects⁷², and variability arising during maintenance^16,61. One proposal is that deviations from normality in the distribution of working memory errors may arise from the same source of stochasticity as the errors themselves, namely Poisson variability in neural spiking⁷³.

Error distributions in delayed estimation are predicted considerably better by a variable-precision model than by alternative models, including the discrete-representation model^15,16,70. In particular, the model accounts for the increase in the ‘guessing rate’ with increasing set size: when a normal + uniform mixture is fitted to recall errors, low-precision trials will be absorbed into the uniform component, even though they might not represent true guesses. Thus, an increase in guessing rate with set size simply reflects an increasing prevalence of low-precision representations. The variable-precision model also provides a good quantitative account for both actual standard deviation and SD_normal as a function of set size¹⁵ (Fig. 5c). These findings further call into question the interpretation of the uniform component in the normal-uniform mixture as being a result of an item limit. More generally, it is important to keep in mind that summary statistics computed using a descriptive model, such as capacity K when using a classic slot model or the guessing rate when using a normal + uniform mixture, are only as good as the model itself. They can be misleading when the model is a poor description of the data. Conclusions from formal model comparison based on individual-trial data are always more reliable than conclusions from summary statistics⁶⁹.

Other findings also point to variability in precision: when subjects are asked on some trials to recall the item they remembered best, performance on those trials was substantially better than on ones on which a random item was probed¹⁶. Furthermore, when participants report the confidence of their estimate, their ratings have a wide distribution and correlate strongly with performance, consistent with variable precision²⁰; indeed, the variable-precision model fits these data well. However, further work is needed to determine the origins of variability in precision, a basis for the particular distributions over precision that fit human data, and how variable precision relates to neural coding of working memory.

Binding errors

Although delayed estimation (Fig. 1) provides advantages over classification tasks such as change detection, the error distributions obtained using delayed estimation are not determined solely by memory quality for the reported feature. This is because observers are required to report a feature of just one of the objects in working memory, uniquely identified by its value on some secondary feature dimension (Fig. 1a,d). In multiple-item arrays, observers must not only hold in memory the features to be reported, but also the features that will identify the relevant object and, crucially, the ‘binding’ information that pairs the two features together (Fig. 6). Errors in storing or maintaining these latter classes of information may result in incorrect retrieval of one of the other items in working memory at test. In other words, memory recall might be systematically corrupted by reporting of features belonging to items retained in working memory other than the probed item.

Figure 6.

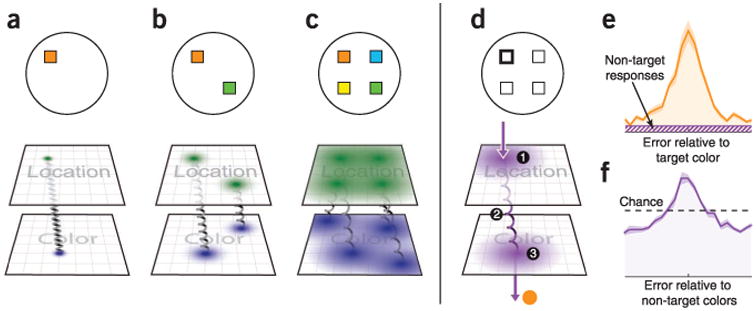
Modes of failure in working memory retrieval. (a) The working memory representation of a colored square can be decomposed into the location of the object in an internal representation of physical space (for example, in posterior parietal cortex; green), the location of the object's color in an internal ‘color space’ (for example, in area V4; blue), and ‘binding’ information that associates the position and color (illustrated here by a spring). (b,c) Increasing working memory load may degrade the quality with which each of the three classes of information is maintained: increasing variability in both color and space representations and making binding information more fragile. (d) To report the color in memory belonging to a given position, the relevant location in internal position space is interrogated, leading via binding information to the corresponding representation in color space. This process can fail in at least three ways. First, variability in position space may cause the wrong position representation to be selected, leading to incorrect report of the color of one of the other objects in memory. Second, binding failure may prevent access to the corresponding color; in this case, a forced response may lead to a random guess from any of the colors in memory. Third, variability in color space may lead to incorrect report of a similar, neighboring color in the internal space. (e) In human data, incorrect reports of non-target objects as a result of the first or second possible sources of failure will produce responses that appear randomly (uniformly) distributed when plotted relative to the target feature value. (f) However, such incorrect reports can be directly observed as a central peak when responses are plotted relative to non-target feature values: if errors were solely a result of variability in the reported feature, this distribution would be flat (data replotted from ref. 9).

In delayed estimation, such non-target or swap errors may be mistaken for random guesses if responses are compared only with the feature value of the probed item⁹. However, in a comparison with all array objects, non-target errors have been directly observed as a clustering of responses around feature values of non-probed items^{9,26,35,49,74}. Such non-target errors grow in prevalence as working memory object load is increased^9,10,26, consistent with the resource principle of a graded decline in representational quality (Fig. 5a–c). Both non-target errors and deviations from normality in target recall (of the kind predicted by variable precision) could account for responses previously attributed to guessing.

There is emerging evidence that failures of binding properties that belong to an object in working memory may have a specific role in forgetting over brief time periods^10,28 and be a crucial component of deficits associated with old age, dementia and medial temporal lobe lesions^28,75–78. Although the principles of neural coding of basic visual features are well established, current neural models of binding remain largely hypothetical. Investigation of the factors that determine binding failure might help constrain neural mechanisms of object representation in working memory.

Computing with working memories: probabilistic inference in change detection

The models described thus far are all concerned with encoding and maintenance: how sensory stimuli are internally represented during a delay period. In many natural and experimental situations, however, working memories are subsequently retrieved and used. For example, in change detection, the memory of a first display is compared with a second one to determine whether a change occurred (Fig. 7a). Because of encoding noise, change detection decisions must be made without exact knowledge of the stimuli in the first display and are therefore a form of inference. In the classic slot model, inference is ignored and decrease of performance with increasing set size is attributed to a limited number of items being held in working memory^5,79. This approach is typically justified by stating that the changes used in the experiments are large. However, how large a change is perceptually depends on the noise level: even seemingly large changes will be difficult to detect when precision is low. In fact, performance in detecting a change between supposedly highly distinct colors strongly depends on the specific colors²³.

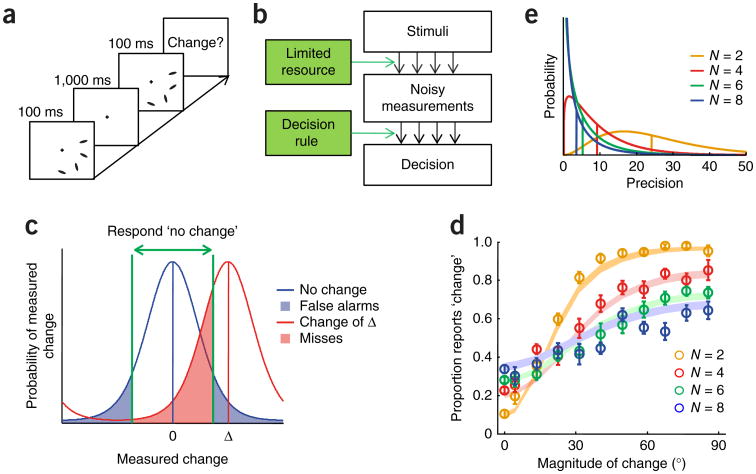
Figure 7.

Changing concepts of change detection. (a) Trial procedure in an orientation change detection task¹³. In contrast with previous studies, the magnitude of the change was varied on a continuum, producing a richer data set. (b) Resource model for change detection. Stimuli in both displays are internally measured in a noisy manner, and an observer applies a decision rule to these measurements to reach a judgment. To maximize accuracy, the decision rule should be based on probabilistic inference. (c) Probabilistic inference in change detection at set size 1 in a resource model, for a circular stimulus variable. The change measured by the observer follows a bell-shaped distribution centered at the true magnitude of change. The observer applies a criterion (green) to decide whether to report a change. At small magnitudes of change, D, the miss rate (red shading) might exceed 50%. Both the width of the distribution and the value of the criterion will depend on noise level and thus on set size. At higher N, the measured changes at different locations are combined nonlinearly before a criterion is applied. (d) Proportion of ‘change’ reports as a function of the magnitude of change, for each set size. Circles and error bars represent data and shaded areas represent variable-precision model with probabilistic inference. In traditional change detection studies, magnitude of change is not varied systematically and these psychometric curves cannot be plotted. (e) Probability distributions over precision in the variable-precision model, as estimated from one subject in a change detection experiment. In the equal-resource model (Fig. 2b), these distributions would be infinitely sharp. All panels except for c are adapted from ref. 13.

Resource models attribute the majority, if not all, of change detection errors to the consequences of noise (Fig. 7b). This idea has been formalized in signal detection theory and Bayesian models of change detection^8,13,25,80, change discrimination^11,60 and change localization^15,23. Bayesian models are signal detection theory models in which observers make the best possible decision based on the noisy evidence on each trial. These models, which are computationally very similar to models of non-memory tasks such as visual search^81,82, account for many observations that are inconsistent with the slot model.

First, in change detection, false alarm rate increases with set size^8,13. Although the slot model predicts no relationship, resource models do: noise causes the internal representation of an individual item to differ between the two displays, even if no physical change occurred (Fig. 7c), and more so when precision is lower. Furthermore, resource models explain the dependence of working memory capacity estimates on stimulus category¹², and the higher difficulty of within-category compared to between-category change detection⁸³: the signal-to-noise ratio will depend on the perceptual space associated with a category and is expected to be lower within a category than between categories. Finally, receiver operating characteristics obtained using a confidence rating procedure follow the predictions of continuous-resource models across a range of set sizes and numbers of changing items⁸.

Surprisingly, researchers have only recently started to systematically vary the magnitude of change in multiple-item change detection^13,25,80 and change localization¹⁵. Manipulating the magnitude of change in addition to set size produces a much richer data set, consisting of a full psychometric curve at each set size, rather than a single hit rate and a single false-alarm rate. The psychometric curves show a gradual increase of performance with magnitude of change (Fig. 7d). This is consistent with resource models, which predict that performance increases continuously with signal-to-noise ratio. When these change detection and change localization data were analyzed using the classic slot model, estimates of K were consistent with earlier studies, but the full psychometric curves revealed that the slot model was inadequate¹³. Instead, a variable-precision model augmented with a Bayesian decision rule provided an accurate account of these data¹³ (Fig. 7d,e). In contrast, a different study concluded that receiver- operating characteristics in a change detection task are consistent with a slot model⁸⁴, but neither variable precision nor a Bayesian decision rule were considered in this work.

A change detection study in which stimulus reliability was unpredictably varied on a trial-to-trial and item-to-item basis found that observers possess knowledge of these variations and take them into account near-optimally during the decision stage⁸⁰. This raises the possibility that not only feature information, but also the corresponding precision (or certainty level), gets stored in working memory on every trial.

Context and ensemble effects

Probabilistic inference may also be involved in delayed estimation. Further computation could consist of combining the sensory measurement at the probed location with summary statistics of the memory display. There is evidence that this happens: for example, a circle is remembered as being slightly bigger than its true size when other circles of the same color were bigger⁸⁵. This illustrates a broader phenomenon, namely that the recalled value of a stimulus might be influenced by the features and positions of other items in the display. A shortcoming of all of the working memory models discussed thus far is that they assume that all items are encoded independently. A recent focus has been on the effect of context on how well we remember^72,85,86. One proposal is that observers store summary statistics, or the ‘gist’, of a scene, such as how correlated the colors of neighboring elements tend to be, in addition to individual items⁷². If working memory resources can be flexibly deployed, stimuli that fit the gist could be safely stored with lower precision, reserving high-precision memory for informative outliers.

Open questions

Taken together, behavioral evidence from multiple tasks supports a continuous-resource account of human working memory and does not support the notion that it is limited by a fixed number of slots that can hold items. However, resources may not be infinitely divisible, and even if they are, outside of laboratory experiments there will always be variations in the salience or importance of environment stimuli that make even allocation over large numbers of objects undesirable. Furthermore, if the quality of item representations in working memory is limited by noise, in practical terms there might be limits to how well a limited working memory resource can be allocated, or thinly spread, over a very large number of items. One direction of future research could be to examine the optimal distribution of resources in situations in which items have unequal probabilities of being tested or are rewarded differentially.

Another direction would be to combine ingredients from existing models in new ways, such as a continuous-resource model with a maximum number of items that can be stored or models in which the number of items stored varies across trials^87,88. However, such models should ideally be informed by biological plausibility and neural data. A recent paper, comparing 32 models in a three-factor space, found that the most successful models incorporated both continuous, variable precision and spatial binding errors, with additional evidence for variability in the number of items stored⁷⁰.

In the slots framework, a long-running debate askes whether slots hold individual features or entire objects^5,48,89,90. In resource models, this question has to be rephrased: do different feature dimensions (for example, colors and orientations) compete for the same resource pool? Present evidence indicates that recall variability depends primarily on the number of competing features in each dimension and that errors arise independently for different features of the same object^{49,74,91–93}.

Generalizations of resource models to more real-world situations remain underexplored. Alphanumeric characters, shapes and line drawings have all been used in previous working memory experiments. In principle, resource models can also be applied to such stimuli. However, the space in which these complex objects are perceptually represented, and how noise corrupts measurements in this space, is not as well understood as for basic visual features. In addition, each such stimulus is part of a large, high-level category of objects, which might affect encoding. Resource models might have an advantage over slot models when dealing with natural or crowded scenes. An ‘item’ is often relatively easy to define in laboratory experiments, but this is not necessarily the case in real scenes. In an image of a bike, for example, is the entire bike the item, or are its wheels or its spokes items? Slot models cannot avoid this question, as the definition of the item determines what goes into a slot. In resource models, resource is easily conceptualized as being allocated to groups of features or spatial locations, rather than to items. However, it remains to be seen how well behavioral data from natural scenes can be described by resource models.

Continuous-resource models might also be extendable beyond visual working memory, to visual long-term memory⁹⁴, other sensory domains⁹⁵ or other multiple-object tasks. Multiple-object tracking, for example, is often considered to be limited by a four-item limit, but this conclusion is being challenged^60,96,97. A similar reexamination may be necessary for subitizing limits⁹⁸. Finally, resource model approaches have now begun to be applied to a range of issues in neuroscience, such as working memory development⁹⁹, aging^77,100 and pathology⁷⁸, where changes in memory quality may have a vital and previously overlooked role.

Recent work that has explored decoding of working memories from neural activity^51–55 opens the door to directly test, at a neural level, the predictions that the various models make for the dependence of precision on set size. Although it is challenging to probe the contents of working memory of all items in a display simultaneously in behavioral experiments, this might be possible when decoding neural signals, thereby providing more power to distinguish between competing models. Moreover, neural data offers the opportunity to study in detail the modulation of working memory when attention is directed to a subset of stored items.

Conclusions

Recent years have seen a resurgence of interest in the nature and limits of short-term storage in the brain, driven by methodological advances in measuring and interpreting recall errors, as well as improved techniques for probing neural representations of memory. In this review, we have presented some of the growing body of evidence from behavior and neurophysiology that suggest that considering only the quantity of representations and ignoring their quality provides an incomplete description of working memory.

An important consequence is that the common practice of characterizing memory ability using a capacity estimate K is increasingly difficult to sustain. Although many researchers use K as a convenient summary statistic, it is important to realize that such an approach is not model free: using K implies committing to a particular slot model^5,6 that has been superseded by both resource models^11,15 and newer slot models¹⁹. A model-agnostic approach would be to simply report the standard deviation of recall errors as a function of set size (Fig. 5) and compare this entire function, for example, between two subject populations. An even better approach would be to fit both slot and resource models, compare their goodness of fit and report the parameters of the best-fitting model.

Clearly, the concept of a limited memory resource has become central to present debates, providing a consistent and intuitive account for both the decline in precision associated with increasing working memory load and the precision gains (and costs) observed for stimuli of differing salience. However, many details in this framework continue to be debated, particularly the extent to which resources are divisible and the degree to which different features tap independent resource pools. Regardless of theoretical position on these issues, the growing sophistication of behavioral analyses combined with an expansion in the range of neurophysiological approaches can only lead to a deeper understanding of how and why individuals remember and forget.