Factorial Comparison of Working Memory Models

Abstract

Three questions have been prominent in the study of visual working memory limitations: (a) What is the nature of mnemonic precision (e.g., quantized or continuous)? (b) How many items are remembered? (c) To what extent do spatial binding errors account for working memory failures? Modeling studies have typically focused on comparing possible answers to a single one of these questions, even though the result of such a comparison might depend on the assumed answers to both others. Here, we consider every possible combination of previously proposed answers to the individual questions. Each model is then a point in a 3-factor model space containing a total of 32 models, of which only 6 have been tested previously. We compare all models on data from 10 delayed-estimation experiments from 6 laboratories (for a total of 164 subjects and 131,452 trials). Consistently across experiments, we find that (a) mnemonic precision is not quantized but continuous and not equal but variable across items and trials; (b) the number of remembered items is likely to be variable across trials, with a mean of 6.4 in the best model (median across subjects); (c) spatial binding errors occur but explain only a small fraction of responses (16.5% at set size 8 in the best model). We find strong evidence against all 6 documented models. Our results demonstrate the value of factorial model comparison in working memory.

The British statistician Ronald Fisher wrote almost a century ago, “No aphorism is more frequently repeated in connection with field trials, than that we must ask Nature few questions, or, ideally, one question, at a time. The writer is convinced that this view is wholly mistaken” (Fisher, 1926, p. 511). He urged the use of factorial designs, an advice that has been fruitfully heeded since. Less widespread but equally useful is the notion of factorially testing models (for recent examples in neuroscience and psychology, see Acerbi, Wolpert, & Vijayakumar, 2012; Daunizeau, Preuschoff, Friston, & Stephan, 2011; Pinto, Doukhan, DiCarlo, & Cox, 2009). Models often consist of distinct concepts that can be mixed and matched in many ways. Comparing all models obtained from this mixing and matching could be called factorial model comparison. The aim of such a comparison is twofold: First, rather than focusing on specific models, it aims to identify which values (levels) of each factor make a model successful; second, in the spirit of Popper (1959), it aims to rule out large numbers of poorly fitting models. Here, we conduct for the first time a factorial comparison of models of working memory limitations and achieve both aims.

Five theoretical ideas have been prominent in the study of visual working memory limitations. The first and oldest idea is that there is an upper limit to the number of items that can be remembered (Cowan, 2001; Miller, 1956; Pashler, 1988). The second idea is that memory limitations can be explained as a consequence of memory noise increasing with set size or, in other words, mnemonic precision decreasing with set size (Palmer, 1990; Wilken & Ma, 2004). Such models are sometimes called continuous-resource or distributed-resource models, in which some continuous sort of memory resource is related in a one-to-one manner to precision and is divided across remembered items. In this article, we mostly use the term precision, not resource, because it is more concrete. The third idea is that mnemonic precision comes in a small number of stackable quanta (Zhang & Luck, 2008). The fourth idea is that mnemonic precision varies across trials and items even when the number of items in a display is kept fixed (Van den Berg, Shin, Chou, George, & Ma, 2012). The fifth idea is that features are sometimes remembered at the wrong locations (Wheeler & Treisman, 2002) and that such misbindings account for a large part of (near-) guessing behavior in working memory tasks (Bays, Catalao, & Husain, 2009). These five ideas do not directly contradict each other and, in fact, can be combined in many ways. For example, even if mnemonic precision is a non-quantized and variable quantity, only a fixed number of items might be remembered. Even if mnemonic precision is quantized, the number of quanta could vary from trial to trial.

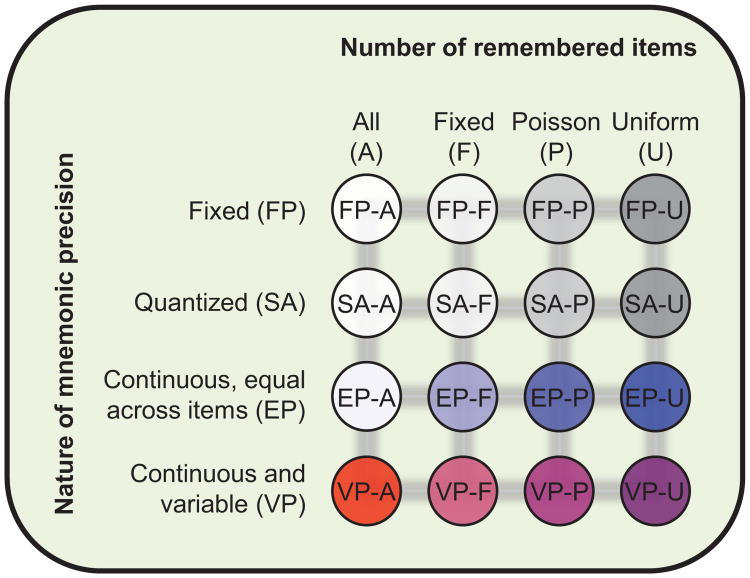
All possible combinations of these model ingredients can be organized in a three-factor (three-dimensional) model space (see Figure 1). One factor is the nature of mnemonic precision, the second the number of remembered items, and the third (not shown in Figure 1) whether incorrect bindings of features to locations occur. As we discuss below, combining previously proposed levels of these three factors produces a total 32 models. Previous studies considered either only a single model or a few of these models at a time (e.g., Anderson & Awh, 2012; Anderson, Vogel, & Awh, 2011; Bays et al., 2009; Bays & Husain, 2008; Fougnie, Suchow, & Alvarez, 2012a; Keshvari, Van den Berg, & Ma, 2013; Rouder et al., 2008; Sims, Jacobs, & Knill, 2012; Van den Berg et al., 2012; Wilken & Ma, 2004; Zhang & Luck, 2008).

Figure 1.

Schematic overview of models of working memory, obtained by factorially combining current theoretical ideas.

Testing small subsets of models is an inefficient approach: For example, if, in each article, two models were compared and the most efficient ranking algorithm were used, then, on average, log₂(32!) ≈ 118 articles would be needed to rank all of the models. A second, more serious problem of comparing small subsets of models is that it easily leads to generalizations that may prove unjustified when considering a more complete set of models. For example, on the basis of comparisons between one particular noise-based model and one particular item-limit model, Wilken and Ma (2004) and Bays and Husain (2008) concluded that working memory precision is continuous and there is no upper limit on the number of items that can be remembered. Using the same experimental paradigm (delayed estimation) but a different subset of models, Zhang and Luck (2008) drew the opposite conclusion, namely, that working memory precision is quantized and no more than about three items can be remembered. They wrote, “This result rules out the entire class of working memory models in which all items are stored but with a resolution or noise level that depends on the number of items in memory” (italics added; Zhang & Luck, 2008, p. 233). These and other studies have all drawn conclusions about entire classes of models (rows and columns in Figure 1) based on comparing individual members of those classes (circles in Figure 1).

Here, we test the full set of 32 models, as well as 118 variants of these models, on 10 data sets from six laboratories. We propose to compare model families instead of only individual models to answer the three questions posed above. Our results provide strong evidence that memory precision is continuous and variable and suggest that the number of remembered items is variable from trial to trial and substantially higher than previously estimated item limits. In addition, although we find evidence for spatial binding errors in working memory, they account for only a small proportion of responses. Finally, the model ranking that we find is not only highly consistent across experiments but also with previous literature. Hence, conflicts in previous literature are only apparent and are resolved when a more complete set of models are tested. Our results highlight the need to factorially test models.

Experiment

Task

In recent years, a popular paradigm for studying the limitations of working memory has been the Wilken and Ma (2004) delayed-estimation paradigm, a multiple-item working memory task that was inspired by a single-item attention task first used by Prinzmetal, Amiri, Allen, and Edwards (1998). In this task, the observer is shown a display containing one or multiple items, followed by a delay, followed by a response screen on which the observer estimates the remembered feature value at a marked location in a near-continuous response space (see Figure 2). The near-continuous response stands in contrast to change detection, where the observer's decision is binary.

Figure 2.

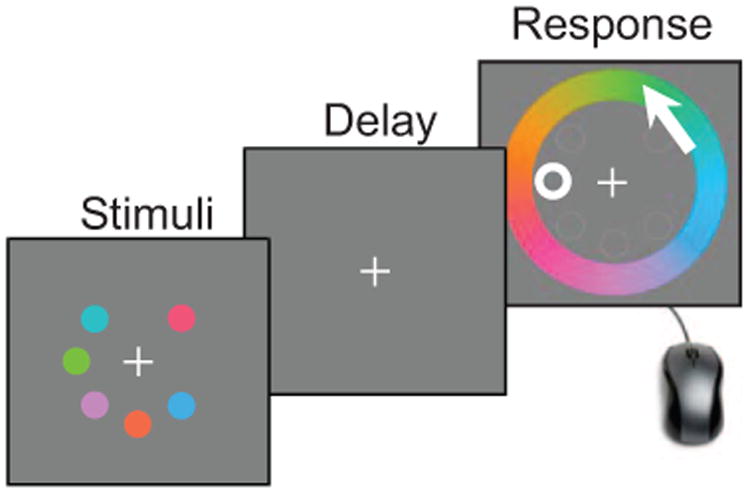
Example trial procedure in delayed estimation of color. Subjects view a set of items and, after a brief delay, they are asked to report the value of one item, for instance, by clicking on a color wheel.

Data Sets

We gathered 10 previously published delayed-estimation data sets collected in six different laboratories, made available by the respective authors (Anderson & Awh, 2012; Anderson et al., 2011; Bays et al., 2009; Rademaker, Tredway, & Tong, 2012; Van den Berg et al., 2012; Wilken & Ma, 2004; Zhang & Luck, 2008; see Table 1). Together, these data sets comprise 164 subjects and 131,452 trials and cover a range of differences in experimental details. The data are available online as a benchmark data set (http://www.cns.nyu.edu/malab/dataandcode.html).

Table 1. Details of the Experiments Whose Data Are Reanalyzed Here.

ID	Article	Location	Feature	Set sizes	Eccentricity (degrees)	Stimulus time (ms)	Delay (ms)	Subjects
E1	Wilken & Ma, 2004	California Institute of Technology	Color (wheel)	1, 2, 4, 8	7.2	100	1,500	15
E2	Zhang & Luck, 2008	University of California, Davis	Color (wheel)	1, 2, 3, 6	4.5	100	900	8
E3	Bays et al., 2009	University College London	Color (wheel)	1, 2, 4, 6	4.5	100, 500, 2,000	900	12
E4	Anderson et al., 2011	University of Oregon	Orientation (360°)	1–4, 6, 8	Variable	200	1,000	45
E5	Anderson & Awh, 2012	University of Oregon	Orientation (180°)	1–4, 6, 8	Variable	200	1,000	23
E6	Anderson & Awh, 2012	University of Oregon	Orientation (360°)	1–4, 6, 8	Variable	200	1,000	23
E7	Van den Berg et al., 2012	Baylor College of Medicine	Color (scrolling)	1–8	4.5	110	1,000	13
E8	Van den Berg et al., 2012	Baylor College of Medicine	Color (wheel)	1–8	4.5	110	1,000	13
E9	Van den Berg et al., 2012	Baylor College of Medicine	Orientation (180°)	2, 4, 6, 8	8.2	110	1,000	6
E10	Rademaker et al., 2012	Vanderbilt University	Orientation (180°)	3, 6	4.0	200	3,000	6

Theoretical Framework

Our model space is spanned by the three model factors mentioned above: the probability distribution of mnemonic precision, the probability distribution of the number of remembered items, and the presence of spatial binding errors. For the distribution of mnemonic precision, we consider four modeling choices or factor levels:

• Level 1: Precision is fixed (fixed precision or FP). This model was originally proposed in the context of the change detection paradigm and it was assumed that mnemonic noise is negligibly low, thus precision was not only assumed fixed but also near infinite (Luck & Vogel, 1997; Pashler, 1988). Because that seems to be an unrealistic assumption in the context of delayed estimation experiments, here we test a more general version of the model, in which precision can take any value but is still fixed across items, trials, and set sizes. Thus, for each subject, a remembered item can only have one possible value of precision.

• Level 2: Precision is quantized in units of a fixed size (slots plus averaging or SA; Zhang & Luck, 2008). Zhang and Luck (2008) use the analogy of standardized bottles of juice, each of which stands for a certain fixed amount of precision with which an item is remembered. For example, if five precision quanta (slots) are available, then among eight items, five will each receive one quantum and three items will be remembered with zero precision, but among three items, two of them will receive two quanta each and one item will receive one quantum. According to this model, precision cannot take intermediate values, for example, corresponding to 1.7 quanta.

• Level 3: Precision is a graded (continuous) quantity and, at a given set size, equal across items and trials (equal precision or EP; Palmer, 1990; Wilken & Ma, 2004). In the realm of attention, this model was first conceived by Shaw (Shaw, 1980), who called it the sample-size model. Precision can depend on set size, typically decreasing with increasing set size. If precision does not depend on set size, then this modeling choice reduces to the FP modeling choice above.

• Level 4: Precision is a continuous quantity and, even at a given set size, can vary randomly across items and trials (variable precision or VP; Fougnie et al., 2012a; Van den Berg, et al., 2012). This model was developed to address shortcomings of the EP model. On any given trial, different items will be remembered with different precision. The mean precision with which an item is remembered will, in general, depend on set size. This is a doubly stochastic model: Precision determines the distribution of the stimulus estimate and is itself also a random variable.

In the EP and VP models, we assume that precision (for VP, trial-averaged precision) depends on set size in a power-law fashion (Bays & Husain, 2008; Elmore et al., 2011; Keshvari et al., 2013; Mazyar, Van den Berg, & Ma, 2012; Van den Berg et al., 2012). Precision determines the width of the distribution of noisy stimulus estimates. In practice, the power law on precision means that the estimates become increasingly noisy as set size increases.

The second factor is the number of remembered items, which we denote by K. The actual number of remembered items on a given trial can never exceed the total number of items on that trial, N, and is therefore equal to the minimum of K and N. Thus, K is, strictly speaking, the number of remembered items only when it does not exceed the number of presented items. For convenience, we usually simply refer to K as the number of remembered items. For the second model factor, we consider the following levels:

• Level 1: All items are remembered (K = ∞; Bays & Husain, 2008; Fougnie et al., 2012a; Palmer, 1990; Van den Berg, et al., 2012; Wilken & Ma, 2004).

• Level 2: The number of remembered items is fixed for a given subject in a given experiment (K is an integer constant; Cowan, 2001; Luck & Vogel, 1997; Miller, 1956; Pashler, 1988; Rouder et al., 2008).

• Level 3: K varies according to a Poisson distribution with mean K_mean.

• Level 4: K varies across trials according to a uniform distribution between 0 and K_max.

The latter two possibilities were inspired by recent suggestions that K varies across trials (Dyrholm, Kyllingsbaek, Espeseth, & Bundesen, 2011; Sims et al., 2012); we return to the exact proposal by Sims et al. later. We label these levels -A, -F, -P, and -U, respectively; for example, SA-P refers to the slots-plus-averaging model with a Poisson-distributed number of remembered items. Note that in all SA models, the number of remembered items is equal to the number of quanta.

The third factor is the presence or absence of spatial binding errors. In the models with spatial binding errors, subjects will sometimes report a nontarget item. We assume that the probability of a nontarget report is proportional to the number of nontarget items. Assuming this proportionality keeps the number of free parameters low and seems reasonable on the basis of the results of Bays et al. (2009). The models with nontarget reports are labeled -NT. For example, SA-P-NT is the slots-plus-averaging model with a Poisson-distributed K and nontarget reports.

In all models, we assume that the observer's report is not identical to the stimulus memory but has been corrupted by response noise.

Considering all combinations, we obtain a model space that contains 4 × 4 × 2 = 32 models (see Figure 1). The six models that are currently documented in the literature are FP-F (Pashler, 1988), EP-A (sample-size model; Palmer, 1990), EP-A-NT (Bays et al., 2009), EP-F (slots plus resources; Anderson et al., 2011; Zhang & Luck, 2008), SA-F (slots plus averaging; Zhang & Luck, 2008), and VP-A (variable precision; Fougnie et al., 2012a; Van den Berg, et al., 2012).

The abbreviations used are listed in Table 2. We now describe the mathematical details of all models.

Table 2. Abbreviations Used to Label the Models.

Abbreviation	Meaning
FP-	Fixed precision: The precision of a remembered item is fixed across items, trials, and set sizes
SA-	Slots plus averaging: The precision of a remembered item is provided by discrete slots and is thus quantized
EP-	Equal precision: The precision of a remembered item is equal across items and trials (but depends in a power law fashion on set size)
VP-	Variable precision: The precision of a remembered item varies across items and trials (mean precision depends in a power law fashion on set size)
-A-	All items are remembered
-F-	There is a fixed number of remembered items
-P-	The number of remembered items varies across trials and follows a Poisson distribution
-U-	The number of remembered items varies across trials and follows a uniform distribution
-NT	Nontarget reports are present; the proportion of trials in which the subject reports a nontarget item is proportional to set size minus 1

Estimate and Response Distributions

We consider tasks in which the observer is asked to estimate a feature s of a target item. In all experiments that we examine, the feature (orientation or color on a color wheel) and the observer's estimate of the feature have a circular domain. For convenience, we mapped all feature domains to [0,2π) radians in all equations. In all models, we assume, following Wilken and Ma (2004), that the observer's estimate of the target, ŝ, follows a Von Mises distribution (a circular version of the normal distribution), centered on the target value, s, and with a concentration parameter, κ:

$$p(\widehat{s}|s)=\frac{1}{2\mathrm{\pi }{I}_0(\mathrm{\kappa })}{e}^{\mathrm{\kappa }cos(\widehat{s}-s)}\equiv \text{VM}(\widehat{s};s,\mathrm{\kappa }),$$ (1)

where I₀ is the modified Bessel function of the first kind of order 0. We further assume in all models that the report r of this estimate is corrupted by Von Mises–distributed response noise,

$$p(r|\widehat{s})=\frac{1}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_{\mathrm{r}})}{e}^{{\mathrm{\kappa }}_{r}cos(r-\widehat{s})}\equiv \text{VM}(r;\widehat{s},{\mathrm{\kappa }}_{\mathrm{r}}).$$

Relationship Between Mnemonic Precision and Stimulus Noise

To mathematically specify mnemonic precision, we need a measure that can be computed for a circular domain; thus, the inverse of the usual variance is inadequate. Ideally, this measure should have a clear relationship with some form of neural resource. Therefore, we follow earlier work (Van den Berg et al., 2012) and express mnemonic precision in terms of Fisher information, denoted J. Fisher information is a general measure of how much information an observable random variable (here, ŝ) carries about an unknown other variable (here, s). Moreover, it reduces to inverse variance in the case of a normally distributed estimate. Fisher information is proportional to the amplitude of activity in a neural population encoding a sensory stimulus (Paradiso, 1988; Seung & Sompolinsky, 1993). Hence, J is a sensible measure of memory precision. For a Von Mises distribution (see Equation 1), J is directly related to the concentration parameter, κ, through

$$J=\mathrm{\kappa }\frac{I_1(\mathrm{\kappa })}{I_0(\mathrm{\kappa })},$$ (2)

where I₁ is the modified Bessel function of the first kind of order 1 (Van den Berg et al., 2012). We denote the inverse relationship by κ = Φ(J). We consistently use the definition of J and Equation 2 in all models.

FP Models With Fixed K

The classic model of working memory has been that memory accuracy is very high and errors arise only because a limited number of slots, K, are available to store items (Cowan, 2001; Miller, 1956; Pashler, 1988). This model was originally proposed in the context of the change detection paradigm, in which it was assumed that the memory of a stored item is essentially perfect (very high precision). Because this appears to be unrealistic in the context of delayed estimation, we give the model a bit more freedom by letting precision be a free parameter. Precision in this model is fixed across items, trials, and set sizes. Therefore, we call it the fixed-precision model (denoted FP). The probability that the target is remembered in an N-item display would equal K/N if K < N and 1 otherwise. When K ≥ N, all items are remembered and the target estimate is a Von Mises distribution,

$$p(\widehat{s}|s)=\text{VM}(r;s,\mathrm{\kappa }),$$

where parameter κ controls the precision with which items are remembered. When K < N, the target estimate follows a mixture distribution consisting of a Von Mises distribution (representing trials on which the target is remembered) and a uniform distribution (representing trials on which the target is not remembered),

$$p(\widehat{s}|s)=\frac{K}{N}\text{VM}(\widehat{s};s,\mathrm{\kappa })+(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }}.$$

Including response noise, the response distributions becomes a convolution of two Von Mises distributions and evaluates to

$$p(r|s)=\frac{K}{N}\frac{I_0\left(\sqrt{{\mathrm{\kappa }}^2+{\mathrm{\kappa }}_{\mathrm{r}}^2+2\mathrm{\kappa }{\mathrm{\kappa }}_{\mathrm{r}}cos(r-s)}\right)}{2\mathrm{\pi }{I}_0(\mathrm{\kappa })I_0({\mathrm{\kappa }}_{\mathrm{r}})}+(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }},$$ (3)

where parameter κ_r controls the amount of response noise.¹

Note that K can only take integer values. This is because we model individual-trial responses, and on an individual trial, the number of remembered items can only be an integer value. When averaging K across subjects or trials, it may take noninteger values. Also note that K is independent of set size in all models, except for model variants we consider in the section Equal and Variable-Precision Models With a Constant Probability of Remembering an Item.

SA Models With Fixed K

In the SA models, working memory consists of a certain number of slots, each of which providing a finite amount of precision that we refer to as a precision quantum. When K ≤ N, K items are remembered with a single quantum of precision and the other items are not remembered at all. Hence, the target estimate follows a mixture of a Von Mises and a uniform distribution,

$$p(\widehat{s}|s)=\frac{K}{N}\text{VM}(\widehat{s};s,{\mathrm{\kappa }}_1)+(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }},$$

where κ₁ is the concentration parameter of the noise distribution corresponding to the precision obtained with a single quantum of precision, which we denote J₁. With response noise, the response distribution is given by

$$p(r|s)=\underset{0}{\overset{2\mathrm{\pi }}{\int }}p(r|\widehat{s})p(\widehat{s}|s)d\widehat{s}=\underset{0}{\overset{2\mathrm{\pi }}{\int }}\text{VM}(r;\widehat{s},{\mathrm{\kappa }}_{\mathrm{r}})(\frac{K}{N}\text{VM}(\widehat{s};s,{\mathrm{\kappa }}_1)+(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }})d\widehat{s}=\frac{K}{N}\frac{I_0\left(\sqrt{{\mathrm{\kappa }}_1^2+{\mathrm{\kappa }}_{\mathrm{r}}^2+2{\mathrm{\kappa }}_1{\mathrm{\kappa }}_{\mathrm{r}}cos(r-s)}\right)}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_1)I_0({\mathrm{\kappa }}_{\mathrm{r}})}+(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }}.$$

When K > N, at least one item will receive more than one quantum of precision. In our main analyses, we assume that quanta are distributed as evenly as possible (a variant in which this is not the case is considered in the subsection Model Variants Under Results). Then, the target is remembered with one of at most two values of precision, J_low or J_high, with corresponding concentration parameters κ_low and κ_high. For example, when N = 3 and K = 4, three items are remembered with one quantum of precision (J_low = J₁) and one item is remembered with two quanta (J_high = 2J₁). Hence, the estimate follows a mixture of two Von Mises distributions:

$$p(\widehat{s}|s)=\frac{KmodN}{N}\frac{1}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_{\text{high}})}{e}^{{\mathrm{\kappa }}_{\text{high}}cos(\widehat{s}-s)}+(1-\frac{KmodN}{N})\frac{1}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_{\text{low}})}{e}^{{\mathrm{\kappa }}_{\text{low}}cos(\widehat{s}-s)}.$$

With response noise, the response distribution for K > N is

$$p(r|s)=\frac{KmodN}{N}\frac{I_0({\mathrm{\kappa }}_{\mathrm{c},\text{high}})}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_{\text{high}})I_0({\mathrm{\kappa }}_{\mathrm{r}})}+(1-\frac{KmodN}{N})\frac{I_0({\mathrm{\kappa }}_{\mathrm{c},\text{low}})}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_{\text{low}})I_0({\mathrm{\kappa }}_{\mathrm{r}})},$$

with

$$\begin{array}{c}{\mathrm{\kappa }}_{\mathrm{c},\text{high}}=\sqrt{{\mathrm{\kappa }}_{\text{high}}^2+{\mathrm{\kappa }}_{\mathrm{r}}^2+2{\mathrm{\kappa }}_{\text{high}}{\mathrm{\kappa }}_{\mathrm{r}}cos(\widehat{s}-s)},\\ {\mathrm{\kappa }}_{\mathrm{c},\text{low}}=\sqrt{{\mathrm{\kappa }}_{\text{low}}^2+{\mathrm{\kappa }}_{\mathrm{r}}^2+2{\mathrm{\kappa }}_{\text{low}}{\mathrm{\kappa }}_{\mathrm{r}}cos(\widehat{s}-s)}.\end{array}$$

EP Models With Fixed K

The main idea behind the EP models is that precision is a graded (continuous) quantity that is equal for all K remembered items. We deliberately do not state that “resource is equally distributed over K items” because resource and precision might not be the same thing (precision will be affected by bottom-up factors such as stimulus contrast). Moreover, this would suggest a set size-independent total, which is unnecessarily restrictive. When all items are always remembered, N can be substituted for K. We assume that the precision per item, denoted J, follows a power-law relationship in N, J = J₁N^α, with J₁ and α as free parameters. When α is negative, a larger set size will cause an item to be remembered with lower precision and the error histogram will be wider. (When fitting the models, we did not constrain α to be negative, but all maximum-likelihood estimates turned out to be negative.) Note that J₁ stands for the precision with which a lone item is remembered, which is different from what we meant by J₁ in the SA models, where it stands for the precision provided by a single slot. When K ≥ N, the response distribution becomes, in a way, similar to the SA model discussed above:

$$p(r|s)=\frac{I_0\left(\sqrt{{\mathrm{\kappa }}^2+{\kappa }_{\mathrm{r}}^2\mathrm{+}2\mathrm{\kappa }{\mathrm{\kappa }}_{\mathrm{r}}cos(r-s)}\right)}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_{\mathrm{r}})I_0(\mathrm{\kappa })},$$

with κ = Φ(J₁N^α). When K < N, the response distribution is again a mixture distribution:

$$p(r|s)=\frac{K}{N}\frac{I_0\left(\sqrt{{\mathrm{\kappa }}^2+{\mathrm{\kappa }}_{\mathrm{r}}^2+2\mathrm{\kappa }{\mathrm{\kappa }}_{\mathrm{r}}cos(r-s)}\right)}{2\mathrm{\pi }{I}_0({\mathrm{\kappa }}_{\mathrm{r}})I_0(\mathrm{\kappa })}+(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }},$$

with κ = Φ(J ₁ K^α).

VP Models With Fixed K

The VP models assume, like the EP models, that mnemonic precision is a continuous variable (instead of quantized, e.g., in the SA model) but also, unlike the EP models, that it varies randomly across items and trials even when set size is kept fixed. This variability is modeled by drawing precision for each item from a gamma distribution with a mean J̄ = J̄₁N^α (when N < K; J̄ = J̄₁K^α otherwise) and a scale parameter τ. This implies that the total precision across items also varies from trial to trial and has no hard upper limit (the sum of gamma-distributed random variables is itself a gamma-distributed random variable). The target estimate has a distribution given by averaging the target estimate distribution for given J, over J:

$$p(\widehat{s}|s;\overline{J},\mathrm{\tau })=(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }}+\frac{K}{N}\int p(\widehat{s}|s;J)p(J|\overline{J};\mathrm{\tau })dJ=(1-\frac{K}{N})\frac{1}{2\mathrm{\pi }}+\frac{K}{N}\int \text{VM}(\widehat{s};s,\mathrm{\Phi }(J))\text{Gamma}(J;\overline{J},\mathrm{\tau })dJ.$$

No analytical expression exists for this integral, and we therefore approximated it using Monte Carlo simulations. Response noise was added in the same way as in the other models.

Models With K = ∞

In the FP and SA model variants with K = ∞ (infinitely many slots), denoted FP-A and SA-A, all items are remembered and their estimates are corrupted by a single source of Von Mises– distributed noise. The EP and VP variants with K = ∞, which we call the EP-A and VP-A models, are equal to the EP and VP models with a fixed K equal to N, for which the response distributions were given above.

Models With a Poisson-Distributed K

Predictions of the FP, SA, EP, and VP models in which K is drawn on each trial from a Poisson distribution with mean K_mean were obtained by first computing predictions of the corresponding models with fixed K and then taking a weighted average. The weight for each value of K was equal to the probability of that K being drawn from a Poisson distribution with a mean K_mean.

Models With a Uniformly Distributed K

Predictions of the FP, SA, EP, and VP models in which K is drawn on each trial from a discrete uniform distribution on [0, K_max] were obtained by averaging predictions of the corresponding models with fixed K, across all values of K between 0 and K_max.

Models With Nontarget Responses

Bays and colleagues have proposed that a large part of (near-) guessing behavior in delayed-estimation tasks can be explained as a result of subjects sometimes reporting an item other than the target, due to spatial binding errors (Bays et al., 2009). They do not specify the functional dependence of the probability of a nontarget report on set size. Here, we assume that the probability of a nontarget response, p_NT, is proportional to the number of nontarget items, N − 1: p_NT = min[γ(N − 1), 1], which seems to be a reasonable approximation to the findings reported by Bays et al. (2009; see their Figures 3e and 3f). Predictions of the models with nontarget responses were computed using the predictions of the models without such responses. If p(r | s) is the response distribution in a model without nontarget responses, then the response distribution of its variant with nontarget responses was computed as

Figure 3.

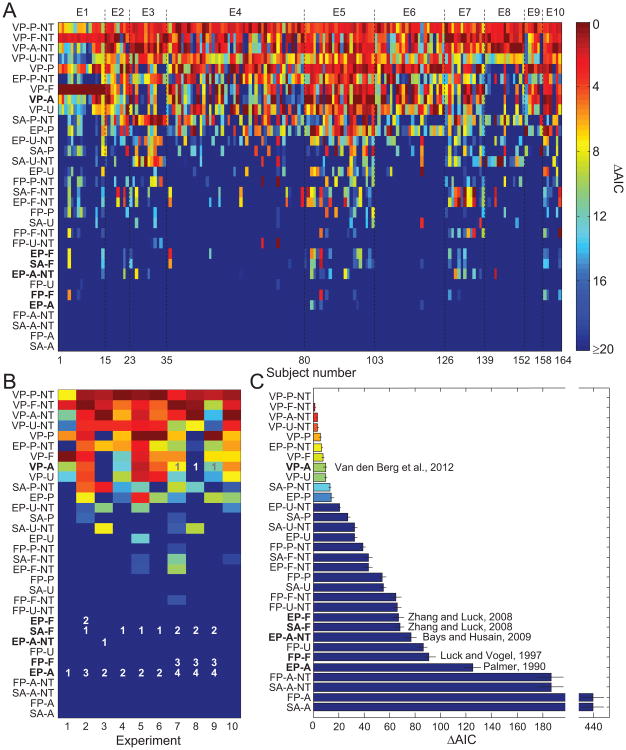
Model comparison between individual models. A. Each column represents a subject, each row a tested model. Cell color indicates a model's Akaike information criterion (AIC) relative to that of the subject's most likely model (a higher value means a worse fit). In all panels, models are sorted by their subject-averaged AIC values and boldface labels indicate previously proposed models. B. AIC values averaged across subjects within an experiment, relative to that of the most likely model. For each experiment, numbers indicate the models that were tested in the original study, ranked by their performance; all rankings are consistent with ours here. C. AIC values minus that of the most likely model, averaged across all subjects. Error bars indicate 1 standard error of the mean. See Table 2 for the model abbreviation key. The articles cited in the figure are the ones in which the respective models were proposed.

$$p_{\text{with nontarget}}(r|\mathbf{s})=(1-p_{\text{NT}})p(r|s_1)+\frac{p_{\text{NT}}}{N-1}\sum _{i=2}^{N}p(r|s_i),$$ (4)

where s₁ is the feature value of the target item and s_2, … s_N are the feature values of the nontarget items. In models in which K items are remembered, Equation 4 could be written out as a sum of four terms, corresponding to the following four scenarios: the target item is reported and was remembered, the target item is reported but was not remembered, a nontarget item is reported and was remembered, and a nontarget item is reported but was not remembered.

Methods

Model Fitting

For each subject and each model, we computed maximum-likelihood estimates of the parameters (see Table A1 in the Appendix) using the following custom-made evolutionary (genetic) algorithm:

1. Draw a population of M = 512 parameter vectors from uniform distributions. Set generation count i to 1.

2. Make a copy of the parameter vectors of the current population and add noise.

3. Compute the fitness (log likelihood) of each parameter vector in the population.

4. If M > 64, decrease M by 2%.

5. Remove all but the M fittest parameter vectors from the current population.

6. Increase i with 1. If i < 256, go back to Step 2. Otherwise, stop.

After this algorithm terminates, the log likelihood of the parameters of the fittest individual in the final population was used as an estimate of the maximum parameter log likelihood.

Because of stochasticity in drawing parameter values and precision values (in the VP models), the output of the optimization method will vary from run to run, even when the subject data are the same. To verify the consistency of the method, we examined how much the estimated value of the maximum log likelihood varied when running the evolutionary algorithm repeatedly on the same data set. For each model, we selected 10 random subjects and ran the evolutionary algorithm 10 times on the data of each of these subjects. We found that the estimates of the maximum log likelihood varied most for the VP-U-NT model, but even for that model, the standard deviation of the estimates was only 0.445 ± 0.080 (mean ± standard error). Averaged across all models, the standard deviation was 0.110 ± 0.028, which turns out to be negligible in comparison with the differences between the models.

Although this indicates that the optimization method is consistent in its output, it is still possible that it is inaccurate, in the sense that it may return biased estimates of the log likelihood. To verify that this was not that case, we also estimated the error in the maximum log likelihood returned by the evolutionary algorithm. We generated 10 synthetic data sets (set sizes 1, 2, 3, 4, 6, and 8; 150 trials per set size) with each FP, SA, and EP model, using maximum-likelihood parameter values from randomly selected subjects. To get an estimate of the true maximum of the likelihood function, we used Matlab's fmin-search routine with initial parameters set to the values that were used to generate the data. This avoided convergence into local minima, as it may be expected that the maximum of the likelihood function lies very close to the starting point. Defining the maximum likelihood returned by fminsearch as the true maximum, we found that the absolute error in the maximum likelihood returned by the evolutionary algorithm was, on average, 0.024 ± 0.006%; the maximum error across all cases was 0.59%. As this error in maximum-likelihood estimates is much smaller than the differences in maximum likelihood between models (as shown below), we consider it negligible. Note that this test could not be done for the VP models, because fminsearch does not converge when the objective function is stochastic. However, because the evolutionary algorithm works the same way for all models, we have no reason to doubt that it also worked well on the VP models.

Model Comparison

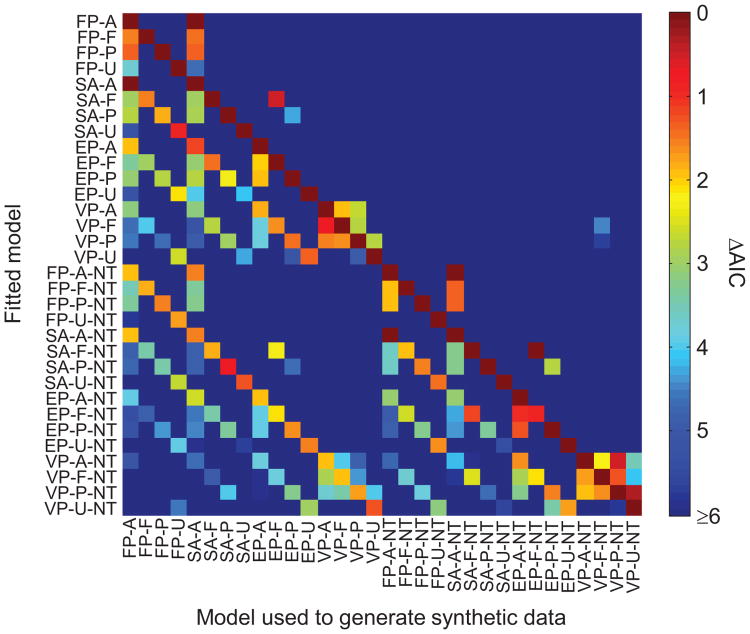
Complex models generally fit data better than simple models but at the cost of having additional parameters. The art of model comparison consists of ranking models in such a way that goodness of fit is properly balanced against model complexity. When penalizing models too harshly for complexity, results will be biased toward simple models; when penalizing too little, results will be biased toward complex models. Two common penalty-based model comparison measures are the Akaike information criterion (AIC; Akaike, 1974) and the Bayesian information criterion (BIC; Schwarz, 1978). We assessed the suitability of these two measures in the context of our 32 models by applying them to synthetic data sets generated by the models (see the Model Recovery Analysis section in the Appendix for details). At the level of individual synthetic data sets, AIC and BIC selected the correct model in about 48.2% and 44.9% of the cases, respectively. At the level of experiments (i.e., results averaged across 16 synthetic data sets), however, AIC selected the correct model in 31 out of 32 cases, whereas BIC made nine mistakes, mostly because it favored models that were simpler than the one that generated a data set. The only selection mistake based on AIC values was that on the EP-F-NT data, the SA-F-NT model was assigned a slightly lower AIC value than the EP-F-NT model itself (ΔAIC = 0.85). On the basis of these model recovery results, we decided to use AIC for all of our model comparisons. We cross-checked the AIC-based results by comparing them with results based on computing Bayes factors and found that these methods gave highly consistent outcomes (see the Appendix).

Summary Statistics

Although AIC values are useful to determine how well a model performs with respect to other models, they do not show how well the model fits the data in an absolute sense. To get an impression of the absolute goodness of fit of the models, we visualized the subject data and model predictions using several summary statistics, as follows. For each subject and each model, we used the maximum-likelihood estimates to generate synthetic data sets, each comprising the same set sizes and number of trials as the corresponding subject data set. We then fitted a mixture of a uniform distribution and a von Mises distribution (Zhang & Luck, 2008) to each subject's data and the corresponding model-generated data at each set size separately,

$$p(r|s)=w_{\text{UVM}}\text{VM}(r;s,{\mathrm{\kappa }}_{\text{UVM}})+(1-w_{\text{UVM}})\frac{1}{2\mathrm{\pi }},$$

where s is the target value. This produced two summary statistics per subject and set size: the mixture proportion of the Von Mises component, denoted w_UVM, and the concentration parameter of the Von Mises component, denoted κ_UVM. We converted the latter to circular variance, CV_UVM, through the relationship

$${\text{CV}}_{\text{UVM}}=1-\frac{I_1({\mathrm{\kappa }}_{\text{UVM}})}{I_0({\mathrm{\kappa }}_{\text{UVM}})}$$

(Mardia & Jupp, 1999). In addition, we computed the residual that remains after subtracting the best fitting uniform–Von Mises mixture from the subject data (Van den Berg et al., 2012).

The estimates of w_UVM and κ_UVM may be biased when the number of data points is low (Anderson & Awh, 2012). To make sure that any possible bias of this sort in the subject data is reproduced in the synthetic data, we set the numbers of trials in the synthetic data sets equal to those in the subject data. Because estimates of w_UVM and κ_UVM thus obtained are noisy as a result of the relatively low number of trials, we generated 10 different synthetic data sets per subject and averaged the estimates of w_UVM and κ_UVM.

One of us has previously argued for examining the correlation between (a) an estimate of the inflection point in a two-piece piecewise linear fit to CV_UVM as a function of set size and (b) an estimate of the probability of remembering an item at a given set size as derived from w_UVM (Anderson & Awh, 2012; Anderson et al., 2011). The presence of a significant correlation was used to argue in favor of a fixed number of remembered items (specifically, the EP-F model). There are three reasons why we do not perform this analysis here. First, we have found that other models (including the VP-A models) also predict significant correlations between these two quantities (Van den Berg & Ma, in press). Second, this correlation is far removed from the data: It is a property of a fit (linear regression) of a parameter (inflection point) obtained from a fit (piecewise linear function) to the set size dependence of a parameter (CSD_UVM) obtained from a fit (uniform–Von Mises mixture) to the data. The value of the correlation, either for model comparison or as a summary statistic, hinges on the validity of the assumptions made in the intermediate fits, and we have found that the uniform–Von Mises mixture fit is not an accurate description of the error histograms (see the Results section). Third, more generally, there is no need to make additional assumptions to derive summary statistics if one's goal is to compare models. By comparing models on the basis of their likelihoods as described above, one incorporates all claims a model makes while staying as close to the raw data as possible.

Results

Comparison of Individual Models

Figure 3A depicts, for each subject, the AIC value of each model relative to the AIC value of the most likely model for that subject (higher values mean worse fits). Most models perform poorly and only a few perform well consistently. To quantify the consistency of model performance across subjects, we ranked, for each subject, the models by AIC and then computed the Spearman rank correlation coefficient between each pair of subjects. The correlation was significant (p < .05) for 99.5% of the 13,336 comparisons, with an average correlation coefficient of 0.78 (SD = 0.14), indicating strong consistency across subjects.

The individual goodness-of-fit values shown in Figure 3A can be summarized in several useful ways. For each experiment, we computed the AIC of each model relative to the best model in that experiment, averaged over all subjects in that experiment (see Figure 3B).² The visual impression is one of high consistency between experiments; indeed, the Spearman rank correlation coefficient between pairs of experiments was significant for all 45 comparisons (p < 10⁻⁵), with a mean of 0.896 (SD = 0.061; see Table 3).

Table 3. Spearman Correlation Coefficients Between Model Rankings Across Experiments.

Model	E1	E2	E3	E4	E5	E6	E7	E8	E9	E10
E1	—	.95	.84	.92	.85	.93	.86	.73	.91	.88
E2		—	.93	.98	.92	.98	.93	.87	.96	.94
E3			—	.94	.80	.90	.86	.95	.86	.85
E4				—	.92	.97	.90	.87	.95	.94
E5					—	.95	.90	.74	.95	.94
E6						—	.89	.81	.96	.93
E7							—	.88	.91	.93
E8								—	.77	.82
E9									—	.92
E10										—

Note. All correlations were significant with p < 10⁻⁵.

Moreover, as the numbers within the figure indicate, with one minor exception, our ranking is consistent with all rankings in previous studies, each of which tested a small subset of the 32 models.³ Somewhat surprisingly, this indicates high consistency rather than conflict among previous studies; the disagreements were only apparent, caused by drawing conclusions from incomplete model comparisons. For example, the findings presented by Zhang and Luck (2008; see E2 in Figure 3) are typically considered to be inconsistent with those presented by, for example, Van den Berg et al. (2012; E7–9 in Figure 3), as these articles draw opposite conclusions. However, Figure 3B shows that their findings are consistent when a more complete model space is considered.

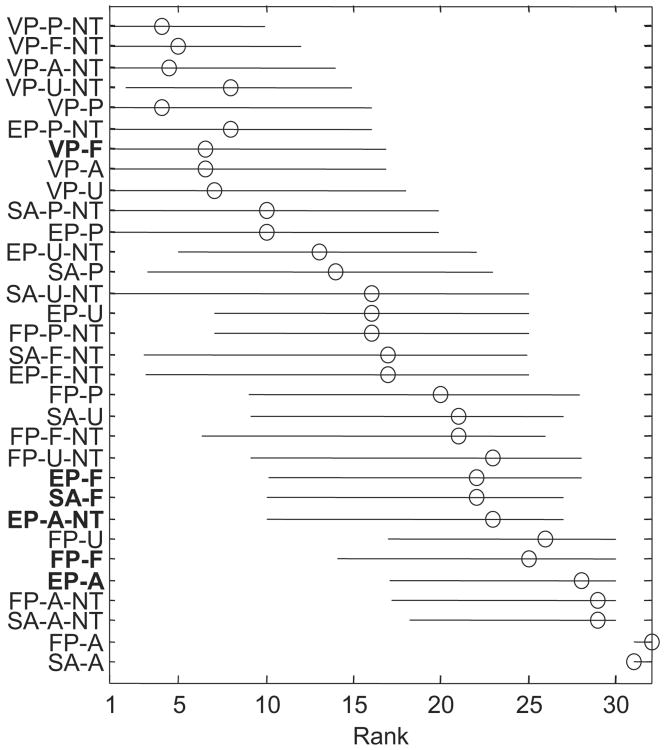
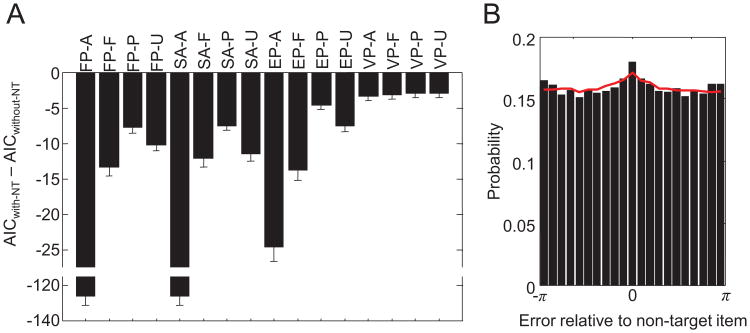
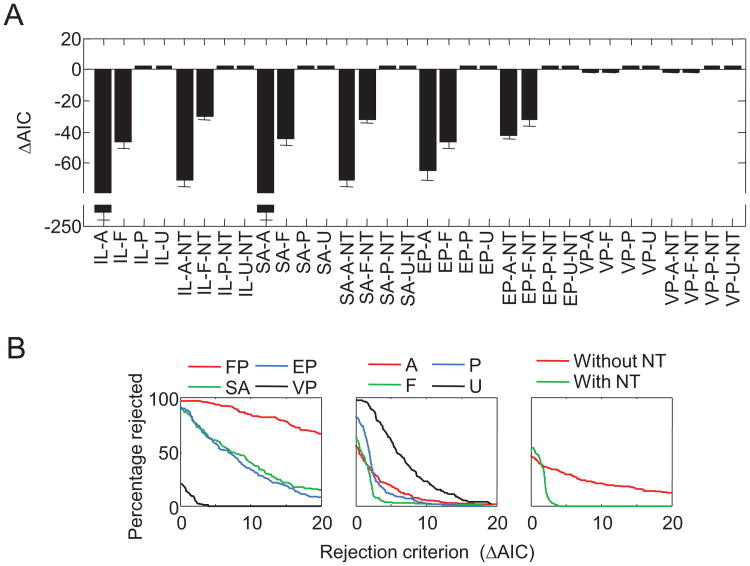
Next, we ranked the models by their AIC values minus the AIC value of the VP-P-NT model, averaged across subjects (see Figure 3C). The top ranks are dominated by members of the VP and NT model families. If we were to use a rejection criterion of 9.2 (which corresponds to a Bayes factor of 1:100 if two models have the same number of free parameters and is considered decisive evidence on Jeffreys's, 1961, scale), all six models that currently exist in the literature (FP-F, SA-F, EP-A, EP-A-NT, EP-F, VP-A) would be rejected, although one (VP-A) lies close to the criterion. The ranking obtained by averaging AIC values is almost identical to the one obtained from averaging the per-subject rankings (see Figure 4).

Figure 4.

Model ranking. Per subject, we ranked models by their AIC values. Shown are the median ranks (circles) and 95% confidence intervals (bars). Models are listed in the same order as in Figure 3C. Boldface labels indicate previously proposed models. See Table 2 for the model abbreviation key.

Comparison of Model Families

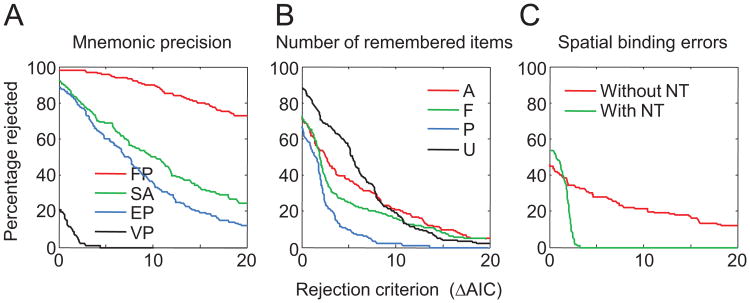
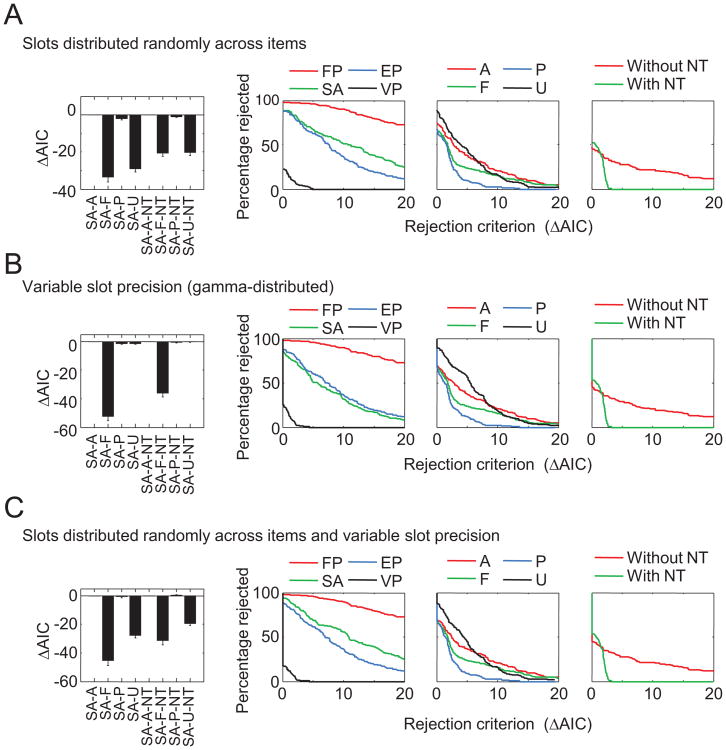
The model ranking in Figure 3C suggests that variable precision and the presence of nontarget responses are important ingredients of successful models. To more directly address the three questions of interest—that is, to determine what levels of each of the three factors describe human working memory best—we define a model family as the subset of all models that share a particular level of a particular factor, regardless of their levels of the other factors. For example, from the first factor, we can construct an FP, an EP, an SA, and a VP model family, each of which has eight members. For each model family, we computed for what percentage of subjects all its members are rejected, as a function of the rejection criterion (the difference in AIC with respect to the winning model for a given subject).

Model Factor 1: Nature of mnemonic precision

Figure 5A shows the results for the first model factor, the nature of mnemonic precision. Regardless of the rejection criterion, the entire family of FP models is rejected in the majority of subjects; for example, even when using a rejection criterion of 20, all FP models would still be rejected in 72.6% of the subjects. The rejection percentages of the SA and EP model families are very similar to each other and lower than those of the FP model family but still substantially higher than those of the VP model family. The percentage of rejections under a rejection criterion of 0 gives the percentage of subjects for whom the winning model belongs to the model family in question. The winning model is a VP model in 79.3% of subjects, while it is an FP, SA, or EP model in only 1.8%, 7.3%, and 11.6% of subjects, respectively. These results provide strong evidence against the notion that memory precision is quantized (Zhang & Luck, 2008) as well as the notion that memory precision is continuous and equal between all items (Palmer, 1990).

Figure 5.

Model comparison between model families (colors), for each model factor (panels). A. Percentage of subjects for whom all models belonging to a certain model family (FP, SA, EP, or VP) are rejected, that is, have an Akaike information criterion (AIC) higher than that of the winning model plus the rejection criterion on the x-axis. For example, when we use a rejection criterion of 10, all models of the FP model family are rejected in about 90% of subjects, all SA and EP models in about 50% of subjects, and all VP models in none of the subjects. B. The same comparison executed for number of remembered items. C. The same comparison executed for number spatial binding errors. See Table 2 for the model abbreviation key.

Model Factor 2: Number of remembered items

Figure 5B shows the rejection percentages for model families in the second model factor, the number of remembered items. The models in which the number of remembered items is uniformly distributed perform worst. There is a clear separation between the other three model families: models with a Poisson-distributed number of remembered items are rejected less often than are models with a fixed number of remembered items, which are rejected less frequently than are models in which all items are remembered. Evidence is strongest for models with a Poisson-distributed number of remembered items, suggesting that the number of remembered items is highly variable. However, this model family does not win as convincingly over the -F and -A model families as the VP model wins over its competitors in Figure 5A, and a better model of the variability in the number of remembered items might be needed. In addition, the mixed result may be due partly to individual differences (e.g., some subjects trying harder to remember all items than others) as well as differences in experimental designs (e.g., models in which all items are remembered are expected to provide better fits when the mean set size in an experiment is low).

Model Factor 3: Presence of nontarget reports

Figure 5C shows that the family of models with nontarget reports outperforms the family without nontarget reports, except when the rejection criterion is very close to zero. It has to be kept in mind that the maximum likelihood of a model with nontarget reports can never be less than that of the equivalent model without nontarget reports. Consequently, a model with nontarget reports can only lose because of the additional AIC penalty of 2 for the extra parameter (because of noise in the maximum likelihood estimates, the difference can sometimes be slightly larger, which is the reason that the percentage of rejections is slightly higher than 0 for rejection criteria greater than 2). If there were no nontarget reports at all, we would expect the rejection percentage of the models with nontarget reports in Figure 5C to be 100% when the rejection criterion is small. Our finding that it is only 54.3% indicates that spatial binding errors do indeed occur but may not be highly prevalent. Additionally, it may be the case that the mixed result reflects individual differences: Some subjects may be more prone than others to making binding errors.

The suggestion that spatial binding errors do occur is supported by our finding that for each of the 4 × 4 models formed by the first two model factors, the variant that includes spatial binding errors outperforms, on average, the variant that does not include them (see Figure 6A). Also, the histogram of errors with respect to nontarget items shows a peak at 0 (see Figure 6B), which is what one would predict in the presence of spatial binding errors. In the model that performed best in the model comparison (VP-P-NT), the percentage of trials on which such errors are made increased with set size, with a slope of 2.35% per item, for a total of 16.5% at set size 8. To assess how well this model reproduces the histogram of errors with respect to nontarget items, we generated synthetic data for each subject using the same set sizes and numbers of trials. The VP-P-NT model fits the peak at 0 reasonably well (see Figure 6B).

Figure 6.

Analysis of nontarget reports. A. Akaike information criterion (AIC) of each model with nontarget reports relative to its variant without nontarget reports. A negative values means that the model with nontarget reports is more likely. Error bars indicate 1 standard error of the mean. B. Histogram of response errors with respect to nontarget items, collapsed across all set sizes and subjects (bars). The bump at the center is evidence for nontarget responses and is fitted reasonably well by the VP-P-NT model (red curve). See Table 2 for the model abbreviation key.

Finally, we examined how strongly the addition of nontarget responses affects conclusions about the other two model factors. We found that the Spearman rank correlation coefficient between the orders of models with and without nontarget responses was .950 ±.006 (mean and standard error across subjects; p < .05 for 163 out of 164 subjects). Hence, although adding nontarget responses to the models improves their fits, they do not substantially affect conclusions about the other two model factors.

Summary Statistics

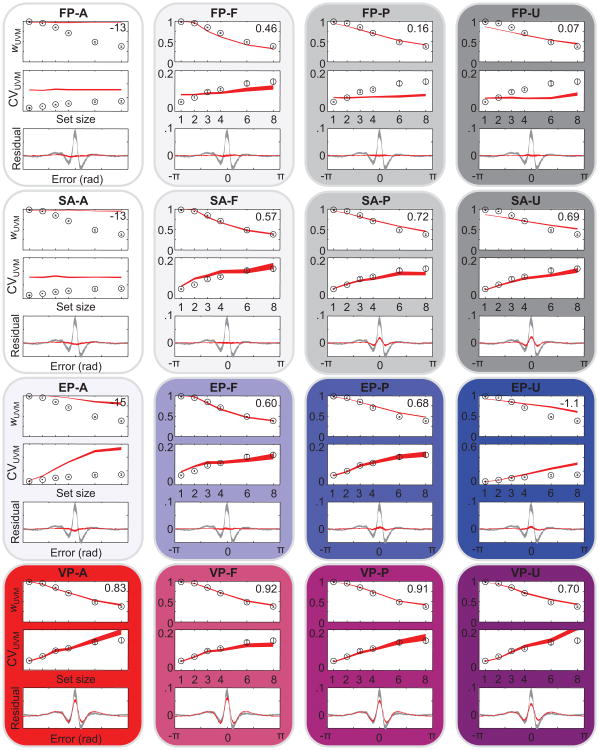
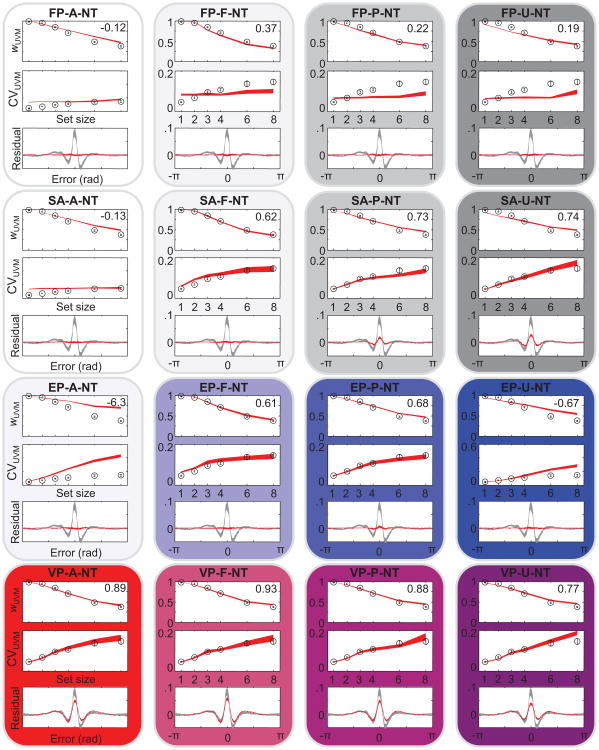
Model comparison based on AIC values shows how well each model is supported by the data compared with the other models, but it does not provide information about what aspects of the data are fitted well or poorly. To that end, we compared summary statistics obtained from the subject data with those obtained from model-generated data (see the Method section). Specifically, we fitted a mixture of a uniform distribution and a Von Mises distribution (Zhang & Luck, 2008) and obtained the weight to the Von Mises component, w_UVM, and the circular variance of the Von Mises component, CV_UVM (see the Method section). Figures 7 and 8 show w_UVM, CV_UVM, and the residual left by the mixture fit (averaged over set sizes), with corresponding predictions from the models without and with nontarget reports, respectively. The fits of the FP models are very poor because they predict no effect of set size on CV_UVM. The EP-A model, in which precision is equally allocated across all items, severely overestimates both w_UVM and CV_UVM. Inclusion of nontarget reports, leading to the EP-A-NT model, helps but not nearly enough. Most models other than FP and EP-A reproduce w_UVM and CV_UVM fairly well. For example, augmenting the EP model with a fixed number of remembered items (EP-F and EP-F-NT) is a great improvement over the EP-A models. The SA-F and SA-P models and all variable-precision models also account well for the first two summary statistics.

Figure 7.

Model predictions for w_UVM, CV_UVM, and residual, averaged over subjects for all models without nontarget reports. Black and gray markings indicate data; red markings depict the model. Shaded areas indicate 1 standard error of the mean. Residuals were averaged over all set sizes. The numbers in the top right corners are the models' R² values averaged over the three summary statistics. Different experiments used different set sizes; shown here are only the most prevalent set sizes. See Table 2 for the model abbreviation key. rad = radians.

Figure 8.

Fits of models with nontarget responses to w_UVM, CV_UVM, and residual, averaged over subjects. Black and gray markings indicate data; red markings depict the model. Shaded areas indicate 1 standard error of the mean. Residuals were averaged over all set sizes. The numbers in the top right corners are the models' R² values averaged over the three summary statistics. Different experiments used different set sizes; shown here are only the most prevalent set sizes. See Table 2 for the model abbreviation key. rad = radians.

The ability of many models to fit CV_UVM implies that for the purpose of distinguishing models based on behavioral data, examining plateaus in the CV_UVM function (Anderson & Awh, 2012; Anderson et al., 2011) is not effective. Variable-precision models, including ones in which all items are remembered, account for those plateaus as well as models in which no more than a fixed number of items are remembered. In particular, it is incorrect that the absence of a significant difference in CV_UVM (or any similar measure of the width of the Von Mises component in the uniform–Von Mises mixture) between two high set sizes “rules out the entire class of working memory models in which all items are stored but with a resolution or noise level that depends on the number of items in memory.” (Zhang & Luck, 2008, p. 233). From among the models of that class considered here, only the EP-A model can be ruled out in this way.

The residual turns out to be a powerful way to qualitatively distinguish the models: Many models predict a nearly flat residual, which is inconsistent with the structured residual observed in the data. Variable-precision models naturally account for the shape of this residual (Van den Berg et al., 2012): Because of the variability in precision, the error distribution is predicted to be not a single Von Mises distribution or a mixture of a Von Mises distribution and a uniform distribution but an infinite mixture of Von Mises distributions with different widths, ranging from a uniform distribution (zero precision) to a sharply peaked distribution (very large precision). Such an infinite mixture distribution will be “peakier” than the best fitting mixture of a single Von Mises and a uniform distribution and will therefore leave a residual that peaks at zero.

To quantify the goodness of fit to the summary statistics, we computed the R² values of the means over subjects for w_UVM, CV_UVM, and residual (averages are shown in Figures 7 and 8). We found that model rankings based on these R² values correlate strongly with the AIC-based ranking shown in Figure 3C. The correlation is strongest when we use the R² values of the residuals, with a Spearman rank correlation coefficient of 0.84. When we use the R² values of the w_UVM and CV_UVM to rank the models, the correlation coefficients are 0.65 and 0.66, respectively. All three correlations were significant with p < .001. Although it is always better to perform model comparisons on the basis of model likelihoods obtained from raw data rather than summary statistics, these results suggests that a model's goodness of fit to the residual is a reasonably good proxy for goodness of fit based on model AICs.

Parameter Estimates

Parameter estimates are given in Table A1 of the Appendix. For the models that have been examined before, parameter estimates found here are consistent with those earlier studies. For example, in the SA-F model, we find K = 2.71 ± 0.08, consistent with the originating article about the SA-F model (Zhang & Luck, 2008), and, in the VP-A model, we find α = −1.54 ± 0.04, consistent with the originating article about that model (Van den Berg et al., 2012). This shows consistency across experiments and suggests that the minor differences in our implementations of some of the models compared with the original articles (e.g., defining precision in terms of Fisher information instead of CV in the SA models) were inconsequential.

In the successful VP-P-NT model (as well as in the VP-P model), however, the mean number of remembered items is estimated to be very high (VP-P-NT: Mdn = 6.4). Because the highest tested set size was 8, this estimated value means that under the VP-F-NT model, on the vast majority of trials, even at set size 8, all items were remembered. In the VP-F-NT model, we find K at least equal to the maximum set size for 39.6% of the subjects.

Characterizing the Models in Terms of Variability

Our results suggest that variability is key in explaining working memory limitations: The most successful models postulate variability in mnemonic precision across remembered items, in the number of remembered items, or in both. Although different in nature, both types of variability contribute to the variability in mnemonic precision for a given item across trials: An item could be remembered with greater precision on one trial than on the next because of random fluctuations in precision, because on this trial, fewer items are remembered than on the next trial, or due to a combination of both effects. Therefore, it is possible that the unsuccessful models are, broadly speaking, characterized by having insufficient variability in mnemonic precision for a given item across trials.

To visualize this variability in each model, we reexpress it in terms of the circular variance of the Von Mises distribution from which a stimulus estimate is drawn, which we denote by CV. In terms of the concentration parameter κ, we have $\text{CV}=1-\frac{I_1(\mathrm{\kappa })}{I_0(\mathrm{\kappa })}$ (Mardia & Jupp, 1999). (This should not be confused with the circular variance of the Von Mises component in the uniform–Von Mises mixture model, CV_UVM.) Noiseless estimation and random guessing constitute the extreme values of CV, namely, CV = 0 and CV = 1, respectively. We computed CV predictions for each model using synthetic data generated using median maximum-likelihood parameter estimates across subjects. Figure 9 shows the predicted distributions of the square root of CV for each model with nontarget responses. The FP models predict that CV equals 0 or 1 on each trial; the SA-F-NT and EP-A-NT models predict that the distribution consists of a small number of possible values for CV; VP models postulate that the CV follows a continuous distribution. What the most successful models have in common is that they have broad distributions over precision, especially at higher set sizes. In the VP-P-NT model, variability in K contributes to the breadth of this distribution. In the VP-U-NT model (the only unsuccessful VP model), there is too much probability mass at CV = 1 when set size is low, that is, it predicts too many pure guesses. Less successful models produce CV distributions that seem to be crude approximations to the broad distributions observed in the most successful models.

Figure 9.

Distribution of square root of the circular variance of the noise distribution in the models with nontarget responses, for set sizes 2, 4, 6, and 8. A value of 0 corresponds to noiseless estimation, 1 to random guessing. For reference, the distribution from the VP-P-NT model is overlaid in the panels of the other models (red curves). Models are ordered as in Figure 3C. See Table 2 for the model abbreviation key.

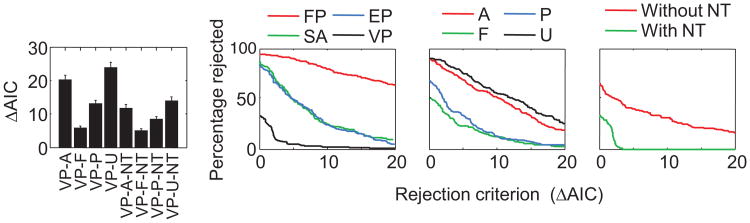
Model Variants

The strongest conclusion from the model family comparison is that memory precision is continuous and variable (VP), instead of fixed (FP), continuous and equal (EP), or quantized (SA). In the context of the ongoing debate between the SA and VP models, our findings strongly favor the latter. However, despite having tested many more models than any working memory study before, we still had to make several choices in the model implementations, for example, regarding how to distribute slots over items (in SA models) and what distribution to use for modeling variability in precision (in VP models). It is possible that the specific choices we made unfairly favored VP over SA models. To verify that this is not the case, we examined how robust our findings are to changes in these choices by testing a range of plausible variants of both SA and VP models. In addition, we examine in this section how important the response noise parameter is and whether adding a set size independent lapse parameter improves the model fits.

SA models with random slots assignment

In the SA models, several possible strategies to assign slots to items exist. Although Zhang and Luck (2008) did not explicitly specify which strategy they had in mind, they did mention that standard deviation in SA is inversely proportional to the square root of the number of slots assigned to the target—this suggests an as-even-as-possible strategy, which seems a plausible choice to us. However, it would be interesting to consider an uneven distribution, as this would introduce some variability in precision and might thus give better results. We tested a variant of the SA model in which each slot is randomly allocated to one of the items. Under this strategy, the number of slots assigned to the target item follows a binomial distribution.

The AIC values of the SA-A models are, by definition, identical under even and random distribution of slots, because the distribution is irrelevant when the number of slots is infinite. It is interesting that the AIC values of the SA-F and SA-U models decrease substantially when slots are assigned randomly instead of evenly to items, but those of the SA-P models remain nearly the same (see Figure 10A, left). This suggests that the Poisson variability in SA-P and SA-P-NT has roughly the same effect as the variability that arises when assigning slots randomly. Overall, SA with random slot assignment still performs poorly compared with the top models: The AIC value of the very best SA model with random slot assignment (SA-P-NT) is 12.2 ± 1.0 points higher than that of VP-P-NT. Moreover, the model family comparison remains largely unchanged (see Figure 10A, right).

Figure 10.

Results of three SA variants. Each row shows a different variant. Left: Akaike information criterion (AIC) values of the SA model variants relative to the original SA models. A positive value means that the fit of the model variant was worse than that of the original model. Error bars indicate 1 standard error of the mean. Right: Rejection rates as in Figure 5, with the SA models replaced by the SA variants. See Table 2 for the model abbreviation key.

SA models with variability in precision

The EP-F and SA-F models perform very similarly to each other, and so do their -NT variants (see Figure 3A). The VP-F and VP-F-NT models account for the data much better. This suggests that the inability of the SA-F model to fit the data well is not due to the quantized nature of precision but due to the lack of variability in precision. The key notion of the standard SA-F model (Zhang & Luck, 2008) is that each slot confers the same, quantized amount of resource or precision to an item (the bottle of juice in their analogy). However, some of the factors that motivate variability in precision in the VP models (e.g., differences in precision across stimulus values and variability in memory decay) may also be relevant in the context of SA models. We therefore consider an SA variant in which the total resource provided by the slots allocated to an item serves as the mean of a gamma distribution, from which precision is then drawn. This model is mathematically equivalent to one in which the amount of precision conferred by each individual slot is variable.

In the limit of large K, this variant of SA-F(-NT) becomes identical to VP-A(-NT) with a power of − 1. The intuition is that if the number of precision quanta is very large, precision is effectively continuous. We found that the AIC values of SA-F and SA-F-NT indeed improve substantially relative to the original SA models without variability in precision (see Figure 10B, left). However, these improvements are not sufficient to make them contenders for a top ranking (cf. Figure 3C): With the improvement, their AIC values are still higher than that of the VP-P-NT model by 15.7 ± 1.2 and 7.99 ± 0.62, respectively. Moreover, the fits of the other six SA models hardly improve, suggesting that variability in the number of slots (-P and -U variants) has a similar effect as variability in slot precision. The rejection rates of SA models with variable slot precision are almost as high as those of the original SA models (see Figure 10B).

In a final variant, we combined the notion of unequal allocation of slots (previous subsection) with variability in precision per slot. The improvements of these models compared with the original SA models (see Figure 10C) are comparable to the improvements achieved by unequal allocation alone (cf. Figure 10A). Hence, SA models improve by adding variability in slot precision on top of other sources of variability but still perform poorly when compared with the VP model. With the improvements, the AIC values of the SA-F, SA-P, SA-F-NT, and SA-P-NT models are still higher than that the AIC value of the VP-P-NT model by 22.4 ± 1.7, 27.1 ± 2.1, 12.6 ± 1.0, and 13.5 ± 1.1, respectively. Therefore, it is not simply a lack of variability in precision that makes the SA models less successful than the VP models.

Taken together, we have tested 32 slots-plus-averaging model variants and found that none of them describes the subject data as well as some of the VP models do. This strongly suggests that the essence of the SA models, the idea that memory precision is quantized, is wrong.

VP models with power = − 1

Why are the VP models so successful, relative to the other models? One part of the answer is clear: If one leaves out the variability in precision, the VP models become EP models, which do not do well—hence, variability in precision must be a key factor. However, compared with the SA models, one could argue that the VP models have more flexibility in the relationship between mean precision and set size. In the SA models, when N < K, each item, on average, is remembered by K/N slots, so its precision will be inversely proportional to N. In the VP models, we assume that mean precision depends on set size in a power law fashion, $\overline{J}\propto \frac{1}{N^{\alpha }}$. Thus, the power α is a free parameter in the VP models (e.g., fitted as −1.25 ± 0.06 in the VP-F-NT model and as −1.67 ± 0.08 in the VP-P-NT model), whereas it is essentially fixed to −1 in the SA models. To test how crucial this extra model flexibility is, we computed the model log likelihoods of VP model variants with the power fixed to −1. We found that all VP models perform worse compared with the variant with a free power (see Figure 11, left panel). However, the most successful VP models (VP-F-NT and VP-P-NT) still outperform all other models by an average of at least 4.6 points. Moreover, the rejection rate remains low for VP and high for all other model groups (see Figure 11, second panel). These results indicate that the continuous, variable nature of precision makes the VP models successful, not the power law in the relationship between mean precision and set size.

Figure 11.

Results of VP variants in which the power in the power law function that relates mean precision to set size is fixed to − 1. Left panel: Akaike information criterion (AIC) values of the VP model variants relative to the original VP models (higher values are worse). Error bars indicate 1 standard error of the mean. Second to fourth panels: Rejection rates as in Figure 5, with the VP models replaced by the VP variants with the power parameter fixed to −1. See Table 2 for the model abbreviation key.

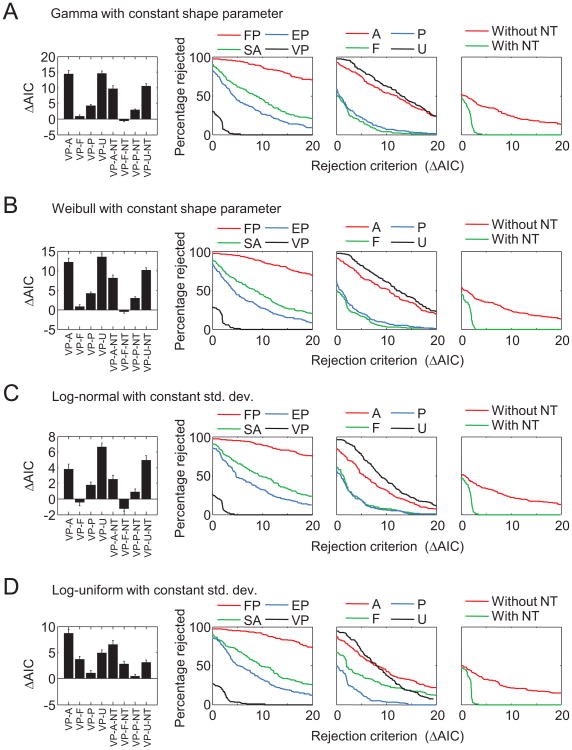
Variable-precision models with different types of distributions over precision

Our results suggest that variability in mnemonic precision is an important factor in the success of the VP models. So far, we have modeled this variability using a gamma distribution with a scale parameter that is constant across set sizes. Because many other choices would have been possible, one may interpret our use of the gamma distribution as an arbitrary behind the scenes decision. The proper way to test the (rather general) concept of variable precision would be to marginalize over all possible ways to implement this variability. Although a full marginalization seems impossible, an approximate assessment of the robustness of the success of the VP concept can be obtained by examining how well it performs under various specific alternative distributions over precision. Therefore, we implemented and tested VP models with the following alternative distributions over precision: (a) a gamma distribution with a constant shape parameter (instead of a constant scale parameter), (b) a Weibull distribution with a constant shape parameter, (c) a log-normal distribution with constant variance, and (d) a log-uniform distribution with constant variance. Although these four variants perform slightly worse than the original VP model (see Figure 12, first column), they all still have rejection rates substantially lower than those of the FP, SA, and EP models (see Figure 12, second to fourth columns). Hence, the success of VP is robust under changes of the assumed distribution over precision.

Figure 12.

Results of VP variants with different distributions of mnemonic precision. Each row shows a different variant. Left: Akaike information criterion (AIC) values of the VP model variants relative to the original VP models. A positive value means that the model variant was worse. Error bars indicate 1 standard error of the mean. Right: Rejection rates as in Figure 5, with the VP models replaced by the VP variants. See Table 2 for the model abbreviation key.

Equal and variable-precision models with a constant probability of remembering an item

Sims et al. (2012) proposed a model in which each item has a probability p of being remembered, with p fitted separately for each set size. Their model is most comparable with our EP-P and VP-P models, with the difference that the number of remembered items follows a binomial instead of Poisson distribution. To examine how much of a difference this makes, we fitted EP and VP variants with a binomial distribution of K, with success probability p fitted separately for each set size. (Note that the mean of K now depends on set size, unlike all models we considered so far.) We term these models EP-B, EP-B-NT, VP-B, and VP-B-NT. We found that the AIC values of EP-B and EP-B-NT are almost the same as those of EP-P and EP-P-NT (the differences were −0.10 ± 0.61 and 1.72 ± 0.53, respectively). This means that the binomial variants of EP are difficult to distinguish from the Poisson variants. The differences were slightly larger for the VP-P models: The AIC values of VP-B and VP-B-NT were 5.03 ± 0.39 and 5.70 ± 0.39 higher than those of VP-P and VP-P-NT, respectively. This means that the Poisson versions of VP are preferred over the binomial variants.

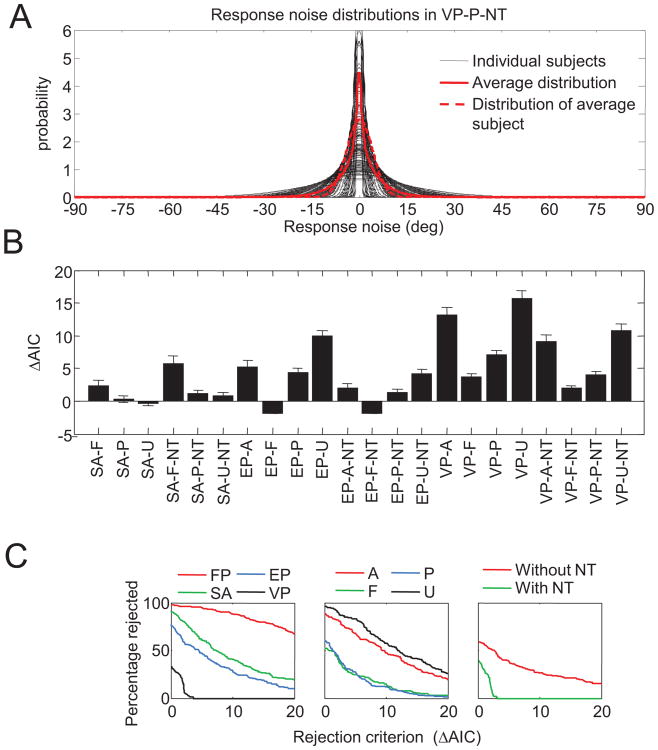
Effect of response noise

All models tested in this article incorporated response noise. One may wonder to what extent our conclusions depend on this modeling choice. Figure 13A shows the estimated response noise distributions in the most successful model (VP-P-NT). The geometric mean of κ_r in this model was 49.7. We found that by converting this to degrees and approximating the Von Mises noise distribution by a Gaussian, this corresponds to a standard deviation of 8.1°. This suggests that response noise is generally small but not necessarily negligible. To assess more directly how important the response noise parameter is, we fitted all 32 models without response noise. We found that removal of response noise led to a small increase in AIC for most models (see Figure 13B) but did not have strong effects on factor rejection rates (see Figure 13C). There is still strong evidence for variable precision and for the presence of nontarget responses. The most notable change is that among models without response noise, -A models fare relatively poorly compared with their performance when we allow for response noise (see Figure 5B). Hence, our conclusions do not strongly depend on whether response noise is included in the models.

Figure 13.

Effect of response noise on model fits. A. Average (red) and individual (black) response noise distributions in the VP-P-NT model. B. Change in Akaike information criterion (AIC) as a result of removing response noise from the models (averages across subjects). Positive values mean that removal of repose noise makes the fit on average worse. Note that this analysis could not be done for the FP models, because in those models there is no distinction between response noise and mnemonic noise. We also excluded SA-A and SA-A-NT, because without response noise, those models would predict noiseless estimates and thus have an infinite AIC. Error bars indicate 1 standard error of the mean. C. Model class rejection rates based on model fits without response noise. Removal of the response noise does not substantially alter the ordering of model factors (cf. Figure 5C). See Table 2 for the model abbreviation key.

Effect of lapse rate

In all tested models, random guesses could arise only from a limitation in the number of items stored in working memory. However, it is conceivable that subjects sometimes also produce a guess because of other factors, such as lapses in attention or blinking during stimulus presentation. We examined the possible contribution of such factors by adding a constant lapse rate to all models and computing how much this changed models' AIC values. We found that adding a constant lapse rate improved the AIC value for all models in which all items are remembered (-A) and for those in which a fixed number are remembered (-F) but made it slightly worse for all models with a variable number of remembered items (see Figure 14A). This can be understood by considering that even without a lapse parameter, the -P- and -U- models can already incorporate some guessing at every set size, whereas the -A- and -F- models cannot. Apparently, adding a constant lapse rate creates a redundancy in the -P- and -U- models but not in the -A- and -F- models. Including a lapse rate does not strongly affect the factor rejection rates (see Figure 14B), indicating that our main conclusion does not heavily rely on this parameter.

Figure 14.

Effect of adding a lapse rate on model fits. A. Change in Akaike information criterion (AIC) as a result of adding a constant lapse rate to the models (averages across subjects). Negative values mean that adding a lapse rate improves the fit. Error bars indicate 1 standard error of the mean. B. Model class rejection rates based on model fits with a constant lapse rate. Adding a lapse rate noise does not substantially alter the ordering of model factors (cf. Figure 5C). See Table 2 for the model abbreviation key.

Ensemble Representations in Working Memory?

All models that we tested here assumed that items in working memory are remembered entirely independently of each other. However, some authors have suggested working memory may have a hierarchical organization: in addition to the individual item values (colors or orientations), subjects may store ensemble statistics, such as the mean and variance of the entire set of items and make use of these statistics when recalling an item (Brady & Alvarez, 2011; Brady & Tenenbaum, 2013; Orhan & Jacobs, 2013). Here, we examine whether the subject data contain evidence of such hierarchical encoding, by examining whether the mean or variance of a stimulus set influenced a subject's response.

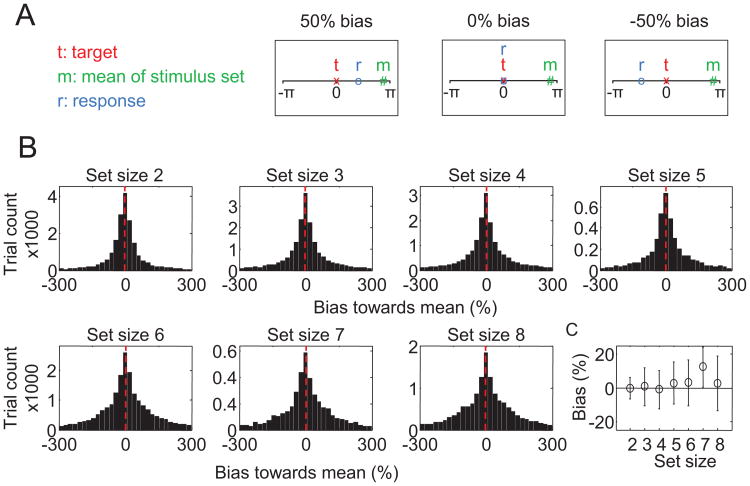
A strong prediction of hierarchical encoding models is that subject responses are biased toward the mean of the stimulus set. To assess whether evidence of such a bias is present in the data that we considered here, we computed for each trial the relative bias toward the mean of the stimulus set as follows. First we subtracted the target value from all stimuli and from the response, r (i.e., we rotated all items such that the target would always be 0). Next, we computed the bias as $\frac{r}{m}·100\%$, where r is the subject's response and m is the circular mean of the stimulus set. Hence, a bias of 0 means that the subject's response was identical to the target value, a negative value means that the subject had a bias away from the mean of the stimulus set, and a positive bias means that the subject had a response bias toward the mean of the stimulus set (see Figure 15A). Figure 15B shows for each set size the distribution of biases across all trials of all subjects. All distributions appear to be centered at and symmetric around 0, which means that there is no clear evidence for a systematic bias toward or away from the mean of the stimulus set. Figure 15C shows the mean bias across subjects. At no set size was the bias significantly different from 0 (Student t test, p > .07, for all comparisons). Thus, in this analysis, we do not find evidence for subjects making use of the mean of the stimulus set when estimating an individual item.

Figure 15.

Response bias analysis. A. Examples illustrating how we defined response bias toward the mean of the stimulus set. B. The histograms show biases pooled across all trials of all 164 subjects, split by set size. The red lines indicate the means of the distributions. C. Mean bias across subjects, as a function of set size. Error bars represent standard errors.

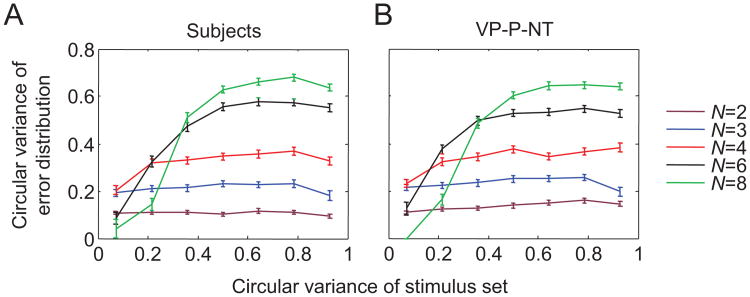
Similarity between items is another ensemble statistic that subjects may encode, because groups of similar items (i.e., lower variance) are possibly remembered more efficiently together. If this is the case, we predict that subjects' estimates are more accurate for homogeneous (low-variance) displays compared with heterogeneous (high-variance) displays. To examine whether there is any evidence for this in the subject data, we plotted the circular variance of the distribution of subjects' estimation errors as a function of the circular variance of the stimulus set on a given trial (see Figure 16). If this particular type of ensemble coding is occurring, one could expect an increasing trend in these curves. At first glance, there indeed seems to be a strong effect of stimulus variance at higher set sizes (see Figure 16A). However, these trends are accurately reproduced by the VP-P-NT model (see Figure 16B), in which the variance of the stimulus set does not play a role in encoding or reporting items. Additional analyses revealed that these trends are due to circular variance being systematically underestimated when the number of trials is low. This bias is strongest in the low-variance bins of the higher set sizes (N = 4, 6, 8), because low circular variance values of the stimulus set are less likely to occur at higher set sizes, with the consequence that the numbers of data trials are relatively low for those bins.

Figure 16.

A. Effect of stimulus variance on estimation error in the subject data. For high set sizes, the variance of the error distribution increases with the variance of the stimulus distribution. B. This effect is reproduced by the VP-P-NT model and can be explained as the result of circular variance being biased when only a few data points are available. The model results were obtained by generating synthetic data for each subject, using the subject's maximum-likelihood parameter estimates and simulating the same number of trials and set sizes as in the subject data. See Table 2 for the model abbreviation key. Error bars indicate 1 standard error of the mean.

Taken together, these results suggest that subjects' estimation errors are independent of both the mean and the variance of the stimulus set. Hence, these data contain no clear evidence for hierarchical encoding in working memory.

General Discussion

In this study, we created a three-factor space of models of working memory limitations based on previously proposed models. This allowed us to identify which levels in each factor make a model a good description of human data and to reject a large number of specific models, including all six previously proposed ones. Our approach limits the space of plausible models and could serve as a guide for future studies. Of course, future studies might also propose factors or levels that we did not include in our analysis; if they do, they should compare the new models against the ones we found to be best here.

Regarding the first factor we examined (the nature of mnemonic precision), we found that mnemonic precision is continuous and variable across items and trials (Van den Berg et al., 2012) instead of being quantized (Zhang & Luck, 2008) or continuous and equal across items and trials (Palmer, 1990; see Figure 5A). This strengthens the conclusion from earlier work (Van den Berg et al., 2012), because here we considered a much larger set of models. Moreover, the superiority of variable-precision models is robust under changes in model assumptions (see Figures 10, 11, and 12), for example, when quantized-precision models are allowed the flexibility of variability in allocation of quanta or in the precision per quantum (see Figure 10). In the VP- models, we found steep decreases of mean precision with increasing set size; the power laws we used to describe these dependencies had powers, on average, more negative than −1.

Although our results strongly support the notion of variability in mnemonic precision, they do not address the origins of this variability. Many sources are conceivable: fluctuations in attention over trials (Cohen & Maunsell, 2010; Nienborg & Cumming, 2009), fluctuations in attention over space (Lara & Wallis, 2012), differences in precision across stimulus values (Bae, Wilson, & Flombaum, 2013; Girshick, Landy, & Simoncelli, 2011), and variability in memory decay rates (Fougnie, Suchow, & Alvarez, 2012b). It is likely that multiple factors contribute, and distinguishing them will be challenging. In fact, not all of these possible factors determining mnemonic precision can be called resource, and, from this perspective, it might be wise to draw a distinction between resource and precision.

Variability in precision might be directly measurable in physiological recordings. For example, if precision were to map to the gain of a neural population encoding the stimulus (Ma, Beck, Latham, & Pouget, 2006; Van den Berg et al., 2012), we would expect variability in gain across trials. This is consistent with observations of doubly stochastic spike counts in macaque cortex (A. K. Churchland et al., 2011; M. M. Churchland et al., 2010; Goris, Movshon, & Simoncelli, 2012). Alternatively, variability in precision might even arise at constant gain simply due to the variability in the total spike count or firing rate (Bays, 2013), which is observed during both perception (Tolhurst, Movshon, & Dean, 1983) and working memory (Shafi et al., 2007). Functional magnetic resonance data might prove valuable in decoding the contents of multiple-item working memory; it was found recently that intersubject differences in the information content of signals in visual cortex are correlated with the precision of individuals' recall (Ester, Anderson, Serences, & Awh, 2013).

Regarding the second factor we examined (the number of remembered items), the evidence is somewhat equivocal: The model family in which all items are remembered performs worse than the model families models with a Poisson-distributed or fixed number of remembered items (see Figure 5B). However, the differences are too small to make very strong statements. Although the currently available delayed-estimation data thus do not allow us to completely resolve the debate about the number of remembered items, our results do suggest that if not all items are remembered, previous literature has severely underestimated the number of remembered items. For example, in the VP-P-NT model, the median value of K_mean was 6.4, much higher than the median K of 3 found in basic models with a fixed number of remembered items (SA-F and EP-F, as well as their -NT variants). Similarly, in the best model with a fixed number of remembered items, the VP-F-NT model, the median K was 6. The difference arises because the SA-F and EP-F models do not take variability in precision and nontarget reports into account, with the consequence that low-precision and nontarget responses can only be explained as non-remembered items.

The mixed conclusion regarding the distribution of the number of remembered items could also reflect individual differences. For example, some subjects may try harder (and therefore succeed more often) to remember all items on all trials than other subjects; the first group is expected to be fitted best by -A models, whereas the other group may be fitted better by -F and -P models. We emphasize that in the -F models, we do not interpret the number of remembered items (when it was smaller than the largest set size) as a limit on the number of remembered items. For example, subjects might sometimes voluntarily remember only a subset of items due to a lack of motivation or due to a desire to achieve a minimum level of precision. In other words, the number of items that are remembered is not necessarily equal to the number of items that can be remembered. In the -P- models, it is obvious that there is no limit on the number of remembered items, because K is drawn from a Poisson distribution. In these models, however, the psychological processes underlying this Poisson distribution are not specified. Thus, the models, in their current forms, do not allow us to determine why some subjects do not seem to remember all items all the time.

Overall, the narrative suggested by our results is that at least at set sizes up to 8, some subjects might occasionally have no memory representation at all of some items, but this is far rarer than previously thought. Instead, the main driver of the deterioration of working memory performance with set size is the decrease in memory quality as set size increases, coupled with variability in this quality.

Regarding the third factor we examined, our results support the existence of nontarget reports in working memory (see Figure 5C), which had been proposed before (Bays et al., 2009) but never been subjected to model comparison. Our findings suggest that the nontarget report rates are relatively low. The origin of the nontarget reports is unclear. If they reflect spatial binding errors, they could be due to positional uncertainty (Hess & Hayes, 1994) or visual crowding (Levi, 2008). Apparent nontarget reports could also arise from a hierarchical representation of information in working memory, which could cause the memory of an individual item to be influenced by other items. Previous studies have found evidence for hierarchical encoding (Brady & Alvarez, 2011; Brady & Tenenbaum, 2013; Orhan & Jacobs, 2013), but the 10 data sets analyzed here do not support this notion (see Figures 15 and 16).

The previous literature on working memory limitations has made conflicting claims. Here, we have shown that once a more complete model space is explored, model comparison results reported in previous articles hold up, but their claims do not. Specifically, Zhang and Luck (2008) found that SA-F fitted better than EP-A and EP-F, Anderson and colleagues (Anderson & Awh, 2012; Anderson et al., 2011) found that SA-F fitted better than EP-A, and Van den Berg et al. (2012) found that VP-A fitted better than SA-F, EP-A, and FP-F. Although the authors of these articles drew conflicting conclusions regarding broad model classes, their rankings of specific models are consistent with each other and also with the ranking of the full set of models in the present study.

Our factorial model comparison was limited to a single dependent measure of working memory performance, namely, the estimation error in delayed estimation. It would be worthwhile to apply the same method to other measures, both to verify the consistency of our conclusions across tasks and to further distinguish models and model families. Accuracy as a function of both set size and change magnitude in change detection (Keshvari et al., 2013; Lara & Wallis, 2012) and change localization (Buschman, Siegel, Roy, & Miller, 2011; Van den Berg et al., 2012) seem to be suitable candidate measures for factorial model comparison. Including reaction time (Donkin, Nosofsky, Gold, & Shiffrin, 2013) or confidence data (Rademaker et al., 2012) in factorial model comparison could further extend the current work.

Factorial model comparison, taken to the extreme, could lead to excessive model proliferation, frequent indistinguishability of models, and delayed graduation of doctoral students. It is important to keep in mind, however, that the factorial method only highlights and does not create the problem that some plausible models are hard to distinguish. In fact, this problem is shared by virtually all behavioral studies of perceptual and cognitive processes. It is inherently difficult to decipher the contents of a black box with many moving parts using just a few thousand observed input–output pairs. Studies that compare only a few models cannot possibly be more conclusive than those that perform a factorial comparison—the former are simply ignoring vast swaths of model space. The modeling of the moving parts can be constrained by general plausibility considerations but, ultimately, plausibility is subjective. Further constraints on models of working memory limitations might have to be derived from physiological experiments, especially neural population recordings coupled with good models of neural coding. In the meantime, factorially comparing models using likelihood-based methods is the fairest and most objective method for drawing conclusions from psychophysical data. If that forces researchers to reduce the level of confidence with which they declare particular models to be good representations of reality, we would consider that a desirable outcome.

Appendix

Parameter Estimates

For a discussion of how the values in Table A1 were calculated, see the Model Fitting section of the main text.

Model Recovery Analysis

We performed a model recovery analysis to test the validity of the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) as measures to distinguish the 32 models considered in this article. For each model, we generated 16 synthetic data sets (fake subjects) with set sizes 1, 2, 3, 4, 6, and 8, and 150 trials per set size; these numbers are representative of subject data sets (see Table 1 in the main text). To ensure that the statistics of the synthetic data sets are representative of those of subject data, we generated the synthetic data using maximum-likelihood parameter estimates from randomly picked subjects. At the level of the 512 individual data sets, AIC selected the correct model 247 times (48.2%) and BIC selected it 230 times (44.9%). There are two possible causes of incorrect model selections: (a) a bias in the model selection method (e.g., favoring simple models too much) and (b) variability in the maximum-likelihood estimates due to the relatively small size of individual data sets. The former explanation would be a reason to reject a model comparison method, whereas the latter can be overcome by averaging across subjects. When averaging across fake subjects, we found that BIC selected a wrong model in nine out of 32 cases, mostly because it favored a simpler model over the one that generated a data set (e.g., VP-A was selected on the VP-F, VP-F-NT, and VP-P data sets; see Table 2 for the model abbreviation key). Hence, BIC seems to be biased and is therefore unsuitable to distinguish the set of models considered in this study. Model recovery based on subject-averaged AIC values was substantially better: The correct model was selected in 31 out of 32 cases (see Figure A1). The only mistake made by the AIC method was that it wrongly selected SA-F-NT as the most likely model for EP-F-NT data (the difference in average AIC was 0.85 in favor of SA-F-NT). These models are quite similar to each other conceptually, and apparently the SA-F-NT model is able to account well for EP-F-NT data, with one parameter less. This means that the SA-F-NT and EP-F-NT may, in practice, be hard to distinguish from each other. However, because both models performed poorly compared with many of the other models, this is not a problem in the present study.

Figure A1.

Model recovery analysis. We tested how well synthetic data sets generated from each model (columns) were fitted by each model (rows). The color in a cell indicates a model's Akaike information criterion (AIC) relative to the winning model. Dark red on the diagonal means that the model used to generate the data was found to be most likely. See Table 2 for the model abbreviation key.

Robustness of Model Comparison Results

To verify the robustness of the model comparison results based on AIC values, we also performed a model comparison based on marginal model log likelihoods (Bayes factors; Kass & Raftery, 1995), approximated through Riemann sums. This method was also successful in model recovery based on synthetic data, indicating that it is suitable for our set of models. Moreover, the model order based on Bayes factors was highly consistent with the order based on AIC values: The Spearman rank correlation coefficient between rankings from the two methods was 0.931 ± 0.009 (mean and standard error across subjects).

Table A1. Maximum Likelihood Estimates per Model.

Model	Parameter	M ± SEM	Mdn	Model	Parameter	M ± SEM	Mdn
FP-A	log κr	0.616 ± 0.027	0.61	FP-A-NT	log κr	1.48 ± 0.04	1.45
					γ	(8.12 ± 0.24) ·10−2	0.08
FP-F	log κr	1.95 ± 0.04	1.94	FP-F-NT	log κr	1.98 ± 0.04	1.94
	K	2.48 ± 0.07	2		K	2.93 ± 0.09	3
					γ	(2.75 ± 0.29) ·10−2	0.02
FP-P	log κr	2.17 ± 0.04	2.2	FP-P-NT	log κr	2.17 ± 0.04	2.19
	K	3.31 ± 0.08	3.15		K	3.93 ± 0.10	3.72
					γ	(4.08 ± 0.28) ·10−2	0.04
FP-U	log κr	2.23 ± 0.04	2.24	FP-U-NT	log κr	2.20 ± 0.04	2.19
	K	8.19 ± 0.66	6.5		K	15.9 ± 1.3	10
					γ	(4.80 ± 0.28) ·10−2	0.05
SA-A	log κr	0.616 ± 0.027	0.61	SA-A-NT	log κr	1.48 ± 0.04	1.45
					γ	(8.12 ± 0.24) ·10−2	0.08
SA-F	log J1	2.78 ± 0.21	1.79	SA-F-NT	log J1	2.60 ± 0.19	1.85
	log κr	7.42 ± 0.24	9.21		log κr	6.35 ± 0.25	8.45
	K	2.71 ± 0.08	3		K	3.40 ± 0.11	3
					γ	(3.01 ± 0.27) ·10−2	0.02
SA-P	log J 1	1.94 ± 0.10	1.78	SA-P-NT	log J1	1.95 ± 0.11	1.79
	log κr	6.73 ± 0.21	8.19		log κr	5.91 ± 0.22	6.56
	Kmean	3.64 ± 0.10	3.48		Kmean	4.41 ± 0.11	4.16
					γ	(3.96 ± 0.28) ·10-2	0.04
SA-U	log J1	1.64 ± 0.10	1.65	SA-U-NT	log J1	1.00 ± 0.11	0.95
	log κr	6.89 ± 0.21	9.09		log κr	5.82 ± 0.20	5.15
	Kmax	11.7 ± 1.2	8		Kmax	30.6 ± 2.2	17.5
					γ	(4.91 ± 0.28) ·10−2	0.05
EP-A	log J1	3.73 ± 0.14	3.28	EP-A-NT	log J1	3.78 ± 0.17	2.9
	α	−2.60 ± 0.09	−2.38		α	−2.07 ±0.11	−1.65
	log κr	6.16 ± 0.25	8.11		log κr	6.51 ± 0.23	8.06
					γ	(5.13 ± 0.27) ·10-2	0.05
EP-F	log J1	2.84 ± 0.13	2.48	EP-F-NT	log J1	3.26 ± 0.16	2.64
	α	−1.10 ±0.10	−1.01		α	−1.16 ±0.10	−0.96
	log κr	8.03 ± 0.16	8.9		log κr	6.98 ± 0.19	7.87
	K	2.76 ± 0.08	3		K	3.41 ± 0.12	3
					γ	(2.82 ± 0.27) ·10-2	0.02
EP-P	log J1	5.74 ± 0.19	6.04	EP-P-NT	log J1	5.15 ± 0.19	4.81
	α	−3.24 ± 0.17	−3.28		α	−2.52 ± 0.16	−2.14
	log κr	3.67 ± 0.14	3.15		log κr	4.02 ± 0.16	3.45
	Kmean	4.13 ± 0.26	3.78		Kmean	5.9 ± 1.3	4.2
					γ	(2.86 ± 0.28) ·10−2	0.02
EP-U	log J1	6.25 ± 0.17	6.59	EP-U-NT	log J1	5.30 ± 0.18	4.96
	α	−3.56 ± 0.14	−3.86		α	−2.67 ± 0.14	−2.44
	log κr	3.47 ± 0.14	3.02		log κr	3.88 ± 0.15	3.29
	Kmax	16.2 ± 0.9	13		Kmax	26.0 ±1.4	19.5
					γ	(3.62 ± 0.29) ·10−2	0.03
VP-A	log J̄1	5.30 ± 0.12	5.39	VP-A-NT	log J̄1	4.99 ± 0.12	5.09
	α	−1.54 ±0.04	−1.59		α	−1.41 ±0.04	−1.47
	log τ	4.54 ± 0.13	4.4		log τ	4.12 ± 0.13	3.95
	log κr	3.40 ± 0.12	3.1		log κr	3.66 ± 0.13	3.28
					γ	(2.40 ± 0.27) ·10−2	0.01
VP-F	log J̄1	4.74 ± 0.12	4.8	VP-F-NT	log J̄1	4.36 ± 0.11	4.5
	α	−1.42 ±0.06	−1.38		α	−1.25 ±0.06	−1.15
	log τ	3.90 ± 0.13	3.81		log τ	3.40 ± 0.12	3.2
	log κr	3.99 ± 0.15	3.47		log κr	4.17 ± 0.15	3.66
	K	5.66 ± 0.16	5.5		K	5.68 ± 0.17	6
					γ	(2.40 ± 0.27) ·10−2	0.01
VP-P	log J̄1	5.06 ± 0.13	5.2	VP-P-NT	log J̄1	4.72 ± 0.13	4.71
	α	−1.88 ±0.08	−1.89		α	−1.67 ±0.08	−1.64
	log τ	3.38 ± 0.14	3.27		log τ	2.93 ± 0.15	2.92
	log κr	3.81 ± 0.15	3.3		log κr	3.91 ± 0.14	3.44
	Kmean	76 ± 49	5.8		Kmean	110 ± 59	6.4
					γ	(2.35 ± 0.27) ·10−2	0.01
VP-U	log J̄1	5.46 ± 0.12	5.52	VP-U-NT	log J̄1	5.12 ± 0.13	5.18
	α	−1.91 ± 0.06	−1.94		α	−1.74 ±0.06	−1.81
	log τ	3.84 ± 0.12	3.7		log τ	3.37 ± 0.14	3.28
	log κr	3.34 ± 0.13	3.03		log κr	3.54 ± 0.13	3.19
	Kmax	42.2 ±1.0	43.5		Kmax	45.0 ± 1.1	46
					γ	(2.27 ± 0.28) ·10−2	0.01

Note. All logarithms have base e. SA-A and FP-A models are identical. See Table 2 for the model abbreviation key. Disclaimer: The meaningfulness of parameter estimates depends on the goodness of fit of the model (for which, see, for instance, Figure 3C).