An Approach to Addressing Selection Bias in Survival Analysis

Abstract

This work proposes a frailty model that accounts for non-random treatment assignment in survival analysis. Using Monte Carlo simulation, we found that estimated treatment parameters from our proposed endogenous selection survival model (esSurv) closely parallel the consistent two-stage residual inclusion (2SRI) results, while offering computational and interpretive advantages. The esSurv method greatly enhances computational speed relative to 2SRI by eliminating the need for bootstrapped standard errors, and generally results in smaller standard errors than those estimated by 2SRI. In addition, esSurv explicitly estimates the correlation of unobservable factors contributing to both treatment assignment and the outcome of interest, providing an interpretive advantage over the residual parameter estimate in the 2SRI method. Comparisons with commonly used propensity score methods and with a model that does not account for non-random treatment assignment show clear bias in these methods that is not mitigated by increased sample size.

We illustrate using actual dialysis patient data comparing mortality of patients with mature arteriovenous grafts for venous access to mortality of patients with grafts placed but not yet ready for use at the initiation of dialysis. We find strong evidence of endogeneity (with estimate of correlation in unobserved factors ρ̂ = 0.55), and estimate a mature-graft hazard ratio of 0.197 in our proposed method, with a similar 0.173 hazard ratio using 2SRI. The 0.630 hazard ratio from a frailty model without a correction for the non-random nature of treatment assignment illustrates the importance of accounting for endogeneity.

1. Introduction

In health services research, randomized controlled experiments are rare. As a result, much effort has been expended developing and adapting methods to control for endogenous selection, a condition that exists when non-random treatment assignment leads to correlation between the treatment (selection) variable and the error term in the outcome of interest. These methods are used to account for potentially endogenous consumer choices and treatment effects [1–3]. For example, an insured person’s endogenous selection of a health plan has the potential to affect medical demand [4], number of provider encounters [5], and wellness activities [6]. Modeling the impact of endogenous treatment effects is also a frequent task in health services research, and is an important factor in analyses supporting the development of clinical guidelines (for example, Kenkel and Terza [7]). Recent focus on patient-centered outcomes research, placed in real-world settings, will increase the demand for methods that account for non-random treatment assignment. This study extends the endogenous selection literature by developing a parametric survival model incorporating a treatment effect, and allowing the treatment effect to be correlated with the patient’s unobserved heterogeneity, captured in a multiplicative frailty term. A key objective in the development of the model was to avoid sophisticated methods such as Markov Chain Monte Carlo estimation, which might limit the accessibility of the technique. This model is easy to implement in any statistical package that allows maximum likelihood estimation using Gauss-Hermite quadrature (e.g., ml with ghquad in Stata or GLIMMIX in SAS). We compare the proposed model to two selection-correction methods previously used in the literature: use of propensity scores and two-stage residual inclusion. We identify advantages of our proposed model in consistency, simplicity of estimation, precision, and interpretation. In addition to simulations, we illustrate the use of this model with mortality data for dialysis patients, adjusting for an endogenous means of vascular access at the start of dialysis treatment.

2. Background

Survival analysis is an important tool used by health services researchers. Whether the event of interest is death, disease incidence, or treatment failure (such as a transplanted organ), accurately modeling the time to the event, or “failure time,” is crucial. In most cases, it is assumed that observed patient characteristics such as age, previous disease burden, or previous health events will influence the failure time. The general form for the hazard of an event, with proportionality in patient i’s observed characteristics captured in x_i, is $h(t\mid x_i)=h_0(t)c(x_i^{\prime }\beta )$ where h₀ (t) is a baseline hazard rate estimated in fully parametric models (e.g., Weibull), or factored out in semi-parametric models (e.g., Cox proportional hazards). The function c(·) is the link function, which has a model-specific, non-negative form. An exponential function is often chosen for c(·), due to its mathematical tractability.

A characteristic of these nonlinear models is that parameter estimation will be biased in the presence of unobserved patient characteristics, even when these unobserved characteristics are uncorrelated with the observed characteristics captured in x_i [8]. Frailty models were developed to account for these unobserved characteristics, summarized nicely in a tutorial by Govindarajulu et al. [9]. In its simplest form, when there is no clustering of observations, this frailty takes the form of a simple univariate random term ε_i within c(·):

$$h(t\mid x_i)=h_0(t)c(x_i^{\prime }\beta +{\epsilon }_i)$$

When the link function is chosen so that time until failure follows a Weibull distribution, this leads to a multiplicative frailty term, θ_i = exp(pε_i), where p is the Weibull shape parameter. (Note that the Weibull hazard model simplifies to the commonly used exponential hazard model when p = 1.) Assuming the baseline hazard is time invariant and captured in an intercept in x_i, hazard in a Weibull survival model takes the form

$$h(t\mid x_i)={\theta }_{i}p{[\text{exp}(x_i^{\prime }\beta )]}^p{t}^{p-1}=p{[\text{exp}(x_i^{\prime }\beta +{\epsilon }_i)]}^p{t}^{p-1}.$$

Often, a “treatment group” variable, d_i ∈ {0,1}, is also included as a regressor so that the hazard can be described as

$$h(t\mid x_i)={\theta }_{i}p{[\text{exp}(x_i^{\prime }\beta +\gamma d_i)]}^p{t}^{p-1}=p{[\text{exp}(x_i^{\prime }\beta +\gamma d_i+{\epsilon }_i)]}^p{t}^{p-1}.$$

Typically, d’s effect on failure time is of primary interest. But because health services research often involves observational or administrative databases, and patients are not randomly assigned to treatment groups, endogenous selection is a concern. If unobservable patient characteristics affecting treatment assignment are correlated with the individual frailty, these unobservable characteristics may confound the effect of treatment on time to the event. To avoid bias in estimation of the treatment parameter, we must recognize this selection effect in our estimation method.

This issue of selection is common in economics, statistics, and epidemiology. Previous authors have demonstrated that endogenous selection leads to biased and inconsistent estimators when a dependent variable is modeled through the usual regression techniques. In a linear setting, much of the seminal work was done by Heckman [1;10] and Lee [11]. Lee’s work [11] extended Heckman’s sample selection methods [1], in which observation of the variable of interest depends on an endogenous selection equation, to a switching model in which two separate equations of interest are estimated, based on an endogenous switch between populations. For example, a researcher might want to model medical care demand in a health maintenance organization plan vs. demand in a fee-for-service plan. In the context of treatment effects, these separate equations of interest are typically simplified to a basic intercept shift, so the researcher models $y_i=x_i^{\prime }\beta +\gamma d_i+{\epsilon }_i$. Chiburis and Lokshin [12] extended the linear case further to allow for several levels of the endogenous treatment variable (e.g., dosage level) using an ordered probit selection model.

This selection analysis has been extended to nonlinear settings. Greene [3], Terza [13], and others developed estimation methods for count data with endogenous selection and switching. Much of this literature is nicely summarized by Greene [14]. Estimation of Poisson models with endogenous dummy variables was operationalized by Miranda [15] in the espoisson Stata command. These methods were generalized by Miranda and Rabe-Hesketh [16] in the ssm Stata command, which allows the dependent variable of interest to be a binary, ordinal, or count variable, with endogenous switching or selection.

In an extension of this work, our model focuses on the presence of an endogenous dummy variable in a Weibull hazard model with a multiplicative frailty term, allowing the estimation of treatment effect on survival. This endogenous selection survival (esSurv) model is an important addition to the literature on this topic.

In practice, a common method of adjusting for selection in survival models has been the use of propensity scores, in a wide variety of formats (see for example Badalato et al. [17], Hadley et al. [18], and Liem et al. [19]). The use of propensity scores is grounded in the seminal paper by Rosenbaum and Rubin [20], in which three methods of using propensity scores are presented: (1) creation of samples matched by propensity score, (2) stratification of the population by propensity score, and (3) inclusion of the propensity score as a regression adjustment. Rosenbaum and Rubin predicated their work on the assumption of strong ignorability, i.e., that the response variable is uncorrelated with the treatment assignment, once one has conditioned on the predictor variables. The difficulty is that many researchers extend these methods without careful consideration of whether strong ignorability holds, instead focusing diagnostics on assessing balance in the observed predictors.

Clearly, propensity score matching violates the requirement that proportional hazard models be based on independent samples [21]. And Terza et al. [22] demonstrate the inconsistency of regression adjustment in nonlinear models, labeling this a two-stage predictor substitution (2SPS) model. Therefore, we compare our proposed esSurv model to only one of Rosenbaum and Rubin’s suggested applications of propensity scores: using propensity scores to stratify the population (PS-strat). In addition, we consider the use of regression weights based on propensity scores (PS-weight), as used by Hadley et al. [18], for example. These two methods are also reviewed by Lunceford and Davidian [23], who do an excellent job of clarifying the often-ignored requirement of strong ignorability. Our simulations deliberately introduce an unobserved covariate to induce endogeneity and thus a violation of strong ignorability, which we expect will lead to inconsistency in both sets of propensity score results, even though we have an instrumental variable to use in the development of our propensity scores.

While demonstrating the inconsistency of 2SPS in nonlinear models, Terza et al. [22] also demonstrate that two-stage residual inclusion (2SRI) methods are generally consistent for nonlinear models. It is thus imperative that we make a third comparison of our model to the model of a 2SRI survival method. In this 2SRI method, a residual from the initial equation that models the probability of treatment is included as a covariate in the second frailty equation.

3. Econometric Models

3.1 Proposed esSurv Model

We observe the time of failure (e.g., death, relapse, organ failure), t_i, for the i^th individual who is characterized by a set of explanatory variables x_i, an endogenous switching variable d_i ∈ {0,1}, and a random error term ε_i. We assume the error term follows a normal distribution with mean zero and variance σ², so that the frailty follows the non-negative lognormal distribution.

If t_i follows a Weibull distribution with a person-specific hazard rate $h_i(t_i)=p{[\text{exp}(x_i^{\prime }\beta +\gamma d_i+{\epsilon }_i)]}^p{t}_i^{p-1}$, then the conditional density for t_i is:

$$f(t_i\mid {\mathrm{\epsilon }}_i,d_i)=p{[\text{exp}(x_i^{\prime }\mathrm{\beta }+\mathrm{\gamma }{d}_i+{\mathrm{\epsilon }}_i)]}^p{t}_i^{p-1}\text{exp}\{-{[\text{exp}(x_i^{\prime }\mathrm{\beta }+\mathrm{\gamma }{d}_i+{\mathrm{\epsilon }}_i)·t_i]}^p\}$$

Let d_i be determined by a standard probit:

$$d_i=\{\begin{array}{ccc}0& \text{if}& z_i^{\prime }\alpha +{\nu }_i\le 0\\ 1& \text{if}& z_i^{\prime }\alpha +{\nu }_i>0\end{array}$$

where the vector of explanatory variables, z_i, may or may not be the same as x_i, and ν_i is a normally distributed error term. Typically, z_i contains x_i and one or more instruments for the switching variable. The instrument for d_i is helpful in identification, though some work suggests that the model is weakly identified due to nonlinearity alone [10;24].

We assume that ε_i and ν_i are bivariate normal:

$$\left[\begin{array}{c}{\epsilon }_i\\ {\nu }_i\end{array}\right]~N\left[0,\mathrm{\sum }\right],\text{where}\mathrm{\sum }=\left[\begin{array}{cc}{\sigma }^2& \sigma \rho \\ \sigma \rho & 1\end{array}\right].$$

It can be shown that the conditional distribution of ν_i given ε_i is then

$${\nu }_i\mid {\epsilon }_i~N[\frac{\rho }{\sigma }{\epsilon }_i,1-{\rho }^2].$$

We can use this distribution to find the conditional probabilities for the endogenous selection variable:

$$\begin{array}{l}P(d_i=1\mid {\epsilon }_i)=P(z_i^{\prime }\alpha +{\nu }_i>0\mid {\epsilon }_i)\\ =P({\nu }_i>-z_i^{\prime }\alpha \mid {\epsilon }_i)\\ =\mathrm{\Phi }\left(\frac{z_i^{\prime }\alpha +\frac{\rho }{\sigma }{\epsilon }_i}{\sqrt{1-{\rho }^2}}\right)\\ P(d_i=0\mid {\epsilon }_i)=1-\mathrm{\Phi }\left(\frac{z_i^{\prime }\alpha +\frac{\rho }{\sigma }{\epsilon }_i}{\sqrt{1-{\rho }^2}}\right)\end{array}$$

The likelihood of the selection-corrected failure time model depends on the joint density

$$\begin{array}{l}f(t_i,d_i)={\int }_{-\infty }^{\infty }f(t_i,d_i\mid {\epsilon }_i)·g({\epsilon }_i)\partial {\epsilon }_i\\ =\frac{1}{\sqrt{2\pi }\sigma }{\int }_{-\infty }^{\infty }\{d_i·f(t_i\mid {\epsilon }_i,d_i=1)P(d_i=1\mid {\epsilon }_i)+(1-d_i)·f(t_i\mid {\epsilon }_i,d_i=0)P(d_i=0\mid {\epsilon }_i)\}·\text{exp}\left[-{\epsilon }_i^2/(2{\sigma }^2)\right]\partial {\epsilon }_i\\ =\frac{1}{\sqrt{2\pi }\sigma }{\int }_{-\infty }^{\infty }\{d_i·f(t_i\mid {\epsilon }_i,d_i=1)\mathrm{\Phi }\left(\frac{z_i^{\prime }\alpha +\frac{\rho }{\sigma }{\epsilon }_i}{\sqrt{1-{\rho }^2}}\right)+(1-d_i)·f(t_i\mid {\mathrm{\epsilon }}_i,d_i=0)\left[1-\mathrm{\Phi }\left(\frac{z_i^{\prime }\mathrm{\alpha }+\frac{\rho }{\sigma }{\mathrm{\epsilon }}_i}{\sqrt{1-{\mathrm{\rho }}^2}}\right)\right]\}·\text{exp}\left[-{\mathrm{\epsilon }}_i^2/(2{\mathrm{\sigma }}^2)\right]\partial {\mathrm{\epsilon }}_i\end{array}$$

To facilitate Gauss-Hermite quadrature in our maximum likelihood estimation, we borrow a technique from Miranda’s count data model [15] and make the variable substitution ${\eta }_i={\epsilon }_i/(\sigma \sqrt{2})$ to express the likelihood as

$$f(t_i,d_i)=\frac{1}{\sqrt{\pi }}{\int }_{-\infty }^{\infty }\{d_i·f(t_i\mid {\epsilon }_i,d_i=1)\mathrm{\Phi }\left(\frac{z_i^{\prime }\alpha +\rho \sqrt{2}{\eta }_i}{\sqrt{1-{\rho }^2}}\right)+(1-d_i)·f(t_i\mid {\epsilon }_i,d_i=0)\left[1-\mathrm{\Phi }\left(\frac{z_i^{\prime }\alpha +\rho \sqrt{2}{\eta }_i}{\sqrt{1-{\rho }^2}}\right)\right]\}·\text{exp}\left[-{\eta }_i^2\right]\partial {\eta }_i.$$

3.2 Comparison Models

The two methods based on propensity score matching first estimate a probit model as described above to capture the estimated parameters α̂. The estimated propensity scores are then computed as ${ps}_i=\mathrm{\Phi }(z_i^{\prime }\widehat{\alpha })$. Under an assumption of strong ignorability, Rosenbaum and Rubin [25] demonstrate that stratifying in quintiles is expected to reduce 90% of the bias in a linear setting. Therefore, in our PS-strat model we divide the population into five strata (indicated by j) based on their estimated propensity scores, despite the fact that we know through our deliberate introduction of endogeneity that strong ignorability is violated. We estimate the form

$$h_{ij}(t_i)=p{[\text{exp}(x_i^{\prime }{\beta }_j+{\gamma }_j{d}_i+{\epsilon }_i)]}^p{t}_i^{p-1}$$

In our simulation results (Table 1), we show the distribution of the estimated treatment parameters averaged across the strata within each Monte Carlo iteration to show the overall treatment effect.

Table 1.

Error in Treatment Parameter Estimation 100-Replication Monte Carlo Simulations by Strength of Correlation (Endogeneity)

	Median [inter-95% range] treatment parameter estimation error, by correlation scenario
	ρ ~50%	ρ ~25%	None
Endogenous switching survival model
N=1000	0.12 [−0.42,0.77]	0.14 [−0.35,0.62]	0.13 [−0.47,0.65]
N=5000	−0.03 [−0.22,0.20]	−0.07 [−0.25,0.18]	−0.05 [−0.27,0.18]
N=10,000	0.01 [−0.20,0.22]	−0.03 [−0.17,0.18]	−0.05 [−0.17,0.15]
Two-stage residual inclusion
N=1000	0.14 [−0.42,0.87]	0.13 [−0.31,0.65]	0.10 [−0.41,0.67]
N=5000	−0.05 [−0.37,0.20]	−0.03 [−0.32,0.16]	−0.03 [−0.31,0.16]
N=10,000	−0.06 [−0.26,0.19]	−0.05 [−0.22,0.16]	−0.04 [−0.20,0.15]
Regression weighted by inverse probability (propensity score)
N=1000	1.30 [0.95,1.59]	0.69 [0.20,1.00]	−0.04 [−0.48,0.44]
N=5000	1.25 [1.10,1.43]	0.61 [0.43,0.81]	−0.01 [−0.21,0.18]
N=10,000	1.23 [1.12,1.33]	0.60 [0.46,0.75]	0.00 [−0.13,0.14]
Regression stratified by propensity score
N=1000	1.26 [0.91,1.52]	0.65 [0.18,1.01]	−0.01 [−0.47,0.53]
N=5000	1.20 [1.07,1.32]	0.57 [0.43,0.77]	−0.01 [−0.20,0.21]
N=10,000	1.20 [1.08,1.27]	0.59 [0.44,0.72]	−0.01 [−0.12,0.15]
Weibull hazard with no endogeneity correction
N=1000	1.07 [0.83,1.33]	0.50 [0.23,0.76]	0.02 [−0.25,0.34]
N=5000	0.99 [0.87,1.08]	0.42 [0.29,0.54]	−0.01 [−0.16,0.12]
N=10,000	1.00 [0.90,1.07]	0.44 [0.34,0.52]	0.00 [−0.04,0.03]

For the PS-weight model, we follow a method used by Hadley et al. [18], applying the regression weight w_i = 1/ps_i for patients who were assigned the treatment and the weight w_i = 1/(1 – ps_i) for patients who did not receive the treatment to an estimation of the general hazard model

$$h_i(t_i)=p{[\text{exp}(x_i^{\prime }\beta +\gamma d_i+{\epsilon }_i)]}^p{t}_i^{p-1}$$

These weights are multiplied by the individual log-likelihoods in the summed overall log-likelihood to be maximized: L = Σ_iw_i ln f(X_i,θ), where X_i captures the observed data, θ is the vector of parameters to be estimated, and f(·) is the individual’s Weibull likelihood function.

Finally, we estimate a 2SRI model by computing the residual ${\widehat{r}}_i=d_i-z_i^{\prime }\widehat{\alpha }$, and including this as a covariate in the hazard model:

$$h_i(t_i)=p{[\text{exp}(x_i^{\prime }\beta +\gamma d_i+\delta {\widehat{r}}_i+{\stackrel{\sim }{\epsilon }}_i)]}^p{t}_i^{p-1}$$

The estimated residual is assumed to capture and correct for the impact of unobserved patient characteristics that are the source of the endogeneity.

4. Simulation Study

4.1 Setting

To demonstrate the impact of the endogeneity in the model, we undertook a series of Monte Carlo simulations. In each simulation, we generated observations with sample size N ∈ {1000; 5000; 10,000} with four continuous covariates, each drawn from a N(0,1) distribution:

• X1 predicts both failure time and treatment assignment, and is observable.

• X2 predicts failure time but not treatment assignment, and is observable.

• X3 predicts treatment assignment but not failure time, and is observable, allowing it to be used as an instrumental variable to identify treatment assignment.

• X4 predicts both failure time and treatment assignment, and is not observed, thus causing the treatment assignment to be endogenous in predicting the failure time.

In order to test the impact of violating Rosenbaum and Rubin’s [20] assumption that treatment assignment is strongly ignorable given the observed x = [X1 X2 X3]′, we include three scenarios for the true X4 parameter in the treatment assignment equation, selected so that the unobserved X4 explains approximately 0%, 5%, and 20% of the treatment assignment, based on partial R² statistics [26].

Once these regressors were generated, we began 100-replication Monte Carlo simulations across the three levels of endogeneity and three sample sizes, simulating two dependent variables: a 0/1 indicator of treatment assignment (d), and time of death (t) measured in months and censored at 12 months, a level of mortality relevant to organ transplant, dialysis, and some cancer diagnoses. Approximately 5% to 10% of the times of death are censored in these simulated data. Distributions used to generate these dependent variables are detailed below:

• d* = x′α + ν = 0.4 +1.0 X1 + 0.0 X2 + 0.8 X3 + α₄ X4 + ν

  where α₄ ∈ {0.00, 0.35, 0.95} controls the level of endogeneity (violation of strong ignorability) in the simulation.

• $d=\{\begin{array}{l}1\text{when}d\ast \ge 0\\ 0\text{when}d\ast <0\end{array}$

• λ = exp[x′β + ε] = exp[1.5 – 1.3 d +1.0 X1 – 0.3 X2 +1.0 X4 + ε]

• f(t|ε) = pλ^pt^p−1 exp[–(λ · t)^p], with Weibull shape parameter p = 0.8

• We drew the error terms ν and ε from independent, standard normal distributions, so we can show that the modified errors that result from the omission of the unobservable X4, ν̃ = α₄X4 + ν and ε̃ = β₄X4 + ε, have joint distribution

  $$\left[\begin{array}{c}\stackrel{\sim }{\nu }\\ \stackrel{\sim }{\epsilon }\end{array}\right]~N\left(0,\left[\begin{array}{cc}{\beta }_4^2+1& {\alpha }_4{\beta }_4\\ {\alpha }_4{\beta }_4& {\alpha }_4^2+1\end{array}\right]\right)$$

  Thus, for the three possible values of α₄ (0.00, 0.35 and 0.95), and the fixed β₄ = 1, our estimations using only observable covariates have true error term correlations of ρ = 0.00, ρ = 0.23, and ρ = 0.49, respectively.

Using each Monte Carlo replication of this generated data, we estimate parameters from a Weibull survival model for each of the five estimation methods (esSurv, 2SRI, regression with weights based on propensity scores, regression with stratification based on propensity scores, and no endogeneity correction), using x_i = [X1 X2]′ in the hazard equation and z_i = [X1 X2 X3]′ in the treatment (propensity score) equation, leveraging the instrumental variable X3.

4.2 Simulation Results

In Table 1 we summarize the results of our simulations, showing the median estimation error [and inter-95% range] of the treatment parameter, γ̂ – γ, from the 100 Monte Carlo replications. These are shown for the five estimation methods at three levels of endogeneity and three sample sizes. The estimation error for the treatment parameter is centered at zero for all five methods when there is no endogeneity (ρ = 0). In the presence of endogeneity (ρ = 0.23 or ρ = 0.49), the propensity score-based and uncorrected regressions have bias in the direction of the correlation of the error terms (negative ρ simulations are available from the corresponding author), and this bias is not mitigated by large sample sizes. Both our proposed esSurv method and the 2SRI method produce estimation errors that are centered on zero across all endogeneity levels and sample sizes.

Replication of the Weibull shape parameter, correlation, and other regression parameters (not shown here) is also quite good for both of these consistent methods. We also compared AIC statistics within Monte Carlo replications to assess model fit. In even the worst case scenario (ρ = 0.49, N = 1000), the median difference AIC_esSurv − AIC_2SRI = −0.7 was not meaningful.

The baseline simulations in Table 1 are based on a fairly strong instrument (X3), with an original true parameter α₃ = 0.80. The effect of eliminating the instrument from the selection equation is a drop in that equation’s pseudo R² of approximately 0.11, from 0.27 to 0.16. To test the importance of the instrument’s strength, we repeated these simulations with smaller true parameters on X3 (α₃ = 0.20 and α₃ = 0.05), equivalent to a contribution to the pseudo R² of 0.01 and 0.002, respectively, in “medium instrument” and “weak instrument” scenarios. Table 2 compares the results of this experiment with the baseline results using the scenarios with the largest endogeneity (ρ ≈ 0.50). As the instrument weakens, we see significant increase in dispersion of the estimates for the two consistent methods (esSurv and 2SRI), but the inter-95% range of the simulations’ errors continues to straddle zero. The small upward bias we see in the median of the weaker instruments is mitigated with increased sample size for these two methods. The inconsistent methods (PS-strat, PS-weight, Uncorrected) continue to show significant upward bias, as in the baseline scenarios, and this bias persists with increased sample size.

Table 2.

Error in Treatment Parameter Estimation 100-Replication Monte Carlo Simulations by Strength of Instrumental Variable

	Median [inter-95% range] treatment parameter estimation error, by strength of instrument (ρ ∼ 50%)
	strong IV (baseline)	medium IV	weak IV
Endogenous switching survival model
N=1000	0.12 [−0.42,0.77]	0.58 [−0.71,2.68]	0.89 [−0.78,2.90]
N=5000	−0.03 [−0.22,0.20]	0.04 [−0.48,0.80]	0.30 [−0.53,1.62]
N=10000	0.01 [−0.20,0.22]	0.11 [−0.30,0.64]	0.20 [−0.32,1.01]
Two-stage residual inclusion
N=1000	0.14 [−0.42,0.87]	0.54 [−1.24,2.29]	0.88 [−1.89,3.49]
N=5000	−0.05 [−0.37,0.20]	0.05 [−0.93,0.96]	0.34 [−0.90,1.57]
N=10000	−0.06 [−0.26,0.19]	−0.05 [−0.67,0.50]	0.04 [−0.84,0.74]
Regression weighted by inverse probability (propensity score)
N=1000	1.30 [0.95,1.59]	1.28 [1.00,1.53]	1.29 [1.00,1.54]
N=5000	1.25 [1.10,1.43]	1.21 [1.07,1.35]	1.22 [1.06,1.34]
N=10000	1.23 [1.12,1.33]	1.20 [1.11,1.29]	1.20 [1.11,1.28]
Regression stratified by propensity score
N=1000	1.26 [0.91,1.52]	1.25 [1.00,1.50]	1.25 [0.97,1.52]
N=5000	1.20 [1.07,1.32]	1.19 [1.06,1.29]	1.18 [1.04,1.30]
N=10000	1.20 [1.08,1.27]	1.18 [1.09,1.26]	1.18 [1.09,1.26]
Weibull hazard with no endogeneity correction
N=1000	1.07 [0.83,1.33]	1.22 [1.00,1.50]	1.23 [1.00,1.51]
N=5000	0.99 [0.87,1.08]	1.14 [1.02,1.24]	1.15 [1.03,1.27]
N=10000	1.00 [0.90,1.07]	1.15 [1.06,1.21]	1.15 [1.07,1.22]

An advantage of the esSurv method is reduced run time because of the full maximum likelihood estimation of all parameters, removing the need for bootstrapping to compute accurate standard errors as is required in the 2SRI method. Though sampling in bootstrap methods is typically done a very large number of times, say 1000 or 10,000 times, preliminary testing indicated that 400 bootstrap iterations provided reasonable convergence in estimation of standard errors for our Monte Carlo replications. Using 400 samples in bootstrapping, the run time for 2SRI Monte Carlo replications was 85 times the run time for the esSurv replications (averaging 20 minutes, 2 seconds for 2SRI vs. 14 seconds for esSurv per 1000-observation replication, using Stata 12), a conservative estimate of the run time difference given the relatively small number of samples in the bootstrap process.

In addition, the esSurv method has some advantages of interpretation over the 2SRI method. As a byproduct of the estimation, we have quantified the correlation estimate ρ̂, a more intuitive measure of endogeneity than the parameter of the estimated residual in the 2SRI model. The 2SRI residual parameter tells the user statistical significance and directionality of the correlation in unobservable factors, but the parameter does not have the intuitive appeal of an actual correlation measure such as the estimate from the esSurv model.

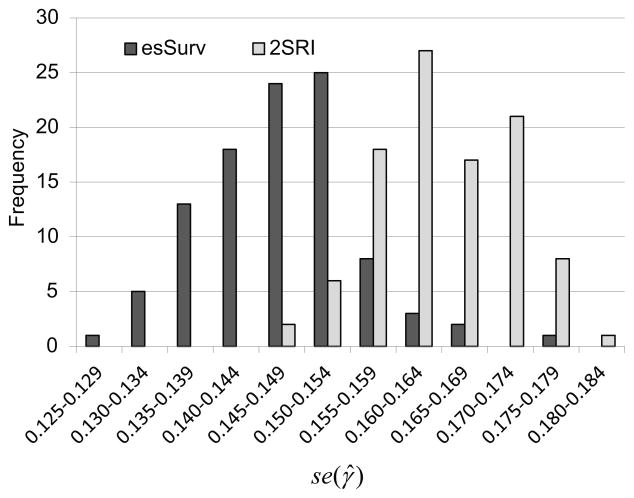
Finally, the results of our bootstrapped standard errors in the 2SRI method, compared to the standard errors of the parameter estimates from the esSurv method, suggest that esSurv produces a more precise estimate of the treatment parameter, compared to the 2SRI method. The distribution of the standard errors of the treatment parameter estimate, se(γ̂), is shown in Figure 1 for both 2SRI and esSurv using 100 bootstrapped Monte Carlo replications in the N = 5000, ρ ≈ 0.50 scenario. The bootstrapped 2SRI standard error is greater than the esSurv standard error in 96% of the replications with a median se^2SRI(γ̂)/se^esSurv(γ̂) ratio of 1.11. Similar results are found across a variety of sample size/endogeneity scenarios. For example when N = 1000, the ρ ≈ 0.50 scenario’s median standard error ratio is 1.12 (2SRI standard error is greater in 81% of the 100 replications) and the ρ ≈ 0.25 scenario’s median standard error ratio is 1.07 (2SRI standard error is greater in 72% of the 100 replications).

Figure 1.

Comparison of treatment parameter standard errors [se(γ̂)] in 100-replication Monte Carlo experiment with N = 5000, α₄ = 0.95 (ρ ≈ 0.50): esSurv vs. Bootstrapped 2SRI.

5. Empirical Application

To illustrate use of this model on real data, we employed data from the United States Renal Data System (USRDS) to investigate the association of the state of a vascular access for hemodialysis to first-year survival. The USRDS database contains information on patients with end-stage renal disease (ESRD), including demographic characteristics and heath encounter information in the form of Medicare claims for eligible patients. A patient is considered to have ESRD when kidney function has declined to the point where either a kidney transplant or regular dialysis is required to survive. The large majority of ESRD patients are treated with regular hemodialysis, in which waste products in the blood are removed by an external dialysis machine. To perform dialysis, access to the circulatory system is needed. The two most common methods of vascular access are temporary catheter and arteriovenous fistula (AVF). Since placing an AVF is a surgical procedure, time is required for the AVF to heal, or “mature,” before it can be used for dialysis. For this reason, clinical guidelines recommend placing the AVF as much as six months before it is estimated that the patient will develop ESRD [27]. Patients whose AVF is not mature at dialysis initiation must dialyze with a temporary catheter until the AVF is ready. Whether or not a patient’s AVF is mature at the time of dialysis initiation is a function of when it was placed and how long it takes to mature. Because dialyzing with an AVF (compared to a catheter) is associated with fewer complications and infections [28–31], as well as lower required doses of typical drug therapies [32;33], AVFs are generally considered to provide superior care and are preferred to catheters. AVF use is also thought to be associated with better first-year survival [34;35]. Our goal was to investigate the magnitude of that association while adjusting for measureable characteristics and accounting for unmeasured characteristics that could lead to selection bias.

From the USRDS database, we identified 5,427 patients who met several criteria: (i) they initiated dialysis at age 67 years or later (to allow for up to two years of Medicare coverage before ESRD onset), (ii) they had continuous Part A and Part B Medicare coverage during the observation period, (iii) their first type of renal replacement therapy was hemodialysis, and (iv) they had an AVF placed before ESRD onset to ensure that all patients in the cohort were deemed viable candidates for AVF. These patients were classified by whether or not the AVF was mature and ready for use by the time they initiated dialysis, which is the comparison of interest. Observable patient characteristics, including general disease burden (identified from claims before ESRD onset), are displayed in Table 3. The two groups appeared to be of similar age. Patients whose AVFs matured before dialysis initiation tended to be more often men (their generally larger veins and arteries can affect the speed of maturation) and to have lower prevalence of several diseases, including atherosclerotic heart disease, congestive heart failure, cerebrovascular attack (stroke), chronic obstructive pulmonary disease, dysrhythmia, and diabetes mellitus. When survival after dialysis initiation was calculated, fewer patients in the mature AVF group died (17% vs. 26%), and mean survival time was longer (174 days vs. 158 days, when censored at 365 days).

Table 3.

Patient Characteristics, End-Stage Renal Disease Example

	Arteriovenous Fistula
	Mature	Maturing
Total n	3,046	2,381
Age, yrs
Mean	76.2	76.4
Median	76	76
67–74	1,291 (42+.4)	999 (42.0)
75–84	1,443 (47.4)	1,135 (47.7)
≥ 85	312 (10.2)	247 (10.4)
Race
White	2,485 (81.6)	1,864 (78.3)
African American	424 (13.9)	436 (18.3)
Other	137 (4.5)	81 (3.4)
Sex
Men	1,951 (64.1)	1,321 (55.5)
Women	1,095 (35.9)	1,060 (44.5)
Comorbid conditions
Atherosclerotic heart disease	1,236 (40.6)	1,102 (46.3)
Congestive heart failure	914 (30.0)	835 (35.1)
Cerebrovascular attack (stroke)	385 (12.6)	344 (14.4)
Peripheral vascular disease	740 (24.3)	594 (24.9)
Other cardiac disease	680 (22.3)	558 (23.4)
Chronic obstructive pulmonary disease	501 (16.4)	441 (18.5)
Gastrointestinal disease	183 (6.0)	157 (6.6)
Liver disease	38 (1.2)	22 (0.9)
Dysrhythmia	733 (24.1)	637 (26.8)
Cancer	401 (13.2)	299 (12.6)
Diabetes	1,658 (54.4)	1,487 (62.5)
Anemia	2,140 (70.3)	1,408 (59.1)
Chronic kidney disease	2,663 (87.4)	1,775 (74.5)
Hypertension	2,827 (92.8)	2,130 (89.5)
Cognitive impairment	43 (1.4)	29 (1.2)
Depression	134 (4.4)	117 (4.9)
Wheelchair use	443 (14.5)	495 (20.8)
Instrumental variable*
First nephrologist claim, mean	546.3	459.6
First nephrologist claim, median	637	555
< 14 days before dialysis initiation	242 (7.9)	241 (10.1)
Died within 1 yr of end-stage renal disease onset	518 (17.0)	612 (25.7)
Mean time to death (patients who died)	174.4	158.5

Note: Unless otherwise indicated, values are n (%).

^*Number of days before starting hemodialysis that patient first saw a nephrologist.

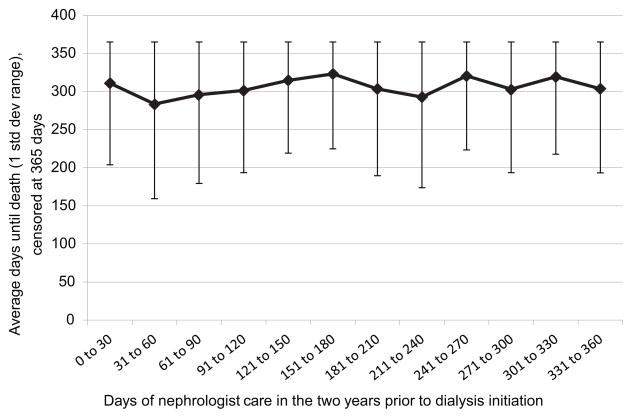
The instrumental variable chosen for this analysis represents the number of days before starting hemodialysis that the patient first saw a nephrologist, as identified from Part B claims during the two years before hemodialysis initiation. Clinically, the earlier a patient sees a nephrologist, the earlier an AVF is likely to be placed, thereby increasing the chance that it will mature by the time of dialysis initiation. At the same time, the timing of the first nephrologist visit should have little direct influence on survival after dialysis begins, as not being under a nephrologist’s care after dialysis initiation is extremely rare. While no formal test is available, the data appear to support the assumption that timing of first nephrologist visit is unrelated to survival after dialysis initiation, as seen in Figure 2, suggesting that this variable can serve as an instrument for maturity of AVF. For patients with no nephrologist claims before dialysis initiation, the “days” variable is set to zero.

Figure 2.

Comparison of time until death to days of nephrologist care prior to dialysis initiation.

Because of space considerations, we do not show the results of the selection equations; they are nearly identical for all models with a selection equation. We include all exogenous variables and the instrumental variable in this equation. The instrumental variable, number of days between first nephrologist visit and dialysis initiation, is parameterized as a categorical variable in deciles. The effect of this instrument is strong (five of the nine parameters have P < 0.01; one has P < 0.05) and nearly monotonic, with a longer nephrologist relationship prior to dialysis initiation predicting higher probabilities of having a mature AVF in place.

Table 4 contrasts the estimation of selected parameters¹ using our proposed esSurv model with estimates using the 2SRI and PS-weight method. Unfortunately, the PS-strat method, with 135 parameters to estimate due to the stratification, would not converge. A Weibull survival model in which the non-random treatment assignment is ignored (“Uncorrected”), incorporating a lognormally distributed multiplicative frailty term, is shown for comparison. We expect to see a monotonically increasing mortality as the duration of dialysis increases, implying an expected shape parameter greater than 1, and indeed we obtain 95% confidence intervals (not shown) for the shape parameter with a lower bound greater than 1 for all but the PS-weight method.

Table 4.

Parameter Estimation, End-Stage Renal Disease Example

Variable	Model Coefficients
	esSurv	2SRI	PS-weight	Uncorrected
Mature AVF	−1.622 ***	−1.752 ***	−0.353 ***	−0.462 ***
Age	0.047 ***	0.048 ***	0.047 ***	0.051 ***
Female sex	−0.068	−0.092	0.005	0.005
African American race	−0.319 ***	−0.334 ***	−0.210 **	−0.238 **
Other race	−0.237	−0.256	−0.287	−0.334 *
Atherosclerotic heart disease	0.129	0.131	0.150 *	0.203 ***
Congestive heart failure	0.246 ***	0.261 ***	0.260 ***	0.292 ***
Stroke/cerebrovascular attack	0.042	0.048	0.054	0.064
Peripheral vascular disease	0.305 ***	0.311 ***	0.228 ***	0.295 ***
Other cardiac disease	0.291 ***	0.309 ***	0.226 ***	0.259 ***
Chronic obstructive pulmonary disease	0.231 **	0.248 ***	0.221 ***	0.268 ***
Gastrointestinal disease	−0.185	−0.145	−0.198	−0.174
Liver disease	0.866 ***	0.803 *	0.607 **	0.705 *
Dysrhythmia	0.063	0.048	0.124	0.067
Cancer	0.118	0.090	0.118	0.092
Diabetes	−0.047	−0.041	0.038	0.034
Wheelchair use	0.329 ***	0.337 ***	0.387 ***	0.427 ***
log(total length of stay)	0.002	0.003	0.052	0.050
Hospitalization	−0.160	−0.169	−0.270 **	−0.284 *
Weibull shape parameter	1.226 ***	1.426 **	1.005 ***	1.423 ***
2SRI residual	---	1.345 ***	---	---
esSurv ρ (correlation estimate)	0.547 ***	---	---	---
Log likelihoods
Selection equation	---	−3501.81	−3501.81	−3501.81
Hazard equation	---	−8987.46	−18333.05+	−8996.57
Total/Joint model	−12490.614	−12489.27	−21834.86	−12498.38
k	64	65	64	64
AIC	25109.228	25108.540	43797.720	25124.760

^*P < 0.1;

^**P < 0.05;

^***P < 0.01

⁺Pseudo loglikelihood

AVF, arteriovenous fistula; HR, hazard ratio.

Note: Reference categories are non-mature AVF, male sex, white race, absence of disease. We have also adjusted for average Medicare reimbursement in the patient’s geographic region using deciles based on data from the Dartmouth Atlas.

We show AIC statistics at the bottom of Table 4 to assist in comparing model fit. These are based on a pseudo log-likelihood for the PS-weight method, and we combine model components when the equations are not jointly estimated to produce comparable measures across methods. Consistent with the Monte Carlo results, we see little difference in fit between the two consistent methods (esSurv and 2SRI).

The estimated treatment parameter from the esSurv model implies a hazard ratio associated with treatment group of 0.197, indicating that the hazard rate for patients with mature AVFs is about 80% lower than for patients with maturing AVFs at dialysis initiation, and 2SRI gives a similar 0.173² hazard ratio. But the estimated parameter from the PS-weight and the Uncorrected survival model produce hazard ratios for treatment group of 0.703 and 0.630, suggesting that patients with a mature AVF at dialysis initiation have only a 30%–37% lower adjusted hazard rate during the first year of dialysis. This is a noticeable difference in hazard ratio estimates for the treatment effect between consistent and inconsistent methods, and would indicate that while the PS-weight and Uncorrected models correctly identify the protective nature of a fully mature AVF, the benefit is dramatically underestimated. These results suggest that the complex nature of a dialysis case includes many unobserved factors affecting mortality, and that these factors are highly correlated with the treatment assignment. Indeed, we see a large estimated correlation of error terms (ρ̂ = 0.55) in the esSurv results and an estimate of the residual’s parameter that is highly statistically significant in the 2SRI model.

6. Conclusion

The issue of non-random treatment assignment appears frequently in observational health care data. Given the importance of survival analysis in health research, proper handling of the bias introduced by selection is an important part of evaluating these nonlinear models. We provide examples, simulated and real, that demonstrate the danger of ignoring the selection issue, or of extending common propensity score methods to this non-linear model when the treatment assignment is endogenous. We provide a solution that closely mirrors the parameter estimation of the consistent two-stage residual inclusion method, while offering significant computational and interpretive advantages. Specifically, the esSurv method enhances computational speed relative to 2SRI by eliminating the need for bootstrapped errors, reducing average run times from more than 20 minutes per Monte Carlo replication to 14 seconds per replication in our testing when N=1000. In addition, esSurv explicitly estimates the correlation of unobservable factors contributing to both treatment assignment and the outcome of interest, providing an interpretive advantage over the residual parameter estimate in the 2SRI method. Finally, we find evidence of better precision in the esSurv method, with 2SRI median standard errors of the estimated treatment effect ranging from 7% to 11% larger than esSurv standard errors in Monte Carlo simulations, and a 2SRI standard error of the estimated treatment effect that is 38% larger than the esSurv standard error in our empirical example.

The application of our model is limited by the use of a fully parametric method that produces a monotone hazard function. The other consistent method proposed, 2SRI, could be applied to proportional hazard models that do not require estimation of the baseline hazard. However, the Weibull hazard model is one of the most widely used parametric models because of its great flexibility. Hazard rates can increase or decrease over time, allowing us to model situations as diverse as the increasing mortality associated with general aging, or the decreasing risk of recurrence of some cancers as the length of remission increases.