Abstract
Geometric accuracy of MRI is one of the main concerns for its use as a sole image modality in precision radiation therapy (RT) planning. In a state-of-art scanner, system level geometric distortions are within acceptable levels for precision RT. However, subject-induced B0 inhomogeneity may vary substantially, especially in air-tissue interfaces. Recent studies have shown distortion levels of more than 2 mm near the sinus and ear canal are possible due to subject-induced field inhomogeneity. These distortions can be corrected with the use of accurate B0 inhomogeneity field maps. Most existing methods estimate these field maps from dual gradient-echo (GRE) images acquired at two different echo-times under the assumption that the GRE images are practically undistorted. However distortion that may exist in the GRE images can result in estimated field maps that are distorted in both geometry and intensity, leading to inaccurate correction of clinical images. This work proposes a method for estimating undistorted field maps from GRE acquisitions using an iterative joint estimation technique. The proposed method yields geometrically corrected GRE images and undistorted field maps that can also be used for the correction of images acquired by other sequences. The proposed method is validated through simulation, phantom experiments and applied to patient data. Our simulation results show that our method reduces the root-mean-squared error of the estimated field map from the ground truth by ten-fold compared to the distorted field map. Both the geometric distortion and the intensity corruption (artifact) in the images caused by the B0 field inhomogeneity are corrected almost completely. Our phantom experiment showed improvement in the geometric correction of approximately 1mm at an air-water interface using the undistorted field map compared to using a distorted field map. The proposed method for undistorted field map estimation can lead to improved geometric distortion correction at air-tissue interfaces, especially in low readout-bandwidth acquisitions, thus making them suitable for clinical use in precision RT without increasing the treatment planning margin.
1 Introduction
Superior multiple contrasts for soft tissue and lesion characterization have made MRI to be considered as a primary imaging modality for radiation therapy (RT) treatment planning and guidance. Currently, MRI is recommended [Pech et al. 2008, Hentschel et al. 2011] for target delineation in many forms of precise radiation treatment [Guo et al. 1993, Chung et al. 2004, Haie-Meder et al. 2005, Lim et al. 2011, Hanvey et al. 2012]. In addition, MRI can provide physiological and metabolic information for evaluating and characterizing tumors and normal tissues, and their responses to radiation therapy. Physiological and metabolic MRI also has the potential to aid in for the definition of a radiation boost target [Cao 2011, Quon and Brizel 2012]. However, MRI technologies have to address several challenges in order to be used as a primary imaging modality for RT planning and guidance.
One of the factors limiting use of MRI as a primary imaging modality for precision RT planning is geometric accuracy, including the sources of distortion at the system-level, e.g., B0 field inhomogeneity, and gradient non-linearity, as well as subject-dependent effects, e.g., susceptibility effect, and chemical shift [Chang and Fitzpatrick 1992, Jezzard and Balaban 1995, Baldwin et al. 2009]. On the state-of-art scanners, the system-level distortions are within acceptable levels due to improved magnet design, and built-in high-order shimming and gradient non-linearity correction. However, the subject-dependent distortions may be non-negligible especially in low readout-bandwidth acquisitions that are often chosen to optimize signal-to-noise or contrast-to-noise ratio in clinical images. Recent studies showed [Wang et al. 2013] that patient-level distortions caused by the susceptibility effect can be up to 2–4 mm in the air-tissue interface at the sinus and ear canal, an amount not within acceptable range for precision RT. These patient-induced distortions can be corrected with the use of B0 inhomogeneity field maps that are commonly estimated from the phase difference of two or more complex gradient echo images acquired at different echo-times [Jezzard and Balaban 1995, Funai et al. 2008]. However, most of the existing methods for distortion correction do not account for the geometrical and intensity distortion in the estimated field maps induced by the susceptibility effect [Jezzard and Balaban 1995, Funai et al. 2008, Baldwin et al. 2009, Crijns et al. 2011]. A distorted field map may not be able to fully correct the geometric inaccuracies in the images to meet the requirements for precision RT, especially for images acquired with a low readout-bandwidth. Herein, we propose a method for estimating undistorted field maps, thus avoiding residual geometric inaccuracies in the corrected images.
Our proposed method uses an iterative refinement process for self-correcting the estimated field maps that start from the k-space data (acquired or re-created via FFT) of the distorted field map. The effectiveness of our method with respect to geometrical and intensity accuracy of the corrected image and the undistorted field map was evaluated through simulations as well as phantom. Finally the proposed method was applied to patient imaging studies.
2 Materials and Methods
Our proposed method to estimate the undistorted field map consists of: 1) acquiring two distorted complex gradient echo images at two different echo times using a 3D gradient echo acquisition; 2) correcting the gradient non-linearity caused system-level distortion using scanner built-in correction; and 3) reconstructing the undistorted field map from the k-space data (re-created from the complex images or acquired) using a published joint reconstruction method [Matakos and Fessler 2010]. This method was developed to estimate undistorted images from modified echo-planar-imaging (EPI) trajectories. Here, we modify the method to estimate the undistorted field map from a single multi-echo acquisition with the standard 3D Cartesian trajectory.
2.1 Undistorted field map and image estimation
The k-space data, denoted as y, of a true underlying object ϱ acquired using a 3D gradient echo (GRE) sequence with a Cartesian k-space trajectory, and zero-mean Gaussian noise, can be modeled as:
| (1) |
where ε is the zero-mean complex Gaussian noise vector, ω = 2πγΔB0 with ΔB0 being the true undistorted field map, and A(ω, t) is the system matrix corresponding to the 3D GRE acquisition with elements given by
| (2) |
Where tm is a discrete acquisition time point, k(tm) = [kx(tm), ky(tm), kz(tm)] is the k-space location at a given time point, rn = [xn, yn, zn] is a discretized image domain location and ωn is the discrete undistorted ΔB0 field value at location rn. In the model, y can be a vector to represent multiple echoes, e.g., two echoes, and is affected by ΔB0. The effect of decay on is ignored for time being.
Using the above model and the joint reconstruction method, an undistorted field map and image can be estimated by solving the following optimization problem
| (3) |
where ŷ are the measured k-space data, and R(ϱ) and R(ω) are regularization terms. To efficiently solve this problem with a stable solution, a linearization technique for the field map along with an alternating minimization scheme is applied similarly to [Matakos and Fessler 2010]. For the regularization terms R(ϱ) and R(ω) we choose quadratic regularizers for efficiency. The quadratic regularization is a natural choice for the field map since they are usually smooth. For the image a non-quadratic regularizer could be used, but that would increase the computational complexity. Since our intent of the use of the image regularizer is to stabilize the solution, the choice of a quadratic regularizer with a small value of the weighting parameter λ1 provides a stable solution without compromising the spatial resolution of the image estimate. Using the analysis method of [Fessler and Rogers 1996] we chose the parameter λ1 to achieve a full-width-half-maximum (FWHM) of the point-spread-function (PSF) of 1.02 pixels, which seems sufficient to provide a stable solution without affecting the spatial resolution of the reconstructed images. For the field map regularization, due to the field map smoothness, we chose the parameter λ2 to achieve a FWHM of the PSF of 1.5 pixels; this choice does not significantly compromise the field map resolution and also helps suppress noise artifacts in the estimated field map. After the linearization approximation and the regularizer choice, the alternating minimization scheme used for image and field map estimations can be expressed as
| (4) |
where D{t} and D{ϱ̂(k+1)} denote diagonal matrixes with elements of the respective vectors along the main diagonal, and C is a second order difference operator.
The system of equations in (4) is now quadratic for both the image ϱ and the field map ω and can be solved efficiently using the conjugate gradient algorithm.
The iterative process is repeated until a convergence criterion is met. The normalized root-mean-squared error (NRMSE) between two consecutive field map updates, defined as
| (5) |
is chosen as the criterion. The convergence of the problem was tested for threshold values of NRMSEs of 0.1% and 0.01%. The output of the final iteration provides the undistorted field map and undistorted image estimates.
The problem of image estimations is convex and subsequently the initialization is not crucial since it will converge to the unique minimizer. However, the field map estimation problem is non-convex and thus the initialization choice is important to guarantee convergence in the correct local minimum. An initialization with a zero estimate for the field map could lead to wraparound artifacts in the field map if the echo-times chosen are spaced too far apart for the given dynamic range of the field map. To avoid this we initialize it with a baseline field map ωb calculated from the phase difference of two distorted gradient echo images as
| (6) |
where ϱ̂1 and ϱ̂2 are distorted complex images acquired from the 3D GRE acquisitions at two different echo times TE1 and TE2, and ∠ denotes the phase operation. Note that the field map obtained from the phase difference of the two gradient echoes is not just distorted geometrically but also corrupted in signal intensity. In addition, this baseline field map can have wraparound artifacts, which can be corrected with the unwrapping method of [Jenkinson 2003] using the FMRIB (Functional MRI of the Brain) Software Library (FSL). The initial field map estimate can also be post-processed using a Gaussian or median filter to remove corruption from noise. The baseline field map after the post-processing steps (unwrapping and/or noise removal) becomes the initial estimate ω̂(0) used in our iterative estimation process. This initial estimate ω̂(0) is also the distorted field map that is used for comparison to our method.
2.2 Experiments
The proposed method for the undistorted field map estimation and image correction was validated through both simulation experiments and phantom studies.
2.2.1 Simulations
The purpose of the simulation experiments was to investigate the geometric accuracy and intensity accuracy of the estimated field map and image comparing to the ground truth. Also, both the average and maximum errors in both the field map and image were determined. The importance of each of the metrics depends upon the utility of the method.
In the simulation experiment, the noiseless k-space data of two gradient echoes were created with standard frequency and phase encodings, a 256×256 acquisition matrix, a readout-bandwidth of 180 Hz/pixel, and echo-times of 3 and 5 ms. The bandwidth was selected as the same as used for a T1-weighted image acquisition in our clinical brain tumor protocol. The maximum inhomogeneity in the field map was chosen to be approximately 900 Hz, which can cause an approximately 5mm distortion in an image acquired with a readout-bandwidth of 180 Hz/pixel. The image and simulated field map are displayed in Figure 1.
Figure 1.

True image (left) and field map (right) used in the simulation experiment with a 50×50 pixel ROI marking the high distortion region. The field map is converted from Hz to mm of distortion in an image acquisition with a frequency-encoding bandwidth of 180 Hz/pixel.
The undistorted field map and images were estimated iteratively and the process was initiated by using the distorted field map. To investigate the convergence of our proposed method and assess the image quality improvement by our proposed method compared to using the distorted field map ω̂(0) for correction, the NRMSEs between the estimated field map or image and the ground truth were calculated in each iteration. To better assess the maximum errors in the field map and corrected image, the NRMS image error and RMS field map error in Hz were measured in a specific 50×50 pixel region-of-interest (ROI) that corresponds to a high-inhomogeneity region in the field map (including the maximum) seen in Figure 1.
2.2.2 Phantom study
A phantom with known geometric specifications (Figure 2), which had a large cylindrical compartment filled with doped water and five cylindrical air pockets was scanned in coronal orientation on a 3T scanner (Skyra, SIEMENS) with two 3D GRE sequences to obtain two-GRE complex image volumes with acquisition matrix of 288×288×104, a field-of-view (FOV) of 280×280×156 mm, flip angle of 15°, and TR of 12ms at echo-times of 4.92 and 7.38ms corresponding to fat-water in phase. To highlight the effects of distortion on the field maps and resulting images, we used a modest-low readout-bandwidth of 300 Hz/pixel in the acquisition.
Figure 2.

Amplitude image of the geometric phantom. An arrow denotes the direction of the main magnetic field B0.
The two distorted complex images, denoted as ϱ̂1 and ϱ̂2, resulting from the 3D GRE acquisitions at the two different echo times, were used to re-create the required k-space data via FFT. The k-space data from the two images ŷ1 = FFT{ϱ̂1} and ŷ2 = FFT{ϱ̂2} were combined into a single data vector
that was subsequently used in the proposed undistorted field map estimation. The two distorted images ϱ̂1 and ϱ̂2 were also used to estimate the distorted initial field maps. Both the distorted and undistorted field maps were then used to self-correct the GRE images. The amount of distortion correction was measured at the air-water interfaces and the corrected images were compared quantitatively to the known geometric specifications of the phantom.
2.2.3 Patient Study
We applied the proposed method to brain MRI data of a patient who participated in an institution-review-board approved protocol. The patient was scanned on a 3T scanner (Skyra, SIEMENS) using a 3D dual GRE sequence with readout gradients of opposite polarities. Two complex image volumes were acquired at echo times of 3.87 and 7.55 ms with acquisition matrix of 128×128×112, field-of-view (FOV) of 240×240×212.8 mm, flip angle of 9°, TR of 12 ms, and readout-bandwidth of 300 Hz/pixel. The echo-times could not be chosen for fat-water in phase as in the phantom due to the use of a single dual-echo acquisition with low readout-bandwidth.
As was done for the phantom study, the two distorted complex image volumes were used to re-create k-space data via FFT and were also used to estimate the distorted initial field maps. The k-space data were used in our joint estimation method to obtain undistorted field maps. Finally both distorted and undistorted field maps were used to self-correct the GRE images.
3 Results
3.1 Simulation study
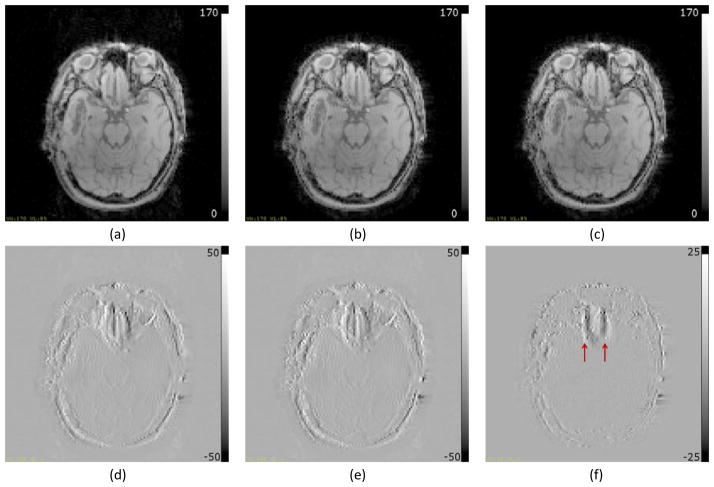
In the simulation study, the RMS error in the field map decreased from the initial 14.8Hz (43.8Hz in the ROI) to 0.8Hz (1.7Hz in the ROI) in the iteratively estimated undistorted field map, and the maximum error decreased from 113Hz to 12Hz, indicating substantial improvement (Figure 3). The reported errors were measured in comparison to the known ground truth field map. This improvement is also reflected in the NRMSE of the reconstructed image where the correction with the distorted field map resulted in an NRMSE of 2.69% whereas correcting with the undistorted field map reduced the NRMSE to 0.43%. In the high-distortion ROI, the NRMS errors decreased from 8.04% using the distorted field map for correction to 0.79% using the undistorted field map for correction (Figure 4). This improvement was also evident visually by comparing the difference between the true and the distorted field maps, and between the true and the undistorted field maps (see Figure 3). As seen in Figure 3a there is significant residual geometric distortion and also residual error in terms of field map intensity. Figure 4a, 4b and 4c show the uncorrected image and the corrected images using the distorted and undistorted field maps respectively, where we see visible residual artifacts in the high-distortion region (Figure 4b) that could cause misdiagnosis in clinical usage, and which are almost completely removed by using the undistorted field map for correction (Figure 4c).
Figure 3.

(a) Difference between the true and the distorted field map, (b) difference between the true and the iteratively corrected undistorted field map
Figure 4.

(a) Uncorrected image. Geometric and intensity distortion artifacts are clearly visible. (b) Corrected image using the distorted field map. Visible artifacts in the regions with high field inhomogeneity. (c) Corrected image using the undistorted field map. No visible artifacts. (d, e, and f) show difference between the true image and figures (a, b, and c) respectively. In all images the scale is in arbitrary intensity units.
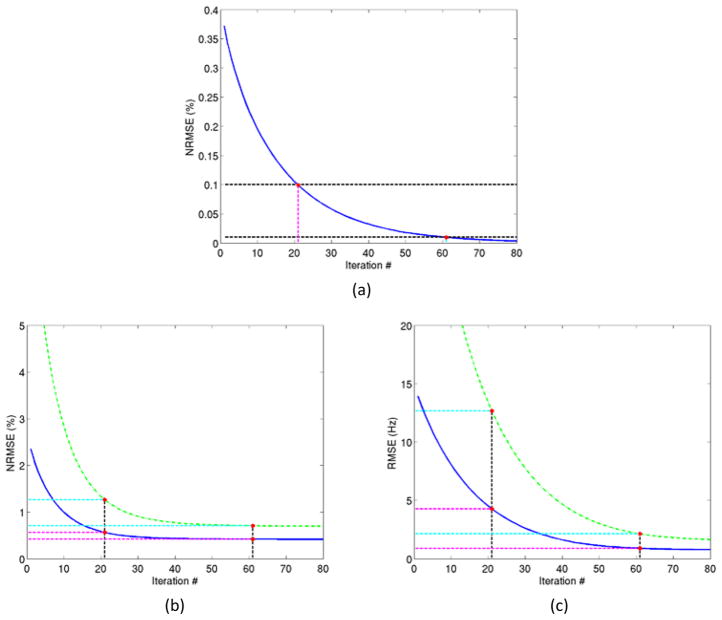
Using a stopping rule of the NRMSE of 0.1% for estimating the~ undistorted field map, the algorithm converged after 21 iterations, and resulted in an RMS error of 4Hz in the entire FOV and ~13Hz in the high-distortion ROI, which are still significant (Figure 5). Using a stopping rule of 0.01%, the method converged after~61 iterations, and yielded substantially lower RMS errors in the field map (<1Hz in the entire FOV and 2Hz in the ROI) (Figure 5). At that point, the errors in both the reconstructed image and field map were practically stable, thus further iterations yielded little to no improvement.
Figure 5.
Algorithm convergence. (a) The NRMSE (%) between consecutive field map updates as given in equation (5) decreases as the number of iterations increases. (b) The NRMSE (%) of the reconstructed image decreases as number of iterations increases. (c) The RMS error (in Hz) of the reconstructed field map decreases with the number of iterations. Blue curves (solid) and green curves (dashed) denote the errors in the entire field of view and in the high distortion ROI of the field map (a and c) or image (b), respectively. Horizontal and vertical dashed lines denote the two stopping criteria of 0.1% and 0.01% of the NRMSEs in the estimated field map, and the respective numbers of iterations of 21 and 61.
3.2 Phantom study
In the uncorrected images, there was about 1.6 mm distortion as well as intensity corruption near the air-water interface (Figure 6). Figure 7 shows the distorted field map (7a), undistorted field map (7b) and their difference (7c) where the improvement in the field map estimation around the air-water interface is clearly illustrated. The undistorted field map corrected the geometric distortion in the image almost completely, whereas the distorted field map corrected the distortion only partially (approximately 1mm of correction, Figure 8). Note that in addition to the geometric distortion correction the intensity corruptions (white and dark spots) near the air-water interface in the original distorted images were corrected (Figure 8b and 8c). The correction effects on both geometry and intensity can be seen in the difference images (Figure 9). Comparing each corrected image to the original distorted one, we see that the distortion correction using the undistorted field map is more effective in the critical regions near the air-water interface than using the distorted field map. Also, the difference between the two corrected images using the distorted and undistorted field maps (Figure 9c) highlights the improvement in the distortion correction at the air-water interface achieved by using the undistorted map.
Figure 6.

The uncorrected image of the phantom overlaid with a color-coded field map that is converted to mm of distortion.
Figure 7.

(a) Initial distorted field map; (b) Iteratively estimated undistorted field map; (c) Difference between the two field maps. The field maps are converted to mm of distortion.
Figure 8.
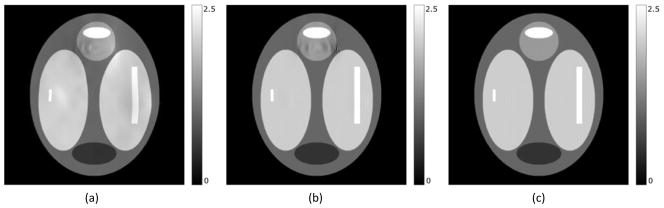
(a) Original distorted image with clearly visible distortion at the air-water interface. (b) Image corrected with the distorted field map. (c) Image corrected with the undistorted field map. (d, e, and f) are zoomed-in regions around the central cylinder from figures (a, b, and c) respectively. Note that there are intensity corruptions at the locations with the geometric distortion in the original distorted image.
Figure 9.

Distortion correction at the air-water interface. Difference images between the uncorrected image and the corrected image using the distorted field map (a), between the uncorrected image and the corrected image using the undistorted field map (b), and between the corrected images using the distorted and the undistorted field maps (c).
The improved correction by the proposed method was also quantified by comparing images to the phantom design specifications. Within the limitation of the image spatial resolution, compared to the corrected images (Figure 8e and 8f), we found that in the uncorrected image (Figure 8d) the top edge of the air cylinder at the phantom center was displaced by 1 mm inferiorly while the horizontal diameter of the cylinder was displaced by approximately 1 mm superiorly, which resulted in the obvious shape distortion seen in Figure 8d. In both corrected images (Figure 8e and 8f) the total displacement and shape distortions were mostly corrected. However, there was residual geometric distortion in the corrected image using the distorted field map (Figure 8e) at the bottom of the cylinder, leading to a measured vertical diameter of 32 voxels (corresponding to 31.1±0.5 mm at spatial resolution of 0.972 mm/voxel), whereas the vertical diameter measured from the corrected image using the undistorted field map (Figure 8f) was 31 voxels (corresponding to 30.1±0.5 mm), which is consistent with the phantom design specification of a cylinder with a diameter of 30.1 mm.
3.3 Patient Study
Figure 10 shows the distorted field map (10a and 10d), undistorted field map (10b and 10e) and their difference (10c and 10f), where white and black edges (arrows) at the high distortion region in the field map difference indicate the field map geometry difference and the improvement in the field map estimation. In the uncorrected images, there was significant distortion (>2 mm) at the region above the sinuses (Figure 10d). The dynamic range of the residual distortion in Figure 10c (about 1 mm) indicates that there may be non-negligible residual geometric and intensity distortions in the corrected images using the distorted field map of Figure 10a. Using the distorted and undistorted field maps to reconstruct images, the geometric accuracies of both corrected images (Figure 11b using distorted field map and Figure 11c using undistorted field map) are substantially improved as illustrated in the difference images (Figure 11d and 11e respectively) where the clearly visible edges indicate the improvement in geometric and intensity accuracy. However, using a distorted field map for correction can result in residual geometric and intensity distortions that are illustrated in Figure 11f that shows the difference between the two corrected images.
Figure 10.
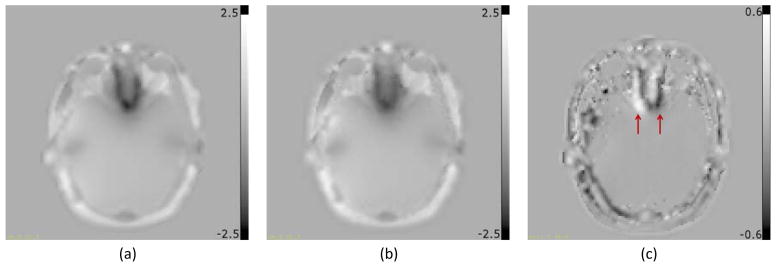
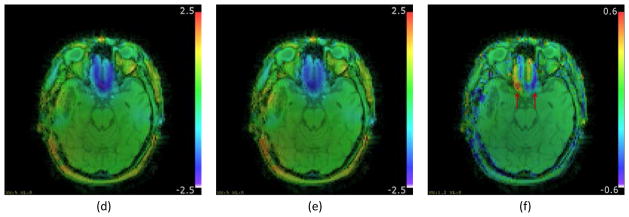
Field maps from patient data converted in mm of distortion at 300Hz/pixel readout bandwidth. (a) Distorted field map; (b) Undistorted field map; (c) Difference between (a) and (b). Figures (d, e, and f) are the same as (a, b and c) respectively, overlaid on the magnitude image. Arrows in (c and f) point to edges in the field map difference indicating geometric distortion at the region of high field inhomogeneity.
Figure 11.
Reconstructed Images from the brain of a patient. (a) Uncorrected image; (b) Image corrected using the distorted field map; (c) Image corrected using the undistorted field map; (d) Difference between (a) and (b); (e) Difference between (a) and (c); (f) Difference between (b) and (c). All intensity images as well as difference images are windowed identically. Visible edges in (d and e) indicate overall geometric distortion correction using field maps. Arrows in (f) point to edges in the difference image indicating geometric distortion correction in the high inhomogeneity region attributed to the use of the undistorted field map.
4 Discussion
Our work presented and evaluated an approach to estimate the undistorted field map and image from a double gradient-echo acquisition by correcting both geometrical and intensity errors caused by magnetic susceptibility effects. We have shown that although the distorted field map (by the magnetic susceptibility effect) can correct both geometry and intensity distortions to some extent, the undistorted field map can correct the distortion almost completely. Estimating the undistorted field map may be beneficial for correcting the images acquired with low readout-bandwidths. Considering that the geometrical distortion in the air-tissue interface is as large as a few mm, the additional improvement in the distortion correction using the undistorted field map can be important for using MRI in precision radiation therapy planning, e.g., stereotactic radiosurgery (SRS) for small brain metastases.
The conventional method to obtain the B0 inhomogeneity field map involves measuring the phase difference of two complex gradient echo images acquired at different echo-times in a single acquisition [Jezzard and Balaban 1995, Funai et al. 2008]. To reduce acquisition time, the clinical pulse sequence is implemented to have the readout gradients of the two echoes in the opposite directions (positive gradient for the first echo and negative gradient for the second one or vice versa). A B0 inhomogeneity field will cause a voxel displaced in the opposite directions in the first and second echo complex images, which results in the phase difference of the two echoes being inaccurate in both frequency and geometry. The geometrical error in the phase difference image could be twice large as that in either the first or second echo amplitude image. Our proposed method addresses this problem in the measured field inhomogeneity map from the phase difference of two gradient echoes.
We investigated the convergence of the proposed algorithm based upon the NRMS errors of the two successive iterations in both the field map and amplitude image. We found that the convergence rate of the image was faster than the field map (Figure 5). Since our main purpose is to estimate the undistorted field map, we chose our convergence criterion based upon the field map convergence. If the proposed algorithm is applied to reconstruct the undistorted image as a main purpose, a different criterion could be used. To reduce the number of iterations required in the computation of the undistorted field map, a fast approximation algorithm can be developed to find a near-optimal solution before applying the proposed algorithm, which will be the future work.
In this work we used modest-low readout-bandwidth acquisitions with the purpose of investigating the effects of field map distortion and avoid noise corruption due to low SNR. However, the regularization used in our method sufficiently suppresses the noise artifacts in the estimated field map. As part of our future work we intend to compare the field map reconstruction quality between low and high bandwidth acquisitions and investigate the tradeoff between low-SNR and low-distortion high-bandwidth acquisitions, and high-SNR and high-distortion low-bandwidth acquisitions. The chemical shift of water and fact signals also causes the relative geometric distortion between the two signals in the frequency-encoding direction in the magnitude images. However, the field map is less affected by the chemical shift due to the small susceptibility difference between fat and water (−8.4 and −8.9 10−6 cm3/mol, respectively). The future works will include the chemical shift effect in the joint reconstruction algorithm for simultaneous estimation of the undistorted image and field map.
We proposed the algorithm based upon a 3D acquisition of double gradient echoes to avoid the complicated susceptibility-caused distortion in the slice selection direction. In the clinical setting, this 3D acquisition that takes approximately two and a half minutes to acquire for volumetric head and neck images with a resolution of 2 mm or less is feasible. However, it is infeasible to acquire every image series by double echoes to apply our proposed method to reconstruct the undistorted images. Nevertheless, in the clinic, some images are acquired with a low readout-bandwidth to achieve better contrast and an adequate signal-to-noise ratio, e.g., 3D T1-weighted gradient-echo brain images. A low readout-bandwidth acquisition is more strongly impacted by the susceptibility-caused geometric distortion. For an SRS treatment plan, a 1 mm margin is often used to handle the geometric uncertainty associated with image-based planning and treatment. However, to use MRI alone for treatment planning, an additional uncertainty in the image geometrical accuracy would require an increase in the treatment plan margin, which is not desirable. Furthermore, for more general RT-planning, MR images of certain body sites are acquired with a large FOV, resulting in part of anatomy being scanned off-center (out of the sweet spot of B0 field homogeneity) where the distortion can be substantial. Our proposed method, in conjugation with the 3D dual gradient echo acquisition, can be used in several different ways. First, the estimated undistorted field map can be used to correct the clinical images. Second, the estimated undistorted images can be used as an undistorted template to register the clinical images. Third, the undistorted field map and/or undistorted images can be used to monitor geometric accuracy of the clinical images patient-by-patient and scan-by-scan for quality assurance (QA). The choice of correcting or not-correcting, and correcting using a distorted or undistorted field maps depends on the imaging sequence and the intended use of the images. When a tumor is located near the air-tissue interface, where the distortion is more profound in a low readout-bandwidth acquisition, the geometric distortion correction using a distorted field map may still not be within acceptable levels for precision RT, thus requiring the use of an undistorted field map. The proposed field map estimation method is being further evaluated in an ongoing patient study using a 3D dual-GRE sequence for estimating an undistorted field map that is subsequently used for geometric and intensity correction of low-bandwidth anatomical T1 images.
Acknowledgments
This work was supported by NIH R01 EB016079.
Bibliography
- Baldwin LN, Wachowicz K, Fallone BG. A two-step scheme for distortion rectification of magnetic resonance images. Med Phys. 2009;36:3917–3926. doi: 10.1118/1.3180107. [DOI] [PubMed] [Google Scholar]
- Cao Y. The promise of dynamic contrast-enhanced imaging in radiation therapy. Semin Radiat Oncol. 2011;21:147–156. doi: 10.1016/j.semradonc.2010.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang H, Fitzpatrick JM. A technique for accurate magnetic resonance imaging in the presence of field inhomogeneities. IEEE Trans Med Imaging. 1992;11:319–329. doi: 10.1109/42.158935. [DOI] [PubMed] [Google Scholar]
- Chung NN, Ting LL, Hsu WC, Lui LT, Wang PM. Impact of magnetic resonance imaging versus CT on nasopharyngeal carcinoma: primary tumor target delineation for radiotherapy. Head Neck. 2004;26:241–246. doi: 10.1002/hed.10378. [DOI] [PubMed] [Google Scholar]
- Crijns SP, Raaymakers BW, Lagendijk JJ. Real-time correction of magnetic field inhomogeneity-induced image distortions for MRI-guided conventional and proton radiotherapy. Phys Med Biol. 2011;56:289–297. doi: 10.1088/0031-9155/56/1/017. [DOI] [PubMed] [Google Scholar]
- Fessler JA, Rogers WL. Spatial resolution properties of penalized-likelihood image reconstruction: space-invariant tomographs. IEEE Trans Image Process. 1996;5:1346–1358. doi: 10.1109/83.535846. [DOI] [PubMed] [Google Scholar]
- Funai AK, Fessler JA, Yeo DT, Olafsson VT, Noll DC. Regularized field map estimation in MRI. IEEE Trans Med Imaging. 2008;27:1484–1494. doi: 10.1109/TMI.2008.923956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo WY, Nordell B, Karlsson B, Soderman M, Lindqvist M, Ericson K, Franck A, Lax I, Lindquist C. Target delineation in radiosurgery for cerebral arteriovenous malformations. Assessment of the value of stereotaxic MR imaging and MR angiography. Acta Radiol. 1993;34:457–463. [PubMed] [Google Scholar]
- Haie-Meder C, et al. Recommendations from Gynaecological (GYN) GEC-ESTRO Working Group (I): concepts and terms in 3D image based 3D treatment planning in cervix cancer brachytherapy with emphasis on MRI assessment of GTV and CTV. Radiother Oncol. 2005;74:235–245. doi: 10.1016/j.radonc.2004.12.015. [DOI] [PubMed] [Google Scholar]
- Hanvey S, Sadozye AH, McJury M, Glegg M, Foster J. The influence of MRI scan position on image registration accuracy, target delineation and calculated dose in prostatic radiotherapy. Br J Radiol. 2012;85:e1256–1262. doi: 10.1259/bjr/26802977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hentschel B, Oehler W, Strauss D, Ulrich A, Malich A. Definition of the CTV prostate in CT and MRI by using CT-MRI image fusion in IMRT planning for prostate cancer. Strahlenther Onkol. 2011;187:183–190. doi: 10.1007/s00066-010-2179-1. [DOI] [PubMed] [Google Scholar]
- Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med. 2003;49:193–197. doi: 10.1002/mrm.10354. [DOI] [PubMed] [Google Scholar]
- Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- Lim K, et al. Consensus guidelines for delineation of clinical target volume for intensity-modulated pelvic radiotherapy for the definitive treatment of cervix cancer. Int J Radiat Oncol Biol Phys. 2011;79:348–355. doi: 10.1016/j.ijrobp.2009.10.075. [DOI] [PubMed] [Google Scholar]
- Matakos A, Fessler JA. Joint Estimation of Image and Fieldmap in Parallel Mri Using Single-Shot Acquisitions. 2010; 7th Ieee International Symposium on Biomedical Imaging: From Nano to Macro; 2010. pp. 984–987. [Google Scholar]
- Pech M, Mohnike K, Wieners G, Bialek E, Dudeck O, Seidensticker M, Peters N, Wust P, Gademann G, Ricke J. Radiotherapy of liver metastases. Comparison of target volumes and dose-volume histograms employing CT- or MRI-based treatment planning. Strahlenther Onkol. 2008;184:256–261. doi: 10.1007/s00066-008-1849-8. [DOI] [PubMed] [Google Scholar]
- Quon H, Brizel DM. Predictive and prognostic role of functional imaging of head and neck squamous cell carcinomas. Semin Radiat Oncol. 2012;22:220–232. doi: 10.1016/j.semradonc.2012.03.007. [DOI] [PubMed] [Google Scholar]
- Wang H, Balter J, Cao Y. Patient-induced susceptibility effect on geometric distortion of clinical brain MRI for radiation treatment planning on a 3T scanner. Phys Med Biol. 2013;58:465–477. doi: 10.1088/0031-9155/58/3/465. [DOI] [PubMed] [Google Scholar]