Who Is Hurt by Procyclical Mortality?

Abstract

There is renewed interest in understanding how fluctuations in mortality or health are related to fluctuations in economic conditions. The traditional perspective that economic recessions lower health and raise mortality has been challenged by recent findings that reveal mortality is actually procyclical. The epidemiology of the phenomenon — traffic accidents, cardiovascular disease, and smoking and drinking — suggests that socioeconomically vulnerable populations might be disproportionately at risk of “working themselves to death” during periods of heightened economic activity. In this paper, I examine mortality by individual characteristic during the 1980s and 1990s using the U.S. National Longitudinal Mortality Study. I find scant evidence that disadvantaged groups are significantly more exposed to procyclical mortality. Rather, working-age men with more education appear to bear a heavier burden, while those with little education experience countercyclical mortality.

Background and motivation

We typically assume that the downside of the business cycle is bad, especially for individuals of lesser means. The rise of the modern welfare state earlier in the past century was a direct effort to limit the pain inflicted by economic recessions, if not head them off entirely. Similarly, the traditional perspective on the health impacts of economic fluctuations held that recessions were bad, especially for the vulnerable (Brenner, 1971, 1975, 1979).

But a number of recent contributions have cast doubt on this view, at least when applied to developed countries with functioning social safety nets. Ruhm (2000, 2003, 2007, 2008), Laporte (2004), Neumayer (2004), Tapia Granados (2005, 2008), Gerdtham and Ruhm (2006), and Tapia Granados and Ionides (2008) all report patterns of procyclical mortality or health, or the worsening of mortality during expansions and improvement during recessions, in the U.S. and European countries. As reviewed by Ruhm (2006, 2007), this finding has become relatively standard, although the recent literature is not completely of one voice. Gerdtham and Johannesson (2005) and Svensson (2007) find countercyclical mortality in Swedish data, while Joyce and Mocan (1993) report no cyclical patterns in infant health.

A central question is precisely who is vulnerable to procyclical mortality. Most of the previous studies in this area have decomposed the phenomenon by age, sex, sometimes race, and cause of death, which is easily done with national vital statistics. Impacts appear to be relatively uniform over age and sex. A key finding is that external causes, in particular traffic accidents, appear to account for a large amount of procyclical mortality. Cardiovascular disease is another commonly identified culprit, as is cirrhosis of the liver and other types of excesses. But an examination focusing solely on the causes of death is limited and somewhat unsatisfactory for researchers and policymakers hoping to improve public health. It is doubtful whether policies designed with current knowledge could effectively ameliorate procyclical mortality without depressing economic activity, or essentially throwing the baby out with the bathwater (Edwards, 2005). We need to know more about the microeconomics of the phenomenon (Ruhm, 2006).

Who are the victims of procyclical mortality? Are they spread evenly across socioeconomic classes, or are they concentrated in a particular range? Information on causes of death does not offer a concise story here. Traffic fatalities could be suburban commuters or inner-city pedestrians. Heart attack victims could be the hard-living working poor, high-stress executives, or some combination. Pollution could affect many individuals, but vulnerable populations like the children, the elderly, and those with asthma may be disproportionately hurt. Edwards (2005) discusses how in the U.S., health insurance coverage is in one sense countercyclical, rising during recessions and falling during expansions. Medicaid, the public medical insurance program for Americans under age 65, is means-tested, so it is naturally countercyclical. We know that a large portion of those without medical insurance in the U.S. are the working poor (Glied, 2001). Given these facts, a key question is to what extent these working poor may be especially vulnerable during periods of rapid economic expansion in the U.S.

In this paper, I examine procyclical mortality in the restricted file of the U.S. National Longitudinal Mortality Study (NLMS), a large dataset of individuals with time-invariant characteristics and a mortality follow-up. After describing the dataset, I first examine aggregate mortality in the NLMS over time. Then I model mortality at the individual level data and test for differential incidence of procyclical mortality. In the last section I discuss the results.

The National Longitudinal Mortality Study

The NLMS is a dataset of individuals who are interviewed once in a Current Population Survey and then subsequently matched to death certificates via the National Death Index. The result is unique among U.S. datasets: a large-scale panel study of mortality connected to a one-time snapshot of covariates such as education, occupation, employment status, and family income. The NDI identifies time of death down to six-hour groupings, along with cause of death and other data from the death certificate. The NLMS is maintained by the National Heart, Lung, and Blood Institute (NHLBI) of the U.S. Census. Further details regarding the NLMS can be found in Rogot et al. (1988, 1992).

One shortcoming of the NLMS data is the data universe. The CPS is representative only of the civilian noninstitutionalized population, and we know that mortality is higher among nursing home residents. This source of bias will gradually evaporate over time, since the NLMS will match the death of any CPS respondent who later entered a nursing home. But as revealed by Preston and Elo (1995), the NLMS yields lower 5-year mortality than do vital statistics because of undersampled institutional mortality. I can do little but acknowledge this shortcoming and suggest that its primary impact is likely to be observable at older ages, while its effect on temporal patterns is wholly unknown. There is no extant literature on short-term trends in institutional mortality, which is typically difficult to measure except in the cross section, so I have no means of directly assessing how its omission early in the NLMS panel may bias this study.

A second shortcoming is that almost all covariates in the NLMS are only measured once, at the time of the initial CPS interview prior to tracking in the NDI. Most characteristics except birth date, sex, race, and education fluctuate over the life cycle, casting considerable doubt on their usefulness in a single snapshot for understanding mortality at a future data. As a result, I plan to emphasize results based on education.

For this study, I examine the restricted version of the NLMS, which follows over a million adults during the 19-year period between 1979 and 1998, about 13 percent of whom died during the panel. In an earlier version of this paper I examined the public file of the NLMS, which ends around 1989 and does not provide exact dates of death or state of residence. To my knowledge, no previous study has examined temporal patterns in the NLMS. I first construct total age and sex-adjusted annual mortality in the NLMS and examine it relative to official vital statistics and to indicators of the business cycle. We are interested in whether these time-averaged NLMS data look like official annual statistics and how they fluctuate with macroeconomic variables.

Aggregated NLMS data

Levels, trends, and volatility in mortality

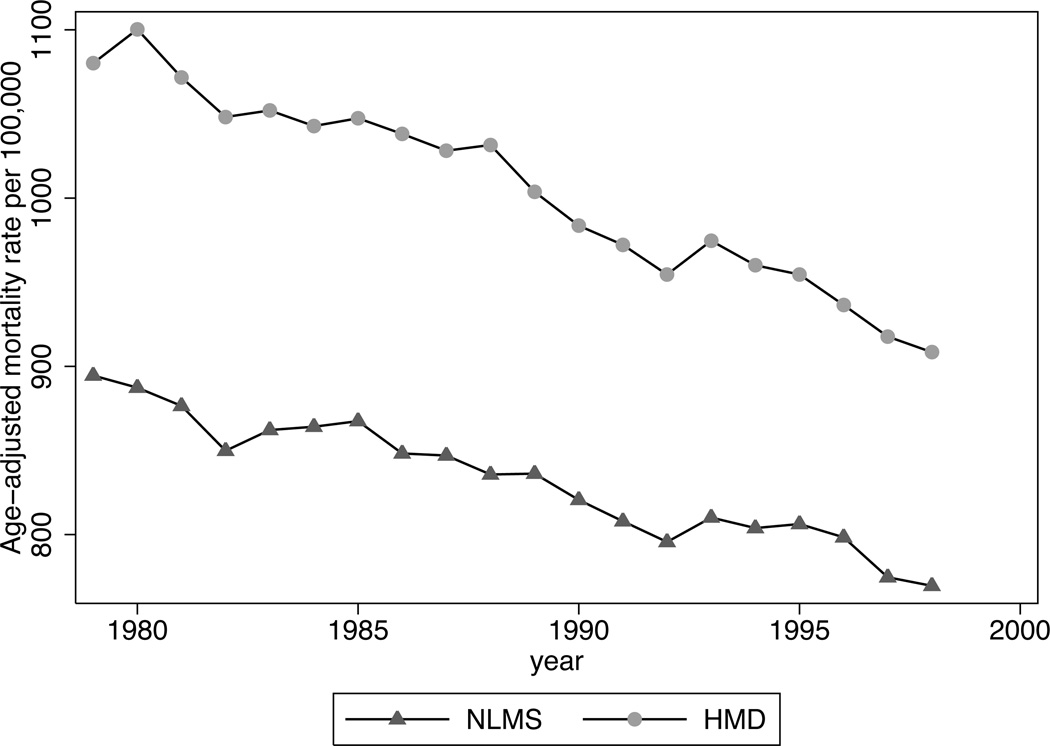
Figure 1 plots two times series of the age-adjusted mortality rate among individuals of both sexes aged 10 and over, one using the NLMS data and the other using data from the Human Mortality Database, which is drawn from national vital statistics. Aggregate mortality in NLMS is about 17 percent lower than in official data, but neither trend nor volatility appears to be substantially dissimilar. The lack of institutional coverage probably accounts for both the reduced level of the NLMS series as well as a slightly less steep downward trend. The NLMS measures CPS respondents who enter and die in nursing homes after the CPS interview, so over time the undersampling bias should fade a little. There are scant differences between the two series in fluctuations around trend, and that is promising for detecting procyclical mortality in the NLMS.

Figure 1.

Age-adjusted Mortality in the NLMS and HMD

Notes: Data are drawn from the National Longitudinal Mortality Study (NLMS) and the Human Mortality Database (HMD). Each series consists of age-adjusted mortality rates for both sexes combined at ages 10 and over calculated by the author using age-specific mortality rates from each source and the age distribution for both sexes combined in 1990 as provided by the HMD.

Procyclical mortality

I posit that the business cycle, indexed by the variable BC_t, impacts mortality m_it for individual i at time t, which rises exponentially in age, x_it:

$$\text{log}{m}_{it}={\alpha }_i+\beta x_{it}+\delta (x_{it})t+\gamma {\mathit{\text{BC}}}_t+\overrightarrow{\theta }\cdot {\overrightarrow{X}}_{it}+{\epsilon }_{it}$$ (1)

where α_i is an individual fixed effect; δ(x_it) < 0 is the rate of temporal decline in mortality at age x_it; X⃗_it is a vector of covariates; and ε_it is a white-noise error. Lee and Carter (1992) reveal that δ varies strongly with age but has remained relatively stable over time. Further, we can conceptualize x and X⃗ as remaining fixed over time for the average individual. With these simplifications, differencing equation (1) produces a relationship for the change in aggregate mortality:

$$\mathrm{\Delta }\text{log}{\overline{m}}_t=\overline{\delta }+\gamma \mathrm{\Delta }{\mathit{\text{BC}}}_t+{\nu }_t,$$ (2)

m̅_t is the age and sex-adjusted mortality rate, δ̅ is the percentage decline in mortality averaged over time and age, and ν_t is the difference in average ε_it’s, also a white noise error.

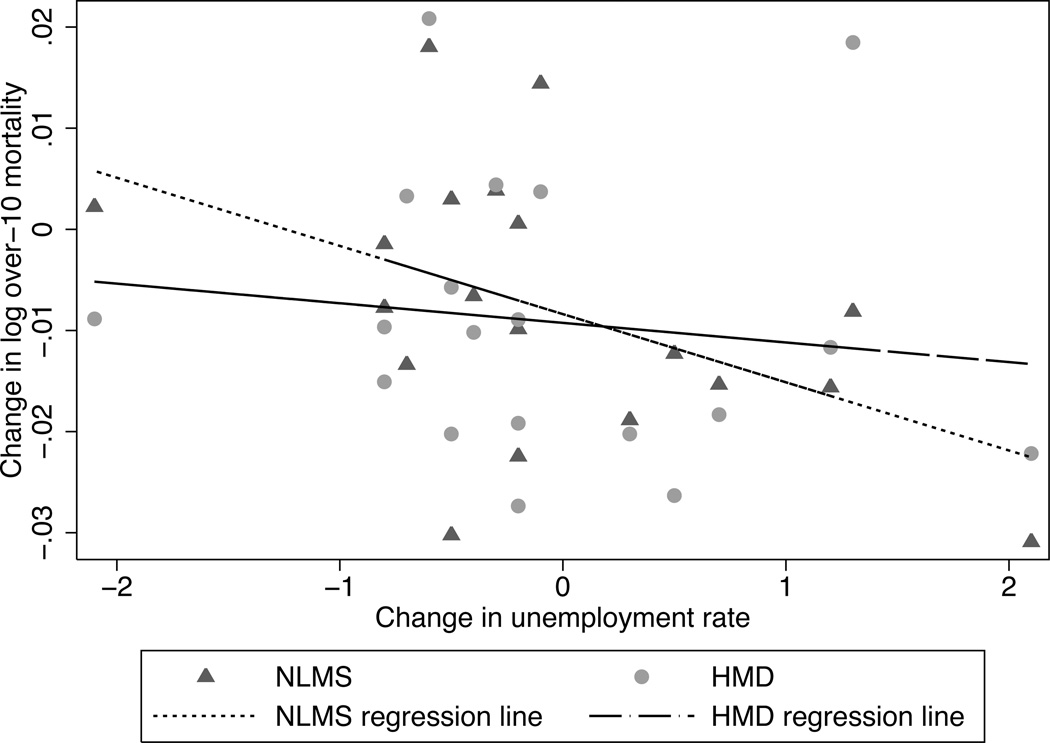
Figure 2 plots annual changes in the age-adjusted log mortality rate for both sexes combined at ages 10 and over along the vertical axis against changes in a key business cycle indicator, the civilian unemployment rate. I plot both the NLMS and the official mortality series to help visually gauge any differences between the two. For each series I estimate equation (2) using ordinary least squares and overlay the trend lines.

Figure 2.

Changes in log mortality versus changes in unemployment 1980–1998

Notes: This figure plots changes in log age-adjusted mortality rates for both sexes combined at ages 10 and over against changes in the civilian unemployment rate. The mortality data are taken from the two series depicted in Figure 1; the unemployment data are provided by the U.S. Bureau of Labor Statistics. Trend lines are ordinary least squares fits of the each data series to a constant and the change in unemployment. In the NLMS data, the slope is estimated at γ̂ = − 0.0067 with a standard error of 0.0003, while in the HMD data, it is γ̂= −0.0019 with a standard error of 0.0036.

The simple bivariate relationship between mortality and unemployment is stronger in the NLMS data, as evidenced by its steeper OLS trend line. The slope, γ̂ in equation (2), is estimated at –0.0067 with a standard error of 0.0003 in the NLMS data, while the HMD data produces γ̂ = −0.0019 with a standard error of 0.0036. That is, a one percentage point increase in the unemployment rate during 1979 to 1998 is associated with a decrease in the aggregate NLMS mortality rate of 0.67 percent, and a decrease in the official U.S. mortality rate of about 0.19 percent. By comparison, estimates of γ̂ in the literature typically range between −0.003 to −0.005 (Ruhm, 2006), with the largest estimate, γ̂ = −0.011, recovered by Neumayer (2004) in German state-level data. Although the HMD data do not exhibit a significant pattern of procyclical mortality during this specific time period, aggregated NLMS mortality data do, and the size of the effect fits neatly into the range of previously reported estimates.

NLMS death probabilities, individual characteristics, and the macroeconomy

With data on individual deaths in the NLMS, I can test for procyclical mortality and examine whether and how it may vary across individuals. In my preferred specification, I model the logit transformation of individual i’s death probability at time t, q_it, which is highly linear in age, x_it (Himes et al., 1994):

$$\text{log}\left(\frac{q_{it}}{1-q_{it}}\right)={\alpha }_i+\beta x_{it}+\delta t+\gamma {\mathit{\text{BC}}}_t+\overrightarrow{\theta }\cdot {\overrightarrow{X}}_i.$$ (3)

I pool annual NLMS data on exposures and deaths and merge with annual macroeconomic data by state of residence during the initial CPS interview. The identifying variation in BC_t is thus both temporal and cross-sectional in nature.

Owing to the limitations of the NLMS design, the covariates in X⃗_i are fixed for individual i over time, since covariates are only measured once in the initial CPS interview. I specify a fixed linear time trend, δ, but I also split the sample into broad age/sex categories so that δ effectively varies by age. I follow Elo and Preston (1996) in focusing on mortality at ages 25–64 and 65–89 separately by sex because of small sample sizes at advanced ages and incomplete education data below age 25. As robustness checks, I tried modeling individual random effects, α_i, and I also estimated a probit of the death probability rather than the logit. Neither variation affected the results appreciably, so I report only the ordinary logit results.

Modeling the level rather than the change in mortality is advantageous for two reasons. The logit and probit models are widely used and well suited to this task, and most of the covariates in X⃗_i do not vary over time, either by construction or due to data limitations. A drawback is that the level of mortality is nonstationary, as are many business cycle variables. Including the linear time trend δ addresses the first problem, but the properties of BC_t remain important.

The most common choice for BC_t is the civilian unemployment rate, which is stationary over long periods of time. Researchers have also used real GDP, industrial production, and hours worked, which are not. In my short panel, the unemployment rate appears to be nonstationary, but the change in unemployment is better behaved and tightly correlated (−0.9054) with the percentage change in real GDP. I therefore use the change in unemployment as my preferred BC_t variable. Gerdtham and Johannesson (2005) find this transformation produces more consistent results in Swedish microdata as well.

Results by age and sex

Table 1 presents the results of estimating equation (3) separately by sex and broad age group for men and women at working ages and older. I use the same array of covariates specified by Elo and Preston (1996), with the addition of the time trend, Hispanic status, and the change in the unemployment rate. Models of mortality at ages under 25 produced statistically insignificant estimates of the procyclical effect, γ̂, so I omit them. That null result is noteworthy because motor vehicle accidents, which tend to be procyclical, are the leading cause of death among children and adolescents in the U.S. But since overall mortality is so low at young ages, power to detect procyclical mortality in individual-level data may be insufficient.

Table 1.

Logit regressions of the annual log odds of dying on the change in the state unemployment rate and individual characteristics, individuals aged 25–89

	Males			Females			Males			Females
	Age 25–64			Age 25–64			Age 65–89			Age 65–89
Δ Unemployment rate	−0.0101	**	(0.0051)	−0.0074		(0.0063)	−0.0180	***	(0.0046)	−0.0281	***	(0.0045)
Time	−0.0060	***	(0.0010)	0.0062	***	(0.0012)	0.0067	***	(0.0009)	0.0153	***	(0.0009)
Age	0.0861	***	(0.0005)	0.0838	***	(0.0006)	0.0639	***	(0.0007)	0.0746	***	(0.0006)
White	---			---			---			---
African American	0.1805	***	(0.0160)	0.2742	***	(0.0176)	−0.1129	***	(0.0186)	−0.1101	***	(0.0171)
Other race	−0.0603	*	(0.0320)	−0.0596		(0.0378)	−0.3680	***	(0.0381)	−0.3811	***	(0.0428)
Non-Hispanic	---			---			---			---
Hispanic	−0.2843	***	(0.0229)	−0.3933	***	(0.0284)	−0.3272	***	(0.0268)	−0.3101	***	(0.0275)
Unknown	−0.1149	***	(0.0259)	−0.1401	***	(0.0336)	−0.1820	***	(0.0250)	−0.1204	***	(0.0233)
Born: Northeast	---			---			---			---
South	0.0465	**	(0.0201)	−0.0135		(0.0237)	−0.0362		(0.0229)	−0.0211		(0.0205)
Midwest	−0.0280		(0.0202)	−0.0338		(0.0241)	−0.0151		(0.0222)	−0.0250		(0.0199)
West	−0.0766	***	(0.0267)	−0.0209		(0.0319)	−0.0973	***	(0.0321)	−0.0404		(0.0300)
Elsewhere	−0.3676	***	(0.0360)	−0.3230	***	(0.0403)	−0.2298	***	(0.0300)	−0.2262	***	(0.0271)
Unknown	−0.0528	***	(0.0166)	−0.0889	***	(0.0198)	−0.0747	***	(0.0184)	−0.1328	***	(0.0165)
0–6 years of school	0.1571	***	(0.0192)	0.2735	***	(0.0240)	0.0868	***	(0.0159)	0.0701	***	(0.0152)
7–8	0.1612	***	(0.0149)	0.2329	***	(0.0180)	0.1073	***	(0.0130)	0.0758	***	(0.0119)
9–11	0.1746	***	(0.0133)	0.2612	***	(0.0148)	0.0988	***	(0.0143)	0.0717	***	(0.0128)
12	---			---			---			---
13–15	−0.0963	***	(0.0147)	−0.1102	***	(0.0179)	−0.0079		(0.0176)	−0.0177		(0.0156)
16+	−0.3958	***	(0.0149)	−0.3099	***	(0.0212)	−0.1285	***	(0.0169)	−0.0467	***	(0.0176)
Education unknown	−0.0284		(0.1209)	0.3833	**	(0.1646)	−0.2763	*	(0.1487)	−0.2164		(0.1452)
Log 1980 family income	−0.1922	***	(0.0053)	−0.1710	***	(0.0064)	−0.1190	***	(0.0061)	−0.0842	***	(0.0056)
Household size (people)	−0.0280	***	(0.0032)	−0.0309	***	(0.0040)	−0.0036		(0.0049)	0.0304	***	(0.0044)
Married	---			---			---			---
Widowed	0.3316	***	(0.0258)	0.1850	***	(0.0167)	0.0845	***	(0.0138)	0.1418	***	(0.0097)
Divorced	0.3145	***	(0.0161)	0.1820	***	(0.0173)	0.1225	***	(0.0216)	0.1710	***	(0.0207)
Never married	0.3109	***	(0.0160)	0.1652	***	(0.0224)	−0.0032		(0.0210)	0.1661	***	(0.0188)
Marital status unknown	−0.0754		(0.1600)	−0.9734	***	(0.2836)	0.3445		(0.2492)	−0.1105		(0.2769)
Not a metro area	---			---			---			---
Live in central city	0.0934	***	(0.0120)	0.0968	***	(0.0141)	0.0097		(0.0114)	0.0059		(0.0104)
Live in metro area	0.0277	**	(0.0109)	0.0520	**	(0.0132)	−0.0102		(0.0106)	0.0209	**	(0.0101)
Unknown	−0.0105		(0.1651)	0.9538	***	(0.3018)	−0.4059		(0.3028)	0.0894		(0.3202)
Constant	4.4401	**	(1.8951)	−20.4462	**	(2.3297)	−19.8964	***	(1.8010)	−38.7370	***	(1.7348)
N	6,160,540			6,817,322			874,891			1,373,046
Chi-square statistic	62,545.46			46,742.32			14,377.45			24,518.16

Notes: Asterisks denote statistical significance at the 1% (three), 5% (two), and 10% (one) levels. Each column shows the coefficient estimates from a logit regression of the log odds of dying during a calendar year between 1979 and 1998. The state unemployment rate is measured in percentage points and is obtained from the U.S. Bureau of Labor Statistics. All other data are from the National Longitudinal Mortality Study (NLMS) restricted file. The time variable starts at 0 and indexes years. The default category is a white non-Hispanic individual born in the Northeast with 12 years of education (if 25 or older), who is married and not living in a metro area. Ethnicity (Hispanic) is a separate question from race.

The top row of Table 1 reveals evidence of significantly procyclical mortality among adults in each age/sex grouping except working-age females. Coefficients on the change in unemployment for the other three groups range between γ̂ = −0.0101 and −0.0281 and are significant at the 5 or 1 percent level. These patterns reflect those revealed by Tapia Granados (2005), who reports smaller procyclical effects during working age as opposed to retirement and larger effects among males. Among working-age females, γ̂ is smaller at −0.0074 and insignificant in this sample. That standard errors are large enough to render insignificant even a relatively large γ̂, by the standards of the literature, is a grim reminder of the limited power of individual-level mortality regressions on even a large-scale sample when mortality is rare.

Other coefficient estimates and their standard errors are similar to those reported by Elo and Preston. An additional year of age raises the odds of dying by about 8 percent. Being African- American raises the log odds of dying among individuals of working age, but the effect switches sign in retirement. Hispanic ethnicity is protective for all age/sex groups. Being born outside of the Northeast is generally associated with lower odds of dying. Education, income, being married, and living in a rural area are all protective. The time trends in mortality, positive for all groups except working-age males, are puzzling but may be capturing the changing coverage of institutional mortality.

Results by race, SES, employment, and occupation

The key advantage of the NLMS is that it measures many more individual characteristics than age and sex, so I can test for differential impacts of procyclical mortality across individual or group characteristics. My estimation strategy is to sequentially interact covariates with the BC_t variable and test the significance of each interaction effect in a separate regression. I choose to estimate each interaction separately because power is limited. I also tried estimating larger models with several categorical interactions included, such as the full set of educational categories. Results using either method were qualitatively similar, likely because the tests are similar. In models with only one interaction, such as those in Table 2, I am testing whether a single group’s treatment differs from the average treatment of all the others; with multiple interactions, I am testing whether a single group differs from a baseline subgroup, where the baseline is typically chosen to be representative of the average. I found that likelihood-ratio tests across nested regressions and simple t-tests of the interaction coefficients produced identical results, so I present the t-tests.

Table 2.

Interaction effects from logit regressions of the annual log odds of dying on the change in the state unemployment rate and individual characteristics

	Males			Females			Males			Females
	Age 25–64			Age 25–64			Age 65–89			Age 65–89
African American	−0.0264	*	(0.0156)	0.0116		(0.0172)	0.0178		(0.0163)	−0.0003		(0.0163)
Hispanic	0.0219		(0.0251)	0.0380		(0.0313)	0.0173		(0.0288)	0.0681		(0.0303)
Educational attainment
0–6 years	0.0368	**	(0.0177)	0.0390	*	(0.0232)	0.0126		(0.0116)	0.0044		(0.0123)
7–8	−0.0041		(0.0145)	−0.0165		(0.0184)	−0.0135		(0.0100)	−0.0115		(0.0100)
9–11	0.0170		(0.0128)	−0.0032		(0.0150)	0.0084		(0.0120)	−0.0093		(0.0116)
12	−0.0264	**	(0.0106)	−0.0035		(0.0125)	0.0010		(0.0109)	0.0173	*	(0.0102)
13–15	−0.0003		(0.0152)	0.0240		(0.0198)	0.0071		(0.0165)	−0.0015		(0.0155)
16+	0.0097		(0.0155)	−0.0345		(0.0240)	−0.0111		(0.0156)	−0.0032		(0.0175)
High school and higher (12+)	−0.0202	**	(0.0102)	−0.0034		(0.0124)	−0.0009		(0.0092)	0.0122		(0.0090)
Family income in 1990 dollars
$0–$7,000	0.0243		(0.0179)	0.0245		(0.0176)	0.0125		(0.0124)	−0.0146		(0.0097)
$7,000–$12,000	−0.0342	*	(0.0196)	0.0188		(0.0197)	−0.0258	**	(0.0117)	−0.0193	*	(0.0110)
$12,000–$20,000	−0.0247	*	(0.0150)	−0.0017		(0.0166)	0.0018		(0.0105)	−0.0012		(0.0113)
$20,000–$30,000	0.0066		(0.0121)	−0.0302	**	(0.0152)	−0.0019		(0.0116)	−0.0036		(0.0129)
$30,000–$40,000	0.0088		(0.0135)	−0.0278		(0.0181)	−0.0019		(0.0156)	0.0285		(0.0177)
$40,000–$75,000	0.0015		(0.0113)	0.0159		(0.0150)	0.0216		(0.0140)	0.0441	***	(0.0158)
$75,000+	0.0021		(0.0212)	0.0137		(0.0290)	0.0208		(0.0246)	0.0537	*	(0.0294)
Urban residence in 1980	−0.0009		(0.0106)	−0.0065		(0.0132)	0.0067		(0.0091)	0.0272	***	(0.0092)
Employment status in 1980
Employed	0.0500	***	(0.0108)	0.0748	***	(0.0121)	0.0188	*	(0.0105)	0.0565	***	(0.0148)
Employed, not working last week	0.0150		(0.0236)	−0.0028		(0.0344)	0.0319		(0.0333)	0.0728		(0.0524)
Unemployed	−0.0757	***	(0.0242)	−0.0283		(0.0365)	0.0797		(0.0491)	0.0112		(0.0754)
Not in the labor force:
Disabled, unable to work	−0.0598	**	(0.0261)	−0.2660	***	(0.0459)	0.0242		(0.0243)	−0.0137		(0.0249)
Retired, housekeeping, student	−0.0434	***	(0.0133)	−0.0538	***	(0.0120)	−0.0260	***	(0.0097)	−0.0429	***	(0.0126)
Occupation
Professional/technical	0.0207		(0.0177)	0.0118		(0.0244)	0.0023		(0.0263)	−0.0006		(0.0339)
Managers/administrators	−0.0055		(0.0157)	0.0768	**	(0.0318)	−0.0054		(0.0229)	0.1028	**	(0.0471)
Sales workers	0.0199		(0.0193)	0.0187		(0.0251)	0.0019		(0.0245)	0.0612	*	(0.0320)
Clerical workers	0.0044		(0.0233)	0.0337	**	(0.0171)	−0.0382		(0.0337)	0.0441		(0.0269)
Craftsmen workers	0.0465	***	(0.0126)	0.0210		(0.0551)	0.0268		(0.0209)	−0.0261		(0.0739)
Operatives except transport	−0.0283		(0.0172)	0.0958	***	(0.0236)	0.0346		(0.0296)	0.0156		(0.0405)
Transport operatives	−0.0127		(0.0192)	−0.1188		(0.0943)	0.0153		(0.0343)	−0.1088		(0.2241)
Laborers, no farm	−0.0322		(0.0233)	0.0353		(0.0526)	0.0497		(0.0359)	0.1482		(0.1010)
Farmers and farm managers	0.0728	**	(0.0316)	0.0751		(0.1230)	0.0324		(0.0270)	0.1188		(0.1174)
Farm laborers/managers	0.0125		(0.0338)	0.1348	*	(0.0767)	0.0177		(0.0381)	0.1567	*	(0.0926)
Service workers	−0.0019		(0.0194)	0.0016		(0.0198)	0.0279		(0.0235)	0.0693	**	(0.0282)
Private household workers	−0.0569		(0.2287)	0.0953		(0.0397)	−0.0547		(0.0660)	0.0198		(0.0390)

Notes: Asterisks denote statistical significance at the 1% (three), 5% (two), and 10% (one) levels. Each column shows the coefficient estimates from a logit regression of the log odds of dying during a calendar year between 1979 and 1998. The state unemployment rate is measured in percentage points and is obtained from the U.S. Bureau of Labor Statistics. All other data are from the National Longitudinal Mortality Study (NLMS) restricted file. The time variable starts at 0 and indexes years. The default category is a white non-Hispanic individual born in the Northeast with 12 years of education (if 25 or older), who is married and not living in a metro area. Ethnicity (Hispanic) is a separate question from race.

Each cell depicts an interaction coefficient and its standard error from a separate logit regression.

Table 2 shows point estimates and standard errors of a wide array of interaction effects, each from a separate logit regression including all the original covariates from Table 1 (not shown) as well as the single interaction effect of interest. The total cyclical effect γ̂ for the particular subgroup is then roughly the sum of the interaction effect in Table 2 and the coefficient in the top row of Table 1.

Point estimates of the interaction effects vary considerably and are sometimes large, but relatively low power hampers inference. The top row of Table 2 explores the interaction of the business cycle variable with race. For males of working age, the interaction with African American is −0.0264, more than twice as large as the γ̂ shown in Table 1 and significant at the 10 percent level. This constitutes weak evidence of a stronger procyclical effect among African American men of working age, what we would consider an example of the disadvantaged “working themselves to death.” But in other age/sex groups, interactions with race are insignificant. Interactions with Hispanic ethnicity are even noisier.

The next set of rows suggests some connection between the level of educational attainment and procyclical mortality, but it is limited to working-age men. Men and women of working age in the lowest attainment group, with 0–6 years of education, seem to experience significantly countercyclical mortality; interaction coefficients are positive, significant, and relatively large at about 0.038. That is, mortality among those with very low education rises, and by quite a bit, during economic bad times. As educational attainment increases, the interaction effect first becomes insignificant and then switches sign and regains significance among working-age males. As shown in the table, the cut point is a high school degree. Those with that level of attainment and higher experience procyclical mortality that is significantly amplified by about −0.020.

Interactions with family income in 1990 dollars measured at the time of the CPS interview appear in the next set of rows in Table 2. No clear robust relationship emerges, although there is some evidence that the lower middle class may suffer disproportionately greater procyclical mortality. Working-age males in households earning $7,000 to $20,000 per year, solidly in the lower middle class, suffer amplified procyclical mortality, but the interactions are significant only at the 10 percent level. Older males in a similar income category also experience more procyclical mortality. Among working-age females, the interaction term is significant for somewhat higher-earning households, which may include two earners. Patterns among older females suggest that high income is protective against the procyclical effect for them, so much so that their mortality may be countercyclical.

Geographic information in the NLMS is relatively limited. Urban versus rural residence, which we can measure and which could matter for exposure to traffic deaths and air pollution, is important for the procyclical effect only among women past retirement age.

The lower half of Table 2 explores patterns in differential effects by employment status and occupation. As is the case with income, these descriptors may have changed considerably during the panel after their initial measurement in the CPS interview. Results show a vastly strengthened procyclical effect among individuals who were unemployed, disabled, or retired at the baseline interview. The table also reveals evidence of strongly countercyclical mortality among those who were employed at baseline. But as with income, the transitory nature of these characteristics in the NLMS sample, where they are only measured once at the beginning, casts doubt on the results. They contrast sharply with those of Ruhm (2003), who finds that bad health is more strongly procyclical among employed individuals in the 1972–1981 National Health Interview Surveys. Since the NHIS measures employment contemporaneously with health, while the NLMS cannot, Ruhm’s results are arguably preferable and call into question the use of volatile snapshot variables like income and employment status in explaining temporal patterns.

At the bottom of Table 2, patterns across occupational categories suggest very little differential incidence, which is surprising. Transport operators ought to be more exposed to the risk of traffic accidents than the average driver, and we know accidents are important for procyclical mortality. Still, workers in many occupations are subject to job-related stress, which we also expect to vary procyclically, and they may engage in unhealthy behaviors in reaction to it. Statistical power is a problem that plagues all the models of covariates interactions equally, so it is probably not specifically at fault here. Taken as a whole, the interaction results suggest that race, education, and possibly income are important in mediating exposure to procyclical mortality, while occupation is not and initial employment status must be too noisy for us to tell.

Results by underlying cause of death

The NLMS codes deaths according to underlying cause of death as reported on the death certificate. I combined deaths classified using the ICD-9 system into 12 functional categories and ran separate logit models on each individual cause of death using the full set of covariates listed in Table 1. For brevity, I summarize results qualitatively because they revealed few statistically significant patterns, probably because of reduced power. Virtually all causes appeared to vary procyclically in the NLMS data, especially among working-age males. For that group, none of the causes appeared to vary countercyclically, even suicides. There was only marginally more variation in cause-specific γ̂ across the among other age/sex groups. Suicides appeared to rise during economic bad times among both men and women over 65.

Discussion

Data from the National Longitudinal Mortality Study reveals that mortality was procyclical in the U.S. during the 1980s and 1990s. This result matches up well with the findings of Ruhm (2000, 2003, 2007, 2008), Laporte (2004), Neumayer (2004), Tapia Granados (2005, 2008), Gerdtham and Ruhm (2006), and Tapia Granados and Ionides (2008), but it conflicts with that of Gerdtham and Johannesson (2005), the only other study that examines cyclical mortality trends using individual-level data. They find countercyclical mortality among men and acyclical mortality among women in Sweden. Precisely why my results differ from theirs in unclear. Gerdtham and Johannesson control for fewer covariates that I do, so omitted variables could be biasing their results. The underlying socioeconomic and sociocultural systems are clearly different in the U.S. compared to Sweden, and that may explain some of the divergence.

The size of the procyclical effect that I recover in NLMS data is somewhat larger than what researchers have found in other datasets. In aggregate NLMS data, the coefficient on the change in unemployment is γ̂ = −0.0067, while in individual-level NLMS mortality, I find effects around γ̂ = −0.01. Although outside the typical range of estimates cited by Ruhm (2006), my coefficients are consistent with those reported by Neumayer (2004). The choice of sample period could explain my somewhat larger estimates; the 1980s were a time of much macroeconomic volatility. The NLMS mortality data may also be more volatile than vital statistics, perhaps due to the smaller sample size or associated with the changing coverage of institutional mortality, if the latter varies differently over the business cycle. Since my results focus on ages 25 and over, they will overstate total procyclical mortality to the extent that infant and child mortality is not procyclical, although this effect probably is not large. Finally, it is possible that the data aggregation in other studies may have dampened previous estimates of the procyclical effect if aggregation combines individuals who experience differential incidence. For example, if incidence varies by education, and if between-state variation is small relative to within-state and total variation in education, then procyclical mortality could appear more muted in state-level data than in the individual-level data I examine here.

Unfortunately the evidence concerning differential incidence of procyclical mortality in the NLMS is mixed, so it is difficult either to assess this last possibility or indeed to answer the central question of this paper without qualifications. As suggested by the standard errors in Table 2, which are rarely smaller in magnitude than the central estimate of γ̂ = −0.01, statistical power to identify differential incidence in the logit is low even in large-scale datasets because effects are small and mortality is rare. Based on approximations provided by Hsieh et al. (1998), a sample of around 40 million can achieve 90 percent power in a test of a logit coefficient equal to 0.01 when the mortality probability averages 0.003 during working ages. As shown in Table 1, even if I combined all four age/sex groups, I would only have 15 million observations.

Still, my results reveal scattered evidence of differential incidence, at least among working-age males. The difficulty is that these findings appear to be at odds with one another. There is weak evidence that some groups with low socioeconomic status might be relatively more exposed to procyclical mortality than those with higher status. Male African Americans of working age appear to suffer amplified procyclical mortality, and groups that were unemployed or out of the labor force at baseline in the initial CPS interview, such as disabled workers, are subject to mortality that was significantly higher during expansions. Males and to some extent females of working age whose family incomes were low but not at the bottom of the distribution also experience amplified procyclical mortality.

Differential incidence across educational groups runs in exactly the opposite direction. Having very low education, 0–6 years, is significantly associated with experiencing countercyclical rather than procyclical mortality, while having a high school degree or more education actually amplifies the procyclical effect. At the high end, education seems to increase the risk of “working too hard,” which is somewhat unexpected. But education also apparently decreases the risk of starving during a recession. It is difficult to reconcile these results with the evidence on race and income, since typically all these variables are correlated. The immutability of education over the life cycle suggests it should be less noisy and thus a more preferable covariate in these data than the income snapshot. Significance levels favor the evidence across educational groups as opposed to race.

If we take education as the best indicator of permanent socioeconomic status, as I believe we should, then the patterns of incidence for working-age males and females in Table 2 weakly suggest an interesting reinterpretation of the phenomenon of cyclical mortality. Individuals with extremely low education and presumably very low wages and wealth are at risk of what Brenner (1971, 1975, 1979) originally perceived: declining health during economic bad times when jobs are lost. But those with a high school degree or more, who presumably have some buffer-stock savings and decent prospects of avoiding long-term unemployment, actually seem to benefit during economic hard times, perhaps from working less hard or being exposed to less pollution.

This perspective, which admittedly is only weakly supported by the results of this study, is certainly interesting and deserving of further inquiry, and not just because it seems to reconcile two disparate perspectives. There are also several unexplored theoretical angles to which these results speak. The basic conceptualization of cyclical mortality with which I started is that it is a bad against which SES should be protective, regardless of whether mortality is falling during bad times and rising during good times or the reverse. Indeed, from a welfare perspective, variation in the quantity of a good, here survivorship, of a given size is painful regardless of the timing of rises and falls.

But welfare is multidimensional. Procyclical mortality implies negative covariance between unemployment and mortality, both of which are economic bads. If improving health during bad economic times provides a hedge against unemployment risk, then procyclical mortality should actually be preferred to countercyclical mortality and perhaps even to acyclical mortality. According to this view, we would expect to see people with low SES and lesser means experiencing either counter or acyclical mortality, while those with high SES might rationally choose procyclical mortality. Another way of stating this perspective is that the economically secure may not find recessions very dangerous because they work very hard during expansions, paying the price of recession insurance in the form of poorer health during periods of hard work. The less educated may be less able to build a buffer of wealth through hard work during expansions, so they suffer during recessions that claim their jobs. The evidence presented here provides weak support for the view that the mortality of individuals at both ends of the socioeconomic spectrum may be relatively more impacted by the business cycle than for those in the middle, although in opposite directions, and perhaps we should expect as much.

These are interesting hypotheses that require further testing with different statistical strategies. It may be fruitful to examine deaths by educational attainment in vital records, although there are concerns about data quality (Sorlie and Johnson, 1996). Exploring mortality at sub-annual frequencies may enhance identification. Optimal policy design requires better knowledge of the target population, and this study has provided some insights along that dimension.