Abstract
Chest physical examination often includes performing chest percussion, which involves introducing sound stimulus to the chest wall and detecting an audible change. This approach relies on observations that underlying acoustic transmission, coupling, and resonance patterns can be altered by chest structure changes due to pathologies. More accurate detection and quantification of these acoustic alterations may provide further useful diagnostic information. To elucidate the physical processes involved, a realistic computer model of sound transmission in the chest is helpful. In the present study, a computational model was developed and validated by comparing its predictions with results from animal and human experiments which involved applying acoustic excitation to the anterior chest while detecting skin vibrations at the posterior chest. To investigate the effect of pathology on sound transmission, the computational model was used to simulate the effects of pneumothorax on sounds introduced at the anterior chest and detected at the posterior. Model predictions and experimental results showed similar trends. The model also predicted wave patterns inside the chest, which may be used to assess results of elastography measurements. Future animal and human tests may expand the predictive power of the model to include acoustic behavior for a wider range of pulmonary conditions.
Keywords: computational modeling, lung acoustics, pneumothorax, percussion, human studies
1. Introduction
1.1 Clinical use of percussion
Percussion is a common component of the clinical chest physical examination, where the objective is often to determine if the area under consideration is air-, fluid- or solid-filled [31]. Such determination can aid in diagnosing pulmonary conditions including pneumothorax, pleural effusion, consolidation and lung masses. During percussion, acoustic energy is introduced at the skin surface and the resulting sound changes are detected. In “conventional percussion” (CP) this is typically accomplished by the clinician placing the middle finger of the non-dominant hand against the chest wall in the area of interest, followed by a rapid wrist flexion of the dominant wrist. The rotational energy of this movement is directed through the middle finger of the moving hand against the outstretched middle finger of the stationary hand while listening for a change in the acoustic chest wall response [19]. An alternative method is auscultatory percussion (AP), which is implemented by tapping on the chest while listening to the posterior chest with a stethoscope [10, 11]. In either case, the clinician listens to the produced sounds, subjectively noting amplitude and pitch (frequency) changes [31]. For example, tympanic “bright” sounds are indicative of air, or “dull” percussive sounds are suggestive of fluid filled or consolidated structures.
Manual implementation of percussion is qualitative, subjective, and skill dependent. This limits the reliability of the method, which may explain the varied levels of clinical utility reported in the literature. For example, a controlled blind study [12] found that AP had 86% sensitivity and 84% specificity and CP had 76% sensitivity and 100% specificity. On the other hand, another study [6] investigated the sensitivity of detecting abnormality in the chest between CP and AP and concluded that the sensitivities of both CP and AP are too low to present acceptable positive predictive values for clinical examinations. The validation of these two techniques was questioned by Bohadana et al. [3] and found that the lung characteristics do not cause significant changes to the transmitted sounds when the AP technique was applied at the sternum. They also suggested that the sound generated by percussion at the sternum propagated to the posterior chest mainly through the chest cage structures [4].
1.2 Other methods of pulmonary diagnosis
Diagnostic methods used to evaluate pulmonary conditions include several imaging modalities such as X-ray, computed tomography (CT), and magnetic resonance imaging (MRI). Imaging methods have continued to improve in their ability to macroscopically image lung anatomy and aid in indirectly assessing lung functional changes. CT and X-ray, however, have the undesirable aspect of ionizing radiation. Ultrasound has limited utility in imaging lung structures due to the acoustic impedance mismatch between the chest wall and air within the lungs. This causes strong reflection of sound waves at the lung interface making it practically infeasible to image areas inside the lungs. Diagnostic methods also include spirometry (the measurement of the volume of inhaled or exhaled air as a function of time), which provides a global measure of lung and airway properties but is patient effort dependent and relatively insensitive to changes in small-airway structure and function. Sputum monitoring and respiratory tests before and after the administration of bronchodilators to assess changes in airway plasticity impose similar constraints by providing global and, at best, indirect information on spatial extent of lung conditions. In addition, MRI using Radio frequency (RF) tagging techniques has been suggested as a method for assessing the regional mechanical properties of the parenchyma [7, 20]; but, this approach is limited to assessing changes in lung volume throughout the respiratory cycle. Finally other pulmonary diagnostic modalities include video bronchoscopy, interventional radiological biopsy, and video assisted or open thoracotomy.
1.3 Use of MR elastography
Recently, the phase contrast-based technique known as magnetic resonance elastography (MRE) has been applied to the lungs in pilot studies with some success [9, 18]. MRE seeks to provide a map of the viscoelastic properties within the region of interest (ROI) [35]. These maps may correlate with injury, the progression of disease, and/or the response to therapy. To obtain the MRE images, shear waves are introduced into to ROI by, for example, a transversely vibrating driver with frequencies in the range of 50 to 200 Hz [18]. Wave motion is then measured and a map of the viscoelastic properties is constructed. Goss et al. applied a longitudinal vibration to the chest wall and hypothesized that the generated compression wave would pass through the chest wall into the lung and the shear wave would be excited due to mode conversion [9]. Since 1995, MRE has been successfully applied in vivo to study of the mechanical properties of a variety of organs including the breast [23], brain [14], kidney [32], prostate [13], liver [28] and muscle [15]. Application to the lungs has proven more challenging because of the poor signal-to-noise available in imaging due to a much lower presence of hydrogen in air than in soft tissue (water), and the complex nature of vibratory wave propagation found in the lungs. Better understanding of mechanical wave motion in the lungs using computational models may aid in the interpretation of the wave images that are acquired using MRE.
1.4 Existing Challenges and Objectives of the Present Study
The main objective of this study is to develop and validate a computational model of sound transmission that can be used to predict chest response to surface excitations (e.g., percussive sounds). The model is validated using experimental measurements in animals and humans. This computer simulation is then used to predict changes in acoustic transmission caused by pneumothorax (PTX) which is an abnormal collection of air or gas in the pleural space separating the lung from the chest wall [16, 17].
Computational models may be also used in future studies to improve our ability to localize sound sources in the chest when acoustic surface measurements are available [1, 22, 26]. There are potential benefits of coupling a multi-point array measurement with an improved computational model of sound propagation to locate acoustic sources in the torso. For example, it was reported that this coupling was significantly superior in identifying the sound source location compared to a simple “ray acoustics” description of sound transmission that neglects the more complex nature of sound transmission in a finite and complex dimensioned structure [22].
In previous studies, most of the acoustic energy of typical chest percussion was limited to frequencies below 200Hz with peak frequencies below 100 Hz [4]. In the present study the frequency range is widened to cover 50-400 Hz in order to further assess the utility of surface excitation in an expanded frequency range. To cover this broader range, a special vibratory excitation was implemented. Sec. 2 describes the computational and experimental methods, while Sec. 3 summarizes the results. Discussion of the results is provided in Sec. 4, followed by the Conclusions in Sec. 5.
2. Materials and Methods
2.1 Numerical simulations: Porcine normal, human normal & collapsed lung cases
To develop a realistic computational model, the three dimensional (3D) geometrical details of the porcine and human torso structures are needed. Dimensions of representative porcine chest structures were determined from computed tomography (CT) of a pig with similar size to those studied in the acoustic experiments. CT scans used 1 mm slice steps and pixel matrix size 512×512 (Brilliance 64, Philips Electronics). To build the 3D geometry of the human subject chest structures, the CT image sets available on line from the Visible Human Male (VHM) [29] were used. The dimensions of the human torso model were rescaled to match the size of the human subjects who participated in the study. To generate the 3D geometries for the computer model of both human and porcine studies, the CT image sets were imported and processed using Mimics V14 (Materialise, Plymouth, MI), which is an image processing software for 3D design and modeling.
The experimental process of vibrating the sternum of all subjects was modeled in a finite element (FE) environment COMSOL® 4.3 (Comsol Inc, Burlington, MA) using the harmonic analysis acoustic-solid interaction module for frequency domain analysis. To run the FE analysis, the material properties of each organ need to be supplied to the model. Properties of the lung parenchyma have been discussed in the literature. For example, one recent study [7] showed that Biot theory of wave propagation in poroviscoelastic media and the effective medium theory has been used to model sound transmission in the lung parenchyma. Furthermore, measurements of compression wave speed and attenuation in freshly excised pig lung matched theoretical predictions based on Biot theory much more closely than the effective medium theory. The shear wave propagation in the lung is also well predicted by the Biot theory. The following set of coupled differential equations (written in the frequency domain neglecting initial conditions, and denoting a derivative with respect to time as multiplication by jω) [7] can be used to describe the steady-state dynamic oscillatory displacement u of the lung parenchyma and dynamic pressure p of the air in the lung:
| (1a) |
| (1b) |
Here, μ is the shear modulus of the lung tissue, Kb is the bulk modulus of the lung tissue when it is inflated. ρ is the lung density, ρf is the air density, φ is the air volume fraction in the lung, α , β and R are the coupling parameters between the lung parenchyma and the air. Fi and a denote external inputs of force per unit volume (e.g. Newtons per cubic meter) and the rate of introduction of gas volume per unit volume (e.g. inverse second), respectively. Suppose that the dilatation ui,i is zero and neglecting external excitations, Eq. (1a) reduces to the following equation, which governs shear wave behavior:
| (1c) |
From Eq. (1c) we can see that the complex-valued wave speed cs and shear wave number ks are
| (2a) |
| (2b) |
The coupled Eqs. (1a-b) lead to two compression waves, a fast wave and a slow wave with much larger attenuation. The compression wave speeds are given by
| (3a) |
| (3b) |
Here, cpf and cps are the fast and slow compression wave speeds, respectively. The corresponding complex-valued wave numbers, kpf and kps, are derived from Eqs. (1a-b). In our frequency range of interest (50-400 Hz), the slow compression wave can't propagate effectively as the relative motion between the lung parenchyma and air is impeded by viscous drag [5]. Hence, only the fast compression wave propagation may be detectable in the parenchyma. As the lung parenchyma is viscoelastic, the shear wave speed is frequency-dependent. The phase speed and attenuation are expressed within the complex valued shear wave speed. The compression wave attenuation is mainly due to the friction between the air and the lung parenchyma. The complex-valued fast compression wave speed is given by Eq. (3a). By implementing the above equations, the frequency dependent compression wave speed and attenuation of compression wave and shear wave in lung parenchyma can be calculated and were completely defined for simulation in COMSOL.
Previous studies [24, 33] suggested that the lung air volume fraction φ = 75%, the lung tissue density ρp =1000 kg/m3, and the air density in the lung ρg =1.21 kg/m3. The lung density is given by:
| (4) |
These properties result in a density of the normal lung ρ = 250.9 kg/m3. When the PTX condition is present in the right chest, the right lung parenchyma was collapsed and thus, had a lower air volume fraction depending on the level of collapse. In this case, the original right lung region in the 3D model was split into two parts, the collapsed parenchymal region and the air region outside the lung. Two different levels of collapse were considered in the current study, which correspond to φ = 28% and φ = 58%. Those two values, respectively, correspond to PTX of 89% and 53% by volume, approximately. The lung compression wave speed and attenuation were then calculated using equation (3) for φ = 75%, φ = 58%, and φ = 28%.
The values of material properties of other parts in the upper torso such as soft tissue, ribcage, sternum, and scapula were based on previous studies [25, 27, 30]. The osseous structure and other biological soft tissue were considered as viscoelastic media and the Voigt model of viscoelasticity was used for these regions. So, the bulk modulus is related to the two complex Lame constants as
| (5) |
Here, λb/t = λb/t1 +jωλb/t2 and μb/t = μb/t1 + jωμb/t2 [27, 30]. The subscript “b” denotes the osseous materials like the ribcage, scapulae and sternum and “t” denotes the soft tissue. Also, λb/t1, λb/t2, μb/t1, and μb/t2 denote volume elasticity, volume viscosity, shear elasticity and shear viscosity, respectively for osseous materials and tissue. In the COMSOL simulation, the lung region was set as a “pressure acoustics model”. The soft tissue and the osseous region were respectively set as the “linear viscoelastic material model” with different material properties assigned as follows: μb1 = 10 GPa, μb2 = 20 Pa-s, λb1=2.6 GPa, λb2 = 0 and density ρb = 1500 kg/m3 for the bone and μt1 = 2.5 kPa μt2 = 5 Pa-s, λt1 = 2.6 GPa, λt2 = 0 and the density ρt = 1000 kg/m3 for the soft tissue such as fat, muscle and connective tissue. Bone and soft tissue volume viscosity λb2 and λt2 are taken to be zero in our frequency range of interest (50-400 Hz) [30]. Harmonic vibratory excitation with displacement amplitude of 1 mm was applied to the sternum. The outside surface of the torso was set as a free boundary condition. The outside surfaces of the lungs were set as an “acoustic-structure boundary” in COMSOL. The number of elements for the porcine simulation was 313,742 and 313,548 for normal case and the PTX case, respectively. The number of elements for the human simulation was 395,788 for the normal case, 392,796 for the PTX = 53% and 392,548 for the PTX = 89%. Element size was set to be smaller than 1/6 of wave length for the acoustic simulation for all regions and frequencies considered.
2.2 Experiment: Porcine studies – Normal and PTX cases
Experiments were carried out on six freshly sacrificed female Landrace and Yorkshire cross pig subjects (weight 30 to 35 kg) after institutional animal care and use committee (IACUC) approval. The experimental setup is shown in Fig. 2(a). Immediately upon sacrifice the lung was kept inflated with air at continuous positive pressure of 5 cm H2O through an endotracheal tube. The pig was then secured in the left lateral decubitus position (right-side-up) with the skin hair of the measurement area shaved completely. P-RETRO-250 glass beads (45 – 63 μm dia., Polytec, Irvine, CA) were applied to the skin surface of subjects to enhance the laser reflectivity to enable an improved signal-to-noise ratio. The anatomy of the pig indicated that its lungs are located roughly between the first and tenth rib. The skin surface velocity was measured by a laser Doppler vibrometer (LDV) (PDV-100, Polytec, Irvine, CA) at 9 evenly spaced points in an array located in the area from the fifth rib to the ninth rib (Fig. 2(a)). A plexiglass disk of radius 15 mm was gently pressed against the chest surface on the top of the sternum and driven by an electromagnetic shaker (ET-132, Lab-Works Inc., Mesa Costa, CA) that was connected to a power amplifier (P 3500S, Yamaha, Buena Park, CA). An impedance head (288D01, PCB Piezotronics, Depew, NY) was mounted on the disk to measure the input acceleration, serving as a reference signal for the LDV measurements. A periodic chirp with spectral content from 50 – 400 Hz was generated from a dynamic signal analyzer (SignalCalc ACE, Data Physics, San Jose, CA) and fed to the amplifier which drives the shaker. The signal analyzer was also used to acquire and analyze the stimulus and output signals, which are the impedance head acceleration at the anterior chest and the LDV surface velocity at the posterior chest, respectively.
Fig. 2.
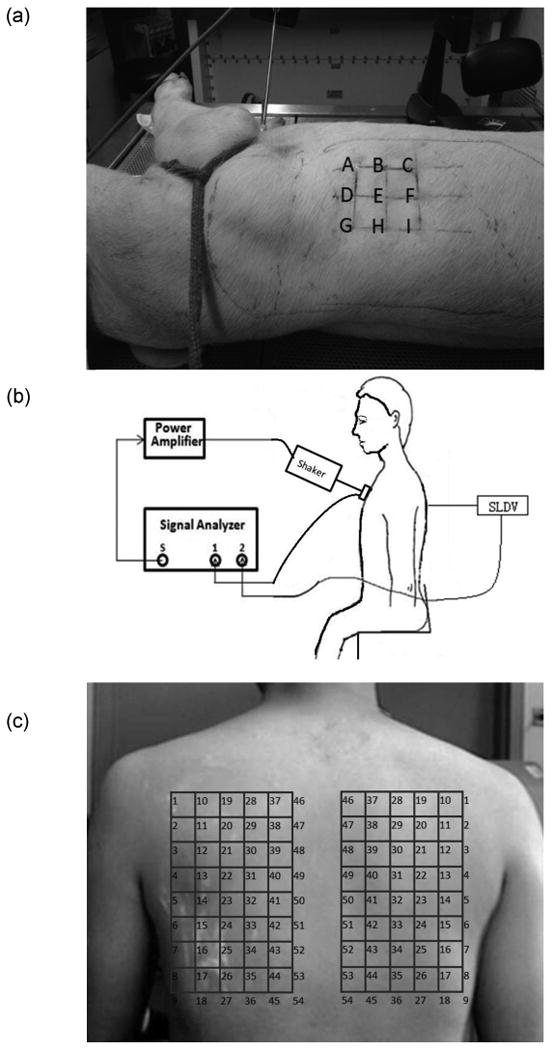
Experimental setup for human and porcine measurements. (a) Experimental setup for the porcine. (b) Schematic diagram of the experimental setup. (c) SLDV scanning points of human posterior.
The signals are analyzed and results are presented in terms of the “frequency response function” (FRF). Here, the FRF is defined as the frequency-dependent ratio between output acceleration, ACCP, (posterior chest) over the stimulus (i.e., reference) acceleration, ACCA, (anterior chest). This acceleration ratio is then converted to the decibel scale and is given by [21]:
| (6) |
The above measurements and analysis were performed for the normal (i.e., intact chest), and PTX states in each animal. PTX was created by making a small incision in the seventh intercostal space in the right mid-axillary line then introducing air through the incision using a syringe. The air pressure for inflating the lungs was set to “0” in the PTX state to allow for full lung collapse. A 5 mm thoracoscopic trocar (Endopath Dilating Tip, model 355, Ethicon, Cincinnati, OH) was inserted into the pleural space and a scope was used to visually confirm the PTX state.
2.3 Experiment: Human Studies – Normal Subjects
Experimental studies were carried out on three healthy human male subjects with ages of 25, 26 and 28, weight of 65, 68, and 67 Kg, and height of 175, 178, and 177 cm, respectively, after receiving appropriate Institutional Review Board (IRB) approval and informed consent. The subject was seated on a chair during the experiment. As shown in Fig. 2 (b), a plexiglass disk, the same as the one used for porcine experiment, was gently applied to the chest surface on the top of the sternum and driven by an electromagnetic shaker connected to a power amplifier. The same chirp signal used in the animal experiments was generated from a scanning laser Doppler vibrometer (SLDV) (PSV-400, Polytec, Irvine, CA) and was fed into the power amplifier that was connected to the electromagnetic shaker. Similar to the animal experiments, the impedance head was mounted on the disk to measure its acceleration, serving as a reference for the SLDV measurement. The amplifier, shaker, and the impedance head were the same as the ones used in the porcine experiment. The reflective glass beads were applied to the skin surface of subjects. The SLDV was used to measure the skin surface velocity at an array of points on the posterior chest of the subject. The measurements were acquired during a coached voluntary breath-hold period at the inspiration end. There were 54 scan points on each side of the back (total of 108 scan points). The experimental setup is shown in Fig. 2(c).
3. Results
First, the results of porcine experimental measurements described in Sec. 2.2 on normal and PTX cases are compared to the simulations described in Sec. 2.1 to validate the FE computer simulation model created in COMSOL. Second, the results of experimental measurements described in Sec. 2.3 of normal human subjects are compared with numerical FE simulations described in Sec. 2.1 to further validate the model for human subjects. Finally, results of numerical simulations of the human normal and PTX case are compared to provide predictions for the effects of PTX in humans.
3.1 Results of Porcine Studies
The FRF from numerical simulations and from experimental measurements in six animals are plotted in Fig. 3(a) for the normal state at point B (see Fig. 2(a) for point location). The labels for different surface points are shown in Fig. 2(a). Both experimental and simulation plots are in the same decibel range. The experimental FRF data of the porcine studies are only plotted at frequencies for which the coherence exceeded 0.85. The data showed similar trends, but with inter-subject variability. Fig. 3 (b) shows the mean FRF of all six pigs with the standard deviation indicated. In this figure, the simulation predication is compared to the mean FRF from all 6 pigs. Similar trends can be seen although the peaks (and valleys) in the experimental results have been minimized due to averaging. Figs. 3(c) and 3(d) show the simulation and experimental results of pigs #1 and #2, respectively, for normal and PTX states at a representative point B. It can be seen that the FRF amplitudes for the PTX state are lower than those for the normal state from 200 to 400 Hz for both simulation and experimental results. Specifically, in the experiment there is an average reduction of 9.15 dB and 9.64 dB over this frequency range for pigs #1 and #2, respectively. The average reduction for all six pigs is 7.97 dB with a standard deviation of 2.60 dB. The simulation predicts a 7.48 dB reduction.
Fig. 3.
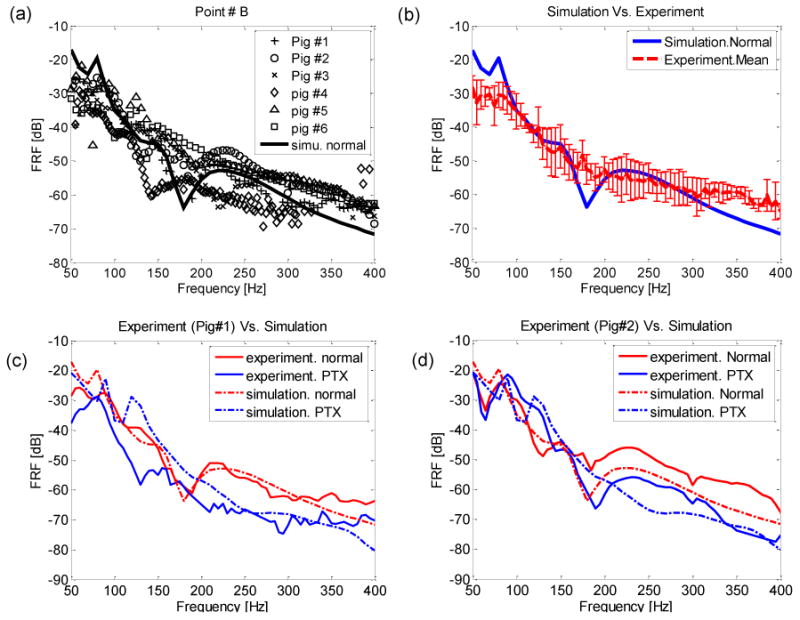
Porcine studies (a) Comparison of simulation and experimental results for normal state (b) Comparison of mean FRF of experiment and simulation for normal state. The error bars indicate standard deviation of six pigs. (c) Comparison of pig#1 experimental and simulation results for normal and PTX cases. (d) Comparison of pig#2 experimental and simulation results for normal and PTX cases.
3.2 Results of Human Studies
In order to compare the results of simulation and experiment for the normal state in humans, FRF maps of the simulation and experiment were generated for the three healthy human subjects. Since the spatial resolution (distance between measurement points) was larger in the experiment, interpolation was used to more closely match the simulation spatial resolution (distance between the finite elements). Fig. 4 shows the FRF results at 60 Hz (Fig. 4(a)-(d)) and at 120 Hz (Fig. 4(e)-(f)), respectively. The simulation results are displayed in Fig. 4(a) and (e) for comparison. The color bar is in the decibel scale and is identical for simulation and experimental results. It can be seen that the FRF amplitudes tend to be larger in the lung region compared to the map boundaries. It also showed more attenuated amplitude over the scapulae, which is more appreciable at the top corners of several maps (e.g., Fig. 4(a-h)). In addition, inter-subject variability and some deviations between the patterns of simulation and experiment can be noticed. However, it is noticeable that the amplitudes of the experiment and simulation are comparable.
Fig. 4.
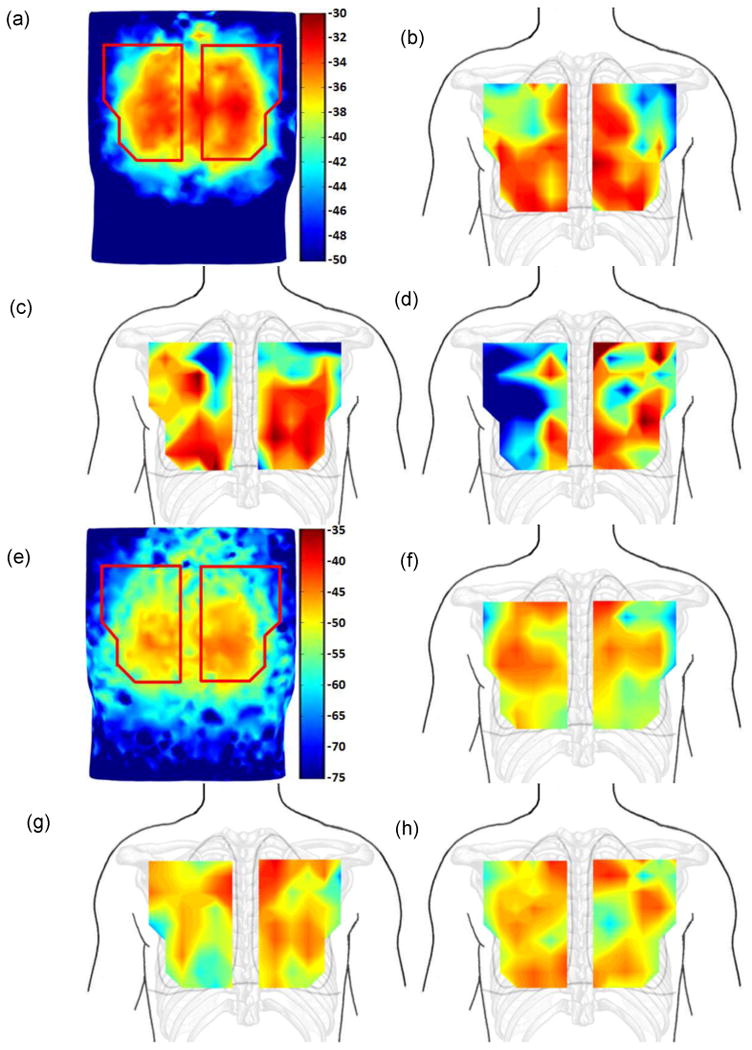
FRF images comparison of healthy human simulation and experimental results at 60 and 120 Hz. (a). Simulation at 60Hz. (b) Experiment: HS#1 at 60Hz. (c). Experiment: HS#2 at 60Hz. (d). Experiment: HS#3 at 60Hz. (e) Simulation at 120Hz. (f) Experiments: HS#1 at 120Hz. (g) Experiment: HS#2 at 120Hz. (h) Experiment: HS#3 at 120Hz. Color bar in dB scale.
In Fig. 5, numerical simulation and experimental measurement of the FRF are compared at three specific scanning points, which are points #15, #24 and #41 (point locations are shown in Fig. 2(c)). These three points on both sides of the back areas were taken in the location avoiding the scapulae, in order to have higher measurement signal-to-noise ratio (SNR). The experimental data are only plotted at frequencies where the coherence exceeded 0.85. Coherence was not good at high frequencies due to low SNR, and hence only the range of 50 – 200 Hz is shown. By comparing the simulation and experimental results of Fig. 5, similar amplitudes and trends can be seen, which further contributes to the validity of the model.
Fig. 5.
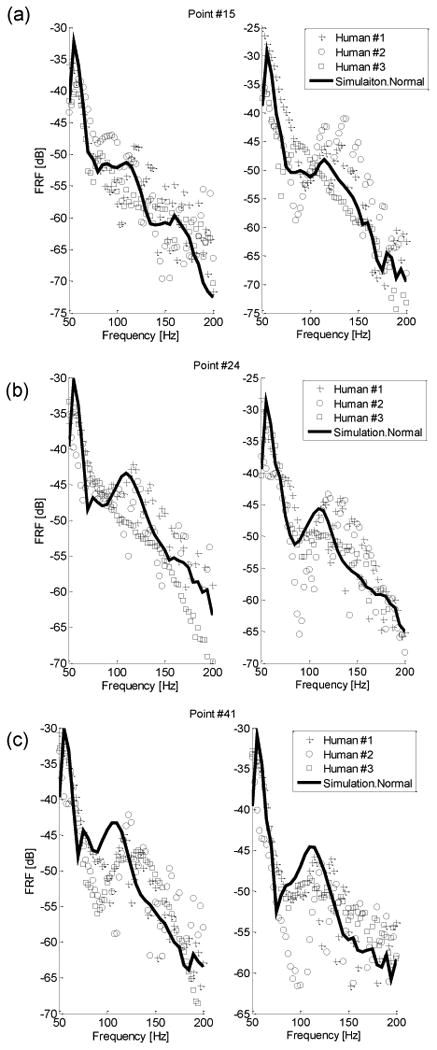
FRF plots at point #15(a), #24(b), and #41(c) on posterior chest (left/right sides correspond to left/right columns). Key: ‘−’ simulation FRF, ‘+’ HS #1 experiment, “(○)” HS #2 experiment, ‘(□)’ HS#3 experiment.
The model was then used to predict FRF values at the posterior chest in a human subject for two different levels of PTX. Simulations were performed for PTX levels of 53% and 89% by volume, which corresponds to a lung air volume fraction of φ = 58% and φ = 28%, respectively. Fig. 6 shows the FRF for the normal and the two PTX states. This prediction suggests that PTX may cause a drop in FRF at frequencies between 100-200 Hz. Specifically, in this frequency range there was an average reduction of 5.61 dB and 9.74 dB for the PTX levels of 53% and 89%, respectively. This is comparable to and consistent with the porcine study results of Fig 3(c), (d). The prediction further suggests that the FRF drop may be higher at larger PTX values and at higher frequencies for the smaller PTX state.
Fig. 6.
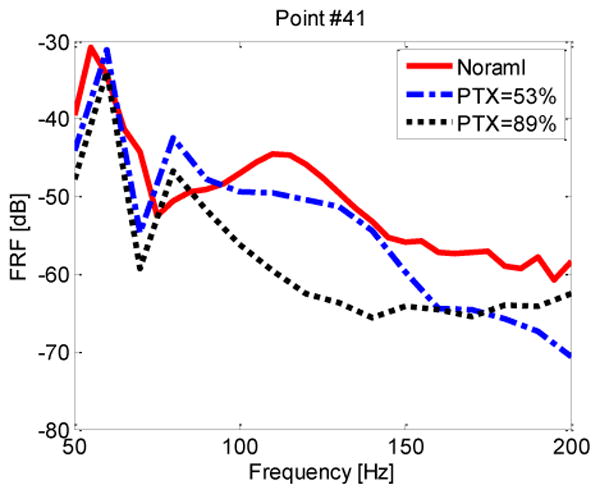
FRF amplitude of points #41 on right side of the posterior chest of the normal and PTX states (human simulation). Key: “—” PTX=0%; “–-–” PTX=53%; “▪▪▪” PTX=89%.
In Fig. 7, the FRF amplitudes are shown for two different PTX levels of 53% and 89% at two specific frequencies 60 Hz and 120 Hz. As seen in the figures, when comparing right to left posterior side FRF amplitudes (only right lung is collapsed), the FRF amplitude reduction caused by PTX is evident, as previously observed in Fig. 6.
Fig. 7.
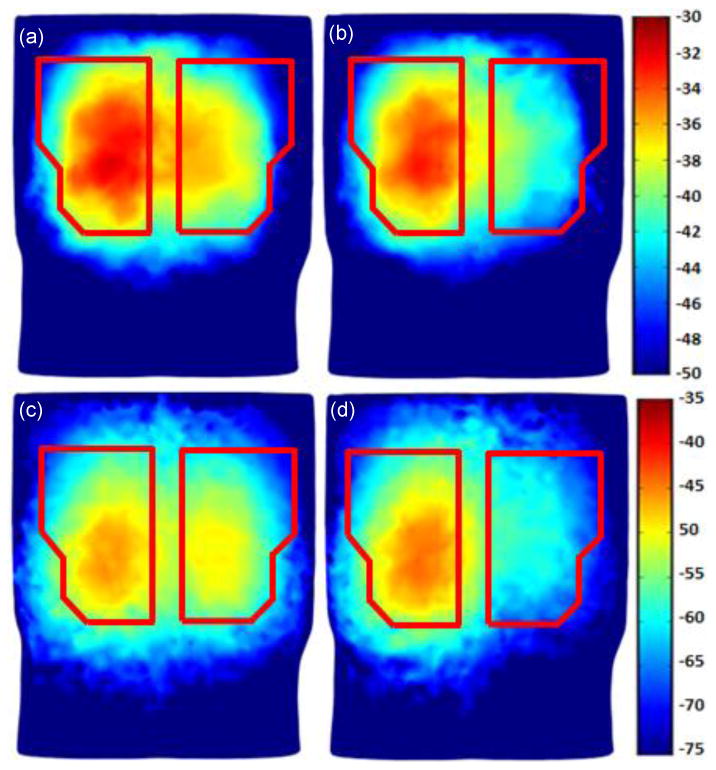
Human simulation results for PTX: (a) PTX = 53% and the excitation frequency is 60 Hz; (b) PTX = 89% and the excitation frequency is 60 Hz; (c) PTX = 53% and the excitation frequency is 120 Hz. (d) PTX= 89% and the excitation frequency is 120 Hz.
The model was also used to simulate the displacement of the lungs and other chest structures in response to surface excitation. Displacement in the anterior posterior direction in a torso cross section is shown in Fig. 8 at two excitation frequencies, namely 60 Hz and 120 Hz. In this simulation, the right lung was collapsed, the left lung was kept normal, and the surface excitation was located at the middle of the top chest surface (over the sternum). Patterns of shear waves emanating from the stimulus and propagating into the chest are evident and are shown as red and blue (indicating high and low amplitude) bands.
Fig.8.
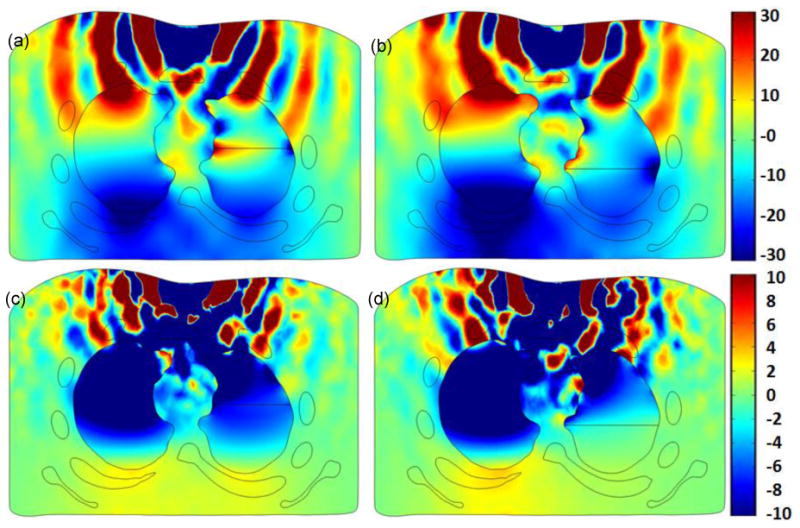
Human simulation at 60 and 120 Hz excitation frequency: cross section of torso showing displacement in the anterior posterior direction for (a) PTX= 53% at 60 Hz, (b) PTX=89% at 60 Hz, (c) PTX= 53% at 120 Hz, and (d) PTX=89% at 120 Hz in the right lung. The color bar shows displacement in [μm]
These patterns are altered in the lung region as the acoustic properties are significantly different from the surrounding tissue. One interesting aspect of this data is that the displacement amplitude in the normal left lung is higher than that in the PTX right lung. As mentioned in the Introduction, simulation images such as those shown in Fig. 8 may provide better understanding on wave motion obtained from MRE and help in estimating soft tissue viscoelastic properties from MRE wave images.
4. Discussion
Percussion is a common procedure during clinical chest exams. The tapping stimulus used in CP and AP, is short and contains relatively low frequencies. The short signal duration limits the amount of energy input. This may lead to low signal-to-noise ratios especially at higher frequencies, which can reduce reliability. In addition, the manual approach of the technique that relies on un-aided listening can be subjective, skill dependent and sometimes tedious. This can pose further limitations on the utility of the technique. The current study attempts to investigate enhancement of the technique by changing the stimulus and analysis methods. Here, input waves are more controlled, introduced for a longer duration (30 seconds vs. < 1 second), and contain a wider frequency band.
The current study is also primarily aimed at developing a finite-element computational model based on tissue properties available in the literature and realistic 3D geometries extracted from actual CT scans of humans and animals. The model was validated for animal and human geometries and computational predictions are consistent with experimental measurements. Though, we note that the human simulation with PTX was not validated experimentally in the present study. But, differences in the human simulation between normal and PTX cases matched those observed in the porcine simulations for normal and PTX cases, both of which were validated experimentally. One underlying hypothesis is that higher-frequency mechanical waves introduced at anterior chest surface propagate to the posterior chest through internal organs lying between the stimulus and measurement points. The change in the relevant intra-thoracic structures would alter the wave propagation through the thorax, and hence results in amplitude modification at the measurement location. Model predictions and experimental results showed that changes in the lung structure due to the presence of PTX (which creates more barriers to the acoustic waves due to additional impedance mismatch between lung, air, and chest wall) caused a drop in the FRF at higher frequencies, which is consistent with this hypothesis. Sound waves at lower frequencies on the other hand (due to their lower attenuation) can travel a longer distance around the internal organs. And consequently, structural changes of the internal organs may have a small effect on the transmission of these waves. This is consistent with the study findings that the presence of PTX had smaller effects on sound transmission at lower frequencies. Given the above hypothesis, one can argue that when PTX is present, the barrier it creates to the sound waves may lead to channeling more acoustic energy around the internal organs. Adding this possibility to the lower attenuation of the low frequency sound waves, an increase in the FRF value at the posterior chest may take place at lower frequencies. This may explain the results of Fig. 3(c) and (d) where a small increase in FRF was seen at low frequencies.
The effect of PTX on transmitted sound (Fig. 3 (c) and (d)) is consistent with earlier reports [17] where the transmitted sound amplitude was investigated in dogs with PTX. In that study the reduction of transmitted sounds with PTX was seen at frequencies 20-1500 Hz, while low frequency (< 100 Hz) transmitted sounds were not significantly affected. That finding also suggests that that FRF drop seen in the current study may continue at frequencies higher than those introduced in the current study. The maximum frequency in the current project was limited 400 Hz to keep the SNR sufficiently high. The frequency range with high SNR may be widened when higher sensitivity sensors are available.
Significant inter-subject variability was seen in pig (Fig. 3(a)) and human (Fig. 5) studies. Variability may be due to the subject anatomical and size differences as well as varied measurement locations and measurement errors including human subject movement. However, there were similar general trends in each subject group and among both groups. For example the FRF decreased by about 30-40 dB as the frequency increased from 50-200 Hz for both the animal and human subjects, as the tissue acoustic properties were close between human and pig. The observed decrease in the transmitted acoustic energy with increasing frequency is consistent with previous studies [17] that suggested that the effect is due to increased attenuations with increasing frequency in biological tissue. It is also worthwhile noting that the FRF amplitude drop in 50-200 Hz range in the current study is comparable to previously reported values in the same frequency range [17] for canine subjects where the chest dimensions were close to half that of the current human subjects. This suggests that chest size may have a small influence (compared, for example, to tissue properties and acoustics barriers like the scapulae) on this frequency dependent attenuation.
In Fig. 5, the measured FRF shows peaks around 130 Hz. This trend is similar to simulation predictions and can be due to resonance in the chest, which is consistent with previous reports [17, 34]. Fig. 6 suggests that larger PTX may cause a larger FRF amplitude drop. This may be due to the increased size of the region of acoustic mismatch, which may be associated with more sound attenuation [8, 17, 33]. This result also suggests that the FRF amplitude drop may be too small to detect a small PTX, which would limit the utility of the current approach, especially when a single point measurement is used. Spatial distributions of the simulated FRF amplitudes at 60 and 120 Hz for PTX of 53% and 89% are shown in Fig. 7. By examining that distribution, a difference of the FRF values over the left vs. right can be seen for both PTX levels. This data suggests that left to right FRF pattern comparisons may be helpful in detecting most moderate PTX. The left to right comparison may be useful in most cases since about 98% of PTX cases are unilateral [2].
As discussed above, sound transmission through the chest may be of value if altered transmission patterns correlate with pathology in ways that can be detected and used to provide a reliable and quantitative diagnosis of the disease or injury. Potential means of detection may be via measurement of the transmitted sounds on the torso surface, as done in this study, or via visualization of internal sound transmission using an imaging technique that measures internal vibratory motion, such as MR elastography. In either case, an accurate computer simulation of sound transmission through the chest and lungs under normal and pathologic conditions (Fig 8) may aid in interpreting experimental measurements [18]. In this study, validated computational acoustic models proved to be capable of simulating transmission and noninvasive measurement of sound and vibration throughout the chest. The outcome of these models may also prove useful in the development of a more effective educational tool for teaching auscultation skills.
5. Conclusion
In the present study, a computational model of sound transmission in the chest for surface acoustic excitation was developed. The model was validated experimentally using data from three healthy human subjects and from six porcine subjects before and after pneumothorax induction. Model predictions were found to be consistent with findings and physical phenomena suggested by the animal and human studies. The tested surface excitation method is an extension of the percussion approach that is commonly used during chest exam. Simulation and experimental findings suggest that surface excitation may be useful in detecting pulmonary abnormalities such as a large PTX. The model may also prove useful for detecting other abnormalities, and developing learning tools. The developed computational models can also predict wave propagation inside the chest which may be of use in assessing the performance of other acoustic diagnostic approaches, such as MR elastography.
Fig. 1.
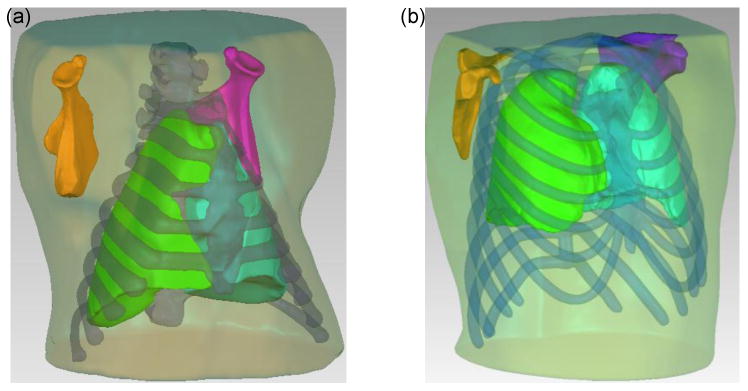
(a) 3-D model of porcine upper torso and internal organs, (b) 3-D model of human upper torso and internal organs.
Acknowledgments
Financial support of the National Institutes of Health (Grant No. EB012142) is acknowledged. The assistance of Mr. Brian Henry is appreciated.
References
- 1.Acikgoz S, Ozer MB, Royston TJ, Mansy HA, Sandler RH. Experimental and computational models for simulating sound propagation within the lungs. ASME J Vib Acoust. 2008;130(2):021010. doi: 10.1115/1.2827358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Athanassiadi K, Kalavrouziotis G, Loutsidis A, Hatzimichalis A, Bellenis I, Exarchos N. Surgical treatment of spontaneous pneumothorax: ten-year experience. World J Surg. 1998;22(8):803–806. doi: 10.1007/s002689900473. [DOI] [PubMed] [Google Scholar]
- 3.Bohadana AB, Kraman S. Transmission of sound generated by sternal percussion. J Appl Physiol. 1989 (1);66(1):273–277. doi: 10.1152/jappl.1989.66.1.273. [DOI] [PubMed] [Google Scholar]
- 4.Bohadana AB, Patel R, Kraman SS. Contour maps of auscultatory percussion in healthy subjects and patients with large intrapulmonary lesions. Lung. 1989 (2);167(1):359–372. doi: 10.1007/BF02714964. [DOI] [PubMed] [Google Scholar]
- 5.Bourbie T, Coussy O, Zinszner B. Acoustics of Porous Media. Gulf Publishing Company; Huston, TX: 1987. pp. 86–87. [Google Scholar]
- 6.Bourke S, Nunes D, Stafford F, Turkey G, Graham I. Percussion of the chest re-visited: A comparison of the diagnostic value of auscultatory and conventional chest percussion. Irish Journal of Medical Science. 1989;158(4):82–84. doi: 10.1007/BF02942111. [DOI] [PubMed] [Google Scholar]
- 7.Dai Z, Peng Y, Royston TJ, Mansy HA. Experimental Comparison of Poroviscoelastic Models for Sound and Vibration in the Lungs. ASME J Vib Acoust. 2013 doi: 10.1115/1.4026436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Goll JH. The design of broad-band fluid-loaded ultrasonic transducers. Sonics and Ultrasonics, IEEE Transactions. 1979;26(6):385–393. [Google Scholar]
- 9.Goss BC, McGee KP, Ehman EC, Manduca A, Ehman RL. Magnetic Resonance Elastography of the lung: Technical feasibility. Magn Reson Med. 2006;56(5):1060–1066. doi: 10.1002/mrm.21053. [DOI] [PubMed] [Google Scholar]
- 10.Guarino J. Auscultation percussion: A new aid in the examination of the chest. The Journal of Kansas Medical Society. 1974;75(6):193–194. [PubMed] [Google Scholar]
- 11.Guarino J. Auscultatory percussion of the chest. The Lancet. 1980;315(8182):1332–1334. doi: 10.1016/s0140-6736(80)91788-2. [DOI] [PubMed] [Google Scholar]
- 12.Hansen LB, Brons M, Nielsen NT. Auscultatory percussion of the lung: prospective comparison of two methods of clinical examination of the lungs. Ugeskrift for laeger. 1986;148(6):323–325. [PubMed] [Google Scholar]
- 13.Kemper J, Sinkus R, Lorenzen J, Nolte-Ernsting C, Stork A, Adam G. RöFo-Fortschritte auf dem Gebiet der Röntgenstrahlen und der bildgebenden Verfahren. 8. Vol. 176. © Georg Thieme Verlag KG Stuttgart·; New York: 2004. MR elastography of the prostate: initial in-vivo application; pp. 1094–1099. [DOI] [PubMed] [Google Scholar]
- 14.Kruse SA, Rose GH, Glaser KJ, Manduca A, Felmlee JP, Jack CR, Jr, Ehman RL. Magnetic resonance elastography of the brain. Neuroimage. 2008;39(1):231–237. doi: 10.1016/j.neuroimage.2007.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, et al. Magnetic resonance elastography: non-invasive mapping of tissue elasticity. Med Image Anal. 2001;5(4):237–254. doi: 10.1016/s1361-8415(00)00039-6. [DOI] [PubMed] [Google Scholar]
- 16.Mansy HA, Balk R, Royston TJ, Sandler RH. Pneumothorax detection using computerized analysis of breath sounds. Med Biol Eng Comput. 2002;40(5):526–532. doi: 10.1007/BF02345450. [DOI] [PubMed] [Google Scholar]
- 17.Mansy HA, Royston TJ, Balk RA, Sandler RH. Pneumothorax detection using pulmonary acoustic transmission measurements. Med Biol Eng Comput. 2002;40(5):520–525. doi: 10.1007/BF02345449. [DOI] [PubMed] [Google Scholar]
- 18.Mariappan YK, Glaser KJ, Hubmayr RD, Manduca A, Ehman RL, McGee KP. MR elastography of human lung parenchyma: technical development, theoretical modeling and in vivo validation. J Magn Reson Im. 2011;33(6):1351–1361. doi: 10.1002/jmri.22550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Murray A, Neilson JMM. Diagnostic percussion sounds: 1. A qualitative analysis. Med Biol Eng Comput. 1975;13(1):19–28. doi: 10.1007/BF02478184. [DOI] [PubMed] [Google Scholar]
- 20.Napadow VJ, Mai V, Bankier A, Gilbert RJ, Edelman R, Chen Q. Determination of regional pulmonary parenchymal strain during normal respiration using spin inversion tagged magnetization MRI. J Magn Reson Im. 2001;13(3):467–474. doi: 10.1002/jmri.1068. [DOI] [PubMed] [Google Scholar]
- 21.Ogata K. System dynamics. 4th edn. Vol. 4. Pearson/Prentice Hall; New Jersey: 2004. p. 107. [Google Scholar]
- 22.Ozer MB, Acikgoz S, Royston TJ, Mansy HA, Sandler RH. Boundary element model for simulating sound propagation and source localization within the lungs. J Acoust Soc Am. 2007;122(1):657–671. doi: 10.1121/1.2715453. [DOI] [PubMed] [Google Scholar]
- 23.Plewes DB, Bishop J, Samani A, Sciarretta J. Visualization and quantification of breast cancer biomechanical properties with magnetic resonance elastography. Phys Med Biol. 2000;45(6):1591. doi: 10.1088/0031-9155/45/6/314. [DOI] [PubMed] [Google Scholar]
- 24.Rice DA. Sound speed in pulmonary parenchyma. J App Physiol. 1983;54:1304–308. doi: 10.1152/jappl.1983.54.1.304. [DOI] [PubMed] [Google Scholar]
- 25.Royston TJ, Dai Z, Chaunsali R, Liu Y, Peng Y, Magin RL. Estimating material viscoelastic properties based on surface wave measurements: A comparison of techniques and modeling assumptions. J Acoust Soc Am. 2011;130(6):4126–4138. doi: 10.1121/1.3655883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Royston TJ, Ozer MB, Acikgoz S, Mansy HA, Sandler RH. Biomedical Applications of Vibration and Acoustics in Imaging and Characterizations. Vol. 9. ASME Press; 2008. Advances in Computational Modeling of Sound Propagation in the Lungs and Torso with Diagnostic Applications; pp. 217–248. [Google Scholar]
- 27.Royston TJ, Zhang X, Mansy HA, Sandler RH. Modeling Sound Transmission Through the Pulmonary System and Chest with Application to Diagnosis of a Collapsed Lung. J Acous Soc Amer. 2002;111:1931–1946. doi: 10.1121/1.1452742. [DOI] [PubMed] [Google Scholar]
- 28.Venkatesh SK, Yin M, Ehman RL. Magnetic resonance elastography of liver: Technique, analysis, and clinical applications. J Magn Reson Im. 2013;37(3):544–555. doi: 10.1002/jmri.23731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Visible Human Project. 2003 www.nlm.nih.gov/research/visible/visible_human.html.
- 30.Von Gierke HE, Oestreicher HL, Franke EK, Parrack HO, von Wittern WW. Physics of vibrations in living tissues. J Appl Physiol. 1952;4(12):886–900. doi: 10.1152/jappl.1952.4.12.886. [DOI] [PubMed] [Google Scholar]
- 31.Walker HK, Hall WD, Hurst JW. The Funduscopic Examination-Clinical Methods: The History, Physical, and Laboratory Examinations. 3rd. Chaper 46. Butterworths; 1990. [PubMed] [Google Scholar]
- 32.Warner L, Yin M, Ehman RL, Lerman LO. Proceedings of the International Society for Magnetic Resonance in Medicine. 2009. Kidney stiffness measured in an animal model of unilateral renal arterial stenosis using 2-D MR Elastography; p. 407. [Google Scholar]
- 33.Wodicka GR, Stevens KN, Golub HL, Cravalho EG, Shannon DC. A Model of Acoustic Transmission in the Respiratory System. IEEE Trans Biomed Eng. 1989;36(9):925–934. doi: 10.1109/10.35301. [DOI] [PubMed] [Google Scholar]
- 34.Wodicka GR, Aguirre A, DeFrain PD, Shannon DC. Phase delay of pulmonary acoustic transmission from trachea to chest wall. Biomedical Engineering, IEEE Transactions on. 1992;39(10):1053–1059. doi: 10.1109/10.161337. [DOI] [PubMed] [Google Scholar]
- 35.Yasar TK, Royston TJ, Magin RL. Wideband MR elastography for viscoelasticity model identification. Magn Reson Med. 2012;70(2):479–489. doi: 10.1002/mrm.24495. [DOI] [PMC free article] [PubMed] [Google Scholar]


