Studies of Hot Photoluminescence in Plasmonically Coupled Silicon via Variable Energy Excitation and Temperature-Dependent Spectroscopy

Abstract

By integrating silicon nanowires (∼150 nm diameter, 20 μm length) with an Ω-shaped plasmonic nanocavity, we are able to generate broadband visible luminescence, which is induced by high order hybrid nanocavity-surface plasmon modes. The nature of this super bandgap emission is explored via photoluminescence spectroscopy studies performed with variable laser excitation energies (1.959 to 2.708 eV) and finite difference time domain simulations. Furthermore, temperature-dependent photoluminescence spectroscopy shows that the observed emission corresponds to radiative recombination of unthermalized (hot) carriers as opposed to a resonant Raman process.

Because of its indirect bandgap, silicon converts excited charge carriers to heat much more readily than to light. In other words, silicon is a “dark” material in comparison to direct bandgap semiconductors, which is the main impediment to the application of Si for light-emitting devices. The exceptionally low quantum yield of silicon stems from the large momentum mismatch between its conduction minima and valence band maxima.¹ To be more specific, it is this momentum mismatch that is predominantly responsible for a slow radiative recombination lifetime of milliseconds once carriers relax to the conduction band minimum (near the X-point), corresponding to a (theoretical) radiative quantum yield of 10^–6.² The low levels of light emission may be circumvented in sub-10 nm quantum confined silicon nanocrystals^3,4 or nanoporous structures but this introduces significant new challenges in their integration with conventional electronic devices.⁵⁻⁷ Previous work has demonstrated efficient emission in bulk silicon diodes (up to 6% at room temperature)⁸ where the emission is enhanced by (1) applying a bias, which exponentially increases the equilibrium photon occupation probability,⁹ (2) patterning the surface to enhance both absorption and emission,¹⁰ and (3) using pristine float-zone silicon to suppress nonradiative scattering centers.¹⁰ In addition to the fabrication costs of these devices, significant limitations include its restriction to band-edge emission (1.12 eV) and slow modulation rates; the recombination lifetime is still in the millisecond range compared to nanoseconds in most direct bandgap materials.^11,12

Recently, Cho et al. demonstrated broadband, superbandgap visible photoluminescence from nonquantum confined silicon nanowires.¹³ Cho et al. were able to significantly enhance the spontaneous emission rate of silicon (and thereby the emission intensity) by intergating silicon with a plasmonic nanocavity to produce highly confined optical modes, using methods similar to those previously applied to cadmium sulfide, a direct bandgap material.¹⁴ However, emission from nonthermalized carriers or “hot luminescence” has similar spectral characteristics to resonant Raman spectroscopy (RRS),¹⁵ such as scattering peaks that occur at fixed phonon energies from the laser line, even though hot luminescence and RRS are fundamentally different processes; the former involves real electronic transitions whereas the latter does not. Thus, experimental verification of hot photoluminescence in silicon, and potentially other plasmonically coupled indirect bandgap materials, is of fundamental importance.

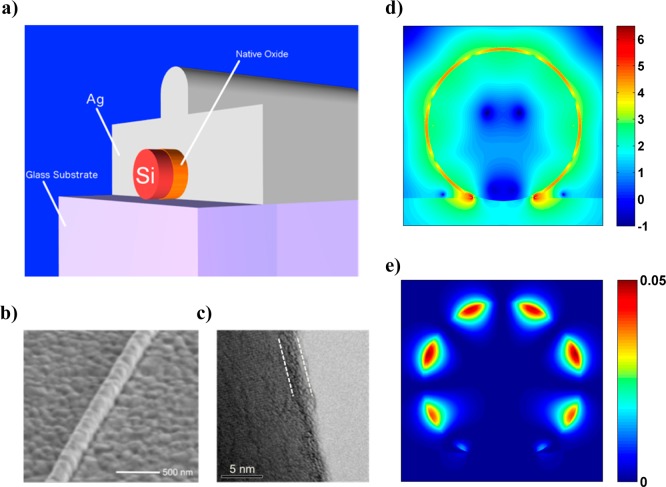
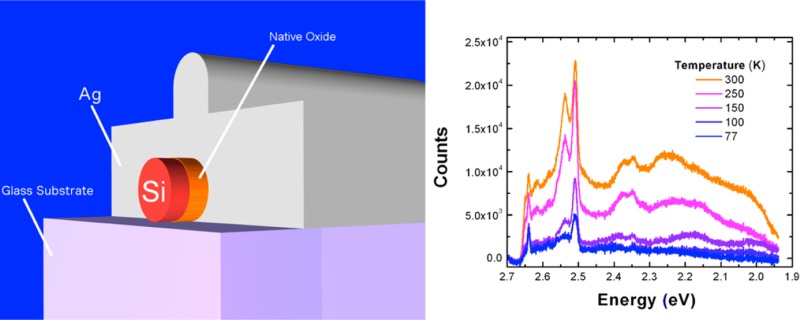
Silicon nanowires were integrated with plasmon nanocavities (Figure 1a,b) following a procedure similar to that previously reported by Cho et al.¹³ However, in contrast to the previous study we used large (d ∼ 150 nm, L ∼ 20 μm) commercially obtained silicon nanowires (Sigma-Aldrich). These nanowires demonstrate superior uniformity in their morphology, while their increased diameters (compared to d = 30–80 nm) result in higher order (plasmonic) cavity modes. High-resolution transmission electron microscopy reveals a native oxide layer on these nanowires of 1.5–2.5 nm thickness (Figure 1c), which is used as an insulating interlayer to separate the active material from the metal and thereby prevent nonradiative recombination of charge carriers at the metal surface.¹⁶ This layer is also used to sustain high intensity surface plasmon fields in the gap between the metal and the silicon core (Figure 1d,e). A thick silver film (300 nm) was deposited atop the silicon nanowires using both thermal and electron beam evaporation techniques. Thermal evaporation was used because it uses a tungsten boat to hold silver source as opposed to a graphite crucible, thereby eliminating a potential source of carbon contamination, which can be an issue with silver (discussed later). During thermal evaporation, particular care was taken to ensure a clean environment by first coating the entire chamber with a 200 nm layer of silver (base pressure of 10^–6 Torr) followed by deposition on the Si nanowires without breaking the vacuum. Samples synthesized using both techniques yield similar results, though for consistency all samples studied for this manuscript were synthesized with a single technique (electron beam evaporation). This highlights precautions taken during silver deposition, which is key for supporting surface plasmon modes in the vicinity of the silicon core, which can span the visible spectral range. Finite difference time domain (FDTD) simulations of the silicon-oxide-silver cavity demonstrate that these nanowires (150 nm diameter) are capable of sustaining high order (m > 7) hybrid surface plasmon modes that can significantly enhance spontaneous emission in silicon via the Purcell effect.^13,14

Figure 1.

(a) Schematic of silicon nanowire integrated with a 300 nm thick silver film to form a plasmonic nanocavity (drawn to scale). The native oxide of silicon (SiO_x) is used to separate the active silicon core from the silver shell. (b) Scanning electron microscope (SEM) of silver-coated silicon nanowire. (c) Transmission electron microscope (TEM) image of a representative bare silicon nanowire demonstrating 1.5–2.5 nm of native oxide (denoted by dashed white lines) on the nanowire surface. (d) Frequency domain spatial distribution of the electric field intensity in Ω-cavity Si (d = 150 nm) demonstrating high order (m = 9) mode (obtained via finite difference time domain simulations) and (e) corresponding magnetic field intensity.

Optical characterization of individual nanowire samples with Ag-based plasmonic nanocavities was carried out using a home-built microscope setup equipped with a 60×, 0.7 NA objective (Nikon) that has a spatial resolution of ∼600 nm. Variable-energy excitation experiments were conducted with five different laser lines obtained from a continuous wave argon-ion laser including 457.9, 488, 496.5, 501.7, and 514.5 nm and a He–Ne laser (633 nm) corresponding to an energy range (1.959–2.708 eV). The incident photon flux at each wavelength was maintained constant by focusing 1 mW of incident laser power to a ∼1 μm spot at all wavelengths. Photoluminescence spectra were collected using a spectrometer (Acton) coupled to a cooled charge-coupled device with a spectral resolution of 0.1 nm. Temperature-dependent measurements were conducted using a liquid nitrogen-cooled cryostat (for temperatures between 77 K and room temperature). We measured plasmonically coupled silicon nanowires with diameters ranging from 148 to 156 nm and at all the laser energies mentioned above.

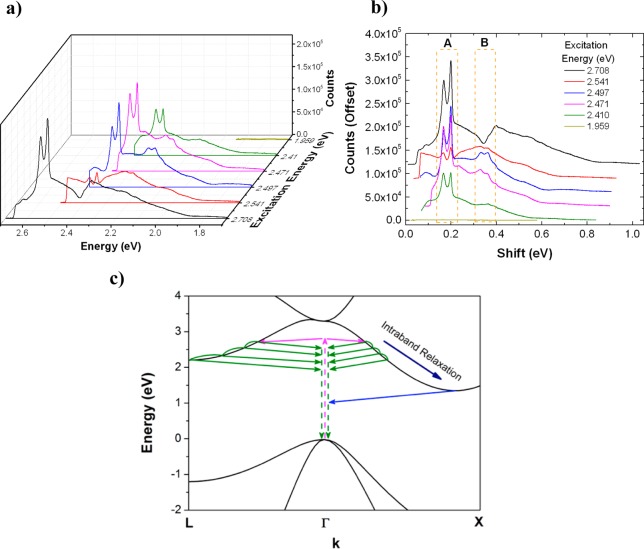
The photoluminescence spectra of a single plasmonically coupled silicon nanowire of diameter d = 150 nm are plotted versus (absolute) emission energy (Figure 2a) for different laser excitation energies. The emission envelope spans the visible range and appears to have a fixed spectral width that is independent of the excitation energy. Plotting the same spectra versus energy shift from the laser line reveals two clear high intensity subbands labeled A and B (Figure 2b), which occur at a fixed distance from the laser line, and are consistent with the previously reported data obtained with 2.708 eV excitation.¹³ The extent of the emission envelope and the occurrence of high intensity bands are related to the electronic structure and phonon dispersion of silicon respectively, which are discussed below.

Figure 2.

Photoluminescence spectrum of plasmonically coupled silicon nanowire (d = 150 nm) plotted versus (a) absolute emission energy and (b) energy shift from the laser line for various excitation energies in the range 1.959–2.708 eV. Spectra in (b) are plotted with a constant offset of 2 × 10³ counts for clarity. The dashed boxes labeled A and B denote high-intensity emission bands. (c) Schematic of the electronic dispersion of silicon featuring carrier excitation (magenta arrows), intraband relaxation and hot luminescence (green arrows), and radiative recombination from thermalized carriers (blue arrows). This process is examined for relaxation toward the selected conduction band minima at both the X-points (1.12 eV) and L-points (∼2.1 eV).

In indirect bandgap semiconductors, once the excited charged carrier is scattered to the electronic branch with momentum q_e and relaxes along the electronic branch by scattering with phonons with momentum q_r, radiative recombination at the light line (with momentum q ∼ 0) will require scattering with phonons of momentum q = −(q_e + ∑q_r) to satisfy momentum conservation (Figure 2c).¹⁷ It should be noted that both energy and momentum must be conserved, thus the emitted photon will have energy E = E_excited – ∑E_q, where E_excited is the excitation energy and ∑E_q is the total energy of all phonons involved in scattering. In silicon, intraband relaxation typically occurs on a picosecond time scale^18,19 while radiative recombination has a ∼10 ns lifetime near the direct bandgap;²⁰ thus radiative recombination is normally observed from carriers that thermalize near the minimum of the conduction band (near X-point) (Figure 2c, blue curves). On the other hand, the spontaneous emission rate of silicon nanowires may be enhanced by up to ∼10²–10³ via the Purcell effect due to highly confined hybrid plasmonic-cavity modes¹³ thereby making spontaneous emission competitive with the intraband relaxation process and enabling luminescence from nonthermalized states, that is, hot photoluminescence.

This competition between intraband relaxation and radiative recombination (Figure 2c, green curves) results in a broad emission envelope (Figure 2a) as carriers scatter back to the almost vertical photon dispersion line near q ∼ 0 (also known as the light line), which leads to radiative recombination, but also as the carriers continue relaxing along the conduction bands. The limited number of available relaxation channels in the electronic dispersion is responsible for the apparent emission cutoff at ∼2 eV. For all excitation energies, examining the electronic structure of silicon, we note the existence of multiple pathways for the relaxation of the excited carrier, that is, toward the two local conduction band minima near the X-point (1.12 eV) and the valley at the L-point (∼2.1 eV).²¹ On the basis of momentum mismatch between the light line at q ∼ 0 and the electronic branch, the two most likely relaxation pathways (toward X- and L-points) are depicted in Figure 2c. A carrier excited with at high energy (>2.1 eV) may relax toward all available conduction band minima, yet once the energy of the excited carrier is <2.1 eV, relaxation toward the L-point will no longer be possible leading to less radiative recombination events and thus a fixed spectral extent of the emission region. In addition, carriers excited with energy <2.1 eV may only be absorbed to the conduction band along the X- and K-points (near the conduction band minima), which are also electronic states that have high-momentum mismatch from the light line (at q ∼ 0). Thus, we expect lower counts from these states due to both the lower number of emission channels and also the low availability of phonons required to scatter back to the light line from near the X-point (see discussion of phonon mediated hot luminescence below). We note that hot emission from states below the L-point bandgap is still possible, albeit at lower counts (Supporting Information Figure S1) due to the requirement of phonons with high density of states (high-DOS) (see discussion below). Indeed, excitation at 1.959 eV yields a nearly background level spectrum (Figure 2b, yellow curve), suggesting the involvement of real electronic states for both absorption and emission. As illustrated in Figure 2c, it can be seen that hot photoluminescence (like thermalized emission) is also an indirect process and requires phonon scattering to satisfy momentum conservation. Depending upon the excitation energy, the excited carriers can occupy the available electronic branches (toward X- and L-points), and they can emit light through the phonon-assisted recombination process during the intraband relaxation. However, for excitation at 1.959 eV, the electronic branch toward L-point becomes inactive, and the excited carriers in the conduction band along the X-point have momentum values that do not correspond to that of phonons with high-DOS,¹³ thus giving rise to the low radiative quantum yield.

The high intensity subbands (Figure 2b, labeled A, B) occur at a fixed energy separation from the laser line and thus are evidence of events, which depend on phonon scattering rather than decay from fixed electronic states. Though the most likely phonons that can participate in this process would be those that have the highest density of states in the phonon dispersion of Si,¹³ labeling of the individual subpeaks within these bands is a significant theoretical problem, which should incorporate potential effects of phonons at the SiO₂–Si interface that are known to play a role in device physics,^22,23 coherent phonons due the high fields involved,²⁴ and correspondingly large phonon population numbers. In this work, we will restrict ourselves to highlighting the experimental results of variable energy excitation spectroscopic measurements, which when plotted as a function of energy shift, reveal a process that is mediated by phonons as expected from hot luminescence.

In addition, because the phonon dispersion around the highest density of states are relatively flat, we also expect scattering from several electronic states that satisfies both momentum and energy conservation with a range of high-DOS phonons.²⁵ Indeed, we observe variation of peak positions in band A by as much as 20 cm^–1 (3 meV) when examining band A of a single 150 nm nanowire at various excitation energies (Supporting Information Figure S2a). We observe even greater scatter in peak positions (40 cm^–1 or 5 meV) as a function of nanowire size at a single excitation energy of 2.541 eV (Supporting Information Figure S2b), a reflection of the fact that phonons from a relatively broad region of the phonon dispersion may be involved in the hot photoluminescence process. Indeed, a similar mechanism of hot photoluminescence was recently observed in organic dye molecules, where surface-plasmon-enhanced spontaneous emission results in a series of peaks at fixed vibrational mode energies (also revealed by variable energy excitation) superimposed on a broadband emission envelope that is restricted due to availability of electronic states.²⁶

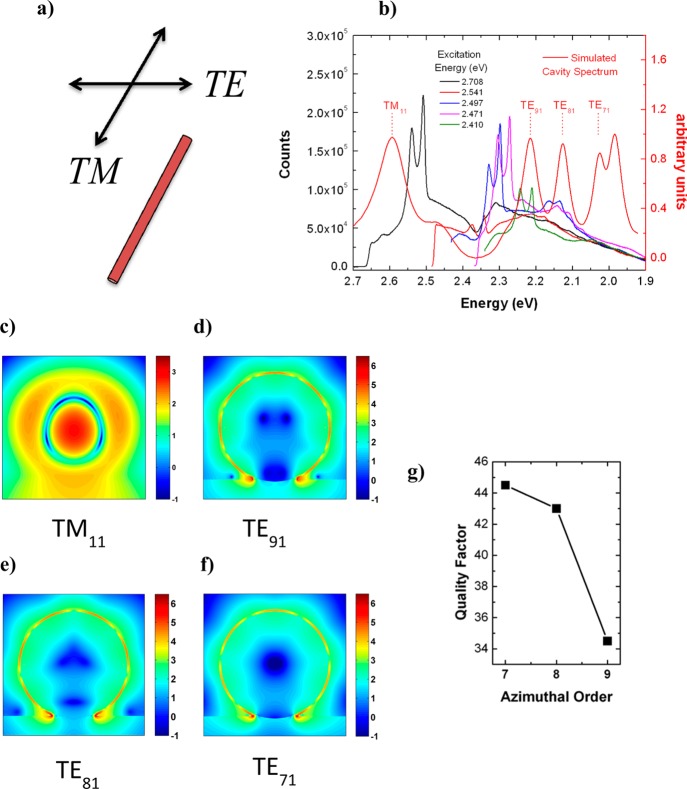
It should be noted that the Purcell-enhanced spontaneous emission of silicon is a highly complex function of the spectral and spatial overlap between cavity modes and states that satisfy momentum and energy conservation, thereby involving three (quasi)-particles, that is, plasmons, carriers, and phonons. Noting that cavity modes for a particular nanowire are spectrally fixed, we expect there to be an excitation energy-dependent modulation of the higher intensity emission bands. As discussed above, these bands occur at fixed energy shifts from the laser line (i.e., bands A and B), thus their spectral positions will change with the exciting laser and be tuned in and out of resonance with the cavity modes that are spectrally fixed for any given geometry. Both the broad emission envelope and the subbands are expected to be strongly modulated as a function of the excitation energy. In order to explore the cavity modes responsible for modulating the emission envelope, we performed FDTD simulations of all experimentally measured samples. The frequency domain response of the sample was obtained by averaging the Fourier transforms of the time domain fields due to all three orthogonal polarizations; that is, two orthogonal polarizations in the plane of the nanowire cross section and a polarization along the nanowire long axis. Unlike the nanowires previously studied in the size range d < 80 nm,¹³ these larger nanowires with diameters d ∼ 150 nm demonstrate markedly different cavity mode spectra characterized by higher order modes with electric field polarizations both perpendicular to the long axis (TE or transverse electric) and parallel to the long axis (TM or transverse magnetic) of the nanowire (Figure 3a). Note this convention is orthogonal to that used in some plasmonics literature where the field polarization is labeled with respect to the plane of incidence,²⁷ but inline with recent nanowire literature where the field polarization is referenced with respect to the nanowire long-axis.²⁸ Figure 3 shows the photoluminescence spectrum of the plasmonically coupled silicon nanowire examined in Figure 2, along with the associated cavity field spectrum (Figure 3b). Note there is a region of low mode activity between peak 1 at 2.58 eV and peak 2 at 2.22 eV of the simulated cavity spectrum. This is responsible for the lower photoluminescence counts in this spectral range. This region of low mode activity is observed all across the measured size range in this work and is due to a lack of high order TE polarized modes and lower order TM modes with both azimuthal and radial components.

Figure 3.

Electromagnetic mode properties of plasmonically coupled silicon analyzed via FDTD simulations and photoluminescence spectroscopy. (a) Nomenclature convention for modes polarized parallel (TM) and perpendicular (TE) to the nanowire long-axis. (b) Variable-energy excitation photoluminescence spectra of d = 150 nm Ω-cavity silicon nanowire juxtaposed with simulated cavity mode spectrum (red curve). (c–f) Frequency domain profiles of the electric intensity (log scale) for cavity modes ordered from highest to lowest energy. (h) Plot of quality factor versus azimuthal index (m), for TE modes in (b) and represented by the field profiles in (d–f).

As can be observed from the frequency domain electric field profiles (Figure 3c–f), these modes resemble whispering gallery modes (WGM) and will be classified as either TE_mn for perpendicular electric field polarization or TM_mn for parallel electric field polarization (with respect to the nanowire long-axis) and where the indices m and n correspond to the integer number of half wavelengths in the azimuthal and radial directions, respectively. It should be noted that for WGM modes the index “m” often refers to an integer number of wavelengths as circularly symmetric structures must observe the periodic boundary condition, which only allows modes at full wavelength multiples.²⁹ The base at the intersection of the nanowire and substrate breaks the circular symmetry and enables modes at half-wavelength multiples.¹³ Following the spectra from right to left (i.e., from low energy to high energy laser excitation in Figure 3b), we observe three modes with perpendicular electric field polarization, which are attributed to the TE₇₁, TE₈₁, and TE₉₁ modes, respectively. These are plasmonic modes similar to those reported by Cho et al. (but of higher order), where the majority of the field is stored near the Si/SiO₂ interface.¹³ The mode at ∼2.6 eV (Figure 3c), on the other hand, is polarized parallel to the nanowire long-axis and has a completely different field profile, where the majority of the field is stored inside the Si core as opposed to the metal interface. This may be classified as the TM₁₁ mode. Referring to Figure 3c–f we note that the field intensities (normalized to the source) within the core in both the TM and TE modes are >10². The TE modes demonstrate >1000 times intensity at the silicon surface, but this is offset by the superior spatial overlap between the active region and the cavity mode in the TM₁₁ mode. It has been previously demonstrated that in silicon–Au plasmonic core–shell nanowire photodetectors, both the TE and TM modes may contribute in similar magnitudes to the spectral characteristics of the system,³⁰ thus given the relative field intensities within the silicon core we expect that both TE and TM modes can mediate the hot PL process.

The question remains, as to why is there a spectral gap in emission between the TE and TM modes in the spectrum (Figure 3b). This may be understood from the inverse relationship between azimuthal mode order and quality factor that exists in plasmonic cavities. In all-dielectric WGM resonators, the quality factor scales proportional to the azimuthal order (and inversely proportional to the radial order),^31,32 in other words this is why larger resonators, which host very high order modes, demonstrate the highest quality factors.³³ The opposite trend is true in plasmonic systems; the quality factor decreases with increasing azimuthal mode order.³⁴ In a surface-plasmon WGM-type resonator, increasing mode order within the same circumference implies increased confinement to the metal-dielectric interface. Metals are very lossy media,^27,35−37 thus higher interaction with the metal interface results in increased damping of the cavity mode. By tracking quality factor of the TE cavity modes as a function of azimuthal order (Figure 3g), we observe that the quality factor drops precipitously with increasing order, which signifies that in our system mode damping becomes prohibitively high for azimuthal mode orders >9. Therefore, due to the highly damped high order TE modes we expect a decreased photoluminescence emission intensity in regions at energies higher than the highest order TE mode, but lower than the lowest order TM mode.

This characteristic of the cavity modes is reflected in the emission spectra of several nanowires, which demonstrate a drop in emission intensity in the region of low mode activity (∼2.3 eV), and which was not observed in previous measurements of smaller (sub-80 nm) plasmonically coupled nanowires.¹³ For 2.708 eV excitation, we observe two broad regions of the emission envelope, one centered around 2.5 eV due to the TM mode and the other centered around 2.2 eV due to the TE modes. Interestingly, in the spectra excited at 2.708 eV, band B is effectively quenched (Figures 2b and 3b, black curves), as it is resonant with this area of low mode activity. Furthermore, the spectra due to excitation at 2.541 eV, where band A (at ∼0.2 eV shift, Figure 2b) is now resonant with the region of low mode activity, also exhibits low intensity in this region when compared with the spectra excited at other laser energies. In fact, the features of the photoluminescence spectra due to excitation at other laser energies in the range 2.541–1.959 eV are all superimposed on the same emission envelope due to the TE cavity modes, but again, restricted in the low energy region due the silicon bandgap at the L-point (discussed above). Therefore, for larger-sized Si nanowires (∼150 nm range) we now exploit both TE and TM modes to generate hot luminescence in larger nanowire cavities.

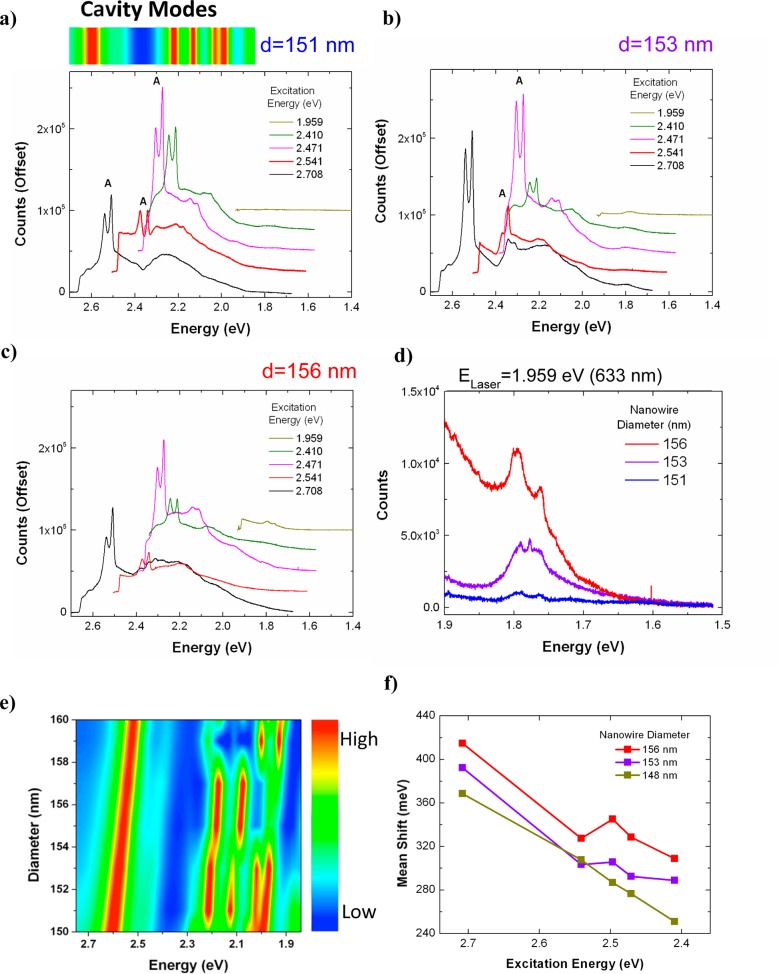
The size dependence (albeit a narrow range of 151 to 156 nm) of the emission is shown in Figure 4. Photoluminescence spectra are analyzed for nanowires with sizes d = 151, 153, and 156 nm, corresponding to Figure 4a–c, respectively, and excited at different laser energies. For d = 151 nm, the emission spectrum excited with the 2.708 eV laser line (Figure 4a, black curve) demonstrates a dip in the emission around 2.38 eV (as in the d = 150 nm sample examined above), which we attribute to cavity mode structure (Figure 4a, top). When the sample is excited with a 2.541 eV (488 nm) laser (Figure 4a, red curve) band A becomes resonant with the local minimum in the cavity field spectrum resulting in significant damping of the emission in this region. Indeed, the entire emission envelope resulting from the excitation energy of 2.541 eV and those at other laser energies up to 1.959 eV also reflects the same structure observed at 2.708 eV excitation. Figure 4e shows simulated cavity spectra for various nanowire diameters, which demonstrate a monotonic redshift in the cavity modes with increasing diameter (as expected). As the nanowire size (although in a small range) increases (Figure 4b,c), the cavity modes redshift (Figure 4e) and the emission envelope shifts to the right (lower energies) leading to a direct modulation of subpeaks in band A (Figure 4b, red curve). The overall redshift of the emission also results in luminescence from lower energy states. Figure 4d is a magnified view of the low-energy region of the spectrum (1.5–1.9 eV), excited at 1.959 eV for all three nanowires. As the intensity of band A significantly decreases under excitation at 1.959 eV, the plasmonic nanowire with d = 153 nm shows a different peak spacing of ∼15 meV, compared to that of ∼30 meV at the other excitation energies, which differs by 1 TA phonon energy. This strongly suggests that because the excitation energy is smaller than the energy gap at L-point (∼2.1 eV), the electronic states along the ⟨111⟩ direction cannot contribute to the hot luminescence process, leading to a dramatic decrease in the counts and also different peak positions. Furthermore, as expected from Figure 4e, increasing nanowire size leads to an increase in measured counts from low energy states due to the increased overlap between the cavity mode and the band A for the larger size nanowires.

Figure 4.

(a–c) Photoluminescence spectra of plasmonically coupled nanowires excited at various laser energies in the range 1.959–2.708 eV for nanowires of size (a) d = 151 nm, (b) d = 153 nm, and (c) d = 156 nm (all spectra are offset by 25 000 counts for clarity). The cavity mode spectrum of the d = 151 nm nanowire is plotted on top of the photoluminescence spectra (high in red to low in blue) using the same energy scale. The variable energy excitation photoluminescence spectra demonstrate the role of mode structure in modulating high intensity subpeaks. In addition to size-dependent peak modulation, the modes, which redshift with increasing size, also enable hot luminescence at lower energies for larger nanowires. (d) Photoluminescence spectrum in low-energy region (excited with 633 nm, He–Ne laser) for samples (a–c). (e) Simulated cavity mode spectra of plasmonically coupled silicon nanowires with diameters in the range d = 150 to 160 nm as a function of energy. (f) Difference between the average emission energy and exciting laser energy (i.e., the mean emission shift) plotted against excitation energy. Large fluctuations in mean emission intensity as a function of size and excitation energy highlight the role of both cavity modes and electronic structure in modulating the emission spectrum.

The observed modulation of individual peaks and spectral features as a function of excitation energy is in contrast to the resonant Raman spectrum of silicon, which demonstrates little or no variation in its spectral features as a function of excitation energy in either the visible³⁸ or infrared frequencies.¹ To further explore the variation of the many spectral features of plasmonically coupled silicon as a function of excitation energy, we use the photoluminescence spectra to extract the mean emission energy of the spectrum and thus the mean energy shift of the spectrum from the exciting laser energy. The mean emission energy was calculated from the photoluminescence spectra via ν̅ = [∫vN(v)dv]/[∫N(v)dv] where N(v) is the number of measured counts at a frequency v.³⁹ The mean emission energy is then hν̅.⁴⁰ Subtracting this value from the exciting laser energy results in a mean emission shift. Plotting the mean emission shift (of the spectrum) as a function of excitation energy (Figure 4f), we observe significant variation in the mean emission energy of individual nanowire samples (>100 meV comparing 2.410 eV excitation with 2.708 eV excitation and >25 meV between 2.410 and 2.541 eV), which is a consequence of the dependence of the emission on both cavity modes and electronic structure as discussed above. Moreover, there is clear size dependence in the mean emission shift where larger wires demonstrate greater mean emission shifts and thus stronger red shifting in the emission envelope. The redshift of the emission envelope as a function of size is consistent with the previous discussion on size-dependent cavity modes (see above and Figure 4e), where lower energy modes (for larger nanowires) enhance scattering from lower energy states. We also note that carbon contamination, and thus Raman activity of carbon, can be an issue especially when combined with silver;⁴¹ however, it is unlikely that trace amounts of carbon can yield such bright white light emission (∼10⁵ peak counts, >10⁶ integrated counts) that the broad emission envelope is very strongly dependent on the excitation energy and that the peaks change their positions and intensities depending on a variety of parameters. These observations are in contrast to the Raman spectrum of silicon where the mean emission energy should show negligible dependence on the exciting laser in this range. It should be noted that surface enhanced Raman spectroscopy (SERS) is known to lead to a broad background, which can depend on plasmon modes.⁴² Still, measurements in the range 2.410–2.541 eV include all TE plasmon modes (see Figure 3b); thus, we expect any possible SERS background to result in little or no net variation of the average emission energy or shift. Furthermore, SERS spectra retain the same Raman spectral features over a broad excitation range,⁴³ where the SERS enhancement is much more sensitive to resonance with electronic states than local field enhancement.⁴⁴

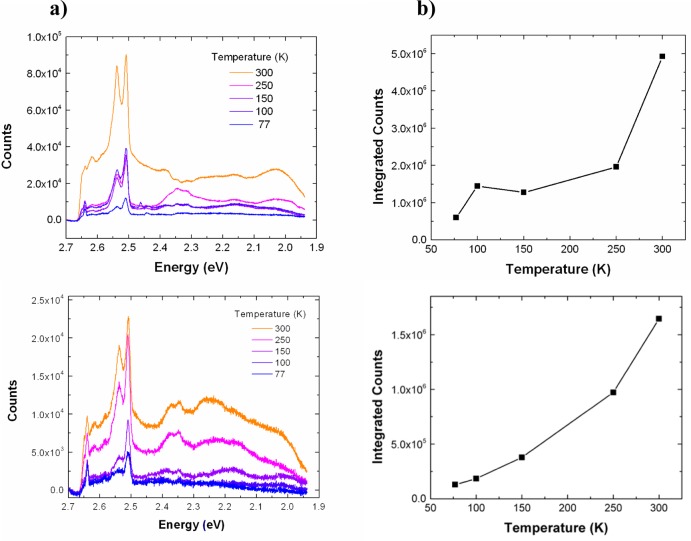
To further test the validity of the hot luminescence process, we examined the temperature dependence of the photoluminescence spectrum from plasmonically coupled silicon and compared it to the known temperature dependence of other radiative and scattering processes. Raman spectroscopy typically shows a decrease in intensity with increasing temperature due to a decrease in the polarizability of a material with temperature.⁴⁵ Resonant Raman spectroscopy of silicon also demonstrates a negative temperature dependence with increasing temperature (as the number of photons involved in electronic absorption increases with temperature due to phonon-mediated indirect absorption thereby limiting the amount of photons involved in the Raman process).^46,47 Likewise, photoluminescence from direct-bandgap materials, such as GaAs⁴⁸ and CdS⁴⁹ also exhibit a negative temperature dependence due to increased nonradiative recombination at higher temperatures.¹⁷ On the other hand, indirect transitions such as hot luminescence from an indirect-bandgap material (i.e., silicon) involve a competition between an increase in the nonradiative decay rate and also an increase in the radiative decay rate with temperature, as phonons are critical to mediating radiative recombination (see discussion above). Previously, a positive temperature dependence was verified for silicon quantum dots, where increased photoluminescence was observed at higher temperatures and attributed to indirect-radiative recombination, as also confirmed by time-resolved photoluminescence measurements.⁵⁰ For our plasmonically coupled silicon samples, we measured the photoluminescence spectrum at temperatures in the range 77–300 K at 2.708 eV excitation and with a fixed laser power. We observed a monotonic increase in counts as a function of increasing temperature (Figure 5) again in contrast to the stokes-Raman spectra, which generally shows a decrease in intensity with increasing temperature. We chose two representative data sets (Figure 5a,b), which exhibit spectra with differing levels of intensity and broad spectral features, while both exhibit a positive temperature dependence in their photoluminescence counts. We observed this positive temperature dependence in all samples measured. It should be noted that at higher temperatures the absorption coefficient of silicon will also increase (as it is phonon mediated), which can lead to a larger concentration of excited carriers and emitted light.⁵¹ However, the ratio of absorption coefficients for silicon (2.708 eV) at 300 and 77 K is 2.4, while the observed ratio of integrated counts (emission) at the same temperatures ranges from 10 to 20 depending on the nanowire size and laser excitation energy. Therefore, the temperature-dependent change in absorption is insufficient to explain an order of magnitude increase in the measured increase in counts. Thus, the temperature dependence of the emission intensity can be best explained by a hot photoluminescence process, where the thermal activation of phonons that are required for intraband and interband relaxation can increase the radiative quantum yield.

Figure 5.

(a) Temperature-dependent photoluminescence spectra of plasmonically coupled silicon (for two different samples) in the range 77–300 K. The increase in overall emission intensity with temperature follows the expected trend for hot luminescence from an indirect bandgap material as the phonon population increases with increasing temperature. (b) Plot of total integrated counts as a function of temperature for samples shown in (a).

In conclusion, we have generated bright luminescence from silicon nanowires coupled with metal nanocavities supported by high order hybrid nanocavity-surface plasmon modes. Photoluminescence spectroscopy at variable excitation energies reveals that silicon’s electronic structure plays a key role in determining the emission intensity, while the individual subfeatures of the spectrum are mediated by phonons in a hot luminescence process. Finite difference time domain simulations elucidate the role of cavity modes in modulating the emission spectrum. Furthermore, temperature-dependent spectroscopy reveals a temperature dependence of the measured intensity that is indicative of hot luminescence and rules out the resonant Raman process. It should also be noted that in addition to this experimental work extensive theoretical work is necessary to analyze this highly complicated system featuring the interplay between phonons (bulk and interfacial for this hybrid system), plasmons, and charge carriers all of which play a role in the radiative recombination process. Finally, a direct measurement of the carrier lifetimes in plasmonically coupled silicon would be highly desirable and is currently being pursued.

Supporting Information Available

Additional discussion and figures. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States