Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Sep 11;4:5864. doi: 10.1038/srep05864

Optical Activity Enhanced by Strong Inter-molecular Coupling in Planar Chiral Metamaterials

Teun-Teun Kim 1,5,6, Sang Soon Oh 2,5, Hyun-Sung Park 1, Rongkuo Zhao 2, Seong-Han Kim 3, Wonjune Choi 4, Bumki Min 1,a, Ortwin Hess 2,b
PMCID: PMC4160707  PMID: 25209452

Abstract

The polarization of light can be rotated in materials with an absence of molecular or structural mirror symmetry. While this rotating ability is normally rather weak in naturally occurring chiral materials, artificial chiral metamaterials have demonstrated extraordinary rotational ability by engineering intra-molecular couplings. However, while in general, chiral metamaterials can exhibit strong rotatory power at or around resonances, they convert linearly polarized waves into elliptically polarized ones. Here, we demonstrate that strong inter-molecular coupling through a small gap between adjacent chiral metamolecules can lead to a broadband enhanced rotating ability with pure rotation of linearly polarized electromagnetic waves. Strong inter-molecular coupling leads to nearly identical behaviour in magnitude, but engenders substantial difference in phase between transmitted left and right-handed waves.

Since its discovery, optical activity has been widely utilized in many fields of science including chemistry, physics, biology, and optics1. It can be measured by the rotation angle of the plane of linearly polarized light2 and is generated in a material with a chiral internal structure lacking mirror symmetry3. While naturally chiral materials such as DNA, sugar and many other bio-molecules display only rather modest optical activity, artificial chiral metamaterials comprised of sub-wavelength metallic resonators have recently been shown to exhibit large optical activity4,5,6. On top of this, chiral metamaterials are also of particular interest for negative refraction7,8,9,10,11, the Casimir effect12, strong nonlinear optical activity13, polarization switching and modulation14,15 as well as various other applications such as broadband circular polarizers and wave plates16,17,18,19. Therefore, significant efforts have been devoted to conceiving and demonstrating various designs of chiral metamaterials for enhanced chirality, including conjugated gammadions20 and double four-U structures21. Strong chirality of various artificial chiral structures has been tested experimentally, which is also theoretically supported by a model taking intra-molecular couplings into consideration22,23. Yet, despite the remarkable possibility of achieving strong chirality, very large ellipticity at resonances remains an obstacle for potential applications of chiral materials as incident linear polarization states become elliptically polarized after being transmitted through the media. Moreover, with only the concept of intra-molecular coupling, the value to which the optical activity can be enhanced is limited and governed by morphological shaping or arrangement of metamolecules so that a degree of freedom in design methodology for chiral metamaterials is seriously restrained.

Here, we experimentally and theoretically demonstrate a new class of bi-layer metamaterial structures that substantially enhance optical activity through strong inter-molecular coupling between adjacent planar chiral metamolecules. This structure, a conjugated double Z metamaterial (CDZM), can maximize inter-molecular capacitive coupling to achieve its remarkable optical activity. On the basis of a semi-analytic coupled RLC resonator model and numerical simulations, we explain qualitatively and quantitatively how the observed optical activity scales with the width of the gap between adjacent planar metamolecules in the CDZM. We show that a strong inter-molecular coupling not only leads to enhanced chirality but also to reduced ellipticity at resonant frequencies.

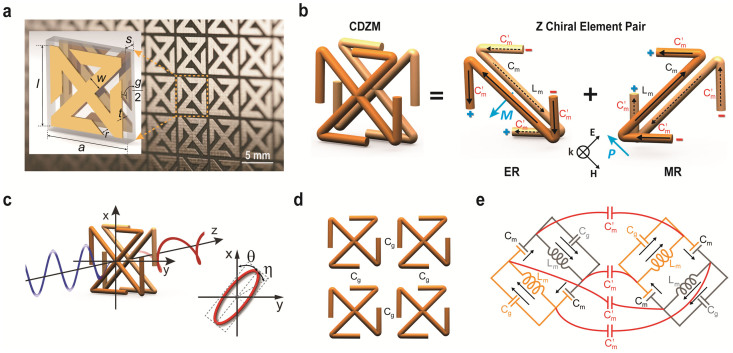
In order to fully exploit the strong inter-molecular capacitive coupling, we designed the CDZM as depicted in Fig. 1a by morphologically transforming a conventional conjugated gammadion structure20 (See Method). The conjugated arrangement of the CDZM maintains resonant chiral properties of the conjugated gammadion structure that exhibits two distinct fundamental resonances in the low frequency range. However, in contrast to the conjugated gammadion structure, each arm of the CDZM is constructed in such a way that a small lateral gap of width g is maintained between adjacent chiral metamolecules for strong capacitive coupling. It can therefore be predicted that g (Fig. 1a) will play a critical role in enhancing the effective chirality parameter in the CDZM. In close analogy to the case of high index metamaterials that utilize strong capacitive coupling24, an effective chirality parameter is expected to scale differently in weak and strong inter-molecular coupled regimes.

Figure 1.

Figure 1

Open in a new tab

Conjugated double Z metamaterial and an equivalent RLC model (a) Schematic view of the unit cell structure and photograph of the CDZM sample with the dimensions indicated in the figure: l = 5.5 mm, w = 0.9 mm, s = 0.5 mm, r = 0.6 mm, and the thickness of the copper t = 18 μm. The gap width between chiral metamolecules is defined by g = a – l. (b) Schematics of the equivalent RLC model for the CDZM. 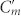Inline graphic is the capacitances of the side strips and Lm and Cm are the inductance and capacitance of the central strips respectively. The incident electric field (E) induces the surface current in the central strip (black arrow) resulting in magnetization (M) and, similarly, the electric charges (represented by +, −) driven by the magnetic field (H) induces electric polarization (P). (c) Ellipticity angle η and azimuthal rotation angle θ represent the polarization state of the transmitted electromagnetic waves. (d) Schematics of CDZM arrays. Cg is the gap capacitance which represents additional inter-molecular coupling between metallic strips in neighbouring unit cells. (e) Equivalent RLC circuits for Z chiral element pairs. For simplicity, the resistor elements have been omitted. The arrow indicates the current direction.

The physical mechanism of optical rotation of CDZM is similar to the one in a type of bilayer chiral metamaterials such as gammadion structures20. For simplicity, the unit cell of CDZM can be decomposed into conjugated Z chiral element pairs as shown in Fig. 1b. Upon a linearly polarized electromagnetic excitation, the external electric field (E) induces an antiparallel current in the central strips resulting in a magnetization (M) in the direction opposite to the incident electric field. Similarly, electric charges driven by the magnetic field (H) result in an electric polarization (P) in the direction opposite to the incident magnetic field. Thus, the coupling between the electric and magnetic fields in the unit cell of a CDZM rotates the polarization plane of linearly polarized light by the azimuthal angle θ as shown in Fig. 1c. This coupling effect can be described by employing an equivalent RLC model. From our simulation results (see Supplementary Information Section SI for field distributions at resonances) we can assign inductive and capacitive coupling elements Lm, Cm, and 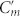Inline graphic (see Fig. 1b). However, it should be noted that, in contrast to bilayer chiral metamaterials demonstrated so far, CDZM exhibit additional strong capacitive coupling between adjacent metamolecules (Cg) shown in Fig. 1d. This characteristic CDZM coupling can be classified as intra-molecular (Lm, Cm and 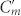Inline graphic) and inter-molecular (Cg) couplings. Here, the intra-molecular coupling refers to capacitive (charge-to-charge) and inductive (current-to-current) coupling between metallic strips in one unit cell and the inter-molecular coupling refers to the coupling between metallic strips in neighbouring unit cells (see Supplementary Information Section SII for details of intra-molecular coupling for CDZM).

To understand this novel coupling property, let us first focus on the role of the inter-molecular coupling Cg in enhancing optical activity. For gap widths comparable to the width of metallic strips w (g ≈ w), Cg is much smaller than Cm and 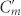Inline graphic since the area per unit length facing each other in Cg is smaller than the ones in Cm and 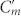Inline graphic (t ≪ w). Therefore, the contribution of Cg to the current induced in the central strips can be ignored. In contrast, when the gap is comparable to t or smaller than t (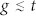Inline graphic), Cg can be increased to a value comparable to Cm and 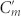Inline graphic or even to an extremely large value since Cg is inversely proportional to the gap width. The increase of capacitance implies that more charge can be accumulated in Cg so that it allows more current to flow in the central strips. As a result, optical activity is enhanced by reducing the gap width. It is worth to point out that the enhancement of optical activity is not restricted to resonant frequencies since the enhanced inter-molecular coupling exists for a wide frequency range25.

To obtain an understanding of the nature and relative role of intra- and inter-molecular coupling, we use a coupled RLC model. As shown in Fig. 1e, each Z chiral element pair in one unit cell is represented by one equivalent RLC circuit and the unit cell is represented by a coupled RLC resonator. For simplicity, the resistor elements have been omitted. It should be noted that the RLC resonators are similar to the one for cut-wire pairs26. By analysing the equivalent RLC circuit, we note that the coupled RLC resonator is, in fact, a combination of three resonators that all share one inductance Lm but are individually distinguished by separate constituting capacitances Cm, 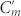Inline graphic and Cg, respectively. From the equations of motion for the electric charge, we obtain expressions for the resonance frequencies f1,2 and the effective chirality parameter of the CDZM (see Supplementary Information Section SI for resonance frequencies of CDZM). 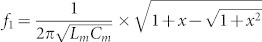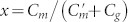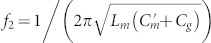The resonance frequencies for the CDZM are given as Inline graphic where Inline graphic and Inline graphic for MR and ER, respectively. As can be confirmed from the expression, the resonance frequency shift for the variation in gap width depends solely on the inter-molecular coupling Cg, because the intra-molecular couplings Cm and Inline graphic are independent of the gap width g. Moreover, the effective chirality parameter is expressed with the chiral resonance strength27, which is inversely proportional to f1,2. Therefore, the optical activity is proportional to the square root of the capacitance of the Z element (see Supplementary Information Section SI for the effective chirality parameters of CDZM).

To shed further light on the chiral response of a CDZM in the regime of strong inter-molecular coupling, we focus on the scaling behaviour of the gap capacitance Cg of the Z element with the gap width g. Using a coplanar strip capacitance formula28, the gap capacitance Cg can be expressed as 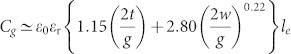Inline graphic, with the vacuum permittivity ε0, the relative permittivity of the substrate material εr, the thickness of the strip t, the effective length of the side strip le and its width w. As can be seen in Fig. S3, three regimes of capacitive coupling are delineated according to the scaling behaviour with the gap width: (1) an intra-molecular coupling regime where the resonance frequencies f1,2 remain almost constant, (2) a weak inter-molecular coupling regime where f1,2 decreases with a rate of g0.11, and (3) a strong inter-molecular coupling regime where f1,2 is proportional to g1/2. In the strong inter-molecular coupled regime, one obtains the relation Ωκ∝g−1/2 between resonant strength coefficients and g (see Supplementary Information Section SI for definition of the three regimes of coupling) resulting in a significant increase of the chirality parameter κ at pure optical activity (i.e., the transmitted wave remains linearly polarized with rotation angle θ) as g becomes very small.

To examine the optical activity of the CDZM, we follow a well-established characterization approach22,27. The measured transmission amplitudes and phases for the RCP and LCP waves through the CDZM are shown in Fig. 2 with a variation in gap width g from 0.1 to 5 mm. As expected from the conjugated design, two strong resonances appear in both transmission amplitude and phase spectra at the frequencies f1 and f2. For the off-resonance frequencies, the transmission amplitudes for the RCP and LCP waves are nearly indistinguishable, which implies that the ellipticity is very small. For the resonance frequencies, the difference in transmission amplitudes for the RCP and LCP waves is significantly reduced as the gap width becomes smaller. In contrast, the phase spectra differ significantly near the resonance frequencies, which is clear evidence of the gigantic optical activity of the CDZM (Fig. 2). More interestingly, in the strong inter-molecular coupled regime (for the case of g = 0.1 mm), the phase difference becomes even larger not only at the resonances but also between the resonances. This suggests that broadband enhanced optical activity is attainable by strong inter-molecular coupling. In addition, the resonance frequencies f1 and f2 are red-shifted with decreasing g, which is consistent with the coupled RLC model. Here, geometrical parameters are chosen such that the resonance frequencies are positioned in the frequency range between 7 and 13 GHz. However, it is worthwhile to note that the concept can be extended to other frequency ranges (see Supplementary Information Section SIV for CDZM at THz frequencies).

Figure 2. Gap-dependent amplitude and phase changes of waves transmitted through the CDZM.

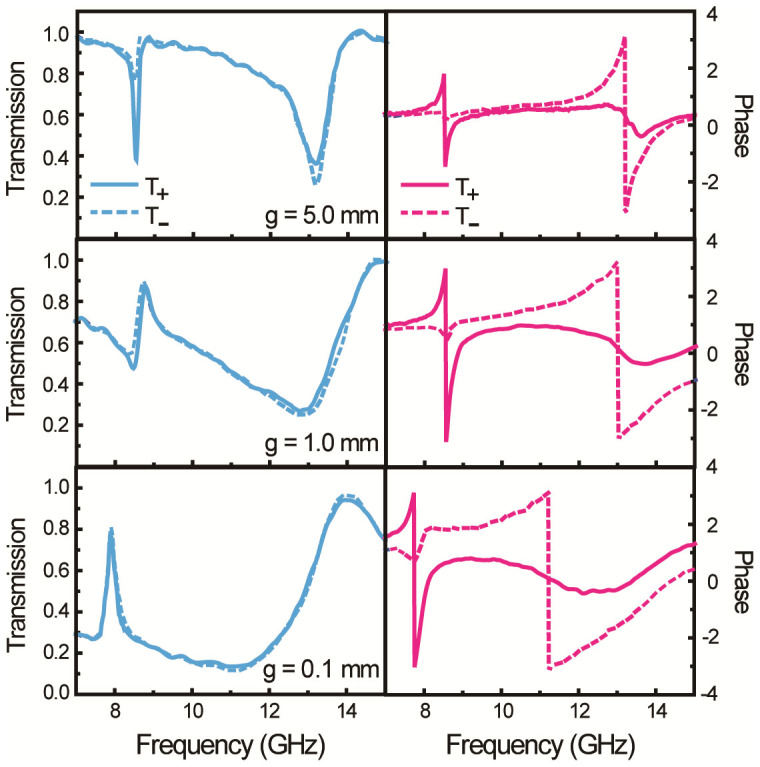
Figure 2

Open in a new tab

Measured transmission spectra and phases of right-handed circularly polarized (RCP, solid line) and left-handed circularly polarized (LCP, dashed line) waves are plotted for different gap widths g. While the transmission difference between RCP and LCP waves is very small due to the small absorption, the phase difference is significant due to the large optical activity.

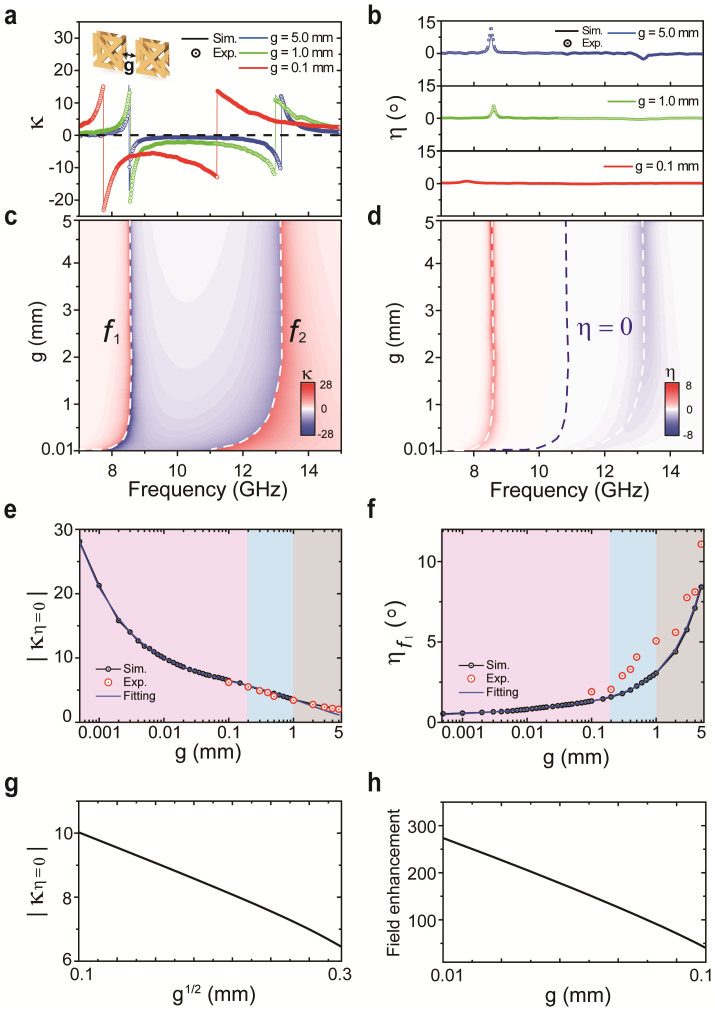
To see how the optical activity scales in different coupling regimes, the chirality parameter κ (Fig. 3a) and ellipticity η (Fig. 3b) are estimated (solid line) from the transmission spectra (Fig. 2) and compared with numerically calculated values (circles) for several values of gap width g. In the strong inter-molecular coupling regime, the ellipticity becomes practically negligible (η ≈ 0) in a broad frequency range between the two resonances, where a substantial amount of pure optical activity can still be observed (highlighted by blue dashed line in Fig. 3d). In this broad frequency range, linearly polarized waves maintain their linearity while being rotated by an angle θ when passing through CDZM. The frequency region of small ellipticity is bounded by the two resonance frequencies where the ellipticity increases due to increased absorption. We note that while a zero-ellipticity frequency, at which the ellipticity becomes zero, is a common feature of bi-layer chiral metamaterials which have two resonances23, the optical activity at that frequency is generally not large enough. Figures 3c,d show simulated values of κ and η as a function of gap width g. The red shift of the resonant frequencies for smaller gap width can be clearly observed, which is consistent with our coupled RLC model above.

Figure 3. Effective parameters as a function of the gap width for the CDZM.

Figure 3

Open in a new tab

Comparisons are made between simulated (solid lines) and measured (circles) (a) chirality κ and (b) ellipticity η for different gap widths g. Simulated effective parameters (c) chirality κ and (d) ellipticity η are plotted with the gap width g ranging from 10 μm to 5 mm. The white dashed lines represent the frequencies f1 and f2, and the blue dashed line represents the region of pure optical activity, η = 0. (e) The chirality κ at the frequencies for which η = 0 and (f) the ellipticity η at the resonant frequency f1 as a function of the gap width g. The black circled line and the red scatters represent simulated and measured results, respectively. The theoretical fitting obtained from the coplanar strip capacitance formula is drawn as a blue line as a function of the gap width g. Three regimes of coupling (uncoupled: grey shaded; weak inter-molecular coupled: blue shaded; strong inter-molecular coupled: red shaded) regimes can be defined for the ranges of gap width. As the gap width decreases, κ increases significantly and η decreases. Comparison between the (g) chirality parameter |κη = 0| and (h) field enhancement factor with varying gap width g in the strong inter-molecular coupled regime.

In order to compare the effective parameters at the frequency of pure optical activity, Fig. 3e shows the dependence of the chirality parameter κ at η = 0 on the gap width. Theoretical chirality parameters κ obtained from the coplanar strip capacitance formula are also plotted in Fig. 3e (see Supplementary Information for details) as well as the theoretical chirality parameter as obtained from the coplanar strip capacitance formula (blue line). As mentioned above, in the strong inter-molecular coupling regime (red shaded region), the chirality parameter κ is proportional to g−1/2 and increases even more rapidly than that in the weak inter-molecular coupled regime (blue shaded region). In the strong inter-molecular coupled regime (g = 0.1 mm), we experimentally achieved very large value of the chirality parameter κ = 6.2 (6.5 in the simulation results) at fη = 0. This corresponds a rotation angle θ of 31.4° at fη = 0 = 9.0 GHz, which means that the rotation angle per wavelength reaches 1933°/λ. Here, the thickness of the sample is 0.536 mm. Simulation results in Fig. 3e show that the chirality parameter can reach up to 28 for g = 0.5 μm.

Moreover, as the gap becomes smaller, the ellipticity η significantly decreases not only at non-resonant frequencies but also at the resonance frequency (Fig. 3f). The theoretical scaling property of the ellipticity η∝1/Cg (blue line) shows an excellent agreement with simulation results and confirms that the near-zero ellipticity indeed is a result of the strong inter-molecular coupling and corresponding field localization effect. In the case of g = 0.1 mm, the ellipticity of the transmitted wave is less than 1.3° (1.9° in the experimental results) across the whole frequency range of interest. Because of this substantial decrease in ellipticity, the transmitted waves at the resonant frequencies remain highly linearly polarized at a rotated angle θ for a linearly polarized incident wave. This is very important for practical applications since the resonance frequencies, where polarization rotation reaches the maximum θ = 90°, can be used for polarization rotation, which has been impossible with conventional bilayer chiral metamaterials. We measured azimuthal rotation angles θ as large as 88.7° at the resonance frequency f1 = 7.8 GHz and 88.0° at f2 = 11.2 GHz. These experimental results show that the rotation angle θ per wavelength reaches values in excess of 6288°/λ and 4383°/λ at f1 and f2, respectively.

To confirm that the enhanced optical activity originates from the strong inter-molecular coupling in the CDZM, we numerically calculated the electric field enhancement in the gap between the two metallic strips using geometric parameters consistent with those of our samples. The induced electric field is expected to increase for smaller gap widths due to an increased capacitance (see Methods). Full-wave electromagnetic simulations confirm electric field enhancements near the metallic strips of CDZM elements. The field enhancement factor (<Egap>/Ein) and retrieved chirality parameter κη = 0 with varying gap width g at resonance frequency fη = 0 are shown in Figs. 3g,h. By reducing the gap width g, we can see that the enhancement factor and κη = 0 are proportional to g−1 and g−1/2, respectively. These pronounced dependencies on the gap width strongly suggest that the enhancement of the optical activity originates from the small-gap effect (see Supplementary Information Section SV for Electric field profiles for CDZM).

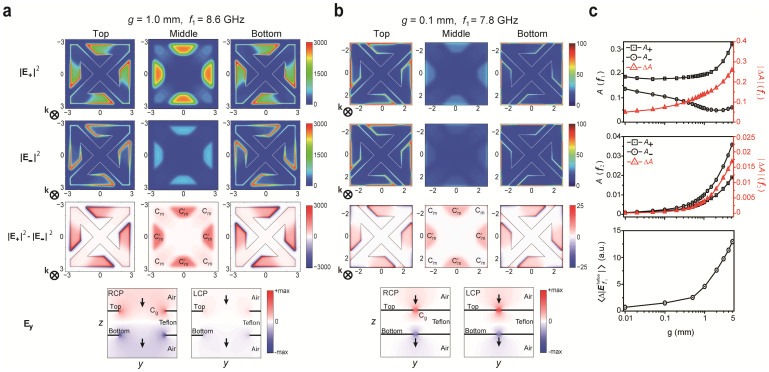
The reduced ellipticity can equally be explained by the strong field localization in the gap and the corresponding decrease in absorption difference (the absorption difference |ΔA| is equal to the difference in transmission because the reflections of RCP and LCP waves are the same). The loss values of the CDZM can be attributed to dissipation in the lossy dielectric substrate as absorption in the metallic elements is negligible at microwave frequencies (see Supplementary Information Section SVI for details of possible loss channels in CDZM). 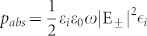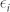To figure out where the absorption occurs in the CDZM, we plot the electric field intensity that is associated with absorbed power per unit volume (Inline graphic where Inline graphic is the imaginary part of the relative permittivity) for the RCP and LCP wave excitations. In the case of g = 1.0 mm (weak inter-molecular coupled regime), as shown in Fig. 4a, electric fields are confined mostly in the lossy dielectric substrates between the top and bottom metal strips of central and side arms (Cm and 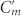Inline graphic in the equivalent circuit); however, for g = 0.1 mm (strong inter-molecular coupled regime) shown in Fig. 4b, the electric fields become more confined to the air gap resulting in a smaller absorption difference for RCP and LCP. For the resonant frequency f1(Fig. 4c), the absorption for the RCP reduces and thereby the absorption difference |ΔA| decreases significantly. In addition, for the resonant frequency f2, both the absorptions for the RCP and LCP waves reduces significantly thereby giving the much smaller absorption difference. In the bottom of Fig. 4c, the difference of the average electric field intensity in the Teflon substrate for RCP and LCP at the resonant frequency f1 is displayed. As the figure shows, the difference of the average electric field intensity decreases for smaller gap widths, which leads to a reduced ellipticity.

Figure 4. Gap dependence of the electric field distribution and absorption.

Figure 4

Open in a new tab

Electric field intensity distribution for RCP (|E+|2) and LCP (|E−|2), the difference of the electric field (|E+|2 − |E−|2) and horizontal electric field amplitude Ey for RCP and LCP in the CDZM with g equal to (a) 1.0 mm and (b) 0.1 mm at the resonance frequency f1. Electric fields are confined in the region denoted as Cm and 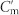Inline graphic for g = 1.0 mm whereas the electric fields are more localized around the gap for g = 0.1 mm reducing the electric fields at Cm and 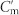Inline graphic significantly. As a result, the difference of the electric field (|E+|2 − |E−|2) for RCP and LCP waves reduces significantly. (c) Absorption A+ (A−) for RCP (LCP) and the absorption difference |ΔA| as a function of the gap width g at f1 (top) and at f2 (middle) and difference of the average field stored in the Teflon substrate for RCP and LCP as a function of g (bottom).

This allows us to conclude that our strong inter-molecular coupling approach in chiral metamaterials is inherently different from previous work where, e.g. coupling of resonances has been employed to engineer bandwidth29,30,31. First, the gap width g, represents an additional and key design parameter that allows us to control the enhancement continuously from a small value to an extremely large one. Second, the strong localization of fields in the small gap provides specific spatial positions where active materials or gain media can be incorporated32 with an aim to tune and further enhance the chiral property of a chiral metamaterial efficiently. Although transmission amplitudes decrease as g becomes smaller (as low as 13% for the broad frequency range near the frequency f2 in the case of g = 0.1 mm), it should be noted that the low transmission does not originate from a large absorption but it is caused by high reflection. Thus, by matching the impedance with a high permeability material or antireflective multiple layer structures, there are, in principle, various ways of increasing the transmission while maintaining large optical activity. This conceivably enables tuneable chiral metamaterials with a wide dynamic range and/or electrical pump switching of chirality.

Methods

Sample fabrication and measurement

The 18 μm thick copper patterned CDZM structures are fabricated on each sides of the Teflon board (Taconic TLX-9) with a thickness s = 0.5 mm by conventional printed circuit board technology. Transmission and reflection measurements were performed using a free-space measurement system with a network analyser (Agilent PNA-L) and two horn antennas (ETS Lindgren 3160), acting as source and receiver, respectively. In order to remove errors associated with the antennas, we used an improved free-space calibration process33 within the Agilent 85071E measurement software. After calibration, the chiral metamaterial sample was placed between the two antennas.

Characterization

Since the signals from the horn antennas were linearly polarized, the transmission coefficients for the linearly polarized waves were measured as Txx, Txy, Tyx, and Tyy, where the first subscript indicates the polarization (x or y) of the transmitted wave and the second subscript indicates the polarization of the incident wave. From these transmission coefficients calculated in a linear basis, the right and left circularly polarized transmission (RCP/LCP) coefficients (T++, T+−, T−+ and T−−) can be obtained20,22.

Numerical modelling

For the modelling of chiral metamaterials, we employed the FEM solver of the commercially available software package (CST Microwave Studio). In the simulations, the unit cell boundary condition was applied. The dielectric constant and loss tangent of the Teflon board are Re(εr) = 2.5 and tan δ = 0.0019 and the metallic strips are considered as a perfect electric conductor.

Gap width vs. field enhancement in a metallic straight strip

To verify quantitatively the dependence of the field enhancement on the gap width, the field enhancement was numerically calculated for the various gap widths. The field enhancement factor is defined by <Egap>/Ein, where Ein and Egap are the electric field amplitudes of the incident field and inside the gap, respectively, and 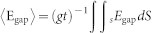Inline graphic.

Author Contributions

T.-T.K., S.S.O., W.C., O.H. and B.M. conceived the original idea. T.-T.K. performed the numerical simulation and the microwave measurement. T.-T.K. and H.-S.P. fabricated the samples and measured THz optical properties. S.S.O., R.Z., S.-H.K. and O.H. developed the analytical model. All the authors analysed the data and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information for

srep05864-s1.docx (2.9MB, docx)

Acknowledgments

We thank B. Kang and Y. Kim for their help, S. Wuestner and A. Pusch for proofreading the manuscript before submission and J.M. Hamm and E. Shamonina for discussions. The work at KAIST (T.-T.K., H.-S.P. and B.M.) was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (No. 2012-0001981, 2012-0006653, 2012-0008746, 2012-0000545, and 2012-054188) and the World Class Institute (WCI) Program of the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology of Korea (MEST). (NRF Grant Number: WCI 2011-001). T.-T.K. was supported by Basic Science Research Program through NRF (No. 2013R1A6A3A03022127). S.S.O., R.Z. and O.H. acknowledge financial support from the Leverhulme Trust, S.S.O. acknowledges financial support from the German Research Foundation (DFG) and R.Z. acknowledges financial support from the Royal Commission for the Exhibition of 1851.

References

  1. Barron L. D.. Molecular Light Scattering and Optical Activity, Cambridge University Press, 2004.4. [Google Scholar]
  2. Hecht E. Optics 4th edn (MA: Addison-Wesley Publishing Company., 2001).
  3. Lindell I. V., Sihvola A. H., Tretyakov S. A. & Viitanen A. J. Electromagnetic Waves in Chiral and Bi-isotropic Media (ArtechHouse, Boston, London, 1994). [Google Scholar]
  4. Rogacheva A. V., Fedotov V. A., Schwanecke A. S. & Zheludev N. I. Giant gyrotropy due to electromagnetic-field coupling in a bilayered chiral structure. Phys. Rev. Lett. 97, 177401 (2006). [DOI] [PubMed] [Google Scholar]
  5. Plum E., Fedotov V. A. & Zheludev N. I. Optical activity in extrinsically chiral metamaterial. Appl. Phys. Lett. 93, 191911 (2008). [Google Scholar]
  6. Decker M. et al. Strong optical activity from twisted-cross photonic metamaterials. Opt. Lett. 34, 2501–2503 (2009). [DOI] [PubMed] [Google Scholar]
  7. Pendry J. B. A chiral route to negative refraction. Science 306, 1353–1355 (2004). [DOI] [PubMed] [Google Scholar]
  8. Plum E. et al. Metamaterial with negative index due to chirality. Phys. Rev. B 79, 035407 (2009). [Google Scholar]
  9. Zhang S. et al. Negative refractive index in chiral metamaterials. Phys. Rev. Lett. 102, 023901 (2009). [DOI] [PubMed] [Google Scholar]
  10. Zhou J. et al. Negative refractive index due to chirality. Phys. Rev. B 79, 121104 (2009). [Google Scholar]
  11. Wiltshire M. C. K., Pendry J. B. & Hajnal J. V. Chiral Swiss rolls show a negative refractive index. J. Phys.: Condens. Matt. 21, 292201 (2009). [DOI] [PubMed] [Google Scholar]
  12. Zhao R., Zhou J., Koschny,. Th.,. Economou E. N. & Soukoulis C. M. Repulsive Casimir Force in Chiral Metamaterials. Phys. Rev. Lett. 103, 103602 (2009). [DOI] [PubMed] [Google Scholar]
  13. Ren M., Plum E., Xu J. & Zheludev N. I. Giant nonlinear optical activity in a plasmonic metamaterial. Nature Comm. 2, 833 (2012). [DOI] [PubMed] [Google Scholar]
  14. Zhang S., Zhou J., Park Y.-S., Rho J., Singh R., Nam S., Azad A. K., Chen H.-T.,. Yin X., Taylor A. J. & Zhang X. Photoinduced handedness switching in terahertz chiral metamolecules. Nature Comm. 3, 942 (2012). [DOI] [PubMed] [Google Scholar]
  15. Zhou J., Chowdhury D. R., Zhao R., Azad A. K., Chen H.-T., Soukoulis C. M., Taylor A. J. & O'Hara J. F. Terahertz chiral metamaterials with giant and dynamically tunable optical activity. Phys. Rev. B. 86, 035448 (2012). [Google Scholar]
  16. Helgert C. et al. Chiral metamaterial composed of three-dimensional plasmonic nanostructures. Nano Lett. 11, 4400–4404 (2011). [DOI] [PubMed] [Google Scholar]
  17. Gansel J. K. et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009). [DOI] [PubMed] [Google Scholar]
  18. Wu C. et al. Metallic helix array as a broadband wave plate. Phys. Rev. Lett. 107, 177401 (2011). [DOI] [PubMed] [Google Scholar]
  19. Zhao Y., Belkin M. A. & Alù A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nature Comm. 3, 870 (2012). [DOI] [PubMed] [Google Scholar]
  20. Zhao R., Zhang L., Zhou J., Koschny T. & Soukoulis C. Conjugated gammadion chiral metamaterial with uniaxial optical activity and negative refractive index. Phys. Rev. B 83, 035105 (2011). [Google Scholar]
  21. Li Z. et al. Chiral metamaterials with negative refractive index based on four “U” split ring resonators. Appl. Phys. Lett. 97, 081901 (2010). [Google Scholar]
  22. Wang B. et al. Chiral metamaterials: simulations and experiments. J. Opt. A: Pure Appl. Opt. 11, 114003 (2009). [Google Scholar]
  23. Kenanakis G. et al. Flexible chiral metamaterials in the terahertz regime: a comparative study of various designs. Opt. Mat. Express 2, 1702–1712 (2012). [Google Scholar]
  24. Choi M. et al. A terahertz metamaterial with unnaturally high refractive index. Nature 470, 369–373 (2011). [DOI] [PubMed] [Google Scholar]
  25. Seo M. et al. Terahertz field enhancement by a metallic nano slit operating beyond the skin-depth limit. Nat. Photonics 3, 152–156 (2009). [Google Scholar]
  26. Zhou J. et al. Unifying approach to left-handed material design. Opt. Lett. 31, 3620 (2006). [DOI] [PubMed] [Google Scholar]
  27. Zhao R., Koschny T. & Soukoulis C. M. Chiral metamaterials: retrieval of the effective parameters with and without substrate. Opt. Express 18, 14553–14567 (2010). [DOI] [PubMed] [Google Scholar]
  28. Sakurai T. & Tamaru K. Simple formulas for two- and three-dimensional capacitances. IEEE Trans. Electron Devices ED-30, 183–185 (1983). [Google Scholar]
  29. Huang X.-R., Peng R.-W., & Fan R.-H. Making Metals Transparent for White Light by Spoof Surface Plasmons. Phys. Rev. Lett. 105, 243901 (2010). [DOI] [PubMed] [Google Scholar]
  30. Foteinopoulou S., Vigneron J., & Vandenbem C. Optical near-field excitations on plasmonic nanoparticle-based structures. Opt. Express 15, 4253–4267 (2007). [DOI] [PubMed] [Google Scholar]
  31. Lei D. Y., Aubry A., Maier S. A. & Pendry J. B. Broadband nano-focusing of light using kissing nanowires. New J. Phys. 12, 093030 (2010). [Google Scholar]
  32. Hess O., Pendry J. B., Maier S. A., Oulton R. F., Hamm J. M. & Tsakmakidis K. L. Active optical metamaterials. Nature Materials 11, 573 (2012). [DOI] [PubMed] [Google Scholar]
  33. Bartley P. G. & Begley S. B. Improved Free-Space S-Parameter Calibration. Instrumentation and Measurement Technology Conference, 2005. IMTC 2005—Proceedings of the IEEE 1, 372 (2005). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information for

srep05864-s1.docx (2.9MB, docx)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES