Prediction of the location and size of the stomach using patient characteristics for retrospective radiation dose estimation following radiotherapy

Abstract

Following cancer radiotherapy, reconstruction of doses to organs, other than the target organ, is of interest for retrospective health risk studies. Reliable estimation of doses to organs that may be partially within or fully outside the treatment field requires reliable knowledge of the location and size of the organs, e.g., the stomach, which is at risk from abdominal irradiation. The stomach location and size are known to be highly variable between individuals, but have been little studied. Moreover, for treatments conducted years ago, medical images of patients are usually not available in medical records to locate the stomach. In light of the poor information available to locate the stomach in historical dose reconstructions, the purpose of this work was to investigate the variability of stomach location and size among adult male patients and to develop prediction models for the stomach location and size using predictor variables generally available in medical records of radiotherapy patients treated in the past. To collect data on stomach size and position, we segmented the contours of the stomach and of the skeleton on contemporary Computed Tomography (CT) images for 30 male patients in supine position. The location and size of the stomach was found to depend on body mass index (BMI), ponderal index (PI), and age. For example, the anteroposterior dimension of the stomach was found to increase with increasing BMI (≈0.25 cm per kg/m²) whereas its craniocaudal dimension decreased with increasing PI (≈ −3.3 cm per kg/m³) and its transverse dimension increased with increasing PI (≈ 2.5 cm per kg/m³). Using the prediction models, we generated three dimensional computational stomach models from a deformable hybrid phantom for three patients of different BMI. Based on a typical radiotherapy treatment, we simulated radiotherapy treatments on the predicted stomach models and on the CT images of the corresponding patients. Those dose calculations demonstrated good agreement between predicted and actual stomachs compared with doses derived from a reference model of the body that might be used in the absence of individual CT scan data.

1. Introduction

Epidemiologic studies of the risk of cancer following radiotherapy treatments require reconstruction of radiation doses to organs of interest(Travis et al 2012). The purpose of such epidemiologic studies is to determine whether the radiation exposure is associated with a risk of late effects, e.g., second cancers, and to determine the shape of the dose-response relationship and the magnitude of its slope. In particular, radiation is known to increase the risk of some gastrointestinal cancers, including stomach cancers, though little is known about the dose-response relationship. Our research group has been studying the risk of stomach cancer after Hodgkin lymphoma (Morton et al 2013) and after cervical cancer (Kleinerman et al 2013). Because the exposures in both studies took place in the past, the exact position of the stomach of each patient was unknown. Moreover, because the location of the organ relative to the radiation field can be a strong determinant of the dose to that organ (Lamart et al 2013), assumptions made in dose estimation can potentially affect the dose-response relationship. For these studies, we needed to assess the stomach location and size for patients in supine position.

Few recommendations exist on estimating the stomach shape, size or location when individual data are not available. International Commission on Radiological Protection (ICRP) Publication 89 states that the stomach “may be cylindrical or roughly crescent-shaped when empty of food, or pear-shaped when partially distended, but the most common form in the upright posture is the fish-hook or J-shape. Typically, the stomach lies obliquely in the upper left quadrant of the abdominal cavity and is directed caudally, anteriorly, and to the right.” (ICRP 2002). Some previous studies have shown that the size, shape and position of the stomach vary considerably depending on the anatomy and stature of the individual (Csendes 2005; Meschan 1953; Poole 1970). However, limitations of previous studies prevent translation of the findings for specifying the stomach size, shape, and location for individuals in the supine position, which is typical for patients receiving chest, abdominal, or pelvic radiotherapy. For example, Meschan et al. (1953) identified four representative stomach shapes and studied the stomach size and location as function of body weight using projection radiography, but patients were in the posterior-anterior and right lateral recumbent positions, and in the left lateral standing position. Poole et al. (1970) identified a linear correlation between the antrum-to-spine distance and body mass using lateral radiography, but stomach position may be different when the body is in the supine position. More recently, Csendes et al. (2005) measured the length of the lesser and greater curvatures and the volume and mass of the stomach of obese patients under bariatric surgery and among cadavers used as control group, but the stomach’s location and size in vivo cannot be derived from their method. One dosimetric study provided stomach dose estimates depending on the stomach size and location using dose measurements from thermoluminescent diodes in a physical phantom (Scarboro et al 2010). Different stomachs were generated by expanding and shifting systematically the boundaries of a stomach of standard location and size. However, the location and size of these different stomachs were not based on actual patients’ images.

In the present work, we characterized the location and size of the stomach in males in a typical radiotherapy treatment position from abdominal computed tomography (CT) images of 30 adult patients scanned in the supine position. From the collected data and using the 10-fold cross-validation technique, we derived multivariate linear regression models to predict stomach location and size from variables that are generally available in the medical records of patients treated years in the past, i.e., age, height, and weight. To illustrate the influence of the location and size of the stomach in radiotherapy dose reconstruction and to assess the performance of our prediction models, we simulated a typical radiotherapy treatment plan on patients with different BMI using 3D computational models based on the predicted location and size of the stomach.

2. Patients and methods

2.1. CT images

We evaluated the abdominal CT images of 30 male patients scanned in the supine position. Because our purpose was to delineate the stomach contours, we selected a CT examination for which an oral contrast agent, in this case, barium, was used to enhance the contrast between the stomach volume and the surrounding soft tissues. The selected patients were enrolled in a protocol approved by our Institutional Review Board and conducted by the National Institute of Child Health & Development at the National Institutes of Health (NIH) Warren Magnuson Clinical Center.

The study patients had all been diagnosed with pheochromocytoma, a tumor of the adrenal gland. Pheochromocytomas are rare tumors (1–2/100,000 individuals), 10% are bilateral, 10% are located outside the adrenal gland, and 10% are malignant. The tumorsvary in size, but are typically between 50 and 200 g (Grant 1997). Review of the CT scans by a radiologist at the NIH Clinical Center confirmed that the presence of pheochromocytoma did not significantly modify either the anatomy of the stomach or the anatomy of the surrounding organs and tissues in these patients.

Several criteria were important for our analysis and limited the number of patients we could include. The requirements were that the CT images had (i) to fully cover the stomach and the outer contour of the body, (ii) to have enough contrast so that the stomach boundaries could easily be distinguished for the segmentation; and (iii) to display a relatively straight vertebral column since we used the vertebrae as a reference to locate the stomach. Finally, the patients’ ages, weights and heights needed to cover a reasonably broad range of values and represent data whose distributions were not excessively skewed because we wanted to assess the effect of these characteristics on typical stomach location and size (Figure 1).

Figure 1.

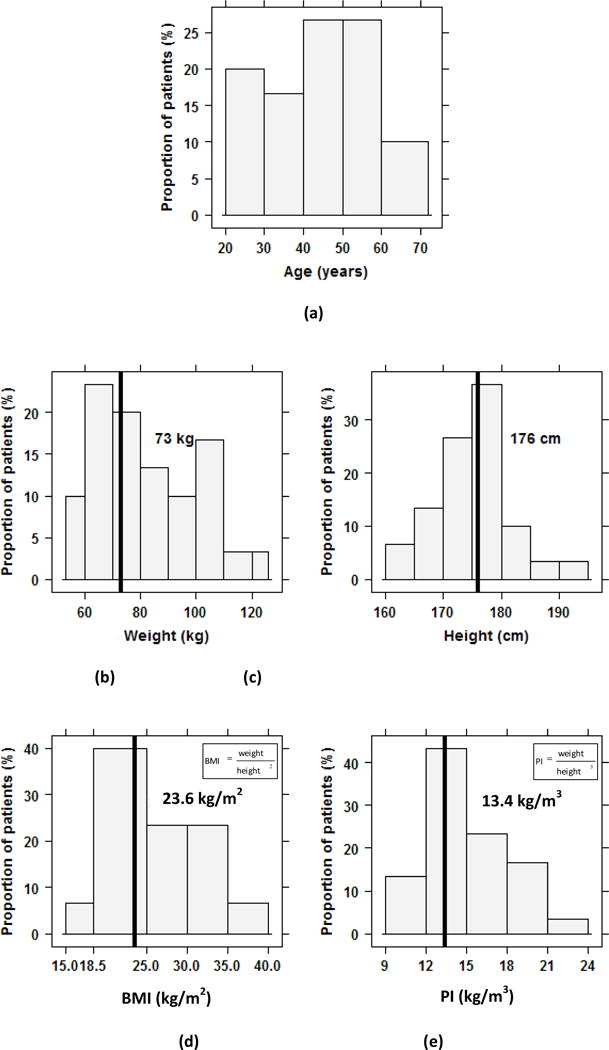
Histograms of the characteristics of patients in this study: (a) age in years, (b) height in cm, (c) weight in kg, (d) body mass index (BMI) in kg/m² and (e) ponderal index (PI) in kg/m³. The corresponding characteristics for the reference adult male from ICRP Publication 89 are specified on each histogram and indicated by a vertical line. There is no specific age for the reference adult male (ICRP 2002).

2.2. Measurement of the location and size of the stomach

Using the segmentation features of an open-source software package¹ and CT images in the DICOM (Digital Imaging and Communications in Medicine) format (Fedorov et al 2012), we manually outlined the stomach contour and set a threshold of Hounsfield number to enable to automatically segment the skeleton. For each patient, we formed three-dimensional (3D) models of the stomach and the skeleton by assembling the segmented areas from the CT slices that encompassed the volume of interest.

We related the stomach position to the skeleton. We analyzed the 3D models of stomach and skeleton using a commercial software package² and we quantified the size and orientation of the stomach by using (i) its volume, (ii) the Cartesian coordinates of the eight vertices of a bounding box created around the stomach that corresponded to the limits of the stomach in three dimensions, and (iii) the transverse, craniocaudal and anteroposterior dimensions of the bounding box (Figure 2). We defined a reference point on the skeleton forall measurements of the stomach position. Because we wanted the reference point to be relatively stable and immovable in the body regardless of body orientation, as well as easy to reproduce, we chose a reference point on the anterior surface of the 12^th thoracic vertebra, midway in its craniocaudal and transverse dimensions. We calculated the location of the boundaries of the stomach relative to this reference point. The six bounding planes of the stomach bounding box were denoted as follow: lower (z₁), upper (z₂), right (x₁), left (x₂), front (y₁) and back (y₂). We defined and computed the transverse, craniocaudal, and anteroposterior dimensions of the bounding box by the differences in the x, y, or z positions, e.g., craniocaudal dimension= z₂−z₁. We quantified the location of the stomach model by the position of its center-of-mass (COM) relative to the T12 reference point (i.e., at x_COM, y_COM, z_COM). To compare our findings on stomach size and location with the ICRP reference man(ICRP 2009), we conducted the same measurements on the ICRP adult male phantom.

Figure 2.

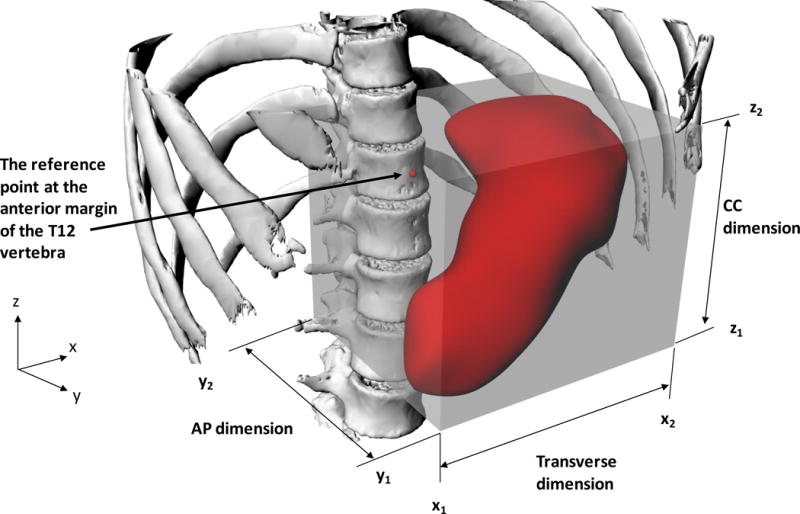
3D visualizations of a computational skeleton-stomach model with the bounding box created around the stomach and showing the reference position on the T12 vertebra. The Cartesian coordinates of the bounding box vertices are defined from a combination of triplets among x₁, x₂, y₁, y₂, z₁ and z₂. The stomach transverse, anteroposterior (AP) and craniocaudal (CC) dimensions correspond to those of the box.

Since we wanted to predict the stomach location and size with respect to body size parameters, we also needed the dimensions of the thoracic cage that partly encloses the stomach as well as the thickness of the body. Hence, in addition to the measurements of stomach size and position, we also measured the anteroposterior dimension of the thoracic cage on the axial CT image at the level of the T9 vertebra, i.e., the distance between the posterior aspect of the spinous process and the anterior surface of the sternum, as well as the anteroposterior dimension of the body at the T9 vertebral level. We used the variables introduced in this section to describe the location and size of the stomach across our sample of patients and to develop predictive models.

2.4 Development of prediction models

Our general goal was to develop predictive models of the stomach location and size by multivariate regression using patient characteristics that are generally available in historical medical patient records. In practice, we aimed at predicting the location and size of the bounding box - a simplified but useful representation of the size and location of the stomach, by predicting its dimensions in the transverse, craniocaudal and anteroposterior directions and the Cartesian coordinates of one vertex of the box. We also developed prediction models for the anteroposterior dimensions of the thoracic cage and of the body at the T9 vertebral level.

We defined a list of 15 possible predictor variables: age, weight, height, BMI and PI, in addition to their respective square and square root. For each dependent variable, we performed linear regressions using 1 and 2 predictors from all possible combinations of predictor variables and allowed for interactions with age, height, weight, BMI and PI. The general form of each possible linear regression model was:

$$\text{Dependant variable}={\beta }_0+{\beta }_1·{\mathrm{x}}_1+{\beta }_2·{\mathrm{x}}_2+{\beta }_{1,2}·{\mathrm{x}}_1·{\mathrm{x}}_2$$ (1)

where x₁ and x₂ are the possible predictors, β₀ is the intercept and β₁, β₂ and β_1,2 are the regression coefficients.

We evaluated the performance of each linear regression model by the 10-fold cross-validation technique which assesses how prediction models perform on an independent dataset and enables one to select the model that has the greatest predictability and that will generalize the best (Stone 1974). The 10-fold cross-validation technique we used involves splitting the variable set into 10 subgroups, using 9 of the subsets together for deriving the predictive model while maintaining one subset for validation, i.e., comparison of predicted values against measured values. The process is then repeated 9 more times, each time keeping a different subset for validation until all 10 subsets have been used for validation. At each step, the squared difference between predictions and measurements is computed where the cross-validation measure (CV) is computed as the mean squared difference. We iterated the 10-fold cross-validation technique on each possible model ten times and ranked the models by increasing order of the averaged CV. We selected the prediction model that had the lowest CV and that was the most parsimonious. We also computed the adjusted R² for the selected models.

2.5 Development of stomach models for radiation dose reconstruction and dose comparison between models and actual patients

We used our predictive models to derive virtual anatomical models of the stomach and the thoraco-abdominal region by modifying an existing adult male hybrid computational phantom with organs of reference mass (ICRP 2002; Lee et al 2010) for three selected patients with low, medium, and high BMI values (18.2, 21.6 and 33.2 kg/m² respectively). Using homothetic transformations², we modified the location and changed the size of the stomach of the hybrid reference phantom so that they matched the predicted location and size of the bounding box, and uniformly scaled the anteroposterior dimension of the existing thoracic cage and of the body thickness to match the predicted dimensions. We did not change the location and size of the other organs and tissues because that was beyond the scope of this work. We surrounded the resulting stomach with soft tissue for dose calculation.

We simulated an identical radiotherapy treatment plan on each of the three patients’ CT images and on the predicted stomach 3D models for each, as well as on the ICRP male phantom taken as reference model. The purposes of the radiotherapy simulations were to (i) assess the influence of the stomach location and size on the radiation dose estimates, and (ii) evaluate the performance of our prediction model regarding the dose estimate by comparing the radiotherapy dose between the actual stomach anatomy and the predicted stomach 3D model. To do these calculations, we first converted the 3D computational models containing the predicted stomachs from their initial surface-based format to a voxel format, including the stomach, skeleton, lungs, muscle and adipose tissue. We developed an algorithm using commercial software³ to create DICOM CT images for each model and for the ICRP phantom, both which we imported to a commercial radiotherapy treatment planning system⁴. We over rode the density of the voxels included in the stomach contours and assigned them the density of water for the CT images and the predicted stomach models to prevent any variation in dose due to the higher density of the barium on the patient’s images. We defined typical radiotherapy fields used to treat the para aortic nodes for Hodgkin disease (Fletcher 1967). These fields were opposed anterior and posterior fields of 10 cm-width spanning from the T8–T9 vertebral interspace to the L4–L5 interspace. We used a 6 MV photon beam and a source-skin distance of 100 cm. We prescribed the dose at patient midplane on the central axes of the fields with a 3:2 anterior weighting. We computed the dose to the bulk of the stomach for the actual patients’ CT images and on the corresponding predicted 3D stomach models. We compared the mean stomach dose across patients and between the actual, the predicted and the ICRP phantoms.

3. RESULTS

3.1. Descriptive statistics of the patients’ characteristics

In the population sample selected in the present study, the mean patient age was 45 years with a range of 21–72 years, the mean weight was 82 kg (54–126 kg) and the mean height was 175 cm (160–193 cm, Figure 1). The height and weight were on average, not too different, from the reference adult male defined in ICRP Publication 89, i.e., 176 cm and 73 kg (ICRP 2002). The mean body mass index was 27 kg/m² (BMI, 18–40 kg/m²) with 53% of patients having a BMI>25 kg/m² and the mean ponderal (or Rohrer’s) index was 15 kg/m³. A variant of BMI, the ponderal index (PI), is defined as the weight divided by the height cubed (Mei et al 2002). The weight, BMI, and PI of the patients were each positively correlated with age (coefficients of correlation, r, were 0.46, 0.53 and 0.53, respectively). Weight was, as expected, also found to be positively correlated with height (r=0.46).

3.2. Descriptive statistics of the stomach location and size

On average, the center of mass (COM) of the stomach was 5 cm to the left of the midline (range 3–7 cm, Figure 3), 7 cm anterior to the T12 reference point (4–11 cm) and at the same level as T12 in the craniocaudal direction (range −5 to 5 cm). Note that the COM would only be located at the center of the bounding box if the stomach model assembled from the CT images was symmetric with respect to the center of the box. In our data, however, the COM and the center of the bounding box were, on average, 1.7 cm apart. We compared the ICRP reference phantom to the actual patients. We found that the height of the ICRP male phantom was similar to the patients’ mean value though the weight was 12% less (ICRP 2002). Of the 9 stomach location variables, seven variables (x_COM, x₂, y₁, y_COM, y₂, z_COM, z₂), derived from the ICRP reference adult phantom were either smaller or larger than the 25%–75% range of the patients. We estimated that the measurement error in the coordinates was less than 1 cm in each Cartesian direction. The mean stomach volume of the patients including the stomach contents, was 372 cm³ which was very similar to the stomach volume of the ICRP reference adult male phantom (368 cm³). As shown in Figure 3, the stomach was on average 13 cm wide (range 9–16 cm), 15 thick (range 10–20 cm) and 10 cm high (range 6–15 cm). The stomach occupied 22% of the bounding box volume (range 11–30%). The stomach transverse, anteroposterior and craniocaudal dimensions of the ICRP phantom were within the 25^th–75^th percentile ranges of the corresponding patients’ distributions.

Figure 3.

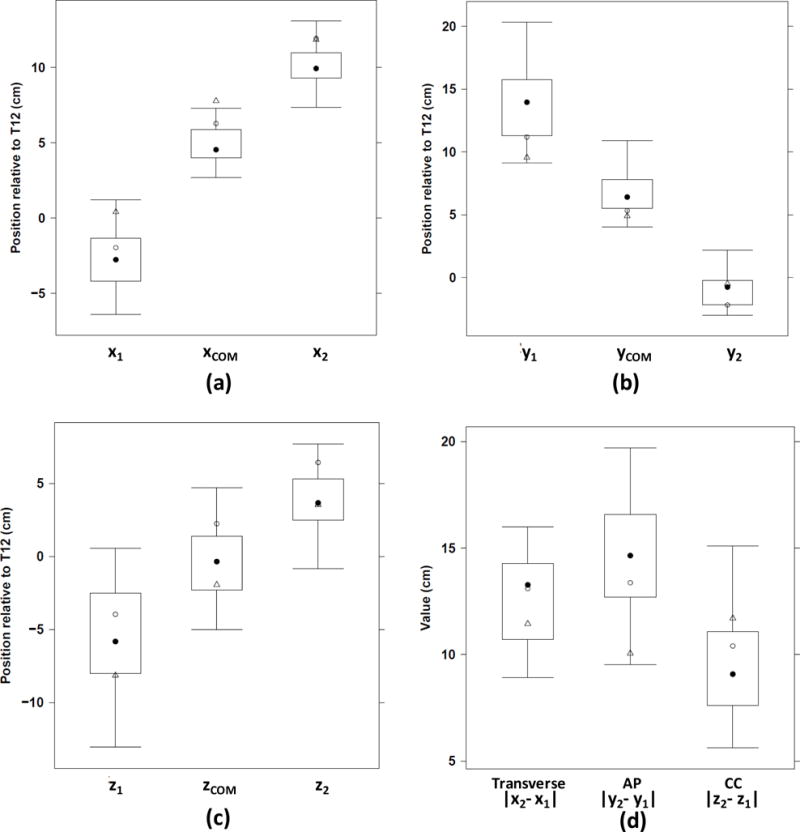
Outer limits of the stomach and of its center of mass along the x-, y- and z-axes: (a) x₁, x_COM, x₂, (b) y₁, y_COM, y₂, (c) z₁, z_COM, z₂ and (d) stomach transverse, anteroposterior (AP) and craniocaudal (CC) dimensions (cm). The corresponding values for the reference ICRP adult male defined in Publication 110 and the adult hybrid male phantom are indicated by open circles and triangles, respectively (ICRP 2009; Lee et al 2010).

Variations in the position of the stomach COM are shown with respect to its anteroposterior dimension (Figure 4, left graph) and its craniocaudal dimension (Figure 4, right graph). The y location of the COM increased with increasing anteroposterior dimension (y_COM, Figure 4, left graph), and the z location of the COM decreased with increasing craniocaudal dimension (z_COM, Figure 4, right graph). These findings indicate that the stomach is located towards the anterior side of the body, and when its anteroposterior dimension increased, its COM moved forward. With respect to the craniocaudal location, the upper boundary z₂ was much less variable than the lower one, z₁. Hence, when the craniocaudal dimension increased, the COM was lower.

Figure 4.

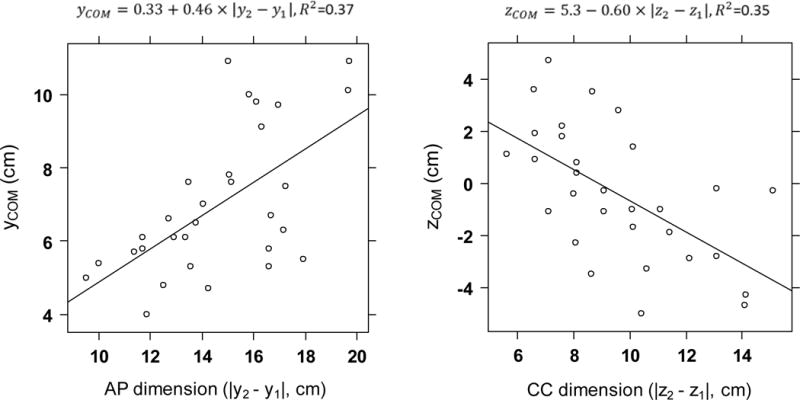
Variation of the position of the stomach center of mass along the y-axis, y_COM, with respect to its anteroposterior dimension (left) and the position of the stomach center of mass along the z-axis, z_COM, with respect to its craniocaudal dimension (right). The linear regression equation and R² are displayed above each graph.

3.3. Predictive model of stomach location and size

To develop prediction models, measured (independent) variables need to have sufficient variability to allow relationships to be quantified. Because the coordinates x₁, y₁, and z₁ had the greatest range of variation among the location variables defining the box bounding the stomach, and because the corresponding values for the ICRP phantoms were within the 25^th to the 75^th percentile range for x₁, y₁ and z₁, we selected this vertex among the eight vertices of the bounding box for our model predictions. We derived multivariate models using linear combinations of age, BMI, PI and weight as predictors in their first or second order form (Table 1). All dependent variables for stomach size and location were highly correlated with either BMI or PI. PI was, in general, a better predictor than BMI. The adjusted R², accounting for the number of predictors in the model, ranged from 0.34 to 0.86. Despite some collinearity between predictor variables, e.g., for BMI and age with a coefficient of correlation of 0.53, each individual predictor variable was statistically significant in the multivariate models shown in Table 1 (p<0.05). In other words, each predictor contributed information to the prediction even in presence of the other variable in the model. Using the simple set of variables that are usually available in patient medical records, we did not find any suitable model to predict stomach volume and the center of mass coordinates.

Table 1.

Fitted coefficients of best multivariate linear models to predict the bounding box location and its size defined by the coordinates of one vertex (x₁,y₁,z₁) and the dimensions of the box (transverse, anteroposterior (AP), and craniocaudal (CC)); and to predict the thoracic cage and body AP dimensions at the T9 vertebra level. BMI: body mass index, PI: ponderal index.

Dependent variable (cm)	Predictive variables and corresponding linear coefficients						Cross-validation measure	Adjusted-R2
	Intercept (β0)	Age	PI	PI2	BMI	Weight
x1	1.99E+01	–	−2.63E+00	7.26E−02	–	–	3.11	0.34
y1	5.51E−01	7.13E−02	–	–	3.72E−01	–	1.73	0.82
z1	−5.07E+01	–	5.27E+00	−1.46E−01	–	–	7.74	0.50
Transverse dimension (|x2− x1|)	−9.02E+00	–	2.50E+00	−6.78E−02	–	–	2.79	0.39
AP dimension (|y2−y1|)	4.49E+00	7.67E−02	–	–	2.51E−01	–	2.74	0.64
CC dimension (|z2−z1|)	3.80E+01	–	− 3.34E+00	9.28E−02	–	–	4.61	0.39
Thoracic cage AP dimension	1.15E+01	4.49E−02	–	–	3.23E−01	–	2.73	0.63
Body AP dimension	1.02E+01	7.10E−02	–	–		1.46E−01	1.79	0.86

3.4. Predicted stomach models and comparison of dose estimates with values from the actual patient’s images

Figure 3 compares against the study samples the location and size of the stomach of the existing hybrid phantom that we subsequently adjusted to derive a virtual 3D computational model including the predicted location and size of the stomach respectively for the three patients selected with low, medium, and high BMI values. The stomach volume of the existing hybrid phantom with which we also made comparisons was 444 cm³ (Figure 3).

Based on a simple visual evaluation, the size and location of the predicted stomach models compared compared well with the actual segmented contours of the three selected patients (Figure 5 Comparison of the actual (upper row) and predicted (lower row) locations and sizes of the stomachs for three selected patients with different BMI values: 18.2 kg/m² (left), 21.6 kg/m² (middle) and 33.2 kg/m² (right). In each patient, the frontal (left) and left lateral (right) views are included.

Figure 5.

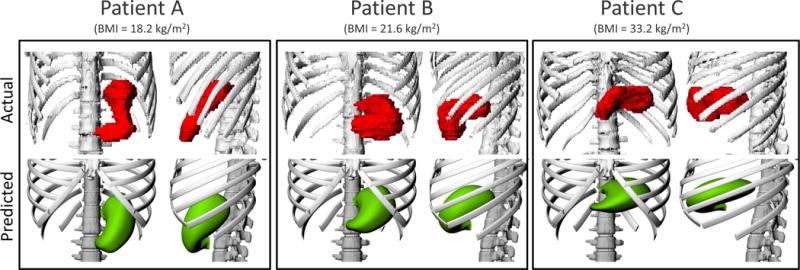
Comparison of the actual (upper row) and predicted (lower row) locations and sizes of the stomachs for three selected patients with different BMI values: 18.2 kg/m² (left), 21.6 kg/m² (middle) and 33.2 kg/m² (right). In each patient, the frontal (left) and left lateral (right) views are included.

Figure 6). We did not attempt to match the actual value of the volume of the predicted stomach for reasons discussed. As derived from our radiotherapy dose estimates, we found mean stomach doses increased with increasing patient’s BMI, e.g., doses were 49% and 82% greater for patient B (21.6kg/m²) and C (33.2 kg/m²) respectively, compared to patient A (18.2 kg/m²) (Table 2). Mean organ absorbed dose to the stomach using the predicted 3D stomach models for each patient compared well with the doses from the actual CT scans of the same patients with values being only 27%, 13% and 12% greater than for patients A, B and C, respectively. Most importantly, the differences between the doses for the predicted stomachs and the doses based on the actual patient’s CT images were smaller than the magnitude of the dose variation across the three patients due only to differences in BMI. The variation of doses between the predicted and actual stomachs was 27% or less while dose variation due to BMI differences (using the patient CT images) was as much as 82%. Similarly, use the ICRP male phantom to estimate patient dose did not provide as good estimates for all patients as using the predicted stomachs. Use of the ICRP phantom resulted in an underestimation of dose by 29% and 42% for patients B and C respectively.

Figure 6.

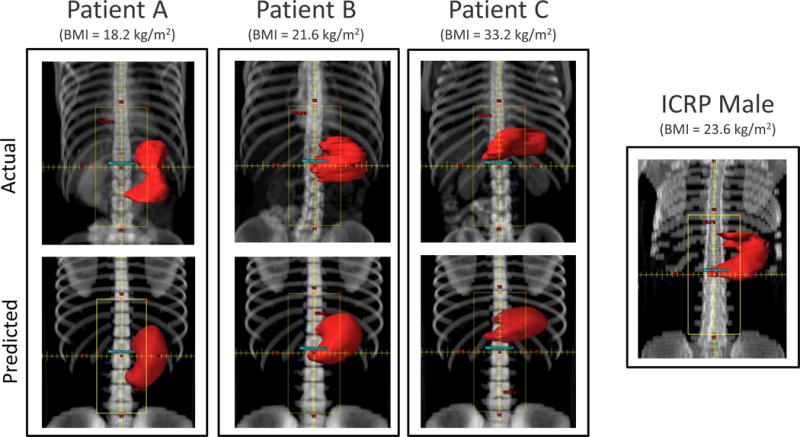
Beam’s eye view of the paraaortic anterior field set-up on three selected patients with different BMI values: 18.2 kg/m2 (left), 21.6 kg/m2 (middle) and 33.2 kg/m2 (right), and for the ICRP male phantom. Comparison between the actual CT images (upper row) and on their predicted phantoms (lower row). The stomach contour is shown in red.

Table 2.

Comparison of the mean stomach doses expressed as percentage of the prescribed dose (%) between the actual patient’s images and the predicted phantoms for three selected patients with different BMI values: 18.2 kg/m² (A), 21.6 kg/m² (B) and 33.2 kg/m² (C), and for the ICRP male phantom taken as reference.

Patient	BMI (kg/m2)	Mean dose (% of the prescribed dose)		Relative dose difference (%)
		Actual	Predicted	Across patients with actual patient A as a reference (Actual − Actual A) / Actual A	Between the predicted and the actual phantoms (Predicted − Actual) / Actual	Between the ICRP phantom taken as reference and the actual patients (ICRP − Actual) / Actual
A	18.2	38	49	0%	27%	5%
B	21.6	57	64	49%	13%	−29%
C	33.2	69	78	82%	12%	−42%
ICRP male	23.6	40

4. Discussion

To predict the location and size of the stomach based on patient’s characteristics, we segmented the contours of the stomach and the skeleton on contemporary CT images of 30 male patients in the supine position and derived multivariate linear regression models using predictor variables (age, height, and weight) often available in medical records of radiotherapy patients treated in the past. The location and size of the stomach was found to depend on BMI, PI and age. For example, the anteroposterior dimension of the stomach increased with increasing BMI (≈2.5 × 10⁻¹ cm per kg/m²) whereas its craniocaudal dimension decreased with increasing PI (≈−3.3 cm per kg/m³) and its transverse dimension increased with increasing PI (≈2.5 cm per kg/m³). Based on the prediction models, we generated three dimensional computational stomach models in a hybrid phantom. Using the predicted stomach models for three selected patients with a range of BMI values (18.2, 21.6 and 33.2 kg/m²), we were able to derive good estimates, with less than 10% to 30% difference, of the stomach doses from the actual patient’s images. These estimates are an improvement in dose estimation precision compared with the estimates that might be derived from the reference ICRP phantom. We found that the imprecision in dose using predicted stomachs compared with using actual CT images of stomachs was less than the imprecision due to BMI alone. In other words, ignoring BMI in dose estimation results in greater error than that introduced by the stomach prediction models. This finding supports that use of these prediction models when CT images are not available.

The absence of relevant literature indicates that the variation in the location and size of the stomach has been little studied. In studies conducted before the development of CT, researchers used anteroposterior and lateral projection radiographic images and identified the dependence of stomach location and size on body weight. For example, Poole (1970) described a positive linear correlation in the lateral recumbent position between the antrum-to-spine distance and body weight. Poole’s findings may not, however, be applicable to radiotherapy patients treated in the supine position. In other work, size measurements were conducted on stomachs extracted from cadavers of obese patients (Csendes 2005) but the actual location and size in vivo cannot be determined from this method. Because we derived the three-dimensional contours of the stomach of patients in the supine position from CT images, we were able to study the location and size of the stomach in vivo with the patient positioned as in most radiotherapy treatments of the chest, abdominal and pelvic regions.

Although we demonstrated that anthropomorphic characteristic scan predict stomach size and location reasonably well, additional parameters which we did not take into account also may affect the stomach contour. Therefore, our models of the stomach may predict sizes and locations that vary from those of actual patients. For example, stomach location, and especially size, may vary due to the volume of food and liquid contents. In our study, patients were fasting but ingested 500–600 ml of a barium-based liquid contrast agent 30 minutes before the CT exam and another 250–300 ml of the same liquid immediately before the exam. Based on radiologic evaluation of stomach wall thickness by one of us (DLM) and the amount of contrast agent contained in the patient’s stomach for the CT images we used, we could assess that extension of the left boundary was small (<1 cm) for 8 patients, moderate (1–2 cm) for 15 patients and large (up to 3 cm) for 7 patients. These modest distensions, however, may not cause deviations larger than food in the stomach. Here we note that patients who received radiotherapy treatments in years past were generally not instructed to arrive for treatment with an empty stomach.

In regard to our dose calculations, because the dose was prescribed at mid-thickness of the body and because the stomach extended close to the anterior surface of the body, the dose incidentally delivered to this organ was found to increase with increasing patient’s thickness and, hence, increasing BMI. Remaining inadequacies between the dose estimates and the reference values were probably mostly due to differences in proportions of the stomach volume included in-field for patients compared with the predicted phantoms.

In summary, using models for predicting stomach size and location derived from real patient data, we were able to provide satisfactory estimates of doses to the stomach for a common Hodgkin’s disease radiotherapy treatment. Because the differences between doses from our predicted stomach and the CT imaged stomachs were smaller than the differences of stomach dose across patients due to actual BMI differences, we believe that modeling the stomach location and size according to the patient’s characteristics can reduce the uncertainty in retrospective dose estimates when CT imaging of the patient is not available. In absence of CT images, dose reconstructions sometimes depend on use of generic models of the human body such as the ICRP reference adult phantom. Here we have demonstrated that the doses derived from the ICRP reference phantom agreed less well with the doses derived from patient CT image than did doses derived from our predictive models coupled with basic patient characteristics. These finding demonstrate the possible improvement in dose estimation when CT images are not available.

5. Conclusion

We developed prediction models of the location and size of the stomach in vivo in adult males using a subject’s age, height and weight, and based on data derived from patient CT images. Based on a typical radiotherapy treatment simulated on predicted stomach phantoms for three patients of different BMI, we showed the effect of body size on the stomach location, size and its absorbed dose. Furthermore, we obtained estimates of the stomach dose from the computational predicted stomach models with greater accuracy than using the reference ICRP male phantom as a default. We have shown that in retrospective studies of radiation dose when CT images are not available, we can reduce the uncertainty in reconstructed dose estimates from past radiotherapy treatments by accounting for patients’ characteristics. Subsequently, our method will assist in improving the assessment of the dose and, hence, the risk estimates in late effect studies of radiation exposure.