Abstract.
Optical coherence tomography (OCT) is an emerging noninvasive imaging technique, which is based on low-coherence interferometry. OCT images suffer from speckle noise, which reduces image contrast. A shrinkage filter based on wave atoms transform is proposed for speckle reduction in OCT images. Wave atoms transform is a new multiscale geometric analysis tool that offers sparser expansion and better representation for images containing oscillatory patterns and textures than other traditional transforms, such as wavelet and curvelet transforms. Cycle spinning-based technology is introduced to avoid visual artifacts, such as Gibbs-like phenomenon, and to develop a translation invariant wave atoms denoising scheme. The speckle suppression degree in the denoised images is controlled by an adjustable parameter that determines the threshold in the wave atoms domain. The experimental results show that the proposed method can effectively remove the speckle noise and improve the OCT image quality. The signal-to-noise ratio, contrast-to-noise ratio, average equivalent number of looks, and cross-correlation (XCOR) values are obtained, and the results are also compared with the wavelet and curvelet thresholding techniques.
Keywords: medical optics and biotechnology, optical coherence tomography, tomographic image processing, image processing, image enhancement
1. Introduction
Optical coherence tomography (OCT) is an emerging, noninvasive imaging technology that can perform high-speed tomographic imaging of biological tissue with micrometer scale resolution. Since it was first demonstrated in 1991,1 OCT has become an important technology and has a variety of clinical and industrial applications.2,3 Because OCT is based on low-coherence interferometry, it suffers from speckle noise, which significantly degrades OCT image quality and makes it difficult to identify the small detailed structures or low-intensity features of the imaged object.4–6
A number of approaches, based on either hardware or software schemes, have been carried out to reduce speckle noise in OCT images. The hardware-based approaches include frequency6–9 and spatial compoundings.10–18 These hardware-based approaches are robust ways for speckle suppression as speckle properties vary across wavelengths or different illumination angles.7 However, these methods require further modification of an existing system and increase a system’s complexity and cost.
Compared to the hardware techniques, the software-based approaches attempt to reduce the speckle noise by applying numerical algorithms or filtering in a certain transform domain to OCT images. Several software-based speckle reduction techniques have been proposed; these include local pixel averaging,19 averaging with rotating kernels,20 numerical frequency compounding,6 nonlinear log–space general Bayesian least-square estimation method,21 Csiszar’s I-divergence regularization,22 adaptive median filtering,23 adaptive Wiener filtering,23 adaptive Lee filtering,23 symmetric nearest neighbor,23 and anisotropic diffusion-based filtering,24–27 as well as wavelet domain filtering,28–32 contourlet domain filtering,33 and curvelet domain filtering.34–37
Wavelet transform is a well-known multiresolution analysis tool capable of conveying accurate temporal and spatial information. Therefore, the application of denoising filters based on wavelet thresholding techniques is suitable for those images which contain discontinuities.29 However, two-dimensional (2-D) tensor products of wavelet based techniques have poor orientation selectivity, and they cannot effectively represent images consisting of different regions separated by boundaries.34 Therefore, wavelet representation does not offer sufficient sparseness for image analysis. The family of wave packets called curvelets is very efficient for representing curved edges in images.34,36 The curvelet transformation concentrates the energy of an object with an arbitrary discontinuity curve in just a few coefficients, giving an optimal sparse representation. This characteristic is due to the fact that curvelets obey a precise parabolic balance between oscillations and support size.34 Therefore, curvelet filtering techniques should be good candidates for speckle reduction. However, the large coefficients in a curvelet decomposition only correspond to directions along the pattern oscillations.
In this paper, we present an effective shrinkage filter for speckle reduction in OCT images based on wave atoms transform. Wave atoms transform is a new multiscale geometric analysis tool that offers sparser expansion and better representation for images containing oscillatory patterns and textures than other traditional transforms, such as wavelet and curvelet transforms.38 Moreover, due to lack of translation invariance of wave atoms transform, cycle spinning-based technology is introduced to avoid visual artifacts, such as Gibbs-like phenomenon, and to develop a translation invariant wave atoms despeckling scheme. The trade-off between speckle suppression degree or image quality is controlled by a single adjustable parameter that determines the threshold value in the wave atoms domain. The experimental results show that the proposed method can effectively remove the speckle noise while simultaneously preserving detail features in the despeckled images. Improvement with the proposed method is quantitatively evaluated in terms of image metrics, such as signal-to-noise ratio (SNR), contrast-to-noise ratio (CNR), average effective number of looks (ENL), and cross-correlation value (XCOR). The results are compared with wavelet and curvelet thresholding filtering techniques.
2. Theory
2.1. Wave Atoms Transform
In this section, we briefly describe a recently developed half multiscale and multidirectional representation called the wave atoms transform.38 Wave atoms can be seen as a variant of 2-D wavelet packets and obey the parabolic scaling of curvelet wavelength . Wave atoms can be adapted to arbitrary local directions of a pattern and also can sparsely represent anisotropic patterns aligned with the axes. Moreover, the warped oscillatory functions and oriented textures in the wave atoms have been proven to have a dramatically sparser expansion compared to some other fixed standard representations, such as Gabor filters, wavelets, and curvelets, which make the wave atoms transform a better option for image characteristic extraction. Wave atoms interpolate precisely between Gabor filters and directional wavelets. Moreover, wave atoms come either as an orthonormal basis or a tight frame of directional wave packets and are particularly well suited for representing oscillatory patterns and textures in the images.39
Let the wave atoms be with the subscript , where the five quantities , , , , and all are integer values. A point (, ) is indexed in phase space by
| (1) |
where and are two positive constants, and their values will be deduced by the specifics of the implementation. Wave atoms, then, need to obey a localization condition around the phase-space point (, ). The position vector is the center of , and the wave vector determines the centers of both bumps of as . The elements of a frame of wave packets are called wave atoms when
| (2) |
and
| (3) |
Here , the oscillations within the envelope of a wave atom in have a wavelength . Here, the subscript indexes different “dyadic coronae,” whereas the additional subscript labels the different wave numbers within each dyadic corona.
Let be a real-valued continuous function with support included in the domain of [, ] and such that for , and . Define as the inverse Fourier transform (FT) and
| (4) |
The FT of is given by38
| (5) |
Here, , and . The function is an appropriate real-valued, bump function, compactly supported on an interval of length . Writing basis functions as , the coefficients of the transform can be obtained by
| (6) |
Assuming that the function is discretized at , and , then we have,
| (7) |
This algorithm can be implemented by the following steps: (1) fast Fourier transform (FFT) of , (2) wrap the product by periodicity inside the interval [, ] for each (, ), and (3) perform an inverse FFT.
By individually taking products of 1-D wave packets, 2-D orthonormal basis functions with four bumps can be formed in frequency.38,39 The 2-D extension can be formed by the products
| (8) |
| (9) |
Here, denotes the Hilbert transform operator. The combinations and from the wave atoms frame are denoted jointly as , and we have
| (10) |
The coefficients of 2-D wave atoms transform can be given by38
| (11) |
where WA is the forward wave atoms transform operator, and denotes the inverse transform. Therefore, the wave atoms shrinkage can be formulated as in which can be determined, for example, as a hard thresholding, , if ; otherwise, , where is a threshold value. The computational complexity of wave atoms is , and a MATLAB software for numerical implementation of WA is given in Ref. 40.
2.2. Wave Atoms Cycle Spinning
Orthogonal wave atoms transform is not translation invariant. This means that visual distortions, such as Gibbs-like phenomenon or ringing effects, will be produced in the image discontinuous point neighborhood area (e.g., edges and textures) due to lack of translation invariant in the translation processing. Fortunately, any denoiser can be turned into a translation invariant denoiser by performing cycle spinning.41 The denoiser is applied to several shifted copies of the image, then the resulting denoised image is shifted back to the original position and the results are averaged. As the wave atoms transform is not a translation invariant, this approach will result in different estimates of the original image with statistically different noises, which are reduced by linear averaging on all denoised results. Denoting the 2-D circular shift by , the forward and inverse wave atoms transform by WA and , and the threshold operator by , therefore the cycle spinning will be performed as41
| (12) |
where denotes the noisy image, and are the maximum number of shifts in the row and column directions, and the subscripts, and , are the translation amount in the row and column directions, respectively.
2.3. Algorithm Implementation
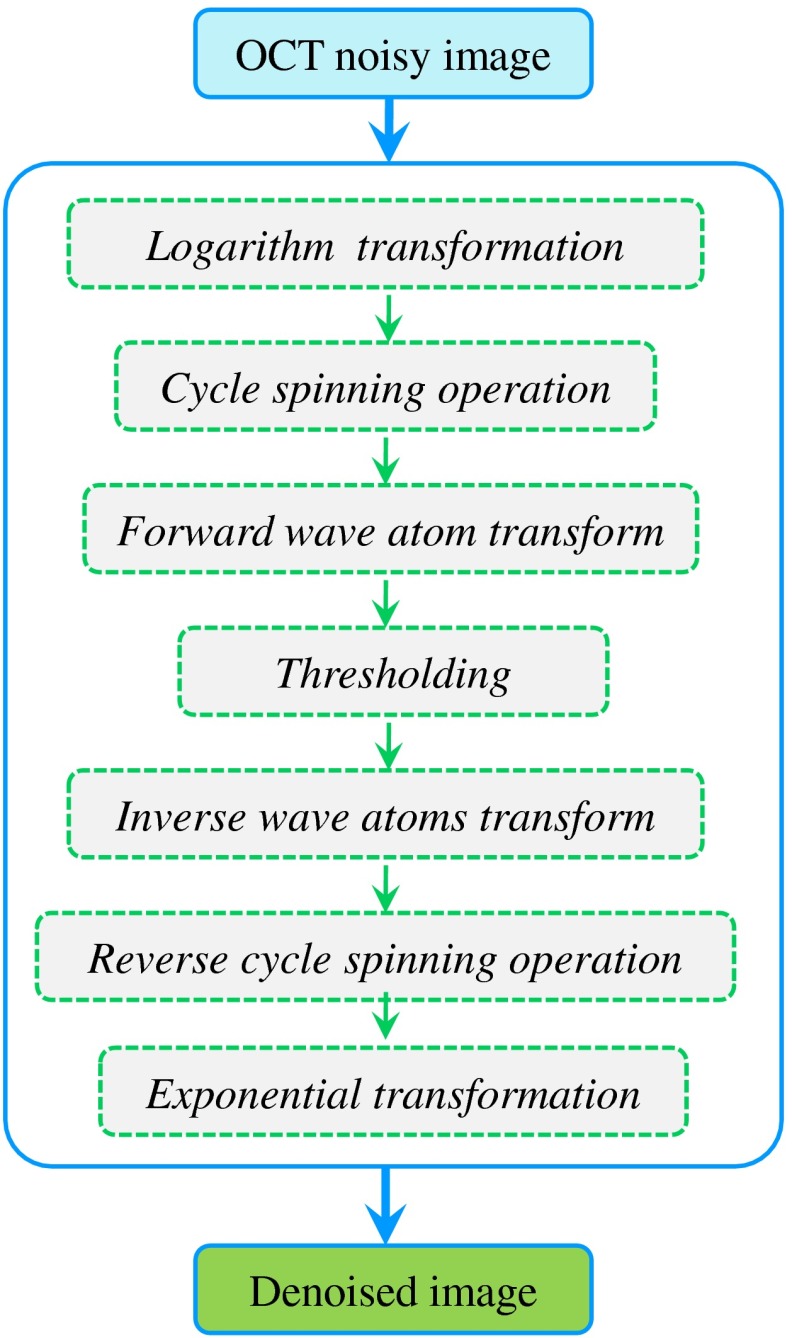
As described in the above section, in order to inhibit visual distortions, such as ringing effects and Gibbs-like phenomenon, the wave atoms based image despeckling algorithm is proposed by combining cycle spinning technology in the process of a hard threshold denoising theme. The denoising procedure of wave atoms cyclic spinning shrinkage is similar to the steps in the traditional wavelet transform method and includes seven steps. The seven steps are: logarithm transformation, cycle spinning operation, forward wave atom transform, thresholding set, inverse wave atoms transform, reverse cycle spinning, and the exponential transformations to convert the denoising images from the logarithmic scale to the linear scale. The procedure for speckle reduction in OCT imaging based on wave atoms cycle spinning shrinkage is shown in Fig. 1.
Fig. 1.
The basic work frame of speckle reduction for OCT images based on wave atoms transform.
The specific algorithm steps are as follows:
-
Step 1
: Take a logarithm operation of the aligned OCT image. The purpose of this is to convert the multiplicative noise into additive noise as it is well known that speckles can be well modeled as multiplicative noise, , where denotes the noisy image, is the noise clean image, and denotes the multiplicative noise in the OCT image. After the logarithm transformation, that is, , where is the measured data, is the noise free signals, and is the speckle noise.
-
Step 2:
Conduct cycle spinning on the noisy image by the use of a cycle spinning operator , and obtain the shifted image .
-
Step 3:
Take the 2-D forward wave atoms transform of the cycle shift data, , to produce the wave atoms coefficients . The transformed coefficient is a function of the scale , direction , and spatial coordinate . Moreover, the wave atoms transform is a linear process, hence the additive noise is still additive after the transform, , where , , and are the coefficients for noisy image, speckle-free signals, and speckle noise, respectively.
-
Step 4:
Process these coefficients using a hard thresholding operator and obtain the denoised coefficient, . A hard threshold is applied to each wave atoms coefficients , so that when , and when .
Note that determination of the threshold value is very critical in the despeckling processing, and its values are based on the noise variance of the corrupted image given by34
where is the standard deviation of speckle noise in the noisy image, and is the standard deviation of speckle noise in the wave atoms domain at a specific scale and direction by Monte Carlo analysis.35 Moreover, in order to account for the slight noise estimation deviation between the actual speckle noise distribution and the estimation, an adjustable parameter is introduced to further reduce noise with a minimal blurring of edge sharpness. The value of is usually obtained by trial and error, and it is used to control the degree of speckle reduction; namely, despeckled image quality metrics such as SNR, CNR, and ENL. The trade-off between speckle reduction degree and edge preservation in denoised images, therefore, is achieved by tuning the value.(13) -
Step 5:
Carry out an inverse wave atoms transformation on the wave atoms coefficient after the hard threshold process and get the denoised image. Take the inverse 2-D wave atoms transform of the attenuated wave atoms coefficients to reconstruct despeckled data, .
-
Step 6:
The restored image can be obtained by reverse cycle spinning on the denoised image , where represents the reverse cycle spinning operator, and the denoised results can be corrected and derived by averaging on all results .
-
Step 7:
The last step is the exponential transformation which converts the denoised images in the logarithmic scale to the linear scale. The obtained data are in the logarithmic scale, hence an exponential calculation of base 10 is applied to convert the despeckled data back to the original linear scale.
3. Results and Discussion
3.1. Quality Metrics
For a quantitative comparison of the various thresholding filters, such as wavelet29 and curvelet,36 we used several blind speckle denoising metrics to quantify the despeckled image quality. The metrics included SNR, CNR, and ENL.29 The CNR measures the contrast between an area of the image feature and an area of background noise, while the ENL measures the smoothness of homogeneous regions of interests (ROIs) that are corrupted by speckle noise. The ENL is a good metric for the quantification of noise reduction in homogeneous areas, and it increases with noise reduction. The ENL in an intensity image is a measurement of the statistical speckle fluctuations. Thus, ENL gives essentially an idea about the smoothness in regions of the images that are supposed to have a homogeneous appearance but are affected by noise.
The definitions for SNR, CNR, and ENL are defined as29
| (14) |
| (15) |
| (16) |
where is the intensity at locations () in the selected ROI. Here, and are the mean of intensity and the standard deviation of the intensity in the background region, respectively; is the mean of the pixel values in the ’th ROI, and is the pixel standard deviation.
Moreover, we also use the cross-correlation (XCOR) value as an indicator of similarity between different speckle fields, which measures the similarity between the images before and after denoising. Its definition is given by36
where is the intensity data before denoising, is the intensity data after denoising, and (, ) are the indices of the images; and , and are the mean of intensity and the standard deviation of the intensity in the denoised image and the noisy images, respectively. The value of XCOR is smaller than 1 and will approach to 1 when the denoised image resembles the original image.
3.2. Results and Discussions
This section gives a detailed qualitative and quantitative analysis of the proposed OCT speckle reduction algorithm based on wave atoms transform. The image data are acquired with a spectrometer-based 890 nm Fourier domain OCT system.42 Briefly, the spectrometer-based Fourier domain OCT uses a super luminescent diode light source, which has a central wavelength of 890 nm and full width at half maximum bandwidth of 150 nm. A modified scanning head from a commercial Zeiss Stratus OCT was used. The optical power on the human eye was set at 650 μW. The charge-coupled device (CCD) integration time was set at 50 μs. The system sensitivity was measured to be about 100 dB at around zero imaging depth. The 6 dB sensitivity roll-off distance was found to be at an imaging depth of 1.6 mm. The imaging process includes background signal subtraction, linear interpolation to convert data from the linear wavelength space to the linear wavenumber space, and numerical dispersion. The lateral and axial resolutions were measured to be 20.0 and 3.5 μm, respectively, in the air.
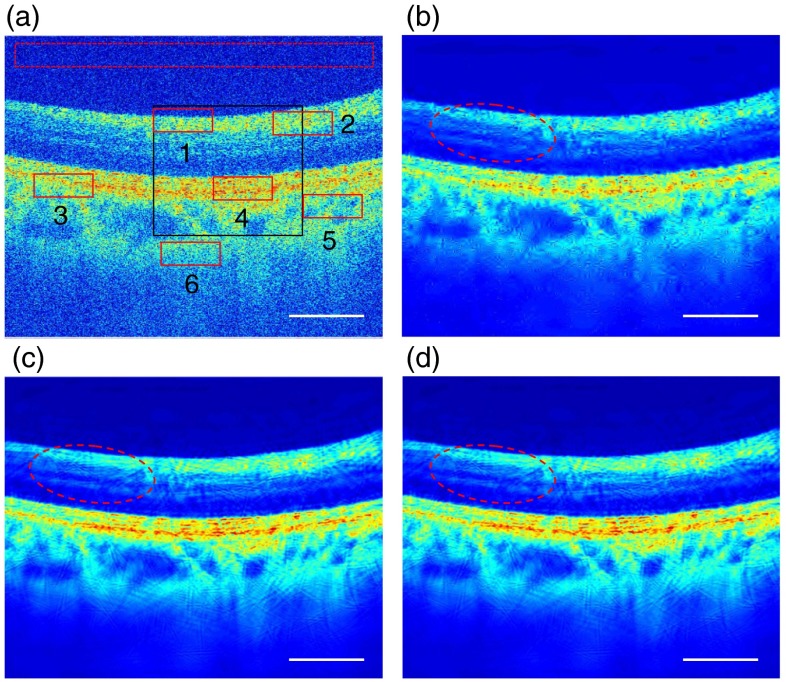
We applied our algorithm to the acquired OCT image of a human retinal image with (). Here, the retinal image was first reduced to by averaging groups of three adjacent axial scans, as shown in Fig. 2(a). As shown in Fig. 2(a), six ROIs, including three nonhomogeneous (labeled 1, 3, and 5) and three homogeneous (labeled 2, 4, and 6) areas, respectively, were selected in the retinal image and marked with solid rectangles in red. Meanwhile, a biological tissue-free area in the top region of the retinal image was selected as a “background” region, which was marked with a dashed rectangle in red and used for calculating SNR of the images. A region in the black rectangle window in Fig. 2(a) was enlarged 1.8 times and used for comparative analysis. Meanwhile, wavelet29 and curvelet35 based thresholding filterings were also applied to the same OCT image. For objective and equivalent comparisons, cycle spinning technology was also applied to remove Gibbs artifacts in the wavelet filtering and curvelet filtering processes. Note that we performed the wavelet- and curvelet-based thresholdings with the best results by obtaining the most appropriate threshold by a trial and error method in the image processing. The threshold is chosen to be 3.6 and 1.1 times of the noise variances, which are obtained from the median estimator of the highest sub-band of the transform for wavelet- and curvelet-based methods, respectively.35,36 Comparing wavelet- and curvelet-based methods with the proposed wave atoms-based methods for a similar cross-correlation XCOR value, the threshold value in the wave atoms despeckling process is chosen to be . In all cases, the images were processed with MATLAB on an Intel dual-core 2.2 GHz laptop.
Fig. 2.
Denoised results of a human retinal image with . (a) Original image, (b) denoised image with wavelet, (c) curvelet, and (d) proposed wave atoms shrinkage, respectively. The areas in solid rectangles (marked in red) are the selected regions of interests (ROIs) and the dashed red rectangle area is the selected background region used for quantitative comparison of the performance of all speckle reduction algorithms based on wavelet, curvelet, and the proposed wave atom transforms applied to the original image. The red elliptical area points to structures with clearer visibility in the denoised OCT images; white scale bars represent 0.80 mm.
Figure 2 shows the original and despeckled OCT images of a human retina. The unprocessed image, shown in Fig. 2(a), has a grainy appearance due to the presence of speckle noise. Figure 2(b) shows the denoised image by the traditional wavelet method and the same OCT image after despeckling by curvelet is shown in Fig. 2(c). Figure 2(d) shows the denoised image using the proposed wave atoms transform method. It can be seen from the results that all three methods can remove most speckle noises and improve the visualization of small morphological features, such as outer plexiform layer (OPL) and retinal pigment epithelium, which are not shown clearly in the original raw OCT image. Meanwhile, it also can be seen that the processed OCT image, as shown in Fig. 2(d) with the proposed wave atoms method, shows much better visual effects and clearer detailed morphological features indicated, for example, by the red elliptical area in Fig. 2(d), than with the wavelet and curvelet methods. However, it needs to be pointed out that, like other image despeckling methods, the proposed wave atoms method also will blur or injure some feature details and edge information in the processed image. For example, there are some discontinuities in the OPL layer in the despeckled image compared to the original image. Therefore, it is necessary to keep a balance between obtaining the highest level of despeckling in the processed image and maintaining minimum damage to the original image in the practice applications.
For further comparative analysis, enlarged views of the region in the solid rectangle marked in black in Fig. 2(a) are presented in Fig. 3. It can be seen from Fig. 3 that there is almost no residual speckle noise pattern in the denoised images with wavelet, curvelet, and wave atoms shrinkages. However, there appears to be significant visual aberration (ringing effects and artificial effect in some areas in the despeckled image) and blurring of features in the denoised images by wavelet- and curvelet-domain filtering methods compared to the proposed wave atoms transform method. Namely, the proposed wave atoms shrinkage method shows much better visual effects and clearer detailed morphological features in the denoised images, as indicated, for example, by the two black arrows in the Fig. 3 (right image), the OPL and external limiting membrane (ELM). For the wavelet method, as shown in Fig. 3 (left), the ELM layer is almost invisible and the OPL layer cannot be resolved easily in the wavelet-based despeckled image, while in the curvelet-based despeckled image, as shown in Fig. 3 (middle), we can see that the ELM layer is distorted and discontinuous. Moreover, the OPL layer edge is distorted with mottling, and it cannot be resolved easily. In the wave atoms-based despeckled image, as shown in Fig. 3 (right), it shows a nicely continuous OPL layer, and the ELM layer is very clear except for where there are a few minor discontinuities as indicated by the white arrow.
Fig. 3.

Enlarged copies of the solid black rectangle region in OCT retinal images [as shown in Fig. 2(a)] for close comparison of the performance of three image processing algorithms. The black arrows point to layer structures with clearer visibility and the white arrow points to the discontinuous layer structure in the denoised OCT images. The white scale bars represent 0.42 mm.
The reason for this performance difference is that the wavelet transform is only optimal in representing 1-D singularities but not optimal in representing 2-D image contours or layers because of poor orientation selectivity and anisotropy. Therefore, it cannot effectively represent images consisting of different regions separated by boundaries that often appear in OCT images. The curvelet transform gives an optimal sparse representation because it obeys a more precise parabolic balance between oscillations and support size, and it concentrates the energy of an object with an arbitrary discontinuity curve in just a few coefficients.34 Meanwhile, wave atoms can be adapted to arbitrary local directions of a pattern and also can sparsely represent anisotropic patterns aligned with the axes. Moreover, the warped oscillatory functions and oriented textures in wave atoms have been proven to have a dramatically sparser expansion compared to wavelets and curvelets, and wave atoms transform is particularly well suited for representing oscillatory patterns and textures in the images39 As a result, the wave atoms transform would generate relatively larger transformed coefficients for such continuous and weak layer features (like ELM), while the wavelet and curvelet coefficients for the weak ELM signals are small and are easily attenuated along with speckle noise. The proposed wave atoms method, therefore, is a highly promising preprocessing approach that can enhance retinal OCT image quality for further quantitative analysis, such as segmentation for retina layer measurement and analysis.
To quantitatively analyze the performance of the proposed algorithm, we also calculated the image quality metrics, such as SNR, CNR, ENL, and XOCR. The CNR values were averaged over six ROIs () within the solid red rectangle in Fig. 2(a). Similarly, the ENL values were averaged over the three ROIs, , 4, 6, in Fig. 2(a). The selected background region in the dashed rectangle was used to calculate the background noise level. Note that the CNR and ENL were computed using a logarithmic scale while SNR and XCOR were calculated using a linear scale. Table 1 gives the results of the qualitative metrics for the original and the filtered images. It clearly shows that the denoised results with curvelet and the proposed wave atoms transforms are better than the traditional wavelet thresholding method. Note that we performed the wavelet- and curvelet-based thresholdings with the best results by obtaining the most appropriate threshold by a trial and error method in the image processing. For similar XCOR values, for example, we took the XCOR values of 0.925, 0.924, and 0.926 for the wavelet-, curvelet-, and wave atoms-based methods, respectively. As shown in Table 1, our proposed wave atoms shrinkage method () made further improvements to the SNR, 8.43 dB and 3.12 dB, compared to the wavelet- and curvelet-based methods, which also greatly improving the image quality of the CNR and ENL.
Table 1.
Image quality metrics for OCT images.
| Methods | SNR (dB) | CNR (dB) | ENL | XCOR |
|---|---|---|---|---|
| Original | 48.72 | 8.49 | 11.83 | 1.000 |
| Wavelet | 98.40 | 15.67 | 39.25 | 0.925 |
| Curvelet | 103.71 | 16.08 | 43.43 | 0.924 |
| Wave atoms () | 105.33 | 16.92 | 53.77 | 0.929 |
| Wave atoms () | 106.83 | 17.43 | 61.36 | 0.926 |
| Wave atoms () | 107.42 | 17.88 | 69.33 | 0.923 |
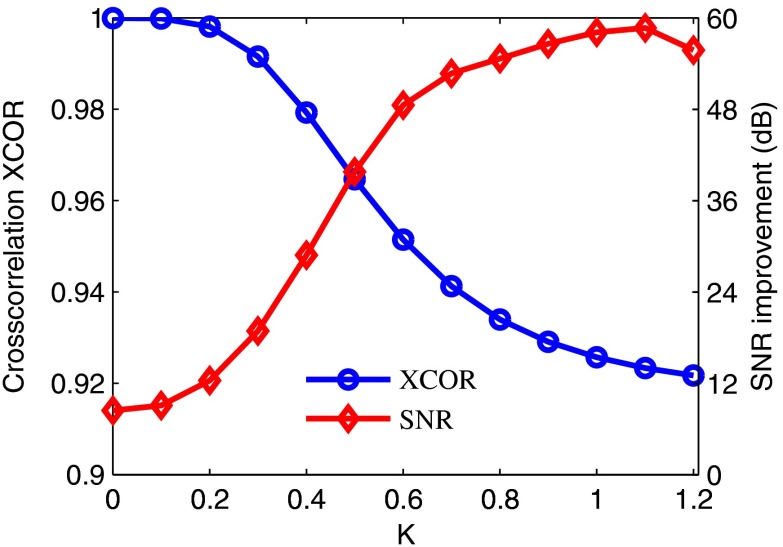
In speckle reduction with wave atoms shrinkage, the parameter controls the degree of speckle reduction, and there is a trade-off between speckle reduction degree and edge preservation in practical applications. Figure 4 shows the trend of SNR improvement and cross-correlation XCOR with a different threshold factor, , in the denoising process. As shown in Fig. 4, the XCOR decreases with the increment of threshold factor . However, SNR increases with the increment of until reaches 1.1. The XCOR decreases sharply initially at small values, and then it does not change significantly for between 0.8 and 1.2. Increasing the threshold further would eventually lead to the loss of image features and decrease the XCOR. Moreover, Fig. 4 also shows acceptable and stable despeckled results (SNR and XCOR) for a wide available range of threshold (from 0.7 to 1.2) in the wave atoms despeckling process.
Fig. 4.
Measurement of SNR improvement and cross-correlation XCOR as a function of different threshold values (from 0 to 1.2) in an OCT retinal image by wave atoms despeckling algorithm. The algorithm improves the maximum SNR of 58.70 dB at , while the cross-correlation XCOR between the original and despeckled images is 0.923.
4. Conclusions
In summary, we presented a recently introduced wave atoms frame of decomposition for speckle reduction in OCT images. The results showed that the proposed approach achieved better SNR improvement and visual effects compared to the traditional wavelet and curvelet shrinkages. Furthermore, the wave atoms algorithm showed good preservation of image detail features, and the trade-off between speckle reductions can be controlled by using an adjustable parameter in the despeckling process. Note that the computational complexity of wave atoms transform is for an image; it shows more complex than wavelet and curvelet methods. Moreover, after using cycle spinning technology, the time consumed by the algorithm is slower and the proposed method was the most time consuming. In our case, the total time for processing a images was about 2.3, 2.7, and 8.1 s using wavelet, curvelet, and the proposed wave atoms algorithm with MATLAB on an Intel dual-core 2.2 GHz laptop, respectively. However, the processing time can be significantly reduced with a C++ program and graphic processing unit.
Acknowledgments
This work was supported by the National Institutes of Health (R01EB-10090, R01EY-021519, R01HL-105215, R01HL-103764, and P41EB-015890), Office of Scientific Research (FA 9550-10-1-0538), and the Beckman Laser Institute Endowment. Yongzhao Du is supported by the Postgraduate Scholarship Program (PhD Joint-Training Program) of the China Scholarship Council (CSC) and Scholarship Award for Excellent Doctoral Student granted by Ministry of Education, China. Dr. Chen has a financial interest in OCT Medical Imaging Inc., which, however, did not support this work.
Biographies
Yongzhao Du received his undergraduate education at Huaqiao University in China, and he started his graduate education major in optical engineering at Sichuan University. His PhD degree studies involved research in new laser technology, optical measurements, and optical imaging. Now he is an assistant specialist at Beckman Laser Institute, University of California, Irvine, and his current research fields focus on optical coherence tomography (OCT), Doppler OCT, and optical image processing.
Zhongping Chen is a professor of biomedical engineering and the director of F-OCT Laboratory at University of California, Irvine. He is a co-founder and the board chairman of OCT Medical Imaging Inc. His research group has pioneered the development of Doppler optical coherence tomography. He has published more than 200 peer-reviewed papers. He is a fellow of the American Institute of Medical and Biological Engineering, a fellow of SPIE, and OSA.
Biographies of the other authors are not available.
References
- 1.Huang D., et al. , “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Drexler W., Fujimoto J. G., Optical Coherence Tomography: Technology and Applications, Springer-Verlag, Berlin Heidelberg: (2008). [Google Scholar]
- 3.Wojtkowski M., “High-speed optical coherence tomography: basics and applications,” Appl. Opt. 49(16), D30–D61 (2010). 10.1364/AO.49.000D30 [DOI] [PubMed] [Google Scholar]
- 4.Xiang S., Zhou L., Schmitt J., “Speckle noise reduction for optical coherence tomography,” Proc. SPIE 3196, 79–88 (1998). 10.1117/12.297921 [DOI] [Google Scholar]
- 5.Bashkansky M., Reintjes J., “Statistics and reduction of speckle in optical coherence tomography,” Opt. Lett. 25(8), 545–547 (2000). 10.1364/OL.25.000545 [DOI] [PubMed] [Google Scholar]
- 6.Schmitt J. M., Xiang S. H., Yung K. M., “Speckle in optical coherence tomography,” J. Biomed. Opt. 4(1), 95 (1999). 10.1117/1.429925 [DOI] [PubMed] [Google Scholar]
- 7.Schmitt J. M., “Array detection for speckle reduction in optical coherence microscopy,” Phys. Med. Biol. 42(7), 1427–39 (1997). 10.1088/0031-9155/42/7/015 [DOI] [PubMed] [Google Scholar]
- 8.Schmitt J. M., “Restoration of optical coherence images of living tissue using the CLEAN algorithm,” J. Biomed. Opt. 3(1), 66–75 (1998). 10.1117/1.429863 [DOI] [PubMed] [Google Scholar]
- 9.Pircher M., et al. , “Speckle reduction in optical coherence tomography by frequency compounding,” J. Biomed. Opt. 8(3), 565–569 (2003). 10.1117/1.1578087 [DOI] [PubMed] [Google Scholar]
- 10.Iftimia N., Bouma B. E., Tearney G. J., “Speckle reduction in optical coherence tomography by “path length encoded” angular compounding,” J. Biomed. Opt. 8(2), 260–263 (2003). 10.1117/1.1559060 [DOI] [PubMed] [Google Scholar]
- 11.Kim J., et al. , “Optical coherence tomography speckle reduction by a partially spatially coherent source,” J. Biomed. Opt. 10(6), 064034 (2005). 10.1117/1.2138031 [DOI] [PubMed] [Google Scholar]
- 12.Desjardins A. E., et al. , “Speckle reduction in OCT using massively-parallel detection and frequency-domain ranging,” Opt. Express 14(11), 4736–4745 (2006). 10.1364/OE.14.004736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Desjardins A. E., et al. , “Angle-resolved optical coherence tomography with sequential angular selectivity for speckle reduction,” Opt. Express 15(10), 6200–6209 (2007). 10.1364/OE.15.006200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Popescu D. P., Hewko M. D., Sowa M. G., “Speckle noise attenuation in optical coherence tomography by compounding images acquired at different positions of the sample,” Opt. Commun. 269(1), 247–251 (2007). 10.1016/j.optcom.2006.07.063 [DOI] [Google Scholar]
- 15.Bajraszewski T., et al. , “Improved spectral optical coherence tomography using optical frequency comb,” Opt. Express 16(6), 4163–4176 (2008). 10.1364/OE.16.004163 [DOI] [PubMed] [Google Scholar]
- 16.Wang H., Rollins A. M., “Speckle reduction in optical coherence tomography using angular compounding by B-scan Doppler-shift encoding,” J. Biomed. Opt. 14(3), 030512 (2009). 10.1117/1.3155523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kennedy B. F., et al. , “Speckle reduction in optical coherence tomography by strain compounding,” Opt. Lett. 35(14), 2445–2447 (2010). 10.1364/OL.35.002445 [DOI] [PubMed] [Google Scholar]
- 18.Klein T., et al. , “Joint aperture detection for speckle reduction and increased collection efficiency in ophthalmic MHz OCT,” Biomed. Opt. Express 4(4), 619–634 (2013). 10.1364/BOE.4.000619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pircher M., et al. , “Measurement and imaging of water concentration in human cornea with differential absorption optical coherence tomography,” Opt. Express 11(18), 2190–2197 (2003). 10.1364/OE.11.002190 [DOI] [PubMed] [Google Scholar]
- 20.Rogowska J., Brezinski M. E., “Evaluation of the adaptive speckle suppression filter for coronary optical coherence tomography imaging,” IEEE Trans. Med. Imaging 19(12), 1261–1266 (2000). 10.1109/42.897820 [DOI] [PubMed] [Google Scholar]
- 21.Wong A., et al. , “General Bayesian estimation for speckle noise reduction in optical coherence tomography retinal imagery,” Opt. Express 18(8), 8338–8352 (2010). 10.1364/OE.18.008338 [DOI] [PubMed] [Google Scholar]
- 22.Marks D. L., Ralston T. S., Boppart S. A., “Speckle reduction by I-divergence regularization in optical coherence tomography,” J. Opt. Soc. Am. A 22(11), 2366 (2005). 10.1364/JOSAA.22.002366 [DOI] [PubMed] [Google Scholar]
- 23.Ozcan A., et al. , “Speckle reduction in optical coherence tomography images using digital filtering,” J. Opt. Soc. Am. A 24(7), 1901 (2007). 10.1364/JOSAA.24.001901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Salinas H. M., Fernández D. C., “Comparison of PDE-based nonlinear diffusion approaches for image enhancement and denoising in optical coherence tomography,” IEEE Trans. Med. Imaging 26(6), 761–771 (2007). 10.1109/TMI.2006.887375 [DOI] [PubMed] [Google Scholar]
- 25.Puvanathasan P., Bizheva K., “Speckle noise reduction algorithm for optical coherence tomography based on interval type II fuzzy set,” Opt. Express 15(24), 15747–15758 (2007). 10.1364/OE.15.015747 [DOI] [PubMed] [Google Scholar]
- 26.Puvanathasan1 P., Bizheva K., “Interval type-II fuzzy anisotropic diffusion algorithm for speckle noise reduction in optical coherence tomography images,” Opt. Express 17(2), 733–746 (2009). 10.1364/OE.17.000733 [DOI] [PubMed] [Google Scholar]
- 27.Bernardes R., et al. , “Improved adaptive complex diffusion despeckling filter,” Opt. Express 18(23), 24048–24059 (2010). 10.1364/OE.18.024048 [DOI] [PubMed] [Google Scholar]
- 28.Chang S. G., Yu B., Vetterli M., “Spatially adaptive wavelet thresholding with context modeling for image denoising,” IEEE Trans. Image Process. 9(9), 1522–1531 (2000). 10.1109/83.862630 [DOI] [PubMed] [Google Scholar]
- 29.Adler D. C., Ko T. H., Fujimoto J. G., “Speckle reduction in optical coherence tomography images by use of a spatially adaptive wavelet filter,” Opt. Lett. 29(24), 2878–2880 (2004). 10.1364/OL.29.002878 [DOI] [PubMed] [Google Scholar]
- 30.Chitchian S., Fiddy M., Fried N., “Denoising during optical coherence tomography of the prostate nerves via wavelet shrinkage using dual-tree complex wavelet transform,” J. Biomed. Opt. 14(1), 014031 (2009). 10.1117/1.3081543 [DOI] [PubMed] [Google Scholar]
- 31.Mayer M., et al. , “Wavelet denoising of multiframe optical coherence tomography data,” Biomed. Opt. Express 3(3), 572–589 (2012). 10.1364/BOE.3.000572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chitchian S., et al. , “Retinal optical coherence tomography image enhancement via shrinkage denoising using double-density dual-tree complex wavelet transform,” J. Biomed. Opt. 17(11), 116009 (2012). 10.1117/1.JBO.17.11.116009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Xu J., et al. , “Speckle reduction of retinal optical coherence tomography based on contourlet shrinkage,” Opt. Lett. 38(15), 2900–2903 (2013). 10.1364/OL.38.002900 [DOI] [PubMed] [Google Scholar]
- 34.Starck J. L., Candes E. J., Donoho D. L., “The curvelet transform for image denoising,” IEEE Trans. Image Process. 11(6), 670–684 (2002). 10.1109/TIP.2002.1014998 [DOI] [PubMed] [Google Scholar]
- 35.Candes E., et al. , “Fast discrete curvelet transforms,” SIAM Multiscale Model. Simul. 5(3), 861–899 (2006). 10.1137/05064182X [DOI] [Google Scholar]
- 36.Jian Z., et al. , “Speckle attenuation in optical coherence tomography by curvelet shrinkage,” Opt. Lett. 34(10), 1516–1518 (2009). 10.1364/OL.34.001516 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jian Z. P., et al. , “Three-dimensional speckle suppression in optical coherence tomography based on the curvelet transform,” Opt. Express 18(2), 1024–1032 (2010). 10.1364/OE.18.001024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Demanet L., “Curvelets, wave atoms and wave equations,” Ph.D. Thesis, California Institute of Technology (2006). [Google Scholar]
- 39.Demanet L., Ying L., “Wave atoms and sparsity of oscillatory patterns,” Appl. Comput. Harmon. Anal 23(3), 368–387 (2007). 10.1016/j.acha.2007.03.003 [DOI] [Google Scholar]
- 40.Demanet Laurent, http://math.stanford.edu/~laurent/html/software.html.
- 41.Coifman R. R., Donoho D. L., “Translation-invariant denoising,” in Lecture Notes in Statistics: Wavelets and Statistics, Antoniadis A., Oppenheim G., Eds., pp. 125–150, Springer-verlag, New York: (1995). [Google Scholar]
- 42.Liu G., et al. , “Real-time bulk-motion-correction free Doppler variance optical coherence tomography for choroidal capillary vasculature imaging,” Opt. Express 19(4), 3657–3666 (2011). 10.1364/OE.19.003657 [DOI] [PMC free article] [PubMed] [Google Scholar]