Like-charge interactions between colloidal particles are asymmetric with respect to sign

Abstract

Two-dimensional dispersions of colloidal particles with a range of surface chemistries and electrostatic potentials are characterized under a series of solution ionic strengths. A combination of optical imaging techniques are employed to monitor both the colloid structure and the electrostatic surface potential of individual particles in situ. We find that like-charge multiparticle interactions can be tuned from exclusively repulsive to long-range attractive by changing the particle surface composition. This behavior is strongly asymmetric with respect to the sign of the surface potential. Collective long-range attractive interactions are only observed among negatively charged particles.

Introduction

The behavior of colloidal particles in water is of paramount importance to numerous scientific problems ranging from photonic and meta-material fabrication to protein oligomerization and cell membrane interactions.^1–5 Dispersions of like-charged colloidal particles exhibit widely varying degrees of order, from randomly dispersed to condensed liquid and crystalline phases. The colloidal structure is determined by interaction forces between particles. These are typically modeled by the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory, which superimposes a short-range attractive van der Waals interaction onto a longer-range electrostatic potential. The electrostatic component of DLVO theory is based on the widely used Poisson–Boltzman model, and is universally repulsive between like charged objects.^6–8 An intriguing observation is that interparticle spacings in condensed phases can be nearly a micron greater than the particle diameter, suggesting a non-monotonic multiparticle interaction potential that is strongly repulsive at intermediate distances and becomes weakly attractive at longer distances. Attractive forces at such distances are well beyond the limits of van der Waals forces or any type of direct salt bridging effect.^6,9 Their physical origin and even existence remains enigmatic. Nevertheless, they appear to dominate the behavior of certain systems.^10–15

Here, we comprehensively study colloidal monolayers of identically charged particles over a wide range of surface chemistries, surface potentials, and electrolyte strengths and compositions. Using a combination of optical imaging techniques to monitor both the colloidal structure and the particle electrostatic potential within each sample, one clear trend emerges. Condensed phases, and the apparent like-charge attraction, are only observed among negatively charged particles. Not only does this contradict the Poisson–Boltzmann model for electrostatic interactions in water,^7,8 no theory that is symmetric with respect to the sign of the charge predicts this asymmetry. Breakdown of the Poisson–Boltzmann theory over molecular length-scales is well established, and can be easily rationalized in terms of the failure of this mean field model to capture molecular aspects of liquids and surfaces. Over larger distances, such as those examined by experiments here, mean field descriptions are expected to become increasingly accurate. It is therefore surprising to find a significant range of conditions, covering a space thought to be well described by Poisson–Boltzmann theory, where not even the direction of electrostatic forces can be predicted.

Critical to this study is the ability to both control and monitor the colloid surface potential, Ψ, in situ. We combine two new techniques to solve this problem. First, lipid membrane coatings are employed to derivatize the colloid surface,^12,14,16 as well as the underlying substrate (Fig. 1). Lipid bilayer vesicles spontaneously adsorb and fuse on silica surfaces, forming a single, continuous bilayer membrane that uniformly coats the substrate.¹⁷ The vesicle fusion process is quite general, accommodating a diversity of membrane lipid compositions and charges. Thus, by varying the fractions of lipids with acidic and basic headgroups, the surface chemistry and resulting surface potential of the coated substrates can be varied continuously over a wide range. Alternative surface coating methods were also used to confirm that none of the results reported below are due to the lipid membrane. Second, we use dual wavelength reflection interference contrast microscopy (RICM) to measure height distributions of the electrostatically levitated particles to a precision of ~5 nm in situ. This precisely determines the separation distance between the particle and substrate surfaces at which the repulsive electrostatic force equals the force of gravity. Thus, different systems can be electrostatically matched in a model independent manner, and to a precision greater than that with which Ψ can be experimentally controlled.

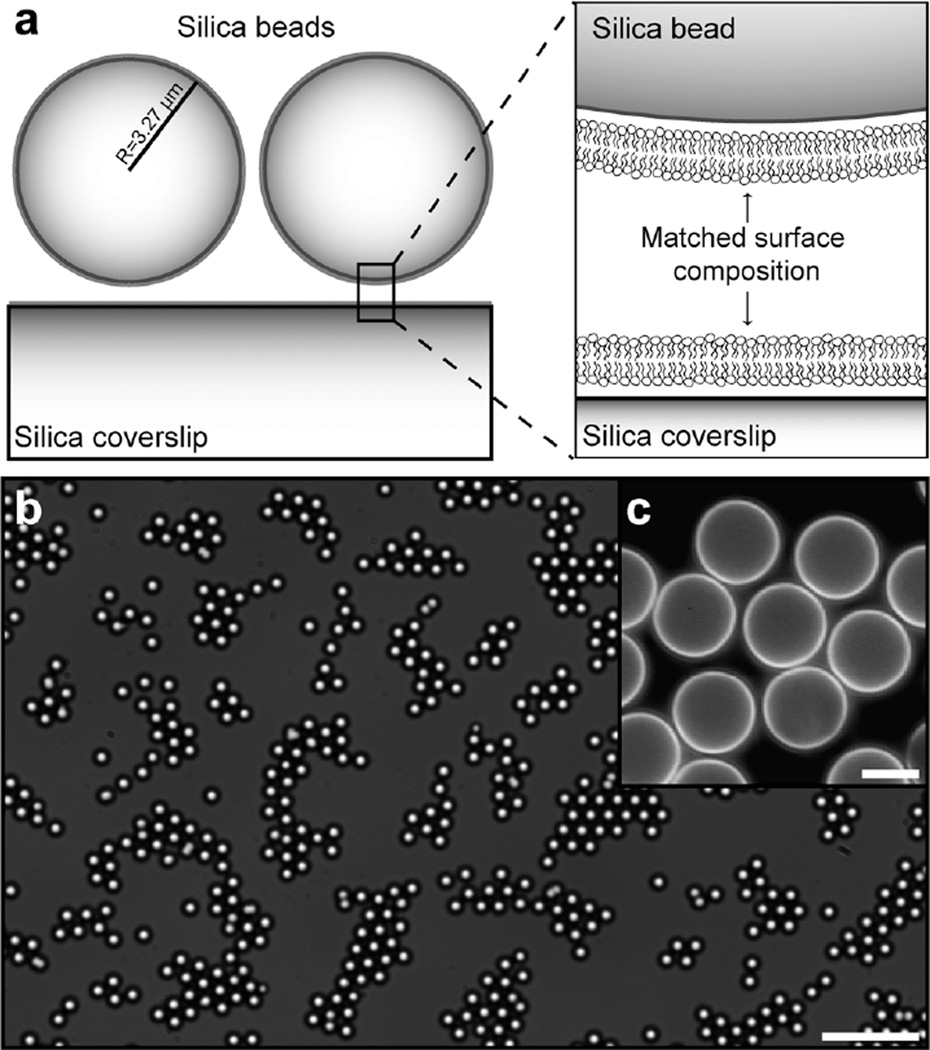
Fig. 1.

Experimental geometry. (a) Silica particles and the underlying planar coverslip are coated by membranes of the same composition. (b) Brightfield image of a two-dimensional dispersion of silica particles where both the particles and the underlying coverslip are coated with negatively charged membranes. Scalebar: 50 µm. (c) Fluorescence image of particles coated with negatively charged membranes containing 0.5 mole % N-(Texas red sulfonyl)-1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine (Texas red-DPPE) as the fluorescent probe. The surfaces of the particles are separated by up to one micron within the condensed regions of the dispersion. Scalebar: 5 µm.

Results and discussion

Variously coated silica particles (6.54 ± 0.65 µm mean diameter) were dispersed into glass-bottom 96-well plates with identical surface coatings. This symmetrical configuration facilitates interpretation of electrostatic measurements, but is not required. Experiments were performed in 18.2 MΩ cm Millipore water or prepared salt solutions. Ultrapure water from multiple sources was examined to confirm generality of the results. Colloids were observed by brightfield microscopy and images were recorded with a charge-coupled device (CCD) camera. Particle positions were determined to a lateral precision of ~25 nm by an object locating algorithm from images (449 × 449 µm²) containing approximately 1650 individual particles.^14,18 This corresponds to a colloid area fraction of ϕ ≈ 0.3; standard deviations in ϕ from independent images were typically less than 3%. Colloid structure was characterized using radial pair distribution functions, g(r), which were compiled from averaging 50–75 independent images for a total of ~100,000 individual particles (see Supplementary discussion^†).

Well plates were left undisturbed on the microscope stage before data collection to allow the particles to settle, gravitationally, to an equilibrium height above the underlying substrate, and for the resultant colloidal monolayer to attain its near equilibrium lateral distribution.¹² In this state, particle motion persists and the system continues to evolve through different microscopic configurations. The overall structure, as measured by g(r), is time-invariant (Fig. S1). Moreover, changing a parameter (e.g. ionic strength) leads to a rapid transition from one stable near-equilibrium distribution to another (Fig. S3). Thus, all data presented herein result from essentially ergodic systems.

Colloids with controllable surface potentials spanning a range of nearly ±60 mV were generated by derivatizing the particles with differing membrane compositions. The actual surface charge is determined by a number of factors including the composition of ionizable lipids, their ionization states, as well as charge contributions from the underlying silica substrate.^14,19 Particle surface potentials were characterized in situ for each experiment from dual wavelength RICM height measurements (see Supplementary discussion). Standard deviations in Ψ for particles within a sample were typically less than 4%. For membrane compositions between 2 and 4 net mol% of excess positively charged lipids, the particles no longer levitate above the underlying substrate; repulsive electrostatic forces are too weak to balance the gravitational force. This indicates the point of zero surface charge, and reveals the residual negative charge from the underlying silica surface. The symmetry about the point of zero charge is confirmed by equivalent heights of oppositely charged particles (counting the offset) above the underlying substrate. Thus within the range of these studies, membrane composition linearly determines surface charge density modulated by a negative offset from the substrate (Fig. S4).

Brightfield images of colloidal monolayers of particles with a range of surface potentials are shown in Fig. 2a with corresponding plots of g(r) in Fig. 2b. Particles with a net negative charge, irrespective of the surface chemistry used to achieve this, condense into hexagonally packed crystallites at low surface densities. In these systems, the first order peak of g(r), corresponding to the interparticle separation distance, occurs at a distance of approximately 7.5 µm. This indicates that surfaces of the 6.54 µm diameter particles in condensed crystallites are separated by nearly a micron. Attractive van der Waals forces, which are limited to distances of <10 nm,⁶ are not expected to play a significant role over distances of this magnitude. A small peak, which occurs exactly at the diameter of the particles, labeled r_o, is a result of a small number of doublet particles and particles in van der Waals contact (see Fig. 2b, inset).

Fig. 2.

Surface potential panel. (a) Brightfield images of colloidal monolayers for a range of surface potentials. Scalebar: 60 µm. (b) Corresponding plots of the radial distribution function, g(r). The inset plots the first peak of g(r). Particles with negative surface potentials form condensed structures and particles with positive surface potentials are dispersed. (c) Plot of the degree of particle localization, G, as a function of the surface potential, Ψ, for a variety of membrane coatings and for Monte Carlo results. Error bars represent one standard deviation.

Colloid systems of equal but opposite charge exhibit drastically different behavior. Condensation into ordered crystallites is strongest for the most negative surface potentials. These apparently attractive multiparticle interactions become progressively weaker with decreasing magnitude of negative Ψ. For positive Ψ, colloids were universally disordered, and exhibited strictly repulsive interactions. Results from Monte Carlo simulations for a pair-wise Poisson–Boltzmann interaction between charged spheres, calculated using the Derjaguin approximation,⁶ are plotted in Fig. 2b (inset) for comparison. No strong ordering is predicted under any of the experimental conditions.

The generality of this charge asymmetric behavior is established through a series of experiments covering a variety of charged lipid species and charge combinations. To simplify comparison of these results, we define a parameter G as:

$$G\equiv \frac{{\int }_{r_o}^{r_1}g(r)r\mathrm{d}r}{{\int }_{r_o}^{r_1}r\mathrm{d}r}$$ (1)

where r_o is the mean bead diameter and r₁ is the outer radius of the first coordination shell.¹⁴ Physically, G measures the degree of localization in these systems. For purely random distributions, G = 1; values of G > 1 indicate ordering, and possibly attraction, while G < 1 is indicative of repulsion. The collective results from all lipid compositions studied are summarized in Fig. 2c and Table 1 in terms of G as a function of the surface potential. The degree of order is roughly equivalent for equivalent surface potentials, regardless of how they were achieved chemically. Ordering is exclusively observed in systems with negative Ψ. Data from bare silica (Ψ = −22.4 mV) and amine-functionalized silica (Ψ = +10.8 mV) colloids are included in Fig. 2c, and confirm that the supported membrane is not responsible for these effects.

Table 1.

Effect of different membrane species on the ordering of two-dimensional dispersions of membrane-coated particles expressed in terms of G. Compositions in bold type exhibit apparently attractive long-range interactions

Membrane species (mol%)
0 DMOPC	(+)		(−)
	DOEPC	DMDAP	DMPS	DMPG	DMPA	TR	Ψ (mV)	G
89	11						+58	0.2
88	11.5					0.5	+53	0.3
92	7.5					0.5	+34	1.0
85	11		4				+24	1.5
84	11.5		4			0.5	+54	0.7
84	11.5			4		0.5	+33	1.1
84	11.5			4		0.5	+34	0.8
84	11.5				4	0.5	+52	1.2
92		7.5				0.5	+35	1.0
84		11.5	4			0.5	+49	0.6
84		11.5		4		0.5	+34	1.4
84		11.5			4	0.5	+53	1.3
77	11		12				−37	3.2
76	11.5			12		0.5	−34	2.9
76	11.5			12		0.5	−26	4.5
99			0.5			0.5	−16	5.0
99				0.5		0.5	−38	5.4
99					0.5	0.5	−16	4.7
73	11		16				−55	5.4
73	11			16			−53	2.8
72	11.5		16			0.5	−41	4.5
72	11.5			16		0.5	−38	4.9
72	11.5				16	0.5	−59	7.0
95			4.5			0.5	−23	4.1
95				4.5		0.5	−40	6.8
95					4.5	0.5	−40	6.0

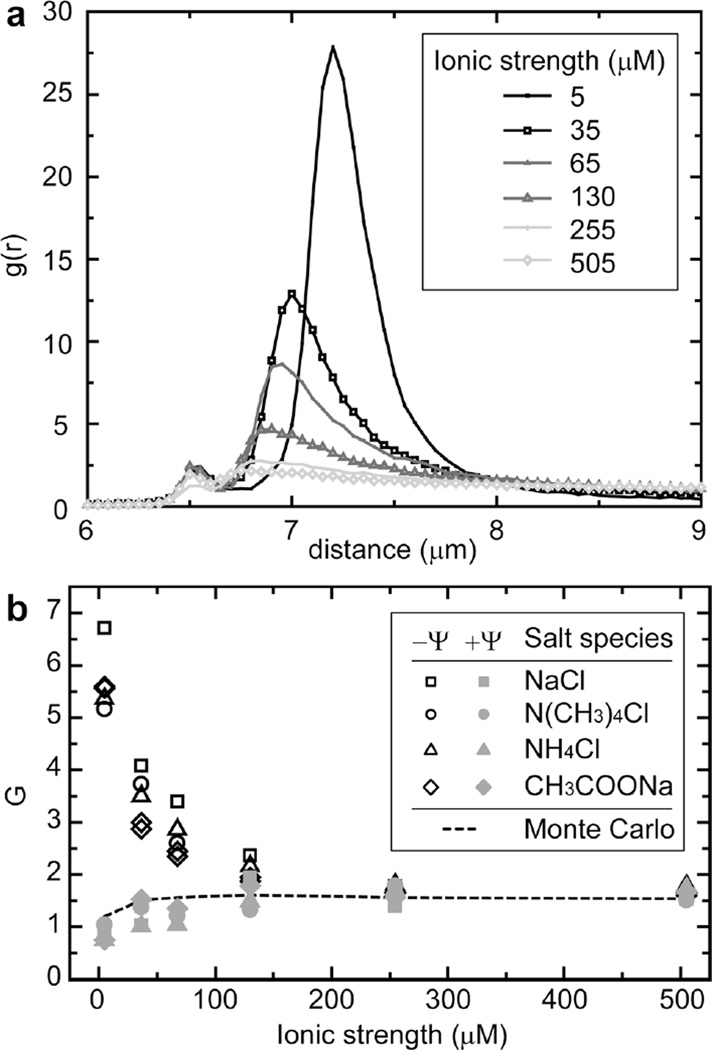
Electrostatic interactions in water are strongly dependent on ionic strength. Therefore, we characterized the effects of ionic strength and electrolyte species on the colloidal structure. Plots of g(r) for a system of negatively charged particles (Ψ ~ −55 mV) under a series of different ionic strengths (NaCl) are presented in Fig. 3a. Ionic strength is adjusted by adding salt to 18.2 MΩ cm water, with an initial ionic strength of ~5 µM, attributed to dissolved CO₂.²⁰ Increasing the ionic strength reduces the degree of condensation and ordering within negatively charged systems. The minimum particle separation distance, marking the point at which electrostatic repulsion overwhelms thermal fluctuations, also decreased with increasing ionic strength for both positive and negative systems. Monte Carlo simulations reveal that this repulsive component of the colloid interaction potential is well described by a pair-wise Poisson–Boltzmann interaction (Fig. S5). All of these ionic effects are independent of monovalent ionic species, as summarized in Fig. 3b (see also Table S1). Small changes in pH, as a result of adding micromolar concentrations of weak acid (NH₄⁺) or weak base (CH₃COO⁻), did not result in appreciable changes in the colloidal ordering.

Fig. 3.

Effect of electrolyte. (a) g(r) plots for negatively charged particles over a range of ionic strengths, prepared from deionized water with an initial ionic strength of ~5 µM attributed to dissolved CO₂. (b) Plot of G as a function of the ionic strength for negative (black, open symbols) and positive (gray, filled symbols) surface potentials (~ ±55 mV) with a variety of monovalent salts. Monte Carlo results as a function of ionic strength for Ψ = ±55 mV are plotted as a dashed line.

Apparently attractive long-range interactions between negatively charged particles (e.g. silica and polystyrene sulfate) have been periodically reported over the years.^10,11 Despite many attempts to explain or refute such observations, no consensus has emerged.^9,11,21–25 The observations reported here support the existence of long-range attractive multiparticle interactions in negatively charged colloids. The charge asymmetry we observe has not been reported previously, and rules out a number of the proposed explanations. It may also help identify the origin of these anomalous electrostatic interactions in water.

The presence of a nearby planar surface introduces several modifications to interactions within two-dimensional colloidal systems. First, the nearby boundary significantly affects local hydrodynamic flows, potentially influencing nearby colloidal particles.²¹ However, such dissipative forces are not relevant in systems at equilibrium (see Supplementary discussion).²⁶ Reversibility of hydrodynamic flow guarantees that all net hydrodynamic forces sum to zero when there is no net motion of the particles. Second, the nearby interfaces affect the distribution of counter-ions in solution that balance surface charges. Speculation as to whether two like-charged particles could attract within a confined geometry under the Poisson–Boltzmann formalism^27,28 has been largely put to rest by several theoretical proofs.^7,8 Additionally, neither of these effects would distinguish between the sign of Ψ.

Measured forces between charge mosaic surfaces, in which positively and negatively charged domains are randomly distributed on a surface, can exhibit a long-range attraction.^29,30 The length scale of the attraction depends on the Debye length and the length scale of the heterogeneity within the system. There are several facts that suggest static charge mosaicism is not responsible for the condensation effects reported here. First, the most strongly attracting systems exhibit an attractive minimum at the largest separation distance (~1 µm). In contrast, interactions between charge mosaic surfaces in water are purely attractive up to surface contact.³⁰ Additionally, the size scale of surface charge heterogeneity would need to be comparable to the separation distance. Fluorescence probe lipids are charged, and exhibit visible concentration variation under surface potential modulation of as little as 5 mV.¹⁹ Membrane coatings on particle and substrate surfaces are uniform when observed by fluorescence microscopy (Fig. 1c and Fig. S6), suggesting that charge heterogeneity is not present on the >200 nm length scale. More generally, it is unlikely that charge mosaic patterns would consistently form over such a wide range of negative surfaces without ever showing up on positively charged surfaces. A dynamic charge mosaic, resulting from spatial fluctuations of the charge state of ionizable groups on the surface, however, may exist. It is plausible that the dynamics of these fluctuations would be different on positive and negative surfaces owing to the intrinsic ionic asymmetry of water. Whether or not this type of mechanism contributes to the effects observed here remains to be determined.

Several studies have shown similar two-dimensional crystalline domain patterns resulting from depletion forces.^31,32 Although depletion may be the source of long-range attraction, extensive purification and analysis reveal no direct evidence of depletant in the solution (see Supplementary discussion). We do note, however, that the strongest and most consistent condensation into crystalline lattices results when the bare silica particles are pre-washed in a base solution (0.1 N NaOH). This suggests that the observed attractive force may be associated with surface characteristics of the particles. The same charge asymmetry behavior was observed when the base treated silica particles were coated with lipid membranes. Other factors such as imaging artifacts,²⁴ particle polydispersity,²⁵ and convection,³³ which are known to influence measured interactions in colloidal systems, are demonstrably inconsequential to the results reported here.

Conclusions

Irrespective of the physical mechanism, we have observed an asymmetrical electrostatic interaction in aqueous colloids. The asymmetrical behavior is not predicted by standard models. There are numerous instances when understanding and controlling particle assembly in aqueous environments is essential. Clearly, more theoretical and experimental work is needed to establish a predictive understanding of electrostatic interactions in water.

Experimental methods

Lipids

The following lipids were purchased from Avanti Polar Lipids (Alabaster, AL): 1,2-dimyristoleoyl-sn-glycero-3-phosphocholine (DMOPC), 1,2-dioleoyl-sn-glycero-3-ethylphosphocholine (DOEPC), 1,2-dimyristoyl-3-dimethylammonium-propane (DMDAP), 1,2-dimyristoyl-sn-glycero-3-(phospho-L-serine) (DMPS), 1,2-dimyristoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (DMPG), and 1,2-dimyristoyl-sn-glycero-3-phosphate (DMPA). The fluorescent lipid probe Texas Red 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine (Texas red DPPE) was purchased from Invitrogen (Carlsbad, CA). The compositions (mole fraction) of the lipid bilayers studied are as follows: 11 mol% basic lipid (DOEPC or DMDAP), 0–16 mol% acidic lipid (DMPS, DMPG, or DMPA), with balance of a zwitterionic lipid (DMOPC). To verify that the membranes uniformly coated the surfaces, 0.5 mol% Texas red DPPE was added to some samples; 11.5 mol% basic lipid was added to these samples to account for the negative charge of Texas red DPPE.

Lipid vesicles

Lipids were mixed in chloroform. The mixture was then dried onto a round-bottom flask followed by desiccation under vacuum for at least 2 hours. Lipid films were then hydrated with 18.2 MΩ cm deionized (DI) water to 2 mg/mL. The resulting suspension was probe sonicated to clarity in an ice bath and ultracentrifuged at 5 °C for 2 hours. The top 1 mL of small unilamellar vesicle (SUV) solution was retained for use in experiments.

Supported lipid bilayers

Supported lipid bilayers were formed by standard vesicle fusion techniques^17,34 onto the surfaces of clean 6.54 µm silica particles (Bangs Laboratories, Fishers, IN) and 96-well optical bottom plates with #1.5 borosilicate coverglass bases (Nalgene NUNC, Rochester, NY). A spreading solution was formed by combining equal volumes of the SUV suspension with buffer (250 mM NaCl, 10 mM Tris, at pH 7.4). Planar supported lipid bilayers were prepared by incubating 25 µL of spreading solution in a well of a glass-bottom 96-well plate for 10 minutes. Wells were rinsed 10 times with 250 µL of working solution (18.2 MΩ cm DI water or salt solution, pH ~5.5). Bilayers were assembled on particles by combining equal volumes of bead stock solution with spreading solution in a small centrifuge tube, followed by pulse vortexing of the mixture. Excess vesicles and salt were removed by rinsing several times with desired working solution. Membrane coated particles were then diluted to the desired working concentration and cast into a well plate for imaging. Each well contained ~250 µl of solution, giving a fluid depth of ~8 mm. Typically, eight wells were prepared per membrane composition.

Silica and amine-functionalized silica systems

For bare silica experiments, silica particles and borosilicate glass surfaces were washed with 0.1 N NaOH followed by extensive rinsing with 18.2 MΩ cm DI water. Particles were then diluted to the desired working concentration and cast into a well plate for imaging. Silica surfaces were functionalized with 3-aminopropyltrimethoxysilane (APTMS, Sigma Aldrich) to create positively charged surfaces. An aliquot of silica particle suspension (10 wt % solids in DI water) was rinsed twice with acetone. The particles were then resuspended in a solution of 2% (v/v) APTMS in acetone and placed on a rotisserie to continuously mix for 3 hours at room temperature. Next, the particles were rinsed with acetone, followed by isopropanol, and lastly in DI water. Amine coated coverslips were prepared by first sonicating 25 mm round borosilicate coverslips in DI water to remove dust. The coverslips were etched in piranha solution (3 parts sulfuric acid (H₂SO₄) to 1 part hydrogen peroxide (H₂O₂) by volume) for 10 minutes, rinsed extensively in DI water, and then dried under a stream of nitrogen. Coverslips were then incubated in 1% (v/v) APTMS in acetone for 80 minutes, followed by rinsing in acetone and isopropanol. The coverlips were then dried under a stream of nitrogen and cured in an oven at 70 °C for 30 min.

Ionic strength

The following salts were purchased from Sigma Aldrich: sodium chloride (NaCl), sodium acetate (CH₃COONa), ammonium chloride (NH₄Cl), and tetramethylammonium chloride (N(CH₃)₄Cl). Ionic strength was adjusted by adding the salt to DI water, with an initial ionic strength of ~5 µM, attributed to dissolved CO₂. Particles and substrates used in ionic strength experiments were rinsed in salt solutions of the desired composition and ionic strength. Membrane-coated particles were then diluted to the desired working concentration in the salt solution and cast into a well plate for imaging.

Microscopy

Colloidal monolayers were imaged by a combination of brightfield and dual wavelength RICM to reveal both the colloid structure and monitor electrostatic potentials of individual particles. These were performed in parallel on the same microscope for each experiment. Brightfield imaging was performed with a 40× air objective using a Nikon TE2000-E inverted fluorescence microscope (Nikon, Japan) equipped with a Coolsnap K4 charge-coupled device camera (Roper Scientific, Dowington, PA). Nine non-overlapping images were taken per well using an automated stage. For fluorescence and dual wavelength RICM, sample illumination was provided by a mercury arc lamp. In dual wavelength RICM experiments the illumination from the mercury arc lamp was filtered using a dual-band pass (460–480 nm and 510–550 nm) excitation filter (Chroma, Rockingham, VT). The aperture diaphragm was set to provide a small illumination numerical aperture (INA = 0.495) and, hence, minimal angular variation in the incident light. This is important for maximizing the contrast between interference fringes. The field diaphragm was partially closed to facilitate reproducible focusing on the coverslip-water interface. Reflected light was imaged onto separate halves of a Cascade 512B CCD camera (Roper Scientific, Dowington, PA) or a Quantix CCD camera (Photometrics, Tucson, AZ) using a DualView (Optical Insights LLC, Tucson, AZ) image splitter interposed between the body of the microscope and the camera. Fluorescence and dual wavelength RICM experiments were performed with a 100× oil objective (NA = 1.3).

Image analysis

Image processing was performed using original software developed for Matlab 7 (Mathworks, Natick, MA). See Supplementary discussion for details regarding radial distribution function and dual wavelength reflection interference contrast microscopy analyses.

Monte Carlo simulations

Metropolis Monte Carlo was used to numerically calculate expected g(r) functions for two-dimensional dispersions of like-charged 6.54 µm diameter hard-sphere particles interacting by pair interactions. The pair interaction used in the simulations was composed of a linear superposition of hard-sphere repulsion and the Poisson–Boltzmann interaction between two spheres as calculated using the Derjaguin approximation. The pair interaction used is equivalent to a DLVO interaction at the large distances that our system explores. Simulations were performed at a particle area fraction of ϕ = 0.3. Trial states were generated by randomly selecting a particle and adjusting the position by a random step size. The maximal step size was adjusted to achieve a target acceptance rate of 30%. The entire system was modeled in a box 150 µm long on each side, which is well beyond the longest particle–particle correlations observed during the calculation. Particle configurations were recorded after every particle in the system had been moved an average of 5 times. After 2 × 10⁵ iterations recorded particle configurations were used to calculate g(r). Monte Carlo was performed using a discrete set of ionic strengths and surface potentials mirroring experimental conditions. Cubic interpolation between these points was used to plot the theoretical results displayed in Fig. 2, 3, and S5.