Role of linear and voltage-dependent ionic currents in the generation of slow wave oscillations

Abstract

Neuronal oscillatory activity is generated by a combination of ionic currents, including at least one inward regenerative current that brings the cell towards depolarized voltages and one outward current that repolarizes the cell. Such currents have traditionally been assumed to require voltage-dependence. Here we test the hypothesis that the voltage dependence of the regenerative inward current is not necessary for generating oscillations. Instead, a current I_NL that is linear in the biological voltage range and has negative conductance is sufficient to produce regenerative activity. The current I_NL can be considered a linear approximation to the negative-conductance region of the current-voltage relationship of a regenerative inward current. Using a simple conductance-based model, we show that I_NL, in conjunction with a voltage-gated, noninactivating outward current, can generate oscillatory activity. We use phase-plane and bifurcation analyses to uncover a rich variety of behaviors as the conductance of I_NL is varied, and show that oscillations emerge as a result of destabilization of the resting state of the model neuron. The model shows the need for well-defined relationships between the inward and outward current conductances, as well as their reversal potentials, in order to produce stable oscillatory activity. Our analysis predicts that a hyperpolarization-activated inward current can play a role in stabilizing oscillatory activity by preventing swings to very negative voltages, which is consistent with what is recorded in biological neurons in general. We confirm this prediction of the model experimentally in neurons from the crab stomatogastric ganglion.

1. Introduction

We are interested in understanding the mechanisms of generation of slow oscillations underlying neuronal bursting. Regenerative inward currents, typically Ca⁺⁺ or Na⁺ currents (Jahnsen and Llinas 1984; Kramer and Zucker 1985; McCormick and Huguenard 1992; Dunmyre et al. 2011; Del Negro et al. 2002), are essential for the generation of neuronal oscillations, from spiking to bursting. They are often targets of modulation by neuroactive substances (Tryba et al. 2006; Cantrell and Catterall 2001) as well as by activity (Swensen and Bean 2005; Desai et al. 1999; Turrigiano et al. 1994; Haedo and Golowasch 2006). For example, in the crab stomatogastric nervous system (STNS), a modulatory inward current (I_MI), believed to be important in generating slow bursting oscillations (Hooper and Marder 1987), is elicited by the release of several neuromodulators (Golowasch and Marder 1992b; Swensen and Marder 2000).

Regenerative inward currents typically have non-linear current-voltage (I-V) curves consisting of three distinct portions. At very low voltages, the curve is close to zero; at low to intermediate voltages, the curve has negative slope; while at higher voltages the curve has positive slope. The negative-slope portion tends to drive the neuron's voltage away from rest, while the other two regions prevent the voltage from becoming unbounded at either lower or higher voltages, respectively. Oscillations are created by inward currents driving the cell away from rest, subsequently shutting down at higher voltages, after which the outward currents bring the voltage down to lower levels. We refer to these inward currents as regenerative pacemaker currents. I_MI is one such current.

Independent of how the inward current is generated, the negative-slope conductance region of the currents primarily allows for continued depolarization of the membrane potential. In a previous experimental study we showed that a linear approximation of this negative conductance region, introduced in a single neuron, is sufficient to generate oscillatory activity in the pyloric network of the crab stomatogastric nervous system (Zhao et al. 2010). The main hypothesis that we examine in the current study is that an inward regenerative current creates the opportunity for oscillations to exist primarily by destabilizing the resting potential of a cell, thereby forcing the membrane potential away from rest.

Linear non-synaptic ionic currents (i.e., leak currents) have been previously shown to be involved in the generation of oscillatory activity (Blethyn et al. 2006; Cymbalyuk et al. 2002; Koizumi and Smith 2008; Lu and Feng 2012; Pang et al. 2009). However, they do so principally by modifying the general excitability of the neurons expressing them (Brickley et al. 2007; Lu and Feng 2012; Rekling et al. 2000) rather than through an independent pacemaker mechanism. In these examples, a reduced leak current typically increases the excitability of the cell, allowing a different current or a synaptic input to drive the membrane potential into a region where a different regenerative (pacemaker) current is activated. In contrast, here we hypothesize that a linear current with negative conductance can act as a regenerative pacemaker current.

Our study has two goals. First, through modeling and experiments, we show that a current that has a negative conductance, but is linear in the biological range, is sufficient to produce the regenerative effect of a pacemaker current. As such, non-linearity in the biological range is not necessary for this purpose. We characterize the minimum set of requirements to obtain stable slow-wave oscillations. We do this by exploring the properties of a simple model consisting of a potassium (recovery) current (I_K) and a current with negative conductance that is linear in the biological range (I_NL). Although I_NL is not a biological current, we show that it serves as a proxy for a nonlinear inward regenerative current that can function as a pacemaker current.

Second, we use I_NL as a modeling and experimental tool to reveal the role of ionic currents other than regenerative ones in shaping oscillations. In particular, using the I_NL protocol, we explore how the addition of an inward hyperpolarization activated current (I_h) may provide oscillation robustness. In fact, we show that in some cases I_h is necessary for the existence of stable oscillations. This minimal model makes several experimental predictions, some of which are verified using experimental data from the crab pyloric dilator (PD) neuron in which I_NL is introduced using the dynamic clamp technique.

2. Methods

2.1. Model

The equations that describe the full negative linear conductance model involve four currents associated with the negative linear conductance, leak, potassium and h currents:

$$\begin{array}{cc}\hfill v^{\prime }=& -{\tilde{g}}_{NL}[v-{\tilde{E}}_{NL}]-g_L[v-E_L]-g_{K}w[v-E_K]-g_{h}h[v-E_h]\hfill \\ \hfill w^{\prime }=& \frac{w_{\infty }\left(v\right)-w}{{\tau }_K\left(v\right)}\hfill \\ \hfill h^{\prime }=& \frac{h_{\infty }\left(v\right)-h}{{\tau }_h\left(v\right)}\hfill \end{array}$$ (1)

The parameters g̃_NL , g_L, g_K, and g_h are the maximal conductances and Ẽ_NL , E_L, E_K, and E_h are the reversal potentials for these currents (see the Appendix for specific equations and parameter values). The value g̃_NL is negative, while the other conductance values are positive. The terms w_∞(v) and h_∞(v) are the steady-state activation functions for the potassium and h currents. By letting g_NL = g̃_NL + g_L, and E_NL = [g̃_L Ẽ_NL + g_L E_L] / [g̃_NL + g_L], we can simplify (1) to

$$\begin{array}{cc}\hfill v^{\prime }=& -g_{NL}[v-E_{NL}]-g_{K}w[v-E_K]-g_{h}h[v-E_h]\hfill \\ \hfill w^{\prime }=& \frac{w_{\infty }\left(v\right)-w}{{\tau }_K\left(v\right)}\hfill \\ \hfill h^{\prime }=& \frac{h_{\infty }\left(v\right)-h}{{\tau }_h\left(v\right)}\hfill \end{array}$$ (2)

Equation (2) makes sense as a model for the negative linear conductance current only if g_NL < 0. Thus, we require that −g̃ _NL > g_L. As discussed below, the introduction of g_NL leads, in some cases, to a destabilization of the rest state that drives the cell to extremely hyperpolarized levels. To avoid this possibility, and to restrict our analysis to a biologically relevant voltage range, we define I_NL = g_NL[v − E_NL]Heav(v − v_cutoff ) where the Heaviside function Heav(x) is a cutoff function that equals 1 when x ≥ 0, and is 0 otherwise. This leads to a corresponding set of equations:

$$\begin{array}{cc}\hfill v^{\prime }=& -g_{NL}[v-E_{NL}]Heav(v-v_{cutoff})-g_{K}w[v-E_K]-g_{h}h[v-E_h]\hfill \\ \hfill w^{\prime }=& \frac{w_{\infty }\left(v\right)-w}{{\tau }_K\left(v\right)}\hfill \\ \hfill h^{\prime }=& \frac{h_{\infty }\left(v\right)-h}{{\tau }_h\left(v\right)}.\hfill \end{array}$$ (3)

In this study, we analyze mainly the case when v_cutoff = E_NL, which restricts our analysis to a biologically relevant voltage range. The special case v_cutoff = -∞ makes I_NL strictly linear with voltage and g_NL[v − E_NL]Heav(v − v_cutoff) reduces to g_NL [v − E_NL].

For much of the analysis, we will simplify I_h to allow us to consider a two-dimensional model. This is achieved by letting h ≡ h_∞(v). We realize that the h current need not be fast; the main purpose in making it instantaneous in this context is to focus, in a simplified setting, on the effects I_NL. We refer to the instantaneous I_h as I_h-fast and the original I_h in equation (3) as I_h-slow. Thus, the simplified equations for the two-dimensional model are

$$\begin{array}{cc}\hfill v^{\prime }=& -g_{NL}[v-E_{NL}]Heav(v-v_{cut-off})-{g_K}^w[v-E_K]-g_h{h}_{\infty }\left(v\right)[v-E_h)\hfill \\ \hfill w^{\prime }=& \frac{w_{\infty }\left(v\right)-w}{{\tau }_K\left(v\right)}.\hfill \end{array}$$ (4)

The nullclines of (4) are found by setting the right-hand side of the equations to 0. This yields the v-nullcline explicitly given by

$$w=\frac{-g_{NL}[v-E_{NL}]Heav(v-v_{cutoff})-g_h{h}_{\infty }\left(v\right)[v-E_h]}{g_K[v-E_K]}$$ (5)

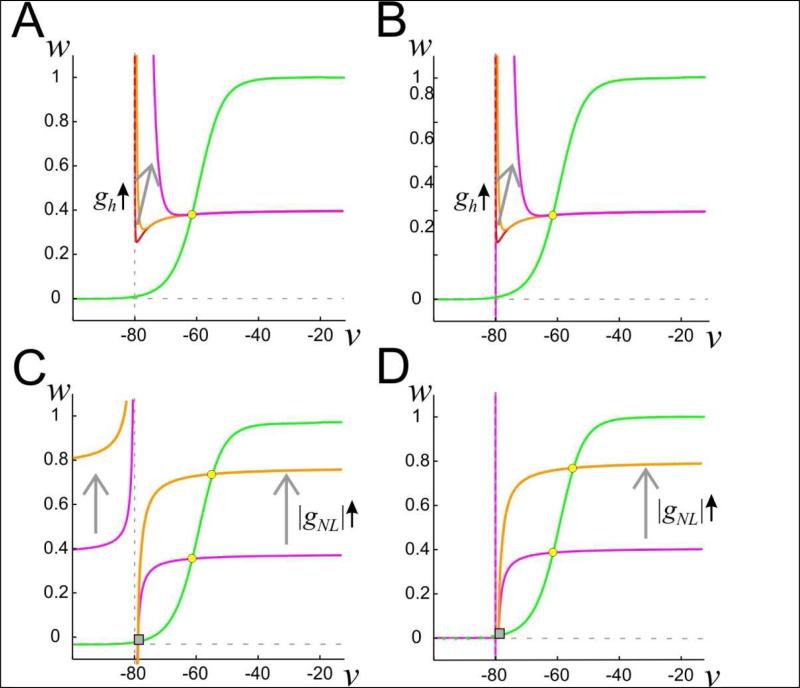
and the w-nullcline given by w = w_∞(v) (Fig. 1). Here we have taken the case E_NL > E_K. For the case in which v_cutoff = -∞ (Fig. 1A), the v-nullcline has two pieces that are separated by the vertical asymptote v = E_K. For the region v > E_K, the v-nullcline has a stable, decreasing, left branch, if g_h is large enough. By stable, we mean that trajectories that start in a neighborhood of this left branch tend to transiently approach the nullcline and remain nearby it until they reach a neighborhood of the local minimum. Depending on other parameters, this nullcline can have an unstable middle branch (Fig. 1A, red and gold), as well as a branch that asymptotes to |g_NL/g_K| as v tends to ∞. By unstable, we mean that nearby trajectories quickly leave a neighborhood of the middle branch. Increases in g_h move the v-nullcline up in the v-w phase space. If g_h is large enough, the v-nullcline is monotone decreasing for v > E_K (Fig. 1A, magenta). For the case in which v_cutoff = E_NL, the v-nullcline has a stable left branch in the region v > E_K if g_h > 0, independent of its size (Fig 1B).

Figure 1. Phase plane structure of the linear negative conductance-based neuron model.

A. The nullclines of the model described by equation (5) with v_cutoff = -∞. The w-nullcline is in green; the v-nullcline in red, gold and magenta (overlapping for large v). Increasing g_h results in a shift up in the v-nullcline for the region v > E_K as indicated by the arrow. B. The corresponding set of nullclines for the v_cutoff = E_NL case. C. The nullclines of the model described by equation (6) and v_cutoff = -∞. The w-nullcline is in green, the v-nullcline in magenta and gold; g_h = 0. Increasing g_NL results in a shift in the v-nullcline as indicated by the arrows. E_K = -80 mV, E_NL = -79 mV. D. The corresponding set of nullclines described by equation (6) for the v_cutoff = E_NL case, and g_h = 0. The w-nullcline is shown as dashed for v < E_K to visualize the horizontal vnullcline at w = 0 in this region. However, in our analysis only the nullclines for v > E_K are relevant.

The first part of the analysis will focus on just the effects of I_K and I_NL. In this case, we set g_h = 0 in equation (4), which reduces it to

$$\begin{array}{cc}\hfill v^{\prime }=& -g_{NL}[v-E_{NL}]Heav(v-v_{cutoff})-g_{K}w[v-E_K]\hfill \\ \hfill w^{\prime }=& \frac{w_{\infty }\left(v\right)-w}{{\tau }_K\left(v\right)}.\hfill \end{array}$$ (6)

Now the v-nullcline is given by

$$w=\frac{-g_{NL}[v-E_{NL}]Heav(v-v_{cutoff})}{g_K[v-E_K]}.$$ (7)

Figure 1C shows the resulting nullclines with v_cutoff = -∞. For v > E_K, the v-nullcline is a monotone increasing, concave down curve that asymptotes to |g_NL/g_K| as v tends to ∞ and towards -∞ as v → E⁺_K (the superscript + denotes limit from above). Increases in |g_NL| move the nullcline up in the phase space. For v < E_K, the nullcline is increasing and concave up as shown. Finally, Figure 1D shows the nullclines for the equations with v_cutoff = E_NL. Note that for E_K < v <E_NL, the v-nullcline is just the line segment w = 0. This produces a stable fixed point at v = E_K, w = w_∞(E_K), since I_NL = 0 there. The v-nullcline for v < E_K is not relevant as the voltage will never reach these values.

2.2. Experimental

Experiments were carried out on identified neurons from the stomatogastric ganglion (STG) of male crabs (Cancer borealis). Animals were obtained from local markets in Newark (NJ) and maintained in seawater tanks at 7–10°C. The entire stomatogastric nervous system, including the anterior commissural and esophageal ganglia, STG and connecting and motor nerves from a crab were dissected out as previously described (Selverston et al. 1976), pinned down on a Sylgard-coated Petri dish, and the STG desheathed to allow electrode penetration of the cell bodies. All preparations were continuously superfused with cooled (10 –13°C) physiological Cancer saline. Saline composition was (in mM) 11 KCl, 440 NaCl, 13 CaCl₂, 26 MgCl₂, 11.2 Trizma base, 5.1 maleic acid, pH 7.4 –7.5.

Extracellular recordings were performed with pin electrodes placed in petroleum jelly wells built around individual nerves and recorded differentially relative to a distant electrode using an A-M Systems 1700 differential amplifier (A-M Systems). Intracellular recordings and current injections were performed with Axoclamp 2B amplifiers (Molecular Devices) using double impalements with 0.6 M K₂SO₄ + 20 mM KCl-filled borosilicate electrodes. Low resistance electrodes (15-20 MΩ ) were used for current injection, and high resistance electrodes (30-40 MΩ ) for voltage measurement. Individual neurons were identified by matching intracellularly recorded action potentials to action potentials on identified motor nerves that innervate known muscles (Selverston et al. 1976).

The crab pyloric network was isolated from all neuromodulatory input by decentralization (Zhao et al. 2010), resulting in quiescent preparations and the pyloric dilator (PD) neurons were recorded. When required, all action potentials (and therefore all modulatory inputs) were removed by bath application of 10^-7M tetrodotoxin (TTX; Biotium). Current injection was performed using the dynamic clamp technique to emulate the activation of I_NL and I_h with a variety of values of the two current's parameters (Sharp et al. 1993; Zhao et al. 2010). For this we used software developed in our laboratories (available for download at http://stg.rutgers.edu/software) in the LabWindows/CVI software environment (National Instruments) on a Windows platform, and using a NI PCI-6070-E board (National Instruments, Austin, TX, USA). Data acquisition was performed using a Digidata 1332A data acquisition board and the pClamp 10.3 software (Molecular Devices).

Injections of current in dynamic clamp were performed at 10 kHz and voltage recordings at 5 kHz. The following equations were used:

$$\begin{array}{cc}\hfill & I_{NL}=g_{NL}[v-E_{NL}]\hfill \\ \hfill & I_{NL-cut}=g_{NL}[v-E_{NL}]Heav(v-E_{NL})\hfill \\ \hfill & I_{MI}=g_{MI}{m}_{\infty }\left(v\right)[v-E_{MI}],m_{\infty }\left(v\right)=\frac{1}{1+e^{-[v+10]∕6}}\hfill \\ \hfill & I_h=g_h{h}_{\infty }\left(v\right)[v-E_h],h_{\infty }\left(v\right)=\frac{1}{1+e^{[v+65]∕10}}\hfill \end{array}$$

The parameter values used were E_NL = −62 to −58 mV, E_MI = 0 mV, E_h = −20 mV, g_NL = -0.04 to -0.2 S, g_MI = 0.08 to 0.2 μS, g_h = 0.1 μS.

3. Results

We will examine, in detail, a minimal model consisting of the biological current I_K and the non-biological current I_NL. We show that as the negative leak conductance g_NL is increased in absolute value, various bifurcations occur that give rise to, and subsequently destroy, oscillations. To obtain oscillations, we show that the negative leak current need only be linear in the biological range of voltages. The insight gained from the bifurcation analysis allows us to then explore a second major goal of this paper, namely to identify the role that I_h has in stabilizing neuronal oscillations. In particular, we will show that the existence of I_h allows the cell to display oscillations over a wider range of parameters and increases the size of the basin of attraction of periodic solutions that already exist. Moreover, we will show that there are circumstances where I_h is necessary to produce oscillations. Using the fully linear version of I_NL, we will show how slow buildup of I_h can explain a curious experimental finding associated with hyperpolarization dips.

Negative linear conductance induces oscillations in a biological system

Figure 2 shows that oscillations in a biological system can result purely from a linear current with negative conductance. Isolated PD neurons were recorded in TTX (initial black trace in Fig. 2B). When an instantaneous regenerative current I_MI (Golowasch and Marder 1992b; Swensen and Marder 2000) with an I-V curve as shown in Figure 2A (red) was injected, oscillatory activity resulted (Fig. 2B, red). Very similar activity was activated when only a linear current, with negative conductance that matched the region of negative conductance of I_MI (Fig. 2A, I_NL with v_cutoff = -∞ (blue), v_cutoff = E_K (aqua)) was introduced in the same cell (Fig. 2B, blue; the two cutoff values produce the same output thus aqua not shown). These results build on previous experiments described by Zhao et al (2010) who showed that the expression of I_NL in the PD neuron in the decentralized pyloric network resulted in the recovery of the full pyloric rhythm. The current experiments show that oscillations can be generated by I_NL in an isolated PD neuron and in the absence of action potentials. Thus, it appears that the activation of oscillatory activity does not require nonlinear regenerative currents.

Figure 2. Linear negative conductance current elicits oscillations in PD neurons.

A. I-V curve for the modulator-activated inward current I_MI (red), I_NL (blue/aqua) which was matched in slope (at the inflection point) to the negative conductance portion of I_MI. The two I_NL curves have v_cutoff = -∞ (solid blue) or v_cutoff = E_NL (dotted aqua). B. PD neuron membrane potential with added I_MI (red), I_NL (blue; the two v_cutoff values produce identical results), showing onset of very similar oscillatory activity immediately after onset of dynamic clamp current (gray traces). Horizontal arrows show –58 mV (top), and 0 nA (bottom).

Oscillations resulting from I_NL and I_K

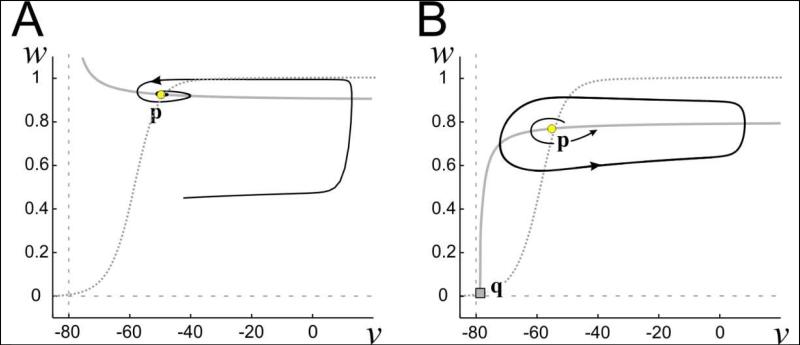
We begin by showing that in certain parameter regimes, I_NL and I_K can together produce stable oscillations. Consider equation (6) in which I_h is not present. When E_K > E_NL, the v-nullcline is a concave-up decreasing curve on the region v > E_K that tends to |g_NL/g_K| as v → (Fig. 3A). Its intersection with the w-nullcline yields a single fixed point p (yellow circle) that is globally attracting. However, when E_NL > E_K, the v-nullcline is instead a concave-down monotone-increasing curve in the region v > E_NL (Fig. 3B). It now intersects the w- nullcline at a second point q that is an unstable saddle point (gray square). Depending on the value of g_NL, a third intersection near w = 1 can also exist (shown and discussed later). In this case, the fixed point p is either unstable or no longer globally attracting. This is the situation on which we will focus, as it is the one that provides the opportunity for oscillations.

Figure 3. Phase plane of the simplified linear negative conductance current model.

Dotted trace is the w-nullcline. Vertical dashed gray line is v=E_K. Continuous gray trace is the v-nullcline. v_cutoff = E_NL. Saddle point q is located at the square, while the circle corresponds to the (spiral) fixed point p. A. E_NL<E_K yields a stable spiral point p. B. E_NL > E_K can yield an unstable spiral point p, which is surrounded by a stable limit cycle. v in mV.

Note that in the region E_K ≤ v < E_NL, the v-nullcline is simply the line segment w = 0, which does not intersect the w-nullcline (Fig. 1D). But at v = E_K, w = w_∞(E_K), there is a stable fixed point, independent of the value of g_NL, because I_NL = 0 there. For clarity, we do not show the v-nullcline in the region v ≤ E_K in Fig. 3.

Consider the linearization of (6) about any of the fixed points, denoted as (v*, w*). The eigenvalues of the corresponding Jacobian matrix satisfy

$$\lambda =\frac{1}{2}\left[F_v+G_w\pm \sqrt{{(F_v-G_w)}^2+4F_w{G}_v}\right]$$ (8)

where F_v = –g_Kw* – g_NL, F_w = –g_K(v* – E_K), G_v = δ[(w_∞(v) – w) / τ_K(v)] / δv, evaluated at (v* , w*), and G_w = −1/τ_K(v*). The lower fixed point q occurs at w*_q ≈ 0 , G_v ≈ 0. The eigenvalues are therefore well approximated by F_v = –g_NL > 0 and G_w = –τ(v*_q) < 0. Thus, the fixed point q is a saddle. The stable and unstable manifolds of this saddle will play an important role in determining the existence and stability of various solutions. The upper fixed point p = (v*_p, w*_p) can be stable or unstable. For small values of |g_NL|, p is always asymptotically stable. As |g_NL| increases, the v-nullcline moves up in the phase space causing p to also move up and w*_p to increase. Note that the v-nulllcline asymptotes to -g_NL/g_K as v → ∞. The w-nullcline asymptotes to 1; thus, when - g_NL=g_K, a third fixed point, denoted r, is created at v = ∞. As |g_NL| increases r moves in from ∞ and eventually collides with p at a bifurcation point as describe below.

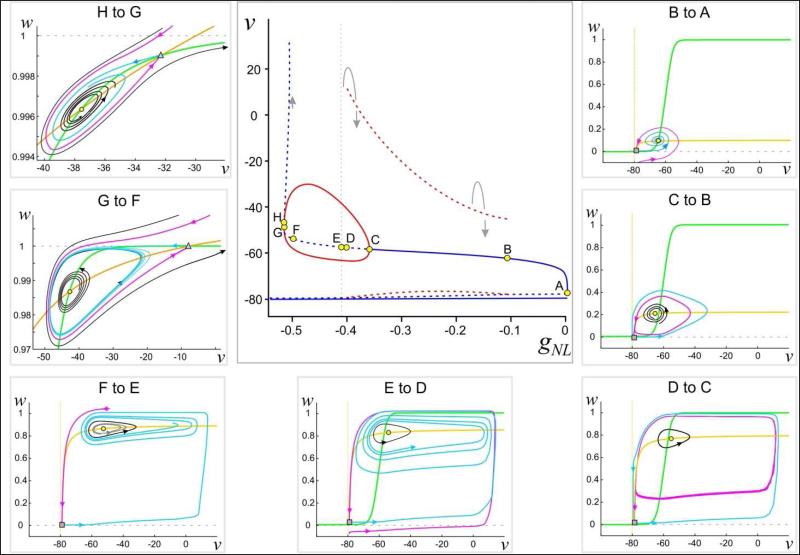
Certain bifurcations may occur as |g_NL| increases, as depicted in Figures 4 and 5 (for different parameter sets). Figures 4 and 5A show bifurcations that lead to periodic solutions. The types of bifurcations in each case are different and lead to distinct behaviors in the system given by equation (6). Figure 5B, by contrast, shows the case where there are no stable oscillations, instead just a stable fixed point. Common to all three figures is a bifurcation that occurs for large values of |g_NL| where p and r collide (H in Fig. 4, I in Fig. 5A, F in Fig. 5B).

Figure 4. Bifurcation diagrams for system (6) and associated phase planes.

Center: Bifurcation diagram with g_NL as parameter. Solid (dashed) lines/curves indicate stable (unstable) fixed points (blue)/periodic orbits (red). Note that the fixed point is stable between H and G. Points marked by letters indicate local or global bifurcation points. Small arrows show the direction of the flow. Horizontal solid line is the fixed point at E_K = −80 mV. The dashed horizontal curve above that is the position of the saddle point Surround: Phase plane diagrams in different regions of the bifurcation diagram (as marked in each panel). The v-nullcline is shown in yellow and the w-nullcline in green. Solid curves indicate trajectories with the direction of the flow shown (closed curves are periodic orbits). The two fixed points p (yellow circle) and q (gray square) as in Fig. 3 are marked. Note that the fixed point p is stable in the region H to G. Magenta and cyan curves respectively indicate the relevant branches of the stable and unstable manifolds of the saddle point q (square in panels showing points from F to A) or r (triangle in panels G to F and H to G). v in mV, g_NL in μS.

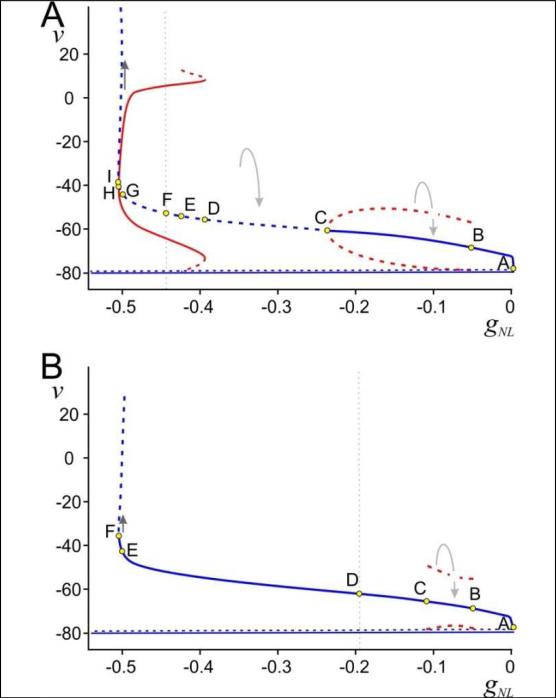
Figure 5. Alternative bifurcation diagrams for system (6).

Bifurcation diagrams with g_NL as parameter. Solid (dashed) lines/curves indicate stable (unstable) fixed points (blue)/periodic orbits (red). Points marked by letters indicate local or global bifurcation points. Small arrows show the direction of the flow. Horizontal solid line is E_K = −80 mV. The dashed horizontal curve above that is the position of the saddle point. A: Bifurcation diagram with τ₁ = 80 ms and k₁ = 4 mV. Note that the fixed point is stable in the region I to H.B: Bifurcation diagram with τ₁ = 60 ms and k₁ = 4 mV. v in mV, g_NL in μS.

To understand the different activity patterns that can arise with different values of g_NL, we will describe Figure 4 in more detail. We have labeled eight points A-H corresponding to different values of g_NL (increasing |g_NL|) at which the structure of the phase space changes. We will describe the bifurcation diagram in this order.

The point A corresponds to g_NL = 0 where a single fixed point exists at v = E_K. As |g_NL| is increased, on the interval (B, A), two new fixed points emerge, a saddle point q near v = E_K and the point p. Note that when v < E_NL , I_NL = 0, therefore v = E_K remains a stable fixed point (this is true for all values of g_NL). On the (B, A) interval, p is asymptotically stable, but has a limited basin of attraction in the phase space. The unstable manifold (cyan) of q with v > E_K approaches p in forward time, while the stable manifold (magenta) of q encircles p as shown in the inset. The stable manifold separates trajectories that are attracted to p versus v = E_K. The stable and unstable manifolds of q meet at a homoclinic bifurcation point B, creating an unstable periodic orbit (dashed red curves) that surrounds p. As |g_NL| is increased, this homoclinic orbit gives rise to an unstable periodic orbit (dashed red curves in bifurcation diagram). On the interval (C, B), the stable and unstable manifolds of q switch their orientation relative to those on the interval (B, A). The stable manifold of q now approaches the unstable periodic orbit in backward time, while the unstable manifold of q asymptotes to v = E_K.

At the point C, p loses stability through a supercritical Hopf bifurcation. The new asymptotically stable periodic orbit (solid red curves in bifurcation diagram) that is created by this bifurcation lies inside the previously created unstable orbit. In (D, C), the stable periodic solution is not globally attracting on the set v > E_K: there still remain trajectories that tend to v = E_K. At the value D, another homoclinic bifurcation occurs that destroys the unstable periodic solution. The orientation of the stable and unstable manifolds of q again switch such that the unstable manifold in forward time approaches the asymptotically stable periodic orbit. On the interval (E, D), there still remain trajectories that tend to v = E_K as the stable manifold of q lies below the line w = 1. At the point E (vertical dashed gray line in the bifurcation diagram), the stable manifold of q asymptotes to w = 1 in backward time. The stable manifold of q now blocks trajectories with initial conditions lying to the right and below it (roughly v > E_NL and w < 1) from converging to v = E_K. The asymptotically stable periodic orbit now attracts every initial condition on this set. This remains the case on the interval (F, E).

At the point F, -g_NL = g_K and as v → ∞, the v-nullcline asymptotes to w = 1. This creates a new fixed point r at +∞ that is a saddle point. As |g_NL| increases, the point r (indicated by the triangle in the G to F and H to G panels of Fig. 4) moves in from +∞. Along the way, the unstable manifold of q intersects the stable manifold of r making a heteroclinic connection (not demarcated in the bifurcation diagram). For (G, F), the asymptotically stable periodic orbit continues to exist. However, now there are initial conditions that lie on trajectories that escape to +∞ (black curve). As |g_NL| is increased further, the periodic orbit finally disappears through a super-critical Hopf bifurcation at G. The fixed point p now becomes a stable spiral on the interval (H, G). As |g_NL| is increased through this interval, the two fixed points p and r move together and collide at H. The point H therefore appears to be a saddle-spiral bifurcation. Such saddle-spiral bifurcations have been shown to exist in the category of co-dimension two Bogdonov-Takens bifurcations (Kuznetsov 2004). A more detailed analysis, beyond the scope of the current discussion, is needed to resolve the exact nature of this bifurcation.

Figure 5A shows a bifurcation structure for a set of parameters different from those in Figure 4. (The time constant τ₁ associated with I_K is changed from 60 to 80 ms and the parameter k₁ associated with the slope of its half-activation from 2 to 4 mV. The effect of these changes is to weaken the effect of I_K.) Here we have labeled 9 points A - I. Points A, B and C are the same as in Figure 4 except that, at C, the Hopf bifurcation is subcritical with the unstable branch of periodic orbits bending back towards smaller values of |g_NL|. Further, on the interval (D, C) all trajectories, except for the stable manifold of q, tend to v = E_K. At D, a saddle node of periodic orbits occurs creating a stable periodic orbit surrounded by an unstable one. At E, a homoclinic bifurcation corresponding to the intersection of the stable and unstable manifolds of q occurs destroying the unstable periodic orbit. The remaining subintervals of (I, E) have the same type of bifurcation structure as the subintervals (H, D) in Figure 4.

Finally, Figure 5B shows that increasing |g_NL| does not necessarily lead to stable oscillations. (Here τ₁ = 60 ms and k₁ = 4 mV). For this set of parameters, p never loses stability. Points B and C are homoclinic bifurcation points of the manifolds of the fixed point q, between which lies an unstable periodic orbit. At D, convergence to v = E_K becomes impossible and, at E, escape to +∞ becomes possible.

We can use the eigenvalues at the linearization given by equation (8) to explain how changes in parameters give rise to different bifurcations of p. In Figures 4 and 5A, p undergoes a Hopf bifurcation as |g_NL| increases. A necessary condition for this type of bifurcation is that the real part of the eigenvalue Reλ=1/2(F_v + G_w) must pass through zero as g_NL changes. From (8),

$$\begin{array}{cc}\hfill \mathrm{Re}\lambda =& \frac{1}{2}\left[-g_k{w}_p^{\ast }-g_{NL}-\frac{1}{{\tau }_K\left(v_p^{\ast }\right)}\right]\hfill \\ \hfill \approx & \frac{1}{2}\left[-g_k{w}_p^{\ast }-g_{NL}-\frac{1}{{\tau }_1}\right]\hfill \end{array}$$ (9)

The second line follows since τ_K(v*_p) is basically constant near p. Note, however, that the value of w*_p depends on the location of the fixed point p and therefore on g_NL, as seen from Equation (7) and Fig. 1. At the point labeled C in Figures 4 and 5A, a Hopf bifurcation occurs, i.e., the right-hand side of (9) is 0. While in Figure 5B, p remains asymptotically stable, i.e., the right-hand side of (9) remains negative for all |g_NL|. The difference between Figures 4 and 5B is simply a change in the parameter k₁ from 2 to 4, which makes the w-nullcline less steep. This, in turn, causes an increase in w* as the fixed point shifts up and to the right in the phase plane. As a result, the right-hand side of (9) decreases, thus keeping it negative. Similarly, the difference between Figures 5A and 5B is a change in τ₁ from 80 to 60. Again, a smaller τ₁ decreases the right-hand side of (9), also keeping it negative. Thus, the eigenvalues in both of these situations remain in the negative half-plane and p remains asymptotically stable.

The above analysis allows us to make several observations. First, in both Figures 4 and 5, there are parameter regimes for which trajectories converge to v = E_K. Thus, the existence of a strong enough depolarizing current is not by itself sufficient to produce oscillations. A second observation from the model is that the voltage under the negative-conductance leak protocol can escape to +∞, which can occur when |g_NL |> g_K. Note that, even when |g_NL |> g_K , stable oscillations can exist (see G to F region in Fig. 4). However, if |_NL|> I_K for all v values (to the left of H in Fig. 4), then the destabilizing drive of the negative-conductance leak current exceeds the stabilizing effect of the potassium current and all orbits (above E_K) escape to +∞.

The role of I_h in stabilizing oscillations

The addition of the hyperpolarization-activated current I_h qualitatively changes the nature of solutions. Indeed, it largely wipes out the interesting bifurcation structure of the previous section and leads typically to stable oscillations or convergence to a stable fixed point. To better understand the roles of I_K and I_h, consider now the simplified model given by equation (4) with v_cutoff = E_NL where I_h is instantaneous, h ≡ h_∞(v), the I_h-fast case (Fig. 6).

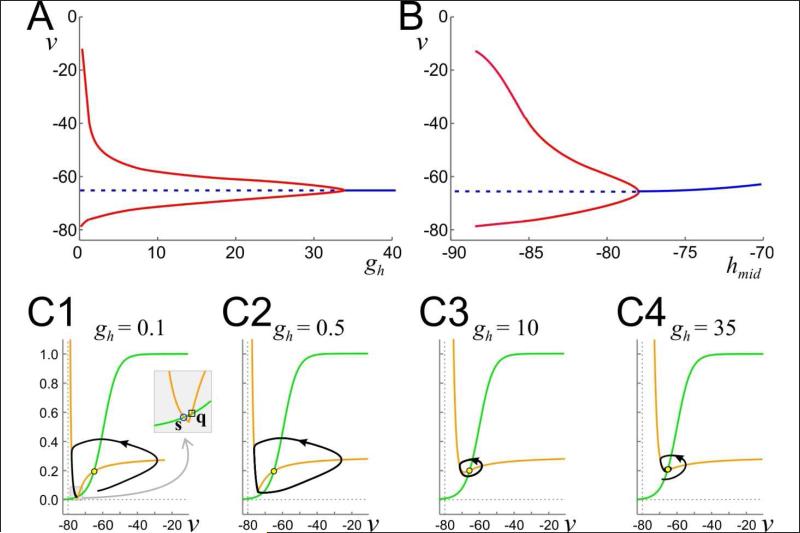
Figure 6. Bifurcation diagrams and phase plane behaviors for system (4) and v_cutoff = E_NL.

A: Bifurcation diagram with g_h as parameter. Solid (dashed) lines/curves indicate stable (unstable) fixed points (blue)/periodic orbits (red). B: Bifurcation diagram with h_mid as parameter and g_h = 1 μS. C1-C4: Phase planes and limit cycles for various values of g_h as noted. v in mV, g_h in μS. Inset in C1 highlights the fixed points q and s.

We start with parameter values taken from Figure 5A in the regime (C, B) where trajectories tend to v = E_K or to p. We fix g_NL = -0.15 μS and increased E_NL = −75mV to better illustrate the results. For g_h > 0, the phase plane changes qualitatively. In particular, for v > E_K, the v-nullcline now has a decreasing left branch, a local minimum and an increasing right branch that asymptotes to |g_NL/g_K|. For fixed values of w, the left branch is attracting. Note that there is a large change in the v-nullcline on the region E_K < v < E_NL. Recall for g_h = 0, this was just the line segment w = 0 (Fig. 1D). In contrast, for g_h > 0, the v-nullcline is a decreasing left branch (Fig.6C). When g_h is small, this left branch intersects the w-nullcline in the region E_K < v < E_NL creating a stable fixed point denoted s (Fig. 6C1). As g_h is increased, the v-nullcline moves up in the phase space and this newly created fixed point collides with q at a saddle-node on an invariant circle bifurcation yielding the first requirement for oscillations. It is quite straightforward to derive the condition on g_h where this occurs. The saddle-node point occurs when the local minimum of the v-nullcline intersects the w-nullcline. Because v_cutoff = E_NL, the v- nullcline must have its local minimum at v = E_NL (see equation (5)). The w value of the vnullcline at v = E_NL is derived from equation (5) while that for the w-nullcline is simply w_∞ (E_NL). Setting the w values of both equal to one another yields the condition

$$g_h{h}_{\infty }\left(E_{NL}\right)=\frac{g_K(E_{NL}-E_K)w_{\infty }\left(E_{NL}\right)}{E_h-E_{NL}}$$ (10)

Let g_min-h denote the right hand side of equation (10). Except for the value of E_h, g_min-h is determined by parameters that are independent of I_h. Moreover, equation (10) is independent of g_NL. Thus the existence of the saddle-node bifurcation can be controlled by the left hand side of (10) which is dependent only on parameters associated with I_h. In particular if gh_∞(E_NL) < g_min-h, then the v-nullcline intersects the w-nullcline twice in a neighborhood of w = 0 and if gh_∞ (E_NL) > g_min-h then it does not. Note that g_h and gh and h_∞ (E_NL) can be modulated separately. The former is the maximal conductance of I_h, while the latter is the fraction of I_h activation at E_NL and is strongly dependent on h_mid, the half-activation value.

A second requirement for the existence of oscillations is the instability of p. The location of p can be estimated as the solution v* of w_∞(v*) = –g_NL / g_K, because h_∞(v) is small in a neighborhood of the intersection and E_NL – E_K is also small. Thus, the location of p is largely independent of g_h, but its stability will depend on local changes in the slope of the v-nullcline which do depend on g_h. Keeping h_∞(E_NL) = −85 mV fixed, Figure 6A shows a bifurcation diagram of how the stability of p changes as a function of g_h. At low values, for gh_∞ (E_NL) < g_min-h , solutions converge to the fixed point s (Fig. 6C1). Oscillations arise when g_h increases so that gh_∞ (E_NL) > g_min-h and continue to exist for intermediate values (Fig. 6C2-C3). At a larger value of g_h , p undergoes a supercritical Hopf bifurcation that destroys oscillations. For sufficiently large values of g_h, the v-nullcline becomes monotone decreasing, stabilizing the spiral fixed point p (Fig. 6C4).

Because of the terms on the left hand side of equation (10), a qualitatively similar set of bifurcations can be obtained by changing h_mid, the half-activation point of the h current, instead of g_h, leading to a limited range of h_mid values over which oscillations are possible (Fig. 6B). At more negative values of h_mid, oscillatory activity ends because the v-nullcline intersects the wnullcline because h_∞(E_NL) becomes too small and the stable fixed point s reappears. Note that h_∞(E_NL) is a monotone-increasing function of h_mid. Thus the model makes a prediction that, for oscillations to exist, the h-current half-activation has to sit at relatively hyperpolarized levels. On the other hand, if h_mid is too large, then I_h never deactivates and the fixed point p is stable. Furthermore, by analyzing equation (10) it can be seen that, h_∞(E_NL) and g_h are inversely related; increasing one decreases the other. Thus if h_mid is relatively large causing h_∞(E_NL) to be relatively large, then a smaller value of g_h is required for oscillatory activity.

As seen in the previous section, the existence of I_h is not necessary to produce oscillations. Indeed, if the model produces stable oscillations when g_h = 0 then those oscillations will continue to exist, qualitatively unchanged, when g_h > 0 but not too large. However, the basin of attraction for those solutions may become larger as the existence of a large enough I_h prevents convergence to either E_K or to s. As a result, stable oscillations become more robust to noise and perturbations. For example, a perturbation introduced to the model consisting of just I_NL and I_K can cause the trajectory to converge to E_K. But when I_h is present, the same perturbation will not. Figure 7 shows modeling and experimental verifications of this. In panel A, g_h = 0 a stable periodic orbit (black trajectory) is perturbed with the injection of an inhibitory external current pulse. The trajectory (red curve) leaves a neighborhood of the stable orbit, dips below E_NL and E_K, after which the external current is removed. The trajectory (gray curve) now is attracted to the stable fixed point at E_K. In contrast, in panel B where g_h > 0, the same type of perturbation prevents the voltage from dipping below E_NL. Thus, after the external current is removed, the solution (gray curve) is attracted back to the original periodic orbit. Panels B and D, show the corresponding experimental realization of such. Finally, if parameters are chosen as in Figure 5B where no oscillations exist over the range of g_NL values, the inclusion of I_h will not enable the model to produce oscillations (not shown).

Figure 7. Perturbation of the periodic orbit of system (4) without and with I_h.

A. When g_h = 0, perturbation (red) of the trajectory along a stable periodic orbit (black) by injecting a hyperpolarizing current pulse causes the trajectory (gray) to converge to the stable fixed point at v = E_K. B. When g_h > 0, the same type of perturbation cannot remove the trajectory from the basin of attraction of the periodic orbit and the ensuing trajectory (gray) is attracted back to the periodic orbit. C. and D. Corresponding voltage traces from a biological PD neuron with I_NL injected using dynamic clamp (and v_cutoff=E_NL). A -5 nA current pulse (red bar) shuts down the oscillations in the absence of I_h (C). In the presence of a dynamic-clamp injected instantaneous I_h, the same current pulse only provides a brief interruption in the oscillations (D).

A fully linear I_NL: setting v_cutoff to -∞

The destabilizing effects of the I_NL current can exist for voltages both above and below E_NL. This will occur if we take the cutoff value of I_NL in equation (6) (the value below which I_NL = 0) to lie below E_NL. For example, if we set v_cutoff = -∞, then I_NL = -g_NL[v - E_NL], and the current will drive the voltage away from E_NL both above and below this value. Consider equation (6) in such a case. The major change is that v = E_K is no longer a stable fixed point. Instead trajectories can now escape to -∞. We recomputed the bifurcation diagrams using the parameter values of Figs. 4 and 5 with v_cutoff = -∞. These diagrams would each show only one change: the stable fixed point at v=E_K (solid blue line) disappears. As an example of this, choose g_NL to have a value between points C and D in Fig. 5A with g_h = 0, and v_cutoff = -∞. Figure 1C shows the nullcline structure for this case. The v-nullcline has two distinct pieces that are separated by the vertical asymptote at v = E_K. There are no stable fixed points or periodic orbits in the phase plane and solutions spiral away from the unstable point p and escape to -∞ (not shown).

An interesting question is what effect the addition of I_h would have for these cases. When I_h-fast is added, the nullcline structure is as in Fig. 1A. Here, the globally destabilizing effect of I_NL is not strong enough to disrupt the stabilization provided by I_h. However, if we instead use a slower version of the h current (I_h-slow), where the activation occurs over a longer time, our model makes dips in voltage to extremely hyperpolarized values, as shown in the left panel of Fig. 8A, preceded by a sequence of oscillations that grow in size. The voltage, however, does not actually escape to -∞, but instead eventually repolarizes back and resumes the oscillatory pattern. It is reasonably straightforward to explain this result using our prior analysis. In the trace shown in Fig. 8A, the voltage begins at a large value (v > E_K) with I_h-slow non-zero and negative. Since the term -I_h-slow appears on the right-hand side of the voltage equation in (3), this current provides a positive contribution which causes the v-nullcline to have a stable left branch (as in Fig. 1A) and oscillations that accompany that nullcline structure. I_h-slow decays towards 0 during this time as the current deactivates. Once it has decayed enough, the left branch of the v-nullcline disappears and the nullcline structure changes to that of Fig. 1C for which escape to -∞ is possible. As the voltage makes its hyperpolarizing dip, I_h-slow activates, eventually pulling the voltage back up and the process repeats. In the right panel of Fig. 8A, I_h-slow was changed to a fast (instantaneous) current I_h-fast in the model and, as expected, the large hyperpolarizing dips disappear because now the nullcline structure of Fig. 1A persists.

Figure 8. Hyperpolarizing dips in system (3) and experimental verification.

A: The model described by equation (3) and v_cutoff = -∞ shows hyperpolarizing dips (left) to very negative membrane potentials when |g_NL| is large enough. Escape to -∞ is prevented by a slow I_h (τ_h1 = 20 ms). Making I_h fast (right) prevents the hyperpolarizing dips. B: The hyperpolarizing dips are observed in the biological PD neuron (left) when I_NL with a large enough conductance (-0.2 μS here) is added with dynamic clamp. As in the model, addition of a fast (instantaneous) I_h (0.1 μS here) via dynamic clamp prevents the hyperpolarizing dips and results in stable oscillations (right). Arrows indicate -60 mV for the voltages and 0 nA for I_dclamp.

Figure 8B shows an experimental validation of the model predictions. In the left panel, the voltage trace shows hyperpolarizing dips. This is done by injecting I_NL with dynamic clamp (see Experimental Methods). The biological PD neuron has a slow h current(Khorkova and Golowasch 2007) that activates by the hyperpolarizing dips that result from I_NL injection with a sufficiently large conductance value. Subsequent addition of I_h-fast with dynamic clamp removes the hyperpolarization dips. There are some differences between the model and experimental results, for example, the local extremes of the latter are much smoother. Despite these differences in the details, the model captures the mechanisms that underlie this phenomenon.

4. Discussion

In this paper we examine whether neuronal regenerative inward currents need to be voltage-dependent to induce oscillatory activity, i.e., be designated as a pacemaker current. Our hypothesis is that voltage-dependence is not required and that a linear current with negative conductance, representing the negative conductance region of a typical regenerative current, is all that is needed. Furthermore, we hypothesize that such a negative conductance current, I_NL, acts by destabilizing the resting potential of a cell.

It is important to note that the current we define as I_NL is not a biological current as such (negative conductance has no physical correlate). Therefore, simply down-regulating leak currents in a cell (Blethyn et al. 2006; Lu and Feng 2012; Pang et al. 2009; Brickley et al. 2007; Rekling et al. 2000) cannot by itself generate oscillations. Here we confirm our hypothesis that a system consisting of only a voltage-gated K⁺ current and I_NL is capable of generating oscillatory activity. We show that the linear properties of I_NL in the biologically relevant voltage range are sufficient to explain the origin of oscillations without the need to resort to any other nonlinearities in the system than those of the recovery outward current. Furthermore, here we describe how a hyperpolarization-activated inward current (I_h) can contribute to stabilize oscillations by preventing excursions of the membrane potential to very negative values. In the case where we allow I_NL to extend below the biological plausible range (i.e. below E_K), the membrane voltage can transiently deflect below E_K. However, this is purely an artifact of the linear current approximation being used outside of a biologically relevant domain.

Furthermore, we show that this system expresses a rich behavioral repertoire as parameters, particularly g_NL, are varied. Additionally, we show that transitions from stable non-oscillatory states to rhythmic activity, as g_NL is varied, occur in phase space through various bifurcations. Interestingly, even in this very simple model, as the value of |g_NL| is increased, oscillations may arise through either a supercritical Hopf bifurcation or through a saddle-node of periodic orbits. The rich bifurcation structure of the model arises through an interaction between I_NL and I_K, resulting in the existence of saddle point q in the phase plane. When E_NL > E_K, the stable and unstable orbits of this saddle point define the boundaries between the basin of attraction of the periodic orbit, the stable fixed points p or E_K and the regions where escape to +∞ is possible. As |g_NL| is increased, these stable and unstable orbits can coincide (e.g., at points B and D of Fig. 4), to result in homoclinic bifurcations.

When assigning an ionic current as a pacemaker current, it is important to distinguish between a current that is necessary for pacemaker activity and one that shifts the membrane potential into a range where other ionic currents drive the oscillation. In the latter case the current can effectively be substituted with a DC current that shifts the membrane potential to the appropriate range, whereas the former is responsible for the regenerative depolarization in each cycle of oscillation. It has been shown that introducing the linear negative-conductance current I_NL by dynamic clamp can induce oscillatory activity in biological neurons of the crab STG (Zhao et al. 2010). However, in this experimental study, it was not possible to eliminate the possibility that I_NL only moves the voltage of the cell into a range in which other currents act as the regenerative pacemaker currents. Our results here, by using a simplified model consisting of only two currents, prove that a linear current with a negative conductance can indeed act as a regenerative, pacemaker current. This does not imply that any current that can be reduced to a negative-conductance current such as I_NL is necessarily a pacemaker current. For example, both the classical axonal Na⁺ current (Hodgkin et al. 1952) and other slow as well as non-inactivating Na⁺ currents (Jahnsen and Llinas 1984) have a region of negative conductance. However, while the axonal Na⁺ current could be said to underlie periodic activity under certain conditions (and thus be labeled ‘pacemaker’), the slow Na⁺ current of thalamic neurons does not play such a role during slow oscillations (Jahnsen and Llinas 1984).

In the stomatogastric pyloric network, which inspired the current work, a voltage-gated inward current, I_MI, is activated by a number of neuromodulatory substances, each of which can turn on oscillations in the pyloric network (Golowasch and Marder 1992b; Hooper and Marder 1987; Swensen and Marder 2000). The negative-slope conductance region of the I-V curve of I_MI can be approximated by the linear I_NL current. In the present study, we show that the PD neurons can generate oscillations with I_NL even when regenerative currents carried by Na⁺ are removed. It is possible that low-threshold Ca⁺⁺ currents contribute to the generation of oscillations in the pyloric pacemaker neurons. However, the results of the present study, together with those of Zhao et al (2010), suggest that I_MI is the pacemaker current of the pyloric network.

Our results indicate a need for a relatively close balance of parameters in order to ensure the generation of oscillatory activity. For example, when E_NL < E_K, the fixed point p is always stable and there is no possibility of stable oscillations (Fig. 3A). What this implies for biological oscillations is that the slope and position of the negative-conductance region of the I-V curve of a regenerative inward current is important for producing stable oscillations. If the linear approximation of the negative-conductance region (blue or aqua in Fig. 2A) intersects the v-axis below E_K (for example, if the I-V curve is not steep enough), oscillations are not possible irrespective of the maximal conductance of this current. The steepness of this region can be changed, however, by increasing the maximal conductance of the regenerative inward current to the point that this linear approximation intersects the v-axis above E_K to allow stable oscillations to exist. If the shape of the I-V curve is known, this simple principle can constrain the range of the maximal conductances of the regenerative inward current in a biological neuron in order to produce stable oscillations.

This kind of relationship between two ionic currents in oscillatory neurons has been shown before in neurons of the rat Pre-Bötzinger complex that drive rhythmic inspiratory activity (Del Negro et al. 2002) and in bursting glutamatergic interneurons within lamina I of the rat spinal cord (Li and Baccei 2011). In both cases, pacemaking is attributed to the activity of a slowly inactivating Na⁺ current, I_NaP, which drives membrane potential oscillations in close concert with a linear leak current. Our analysis shows that a close relationship between conductances is necessary in order to maintain the dynamical properties that allow oscillatory activity to emerge. Thus, as has been shown previously, we conclude that the relative expression of ionic conductances needs to be constrained to restricted ranges to produce oscillatory activity (see (Del Negro et al. 2002; Prinz et al. 2004; Ball et al. 2010; Goldman et al. 2001). We further show that parameters other than conductances, such as half-activation values (e.g. h_mid), may also be subject to such constraints.

An interesting prediction of our model is that the principal role of the hyperpolarization-activated inward current, I_h, in oscillatory neurons is not to generate pacemaker activity as proposed previously (Jahnsen and Llinas 1984; McCormick and Bal 1997; DiFrancesco 2005), but rather to stabilize oscillations. This stabilization is principally achieved by preventing excursions of the membrane potential towards negative voltages (see also (Robinson and Siegelbaum 2003). In this case, we find that a balance between conductances, in this case between g_NL and g_h, is also required to ensure the ability of the cell to oscillate. A very large conductance g_h results in an increase of the input conductance of the cell to a point where the unstable fixed point needed for oscillatory activity becomes stable. On the other hand, too much g_NL results in excursions of the membrane potential to negative or positive values. Interestingly, this balance seems to constrain g_h to be small relative to most other conductances in neurons, which is confirmed by experimental measurements in a variety of systems (Golowasch and Marder 1992a; Bazhenov et al. 2002; Tobin et al. 2006). We note that a finite non-zero g_h value is not necessarily required to ensure oscillations, which can be generated even when g_h = 0. However, a non-zero g_h can ensure that perturbations (such as inhibitory synaptic inputs) do not push the voltage to a stable rest state and thus destroy the oscillations.

In our model, trajectories cannot escape to +∞ so long as |g_NL |> g_K , but large depolarizing excursions are possible. Just as I_h can stabilize oscillations by preventing large hyperpolarizing excursions of the membrane potential, one role of the voltage-gated outward currents (such as I_K in our model) is to stabilize oscillations by preventing such large depolarizing excursions. The stabilizing effect of I_K depends on both its maximal conductance and how fast it activates. Biological neurons typically have a number of different voltage gated outward currents and the conductances of these currents are usually large compared to the regenerative inward pacemaker currents (Golowasch and Marder 1992a; Bazhenov et al. 2002; Tobin et al. 2006). As a result, once the membrane potential is depolarized enough, the pacemaker current is dominated by the outward currents which guarantee the stability of oscillations in the depolarizing direction.

In conclusion, we have shown that a linear current with negative conductance is sufficient to generate oscillatory activity in conjunction with a simple delayed rectifier voltage-dependent K⁺ current. Our results predict a stabilizing role for hyperpolarization activated inward currents in addition to their known role in determining the rate of oscillations. Our results also suggest that stability of oscillations requires a balance of the conductance levels of specific ionic currents, which is confirmed by recent models and experimental observations in various systems.

5. Appendix

We used the following set of equations for simulations associated with Figures 4-8.

$$\begin{array}{cc}\hfill v^{\prime }=& [I_{ext}-I_{NL}^{\ast }\left(v\right)-I_K(v,w)-I_h(v,h)]∕C_m\hfill \\ \hfill w^{\prime }=& \frac{w_{\infty }\left(v\right)-w}{{\tau }_K\left(v\right)}\hfill \\ \hfill h^{\prime }=& \frac{h_{\infty }\left(v\right)-h}{{\tau }_h\left(v\right)}\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & I_K(v,w)=g_{K}w[v-E_K]\hfill \\ \hfill & I_{NL}^{\ast }=\{\begin{array}{c}{g}_{NL}[v-E_{NL}]Heav(v-E_{NL}),\text{for}\text{Figs.}4-7\hfill \\ g_{NL}[v-E_{NL}],\text{for}\text{Fig.}8\hfill \end{array}\phantom{\}}\hfill \\ \hfill & I_h=g_{h}h[v-E_h]\hfill \end{array}$$

The gating functions are

$$\begin{array}{cc}\hfill & w_{\infty }\left(v\right)=1∕[1+\exp (-[v-w_{mid}]∕k_1)]\hfill \\ \hfill & h_{\infty }\left(v\right)=1∕[1+\exp ([v-h_{mid}]∕h_1)]\hfill \end{array}$$

and the time constants are given by τ_K (v)=τ₁ / [1+exp(v/k_s)] and τ_h (v) = τ_h1 ms. The following parameter values were used in all simulations E_K = −80 mV, g_K = 0.5, I_ext = 0, andC_m = 1.0 nF

In Figures 4 and 5 there was no h current, which we modeled simply by setting g_h = 0 μS. We let E_NL = −79 mV, w_mid = -60 mV, k_s = 2 mV. For Figure 4, we used k₁ = 2 mV and τ₁ = 60 ms. For Figure 5A, we used k₁ = 4 mV and τ₁ = 80 ms. For Figure 5B, we used k₁ = 4 mV and τ₁ = 60 ms.

In Figure 6, an instantaneous version of the h current was used, i.e., the equation for h’ was replaced with h ≡ h_∞ (v). For this figure, parameter values from Figure 5A were used. In addition, E_h = −30 mV, h_mid = −85 mV, h₁ = 2 mV , E_NL = -75 mV and g_NL = −0.15 μS. Figure 6B was obtained by varying h_mid while g_h = 1 μS was fixed.

In Figure 7, we used parameter values from Figure 5A with g_NL = −0.45 μS, E_NL = -75 mV, g_h = 1. The perturbation was achieved be setting I_ext = -1 for 50 mS.

In Figure 8, we used C_m = 10.0 nF, τ_h1 = 200 ms, τ₁ = 600 ms to match the biological timescale. Additionally, we set with k_s(v) = τ₁ / cosh((v – w_mid)) / k_s) with k_s = 5.6 mV, g_NL = −0.45 μS, E_NL = −65 mV, w_mid = −40 mV, g_h = 0.8 μS and h₁ = 6mV.