Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Oct 1.
Published in final edited form as: J Comput Neurosci. 2014 Jun 14;37(2):377–386. doi: 10.1007/s10827-014-0510-z

Effect of non-symmetric waveform on conduction block induced by high-frequency (kHz) biphasic stimulation in unmyelinated axon

Shouguo Zhao 1,2, Guangning Yang 3,4, Jicheng Wang 5, James R Roppolo 6, William C de Groat 7, Changfeng Tai 8,9,✉
PMCID: PMC4161638  NIHMSID: NIHMS605298  PMID: 24928360

Abstract

The effect of a non-symmetric waveform on nerve conduction block induced by high-frequency biphasic stimulation is investigated using a lumped circuit model of the unmyelinated axon based on Hodgkin-Huxley equations. The simulation results reveal that the block threshold monotonically increases with the stimulation frequency for the symmetric stimulation waveform. However, a non-monotonic relationship between block threshold and stimulation frequency is observed when the stimulation waveform is non-symmetric. Constant activation of potassium channels by the high-frequency stimulation results in the increase of block threshold with increasing frequency. The non-symmetric waveform with a positive pulse 0.4–0.8 µs longer than the negative pulse blocks axonal conduction by hyperpolarizing the membrane and causes a decrease in block threshold as the frequency increases above 12–16 kHz. On the other hand, the non-symmetric waveform with a negative pulse 0.4–0.8 µs longer than the positive pulse blocks axonal conduction by depolarizing the membrane and causes a decrease in block threshold as the frequency increases above 40–53 kHz. This simulation study is important for understanding the potential mechanisms underlying the nerve block observed in animal studies, and may also help to design new animal experiments to further improve the nerve block method for clinical applications.

Keywords: Nerve block, High-frequency, Stimulation, Sodium, Potassium

1 Introduction

It has been known for about 80 years that high-frequency biphasic stimulation can block conduction of myelinated axons at a minimal frequency of approximately 5 kHz (Cattell and Gerard 1935; Reboul and Rosenblueth 1939; Rosenblueth and Reboul 1939). Recently this nerve block method has been applied to treat obesity (Camilleri et al. 2009; Wattaja et al. 2011), block chronic pain of peripheral origin (Cuellar et al. 2013; van Buyten et al. 2013), or restore urinary function after spinal cord injury (Gaunt and Prochazka 2009; Tai et al. 2004). However, the mechanisms underlying this conduction block are still unknown. It has been proposed that high-frequency biphasic stimulation causes extracellular accumulation of potassium (Cattell and Gerard 1935) or constant depolarization of the axonal membrane (Tanner 1962) to induce the block. Although the patch-clamp technique has significantly increased our understanding of sodium and potassium channel properties of the axonal membrane (Catterall 2012; Jan and Jan 2012; Schwarz et al. 1995; Vasylyev and Waxman 2012; Waxman 2012), it has not been used to investigate axonal responses to high-frequency (>5 kHz) biphasic stimulation leaving the above proposals unconfirmed.

Recent studies of unmyelinated axons using sea slugs and frogs (Joseph and Butera 2009, 2011) have further shown that the high-frequency biphasic stimulation has a maximal block threshold at 12–15 kHz. This observation provides a new challenge and/or opportunity for testing the different hypotheses regarding the blocking mechanism. It seems likely that a single mechanism as proposed above (Cattell and Gerard 1935; Tanner 1962) would not explain the two critical frequencies (5 kHz and 12–15 kHz) of conduction block by high-frequency stimulation. Therefore, in this study we investigated the role that both sodium and potassium channel kinetics might play in the block of unmyelinated axons induced by high-frequency biphasic stimulation.

It is a technical challenge to generate a perfectly symmetric biphasic waveform due to the limitations of the electronic generators. Therefore, as the stimulation frequency becomes very high (>10 kHz), a small difference (<1 µs) in the duration of the positive and negative pulses of the biphasic waveform could lead to a significantly different response of the axonal membrane. In the present study we investigated the effect of a non-symmetric waveform on high-frequency nerve conduction block. Because it is technically difficult to measure sodium and potassium channel activity during the biphasic high-frequency stimulation due to the strong electrical artifacts, we used an axonal cable model based on Hodgkin-Huxley equations (Hodgkin and Huxley 1952) to simulate the response of an unmyelinated axon to high-frequency biphasic stimulation to determine: (1) whether the model can predict the minimal frequency (about 5 kHz) for nerve block and the frequencies (about 12–15 kHz) for a maximal block threshold; (2) whether sodium and/or potassium channel kinetics determine these critical blocking frequencies. Answering these questions might not only reveal the physiological mechanisms underlying nerve conduction block, but may also guide future animal experiments and clinical applications of nerve conduction block induced by high-frequency biphasic stimulation (Camilleri et al. 2009; Cuellar et al. 2013; Gaunt and Prochazka 2009; Tai et al. 2004; Wattaja et al. 2011; van Buyten et al. 2013).

2 Methods

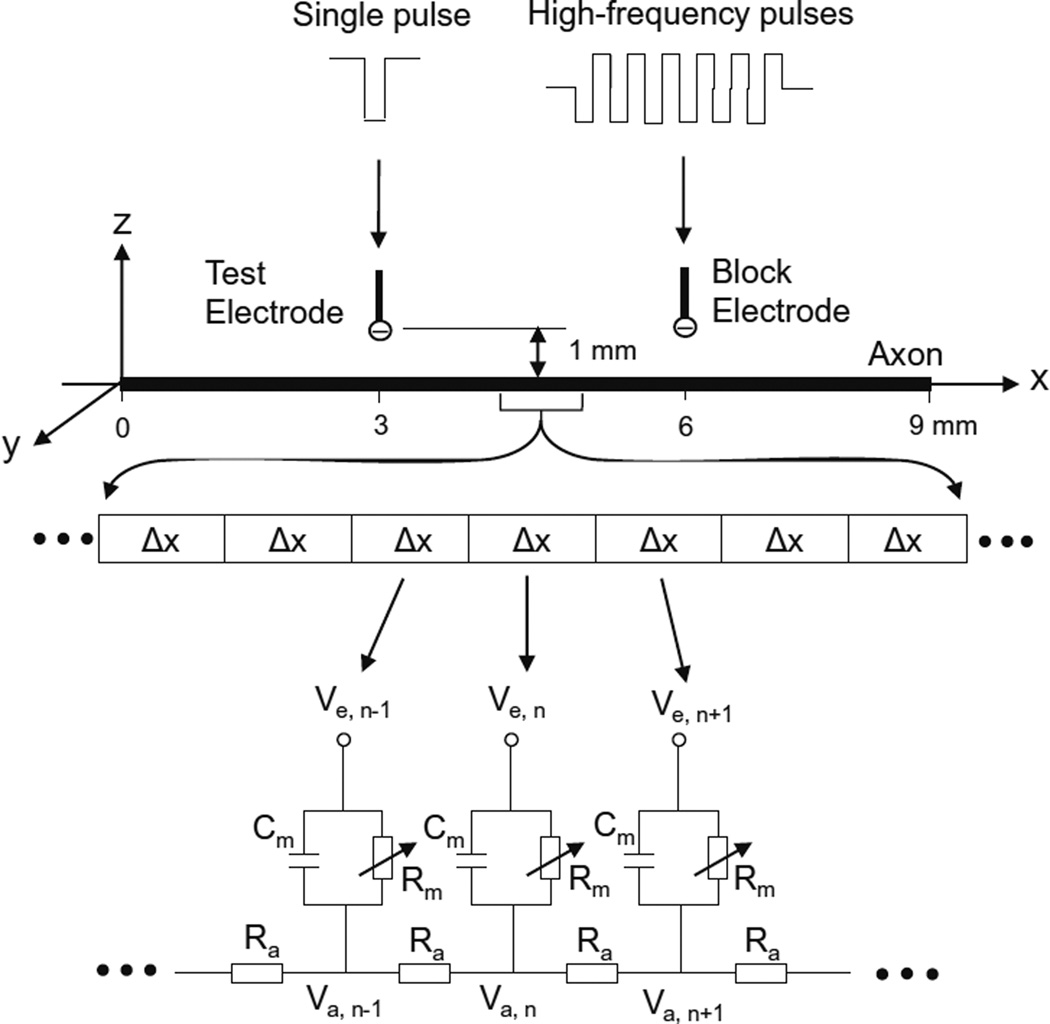
The unmyelinated axon model (Fig. 1) consists of a 9-mmlong axon segmented into many small cylinders of length Δx=0.25 mm, each of which is modeled by a resistance-capacitance circuitry. The ionic currents passing through the variable membrane resistance are described by Hodgkin–Huxley equations (Hodgkin and Huxley 1952). Two mono polar electrodes (with the indifferent electrodes at infinity) are placed at 1 mm distance from the unmyelinated axon. One is the block electrode at the 6 mm location along the axon, where the high-frequency biphasic electrical current is delivered. The other is the test electrode at the 3 mm location, which delivers a uniphasic single pulse (pulse width: 0.1 ms; intensity: 10–15 mA) to evoke an action potential that can propagate through the site of the block electrode. The test electrode is always the cathode (negative pulse). The block electrode always delivers the high-frequency biphasic current with the cathodal phase first.

Fig. 1.

Fig. 1

Open in a new tab

Unmyelinated axon model to simulate conduction block induced by high-frequency biphasic electrical current. The unmyelinated axon is segmented into many small cylinders of length Δx, each of which is modeled by a resistance-capacitance circuit based on the Hodgkin–Huxley model. Ra: Axoplasm resistance. Rm: Membrane resistance. Cm: Membrane capacitance. Va: Intracellular potential. Ve: Extracellular Potential

We assume that the unmyelinated axon is in an infinite homogeneous medium (resistivity ρe=300 Ωcm). After neglecting the small influence of the axon in the homogeneous medium, the extracellular potential Ve,n at the nth segment along the axon can be described by:

Ve,n=ρe4π[Iblock(t)(nΔx−x0)2+z02+Itest(t)(nΔx−x1)2+z12]

Where Iblock(t) is the high-frequency biphasic current delivered to the block electrode (at location x0=6 mm, z0=1 mm); Itest(t) is the single test pulse delivered to the test electrode (at location x1=3 mm, z1=1 mm).

The change of the membrane potential Vn at the nth segment of the unmyelinated axon is described by:

dVndt=[d4ρi(Vn−1−2Vn+Vn+1Δx2+Ve,n−1−2Ve,n+Ve,n+1Δx2)−Ii,n]/Cm

Where Vn=Va,n−Ve,n−Vrest;Va,n is the intracellular potential at the nth segment; Ve,n is the extracellular potential at the nth segment; Vrest is the resting membrane potential; d is the unmyelinated axon diameter; ρi is the resistivity of axoplasm (34.5 Ωcm); cm is the capacity of the membrane (1 uF/cm2); Ii,n is the ionic current at the nth segment described by Hodgkin–Huxley equations (Hodgkin and Huxley 1952; Rattay 1989; Rattay and Aberham 1993; Tai et al. 2005a, 2005b).

The model equations were solved by the Runge–Kutta method (Boyce and Diprima 1997) with a time step of 0.2 µsec. A smaller time step (0.05 µsec) or Runge–Kutta-Fehlberg method (Heinbockel 2005) with an adaptive time step was also used to confirm some of the key results. The temperature parameter was set at T=18.5 °C. The simulation was always started at initial condition Vn=0. The membrane potentials at the two end segments of the modeled axon were always equal to the membrane potentials of their closest neighbors, which implemented sealed boundary conditions (no longitudinal currents) at the two ends of the modeled axon. The block threshold intensity was determined with a resolution of 1 mA.

3 Results

3.1 Conduction block by symmetric and non-symmetric biphasic stimulation waveforms

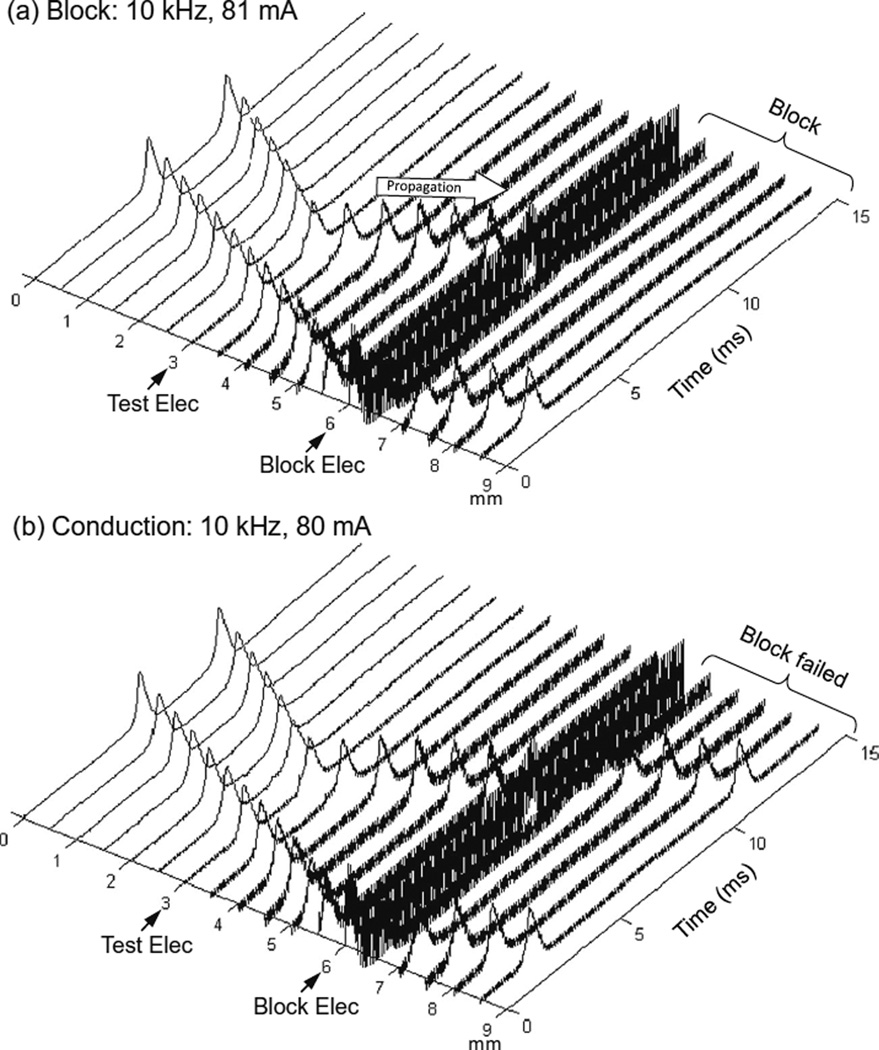
Figure 2 shows that in an unmyelinated axon the Hodgkin–Huxley model can successfully simulate the conduction block induced by high-frequency (10 kHz) symmetric biphasic stimulation. In Fig. 2a the 10 kHz blocking stimulation (81 mA) generates an initial action potential propagating in both directions. At 5 ms after the start of blocking stimulation, the test electrode delivers a single pulse that generates another action potential propagating toward the block electrode (see the white arrow in Fig. 2a). This action potential fails to propagate through the block electrode due to the presence of the high-frequency biphasic stimulation. However, at a lower stimulation intensity (80 mA in Fig. 2b) the 10 kHz stimulation does not block nerve conduction and the action potential propagates through the site of the block electrode. Similar conduction block was also successfully simulated for non-symmetric biphasic stimulation wave-forms where either the positive pulse is 0.4 or 0.8 µs longer than the negative pulse, or the reverse of this condition.

Fig. 2.

Fig. 2

Open in a new tab

Blocking the propagation of action potentials along an unmyelinated axon by high-frequency symmetric biphasic stimulation. High-frequency (10 kHz) stimulation is continuously delivered at the block electrode, which initiated an initial action potential. Another action potential is initiated via the test electrode at 5 ms after starting the high-frequency stimulation, and propagates towards both ends of the axon. The 10 kHz stimulation blocks nerve conduction at the intensity of 81 mA (a), but not at 80 mA (b). The short arrows mark the locations of test and block electrodes along the axon. The white arrow indicates propagation of the action potential to the location of the 10 kHz blocking stimulation. Axon diameter: 2 µm

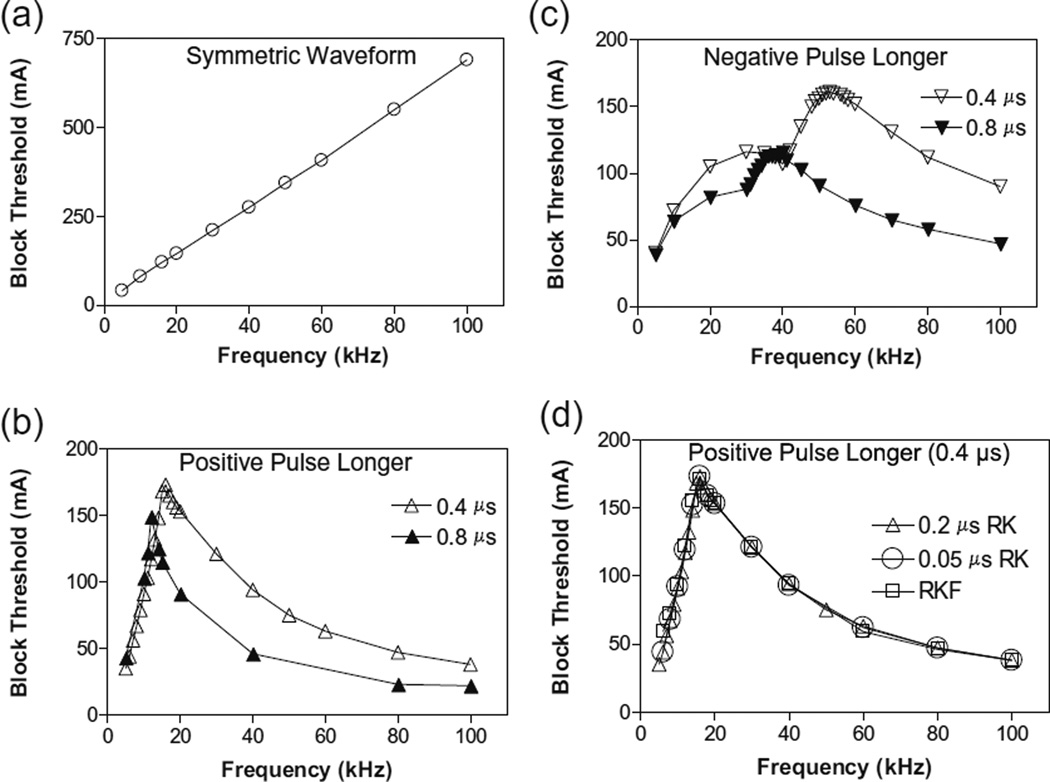
Figure 3 shows the intensity thresholds for inducing conduction block at different frequencies (5–100 kHz) for an unmyelinated axon of 2 µm diameter. For the symmetric biphasic waveform (Fig. 3a), the block threshold monotonically increases as the stimulation frequency increases. However, if the biphasic waveform is not symmetric (Fig. 3b and c), the block threshold increases initially and then decreases with increasing stimulation frequency, showing a non-monotonic relationship between block threshold and stimulation frequency. If the positive pulse is 0.4 or 0.8 µs longer than the negative pulse, the block threshold peaks between 12 kHz and 16 kHz (Fig. 3b). However, if the negative pulse is 0.4–0.8 µs longer than the positive pulse, the block threshold peaks at a frequency of 40–53 kHz (Fig. 3c). For the symmetric waveform, nerve block is not observed at frequencies below 5 kHz, indicating that the minimal frequency for inducing nerve block is about 5 kHz (Fig. 3). To evaluate the possibility that the numerical integration method might cause the effect of asymmetric stimulation waveform, we also calculated the result shown in Fig. 3b using a smaller time step of 0.05 µs or using Runge–Kutta-Fehlberg method with an adaptive time step. These methods did not change the results (see Fig. 3d).

Fig. 3.

Fig. 3

Open in a new tab

The threshold intensity to block nerve conduction changes with the stimulation frequency. (a). For the symmetric waveform, the block threshold monotonically increases as the frequency increases. (b). If the positive pulse is longer (0.4 or 0.8 µs), the block threshold peaks at 12–16 kHz and then gradually decreases as the frequency increases. (c). If the negative pulse is longer (0.4 or 0.8 µs), the block threshold peaks at 40–53 kHz. (d). The same results were also obtained by Runge–Kutta (RK) numerical integration method with a smaller time step of 0.05 µs or by Runge–Kutta-Fehlberg (RKF) numerical integration method with an adaptive time step. Axon diameter: 2 µm

3.2 Mechanisms of the conduction block by symmetric and non-symmetric waveforms

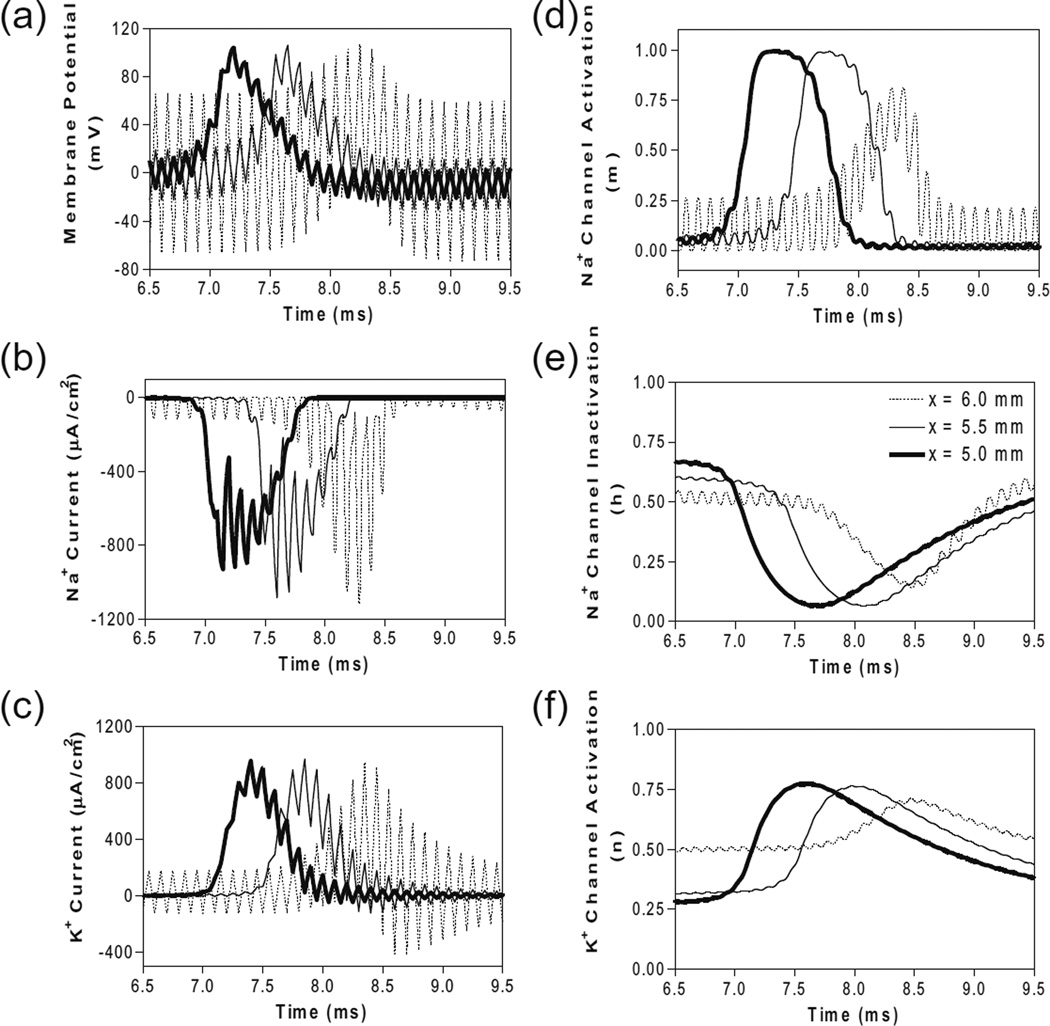
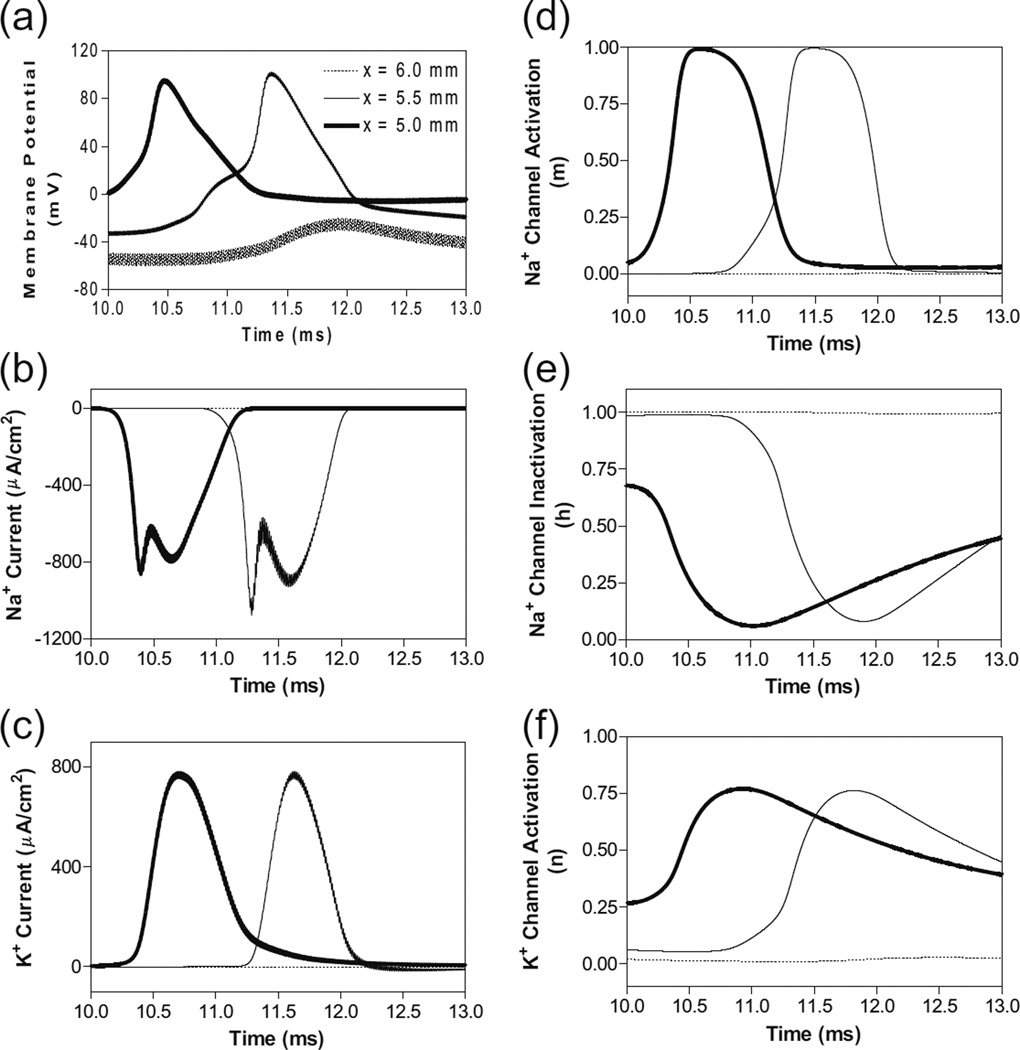
Figure 4 shows the same simulation as in Fig. 2a for the 10 kHz symmetric biphasic waveform but including more detailed information for the 3 consecutive axon segments at distances of 0–1 mm from the block electrode (the location at 6.0 mm is under the block electrode). Figure 4a-c show the action potential, sodium current, and potassium current at different locations approaching the block electrode. This action potential propagation is disrupted at the location (6.0 mm) under the block electrode, where axon membrane is alternately depolarized and hyperpolarized with large pulsed sodium and potassium currents. The behavior of the membrane potential and ionic currents can be further explained by the activation/inactivation of the sodium and potassium channels as shown in Fig. 4d-f. As the action potential propagates toward the block electrode, the activation (m) of sodium channels also changes at each location and becomes weaker and oscillatory at the location under the block electrode (Fig. 4d). Meanwhile, the inactivation of sodium channels is kept at a low level (i.e., h is a high value) under the block electrode (Fig. 4e). The combination of activation and inactivation of sodium channels (Fig. 4d-e) determines that the sodium current becomes a pulsed inward current under the block electrode (Fig. 4b). Therefore, the sodium channels are never completely blocked when conduction block occurs. However, the change in potassium activation (n) induced by the action potential becomes smaller under the block electrode (Fig. 4f) because potassium channels are constantly activated at this location, resulting in a large pulsed outward potassium current (Fig. 4c). This large outward potassium current opposes the large inward sodium current, causing the membrane under the block electrode to become un-excitable leading to the block of action potential conduction. This blocking mechanism is observed for the symmetric waveform in the frequency range of 5–100 kHz (Fig. 3a). Our previous simulation studies of an unmyelinated axon (Tai et al. 2005a, 2005b) also revealed that the constant activation of potassium channels by high-frequency symmetric biphasic stimulation requires higher stimulation intensity as the frequency increases, because a lower frequency can maintain a higher activation level of potassium channels than a higher frequency.

Fig. 4.

Fig. 4

Open in a new tab

The changes in membrane potential, ionic currents and activation/inactivation of ion channels near the block electrode when conduction block occurs as shown in Fig. 2 (a) during stimulation with a symmetric waveform. The legends in (e) indicate the location of each axon segment. Node at 6.0 mm is under the block electrode. (a) Change in membrane potential, (b) Na+ current, (c) K+ current, (d) Na+ channel activation, (e) Na+ channel inactivation, (f) K+ channel activation. Symmetric stimulation waveform: 10 kHz, 81 mA. Axon diameter: 2 µm. Abscissa: time in ms after the start of blocking stimulation

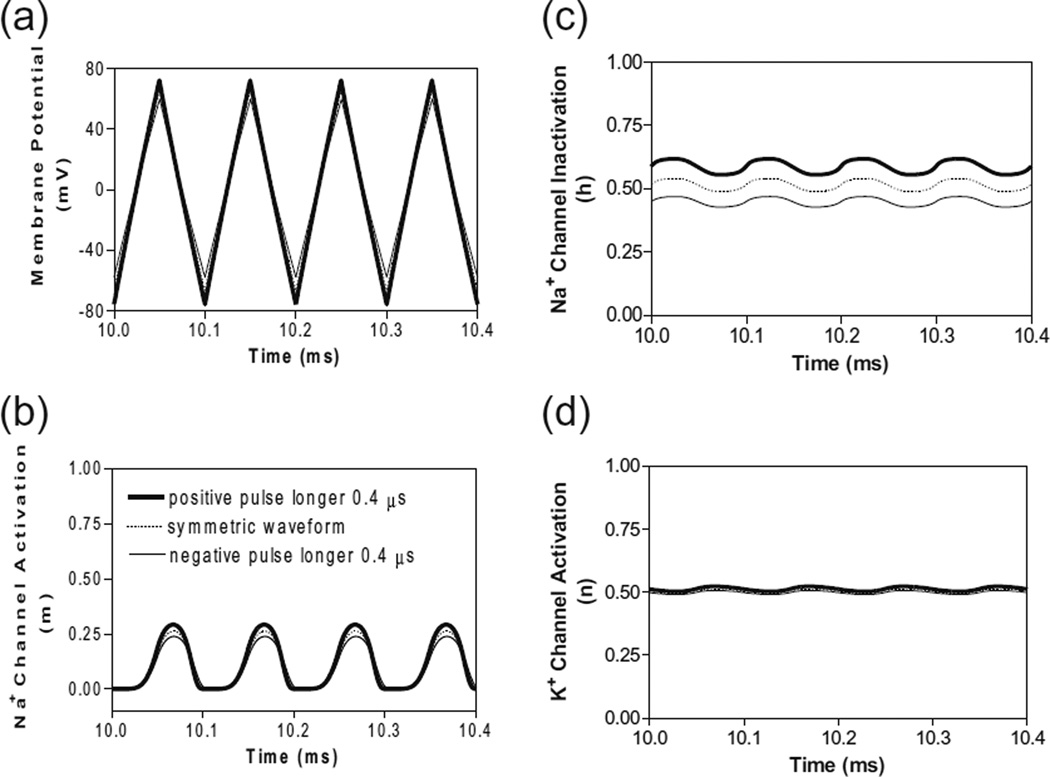
A similar blocking mechanism is also observed for non-symmetric waveforms at frequencies below the peak block threshold frequency (Fig. 3b and c). Figure 5 shows that at 10 kHz the symmetric and non-symmetric waveforms produce almost the same alternating membrane depolarization/ hyperpolarization (Fig. 5a) and very similar ion channel activation/inactivation (Fig. 5b-d). It is also worth noting that the 0.4 µs difference between the positive and negative pulses produces no difference in potassium channel activation (Fig. 5d).

Fig. 5.

Fig. 5

Open in a new tab

The effects of non-symmetric waveforms on membrane potential and activation/inactivation of ion channels under the block electrode when stimulation frequency is 10 kHz. The legends in (b) indicate the types of waveform: symmetric and non-symmetric with a 0.4 µs difference in pulse width between the positive and negative pulses. (a) Change of membrane potential, (b) Na+ channel activation, (c) Na+ channel inactivation, (d) K+ channel activation. Stimulation waveforms: 10 kHz at block threshold intensities. Axon diameter: 2 µm. Abscissa: time in ms after the start of blocking stimulation

In order to understand why the block threshold with the non-symmetric waveform starts to decrease at frequencies above the peak block threshold frequency (Fig. 3b and c), we further investigated the changes in membrane potential, ionic currents, and activation/inactivation of the sodium and potassium channels at frequencies between 12–100 kHz. Figure 6 shows the conduction block by the 80 kHz non-symmetric waveform with a positive pulse 0.4 µs longer than the negative pulse. Action potential propagation is completely abolished at the location (6.0 mm) under the block electrode, where the axon membrane is hyperpolarized to about −120 mV [(−50 mV)+(−70 mV resting potential), see Fig. 6a]. This hyperpolarization is caused by the accumulation of 0.4 µs longer positive pulses, which completely deactivates both sodium and potassium channels (Fig. 6d and f) and eliminates both sodium and potassium currents (Fig. 6b and c) thereby resulting in a conduction block at the location (6.0 mm) under the block electrode. Meanwhile, inactivation (h) of sodium channels is minimal (≈1) under the block electrode (Fig. 6e). The same blocking mechanism is observed at frequencies greater than 12–16 kHz for non-symmetric waveforms with the positive pulse 0.4 or 0.8 µs longer than the negative pulse (Fig. 3b). As the frequency is increased, the accumulation of positive charges due to the longer positive pulses is greater and produces the same level of hyperpolarization at a lower stimulus intensity. Therefore, the block threshold decreases as the frequency increases (Fig. 3b).

Fig. 6.

Fig. 6

Open in a new tab

The changes in membrane potential, ionic currents and activation/inactivation of ion channels near the block electrode when conduction block is induced by a 80 kHz non-symmetric waveform with the positive pulse 0.4 µs longer than the negative pulse. The legends in (a) indicate the location of each axon segment. Node at 6.0 mm is under the block electrode. (a) Change in membrane potential, (b) Na+ current, (c) K+ current, (d) Na+ channel activation, (e) Na+ channel inactivation, (f) K+ channel activation. Non-symmetric stimulation waveform: 80 kHz, 48 mA. Axon diameter: 2 µm. Abscissa: time in ms after the start of blocking stimulation

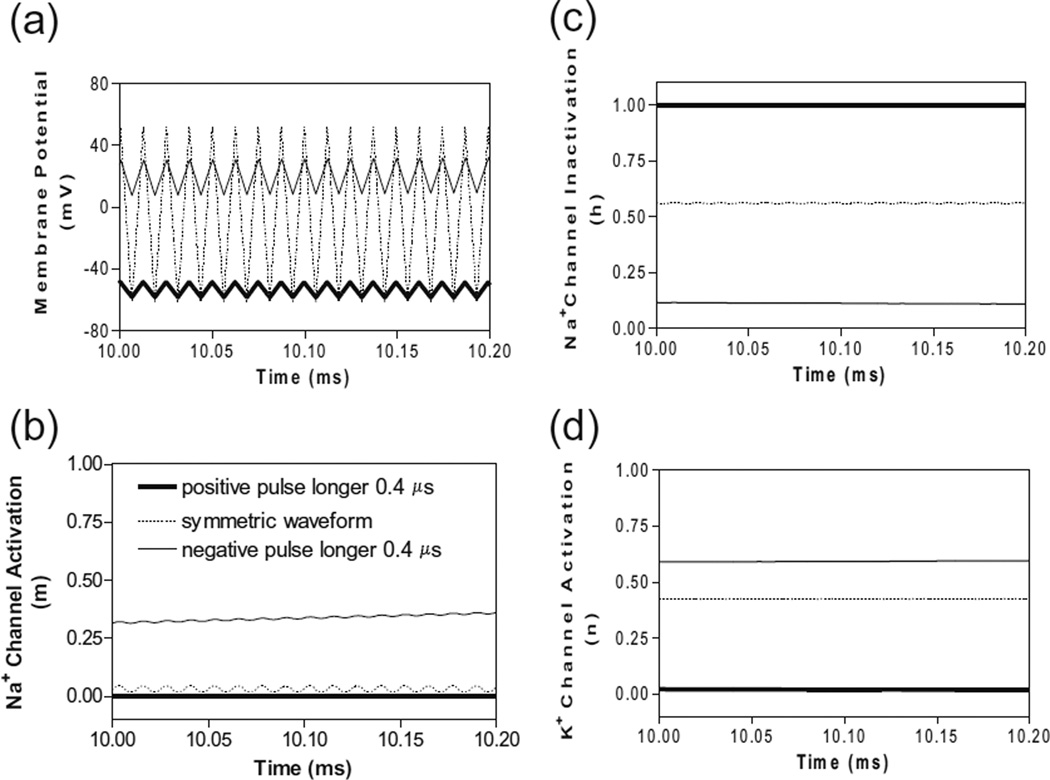
However, if the non-symmetric waveform has a longer negative pulse, it generates a constant depolarization under the block electrode instead of a hyperpolarization. Figure 7 shows the membrane potentials and ion channel activation/ inactivation for the symmetric and non-symmetric waveforms at 80 kHz. Although the 0.4 µs difference between the positive and negative pulses does not produce a different membrane response at 10 kHz (Fig. 5), it can generate a significantly different response at 80 kHz (Fig. 7). The non-symmetric waveform with the negative pulse 0.4 µs longer than the positive pulse produces a constant depolarization about 20 mV (Fig. 7 a), which causes a significant inactivation of sodium channels (Fig. 7c) resulting in a conduction block. The accumulation of negative charges due to longer negative pulses is greater for a higher frequency, thereby producing the same level of depolarization at a lower block threshold (Fig. 3c).

Fig. 7.

Fig. 7

Open in a new tab

The effects of non-symmetric waveforms on membrane potential and activation/inactivation of ion channels under the block electrode when stimulation frequency is 80 kHz. The legends in (b) indicate the types of waveform: symmetric and non-symmetric with a 0.4 µs difference in pulse width between the positive and negative pulses. (a) Change of membrane potentials, (b) Na+ channel activation, (c) Na+ channel inactivation, (d) K+ channel activation. Stimulation waveforms: 80 kHz at block threshold intensities. Axon diameter: 2 µm. Abscissa: time in ms after the start of blocking stimulation

4 Discussion

This study employed the Hodgkin–Huxley axonal model to simulate nerve conduction block by high-frequency (5– 100 kHz) biphasic stimulation in an unmyelinated axon (Figs. 1–2). It revealed that the block threshold monotonically increases with the stimulation frequency if the biphasic stimulation waveform is symmetric (Fig. 3a). A non-monotonic relationship between block threshold and stimulation frequency can only be observed when the biphasic stimulation wave-form is non-symmetric (Fig. 3b and c). Constant activation of potassium channels by high-frequency stimulation is the underlying mechanism for the increase of block threshold with increasing frequency (Figs. 4 and 5). The non-symmetric waveform consisting of longer positive pulses blocks axonal conduction by hyperpolarizing the membrane (Fig. 6), which causes a decrease in block threshold as the frequency increases above 12–16 kHz (Fig. 3b). On the other hand, the non-symmetric waveform consisting of longer negative pulses blocks axonal conduction by depolarizing the membrane (Fig. 7), which causes a decrease in block threshold as the frequency increases above 40–53 kHz (Fig. 3c).

This study and our previous studies (Tai et al. 2005a, 2005b) using the unmyelinated axonal model (Hodgkin–Huxley model) have successfully predicted the minimal blocking frequency (5 kHz) (Bowman and McNeal 1986; Reboul and Rosenblueth 1939; Rosenblueth and Reboul 1939). However, the peak block threshold frequencies (12–15 kHz) discovered recently in unmyelinated axons of sea-slugs and frogs (Joseph and Butera 2009, 2011) can only be observed in this simulation study using non-symmetric waveforms with a positive pulse 0.4 or 0.8 µs longer than the negative pulse (Fig. 3). Since the animal studies (Joseph and Butera 2009, 2011) did not report the accuracy of the stimulation waveform, it is difficult to know whether the peak block threshold frequencies (12–15 kHz) were caused by a slightly non-symmetric wave-form used in those studies. Additional animal studies with accurate information about the symmetry of the stimulation waveform are needed in order to confirm the results from this simulation study.

However, the animal study (Joseph and Butera 2011) using the same stimulation waveform also showed that in a myelinated axon the block threshold monotonically increases with stimulation frequency up to 50 kHz. Our previous simulation study (Tai et al. 2011) using a myelinated axon model (Frankenhaeuser-Huxley model) showed the same monotonic increase in block threshold at frequencies up to 100 kHz for axons of diameter 10–20 µm. However, the effect of non-symmetric waveforms on conduction block of myelinated axon has not been investigated. Since the ion channels in myelinated axons (Frankenhaeuser 1960) have much faster kinetics than in unmyelinated axons (Hodgkin and Huxley 1952), it is possible that a frequency greater than 50 kHz might be needed in order to induce a constant hyperpolarization and a decrease in block threshold by the non-symmetric waveform with a slightly longer positive pulses. Therefore, more studies are warranted to investigate nerve conduction block in myelinated axons using non-symmetric stimulation waveforms.

The results in this study emphasize the importance of using a symmetric biphasic waveform for high-frequency nerve block, especially when the frequency is above 10 kHz. The small difference of 0.4 µs between the positive and negative pulses (less than 0.8 % difference in pulse width) may not make a difference in nerve block at frequencies below 10 kHz (Figs. 4–5), but can make a significant difference at frequencies of 20–100 kHz (1.6–8 % difference in pulse width) causing a decrease in block threshold (Fig. 3b and c) by constantly hyperpolarizing or depolarizing the axonal membrane (Figs. 6–7). The net effect of the non-symmetric waveform on axonal conduction is equivalent to that caused by direct current (DC). The non-symmetric waveform with a longer positive (or negative) pulse blocks nerve conduction by inducing a constant hyperpolarization (or depolarization) of the axon membrane, which is similar to the nerve conduction block induced by an anodal (or cathodal) DC (Tai et al. 2009). It is known that DC can damage nerves during long-term application due to the accumulation of electrical charges that can cause irreversible chemical reactions. Electrical charges could accumulate more rapidly when the stimulation frequency is high (such as >10 kHz, see Fig. 7) even with a very small difference between the durations (such as 0.4 µs) of the positive and negative pulses of the non-symmetric wave-form. Therefore, the results from this simulation study suggest that waveform symmetry needs to be carefully examined when the high-frequency (kHz) biphasic stimulation is to be used in clinical applications.

It has been proposed that high-frequency biphasic stimulation might induce block by producing a constant depolarization of the axonal membrane (Tanner 1962). However, the results in this simulation study show that a constant depolarization is only possible when the biphasic waveform is non-symmetric with a longer negative pulse than positive pulse (Fig. 7). If the biphasic waveform is symmetric (i.e., charge-balanced), it will not produce a constant depolarization. Instead, the axonal membrane will be alternately depolarized and hyperpolarized (Fig. 7a) causing a constant activation of the potassium channels (Fig. 4f and Fig. 7d). Therefore, it is possible that extracellular accumulation of potassium as proposed previously (Cattell and Gerard 1935) could contribute to the nerve conduction block. However, this blocking mechanism will depend on how fast the potassium can diffuse in the extracellular space. In this simulation study the extracellular accumulation of potassium is not considered but the nerve conduction block is still successfully simulated, indicating that the extracellular accumulation of potassium might not be a necessary factor in the block induced by high-frequency (kHz) biphasic stimulation.

The results in this study and our previous studies using an unmyelinated axonal model (Tai et al. 2005a, 2005b) indicate that the kinetics of ion channel gating play a major role in the conduction block induced by high-frequency biphasic stimulation. For example, the kinetics of the potassium channel are slow compared to the sodium channel. Therefore, opening and closing of the potassium channel cannot follow higher frequencies. Hence, it is constantly open as the frequency increases to the minimal blocking frequency of about 5 kHz (Fig. 4) (Tai et al. 2005a, 2005b), which results in a potassium current that opposes the sodium current induced by the arrival of the action potential and thereby elicits a conduction block (Fig. 4). This potassium channel mechanism causes the monotonic increase in block threshold as the stimulation frequency increases (Figs. 3–5) because a lower frequency can maintain a higher activation level of potassium channels (Tai et al. 2005a, 2005b). However, the blocking mechanisms identified in this simulation study still need to be confirmed by animal studies using patch-clamp techniques to examine the ion channel kinetics (Vasylyev and Waxman 2012). In addition, the responses of different subtypes of sodium and potassium channels to high-frequency biphasic stimulation also need to be investigated using patch-clamp techniques (Vasylyev and Waxman 2012) or by simulation studies using the kinetics of different subtypes of ion channels (Catterall 2012; Jan and Jan 2012; Waxman 2012).

It is worth noting that the block threshold calculated in this model study is much higher than the measurements from animal studies (Gaunt and Prochazka 2009; Joseph and Butera 2009, 2011). This is mainly due to the 1 mm distance between the block electrode and the axon (Fig. 1), while the electrode in animal studies is in close contact with the nerve. In addition, the extracellular medium resistivity (ρe=300 Ωcm) in this model study is probably higher than in animal studies, which can also cause a higher block threshold. Currently nerve conduction block by high-frequency biphasic stimulation has been shown both in small (<1 µm diameter) unmyelinated axons of rat vagus nerve (Wattaja et al. 2011) and in large (2–20 µm diameter) unmyelinated axons of Aplysia (Joseph and Butera 2009). Therefore, we chose an unmyelinated axon of 2 µm diameter as the representative in this study to investigate the effect of stimulation waveform asymmetry.

Nerve conduction block induced by high-frequency biphasic stimulation has many potential applications in both clinical medicine and basic neuroscience research (Camilleri et al. 2009; Gaunt and Prochazka 2009; Tai et al. 2004;Wattaja et al. 2011). The results about nerve block of umyelinated axons in this study are especially useful for clinical applications to block chronic pain (Cuellar et al. 2013; van Buyten et al. 2013). Understanding the mechanisms underlying this type of nerve block could improve the design of new stimulation waveforms (Roth 1994, 1995) and further promote clinical application (Leob 1989; Song et al. 2008). Simulation analysis using computer models provides a tool to reveal the possible blocking mechanisms and may help to design new animal experiments to further improve the nerve blocking method.

Acknowledgments

This study is supported by DOD Spinal Cord Injury Program under grant W81XWH-11-1-0819 and by NIH under grant DK-068566.

Footnotes

Conflict of interest The authors declare that they have no conflict of interest.

Contributor Information

Shouguo Zhao, Department of Urology, University of Pittsburgh, 700 Kaufmann Building, 15213 Pittsburgh, PA, USA; Department of Biomedical Engineering, Beijing Jiaotong University, Beijing, Peoples Republic China.

Guangning Yang, Department of Urology, University of Pittsburgh, 700 Kaufmann Building, 15213 Pittsburgh, PA, USA; Department of Biomedical Engineering, Beijing Jiaotong University, Beijing, Peoples Republic China.

Jicheng Wang, Department of Urology, University of Pittsburgh, 700 Kaufmann Building, 15213 Pittsburgh, PA, USA.

James R. Roppolo, Department of Pharmacology and Chemical Biology, University of Pittsburgh, Pittsburgh, PA, USA

William C. de Groat, Department of Pharmacology and Chemical Biology, University of Pittsburgh, Pittsburgh, PA, USA

Changfeng Tai, Email: cftai@pitt.edu, Department of Urology, University of Pittsburgh, 700 Kaufmann Building, 15213 Pittsburgh, PA, USA; Department of Pharmacology and Chemical Biology, University of Pittsburgh, Pittsburgh, PA, USA.

References

  1. Bowman BR, McNeal DR. Response of single alpha motoneurons to high-frequency pulse train: firing behavior and conduction block phenomenon. Applied Neurophysiology. 1986;49:121–138. doi: 10.1159/000100137. [DOI] [PubMed] [Google Scholar]
  2. Boyce WE, Diprima RC. Elementary differential equations and boundary value problems. 6th ed. John Wiley & Sons Inc.; 1997. pp. 436–457. [Google Scholar]
  3. Camilleri M, Toouli J, Herrera MF, Kow L, Pantoja JP, Billington CJ, Tweden KS, Wilson RR, Moody FG. Selection of electrical algorithms to treat obesity with intermittent vagal block using an implantable medical device. Surgery for Obesity and Related Diseases. 2009;5:224–230. doi: 10.1016/j.soard.2008.09.006. [DOI] [PubMed] [Google Scholar]
  4. Cattell M, Gerard RW. The “inhibitory” effect of high-frequency stimulation and the excitation state of nerve. Journal of Physiology. 1935;83:407–415. doi: 10.1113/jphysiol.1935.sp003238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Catterall WA. Voltage-gated sodium channels at 60: structure, function and pathophysiology. Journal of Physiology. 2012;590:2577–2589. doi: 10.1113/jphysiol.2011.224204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cuellar JM, Alataris K, Walker A, Yeomans DC, Antognini JF. Effect of high-frequency alternating current on spinal afferent nociceptive transmission. Neuromodulation. 2013;16:318–327. doi: 10.1111/ner.12015. [DOI] [PubMed] [Google Scholar]
  7. Frankenhaeuser B. Quantitative description of sodium currents in myelinated nerve fibres of xenopus laevis. Journal of Physiology (London) 1960;151:491–501. doi: 10.1113/jphysiol.1960.sp006455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gaunt RA, Prochazka A. Transcutaneously coupled, high-frequency electrical stimulation of the pudendal nerve blocks external urethral sphincter contractions. Neurorehab. Neural Repair. 2009;23:615–626. doi: 10.1177/1545968308328723. [DOI] [PubMed] [Google Scholar]
  9. Heinbockel JH. Numerical Methods for Scientific Computing. Trafford Publishing; 2005. [Google Scholar]
  10. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology (London) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Jan LY, Jan YN. Voltage-gated potassium channels and the diversity of electrical signalling. Journal of Physiology (London) 2012;590:2591–2599. doi: 10.1113/jphysiol.2011.224212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Joseph L, Butera R. Unmyelinated aplysia nerves exhibit a nonmonotonic blocking response to high-frequency stimulation. IEEE Trans Neural Syst Rehab Eng. 2009;17:537–544. doi: 10.1109/TNSRE.2009.2029490. [DOI] [PubMed] [Google Scholar]
  13. Joseph L, Butera R. High-frequency stimulation selectively blocks different types of fibers in frog sciatic nerve. IEEE Trans Neural Syst Rehab Eng. 2011;19:550–557. doi: 10.1109/TNSRE.2011.2163082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Leob GE. Neural prosthetic interfaces with the nervous system. Trends in Neurosciences. 1989;12:195–201. doi: 10.1016/0166-2236(89)90071-4. [DOI] [PubMed] [Google Scholar]
  15. Rattay F. Analysis of models for extracellular fiber stimulation. IEEE Transactions on Biomedical Engineering. 1989;36:676–682. doi: 10.1109/10.32099. [DOI] [PubMed] [Google Scholar]
  16. Rattay F, Aberham M. Modeling axon membranes for functional electrical stimulation. IEEE Transactions on Biomedical Engineering. 1993;40:1201–1209. doi: 10.1109/10.250575. [DOI] [PubMed] [Google Scholar]
  17. Reboul J, Rosenblueth A. The action of alternating currents upon the electrical excitability of nerve. American Journal of Physiology. 1939;125:205–215. [Google Scholar]
  18. Rosenblueth A, Reboul J. The blocking and deblocking effects of alternating currents on nerve. American Journal of Physiology. 1939;125:251–264. [Google Scholar]
  19. Roth BJ. Mechanisms for electrical stimulation of excitable tissue. Critical Rev Biomed Eng. 1994;22:253–305. [PubMed] [Google Scholar]
  20. Roth BJ. A mathematical model of make and break electrical stimulation of cardiac tissue by a unipolar anode or cathode. IEEE Transactions on Biomedical Engineering. 1995;42:1174–1184. doi: 10.1109/10.476124. [DOI] [PubMed] [Google Scholar]
  21. Schwarz JR, Reid G, Bostock H. Action potentials and membrane currents in the human node of Ranvier. Pflügers Archiv. 1995;430:283–292. doi: 10.1007/BF00374660. [DOI] [PubMed] [Google Scholar]
  22. Song D, Raphael G, Lan N, Loeb GE. Computationally efficient models of neuromuscular recruitment and mechanics. Journal of Neural Engineering. 2008;5:175–184. doi: 10.1088/1741-2560/5/2/008. [DOI] [PubMed] [Google Scholar]
  23. Tai C, Roppolo JR, de Groat WC. Block of external urethral sphincter contraction by high frequency electrical stimulation of pudendal nerve. Journal of Urology. 2004;172:2069–2072. doi: 10.1097/01.ju.0000140709.71932.f0. [DOI] [PubMed] [Google Scholar]
  24. Tai C, de Groat WC, Roppolo JR. Simulation analysis of conduction block in unmyelinated axons induced by high-frequency biphasic electrical currents. IEEE Transactions on Biomedical Engineering. 2005a;52:1323–1332. doi: 10.1109/tbme.2005.847561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Tai C, de Groat WC, Roppolo JR. Simulation of nerve block by high-frequency sinusoidal electrical current based on the Hodgkin- Huxley model. IEEE Trans Neural Syst Rehab Eng. 2005b;13:415–422. doi: 10.1109/TNSRE.2005.847356. [DOI] [PubMed] [Google Scholar]
  26. Tai C, Roppolo JR, de Groat WC. Analysis of nerve conduction block induced by direct current. Journal of Computational Neuroscience. 2009;27:201–210. doi: 10.1007/s10827-009-0137-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Tai C, Guo D, Wang J, Roppolo JR, de Groat WC. Mechanism of conduction block in amphibian myelinated axon induced by biphasic electrical current at ultra-high frequency. Journal of Computational Neuroscience. 2011;31:615–623. doi: 10.1007/s10827-011-0329-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Tanner JA. Reversible blocking of nerve conduction by alternating-current excitation. Nature. 1962;195:712–713. doi: 10.1038/195712b0. [DOI] [PubMed] [Google Scholar]
  29. van Buyten JP, Al-Kaisy A, Smet I, Palmisani S, Smith T. High-frequency spinal cord stimulation for the treatment of chronic back pain patients: results of a prospective multicenter European clinical study. Neuromodulation. 2013;16:59–65. doi: 10.1111/ner.12006. [DOI] [PubMed] [Google Scholar]
  30. Vasylyev DV, Waxman SG. Membrane properties and electrogenesis in the distal axons of small dorsal root ganglion neurons. in vitro. Journal of Neurophysiology. 2012;108:729–740. doi: 10.1152/jn.00091.2012. [DOI] [PubMed] [Google Scholar]
  31. Wattaja JJ, Tweden KS, Honda CN. Effects of high frequency alternating current on axonal conduction through the vagus nerve. Journal of Neural Engineering. 2011;8:056031. doi: 10.1088/1741-2560/8/5/056013. [DOI] [PubMed] [Google Scholar]
  32. Waxman SG. Sodium channels, the electrogenisome and the electrogenistat: lessons and questions from the clinic. Journal of Physiology (London) 2012;590:2601–2612. doi: 10.1113/jphysiol.2012.228460. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES