Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Sep 12;4:6318. doi: 10.1038/srep06318

Male motion coordination in anopheline mating swarms

Daigo Shishika 1, Nicholas C Manoukis 2, Sachit Butail 3, Derek A Paley 4,a
PMCID: PMC4161964  PMID: 25212874

Abstract

The Anopheles gambiae species complex comprises the primary vectors of malaria in much of sub-Saharan Africa. Most of the mating in these species occurs in swarms composed almost entirely of males. Intermittent, organized patterns in such swarms have been observed, but a detailed description of male-male interactions has not previously been available. We identify frequent, time-varying interactions characterized by periods of parallel flight in data from 8 swarms of Anopheles gambiae and 3 swarms of Anopheles coluzzii filmed in 2010 and 2011 in the village of Donéguébogou, Mali. We use the cross correlation of flight direction to quantify these interactions and to induce interaction graphs, which show that males form synchronized subgroups whose size and membership change rapidly. A swarming model with damped springs between each male and the swarm centroid shows good agreement with the correlation data, provided that local interactions represented by damping of relative velocity between males are included.

Collective movement of animals exemplified by birds1,2,3, fish4,5,6, and insects7,8,9 can be broadly divided into polarized motion and unpolarized motion. For example, members of a pigeon flock3 fly in parallel, whereas swarming midges7,8,10 fly in seemingly random directions while aggregating around a single point. The swarming behavior of malarial mosquitoes in the Anopheles gambiae species complex would appear to be unpolarized, but it contains unexpectedly frequent occurrences of intermittent, parallel flight. Analysis of motion coordination between males provides insight into the cause and function of swarming behavior, furthering our understanding of mating in anophelines.

Crepuscular swarms of An. gambiae and Anopheles coluzzii, formerly the M and S “molecular forms”11, can be described as three-dimensional leks with characteristics of scramble competition by numerous males for a few females12. The behavioral and evolutionary basis of mating swarms in this species has only recently been examined in detail and observations to date suggest that it does not fall neatly into a single category12,13,14. One important area of investigation in the mating system of these malaria vectors is the nature and extent of male-male interaction in the swarm. Male-male interactions are representated in theories of lek-formation, where they range from aggression or arena defense15 to collectively increased signaling to females16 and association with successful males17.

The interactions between An. gambiae males in mating swarms have not been analyzed previously. Butail et al. obtained three-dimensional positions and velocities of swarming mosquitoes from stereoscopic video sequences and described the oscillatory motion of male mosquitoes in the swarm18 using the dynamic model of Okubo19. Evidence for interactions in mosquito swarms18 was suggested by analyzing the velocity disagreement between neighbors and for midge swarms8 using speed distributions and the statistics of spatial arrangement. For midge swarms7, Attanasi et al. showed the existence of metric-based interaction and estimated the effective interaction range using a correlation function similar to that used here. Inspired by studies of neural networks that show incidence of correlated signals20, we analyze the interaction networks in a mosquito swarm using the unit-velocity cross correlation to classify mosquito pairs as interacting or non-interacting.

Cross correlation measures the similarity between two signals taking time delay or lag into account2,3,7. The cross-correlation value of two discrete, scalar signals f(t) and g(t) with time lag m is 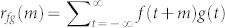Inline graphic. Maximum correlation at a positive lag m indicates that f is lagging behind g. We use as signals the three-dimensional velocity V of each mosquito obtained from stereo-video tracking in the field (see Methods). Let T be an even integer that specifies the time window in which we calculate the correlation value and · denote the vector inner product. The velocity cross correlation of mosquito i and j at time t and lag m is

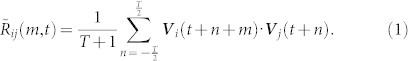graphic file with name srep06318-m1.jpg

When T = 0, 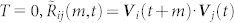Inline graphic represents an instantaneous measure of correlation; when T ≥ 2, 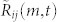Inline graphic is averaged over T + 1 video frames. Since we wish to know at each instant whether a given pair of mosquitoes is interacting, the instantaneous correlation T = 0 is problematic because it fails to reject incidental velocity alignment. Further details for choosing T are described in Methods.

The cross correlation (1) is positive when the angular disagreement in the direction of motion is less than π/2 radians; otherwise it is negative. The value (1) is also affected by flight speed in the following sense: the (absolute value of) 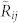Inline graphic is large when either insect is flying at high speed, even if the direction of motion is not well aligned. In order to focus on the directional alignment, we consider the unit velocity 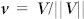Inline graphic of each mosquito and define the unit-velocity cross correlation as

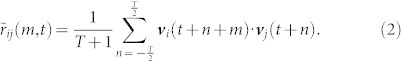graphic file with name srep06318-m2.jpg

The unit-velocity cross correlation (2) takes values in the range [−1, 1]; the value +1 (resp. −1) occurs when the direction of motion is completely parallel (resp. anti-parallel) throughout the time interval of length T. Figure 1 illustrates the calculation of the unit-velocity cross correlation. Although the unit-velocity cross correlation ignores speed (i.e., velocity magnitude), its value is easier to interpret than the velocity cross correlation because it represents the degree of alignment in the direction of motion.

Figure 1. Calculation of unit-velocity cross correlation.

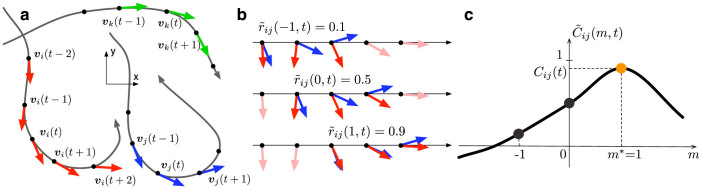
Figure 1

Open in a new tab

(a), Three hypothetical flight trajectories and direction of motion projected on a plane (actual calculation is performed with three-dimensional velocities). Mosquito k is included to show the risk of using T = 0; i.e., vi(t+2) and vk(t) are well aligned, which leads to a high correlation value 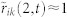Inline graphic, although there is no motion coordination between i and k. (b), Calculation of cross correlation (2) between i and j with T = 2, using three data points from each trajectory. Cross correlation between vi and vj at time t is shown for lags m = −1, 0, and +1. (c), Determining the optimal lag m* and cross correlation Cij(t) by choosing the peak from 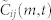Inline graphic. A positive lag indicates that i is following j.

Results

Induced interaction graph

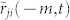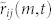The unit-velocity cross correlation measures the degree of interaction (if any) between two mosquitoes according to the alignment in their direction of motion. The choice of T = 10 is based on the average frequency (approximately 3 Hz) with which mosquitoes change their direction of motion (see Methods). The quantities Inline graphic and Inline graphic are averaged to obtain the correlation value 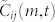Inline graphic. Using the lag value m* that maximizes 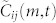Inline graphic, we obtain the correlation value 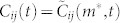Inline graphic for every pair of mosquitoes in a swarm sequence (see Methods). Figure 2a shows the probability density for the correlation values taken from 8 swarms of An. gambiae (approximately 450,000 data points). These data are compared to simulated data from a random-walk model, simulated data from a swarming model without interaction, and field data from 8 male-female coupling events (about 200 data points). Construction of the simulated swarm is described in Methods.

Figure 2. Frequency distribution of correlation values and optimal lags for real and simulated swarms.

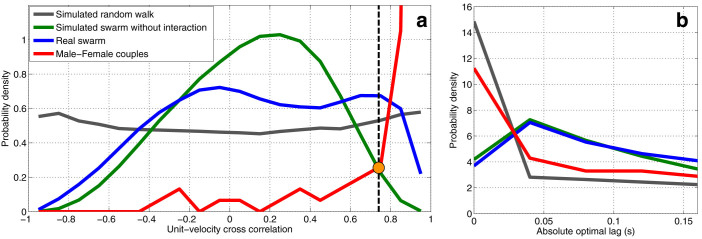
Figure 2

Open in a new tab

(a), Unit-velocity cross correlation probabilities calculated for 8 real swarms and 8 coupling flights, normalized to have unit integral. The vertical dashed line passing through the orange dot indicates the threshold for interaction. The area under each curve to the right of the threshold shows the proportion of the pairs that are classified as interacting. (b), Probability density of optimal lags calculated for interacting pairs; by symmetry, the absolute value is used.

Comparing the simulated swarm and the real swarm to the simulated random walk, we see that the first two have their peak-probability correlation values near zero, whereas the latter has an almost uniform distribution in the interval [−1, 1]. Although the simulated swarm without interaction captures some of the features of the real swarm, the real swarm exhibits an elevated probability of high correlation values as compared to the simulated swarm. To detect interactions, we define a threshold on the correlation value inspired by Bayes' decision rule21, using the intersection at 0.75 of the green curve (simulated swarm without interaction) and the red curve (male-female couples). This choice ensures minimum error rate in classification, assuming that it is equally probable for a pair of mosquitoes to be interacting or not21. We label pairs that have a correlation value greater than the threshold as interacting; otherwise we label them as non-interacting.

For an interacting pair, a nonzero lag value m* that maximizes the correlation indicates an instantaneous following behavior3. A positive lag for Cij (or a negative lag for Cji) indicates that mosquito i is following the motion of mosquito j. (Note that this does not necessarily imply i is chasing j; simply that i is matching its direction of motion to that of j.) Figure 2b shows the probability density of the optimal lags calculated for pairs defined as interacting. The male-female coupling flight has high probability at zero lag, indicating that their interactions tend to be bidirectional more often than male-male interactions. The simulated random walk has a similar distribution, but this is caused by the absence of critical points in 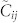Inline graphic (see Methods). The interaction lag analysis, combined with the cross-correlation threshold, induces a directed graph3,20 that describes the instantaneous interaction topology in the swarm. Each node represents a mosquito and the edges are directed towards the followers. Figure 3a depicts the instantaneous interaction graph for a real swarm. Figure 3b depicts the interval graph23. Note that, although males in the simulated swarm are not directly interacting, pairs with correlation value above the threshold are misclassified as interacting; the area under the green curve above the threshold, which corresponds to the misclassified data, accounts for less than 2% of the area under the curve.

Figure 3. Visualization of interaction network.

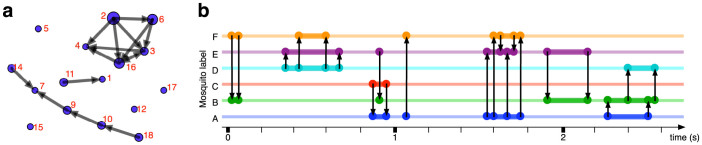
Figure 3

Open in a new tab

(a), Visualization of interaction graph generated by software “SoNIA” [McFarland, D., BenderedeMoll, S., SoNIA: Social Network Image Animator. Available from http://www.stanford.edu/group/sonia]. The figure shows an instantaneous interaction graph. Each node represents a mosquito and each edge directed towards a follower represents an interaction. The size of a node is proportional to the number of incident edges originating from it. Note that the distance in this figure does not represent Euclidean distance. Nodes without edges are located randomly. The animation of the time-varying interaction graph can be found at the following link: http://youtu.be/XgfShZpwYoY. (b), Interval graph. Directed edges are shown at the starting and the ending point of each pairwise interaction. The thick line indicates that the mosquito is in an interacting state.

Features of pairwise interaction network

Here we analyze the characteristics of the interactions that occur between pairs of males in the An. gambiae swarms, as well as the subgroups that are defined by those pairwise interactions. Figure 4a plots the probability density of the distance between all pairs of males. The curve for interacting pairs lies to the left of the curve for non-interacting pairs, which indicates that an interacting pair is likely to fly closer together than a non-interacting pair. Figure 4b shows the neighbors with which each male is interacting, sorted by their relative proximity. When a male is interacting with more than one other male at the same time, the plot shows the one with the greatest correlation value. The probability of interaction decreases as the neighbor number increases. Figure 4c shows the duration of interaction (i.e., the period of time that the correlation value stays above the threshold). The resolution of this analysis is equal to the video frame rate (0.04 s).

Figure 4. Features of interaction and network.

Figure 4

Open in a new tab

(a), Probability density of distance between two males, for interacting and non-interacting pairs. (b), Probability of interacting with kth-neighbor. (c), Duration of interaction, i.e., the period of time that the correlation value stays above the threshold. (d), Probability of the size of subgroup in which a male may be included at each moment for subgroup sizes greater than one. The result is compared to a reference null model with randomized edges23. (e), Number of subgroups versus swarm size with linear regression passing through the origin.

Consider a subgroup of a swarm to be defined as the weakly connected component of an interaction graph induced as in the preceding section. A weakly connected component is a set 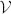Inline graphic of nodes that are connected to each other by edges; treating the edges as undirected, each node in 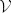Inline graphic is reachable from any other node in 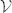Inline graphic22. For example, if i is following j and j is following k, then {i, j, k} are in the same subgroup. If i and j are both following k, they are also in the same subgroup. Figure 4d shows the instantaneous probability of the subgroup size in which a male may be included—omitting subgroup size 1, which corresponds to no interaction. In order to find the type of subgraph that is overrepresented in the mosquito swarm, called a motif23, compare the result to a randomized edges model; in this model the connected pairs are randomly shuffled while the number of edges at each time remains the same as in the real data. Figure 4e shows the number of subgroups versus swarm size in 8 swarm sequences (regression slope = 0.427, adjusted R2 = 0.612).

Simulation model with interaction

The dynamic swarming model18,19 is based on a damped, spring-like force between each insect and the swarm centroid (see Methods). Although such a central-force model reproduces the cohesive motion of males in the swarm, it does not match the unit-velocity cross correlation probability density of the real swarms (see Fig. 2a). In the real swarms, we observed a velocity-matching behavior of the males. Velocity matching can be achieved if the interacting males reduce their relative velocity. In order to model this behavior, we used a damper as the interacting force. In the augmented model, males in the interacting state are subject to an additional force modeled as a velocity damper (see Methods). The damper aligns the velocity of interacting males; only the follower feels the interaction force. For males in the interacting state, the random force is decreased proportionally to the gain λ ∈ (0, 1]. The damper is eliminated when a male is in the non-interacting state. Figure 5a illustrates the augmented swarming model. The interaction topology is determined as follows: males interact if the disagreement in the direction of their motion is less than the threshold 0.75; one is picked randomly to be the follower for the duration of interaction. Figure 5b shows the unit-velocity cross correlation of the simulation model with interaction, which has elevated probability of high values as compared to the model without velocity damping (see Methods for model parameters). Nonparametric Kruskal-Wallis comparison of the mean squared error E between the probability distributions of real and simulated data for the 8 swarms reveal a significant reduction in error (p = 0.011, χ2 = 6.35) from using the model without interaction (E = 0.072 ± 0.06) to the new model with interaction (E = 0.024 ± 0.02).

Figure 5. Augmented swarming model with interaction.

Figure 5

Open in a new tab

(a), Illustration of the augmented swarming model with five males. All five are connected to the swarm centroid by a damped spring. At the instant shown, male i is in the interacting state and is subject to the (uni-directional) force from the damper connected to j; the random force is weakened proportionally. Male j does not feel this damper force. (b), Model fit to swarming data from two real swarms of An. gambiae. The simulated swarm with interaction (red) fits the real data better than the original swarming model without interaction (green).

Differences between species

Along with data on 8 swarms of An. gambiae, we have sequences of positions from 3 swarms of An. coluzzii, formerly known as the Anopheles gambiae M form11. We performed the same unit-velocity cross correlation analysis on the flight data from An. coluzzii, and compared the results with those from An. gambiae. In order to test whether the difference in the species affects the degree of male-male interactions, we used a linear regression model with the proportion of time each male spends interacting with other males as the response variable; the species and the mean swarm size were fixed effects. Data were averaged over entire swarms. Table 1 indicates a significant positive relationship between swarm size and the proportion of time individuals spent interacting but no significant differences between the species. An interaction term for the fixed effects was included in a separate model but found to be not statistically significant (results not shown).

Table 1. Linear regression model. The effect of the species and swarm size on the proportion of time each male spends interacting with another male. Standard error (SE), t-statistics (t), and p-values (p) are shown.

source value SE t p
Intercept 0.239 0.145 1.643 0.139
Species −0.106 0.108 −0.976 0.358
Mean Swarm Size 0.025 0.009 2.772 0.024
Open in a new tab

Residual SE = 0.155 (8df); adjusted R2 = 0.469; model F2,8 = 5.418; p = 0.033

Discussion

The results presented here strongly support the hypothesis that there is significant male-male interaction in mating swarms of An. gambiae and An. coluzzii and that these interactions go beyond simple collision avoidance. Indeed, there is regular occurrence of parallel flight between pairs and within subgroups of swarming males. The presence of clusters of coordinated individuals has been found in midge swarms7. We have described a similar clustering occurring in anopheline swarms, and further studied the directed interaction to describe the time-varying interaction network. Our observation of parallel flights and the basis and function of male-male interactions have important implications on the origins of swarming behavior and for mating in An. gambiae and An. coluzzii.

Observed parallel flight behavior may result from velocity-matching behavior by each male. It is possible that males would perform velocity-matching to any nearby flying insect in a swarm to allow mate recognition via wingbeat frequency matching24 or potentially volatile pheromone communication, though as yet there is no evidence of the latter25. In mating swarms, behavioral sequences leading to insemination may be initiated by a couple matching their velocities.

A second possibility is that the observed interactions represent a means of obtaining information on what may be occurring in a part of the swarm outside an individual's perceptive range. For example, if a female enters the swarm at a point distant from a given male, but other males are responding to her by altering their flight patterns, then information may be transmitted from male to male by velocity matching. Such a scenario may be amenable to further analysis via information theory26; interestingly, males nearest to the female should be disadvantaged by communicating that fact, so data transmission in the context of the swarm may be viewed as detrimental for the transmitter but beneficial for the receiver.

A third interpretation of the interactions in the swarm is that males are competing for space in the lek, so that parallel flight is a form of ritualized aggression27 between males, such as is observed in the dragonfly Plathemis lydia28. Early theories of lek formation included elements of male-male competition (see review in29). However, this hypothesis is opposed by limits to the visual acuity of An. gambiae and An. coluzzii and by the absence of individual territories even within the denser swarm centroid, a location suggested to be advantageous for males seeking females18,30.

An important contribution of the current work is the improved model of male An. gambiae swarming over the previous approach18. The model presented here (see equations (5), (6), and (7) in Methods) includes a term representing male-male interaction: velocity correlation between males is initiated randomly, but once it occurs individuals attempt to maintain a high correlation. Incorporation of male-male interactions in an improved mathematical characterization of the swarms significantly improves the statistical fit of the model to real swarm data. Therefore the new model provides a better null hypothesis against which to test deviations from normal swarming behavior.

Male-male interactions were not found to vary significantly between species. It has been generally observed that An. coluzzii males swarm over markers of contrast on the ground, such as a well or a pile of refuse, whereas An. gambiae males swarm over bare ground13,30,31. In this respect, the degree of male-male interaction might be expected to vary between these species31, since the external marker may serve as an attractor. As a result, one might predict that a higher degree of male-male interaction is required to maintain swarm cohesion for An. gambiae, which do not swarm over a marker in the study area, compared with An. coluzzii, which do. While our analysis does not support this prediction, it is possible that a better test would require a larger dataset on An. coluzzii, similar to the one we collected for An. gambiae.

Genetic control of the degree of velocity matching may be through one or a few linked loci and thus be a trait that can drive the speciation in the An. gambiae complex32, in this case between An. gambiae and An. coluzzii. The genetic basis of male-male interaction will also be critical for any release-based program of malaria vector control such as one based on Sterile Insect Technique33 or Genetic Modification34. Such releases will almost certainly involve colony-reared males that will have to successfully inseminate wild females, probably by mating with them in swarms. Therefore understanding and regulating the genetic basis of swarming behavior for these purposes may be critical to these programs. Future experiments could include correlations between swarming behaviors and genetics to elucidate the link between the two.

Methods

Obtaining flight data

Mosquito swarms were filmed between 17 August, 2010 and 2 September, 2010 and again between 6 October, 2011 and 9 October, 2011 in the village of Donéguébogou, Mali, Africa. Donéguébogou has been the site of previous An. gambiae related research including studies on mating swarms30. The filming was performed at approximately 7 pm local time. Two identical stereo camera systems, each consisting of a pair of parallel-mounted Hitachi KP-F120CL cameras (Hitachi- Kokusai, Tokyo, Japan) with HF12.5SA-1 Fujinon lenses (Fujifilm, Valhalla, NY), an Imperx FrameLink Express frame grabber (Imperx Inc., Boca Raton, FL USA), and a 2.8 GHz quad core laptop running STREAMPIX v. 5 software (Norpix Inc, Quebec, Canada) were used to film 25 different swarms during this period. During filming, weather data such as wind velocity and temperature were recorded at 0.1 Hz with a Kestrel 4500 portable weather station (Nielsen-Kellerman, Boothwyn, PA, USA). A sample of males was captured from each swarm with a hand net for later PCR-based species identification. To transform the resulting mosquito trajectories into a world reference frame, the inclination, magnetic direction, and height of the camera system were recorded prior to filming.

Time-synchronized video data were post-processed using a multi-target tracking algorithm35. The tracking algorithm used a nonlinear estimation technique called particle filtering36 along with multi-hypothesis assignment37 to automatically reconstruct three-dimensional trajectory segments corresponding to individual mosquito flight patterns in the stereo images. Image sections were adaptively thresholded to isolate faded mosquito streaks and nonlinear optimization fitting of foreground blobs was used to resolve occlusions. Trajectory segments produced by the automatic tracking algorithm were verified and spliced together into full-length tracks using a custom graphical user interface. A total of 11 mosquito swarming events from various locations in Donéguébogou were reconstructed using this method.

Correlation value

The correlation value Cij(t) between mosquito i and mosquito j at time t with a time window T is calculated using (2) as follows:

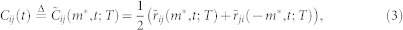graphic file with name srep06318-m3.jpg
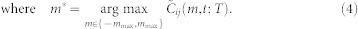graphic file with name srep06318-m4.jpg

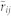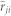Taking the mean of Inline graphic and Inline graphic ensures the relation between i and j is consistent, i.e., i and j do not lag behind each other at the same time. The parameter T affects the correlation value in various ways. First, it specifies the number of the data points used to find the similarity between the direction of motion of two mosquitoes. Therefore, a smaller value of T leads to a higher risk of detecting accidental coordination. Second, since we average the value over T + 1 frames, the true correlation may be suppressed if we choose T to be too large. Considering these two points, we base the choice of T on the frequency of the flight turns that the males make. Figure 6a shows the cumulative probability of the curvature κ in a male's flight trajectory. Using this figure, we set a threshold of 0.1 (cm−1) on the value of the curvature to define tight turns. Figure 6b shows that the interval between tight turns so defined has its peak probability at 8 frames (0.32 s). We choose T = 10 frames (0.40 s) so that these turning flights are typically included in every sliding time window.

Figure 6. Interval between tight turns.

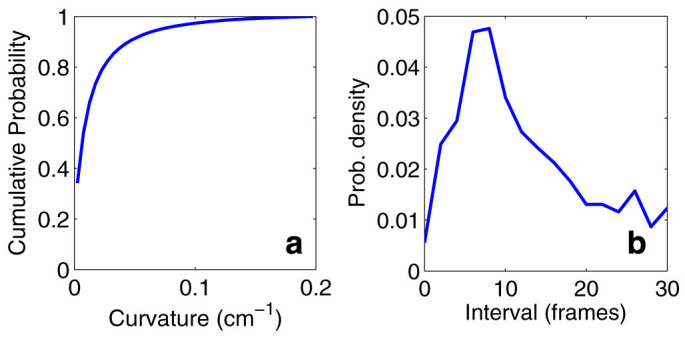
Figure 6

Open in a new tab

(a), Cumulative probability of curvature value. A tight turn is defined as a turn with curvature greater than 0.1 (cm−1). (b), Interval between tight turns. The peak is at 8 frames (0.32 s).

We set two restrictions on the optimal lag m* when we search for the maximum in (4). First, to avoid erroneous correlation, we set an upper and a lower bound on m* given by mmax = 4 frames (0.16 s), based on the frequency of the tight turns as described above. Second, since the optimal m* in terms of matching two signals should be a critical point in the curve of 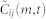Inline graphic as shown in Figure 1c, we restrict the candidates for m* to those m that achieve local maxima. When there are multiple local maxima, we use m* with the largest 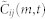Inline graphic among those candidates; when there is no critical point within the range [−mmax, mmax], then we use the value m* = 0.

Simulated swarm model

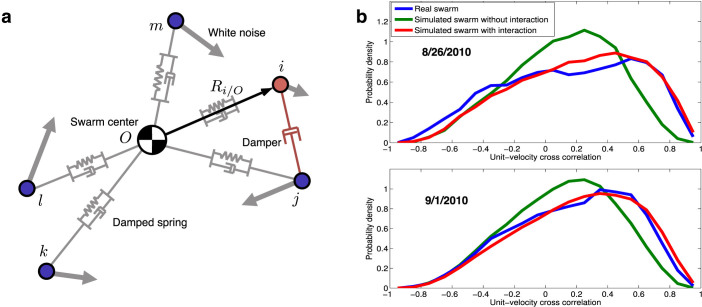
Let 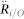Inline graphic be the acceleration of mosquito i with respect to an inertial point O and m denote the mass. Following Okubo19, we model the force on mosquito i as a linear combination of the external force 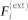Inline graphic, the drag force 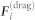Inline graphic, and the interaction force 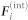Inline graphic, i.e.,

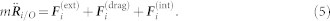graphic file with name srep06318-m5.jpg

Velocity fluctuation is modeled as a damped oscillator18; the frequency ω0 and damping ratio ξ are obtained from the velocity autocorrelation. Based on this previous analysis, we model the first two components in (5) as resulting from a damped spring that connects the mosquito to the centroid of the swarm. Let ri = Ri/O/||Ri/O||. Assuming the centroid is fixed in an inertial frame (only approximately true in real data), then we can without loss of generality attach the spring to the point O, i.e.,

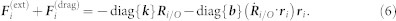graphic file with name srep06318-m6.jpg

The parameters k and b denote the three-dimensional spring and damping constants, respectively; since they are vector quantities, the spring has different constants in each direction (e.g., down-wind, cross-wind, and vertical)18. Since we do not know the internal interaction force, we assign white noise as the third component, i.e., F(int) = W, where the random process W(t) has the autocorrelation RW(τ) = Aδ(τ). The intensity A of the white noise was determined previously18. We discretize W(t) in the numerical integration with the integration time step Δt = 0.04 (s), equal to the video frame rate. Note that fitting the model to each of the 8 real swarms yields a unique set of parameters. Table 2 shows the mean and standard deviation of the parameter values from all 8 An. gambiae swarm sequences.

Table 2. Parameters for the swarm simulation. The four parameters at the bottom are used only in the simulation with interaction. Three components in each of k and b correspond to the values used for down-wind, cross-wind and vertical direction, respectively.

  mean SD units
Cohesive motion
mass of mosquito m = 10−6 N/A kg
rest length of spring l0 = 0 N/A m
spring constants k = [35, 27, 10] × 10−6 ±[23, 20, 21] × 10−6 N/m
damping constants b = [5.4, 4.5, 5.4] × 10−6 ±[2.0, 1.5, 2.7] × 10−6 N·s/m
integration time step Δt = 0.04 N/A s
intensity of random forcing 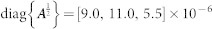Inline graphic ±[6.5, 7.1, 4.6] × 10−6 N
Interaction      
damping constant for interaction bint = 116 × 10−6 ±66 × 10−6 N· s/m
threshold for velocity alignment r* = 0.75 N/A  
gain of damping term λ = 0.73 ±0.12  
Open in a new tab

Simulated swarm model with interaction

In order to model coordinated behavior using velocity alignment, we introduce a damper between interacting males. The damper is compatible with a dynamical modeling viewpoint, in contrast to other self-propelled particle models in which agents have constant speed. Let Inline graphic denote the set of mosquitoes interacting with mosquito i and W denote white noise with zero mean and intensity A. Let Rj/i = Rj − Ri, and rj/i = Rj/i/||Rj/i||. The interaction force model is

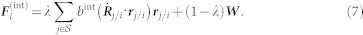graphic file with name srep06318-m7.jpg

The gain λ ∈ (0, 1] creates a convex combination of the damping force and the random force when mosquito i is in the interacting state; λ = 0 eliminates the damping term when it is in the non-interacting state. Whenever two particles are connected by a velocity damper, it decreases the relative velocity between them and increases the velocity alignment.

We created the following model for determining the interaction topology as described in Results: a pair of males interact if the agreement in their direction of motion is greater than the threshold 0.75; one of the two is picked randomly to be the follower for the duration of interaction. The remaining model parameters are the damping constant bint and the gain λ. We used a probabilistic search method called simulated annealing38 to obtain the values of bint and λ that best fit the real swarm in terms of the correlation probabilities. Table 2 shows the parameters that are used in the simulation model.

Author Contributions

D.A.P designed the study, N.C.M. and S.B collected the data, D.S., S.B. and N.C.M. analyzed the data. All authors discussed the results and analysis. D.S. and D.A.P. wrote the main text, N.C.M. wrote the Discussion, and S.B. wrote the section “Obtaining flight data“ in the Methods.

Acknowledgments

We would like to recognize the important contributions of José M. C. Ribeiro from National Institute of Allergy and Infectious Diseases. We also thank our colleagues, particularly Moussa Diallo, at the Malaria Research and Training Center (MRTC) in Bamako for assitance collecting image data. Opinions, findings, conclusions, or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of the USDA. USDA is an equal opportunity provider and employer.

References

  1. Ballerini M. et al. Empirical investigation of starling flocks: a benchmark study in collective animal behaviour. Animal Behaviour 76, 201–215 (2008). [Google Scholar]
  2. Cavagna A. et al. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 107, 11865–11870 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Nagy M., Akos Z., Biro D. & Vicsek T. Hierarchical group dynamics in pigeon flocks. Nature 464, 890–893 (2010). [DOI] [PubMed] [Google Scholar]
  4. Couzin I. D. et al. Uninformed individuals promote democratic consensus in animal groups. Science 334, 1578–1580 (2011). [DOI] [PubMed] [Google Scholar]
  5. Becco C., Vandewalle N., Delcourt J. & Poncin P. Experimental evidences of a structural and dynamical transition in fish school. Phys. A 367, 487–493 (2006). [Google Scholar]
  6. Killen S. S., Marras S., Steffensen J. F. & McKenzie D. J. Aerobic capacity influences the spatial position of individuals within fish schools. Proc. Biol. Sci. 279, 357–64 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Attanasi A. et al. Collective behavior without collective order in wild swarms of midges. Cornell University Library. 1–15 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kelley D. H. & Ouellette N. T. Emergent dynamics of laboratory insect swarms. Sci. Rep. 3 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Buhl J. et al. From disorder to order in marching locusts. Science 312, 1402–1406 (2006). [DOI] [PubMed] [Google Scholar]
  10. Okubo A. & Chiang H. C. An analysis of the kinematics of swarming of Anarete Pritchardi Kim (Diptera: Cecidomyiidae). Res. Popul. Ecol. 16, 1–42 (1974). [Google Scholar]
  11. Coetzee M. et al. Anopheles coluzzii and Anopheles amharicus, new members of the Anopheles gambiae complex. Zootaxa 3619, 246–274 (2013). [PubMed] [Google Scholar]
  12. Diabaté A. et al. Spatial distribution and male mating success of Anopheles gambiae swarms. BMC Evol. Biol. 11, 184 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Sawadogo P. S. et al. Swarming behaviour in natural populations of Anopheles gambiae and An. coluzzii: Review of 4 years survey in rural areas of sympatry, Burkina Faso (West Africa). Acta Trop (2013). [DOI] [PubMed] [Google Scholar]
  14. Howell P. I. & Knols B. G. J. Male mating biology. Malaria J. 8, S8 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Prokopy R. J. & Hendrichs J. Mating behavior of Ceratitis capitata1 on a field-caged host tree. Ann. Entomol. Soc. Am. 72, 642–648 (1979). [Google Scholar]
  16. Snow D. W. A field study of the Black and White Manakin, Manacus manacus, in Trinidad. N. Y. Zool. Soc. (1962). [Google Scholar]
  17. Beehler B. M. & Foster M. S. Hotshots, hotspots, and female preference in the organization of lek mating systems. Amer. Nat. 203–219 (1988). [Google Scholar]
  18. Butail S., Manoukis N. & Diallo M. The dance of male Anopheles gambiae in wild mating swarms. J. Med. Entomol. 50, 552–559 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. A. Okubo. Dynamical aspects of animal grouping: swarms, schools, flocks, and herds. Adv Biophys. 22, 1–94 (1986). [DOI] [PubMed] [Google Scholar]
  20. Bullmore E. & Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009). [DOI] [PubMed] [Google Scholar]
  21. Duda R. O., Hart P. E. & Stork D. G. Pattern Classification (John Wiley & Sons, 2012). [Google Scholar]
  22. Godsil C. D. & Royle G. Algebraic Graph Theory (Springer, New York, 2001). [Google Scholar]
  23. Holme P. & Saramäki J. Temporal networks. Phys. Rep. 519, 1–28 (2012). [Google Scholar]
  24. Pennetier C., Warren B., Dabiré K. R., Russell I. J. & Gibson G. “Singing on the wing” as a mechanism for species recognition in the malarial mosquito Anopheles gambiae. Curr. Biol. 20, 131–136 (2010). [DOI] [PubMed] [Google Scholar]
  25. Takken W. & Knols B. G. J. Odor-mediated behavior of Afrotropical malaria mosquitoes. Annu. Rev. Entomol. 44, 131–157 (1999). [DOI] [PubMed] [Google Scholar]
  26. Shannon C. E. A mathematical theory of communication. ACM SIGMOBILE MC2R 5, 3–55 (2001). [Google Scholar]
  27. Lorenz K. Ritualized fighting. The Natural History of Aggression 7 (1964). [Google Scholar]
  28. Matthews R. W. & Matthews J. R. Insect Behavior (Springer, The Netherlands, 2010). [Google Scholar]
  29. Bradbury J. W. [The evolution of leks] Natural Selection and Social Behavior. [138–169] (Chiron Press, New York, 1981).
  30. Manoukis N. C. & Diabate A. Structure and dynamics of male swarms of Anopheles gambiae. J. Med. Entomol. 46 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Diabaté A. et al. Spatial swarm segregation and reproductive isolation between the molecular forms of Anopheles gambiae. Proc. R. Soc. B. 276, 4215–4222 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Manoukis N. C. et al. A test of the chromosomal theory of ecotypic speciation in Anopheles gambiae. Proc. Natl. Acad. Sci. USA 105, 2940–2945 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Knipling E. F. The basic principles of insect population suppression and management. Agriculture hand-book. USDA 512 (1979). [Google Scholar]
  34. Aultman K. S., Beaty B. J. & Walker E. D. Genetically manipulated vectors of human disease: a practical overview. Trends in Parasitology 17, 507–510 (2001). [DOI] [PubMed] [Google Scholar]
  35. Butail S. et al. Reconstructing the flight kinematics of swarming and mating in wild mosquitoes. J. R. Soc. Interface. 9, 2624–2638 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ristic B., Arulampalm S. & Gordon N. J. Beyond The Kalman Filter: Particle Filters For Tracking Applications (Artech house, 2004). [Google Scholar]
  37. Reid D. An algorithm for tracking multiple targets. IEEE T. Automat. Contr. 24, 843–854 (1979). [Google Scholar]
  38. Kirkpatrick S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 34, 975–986 (1984). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES