SPONTANEOUS TRANSMEMBRANE HELIX INSERTION THERMODYNAMICALLY MIMICS TRANSLOCON-GUIDED INSERTION

Abstract

The favorable transfer free energy for a transmembrane (TM) α-helix between the aqueous phase and lipid bilayer underlies the stability of membrane proteins. However, the connection between the energetics and process of membrane protein assembly by the Sec61/SecY translocon complex in vivo is not clear. Here, we directly determine the partitioning free energies of a family of designed peptides using three independent approaches: an experimental microsomal Sec61 translocon assay, a biophysical (spectroscopic) characterization of peptide insertion into hydrated planar lipid bilayer arrays, and an unbiased atomic-detail equilibrium folding-partitioning molecular dynamics simulation. Remarkably, the measured free energies of insertion are quantitatively similar for all three approaches. The molecular dynamics simulations show that TM helix insertion involves equilibrium with the membrane interface, suggesting that the interface may play a role in translocon-guided insertion.

Introduction

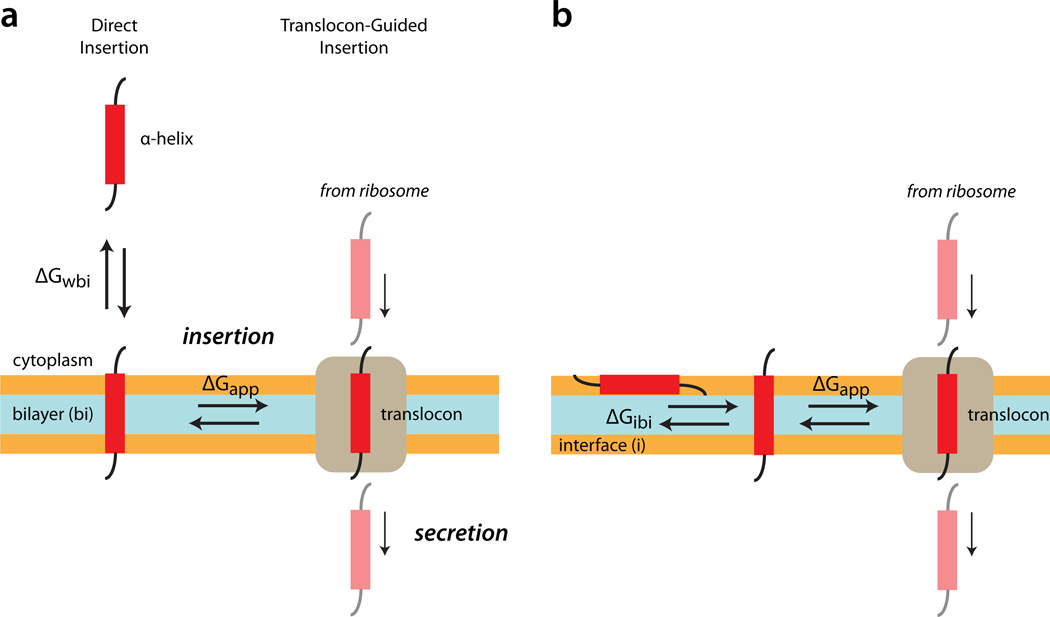
Transmembrane (TM) α-helices of proteins embedded in plasma membranes are highly enriched in amino acids with non-polar sidechains, such as leucine and isoleucine. Potential TM helices in an amino acid sequence can be identified using hydropathy plots^1,2, which are based upon the sliding-window method³. If a true thermodynamic hydrophobicity scale is used⁴ with a sliding window of about 20 amino acids, the window sum is an estimate of the free energy of transfer of an α-helix between the aqueous phase and the 30 Å-thick hydrocarbon core of the lipid bilayer (ΔG_wbi, Fig. 1a). Although this free energy is clearly relevant to the question of transmembrane helix stability, its connection to the energetics of TM helix insertion in vivo by the Sec translocon (ΔG_app, Fig. 1a) is far from clear. Understanding the connection between ΔG_wbi and ΔG_app, which is the goal of the work presented here, is crucial for a quantitative description of membrane protein assembly, folding, and stability.

Figure 1.

Schematic comparisons of spontaneous transmembrane (TM) helix insertion with translocon guided insertion. (a) The thermodynamic stability of TM helices is generally thought of as the free energy of transfer ΔG_wbi of a helix from water to bilayer. Translocon-guided Insertion of helices is characterized by an apparent free energy of transfer ΔG_app from translocon to bilayer. The fundamental question addressed in this paper is the relationship between the two free energy values. (b) All-atom equilibrium simulations presented in this paper show that helical peptides are either across the membrane (TM) or on the membrane interfaces, indicating that the actual free energy determined by the simulations ΔG_ibi is for transfer from the bilayer interface to TM. Figure based upon Fig. 7 of Schow et al.²⁴.

Membrane proteins are assembled with the aid of the heterotrimeric Sec translocon, specifically Sec61αβγ in mammals and SecYEG in bacteria^5–8. The SecY/Sec61 complex also guides the secretion of soluble proteins. Insertion and secretion of polypeptides occur cotranslationally in eukaryotes as the nascent chain emerges from translocon-docked ribosomes. The Sec61 complex acts as a switch that directs sufficiently hydrophobic segments of elongating nascent chains into the membrane as transmembrane helices while allowing more polar secreted segments to pass through the membrane into the interior of the endoplasmic reticulum (ER). The TM selection rules followed by the Sec61 complex have been determined^9,10 by means of an in vitro expression system supplemented with dog pancreas ER vesicles (rough microsomes) using hundreds of so-called H-segments inserted into a host protein, Escherichia coli leader peptidase¹¹. The rules are described by means of apparent free energies of transfer (ΔG_app) of helices between translocon and bilayer (Fig. 1).

Establishing a quantitative relationship between ΔG_app and the water-to-bilayer free energy of transfer is problematic, because direct experimental determinations of ΔG_wbi are rarely possible due to aggregation of highly hydrophobic peptides in the aqueous phase¹². Direct determinations are theoretically possible at aqueous concentrations low enough to prevent aggregation, but the concentrations required are so low as to be impractical to measure accurately in most cases. The only practical approach is to use microsecond-scale equilibrium molecular dynamics simulations, which can measure, in essence, water-to-bilayer partitioning at infinite dilution. Using this approach, Ulmschneider et al.¹³ measured the partitioning of ace-L_n-amide and ace-GGPG-L_n-GPGG-amide peptides (n = 5 … 12) into palmitoyloleoylphosphatidycholine (POPC) bilayers and compared the resulting ΔG_wbi free energies with experimental measurements¹⁴ of ΔG_app. Two important observations resulted. First, consistent with the very low aqueous solubility of hydrophobic peptides, the simulations revealed that the peptides quickly adsorbed at the membrane interface and never subsequently desorbed. The measured values of ΔG_wbi thus corresponded to transfer free energies from the bilayer interface to TM orientations across the bilayer hydrocarbon core. This observation is completely consistent with extensive studies of the interfacial partitioning of peptides². The second important observation was that the ΔG_wbi(n) values exactly paralleled the ΔG_app(n) values with a simple offset of about −2 kcal mol⁻¹ with ΔG_wbi(n).

A fundamental question is how the observed offset would be affected by changing the polarity of the H-segment. To begin answering that question, we have altered the polarity of the segment by introducing a single arginine at the center of the polyleucine H-segment. We chose arginine for three reasons. First, the introduction of a charged residue should cause a strong perturbation of H-segment polarity. Second, Arg cannot be deprotonated when inserted into the center of a lipid bilayer based upon NMR measurements¹⁵ and simulations¹⁶; this eliminates complications that might arise from protonation-deprotonation reactions. Third, the use of Arg provided an opportunity to examine further the contentious finding of Hessa et al.¹⁰ that the free energy cost $\Delta G_{\mathit{\text{app}}}^{\mathit{\text{Arg}}}$ of inserting a single arginine into the center of a TM helix is only +2 kcal mol⁻¹.

This small value of $\Delta G_{\mathit{\text{app}}}^{\mathit{\text{Arg}}}$ was contentious, because computational models predicted prohibitively large penalties of 15 kcal mol⁻¹ or more^17–26. Much of the disagreement has been due to disconnection between the quantities that the simulations and experiments actually measure. While the experimental assay measured the propensity with which the mammalian Sec61 translocon inserts 19-residue arginine-containing TM segments into the ER membrane, the computational methods calculated the free energy of burying an isolated guanidinium group in the hydrophobic core of a lipid bilayer. Attempts have been made to connect the two results via thermodynamic cycles^24–27. However, accurate determination of the free energy components of a thermodynamic cycle depends crucially on a detailed knowledge of the structural and conformational ensemble of the equilibrium states, between which the free energies are to be determined. For the translocon assay, these states are currently not known^9,10,26, while the computational free energy calculations are based on empirical assumptions about the nature of these states.

In the experiments reported here, we used three independent approaches to examine polyleucine segments carrying a central Arg residue: (a) an experimental microsomal Sec61 translocon assay, (b) spectroscopic characterization of peptide insertion into hydrated planar lipid bilayer arrays, and (c) an unbiased atomic-detail equilibrium folding-partitioning molecular dynamics simulation. Great care was taken to design the study such that all three methods could be compared directly with each other.

Direct quantification, both experimentally and computationally, of the free energy difference (ΔG) between two states requires that both states be measurably populated at equilibrium. In the present context, this is best achieved by designing TM segments that have partitioning free energies close to ΔG = 0 so that the populations of both the inserted and non-inserted states are about equal. Because the ΔG of a peptide can only be estimated at the design stage, we chose a series of symmetric polyleucine peptides of the type G-L_nRL_n-G (n = 5, 6, 7, 8). Varying the number of flanking leucine residues on either side of the central arginine allowed the partitioning free energy to be modulated systematically, with longer peptides expected to insert more favorably into the lipid bilayer than shorter segments, which cannot fully span the bilayer. This allowed selection of peptides for which ΔG could be determined accurately from the inserted- and non-inserted-state populations. A polyleucine scaffold was chosen, because it forms near perfect α-helices, thus minimizing the risk of guanidinium sidechain interactions with the peptide backbone. The peptide termini were acetylated (N-terminus) and amidated (C-terminus) to avoid kinetic barriers that arise from having to transport charged end-groups across the hydrophobic bilayer core.

Results

ΔG from the translocon assay

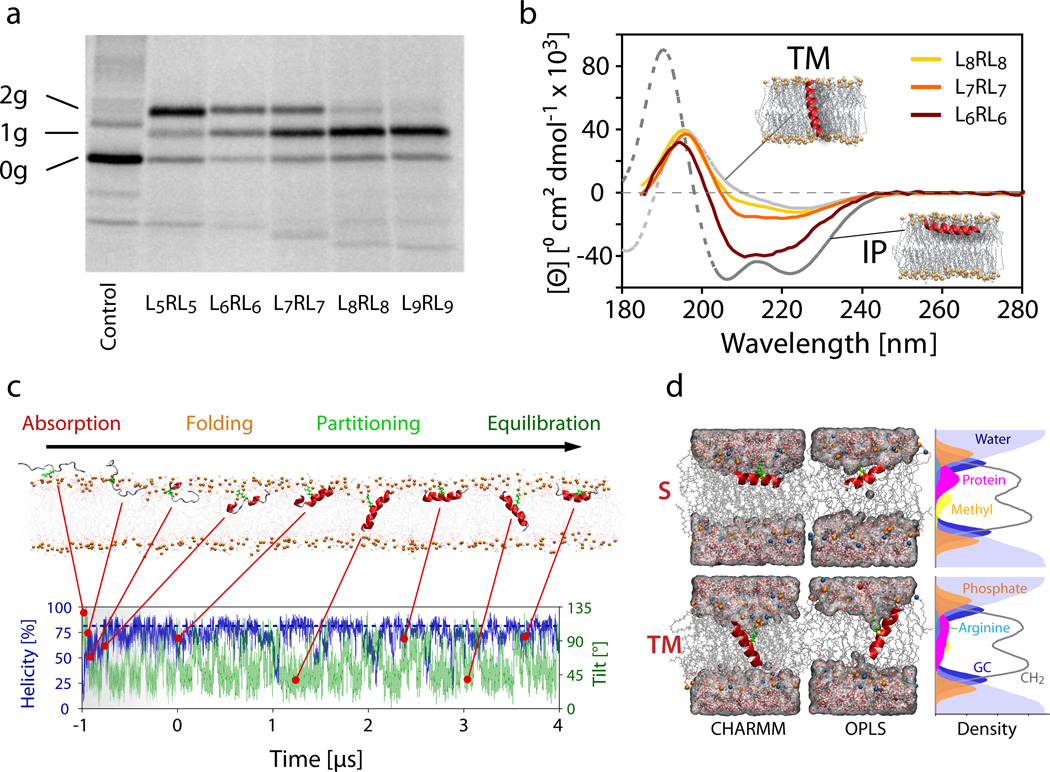
The insertion propensity of the peptides into the ER membrane was determined using a microsomal translocation assay^9,10. Each peptide sequence was introduced as an extra H-segment into the large luminal P2 domain of the model protein leader peptidase (LepB) from Escherichia coli. Each H-segment was flanked by GGPG– and –GPGG tetrapeptides at its N- and C-termini, respectively, to ‘insulate’ the H-segment from the LepB carrier protein^9,10. Glycosylation sites were placed on either side of the segment to allow quantitation of the insertion propensity. The protein was then expressed in vitro in the presence of ER-derived dog pancreas rough microsomes. Because glycosylation only takes place in the interior of the microsome, membrane-inserted segments are singly-glycosylated whereas translocated segments are doubly-glycosylated. The insertion propensity P_TM = f_1g/(f_1g + f_2g) of the segment was determined by phosphoimager scans of SDS-PAGE gels that measure the fractions of singly (f_1g) and doubly (f_2g) glycosylated proteins. As shown in Fig. 2a and Supplementary Figure 1, the SDS-PAGE results reveal that increasing the number of leucine residues shifts the insertion propensity from a predominantly non-inserted configuration (for L₅RL₅), towards a fully inserted configuration (for L₈RL₈).

Figure 2.

Experimental data for in vitro translocon-guided insertion, orientation of synthetic peptides in POPC lipid bilayers, and simulations of spontaneous insertion. (a) SDS-PAGE analysis of LepB constructs containing the GGPG-L_nRL_n-GPGG peptides as an added H-segment. Glycosylation sites on either side of the segment allow quantification of inserted (singly glycosylated, 1g) and non-inserted (doubly glycosylated, 2g) configurations. Increasing the number of leucine residues in the H-segment shifts the equilibrium from doubly to singly glycosylated peptides, with L₆RL₆ and L₇RL₇ showing substantial populations of both forms. Proteins that remain unglycosylated (0g), never entered the translocon and are excluded from the measurement. The full SDS-PAGE gel is presented in Supplementary Figure 1. (b) Oriented synchrotron radiation circular dichroism (O-SRCD) spectra of the G-WL_n-1RL_n-G peptides in stacked POPC lipid bilayers (peptide/lipid = 1/100, relative hydration = 100%). Theoretical reference spectra^31,32 for α-helical peptides oriented parallel (TM, tilt angle ≈ 0°) and perpendicular (IP, tilt angle ≈ 90°) to the membrane normal (coaxial to the light beam) are shown in grey. (c) Unbiased folding-partitioning simulation of the G-L₇RL₇-G (L₇RL₇) peptide (c.f. Table 1). Absorption and interfacial folding is rapid and typically completed within 400 ns. The arginine residue, which is highlighted in green, retains contact with the lipid head group phosphates at all times (see Supplementary Table 1). (d) Representative snapshots of the L₇RL₇ peptide simulation showing the two dominant states present at equilibrium. The configurations consist of a surface (S) adsorbed and a transmembrane (TM) inserted helical peptide, irrespective of the force field employed. The density profiles are averages over the S and TM states of the OPLS simulation of L₇RL₇ (t_S = 70 ns, t_TM = 130 ns). In the TM state, the arginine residue is buried more deeply in the hydrophobic region of the bilayer. Phosphates (orange spheres) and water are frequently pulled into the bilayer to help solvate the charged guanidinium group. The Gaussian distribution of the peptide on the bilayer leaflet is noticeably broader and reaches deeper into the hydrophobic bilayer core.

ΔG from synthetic peptides in oriented lipid bilayers

To analyze insertion of the corresponding synthetic L_nRL_n peptides, the time-averaged orientation of the peptides in oriented planar lipid bilayer arrays was determined using oriented synchrotron-radiation circular dichroism (OSRCD) spectroscopy. All four peptides were synthesized using solid-phase synthesis and purified using reverse-phase high-pressure liquid chromatography (see Supplementary Information). The sequences differed from the equivalent H-segments in that the GGPG- and -GPGG insulating flanks were replaced by a single glycine, which avoids dilution of the helical circular dichroism spectrum of the L_nRL_n segment by the unstructured flanks (see Methods). To facilitate purification and concentration measurements, the N-terminal leucine of each peptide was replaced by a tryptophan, which has the same ΔG_app as leucine in the translocon assay when near the ends the TM helices. The validity of this approach was verified by control simulations of the GWL₆RL₇G peptide, which showed the insertion probability to be identical to that of the GL₇RL₇G peptide (see Supplementary Fig. 2 and Table 1). Oriented multi-bilayer arrays were formed by depositing an organic solution containing both peptide and lipid onto quartz substrates. Highly oriented arrays form spontaneously after slow evaporation of the organic solvent followed by vapor-phase hydration at 100% relative humidity^12,28,29. Films formed in this way typically contain stacks of ~1000 bilayers highly aligned parallel to the quartz substrate, as determined by neutron diffraction³⁰.

Table 1.

Summary of simulation results for polyleucine-based peptides in POPC lipid bilayers. In the table, T = temperature, N_trans = number of insertion/exit events, <t>_TM = average lifetime of the TM state, <t>_S = average lifetime of the S state, P_TM = propensity of the TM state, and ΔG_S→TM = insertion free energy. The total simulation time was 35 µs. See Methods and Supplementary Information for details.

Peptide Sequence	Length [µs]	T [°C]	Helicity [%]	Ntrans [#]	<t>TM† [ns]	<t>S† [ns]	PTM [%]	ΔGS→TM [kcal mol−1]
GL5RL5G	4	140	64 ± 23	146	4 ± 3	49 ± 56	7.0 ± 1.6	2.1 ± 0.2
GL6RL6G	4	140	80 ± 14	259	10 ± 23	19 ± 26	35.3 ± 7.6	0.5 ± 0.3
GL7RL7G	1 + 4	140	77 ± 13	262	20 ± 1	11 ± 1	64.2 ± 5.3	−0.5 ± 0.2
GL7RL7G‡	4	140	93 ± 6	36	170 ± 219	52 ± 72	76.8 ± 11.5	−1.0 ± 0.6
GL8RL8G	4	140	79 ± 10	106	63 ± 73	10 ± 24	86.2 ± 4.7	−1.5 ± 0.3
GL6RL6G	6	90	68 ± 13	65	37 ± 65	125 ± 165	29.9 ± 24.4	0.8 ± 1.4
2× GL6RL6G*	4	140	70 ± 13	170 ± 29	14 ± 17	33 ± 39	30.2 ± 7.9	0.7 ± 0.4
GWL6RL7G	4	140	83 ± 8	163	32 ± 34	16 ± 24	65.8 ± 9.1	−0.5 ± 0.4

^†All averages are over the last 3.6 µs of the equilibrium phase of the simulations (i.e. excluding the initial folding stage, which spanned the range 50–350 ns).

^‡Control simulation with the CHARMM force field (CHARMM27 protein, CHARMM36 lipids, and TIP3P water). All other simulations were carried out with the OPLS force field (OPLS-AA protein, OPLS-UA lipids, and TIP3P water).

^*Control simulation with two peptides.

The net orientation of the synthetic peptides inside the planar POPC bilayer stacks was determined by recording SRCD spectra with the light beam perpendicular to the quartz substrate^31,32. Figure 2b shows the measured spectra together with the theoretically predicted spectra for α-helices aligned perpendicular and parallel to the bilayer normal. Spectra could only be obtained for two peptides: The spectrum of L₈RL₈ is typical for a TM helix, while the spectra for L₇RL₇ and L₆RL₆ suggest that the conformational population averages contain an increasing proportion of surface bound helical conformers. For L₆RL₆, P_TM ≈ 30–50 %, ΔG ≈ 0 to 0.5 kcal mol⁻¹) and for L₇RL₇, P_TM ≈ 70–90 %, ΔG ≈ −0.5 to −1.1 kcal mol⁻¹. The spectrum for L₅RL₅ is atypical, with peaks at 229 nm indicative of interfacial aggregates (Supplementary Figure 3).

ΔG from folding-partitioning simulations

Finally, to determine computationally the free energy of peptide insertion into the membrane of glycine-flanked segments (see Methods), we used unbiased multi-microsecond atomic-detail folding-partitioning simulations at an elevated temperature of 140 °C. We have recently demonstrated that this in silico approach allows direct quantification of the transfer free energy of thermostable peptides from the equilibrium ensembles of peptide configurations in the presence of a lipid bilayer^13,33,34. As in the synthetic implementation, the GGPG- and -GPGG insulating flanks were replaced by a single glycine, to make them identical to the synthetic implementation and to speed up partitioning kinetics, because transporting the unstructured GGPG/GPGG flanks across the hydrophobic bilayer core during transmembrane insertion of the peptide is associated with a large energetic penalty. The removal of the flanking segments has been shown not affect the overall partitioning free energies for a related series of polyleucine peptides¹³.

At the beginning of each simulation, a single peptide was placed in bulk water about 15 Å from the surface of a POPC lipid bilayer in a completely extended configuration. The peptide was then allowed to fold freely, as well as partition spontaneously into and out of the lipid bilayer. No restraints or biasing potentials were applied. Simulation timescales of <400 ns were sufficient to capture the initial non-equilibrium bilayer absorption and folding of the peptide, while a full characterization of the structural and configurational ensemble present at equilibrium typically required several microseconds. Figure 2c summarizes this method. The non-equilibrium part of the simulations is much shorter than for globular proteins of similar size. This is because the cost of a single unpaired backbone hydrogen-bonding group in the bilayer is very large² (≈5 kcal mol⁻¹), which drives rapid secondary structure formation.

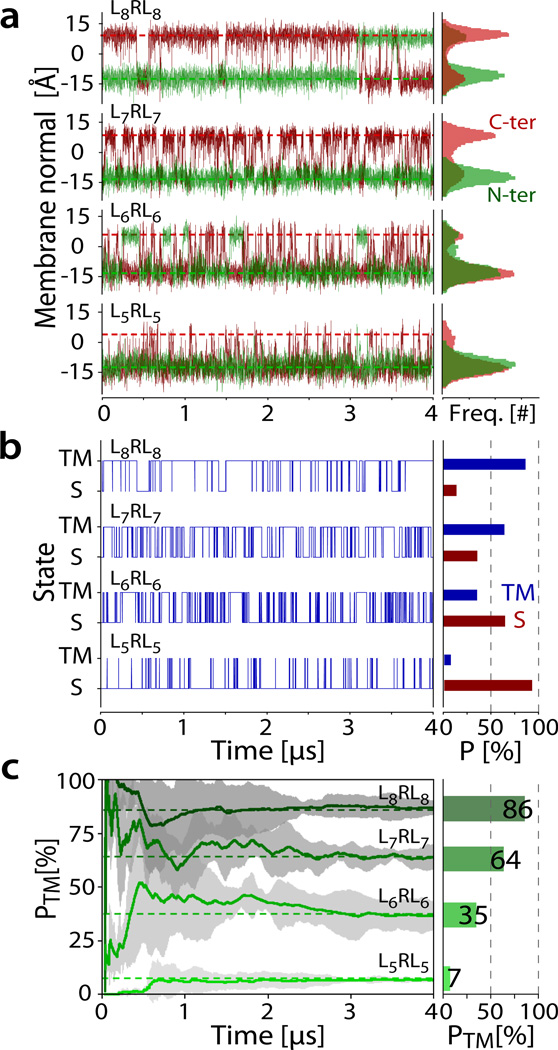
Table 1 summarizes the thermodynamic and kinetic quantities observed from the simulations. All peptides show only two states at equilibrium, with the first state (S) consisting of a surface absorbed, predominantly helical peptide tilted at an angle of ~90° with respect to the membrane normal, and the second state (TM) consisting of a transmembrane inserted helix with a tilt of ~30° (Figure 3). Each state is represented by a configurational and conformational ensemble (Supplementary Figure 4), which is dominated by helical conformers (Supplementary Figure 5). The bilayer responds to burial of the charged arginine sidechain by localized deformation (Supplementary Figure 6), caused by tight hydrogen-bonding interactions that pull down lipid phosphate headgroups into the bilayer core (Supplementary Table 1). This enables the guanidinium group to remain in contact with water even when deeply buried (Supplementary Figure 7). No bulk-phase aqueous states are sampled at equilibrium, consistent with the experimentally confirmed insolubility of the peptides. That is, only two states are observed (see Fig. 4a): interface (S) and transmembrane (TM).

Figure 3.

Quantification of the kinetics and thermodynamics of peptide partitioning derived from equilibrium simulations. (a) Analysis of the positions of the peptide N-termini (green) and C-termini (red) along the membrane normal reveals the two-state behavior of the system. (b) Peptides in the transmembrane (TM) state have one terminus at each of the two membrane interfaces, while peptides in the surface bound (S) state have both termini in the same membrane interface. This allows plotting the state transitions from the analysis of the peptide termini position along the membrane normal (panel a). Knowledge of the state as a function of simulation time allows direct determination of the S and TM population averages, as well as analysis of state lifetimes, transition rates, and related kinetics. The populations and associated free energies are given in Table 1. (c) Plots of the block-averaged TM state propensity against the simulation time shows that the systems require at least 3 µs for full convergence. The equivalent kinetics for the L₇RL₇ CHARMM simulation shows similar ΔG, but much slower kinetics (see Supplementary Figure 5).

Figure 4.

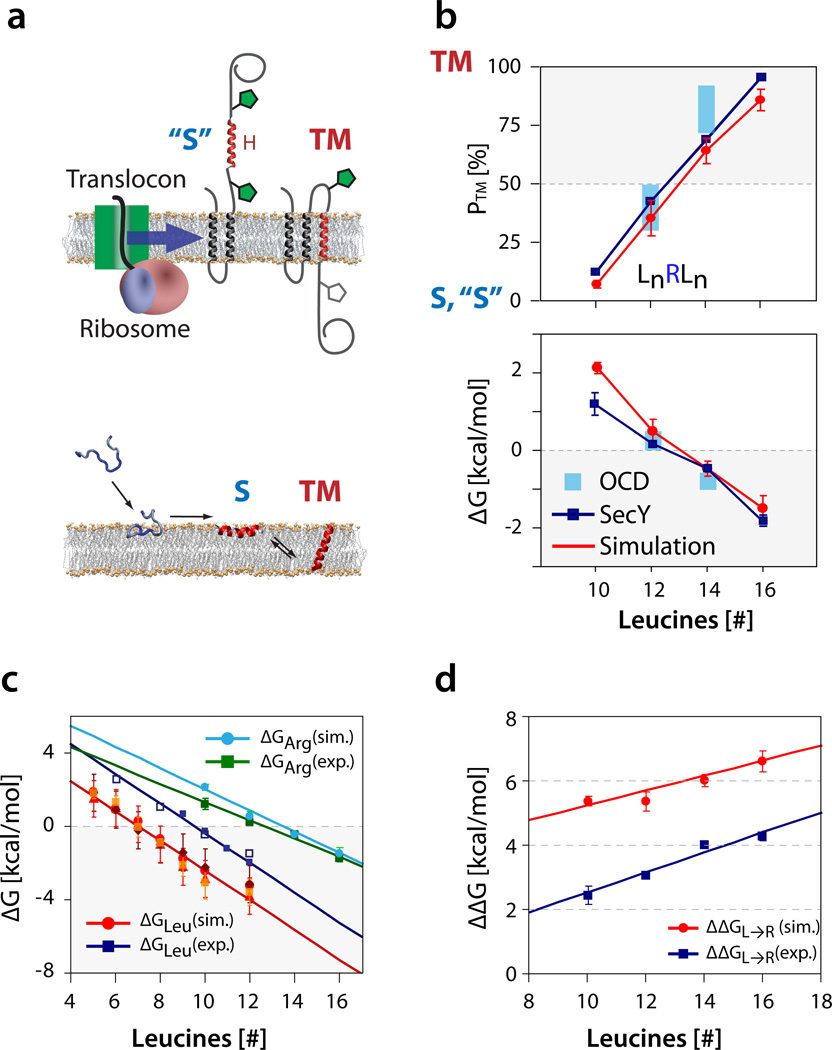
Summary of insertion L_nRL_n propensity data and comparison with L_2n data. The error bars are given by ±σ, where σ is the standard deviation of the mean. (a) Schematic comparison of translocon-guided insertion (upper panel) with simulated spontaneous partitioning (lower panel). (b) Whole-peptide partitioning propensity (P_TM) and insertion free energy (ΔG) as a function of the total number of leucines of the L_nRL_n peptides. Data in red circles () show the results from the monomeric partitioning simulations (c.f. Table 1). The blue squares () show the experimental apparent insertion propensities measured from the Sec61 translocon assay, and the green data points () show the results from the oriented circular dichroism (OCD) experiments, which could only be obtained for two peptides: L₆RL₆ (P_TM ≈ 30–50 %, ΔG ≈ 0 to 0.5 kcal mol⁻¹) and L₇RL₇ (P_TM ≈ 70–90 %, ΔG ≈ −0.5 to −1.1 kcal mol⁻¹). The structure of the singly-glycosylated species is a TM helix, the structure and configuration of the doubly-glycosylated peptide variant (corresponding to the S state) is not known, and is thus denoted “S”. (c) Comparison of polyleucine data with L_nRL_n data. The previously determined free energy of peptide insertion ΔG as a function of the total number of leucine residues (red curve) shows a ~2 kcal mol⁻¹ offset between translocon experimental values (blue) and simulation-derived values (red) for pure polyleucine sequences^13,14. However, for polyleucine sequences carrying a central arginine, the translocon-based experimental free energies (dark green) and simulation-derived partitioning free energies (light green) are almost identical. (d) The free energy penalty of replacing the central leucine with an arginine residue (ΔΔG_L→R) is calculated by subtracting the ΔG of the equivalent polyleucine (L_n) peptide from the ΔG of the L_nRL_n peptide (e.g. L₁₁ for L₅RL₅). The difference between the experimental (blue) and simulation (red) ΔΔG is almost entirely due to the constant free energy offset of the polyleucine peptides, with a small contribution due to differing slopes of the arginine-containing peptides. Due to deeper burial of the guanidinium sidechain for longer peptides, the penalty of swapping a leucine with an arginine at the center of a polyleucine segment increases linearly with peptide length (see Figure 3 and Supplementary Table 2).

The partitioning equilibrium can be summarized in a peptide-tilt versus insertion-depth free energy surface (Supplementary Figure 8). The data confirm that the equilibrium is between surface bound and transmembrane configurations for all peptides. Separation of the configurational ensemble into equilibrium states can be achieved by tracking the motion of the peptide termini along the membrane normal over the course of the simulation. Figure 3 demonstrates that this approach separates a TM configuration (where each bilayer interface hosts exactly one peptide terminus), from a surface bound one (where one interface harbors both termini). Apart from allowing an accurate quantification of the S and TM state populations, this analysis allows calculation of kinetic properties such as the number of transitions and the average lifetimes of the states. All thermodynamic and kinetic data derived from Figure 3 are summarized in Table 1, revealing a large number of equilibrium transitions between the S and TM states for all peptides.

Configurational equilibria in molecular dynamics simulations rely crucially on accurate force field parameters. To exclude a force field dependency of the results, the L₇RL₇ peptide simulation was repeated using the CHARMM force field (see Methods). This simulation showed a slightly more helical and less flexible peptide (Supplementary Figure 9). The kinetics were seven-fold slower than for the equivalent OPLS simulation, but resulted in a very similar insertion free energy (Table 1). The difference in kinetics between the OPLS and CHARMM simulations is most likely due to the united-atom (OPLS) versus all-atom (CHARMM) nature of the lipid force fields^35,36; the protein force field was all-atom in both cases.

For accurate determination of thermodynamic and kinetic quantities from folding-partitioning simulations, all thermally accessible states of the system must be fully sampled. Furthermore, great care must be taken to check that the resulting thermodynamic ensemble is fully converged and that the relative populations of the states present at equilibriums have stabilized at their equilibrium values. Tracking the running average of the TM state propensity (P_TM) shows that at least 3 µs are required for convergence (Figure 3c). Population averages derived from a higher number of transitions between states are more reliable. Because the rate of transitions between states decline exponentially with increasing free energy differences, the L₆RL₆ and L₇RL₇ peptides have the most reliable free energies (Supplementary Figure 10).

Faster convergence of the thermodynamic equilibrium was achieved when the simulation temperature was elevated to 140 °C. We have previously shown that such high temperatures do not affect the thermodynamic equilibrium, because TM helices are highly stable against thermal denaturation due to the large penalty associated with breaking a peptide hydrogen bond in the hydrophobic membrane interior¹³ and the decreased aqueous solubility of hydrophobic molecules at elevated temperatures. Consequently, the conformational ensemble of the peptide does not change measurably with temperature. We experimentally verified the thermostability of the peptides embedded in POPC vesicles using synchrotron radiation circular dichroism spectroscopy, with essentially no unfolding detected at temperatures up to 85 °C (see Supplementary Figure 11). To verify that the partitioning behaves similarly above the boiling point, we carried out a 6 µs control simulation of L₆RL₆ at 90 °C. The results show that the insertion propensity P_TM = 29.9±24.4 (s.d.) at 90 °C is similar to the 140 °C system (P_TM = 35.3 ± 7.6 (s.d.)) (see Table 1). However, the much smaller number of transitions at the lower temperature resulted in large errors and poor convergence (see Supplementary Figure 10). We estimate that even at 90 °C the simulation would have to be extended by roughly an order of magnitude to achieve the same level of convergence as the 140 °C system.

Discussion

Figure 4a compares the propensity P_TM and free energy ΔG_TM of TM insertion obtained from the simulations and experiments. Even though the OSRCD measurements could only provide estimates of the orientation state population for L₆RL₆ and L₇RL₇, the general agreement between all methods is remarkable. The results suggest that 14 or more leucine residues are sufficient for favorable TM insertion of a hydrophobic polyleucine segment containing a central arginine.

We have previously determined the transfer free energies of polyleucine peptides using both folding-partitioning simulations as well as the translocon assay described above^13,14. The contribution of the added arginine sidechain to the transfer free energies of the peptides can be estimated by subtracting the transfer free energy of the corresponding polyleucine segments. The analysis reveals that replacing a leucine with an arginine residue at the center of a polyleucine segment results in a free energy penalty that rises linearly with the length of the peptide (Figure 4b and Supplementary Table 2). The linear rise occurs because longer peptides result in deeper burial of the guanidinium group (Supplementary Figure 6). For translocon partitioning, the free energy penalty rises from 2.4 kcal mol⁻¹ for replacing the central leucine of L₁₁ with an arginine, to 4.3 kcal mol⁻¹ for L₁₇. Swapping the central leucine with an arginine is more costly in the simulations, with a penalty of 5.4 kcal mol⁻¹ for L₁₁ and a 6.8 kcal mol⁻¹ for L₁₇. The discrepancy between the experimental and simulation data seems exclusively due to the constant offset of 2 kcal mol⁻¹ observed between simulation and translocon derived insertion free energies of pure polyleucine peptides (Supplementary Table 2).

Overall, the free energy penalty for burial of a charged guanidinium group at the heart of a hydrophobic membrane-spanning segment is moderate and consistent with earlier translocon data, which measured only minor energetic penalties^9,10. The present approach suggests that using simulations to provide an atomic detail picture of the system can provide complementary insights for experimental measurements that are not possible to achieve with either approach individually. In the present case, the experimental OSRCD and translocon measurements provide time-averaged structural and energetic equilibrium data, while the simulations report the peptide configurations and dynamics in the bilayer that give rise to these thermodynamic measurements. This knowledge of the equilibrium states, between which the equilibrium is measured, is vital for the development of accurate models.

The reasons for the offset of the polyleucine partitioning free energies, especially in light of the excellent agreement between translocon and simulation data for the arginine-containing peptides presented here, are currently not clear. One interpretation might be that a charge inside the hydrophobic segment might give the translocon less leeway than a pure hydrophobic segment. It has been suggested that arginine insertion into bilayers is favorable due to dimerization²⁵. Although the simulation data show that the peptides insert efficiently as monomers this does not preclude a further lowering of the insertion free energy for dimeric TM configurations, which might reintroduce the offset between translocon and simulation data observed for pure polyleucine peptides.

To test the dimerization hypothesis, we performed a simulation with two L₆RL₆ peptides in the same bilayer patch. The results, summarized in Fig. 5, show that although the peptides meet many times during the course of the simulation, and occasionally form a common defect in the membrane, aggregates have a short lifetime. We conclude that the two peptides generally partition independently of each other, particularly because the insertion propensities P_TM = 30.2±7.9 % is similar for both peptides and close to the value observed for the single peptide simulation (35.3±7.6 %). Furthermore, the two-peptide data suggest that partitioning of the peptides is monomeric, with no further energetic gain through aggregate formation, although it should be noted that the timescale of the simulations might be too short to capture the formation of a stable aggregate.

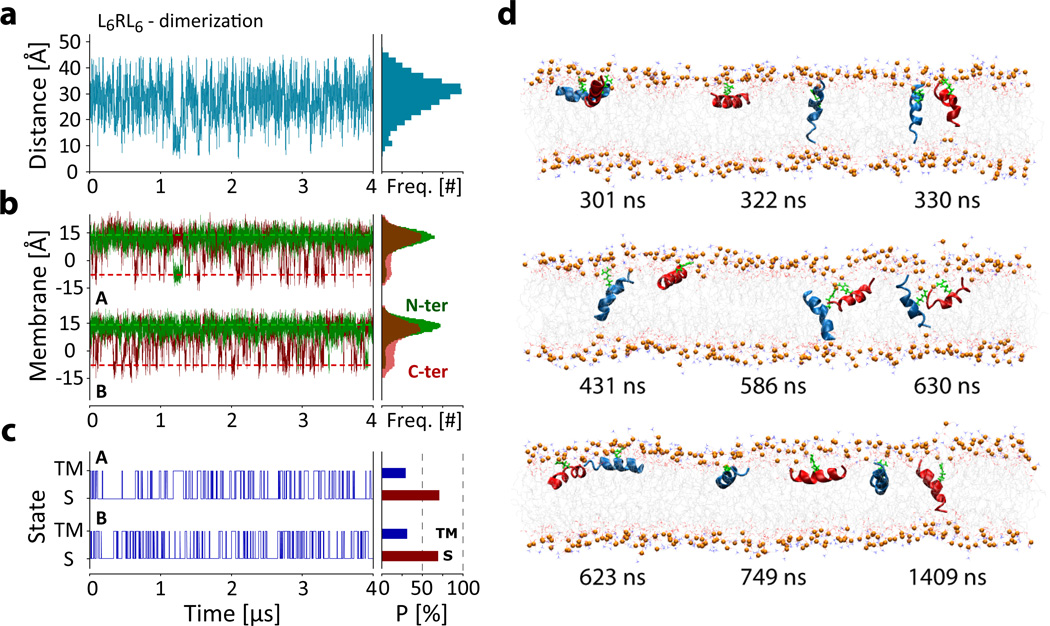
Figure 5.

Equilibrium simulation (4 µsec) of two L₆RL₆ peptides to test for dimerization. (a) Analysis of the inter-arginine distance. The figure plots the distance between the C_Z atoms of the two guanidinium sidechains. The figure shows that the peptides diffuse randomly, independent of each other and any aggregate formation is short-lived, with the longest observed contact lasting ~90 ns (at 1.17 µs). (b) Analysis of the positions of the peptide N-termini (green) and C-termini (red) along the membrane normal reveals that each peptide partitions independently of the other. (c) The state transitions from the analysis of the peptide termini position along the membrane normal (panel B) show that both peptides have similar S and TM state populations and associated free energies (see Table 1). (d) Snapshots of the dimer simulation show independent partitioning of the peptides with occasional random collision, no stable aggregate formation was observed. See movies LnRLn_dimer_side.mov and LnRLn_dimer_top.mov in online Supplementary Information.

A particularly important observation is that during the simulations the initially unfolded peptides in solution quickly partition into the lipid bilayer interface, never to leave, so that the equilibrium states observed are interfacial and transmembrane. This means that the free energies measured in the simulation are those for transferring the helices from the bilayer interface into and across the bilayer (Figure 1B). The interfacial location is expected from extensive experimental studies of the partitioning amphipathic peptides, such as melittin^37–40. A folded interfacial state is preferred because of the high cost of partitioning peptide bonds into the interface or across the bilayer². The formation of intramolecular hydrogen bonds of α-helices dramatically reduces the cost of partitioning, making the folded interfacial state the preferred state, as observed here. There is no reason to believe that interfacial folding is not also important biologically. Unless the translocon completely isolates nascent helices emerging from the ribosome, helix-interface interactions are likely to be important in translocon-guided insertion. In fact, we know that the translocon-ribosome connection is quite exposed to the cytoplasm^41–44. One might thus speculate that the membrane interface in the vicinity of the translocon plays an important role in translocon-guided TM helix insertion.

Methods

Peptide designs

Translocon experiments

The flanks of the L_nRL_n hydrophobic segment were extended to include -GGPG- at the N-terminal end and -GPGG- at the C-terminal end to insulate the hydrophobic segment from the surrounding LepB carrier protein.

Synthetic experiments

Acetyl-GWL_n-1-R-L_nG-amide (n = 5 – 8). The N-terminal leucine of each peptide was replaced with a tryptophan to aid purification and quantification of peptide concentration for the spectroscopic experiments, exploiting the average molar extinction coefficient of ε = 5,600 M⁻¹cm⁻¹ of the tryptophan indole moiety at 280 nm⁴⁵.

Computational experiments

Ace-GL_n-R-L_nG-ame (n = 5 – 8). The N- and C-termini were acetylated (ace) and amidated (ame), respectively, to reduce the kinetic barrier associated with TM insertion of the peptide, which involves transport of a polar peptide terminus across the hydrophobic membrane core.

Sec61 translocon insertion assay

Enzymes and chemicals

Unless stated otherwise, all chemicals were from Sigma-Aldrich (St. Louis, MO). Oligonucleotides were purchased from MWG Biotech AG (Ebersberg, Germany). Pfu Turbo DNA polymerase was purchased from Agilent Technologies. All other enzymes were from Fermentas. The plasmid pGEM-1 and the TNT® SP6 Transcription/Translation System were from Promega. [³⁵S]Met was from PerkinElmer.

DNA manipulations

All LepB constructs used carried one acceptor site for N-linked glycosylation in positions 97–99 (Asn-Ser-Thr) and the naturally present acceptor site in positions 215–217 (Asn-Glu-Thr). LepB constructs encoding H-segments with different numbers of leucines were generated by modifying the lepB gene in the pGEM-1 vector containing SpeI and KpnI restriction sites⁹. Double-stranded oligonucleotides encoding H segments with GGPG/GPGG flanks including either N-terminally a SpeI or C-terminally a KpnI restriction site were created by annealing two pairs of complementary oligonucleotides with overlapping overhangs. All sequences encoding different H segments and the pGEM-1 vector were digested with SpeI and KpnI, followed by insertion of the H segments into the cut vector by ligation. Oligonucleotides were diluted to a concentration of 20 µM. 20 µl of each forward and reverse complementary segments (sample 1: forward1 + reverse1; sample 2: forward2 + reverse2) were mixed with 4.4 µl annealing oligonucleotide buffer (20 mM Tris-HCL pH 7.4, 20 mM MgCl₂ and 500mM NaCl) and heated at 85 °C for 10 minutes. Samples were left in the heating block until the temperature was below 30 °C. 20 µl each of the annealed samples 1 and 2 were mixed and heated at 65 °C for 5 minutes. Samples were left in the heating block until the temperature was below 30 °C. The annealed H segment was ligated into the cut vector overnight at 16 °C followed by transformation. All inserts and mutagenesis were confirmed by sequencing of plasmid DNA at Eurofins MWG Operon (Ebersberg, Germany). Oligonucleotide sequences were as follows:

• L₅RL₅: Forward first part: 5’-P-CTAGTGGTGGTCCTGGActgcttctgcttctgcgtctg-3’; forward second part: 5’-P-cttctgcttctgGGACCTGGTGGGGTAC-3’; reverse first part: 5’-P-cagaagcagTCCAGGACCACCA-3’; reverse second part: 5’-P-CCCACCAGGTCCcagaagcagaagcagacgcagaag-3’

• L₆RL₆: Forward first part: 5’-P-CTAGTGGTGGTCCTGGActgctgcttctgcttctgcgtctg-3’; Forward second part: 5’-P-cttctgcttctgctgGGACCTGGTGGGGTAC-3’; reverse first part: 5’-P-cagaagcagcagTCCAGGACCACCA-3’; reverse second part: 5’-P-CCCACCAGGTCCcagcagaagcagaagcagacgcagaag-3’

• L₇RL₇: Forward first part: 5’-P-CTAGTGGTGGTCCTGGActgctgctgcttctgcttctgcgtctg-3’; forward second part: 5’-P-cttctgcttctgctgctgGGACCTGGTGGGGTAC-3’; reverse first part: 5’-P-cagaagcagcagcagTCCAGGACCACCA-3’; reverse second part: 5’-P-CCCACCAGGTCCcagcagcagaagcagaagcagacgcagaag-3’

• L₈RL₈: Forward first part:5’-P-CTAGTGGTGGTCCTGGActgctgctgctgcttctgcttctgcgtctg-3’; forward second part: 5’-P-cttctgcttctgctgctgctgGGACCTGGTGGGGTAC-3’; reverse first part: 5’-P-cagaagcagcagcagcagTCCAGGACCACCA-3’; reverse second part: 5’-P-CCCACCAGGTCCcagcagcagcagaagcagaagcagacgcagaag-3’

• L₉RL₉: Forward first part: 5’-P-CTAGTGGTGGTCCTGGActgctgctgctgctgcttctgcttctgcgtctg-3’; forward second part: 5’-P-cttctgcttctgctgctgctgctgGGACCTGGTGGGGTAC-3’; reverse first part: 5’-P- cagaagcagcagcagcagcagTCCAGGACCACCA-3’; reverse second part: 5’-P-CCCACCAGGTCCcagcagcagcagcagaagcagaagcagacgcagaag-3’

Expression in vitro

Constructs cloned in pGEM1 were transcribed and translated in the TNT^® Quick coupled transcription/translation system. One microgram of DNA template, 1 µl of [³⁵S]Met (10 µCi; 1 Ci = 37 GBq), 1µl of RNasin, 1 µl of a mixture of all 20 natural amino amino acids minus methionine, and 1 ¼l of dog pancreas RMs were mixed with 9 µl of TNT^®lysate mix, and samples were incubated for 90 min at 30°C. The sample was mixed with SDS sample buffer¹⁰ and incubated at 90°C for 5 min before loading on a 12% SDS/polyacrylamide gel. Proteins bands were visualized in a Fuji FLA-3000 phosphoimager (Fujifilm, Tokyo, JP). The Image Gauge V 4.23 software (Fujifilm) was used to generate a 2D intensity profile of each gel lane and the multi-Gaussian fit program from the Qtiplot software package (www.qtiplot.ro) was used to calculate the peak areas of the protein bands. An apparent equilibrium constant between the membrane-integrated and non-integrated forms was calculated as: K_app = f_1g/f_2g, where f_1g is the fraction of singly glycosylated LepB molecules and f_2g is the fraction of doubly glycosylated LepB molecules. The results were then converted to apparent free energies, ΔG_app = −RT lnK_app.

Synthetic peptide experiments

Synthesis and purification

All peptides were solid-state synthesized on amide resins using standard FMOC/HBTU chemistry, purified using reverse phase high-pressure liquid chromatography (HPLC), and quantified using mass spectroscopy. The peptides were injected in 100% formic acid and separated using C4-C18 columns with acetonitrile-water gradients (0.1% TFA) and lyophilized.

Sample preparation

Samples were prepared by mixing stock solutions of peptide in trifluorethanol (TFE) and palmitoyloleoylphosphocholine (POPC) lipids in chloroform (Avanti Polar Lipids, Alabaster, AL, USA). The mixture was desolvated under a stream of nitrogen with subsequent overnight incubation under vacuum to remove all solvent traces. Vesicles were prepared by re-hydrating dry peptide/lipid films in distilled water at room temperature. Vesicles were prepared by extrusion through membranes with 200 nm pores. The peptide concentration in all samples was 30 µM, and the molar peptide/lipid ratio was 1/100. Stacked lipid bilayers were prepared by dissolving peptide/lipid mixtures in TFE and application to Suprasil quartz slides at peptide/lipid ratios of 1/20 – 1/200, and hydrating them in a specially designed sample chamber⁴⁹. The peptide concentrations of all samples were 1 mg/mL.

Synchrotron radiation circular dichroism spectroscopy⁴⁸

Circular dichroism spectra were collected at the CD-12 beamline at ANKA, Karlsruhe, Germany, the CD1 beam line at ASTRID, ISA, Århus, Denmark, and beamline 4B8 at the Beijing Synchrotron Radiation Facility (China). Oriented synchrotron radiation circular dichroism (OSRCD) spectra were collected for 8 rotation angles of the quartz substrate around the axis of the beam and averaged to limit linear dichroism effects. Data was collected from 280 to 180 nm with 1 nm resolution and 1 nm bandwidth. The response time was 2–4 s at each wavelength and each measurement was an average of 4 scans. Temperature was controlled with a Peltier device, and varied between 20 and 85 °C in 5° steps. Samples were equilibrated for at least 5 minutes at each temperature before data collection. All spectra were corrected for background scattering by subtracting the corresponding vesicle-only spectrum measured over the same temperature range. Spectral and metadata deposited in the Protein Circular Dichroism Data Bank will be released upon publication.

Molecular dynamics Simulations

Simulations were performed and analyzed with Gromacs 4.5 (www.gromacs.org)⁴⁶ and hippo beta (www.biowerkzeug.com), using the OPLS all-atom protein force field⁴⁷ in conjunction with the TIP3P water model⁴⁸. OPLS united atom lipid parameters for POPC (palmitoyloleoylphosphocholine) were taken from Ulmschneider et al.³⁵. Control simulations were carrier out with the CHARMM27 protein, and CHARMM36 lipid force fields, with TIP3P water. Electrostatic interactions were computed using PME, and a cutoff of 10 Å was used for van der Waals interactions. Bonds involving hydrogen atoms were constrained using LINCS⁴⁹. The integration time-step was 2 fs and neighbor lists were updated every 5 steps. All simulations were performed in the NPT ensemble, without any restraints or biasing potentials. Water, lipids, and the protein were each coupled separately to a heat bath with time constant τ_T = 0.1 ps using weak temperature coupling⁵⁰. Atmospheric pressure of 1 bar was maintained⁵¹ using weak semi-isotropic pressure coupling with compressibility κ_z = κ_xy = 4.6 · 10⁻⁵ bar⁻¹ and time constant τ_P = 1 ps. Before production runs all systems were equilibrated for 2–10 ns.

Free energy surfaces

The free-energy surfaces were calculated as a function of the peptide’s center-of-mass position along the membrane normal and the tilt angle. A two-dimensional normalized histogram was calculated over the equilibrium phase of the simulations. Each ‘bin’ contains the probability p_i of finding the peptide in state i. For a system in thermodynamic equilibrium, the change in free energy on going from one state to another is given by

$$\mathrm{\Delta }G=-RT\text{ln}\frac{p_1}{p_2}$$ (1)

where R is the ideal gas constant and T is the temperature. The relative free energy was calculated for each bin, and the minimum was shifted to zero.

Insertion propensity and free energy

The insertion propensity P_TM = f_TM/(f_TM + f_S) of each peptide is calculated as the probability of the peptide being in the TM state. To distinguish the TM state from the S conformations the position of the peptide termini along the membrane normal was tracked.

The insertion free energy, or ‘free energy of partitioning’ can be directly calculated from the TM state propensity using

$$\mathrm{\Delta }{G}_{S\to TM}=-RT\ln (1/P_{TM}-1)$$ (2)

Helicity

The helicities of the peptides were calculated for each residue, and then averaged over the complete sequence. A residue is considered helical if its backbone dihedral angles are within ±40° from the ideal α-helical values (Φ = −57°, Ψ = −47°).

Error estimates

In all figures, we determined error bar estimates by dividing the simulations into a series of 10 blocks of equal length, and then performing averaging for each block. The error bars are given by ±σ, where σ is the standard deviation of the mean, i.e. the standard deviation of the individual block averages with respect to the overall average.