Computational modeling of skin: Using stress profiles as predictor for tissue necrosis in reconstructive surgery

Abstract

Local skin flaps have revolutionized reconstructive surgery. Mechanical loading is critical for flap survival: Excessive tissue tension reduces blood supply and induces tissue necrosis. However, skin flaps have never been analyzed mechanically. Here we explore the stress profiles of two common flap designs, direct advancement flaps and double back-cut flaps. Our simulations predict a direct correlation between regions of maximum stress and tissue necrosis. This suggests that elevated stress could serve as predictor for flap failure. Our model is a promising step towards computer-guided reconstructive surgery with the goal to minimize stress, accelerate healing, minimize scarring, and optimize tissue use.

1. Motivation

Tissue expansion is a reconstructive surgical technique that has established itself as a reliable method to correct birth defects, burns injuries, and regions of tumor removal [20]. The procedure was introduced fifty years ago, when the first implanted balloon was successively inflated to grow skin in situ to resurface a damaged ear [43]. Since then, skin expansion has been eagerly adopted by clinicians and has revolutionized the field of plastic and reconstructive surgery. Skin expansion creates new skin with the same mechanical, hair bearing, color, and texture characteristics as the surrounding tissue, which is ideal from an aesthetic point of view [52].

In current clinical practice, a medical device that resembles a fluid-filled balloon is implanted subcutaneously and inflated gradually over a period of weeks. Skin responds to controlled over-stretch by growing in area to recover its homeostatic state [13, 53]. When the device is removed, the newly grown skin is made available for reconstructive purposes through a process called flap design [27]. Careful planning of flap design is key to successful defect repair [11]. Yet, since most efforts of pre-operative planning focus exclusively on kinematic issues [25], flap failure remains a major complication in plastic and reconstructive surgery [38]. Obviously, the plain survival of the flap has the top-most priority. However, sub-optimal flap design can also compromise healing and trigger keloid formation and hypertrophic scarring [60].

The causes of flap complications are numerous, but mechanical factors are hypothesized to play a central role [45]: Excessive tissue tension can create compression of the pedicle, compromise blood supply, and trigger tissue necrosis [58]. Figure 1 illustrates a clinical example of flap necrosis as a result of excessive tissue tension. To resurface a giant birth defect, two tissue expanders were inserted into the right leg. After the expanders were fully inflated, two flaps were designed from the newly grown tissue and advanced to cover the excised defect. Two days after flap advancement, the distal leg displayed severe flap necrosis. The necrotic tissue had to be removed in a secondary procedure to promote healing. There is a general agreement that mechanical loading greatly influences the success of the reconstructive procedure. Surprisingly, despite all these evidences, the design of tissue flaps has never been analyzed from a mechanistic point of view.

Fig. 1.

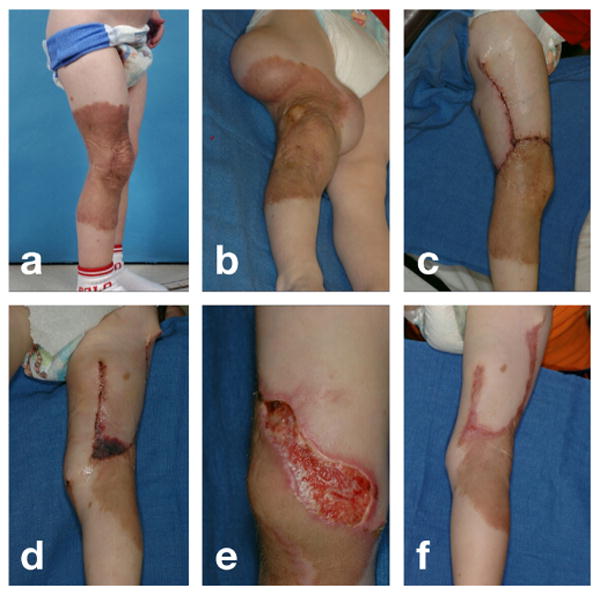
Distal flap necrosis induced by excessive tissue tension. a) Giant congenital pigmented nevus on the right lower leg of a two-year old boy. b) Tissue expanders inserted on the lateral and medial sides of the upper thigh, filled to capacity. c) Lateral leg two days after resurfacing with rotation-advancement flap from expanded lateral thigh tissue. d) Medial leg two days after resurfacing with direct-advancement flap from expanded medial thigh tissue demonstrating distal flap necrosis. e) Necrotic tissue of distal flap debrided to promote healing by secondary intention. f) Medial leg two months after flap advancement, with healing of distal aspect of flap by secondary intention.

A major cause for recurring flap failure arises from the difficulty to determine tissue stress in vivo, a problem that spans all surgical disciplines [62]. Even if mechanical cues are recognized as critical factors, measuring the stress profile in the clinical setting is virtually impossible. Computational models offer an excellent alternative to predict tissue stresses, provided the underlying constitutive models are appropriately calibrated [10, 39]. The past two decades have seen remarkable advances in computational modeling as a useful tool in surgery planning and treatment optimization [61, 64]. For skin, computational modeling has only recently received increased attention [31, 47].

Skin is a remarkable tissue and the largest organ of our body. In the adult, it covers an area of approximately 2m² and weights about 3.5kg. The main functions of skin are to protect our interior body from the outside world, to regulate temperature and water exchange, and insulate our internal machinery from harmful substances and solar radiation [49]. Additionally, skin is densely packed with neural receptors that make it our largest sensor, the one responsible for our tactile sense [12]. Although it is a very thin membrane, only 8 to 14mm thick, skin consists of three distinct layers [66]. The outermost layer, the epidermis, consists of several sublayers of cells stacked on top of one another. Cells in the inner epidermis undergo constant mitosis to continuously regenerate the epidermis; cells in the outer epidermis are dead [54]. The inner epidermis is connected to the dermis, the main load bearing layer of skin [55]. It consists of a water-based matrix that serves as a scaffold for its collagen and elastin fiber network. The hypodermis, which lies underneath the dermis, consists primarily of fat. Its function is to anchor the skin to the underlying bone and muscle tissue.

From a mechanical point of view, skin is a unique material [37]. Like in many other collagenous tissues, the collagenous network of the dermis is the key contributor to its mechanical function [33]. Skin is highly anisotropic. Its collagen bundles form an interwoven network aligned with a preferred microstructural direction [34]. This was first summarized more than a century ago in a comprehensive map of collagen orientations across the human body [32]. Collagen fibers undulation creates a characteristic non-linear response with locking stretches above which skin stiffens significantly [4, 30]. It is not surprising that determining a suitable material model for skin and accurately identifying its parameters is not a trivial task [18].

One of the pioneering constitutive models for skin used biaxial tests of rabbit skin and fitted the data to an exponential strain energy function [57]. A following, more advanced model introduced a microstructurally motivated strain energy function with separate contributions for matrix and fibers [35]. This model was recently calibrated using pig skin experiments [26]. Latterly, an invariant formulation, initially designed to model the arterial wall, was adopted to model skin [23, 44]. Several groups have tested skin in uniaxial tension [57], biaxial stretch [33], oscillatory shear [31], indentation [46], or general three-dimensional loading scenarios [16] to determine its material parameters. However, the underlying constitutive models vary from one group to another: Some assume isotropy as a pragmatic simplification [2, 14, 22], others claim that an accurate model should incorporate the anisotropic response [15, 56].

In flap design, when stress profiles are critical for pre-operative planning, we need to carefully select the constitutive model and its material parameters. An accurate model of the skin's acute behavior will improve our understanding of the chronic adaptation in response to a surgical procedure. However, determining the stress distribution during flap design poses several challenges: Following tissue expansion, the newly grown skin takes a complex three-dimensional dome-like shape [25], which needs to be stretched to resurface planar two regions [19]. During this process, skin undergoes extreme deformations including kinematic and constitutive nonlinearities, anisotropy, and stretch locking. Accurately simulating these characteristics presents tremendous opportunities for computational structural mechanics. The objective of this manuscript is to illustrate the use of computational structural mechanics to identify regions of maximum stress as potential indicators for tissue necrosis and clinical complication.

The manuscript is organized as follows. In Section 2, we summarize the constitutive equations used for the continuum mechanics modeling of skin. To model skin we use a microstructurally motivated, invariant-based, hyperelastic constitutive model. In Section 3, we present the finite element formulation of the problem. In Section 4, we investigate the two most common flap designs used following skin expansion, the direct advancement flap and the double back-cut flap. In Section 5, we draw important conclusions and discuss the potential of the proposed method to improve surgical outcomes in the plastic and reconstructive surgery field.

2. Governing equations

We begin by briefly summarizing the governing equations to model skin. Let B ⊂ ℝ³ be the reference configuration of a body that occupies S ⊂ ℝ³ in the deformed state. Material points X ∈ B are mapped to points x ∈ S trough the deformation map φ. We introduce the deformation gradient F = ▽φ as the spatial gradient of the deformation map, which relates the tangent space of the reference configuration to the tangent space of the current configuration. Due to the incompressible nature of skin, we multiplicatively decompose F into a volumetric and an isochoric part,

$$\mathit{F}={\mathit{F}}^{\text{vol}}·\overline{\mathit{F}}\text{with}{\mathit{F}}^{\text{vol}}=J^{\stackrel{1}{}/\underset{3}{}}\mathit{I}\text{and}\overline{\mathit{F}}=J^{–\stackrel{1}{}/\underset{3}{}}\mathit{F}.$$ (1)

Here, J = det(F) denotes the Jacobian, which characterizes the mapping of volume elements. Incompressibility implies that det(F̄) = 1 and, consequently, J = det(F) = det(F^vol) ≥ 0. Local deformation is represented through the right Cauchy-Green deformation tensor C and its isochoric part C̄,

$$\mathit{C}={\mathit{F}}^{\mathrm{t}}·\mathit{F}=J^{\stackrel{2}{}/\underset{3}{}}\overline{\mathit{F}}\text{with}\overline{\mathit{C}}={\overline{\mathit{F}}}^{\mathrm{t}}·\overline{\mathit{F}}.$$ (2)

To account for transverse isotropy, we introduce the preferred collagen orientation through the undeformed unit vector n₀ and its structural tensor N,

$$\mathit{N}={\mathit{n}}_0\otimes {\mathit{n}}_0\text{with}\parallel {\mathit{n}}_0\parallel =1.$$ (3)

Three principal invariants and two pseudo-invariants characterize a generic transversely isotropic constitutive behavior. Here we select the Jacobian J to represent the incompressible response, the first isochoric invariant Ī₁ to represent the isotropic response, and the fourth isochoric invariant Ī₄ to represent the anisotropic response,

$$\begin{array}{lll}J=\text{det}(\mathit{F})& & {\partial }_{C}J=\frac{1}{2}J{\mathit{C}}^{-1}\\ {\overline{I}}_1=\overline{\mathit{C}}:\mathit{I}& \text{with}& {\partial }_{\overline{C}}{\overline{I}}_1=\mathit{I}\\ {\overline{I}}_4=\overline{\mathit{C}}:\mathit{N}& & {\partial }_{\overline{C}}{I}_4.=\mathit{N}\end{array}$$ (4)

We can now define the incompressible, transversely isotropic, hyperelastic free energy function,

$$\psi ={\psi }^{\text{vol}}(J)+\overline{\psi }({\overline{I}}_1,{\overline{I}}_4)$$ (5)

which consists of a volumetric part ψ^vol and anisochoric part ψ̄, parameterized in terms of the first and fourth isochoric invariants Ī₁ and Ī₄ [17],

$$\overline{\psi }=c_0[{\overline{I}}_1-3]+\frac{c_1}{2c_2}[\text{exp}(c_2{[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]}^2)-1].$$ (6)

The first term mimics a Neo-Hookean response parameterized in terms of the shear modulus c₀ = μ / 2. The second term mimics the collagen fiber contribution parametrized in terms of c₁, and c₂. The anisotropic term acts in tension only, if Ī₄ ≥ 1, and is inactive under compressive loading, if Ī₄ < 0 [24]. In contrast to original Holzapfel model [23], this revised version accounts for a constitutive coupling of the first and fourth invariants through the additional parameter κ to incorporate microstructural fiber dispersion [17]. The lower limit of κ = 0 recovers the initial model without fiber dispersion and suppresses the constitutive coupling between the first and fourth invariants; the upper limit of κ = 1/3 mimics a random fiber dispersion associated with an isotropic response. The additive decomposition of the strain energy function translates into the decomposition of the second Piola-Kirchhoff stress,

$$\mathit{S}=2\frac{\partial \psi }{\partial \mathit{C}}={\mathit{S}}^{\text{vol}}+{\mathit{S}}^{\text{iso}},$$ (7)

into volumetric and isochoric parts,

$$\begin{array}{l}{\mathit{S}}^{\text{vol}}=2\frac{\partial {\psi }^{\text{vol}}}{\partial \mathit{C}}=Jp{\mathit{C}}^{-1}\\ {\mathit{S}}^{\text{iso}}=2\frac{\partial \overline{\psi }}{\partial \mathit{C}}=J^{-\stackrel{2}{}/\underset{3}{}}\mathbb{P}:\overline{\mathit{S}}.\end{array}$$ (8)

The scalar p = ∂ψ^vol / ∂J denotes the pressure, which we prescribe constitutively. The fourth order tensor $\mathbb{P}=\mathbb{I}-\frac{1}{3}{\mathit{C}}^{-1}\otimes \mathit{C}$ denotes the isochoric projection tensor, where $\mathbb{I}=\frac{1}{2}[\mathit{I}\overline{\otimes }\mathit{I}+\mathit{I}\underset{\_}{\otimes }\mathit{I}]$ is the fourth order identity tensor with ${\{•\stackrel{\_}{\otimes }\circ \}}_{ijkl}={\{•\}}_{ik}{\{\circ \}}_{jl}$ and ${\{•\underset{\_}{\otimes }\circ \}}_{ijkl}={\{•\}}_{il}{\{\circ \}}_{jk}$. The second order tensor

$$\overline{\mathit{S}}=2\frac{\partial \stackrel{\_}{\psi }}{\partial \overline{\mathit{C}}}=2{\overline{\psi }}_1\mathit{I}+2{\overline{\psi }}_4\mathit{N}$$ (9)

mimics the isochoric response in terms of the derivatives ψ̄_i = ∂ψ̄/∂I_t of the isochoric free energy function ¯ψ with respect to the isochoric invariants,

$$\begin{array}{ll}{\overline{\psi }}_1=& c_0+c_1\kappa [\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]\\ & \text{exp}(c_2{[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]}^2)\\ {\overline{\psi }}_4=& c_1[1-3\kappa ][\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]\\ & \text{exp}(c_2{[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]}^2).\end{array}$$ (10)

To solve for the deformation within a standard nonlinear finite element framework, we require the linearization of the Piola-Kirchhoff stress S with respect to the right Cauchy-Green deformation tensor C, which defines the fourth order tangent moduli,

$$ℂ=4\frac{{\partial }^2\psi }{\partial \mathit{C}\otimes \partial \mathit{C}}=2\frac{\partial \mathit{S}}{\partial \mathit{C}}={ℂ}^{\text{vol}}+{ℂ}^{\text{iso}},$$ (11)

which again consist of volumetric and isochoric parts,

$$\begin{array}{l}{ℂ}^{\text{vol}}=2\frac{\partial {\mathit{S}}^{\text{vol}}}{\partial \mathit{C}}=\stackrel{\sim }{p}{\mathit{C}}^{-1}\otimes {\mathit{C}}^{-1}-2Jp{\mathbb{I}}_{C^{-1}}\hfill \\ {ℂ}^{\text{iso}}=2\frac{\partial {\mathit{S}}^{\text{iso}}}{\partial \mathit{C}}=J^{-4/3}\mathbb{P}:\overline{ℂ}:{\mathbb{P}}^{\mathrm{t}}+\frac{2}{3}[J^{-\stackrel{2}{}/\underset{3}{}}\overline{\mathit{S}}:\mathit{C}\overline{\mathbb{P}}-{[\overline{\mathit{S}}\otimes {\mathit{C}}^{-1}]}^{\text{sym}}].\hfill \end{array}$$ (12)

The linearization introduces the derivative of the pressure with respect to the Jacobian, p̃ = Jp + J² ∂p/∂J. The first term in the isochoric tangent results from the derivative of S̄ with C̄,

$$\overline{ℂ}=2\frac{\partial \overline{S}}{\partial \overline{\mathit{C}}}=4[{\overline{\psi }}_{11}\mathit{I}\otimes \mathit{I}+2{\overline{\psi }}_{14}{[\mathit{I}\otimes \mathit{N}]}^{\text{sym}}+{\overline{\psi }}_{44}\mathit{N}\otimes \mathit{N}],$$ (13)

where we have used the common abbreviation, ψ̄_ij = ∂²ψ̄/∂Ī_iĪ_j, for the second derivatives of the isochoric free energy,

$$\begin{array}{ll}{\overline{\psi }}_{11}& =c_1{\kappa }^2[1+2c_2[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]]\\ & \text{exp}(c_2{[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]}^2)\\ {\overline{\psi }}_{14}& =c_1\kappa [1-3\kappa ][1+2c_2[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]]\\ & \text{exp}(c_2{[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]}^2)\\ {\overline{\psi }}_{44}& =c_1{[1-3\kappa ]}^2[1+2c_2[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]]\\ & \text{exp}(c_2{[\kappa {\overline{I}}_1+[1-3\kappa ]{\overline{I}}_4-1]}^2).\end{array}$$ (14)

The second term of the isochoric tangent introduces another fourth order projection tensor $\overline{\mathbb{P}}={\mathbb{I}}_{C^{-1}}-\frac{1}{3}{\mathit{C}}^{-1}\otimes {\mathit{C}}^{-1}$, where ${\mathbb{I}}_{C^{-1}}=\frac{1}{2}[{\mathit{C}}^{-1}\overline{\otimes }{\mathit{C}}^{-1}+{\mathit{C}}^{-1}\underset{\_}{\otimes }{\mathit{C}}^{-1}]$. The outlined derivation defines the constitutive equations in the Lagrangian setting. To obtain the Cauchy stress σ and the Eulerian tangent moduli c used in most common finite element packages, we perform push forward operations of the second Piola-Kirchhoff stress, $\sigma =\frac{1}{J}\mathit{F}•\mathit{S}•{\mathit{F}}^{\mathrm{t}}$, and the Lagrangian tangent moduli, $c=\frac{1}{J}[\mathit{F}\overline{\otimes }\mathit{F}]:ℂ:[{\mathit{F}}^{\mathrm{t}}\overline{\otimes }{\mathit{F}}^{\mathrm{t}}]$.

3. Finite element model

We performed all simulations using a commercially available, general purpose, implicit finite element solver, Abaqus/Standard Version 6.13 [1]. Our simulations followed the common two-step clinical protocol of tissue expansion: In the first step, we gradually grew skin to create skin flaps for defect repair. In the second step, we removed the defect, cut the flap, and advanced it to cover the defect region.

For the first step, to create the dome-like three-dimensional geometry for defect repair, we virtually grew skin by inflating a flat tissue sample with a computational tool previously developed and published by our group [3]. This skin growth tool was implemented as a user-defined constitutive subroutine into Abaqus/Standard [68]. We grew two different skin geometries for two different flap designs. The first geometry was a rectangular skin sample of dimension 26 × 26 × 0.5 cm³, which we discretized using 3,328 trilinear brick elements. The second geometry had dimensions of 24 × 22 × 0.5 cm³, which we discretized using 4,224 trilinear brick elements. In both cases, we used two layers of elements across the skin thickness.

To induce tissue growth, we applied pressure underneath a tissue region of 11 × 11 cm², while the surrounding tissue was fixed in space using homogeneous Dirichlet boundary conditions [68]. Computationally, this was achieved by the multiplicative decomposition of the deformation gradients into a growth part and an elastic part [3]. We modeled skin growth as a stretch-driven process, such that deforming the skin patch beyond a physiological limit translated in area growth [4]. Once we achieved the desired area gain, we released the pressure to allow for the elastic part of the deformation to vanish. The net area gain was 40.9% corresponding to 49.6 cm². Growth-induced residual stresses did not fully disappear, even after expander removal [67]. Yet, growth-induced stresses were more than an order of magnitude smaller than the physiological state of tissue pre-tension. We thus considered the resulting deflated geometry as stress free for the purpose of the flap design simulations. At the end of this step, the skin geometry was no longer a two-dimensional flat patch, but a complex three-dimensional geometry [25], similar to the complex shape that surgeons find during clinical practice [59].

For the second step, we used the grown skin geometries to simulate two common flap designs, the direct advancement flap and the double back-cut flap [65]. To account for tissue anisotropy, we converted the material parameters from pig skin for the Lanir model [35] to the Holzapfel model [17] used here. For our simulations we used c₀ = 0.0511MPa, c₁ = 0.015MPa, c₂ = 0.0418, and a fiber dispersion of κ = 0.05. To simulate flap advancement, we placed connector elements between pairs of nodes on the flap edge and on the defect edge. In Abaqus/Standard, connector elements provide an easy and versatile way to model physical mechanisms with discrete node-to-node geometry [1]. We pulled these nodes together by prescribing displacement-controlled actuation to gradually reduce the distance between two pairs of nodes to zero. This resembles the surgical scenario, in which opposite skin edges are pulled together using sutures at discrete locations.

3.1 Direct advancement flap

Figure 2 shows the schematic design of the direct advancement flap. To create this flap from our grown skin geometry, we virtually cut along the base of the expander parallel to the direction of advancement by removing the connectivity between the corresponding nodes. We then excised the damaged region adjacent to the grown skin. To complete the pre-processing of the finite element discretization, we added connector elements between pairs of nodes of the flap edge and the defect edge. This allowed us to model flap advancement by gradually reducing the distance between these pairs of nodes.

Fig. 2.

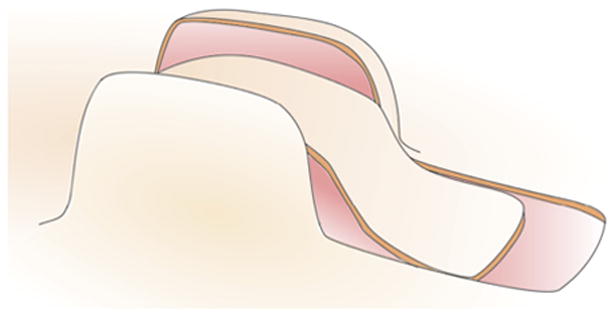
Direct advancement flap. The skin is cut along the base of the expander in the direction of advancement. The damaged tissue is removed and the flap is advanced to cover the excised area. The lateral sides of the grown skin cannot be used and are are discarded.

The direct advancement flap is the simplest of all available flap designs. Its major advantage is that it facilitates the estimate of required tissue. However, its major disadvantage is that it wastes a large amount of tissue on the lateral sides. While its handling is simple, the direct advancement flap is not the most efficient of all flap designs.

3.2 Double back-cut flap

Figure 3 illustrates schematically the design of the double back-cut flap. To create this flap from our grown skin geometry, we virtually cut along the base of the expander, parallel to the advancement direction, from the distal edge towards the middle of the expanded region. Then we cut towards the center of the expander and removed the connectivity between the corresponding nodes. We virtually excised the damaged region of tissue adjacent to the expanded skin. To control flap advancement, we added connector elements between pairs of nodes at the flap and defect edges and gradually reduced their distance to zero.

Fig. 3.

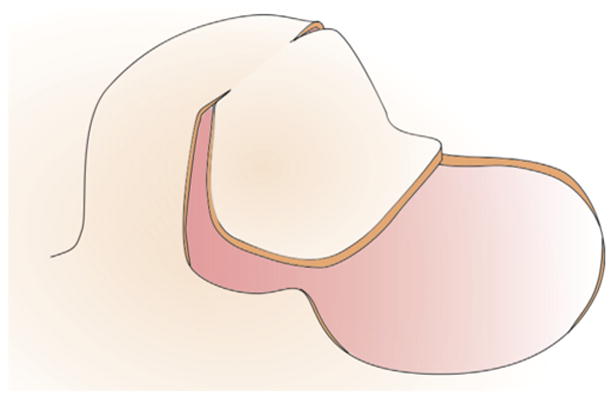
Double back-cut flap. The skin is first cut half way along the base parallel to the direction of advancement, before is is cut perpendicular towards the center. The damaged tissue is removed and the flap is advanced to cover the excised area. The lateral sides of the grown skin are partly used to cover the damaged region.

The double back-cut flap is slightly more complex than the direct advancement flap. Its major advantage is that it does not discard the newly grown skin. However, its major disadvantage is that it induces a combination of advancement and rotation, which creates a non-intuitive mechanical deformation and a rotation of Langer's lines with respect to the reference configuration. While it is efficient and resourceful in terms of tissue utilization, the double back-cut flap partially rotates the direction of maximum tissue stiffness.

4. Results

To explore the evolution of tissue tension during flap advancement, we performed two sets of simulations for each flap design, one with the collagen fibers parallel, and one with the fibers perpendicular to the direction of flap advancement.

4.1 Direct advancement flap

Figures 4 and 5 illustrate the simulation of the direct advancement flap, Figure 4 with parallel and Figures 5 with perpendicular collagen fiber orientations.

Fig. 4.

Direct advancement flap with collagen fibers oriented parallel to the direction of advancement. Color code represents the von Mises stress with maximum values at the distal and proximal edges.

Fig. 5.

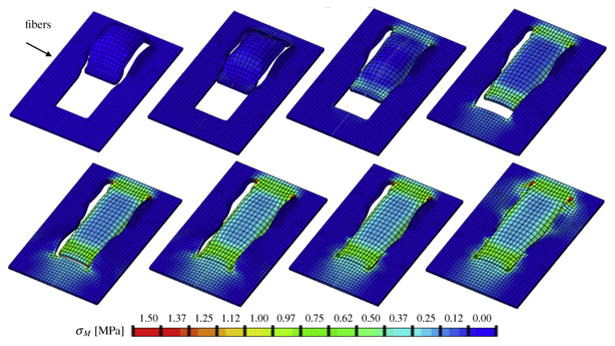
Direct advancement flap with collagen fibers oriented perpendicular to the direction of advancement. Color code represents the von Mises stress with maximum values in all four flap corners.

In both cases, maximum stresses were located at the distal and proximal edges of the flap. For the parallel orientation, maximum stresses were twice as high as for the perpendicular orientation. Figure 4 shows the highly heterogeneous stress profile for the parallel fiber orientation with maximum values of up to 2.00MPa. Figure 5 illustrates the rather smooth stress profile for the perpendicular orientation with local stress maxima of up to 1.00MPa in the flap corners. This side-by-side comparison demonstrates the importance of skin anisotropy and indicates that tissue tension can be reduced when advancing the flap perpendicular to Langer's lines rather than parallel.

4.2 Double back-cut flap

Figures 6 and 7 illustrate the simulation of the double back-cut flap, Figure 6 with parallel and Figures 7 with perpendicular collagen fiber orientations. In both cases, maximum stresses were located at the distal and proximal edges of the flap, but also at the lateral corners were skin was not only stretched along the advancement direction but also rotated towards the sides. For the parallel orientation, maximum stresses were generally higher than for the perpendicular orientation. Figure 6 shows the highly heterogeneous stress profile for the parallel fiber orientation with maximum values of up to 1.50MPa. Figure 7 illustrates the the stress profile for the perpendicular orientation with local stress maxima of up to 1.00MPa in the distal and lateral corners. This side-by-side comparison confirms the crucial role of skin anisotropy analogously to the simulations of the direct advancement flap. In agreement with engineering intuition, the double-back cut flaps adds critical regions of high stress at the lateral corners where cutting introduces sharp geometric singularities.

Fig. 6.

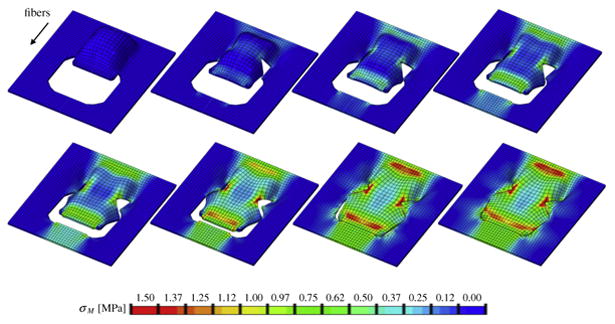
Double back-cut flap with collagen fibers oriented parallel to the direction of advancement. Color code represents the von Mises stress with maximum values at the distal and proximal edges and at the lateral region of local flap rotation.

Fig. 7.

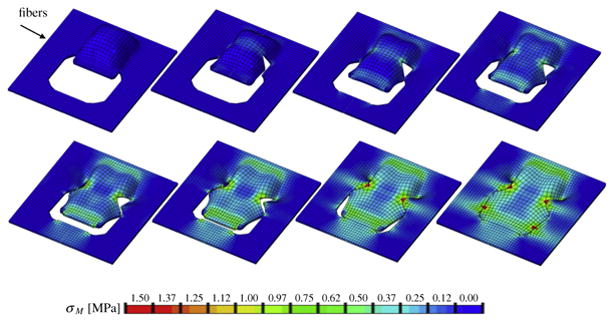
Double back-cut flap with collagen fibers oriented perpendicular to the direction of advancement. Color code represents the von Mises stress with maximum values at the corners of the distal edge and at the lateral corners of local flap rotation.

5. Discussion

In this manuscript, we have demonstrated the potential of finite element analysis in reconstructive surgery. We have presented the continuum mechanics framework to model skin as a hyperelastic, transversely isotropic material characterized by a preferred orientation of collagen fibers. Our constitutive equations are inspired by the collagenous tissue microstructure and closely follow successful models for other soft collagenous tissues [17]. We have applied our model to simulate flap design after skin expansion, a clinically relevant scenario, in which accurate prediction of stress is peremptory, yet challenging, since skin flaps undergo extreme deformations. We have simulated the direct advancement flap and the double back-cut flap, two widely popular flap designs, with collagen fibers oriented parallel and perpendicular to the direction of flap advancement.

Computational modeling is a powerful tool to predict stress profiles, especially in in vivo scenarios where it is impossible to measure stresses experimentally [9, 21,42]. Yet, their success critically depends on the appropriate calibration of the underlying constitutive model, e.g., through inverse finite element analysis [28, 51]. The outcome of a reconstructive procedure is greatly affected by the mechanical microenvironment and local stress concentrations play a critical role throughout the healing process. Extreme loading conditions on skin can dramatically impair the success of an intervention, compromise blood supply, and cause tissue necrosis [6]. Even moderate deviations from the physiological force and stretch regimes can trigger an undesired pathological response such as hypertrophic scarring [63]. Motivated by these needs, several groups are now modeling skin and use finite element methods to simulate reconstructive procedures, however, simplified to idealized geometries and isotropic responses [36]. In its physiological setting, skin is a highly anisotropic, thin, three-dimensional membrane subjected to extreme deformations [29], which we account for in the present model.

In the present model, we have neglected the effect of the hypodermis, the complaint connective tissue layer that connects the dermis to the underlying bone and muscle [68]. We have also neglected the effect of prestrain. Recent studies have shown that prestrain in living skin is of the order of 44% [7]. While incorporating prestrain would directly affect the absolute values of maximum and minimum stress, the main result of this study, the regions of maximum stress, might only be mildly affected by including prestrain. Yet, incorporating prestrain [50], damage [48], growth [3], remodeling [30], and healing [5] would be the logical next steps in refining the model towards reliably predicting the long-term success of surgical intervention.

Here we explored, for the first time, the mechanical environment of skin flap design, a relevant, yet understudied contributor to flap failure [41]. Most existing studies focus exclusively on flap kinematics and on the resourceful use of grown tissue [8, 25] while neglecting the mechanical effects of forces and stress [40]. Some are solely based on simple model systems of cutting fabric sheets, which cover a circular balloon [11]. Here we simulated and compared the stress profiles for a direct advancement flap and a double back-cut flap [65]. For the direct advancement flap, we observed stress concentrations at the distal and proximal edges, both with parallel and perpendicular fiber orientations. However, the overall stress distribution was more heterogeneous for the parallel fiber orientation with the maximum stresses about twice as large as for the perpendicular orientation. For the double back-cut flap, we found additional regions of high stress concentrations located at the lateral corners of local flap rotation. Again, maximum stresses were larger for the parallel fiber orientation as compared to the perpendicular orientation.

The results of our simulation are consistent with common complications encountered in clinical practice: While all flap designs induce high stresses at the base of the flap, the distal edge experiences peak stresses when the fibers are aligned with the direction of flap advancement. The stress concentrations at the distal edge correspond to the regions with frequent occurrence of flap necrosis [6]. Our side-by-side comparison of different flap designs and different fiber orientations allow us to make three recommendations to plastic and reconstructive surgeons: First, to minimize tissue necrosis, we recommend to pay special attention to the distal edge, where stress concentrations are highest in all four cases, but also to the proximal edge and, for the double back-cut flap, to the lateral corners. Second, to reduce peak stresses and obtain a more homogeneous stress profile, we recommend to place the expander such that the flap can be advanced perpendicular to the collagen fiber orientation. Third, to minimize the amount of wasted tissue and maximize the resurfaced area, we recommend to use the double back-cut flap, since its stress maxima are similar to those of the advancement flap, while being more resourceful.

Our simulations represent a first step towards the systematic optimization of reconstructive procedures using the nonlinear field theories of mechanics. We believe that our results set the stage for patient-specific, computer-aided pre-operative planning, which would induce a major breakthrough in plastic and reconstructive surgery.