Abstract
Generating numerical solutions to the eikonal equation and its many variations has a broad range of applications in both the natural and computational sciences. Efficient solvers on cutting-edge, parallel architectures require new algorithms that may not be theoretically optimal, but that are designed to allow asynchronous solution updates and have limited memory access patterns. This paper presents a parallel algorithm for solving the eikonal equation on fully unstructured tetrahedral meshes. The method is appropriate for the type of fine-grained parallelism found on modern massively-SIMD architectures such as graphics processors and takes into account the particular constraints and capabilities of these computing platforms. This work builds on previous work for solving these equations on triangle meshes; in this paper we adapt and extend previous two-dimensional strategies to accommodate three-dimensional, unstructured, tetrahedralized domains. These new developments include a local update strategy with data compaction for tetrahedral meshes that provides solutions on both serial and parallel architectures, with a generalization to inhomogeneous, anisotropic speed functions. We also propose two new update schemes, specialized to mitigate the natural data increase observed when moving to three dimensions, and the data structures necessary for efficiently mapping data to parallel SIMD processors in a way that maintains computational density. Finally, we present descriptions of the implementations for a single CPU, as well as multicore CPUs with shared memory and SIMD architectures, with comparative results against state-of-the-art eikonal solvers.
Keywords: Hamilton–Jacobi equation, eikonal equation, tetrahedral mesh, parallel algorithm, shared memory multiple-processor computer system, graphics processing unit
1. Introduction
The eikonal equation and its variations (forms of the static Hamilton–Jacobi and level-set equations) are used as models in a variety of applications, ranging from robotics and seismology to geometric optics. These applications include virtually any problem that entails the finding of shortest paths, possibly with inhomogeneous or anisotropic metrics (e.g., due to material properties). In seismology, for example, the eikonal equation describes the travel time of the optimal trajectories of seismic waves traveling through inhomogeneous anisotropic media [23]. In cardiac electrophysiology [20], action potentials on the heart can be represented as moving interfaces that can be modeled with certain forms for the eikonal equation [6, 14]. The eikonal equation also describes the limiting behavior of Maxwell’s equations [8], and is therefore useful in geometric optics (e.g., [5, 19]).
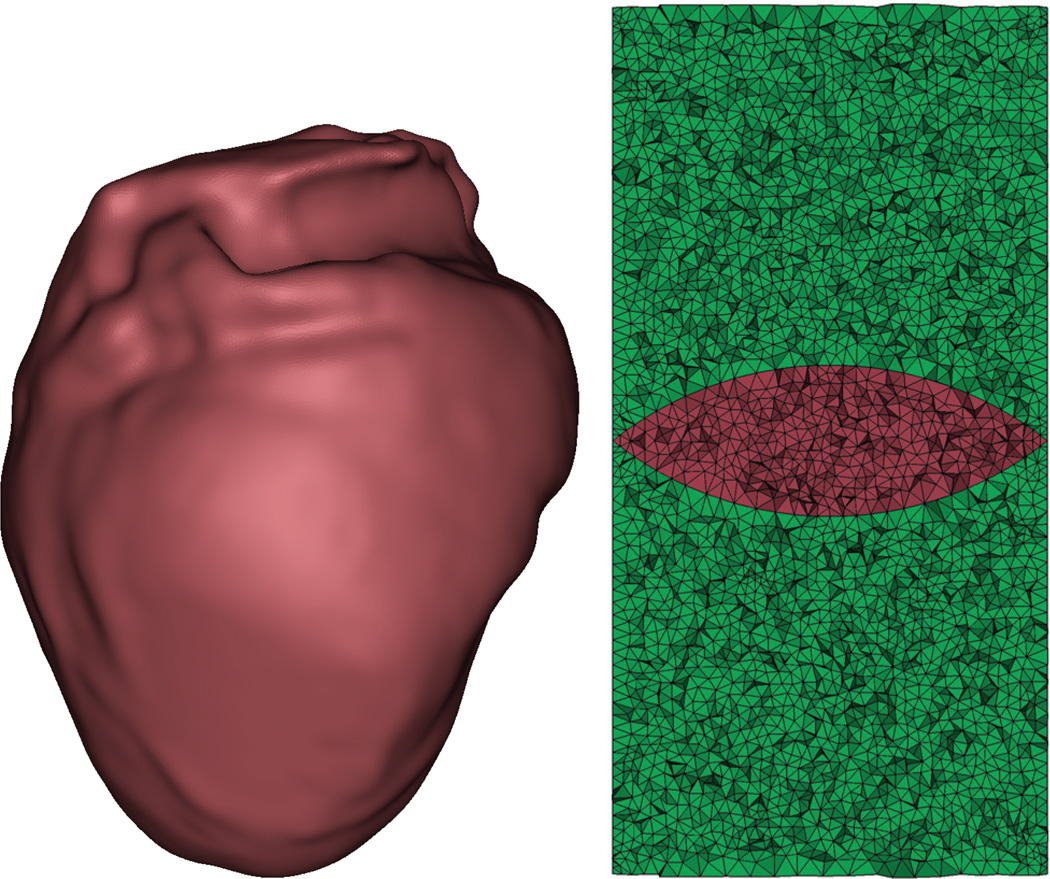
As described in [3], many of these cases present a clear need to solve such problems on fully unstructured meshes. In particular, in this work, the use of unstructured meshes is motivated by the need for body-fitting meshes. In certain problems, such as cardiac simulations, the domain is a volume bounded by a smooth, curved surface, and triangle meshing strategies for surfaces combined with tetrahedral meshing of the interior can accurately and efficiently capture these irregular domains (e.g., see Figure 1.1(left). In other problems, such as in the case of geometric optics (Figure 1.1-right) or in geophysics applications, irregular unstructured meshes allow for accurate, efficient modeling of material discontinuities that are represented as triangulated surfaces embedded in a tetrahedral mesh.
Fig. 1.1.
Examples of body-fitting meshes used for numerical simulation. On the left, we present the surface of a heart model mesh used for bioelectric computation. On the right, we present a cross section of a lens model used for the simulation of geometric optics (the green region denotes air while red denotes the location of the lens).
While solutions of the eikonal equation are used in their own right in many physical problems, such solutions are also used as building blocks in more general computational schemes such as in remeshing and in image/volume analysis (e.g., [1, 2, 4, 25]). When used as part of a more general computational pipeline, it is essential that effort be expended to minimize the computational cost of this component in an attempt to optimize the time of employing the pipeline. There is a clear need for the development of fast algorithms that provide solutions of the eikonal equation on unstructured three-dimensional (3D) meshes.
Recent developments in computer hardware show that performance improvements will no longer be driven primarily by increased clock speeds, but by parallelism and hardware specialization. Single-core performance is leveling off, while hex-core CPUs are available as commodities; soon, conventional CPUs will have tens of parallel cores. Commodity multimedia processors such as the IBM Cell and graphics processing units (GPUs) are considered forerunners of this trend. To obtain solutions in an efficient manner on these state-of-the-art single-instruction-multiple-data (SIMD)-type computer architectures places particular constraints on the data dependencies, memory access, and scale of logical operations for such algorithms.
Building an efficient 3D tetrahedral eikonal solver for multicore and SIMD architectures poses many challenges, some unique to working with 3D data. First of all, as in two dimensions, the update scheme of the solver needs to be easily parallelizable and pose no data dependencies for the active computational domain, which will change as the solution progresses. Second, representing the topology of an unstructured 3D mesh imposes a significant memory footprint compared to its two-dimensional (2D) counterpart, creating challenges in achieving the computational density necessary to make use of the limited memory, registers, and bandwidth on massively parallel SIMD machines. Third, the vertex valences of the 3D unstructured meshes can be both quite high and can be highly variable across the mesh, posing additional challenges to SIMD efficiency.
In the past several decades, many methods have been proposed to efficiently solve the eikonal equations on regular and unstructured grids. The fast marching method (FMM) by Kimmel and Sethian [15] (a triangular mesh extension of [26]) is often considered the de facto state of the art for solving the eikonal equation; its asymptotic worse case complexity, O(N logN), was shown to be optimal. It attains optimality by maintaining a heap data structure with a list of active nodes, on a moving front, that are candidates for updating. The node with the shortest travel time is considered to be solved, removed from the list, and never visited again. This active list contains only a (relatively small) subset of the nodes within the entire mesh. Though it provides worst-case optimality for the serial case, the use of a heap data structure greatly limits the parallelization of the approach. Zhao [31] and Tsai et al. [29] introduced an alternative approach, the fast sweeping method (FSM), which uses a Gauss–Seidel style update strategy to progress across the domain in an incremental grid-aligned sweep. Thismethod does not employ the sorting strategy found in FMM, and hence is amenable to coarse-grained parallelization [9, 30, 32]. The Gauss–Seidel style sweeping approach of FSM, however, is a significant limitation when attempting to build a general, efficient fine-grained parallel eikonal solver over tetrahedral meshes. Although one can do as is traditionally done in parallel computing and employ coloring techniques (e.g., red-black) to attempt to mitigate this issue [28], one cannot push this strategy to the levels needed for the fine-grain parallelization required on current streaming architectures. Furthermore, any gains through parallelism must offset any suboptimal behavior; previous work has shown that FSM introduces a large amount of excess computation for certain classes of realistic input data [12].
In this paper we put forward a new local solver specially designed for tetrahedral meshes and anisotropic speed functions, propose a data compaction strategy to reduce the memory footprint (and hence reduce costly memory loads) of the local solver, design new data structures to better suit the high valence numbers typically experienced in 3D meshes, and also propose a GPU-suitable sorting-based method to generate the gather-lists to enable a lock-free update. We also propose a new computational method to solve the eikonal equation on 3D tetrahedral meshes efficiently on parallel streaming architectures; we call our method the tetrahedral fast iterative method (tetFIM). The framework is conceptually similar to the previously proposed FIM methodology [7, 12] for trianglular meshes, but the move to three-dimensions for solving realistic physics-based problems requires two significant extensions. First is a principles-based local solver which handles anisotropic material (which is needed for realistic 3D physics-based simulations such as in geometric optics and seismology). Second is the corresponding reevaluation and redesign of the computational methodology for triangles in order to fully exploit streaming hardware in light of the additional mathematical complexities required for solving the eikonal equation in inhomogeneous, anisotropic media on fully 3D tetrahedralizations. This paper also provides algorithmic and implementation details, as well as a comparative evaluation, for two data structures designed to efficiently manage 3D unstructured meshes on GPUs. The data-structure issue is particularly important in three dimensions, because of the increased connectivity of the mesh and the need to mitigate the cost of loading 3D data to processor cores in order to keep the computational density high.
The remainder of the paper proceeds as follows. In section 2, we present the mathematical and algorithmic description of the FIM for solving the inhomogeneous anisotropic eikonal equation on fully unstructured tetrahedral domains. We then in section 3 describe how the proposed algorithm can be efficiently mapped to serial and multithreaded CPUs and to streaming architectures such as the GPU. In section 4 we provide results that compare both our CPU and GPU implementations against other widely used methods and discuss the benefits of our method. We present conclusions and future work in section 5.
2. Mathematical and algorithmic description
In this section, we describe the mathematics associated with the eikonal equation and the corresponding algorithm we propose for its solution. The main building blocks of the method are a new local solver and the active list update scheme. The local solver, upon being given a proposed solution of the eikonal equation on three of the four vertices of a tetrahedron, updates the fourth vertex value in a manner that is consistent with the characteristics of the solution. The update scheme is the management strategy for the active list, consisting of the rules for when vertices are to be added, removed, or remain on the list. We refer to the combination of these two building blocks as tetFIM.
2.1. Notation and definitions
The eikonal equation is a special case of non-linear Hamilton–Jacobi partial differential equations (PDEs). In this paper, we consider the numerical solution of this equation on a 3D domain with an inhomogeneous, anisotropic speed function:
| (2.1) |
where Ω is a 3D domain, ϕ(x) is the travel time at position x from a collection of given (known) sources within the domain, M(x) is a 3×3 symmetric positive-definite matrix encoding the speed information on Ω, and ℬ is a set of smooth boundary conditions which adhere to the consistency requirements of the PDE. We approximate the domain Ω by a planar-sided tetrahedralization denoted by ΩT. Based upon this tetrahedralization, we form a piecewise linear approximation of the solution by maintaining the values of the approximation on the set of vertices V and employing linear interpolation within each tetrahedral element in ΩT. We let M be constant per tetrahedral element, which is consistent with a model of linear paths within each element. vi denotes the ith vertex in V whose position is denoted by a 3-tuple xi = (x, y, z)T, where x, y, z ∈ ℝ. An edge is a line segment connecting two vertices (vi, vj) in ℝ3 and is denoted by ei,j. Two vertices that are connected by an edge are neighbors of each other. ei,j denotes the vector from vertex vi to vertex vj and ei,j = xj −xi. The angle between ei,j and ei,k is denoted by ∠i or ∠j,i,k.
A tetrahedron, denoted Ti,j,k,l, is a set of four vertices vi, vj, vk, vl that are each connected to the others by an edge. A tetrahedral face, the triangle defined by vertices vi, vj, and vk of Ti,j,k,l, is denoted Δi,j,k. The solid angle ωi at vertex vi subtended by the tetrahedral face vj, vk, vl is given by ωi = ξj,k + ξk,l + ξl,j, where ξj,k is the dihedral angle between the planes that contain the tetrahedral faces Δi,j,l and Δi,k,l and define ξk,l and ξl,j correspondingly. We define a tetrahedron as an acute tetrahedron when all its solid angles are smaller than 90 degrees while we define an obtuse tetrahedron as one in which one or more of its solid angles is larger than 90 degrees. We note that one can define both an acute and obtuse tetrahedron in terms of dihedral angle, which is equivalent to the proposed definition. We call the vertices connected to vertex vi by an edge the one-ring neighbors of vi, and the tetrahedra sharing vertex vi are called the one-ring tetrahedra of vi. We denote the discrete approximation to the true solution ϕ at vertex vi by Φi.
2.2. Definition of the local solver
One of the main building blocks of the proposed algorithm is the local solver, a method for determining the arrival time at a vertex assuming a linear characteristic across a tetrahedron emanating from the planar face defined by the other three vertices—whose solution values are presumed known. In this section, we define the actions of the local solver for both acute and obtuse tetrahedron.
Given a tetrahedralization ΩT of the domain, the numerical approximation, which is linear within each tetrahedron, is given by Φ(x) and is defined by specifying the values of the approximation at the vertices of the tetrahedra. The solution (travel time) at each vertex is computed from the linear approximations on its one-ring tetrahedra. From the computational point of view, the bulk of the work is in the computation of the approximations from the adjacent tetrahedra of each vertex—work accomplished by the local solver.
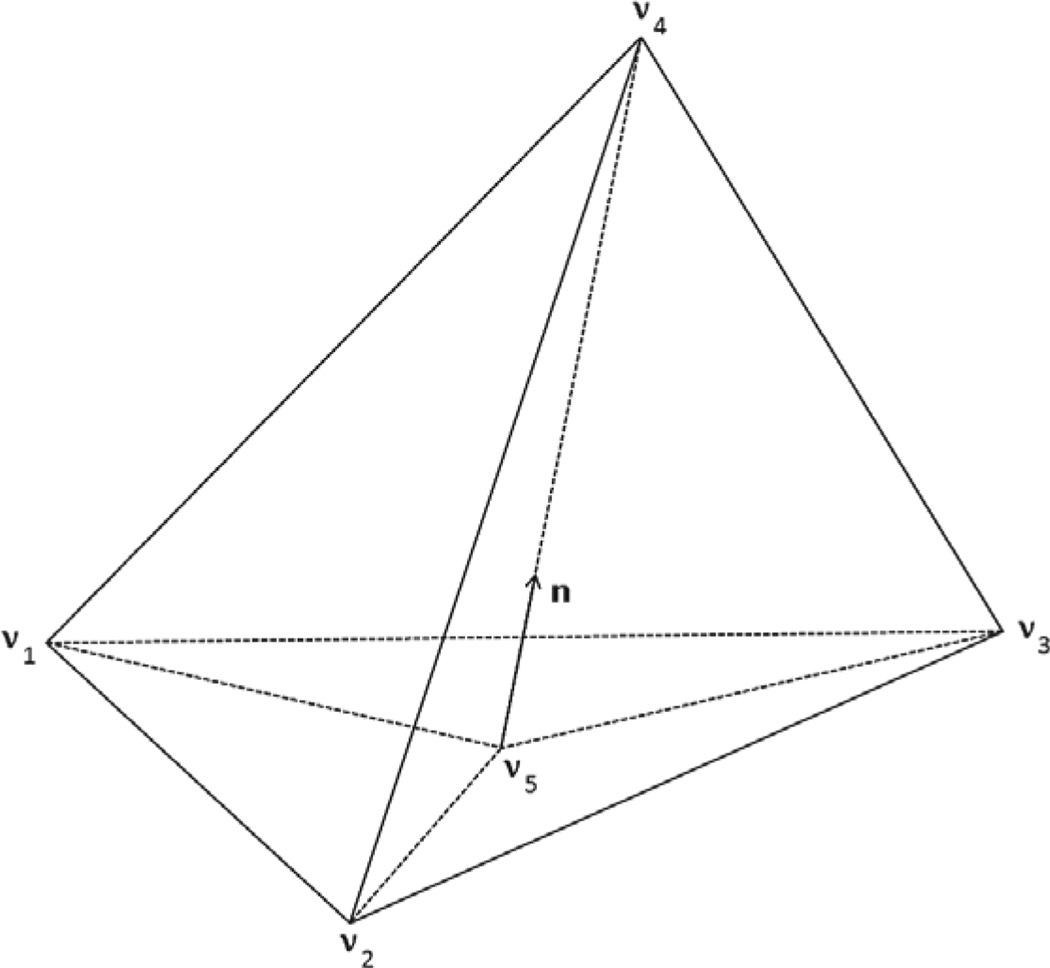
Because acute tetrahedra are essential for proper numerical consistency [15], we consider the case of acute tetrahedra first and then discuss obtuse tetrahedra subsequently. The specific calculation on each acute tetrahedron is as follows. Considering the tetrahedron T1,2,3,4 depicted in Figure 2.1, we use an upwind scheme to compute the solution Φ4, assuming the values Φ1, Φ2, and Φ3 comply with the causality property of the eikonal solutions [22]. The speed function within each tetrahedron is constant, so the travel time to v4 is determined by the time/cost associated with a line segment lying within the tetrahedron T1,2,3,4, and this line segment is along the wave front normal direction that minimizes the value at v4. The key step is to determine the normal direction n of the wavefront and establish whether or not the causality condition is satisfied. The ray that has a direction n and passes through the vertex v4 must fall inside the tetrahedron T1,2,3,4 in order to satisfy the causality condition. To check such a causality condition numerically, we first compute the coordinates of the point v5 at which the ray passing through v4 with direction n intersects the plane spanned by v1, v2, and v3 and then then check to see whether or not v5 is inside the triangle Δ1,2,3.
Fig. 2.1.
Diagram denoting components of the local solver. We compute the value of the approximation at the vertex v4 from the values at vertices v1, v2 and v3. The vector n denotes the wave propagation direction that intersects with the triangle Δ1,2,3 at v5.
We denote the travel time for the wave to propagate from the vertex vi to the vertex vj as Φi,j = Φj − Φi, and therefore the travel time from v5 to v4 is given by , according to the Fermat principle as it applies to Hamilton–Jacobi equations [29]. An alternative derivation of this principle from the perspective of geometric mechanics is given in [10]. Using the linear model within each cell and barycentric coordinates (λ1, λ2, λ3) to denote the position of v5 on the tetrahedral face, we can express the approximate solution at v5 as Φ5 = λ1Φ1+λ2Φ2+λ3Φ3, where the position is given by x5 = λ1x1+λ2x2+λ3x3. Here, λ1, λ2, λ3 satisfy that λ1 + λ2 + λ3 = 1. This gives the following expression for Φ4:
| (2.2) |
The goal is to find the location of v5 that minimizes Φ4. Thus, we take the partial derivatives of (2.2) with respect to λ1 and λ2 and equate them with zero to obtain the conditions on the interaction of the characteristic and the opposite face:
| (2.3) |
If Φ1,3 and Φ2,3 are not both zero, we have the following linear equation:
| (2.4) |
We must now solve (2.4) and either one of (2.3) for λ1 and λ2. If no root exists, or if λ1 or λ2 falls outside the range of [0, 1] (that is, the characteristic direction does not reside within the tetrahedron), we then apply the 2D local solver used in [7] to the faces Δ1,2,4, Δ1,3,4, and Δ2,3,4 and select the minimal solution from among the three. The surface solutions allow for the same constraint, and if the minimal solutions falls outside of the tetrahedral face, we consider the solutions along the edges for which we are guaranteed a minimum solution exists. Because of the quantity being minimized, there can be only one minimum, and the optimal solution associated with that element must pass through the tetrahedron or along one of its faces/edges.
In the case of parallel architectures with limited high-bandwidth memory, the memory footprint of the local solver becomes a bottleneck to performance. The smaller the memory footprint of the local solver, the higher the computational density one can achieve on the streaming processors, and the closer one gets to the 100–200× raw improvement in processing power (relative to a conventional CPU). Here we explore the algebra a little more carefully to reduce these computations to their fundamental degrees of freedom. Solving (2.3)–(2.4) directly requires storing all the coordinates of the vertices and the components of M, which is 18 floating point values in total. In practice, we can reduce the computations and memory storage based on the observation that e5,4 can be reformatted as: e5,4 = x4 − x5 = x4 − (λ1x1+λ2x2+λ3x3) = [e1,3 e2,3 e3,4]λ, where λ = [λ1 λ2 1]T. Hence we obtain
| (2.5) |
where M′ = [α β θ] with
| (2.6) |
and
| (2.7) |
Plugging (2.5), (2.6) and (2.7) into (2.3) and (2.4) we obtain
| (2.8) |
Solving (2.8) only requires storing M′, which is symmetric so only requires six floats per tetrahedron.
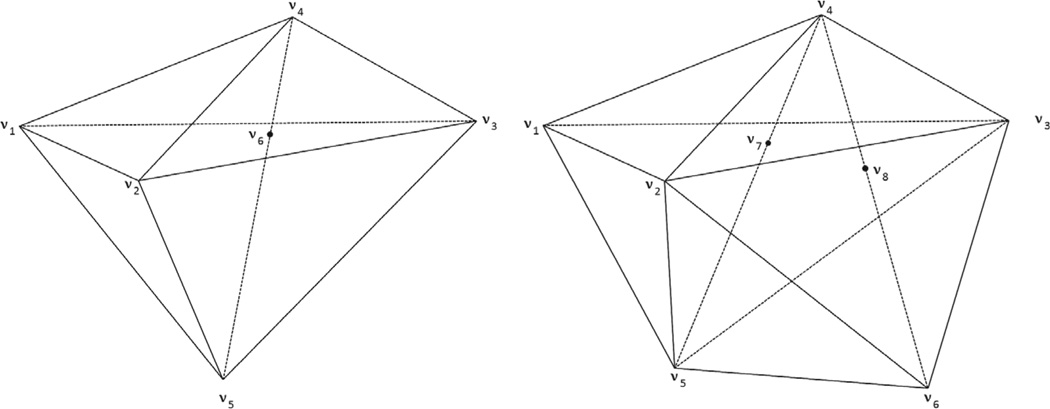
Having defined the acute tetrahedron local solver, we now discuss the case of obtuse tetrahedra. The computation of the solution for linear approximations on tetrahedral elements has poor approximation properties when applied to obtuse tetrahedra [24]. The issue of dealing with good versus bad meshes is not the main focus of this paper or the proposed algorithm, but limited incidences of obtuse tetrahedra can be addressed within the local solver. To accomplish this, we extend the method proposed in [15], originally designed for triangular meshes to work for tetrahedral meshes. As shown in Figure 2.2, where ω4 is obtuse, we connect v4 to the vertex v5 of a neighboring tetrahedron and thereby cut the obtuse solid angle into three smaller solid angles. If these three solid angles are all acute, then the process stops as shown in Figure 2.2(left); otherwise, if one of the smaller solid angles is still obtuse, then we connect v4 to the vertex v6 of another neighboring tetrahedron. This process is performed recursively until all new solid angles at v4 are acute as shown in Figure 2.2(right), or the opposite triangular faces coincides with a boundary. Note that algorithmically, these added edges and tetrahedra are not considered part of the mesh; they are considered virtual and only used within the local solver for updating the solution at v4. We cannot prove the convergence of this refinement algorithm, and the above recursion could propagate extensively throughout the mesh in extraordinary cases. In practice, the algorithm would be forced to terminate after a fixed number of splits emanating from a single vertex—in all of the meshes in this paper, the algorithm had no more than one recursion.
Fig. 2.2.
Diagram denoting the strategy used to deal with obtuse tetrahedra. We split the obtuse angle ω4 to create three virtual tetrahedra used within the local solver.
2.3. Active list update scheme
The proposed algorithm uses a modification of the active list update scheme as presented in [7, 12] combined with the new local solver described above designed for unstructured tetrahedral meshes with inhomogeneous anisotropic speed functions.
The algorithm is iterative, but for efficiency, the updates are limited to a relatively small domain that forms a collection of narrow bands that form wavefronts of values that require updating. This narrow banding scheme uses a data structure, called active list, to store the vertices or tetrahedra slated for revision and these vertices/tetrahedra are called active vertices/tetrahedra. During each iteration, active vertices/tetrahedra can be updated in parallel and after the updates of all the active vertices/tetrahedra, the active list is modified to eliminate vertices whose solutions are consistent with their neighbors and to include vertices that could be affected by the last set of updates. Convergence of the algorithm to a valid approximation of the eikonal equation was proven in [12].
3. tetFIM serial and parallel implementations
In this section, we provide implementation details in terms of methods and data structures necessary for the efficient instantiation of our local solver and active list update scheme on serial CPUs, multithreaded CPUs, and streaming SIMD parallel architectures.
3.1. Implementation on serial and multithreaded CPUs
The proposed method builds on the FIM proposed for structured meshes [12], which operates as follows. Nodes on the active list are revised individually, and the corresponding values remain consistent with their upwind neighbors. Then, each updated value immediately overwrites the previous solution. The algorithm runs through the active list, constantly revising values, and at the end of the list, it loops back to the beginning. As such, the list has no real beginning or end. A vertex is removed from the active list when the difference between its old and revised values is below a predetermined tolerance—effectively, the value at the vertex does not change within the range of the prescribed tolerance from the previous update. We specify a vertex whose value remains unchanged (within some tolerance ε) as ε-converged. As each ε-converged vertex is removed from the active list, all of its potentially downwind neighbors (neighbors with larger value) are updated. If their values are not ε-converged (i.e., they deviate significantly), they are included in the active list. The algorithm keeps updating the vertices in the active list until the list is empty.
The update of an active vertex does not depend on the other updates, hence we can extend the single-threaded algorithm to shared memory multiprocessor systems by simply partitioning arbitrarily, at each iteration, the active list into N sublists and assigning the sublists to N threads. Each thread asynchronously updates the vertices within the sublist. These updates are done by applying the updating step to each partition of the active list. In practice, we choose N to be twice the number of CPU cores to take full advantage of Intel’s hyperthreading technology. At the beginning of an iteration, if there are n nodes in the active list, the sublist size M is given by . The active list is evenly divided into N sublists, each containing M consecutive active nodes except for the last sublist which may contain fewer than M active nodes. These N sublists are then assigned to N threads.
3.2. Implementation on streaming SIMD parallel architectures
To exploit the GPU performance advantage, we propose a variation of tetFIM, called tetFIM-A, that adapts well on SIMD architectures by combining an agglomeration-based update strategy that is divided across blocks and carefully designed data structures for 3D tetrahedral meshes. In this method, the computational domain (mesh) is split into minimally overlapping agglomerates (sharing only one layer of tetrahedra) and each agglomerate is treated with logical correspondence to a vertex in the original tetFIM. The vertices in each agglomerate are updated in an SIMD fashion on a block, and the on-chip cache is employed to store the agglomerate data and the intermediate results. Similar to the CPU variants of tetFIM, a narrow banding scheme is used to focus the computation in terms of the necessary computational region. The active list consists of a set of active agglomerates instead of active vertices.
In an iteration, each active agglomerate is loaded from the global memory to a block, and the values of all vertices in this agglomerate are updated by a sequence of SIMD iterations which we call internal iterations. The agglomerate data are copied to the on-chip memory space, and the internal iterations are performed to revise the solutions of the vertices in that agglomerate. In general, the whole computation consists of two steps: the preprocessing and the iteration.
Preprocessing
The tetFIM-A requires setup or preprocessing before the computation of the solution. First, we divide the mesh into agglomerations through a multilevel partitioning scheme described in [13]. The specific algorithm for mesh partitioning is not essential to the suggested algorithm, except that efficiency is achieved for agglomerates with matching numbers of vertices/tetrahedra and relatively few vertices on the agglomerate boundaries. We also precompute the static mesh information including the extra information associated with the obtuse tetrahedra and prepare the necessary data for the iteration step including compaction of the speed and geometric data and generation of the gather-lists which will be described below.
Iteration step
In this step, each agglomerate is treated just like a vertex in tetFIM, and the main iteration continues until the active list becomes empty. The main iteration consists of three stages as outlined below. First, each agglomerate in the active list is assigned to an SIMD computing unit. Second, once the agglomerate is updated, we check to see if the agglomerate is ε-converged, i.e., all vertices in an agglomerate are ε-converged. Checking the agglomerate convergence entails updating the entire agglomerate once and seeing if there exists a vertex with a changed solution. This is done with a reduction operation, which is commonly employed in the streaming programming model to efficiently produce aggregate measures (sum, max, etc.) from a stream of data [21]. Finally, we deal with the effects of an update on the active list. If an agglomerate is not ε-converged, we add it into the active list, otherwise we add its neighboring agglomerates to the active list and then go to the first stage and repeat the update again (see Algorithm 1).
This agglomeration strategy is meant to exploit the high computing power from modern SIMD processors. However, the 3D tetrahedral mesh and anisotropy of the speed function pose some challenges for this strategy to achieve good performance. First, representing the topology of an unstructured 3D mesh and storing the speed matrices imposes a large memory footprint. In juxtaposition to this, high local memory residency and sufficient computational density are desired to hide the memory access latency. Due to the large memory footprint, the agglomerate size must be small enough so that the limited on-chip fast memory space of the SIMD processor can accommodate all the agglomerate data. However, small agglomerate sizes leads to larger boundary and more global communication which is slow for SIMD architectures. In addition, unstructured 3D meshes can have large and highly variant vertex valences which result in uneven workload for the threads and an incoherent memory access pattern that affects the achieved bandwidth. To address all these challenges, it is essential to carefully design the data structure used for the agglomeration strategy so that the data structure is compact and regular. We explore here two different data structures for representing tetrahedral agglomeration yielding high computational density for the SIMD processing of tetrahedral meshes on blocks. We call these two representations the one-ring-strip and the cell-assembly data structures.
Algorithm 1. meshFIM(A,L) (A: set of agglomerates, L: active agglomerate list).
| comment: initialize the active list L |
| for all a ∈ A do |
| for all v ∈ a do |
| if any v ∈ S then |
| add a to L |
| end if |
| end for |
| end for |
| comment: iterate until L is empty |
| while L is not empty do |
| for all a ∈ L do |
| update the values of the node in each a |
| end for |
| for all a ∈ L do |
| check if a is converged with reduction operation |
| end for |
| for all a ∈ L do |
| if a is converged then |
| add neighboring agglomerates of a into a temporary list Ltemp |
| end if |
| end for |
| clear active list L |
| for all a ∈ Ltemp do |
| perform 1 internal iteration for a |
| end for |
| for all a ∈ Ltemp do |
| check if a is converged with reduction operation |
| end for |
| for all a ∈ Ltemp do |
| if a is converged then |
| add a into active list L |
| end if |
| end for |
| end while |
3.2.1. Description of one-ring-strip data structure
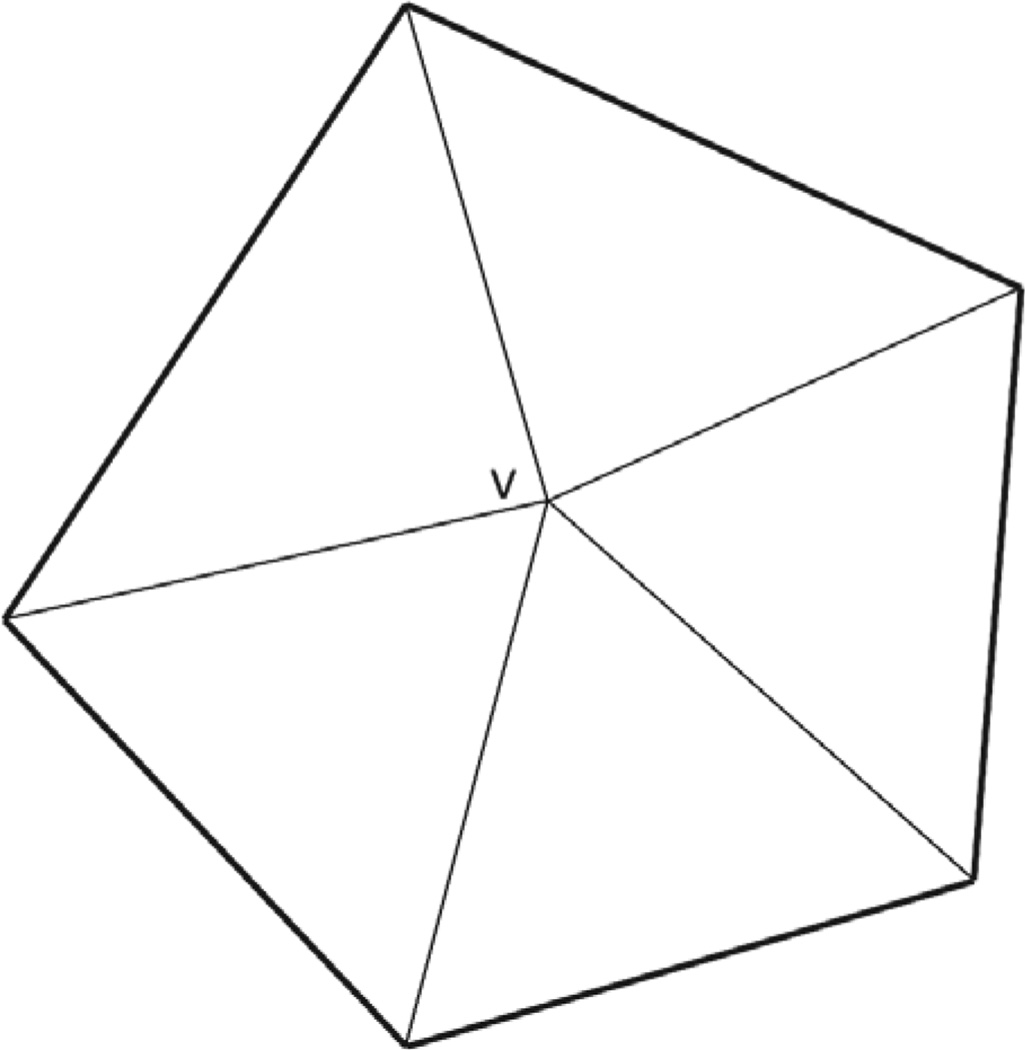
The one-ring-strip data structure is efficient only for the case of isotropic speed functions because its run-time effectiveness is offset by the memory footprint of the geometric and speed information in the anisotropic case. We discuss it here as it provides better performance for this very important special case. As in tetFIM, the update for one vertex includes computing solutions from its one-ring tetrahedra and taking the minimum solution as the new updated value. In order to minimize memory usage, we store for each vertex its one-ring tetrahedra by storing the outer-facing triangles on the polyhedron formed by the union of the one-ring tetrahedra. To further improve memory usage, these triangles are stored in “strips” as commonly used in computer graphics [18]. Specifically, for a given vertex within the mesh, the faces of its one-ring tetrahedra that are opposite the vertex form a triangular surface (see Figure 3.1) from which we generate a triangular strip and store this strip instead of storing the entire one-ring tetrahedra list.
Fig. 3.1.
2D representation of the outer surface of vertex v formed by the one-ring tetrahedra: the polygon formed by the bold line segments is analogous to the outer triangular surface in a tetrahedral mesh.
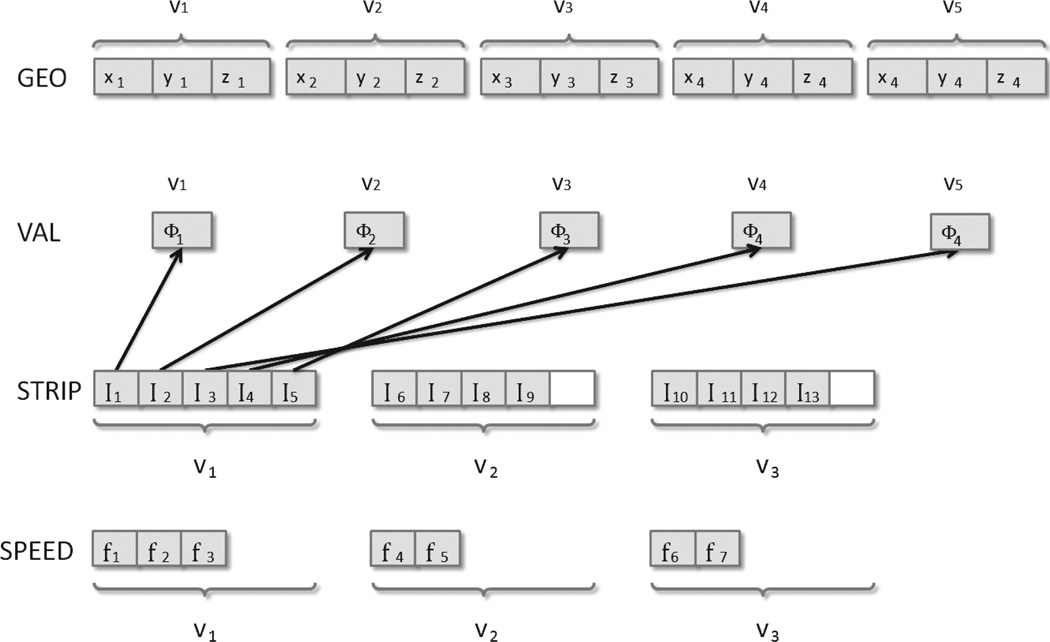
In practice, the one-ring-strip data structure consists of four arrays: VAL, STRIP, GEO, and SPEED. GEO is the array storing the per-vertex geometry information required to solve the eikonal equation. It is divided into subsegments with a predefined size that is determined by the largest agglomeration among all the agglomerates. Each subsegment stores a set of three floating point variables (floats) for the vertex coordinates of each vertex. VAL is the array storing the per-vertex values of the solution of the eikonal equation. It is also divided into subsegments, and solutions on the vertex are stored. The algorithm requires two VAL arrays, one for the input and the other for the output, in order to avoid memory conflicts. Vertices on the boundaries between agglomerates are duplicated so that each agglomerate has access to vertices on neighboring agglomerates, which are treated as fixed boundary conditions for each agglomerate iteration. The STRIP array stores both indices to GEO and VAL, respectively, for the geometric information and the current solution at each vertex within the strip. The SPEED array stores per-tetrahedron speed values corresponding to the tetrahedral strip of a vertex. This data structure is not suited for the anisotropic case since the speed matrix requires significant memory. Anisotropic speed functions require that six floating point numbers of the speed matrix be stored for each adjacent tetrahedron of a node, while isotropic speed functions require only one floating point number per adjacent tetrahedron. Figure 3.2 depicts the data structure introduced above. In a single internal iteration on an agglomerate, the one-ring-strip data structure employs a vertex-based parallelism, i.e., each thread in a block is in charge of the update of a vertex which includes computing the potential values from the one-ring tetrahedra of this vertex and then taking the minimum as the final result.
Fig. 3.2.
One-ring-strip data structure: in this figure, Ti is a tetrahedron, xi, yi and zi represent the coordinates of the ith vertex, fi is the inverse of speed on a vertex. Φi denotes the value of the solution at the ith vertex. Ii in STRIP represents the data structure for the one-ring strip of the ith vertex each of which has q indices pointing (shown as arrows) to the value array.
3.2.2. Description of cell-assembly data structure
The cell-assembly data structure is an extension of the data structure described in [7] for triangular meshes. However, especially for the tetrahedral meshes, we have designed a new data compaction scheme to combine the anisotropic speed matrices with the geometric information. In addition, instead of using a fixed length array NBH to store the memory locations for a thread to gather data, we use a more compact data structure to store these locations. Also, we propose a lock-free strategy to generate the gather-lists which are needed in the computation to find the minimum of the potential values of each node. The cell-assembly works for both the isotropic and anisotropic cases, although it is slightly less efficient in terms of run-time performance for some isotropic cases than the one-ring-strip data structure.
The cell-assembly data structure includes four arrays, that are labeled GEO, VAL, OFFSETS, and GATHER. GEO stores compacted geometry and speed information, and the compaction scheme is described below. This is different from the cell-assembly for the 2D meshes described in [7] which stores the speed and geometric information separately. GEO is also divided into subsegments with a predefined size that is determined by the largest agglomeration. VAL stores per-tetrahedron values of the solution of the eikonal equation. As with the one-ring strip, we simply duplicate and store the exterior boundary vertices for each agglomeration and treat the data on those vertices as fixed boundary conditions for each agglomerate iteration to deal with agglomerate boundaries. The GATHER array stores concatenated per-vertex gather-lists which are the indices to VAL for the per-vertex solution, and the OFFSETS array indicates the starting and ending of the gather-list of each node in the GATHER array. These gather-lists are stored differently because a tetrahedral mesh may have very varied valences, and the fixed length data structure used in [7] may waste a lot of memory space and bandwidth for the sentinel values.
For cell assembly, the updates of the intermediate (potential) vertex values in an agglomerate employ tetrahedron-based parallelism. Each thread of a block is responsible for updating all four vertex values of a tetrahedron, and the intermediate results are stored in the VAL array. Then we need to find the final value of a node, which is the minimum of its potential values which are stored in the per-tetrahedron VAL array. Typically, an atomic minimum operation is then needed to find the minimum for each node in parallel. However, atomic operations are costly on GPUs, and we avoid them by switching to a vertex-based parallelism strategy using gather-lists. A gather-list stores indices to VAL and tells the thread where to fetch potential values in the VAL array for a node. A gather-then-scatteRlike operation is then used to find the minimum value of a vertex from its one-ring tetrahedra and reconcile all the values of this vertex according to the gather-lists. Generating the gather-lists efficiently on GPUs is not a trivial task, given only the geometric information of the mesh—the element list and the node coordinate list. We use a sorting strategy to achieve this. Given a copy of the element list ELE which stores the vertex indices of each tetrahedron, we create an auxiliary array AUX of the same size and fill it with an integer sequence. Specifically, if the size of ELE is n, AUX is initialized to {0, 1, 2, …, n − 1}. We sort ELE and permute AUX according to the sorting. Now AUX stores the concatenated gather-lists all the nodes, but we need to know the starting and ending positions of the gather-list of each node, which is achieved by a reduction and a scan operation on the ELE array. These operations—sorting, reduction and scan—are all very efficient on GPUs, and we use the CUDA thrust library [16] in our implementation. Now ELE and AUX are, respectively, the OFFSETS and GATHER arrays we need.
Next, we describe how we combine the speed matrix and geometric information in practice. As shown in section 2.2, the local solver for updating a vertex requires six floats to store the symmetric speed matrix M′, so a total of 24 floats are needed to update all four vertices on a tetrahedron. However, based on the topology of the tetrahedron and some algebric reductions, we have
| (3.1) |
| (3.2) |
| (3.3) |
where v1, v2, and v3 are arbitrary vectors. According to these properties, we can calculate all the four M′ elements from the six values: , and . Precomputing these values, we need only store six floats for each tetrahedron which are stored in the GEO array.
Compared to the one-ring-strip data structure, the advantage of cell assembly is that the computational work is almost the same for each SIMD thread independent of the valences of the vertices, while for one-ring-strip, the computational work per thread is determined by the valences of the vertices. More homogeneity in the valences of the vertices results in better load balancing for the different threads. However, the one-ring-strip data structure has a smaller memory footprint and higher computation density since each SIMD thread computes the local solver on each tetrahedron of a one-ring strip. We evaluate the performance of each data structure empirically in the next section.
4. Results and discussion
In this section, we discuss the performance of the proposed algorithms in realistic settings compared to two widely used competing methods: the FMM and the FSM. Serial CPU implementations were generated which strictly follow the algorithms as articulated in the (previously) cited references. We rely on a collection of unstructured meshes having variable complexities to illustrate the performance of each method. For this set of meshes, we examine how the performance of these methods is affected by four different speed functions—a homogeneous isotropic speed, a homogeneous anisotropic speed, a heterogeneous anisotropic random speed, and a speed function for the geometric optics/lens example. We first show the error analysis of the proposed first order numerical scheme. Next, we show the results of the single-threaded (serial) CPU implementation of tetFIM, FMM, and FSM, and review the typical performance characteristics of the existing algorithms. We then detail the results of our multithreaded CPU implementation and discuss the scalability of the proposed algorithm on shared memory multiprocessor computer systems. Finally, we present the results of our GPU implementation to demonstrate the performance of the proposed method on massively SIMD streaming parallel architectures. For consistency of evaluation, single precision was used in all algorithms and for all experiments presented herein.
The meshes and speed functions for the experiments in this section1 are as follows:
Mesh 1: a regularly tetrahedralized cube with 1,500,282 tetrahedra (63 × 63 × 63 regular grid) whose maximum valence is 24;
Mesh 2: a irregularly tetrahedralized cube with 197,561 vertices and 1,122,304 tetrahedra whose maximum valence is 54;
Mesh 3: a heart model with 437,355 vertices and 2,306,717 tetrahedra whose maximum valence is 68 (Figure 1.1(left));
Mesh 4: a lens model with 260,908 vertices and 1,561,642 tetrahedra whose maximum valence is 58 (Figure 1.1(right)); and
Mesh 5: a 3D model with irregular geometries, which we call blobs, with 437,355 vertices and 2,306,717 tetrahedra whose maximum valence is 88 (Figure 4.1).
Speed 1: a homogeneous isotropic speed of constant 1.0;
Speed 2: a homogeneous anisotropic diagonal speed tensor with diagonal entries 1.0, 4.0, and 9.0;
Speed 3: a heterogeneous anisotropic correlated randomsymmetric positive-definite speed tensor;
Speed 4: a heterogeneous isotropic speed for a lens model; and
Speed 5: a heterogeneous isotropic speed for a lava lamp model.
Fig. 4.1.
Blobs mesh and its cross section. The different colors in the cross section represent different materials indices of refraction (speed functions).
4.1. Error analysis
To show that the proposed algorithm achieves the first-order accuracy we would expect from the piecewise linear approximation used within the solver, we performed a convergence analysis on a problem with a known solution. We use six regularly tetrahedralized cube meshes, representing a 256×256×256 block within ℝ3, with the number of vertices on each side ranging from 17 to 513. We use an ellipse octant (placing the center of the ellipse at the corner of the cube domain) of the form x2 + 4y2 + 9z2 = R2, where R = 40 as the source. Boundary conditions were projected onto the vertices using the nearest vertices to the sphere. We then solve for the distances to these boundaries for the entire domain using the tetFIM eikonal solver with an anisotropic diagonal speed matrix with diagonal numbers 1, 4, and 9 and compare them against analytical results at the vertices using the L1 error. L1 errors are computed in this way. First, for each tetrahedron, take the average of the errors at the vertices and multiply by the volume of the tetrahedron. We then sum up the products over all tetrahedra and divide the sum by the volume of the whole domain. Finally, we calculate the error orders of any two consecutive meshes. The results are presented in Table 4.1. The table shows that the order of the error is approaching 1.0 with increasing resolution, which is consistent with our claim that tetFIM is asymptotically first-order accurate.
Table 4.1.
Table presenting our convergence results (L1 error) and the order of convergence as computed from subsequent levels of refinement.
| Speed 1 | Speed 2 | |||
|---|---|---|---|---|
| Mesh sizes | L1 Error | Order | L1 Error | Order |
| 17 | 8.073934 | — | 15.399447 | — |
| 33 | 4.688324 | 0.78 | 9.232588 | 0.74 |
| 65 | 2.606537 | 0.85 | 5.347424 | 0.79 |
| 129 | 1.396091 | 0.90 | 2.967363 | 0.85 |
| 257 | 0.721630 | 0.95 | 1.558972 | 0.93 |
| 513 | 0.362584 | 0.99 | 0.789725 | 0.98 |
4.2. CPU implementation results and performance comparison
We have tested our CPU implementation on a Windows 7 PC equipped with an Intel i7 965 Extreme CPU running at 3.2 GHz. All codes were compiled with Visual Studio 2010 using compiler options /O2 and /arch:SSE2 to enable SIMD instructions. (We accomplished a comparison using the Intel Sandy Bridge CPU to run some of the tests. The results show the Sandy bridge CPU is around twice as fast as the i7 965. All results presented herein can be scaled appropriately to interpret the results against the Sandy Bridge processor.) First, we focus on the performance of the CPU implementations of our tetFIM method compared against serial FMM and FSM on three different meshes with differing complexities (Mesh 1, Mesh 2, and Mesh 3) using various speed functions. The anisotropic version of FMM [27] is no longer local in nature (as it requires a larger multielement upwind stencil) and hence we did not include anisotropic FMM in our comparisons. We call the serial version of our CPU method tetFIM-ST and the multithreaded version tetFIM-MT (in all cases, we use four threads). In all these experiments, a single source point is selected at around the center of the cube. For the FSM, we select the reference points to be the eight corners of the cube and the run time for FSM does not include the sorting time required to sort vertices according to their Euclidean distances to the reference points. Tables 4.2, 4.3, and 4.4 show the computational results for this set of experiments.
Table 4.2.
Run time (in seconds) of FMM, FSM, tetFIM-ST, and tetFIM-MT on Meshes 1 with Speeds 1, 2, and 3.
| Speed 1 | Speed 2 | Speed 3 | |
|---|---|---|---|
| FMM | 69 | — | — |
| FSM | 213 | 216 | 680 |
| tetFIM-ST | 80 | 81 | 107 |
| tetFIM-MT | 27 | 28 | 41 |
Table 4.3.
Run time (in seconds) of FMM, FSM, tetFIM-ST, and tetFIM-MT on Mesh 2 with Speeds 1, 2, and 3.
| Speed 1 | Speed 2 | Speed 3 | |
|---|---|---|---|
| FMM | 42 | — | — |
| FSM | 407 | 409 | 674 |
| tetFIM-ST | 60 | 59 | 175 |
| tetFIM-MT | 22 | 23 | 55 |
Table 4.4.
Run time (in seconds) of FMM, FSM, tetFIM-ST, and tetFIM-MT on Mesh 3 with Speeds 1, 2, and 3.
| Speed 1 | Speed 2 | Speed 3 | |
|---|---|---|---|
| FMM | 71 | — | — |
| FSM | 807 | 823 | 1307 |
| tetFIM-ST | 113 | 122 | 173 |
| tetFIM-MT | 46 | 48 | 56 |
As shown in Tables 4.2, 4.3, and 4.4, FMM outperforms both tetFIM and FSM on all isotropic cases. This is to be expected as FMM is a worst-case optimal method and its performance is not significantly impacted by the complexity of the mesh or the speed function as observed previously in [12] and [7]. FIM outperforms the FSM on all the test cases. For simpler speed functions like Speeds 1 and 2, the FSM requires only two iterations to converge, because the characteristics are well captured thanks to the reference point choice. FSM, however, requires the update of all the vertices in the mesh according to their distance to each reference point in both ascending order and descending order. So for the eight reference points in these experiments, FSM needs to update all vertices 16 times in one iteration, which amounts to 32 total updates for each vertex. On the other hand, tetFIM needs fewer updates for the mesh vertices when the wavefront passes through the whole domain from the source in the direction of the characteristics. Indeed, the average valence of the mesh is 24, and assuming that half of the neighbors of a vertex are fixed when a vertex is being updated, each vertex needs to be updated only 12 times on average. As pointed out in [11], when the speed function becomes more complex (i.e., characteristics change frequently), FSM performs even worse when compared to FIM, which can be shown in our Speed 3 case where FSM needs six iterations to converge and tetFIM runs about seven times faster. Moving to the more complex Mesh 2, FSM’s performance is dramatically degraded, needing five iterations for simpler Speeds 1 and 2 and eight iterations for Speed 3. The tetFIM’s performance, however, is inconsequentially impacted by the complexity of the mesh.
The tetFIM algorithm is designed for parallelism, and the results on the multithreaded system bear this out. The fourth rows in Tables 4.2, 4.3, and 4.4 show the run times of multithreaded tetFIM using four CPU cores. Note that tetFIM scales well on multicore systems. On a quad-core processor, we observe a nearly three times speedup from tetFIM-ST to tetFIM-MT on all cases. The reduction from perfect scaling can be attributed to the fact that due to the partitioning of the active list at each time step, the multithreaded version accomplishes more updates per vertex than the serial version. In the single-threaded version, a single active list implies that updated information is available immediately once a computation is done, analogous to a Gauss–Seidel iteration; in the multithreaded case, the active list partitioning enforces a synchronization in terms of exchange of information between threads, analogous to a red-black Gauss–Seidel iteration.
4.3. GPU implementation results
To demonstrate the performance on SIMD parallel architectures of tetFIM, we have implemented and tested tetFIM-A on an NVIDIA Fermi GPU using the NVIDIA CUDA API [17]. The NVIDIA GeForce GTX 580 graphics card has 1.5 GBytes of global memory and 16 microprocessors, where each microprocessor consists of 32 SIMD computing cores that run at 1.544 GHz. Each computing core has configurable 16 or 48 KBytes of on-chip shared memory, for quick access to local data. Computation on the GPU entails running a kernel with a batch process of a large group of fixed size thread blocks, which maps well to the tetFIM-A algorithm that employs agglomeration-based update methods. A single agglomerate is assigned to a CUDA thread block. For the one-ring-strip data structure, each vertex in the agglomerate is assigned to a single thread in the block, while in cell-assembly data structures, each tetrahedron is assigned to a thread. These two variants of the tetFIM-A algorithm are called tetFIM-A-ORS and tetFIM-A-CA, respectively.
The agglomerate scheme seeks to place the agglomerated data into the GPU cache (registers and shared memory). However, the GPU cache size is very limited, and hence we have to use agglomerates with smaller diameters compared to what can be used in triangular mesh cases. This implies that we perform fewer internal iterations in the 3D case versus the 2D case, which leads to lower computational density. On the other hand, performing fewer internal iterations reduces the number of redundant internal iterations caused by outdated boundary information. In addition, the local solver for tetrahedral mesh requires more computations. Table 4.5 demonstrates that our agglomerate scheme balances the trade-off between the agglomerate size, the number of internal iterations, and computational density very well on the GPU; the speedup values increase in three dimensions over previously published 2D results [7]. In addition, our GPU implementations perform much better than all the CPU implementations. Section 4.5.2 provides detailed analysis of the parameter choice.
Table 4.5.
Run times (in seconds) and speedup factors (against tetFIM-ST) for the different algorithms and architectures on all meshes with Speed 1. Data in first row are from Tables 4.2, 4.3, and 4.4.
| Mesh 1 | Mesh 2 | Mesh 3 | |
|---|---|---|---|
| tetFIM-ST | 80 | 60 | 113 |
| tetFIM-MT | 27 | 22 | 46 |
| tetFIM-A-ORS | 0.396 | 1.412 | 2.694 |
| tetFIM-A-CA | 0.587 | 0.939 | 1.911 |
| Speedup 1 | 202× | 42× | 42× |
| Speedup 2 | 136× | 64× | 59× |
Table 4.5 also shows the performance comparison of the two tetFIM-A variants, tetFIM-A-ORS and tetFIM-A-CA with the single-threaded CPU implementation (tetFIM) on the same meshes and the isotropic speed function, and shows the speedup factors of tetFIM-A over the CPU method. Communication times between CPU and GPU, which are only about one tenth of the run times in our experiments, are not included for tetFIM-A to give a more accurate comparison of the methods. As shown in this result, tetFIM-A-ORS performs better than tetFIM-A-CA for Mesh 1, which is a regularly tetrahedralized cube. This is because a one-ring-strip data structure consumes less shared memory so as to allow larger agglomerates. Large agglomerates need more inside iterations to converge, hence the computational density is increased due to fast shared memory usage for inside iterations. While for the more complex irregular meshes like Mesh 3 in this comparison, tetFIM-A-CA has a performance advantage. The reason is that for irregular meshes, the valences of the vertices vary greatly, hence the computational density of tetFIM-A-ORS for each thread is sufficiently unbalanced that computing power is wasted when faster threads are waiting for the slower ones to finish. On the other hand, the two tetFIM-A algorithms achieve a good performance gain over both the serial and multithreaded CPU solvers. On a simple case such as Mesh 1 with Speed 1, tetFIM-A-ORS runs about 201 times faster than tetFIM-ST while tetFIM-A-CA runs about 131 times faster than tetFIM-ST. On the other more complex cases, tetFIM-A-ORS runs up to 23 times faster than tetFIM-ST while tetFIM-A-CA is 37 times faster. See Figure 4.2 for visualizations of the resulting solutions.
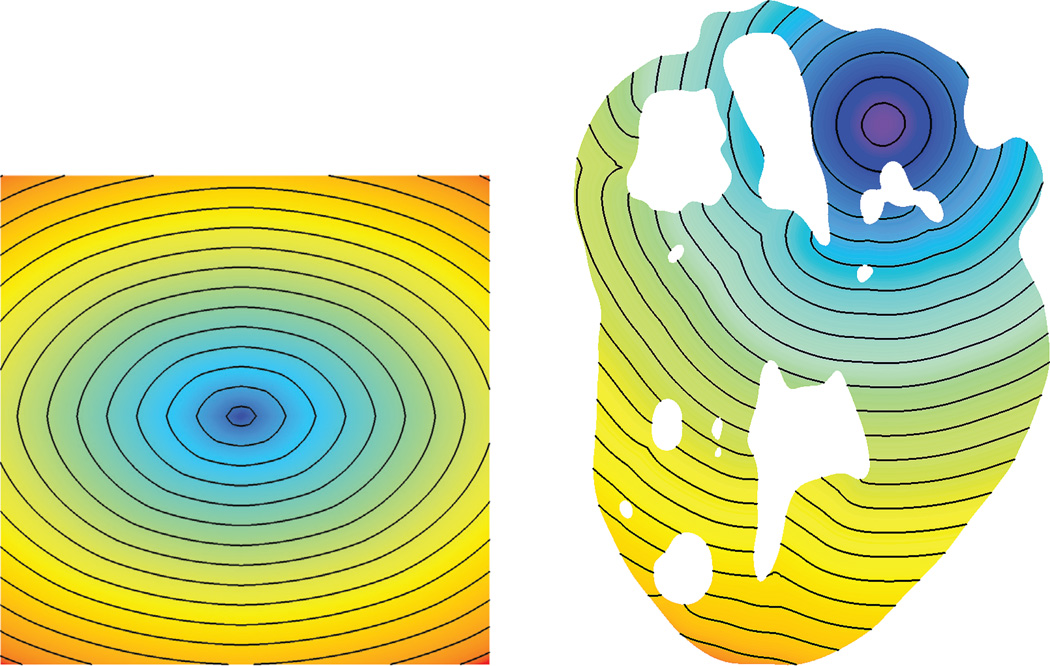
Fig. 4.2.
Color maps and level curves of the solutions on the cube and heart meshes. Left: the ellipse speed function (Speed 2). Right: the isotropic constant function (Speed 1).
We also observe that SIMD efficiency of the tetFIM algorithm depends on the input mesh configuration (i.e., the average vertex valence relative to the highest valence). As seen form Table 4.5, both GPU implementations achieve the highest speedups on Mesh 1 compared to the CPU implementation while achieving the lowest speedups on Mesh 3 which has much greater maximum vertex valence. This is because the highly unstructured mesh, e.g., Mesh 3, leads to unbalanced word load and waste of memory bandwidth on SIMD architectures.
Next, we show the tetFIM-A applied to the anisotropic cases. Because the one-ring-strip data structure is not suitable for this case, we include only the performance result of cell-assembly data structure variant tetFIM-A-CA. Table 4.6 clearly shows that the tetFIM-A which is implemented on the GPU performs much better than the CPU implementation on all the examples we tested, regardless of the mesh configuration and speed function.
Table 4.6.
Run times (in seconds) and speedup factors for the different algorithms and architectures. Data in first row are from Tables 4.2, 4.3, and 4.4.
| Mesh 1 Speed 2 |
Mesh 2 Speed 2 |
Mesh 3 Speed 2 |
Mesh 1 Speed 3 |
Mesh 2 Speed 3 |
Mesh 3 Speed 3 |
|
|---|---|---|---|---|---|---|
| tetFIM-ST | 81 | 59 | 113 | 107 | 175 | 173 |
| tetFIM-A-CA | 0.580 | 0.958 | 1.986 | 1.356 | 2.079 | 2.413 |
| Speedup | 140× | 62× | 57× | 79× | 84× | 72× |
Finally, Table 4.7 shows the preprocessing time for Meshes 1, 2, and 3. The preprocessing is performed on the GPU and includes permuting the geometric information (element list and vertex coordinate list) according to the mesh partition using METIS and generating the gather-lists for the cell-assembly data structure. The graph partitioning and triangle strip generation time are not included since they are not essential parts of our algorithm.
Table 4.7.
Run times (in seconds) of the preprocessing step for Meshes 1, 2, and 3.
| Mesh 1 | Mesh 2 | Mesh 3 |
|---|---|---|
| 0.150 | 0.120 | 0.209 |
4.4. Meshes for complex surfaces
We have also tested this method on meshes with more complex conformal surfaces (Meshes 4 and 5) to show that the proposed method works correctly when applied to scenarios that resemble physical simulation associated with target applications. Figures 4.3 and 4.4 show the results of the simulation on the lens model and the blobs model. The green region in the lens model (Figure 1.1(right)) has a speed functions of 1.0, which represent the refractive index of air, and the red region models a lens whose refractive index is 2.419. Similarly, in the blobs model, the red and green regions have constant speed functions of 1.0 and 10.0, respectively. Table 4.8 shows the performance of all the methods for Meshes 4 and 5.
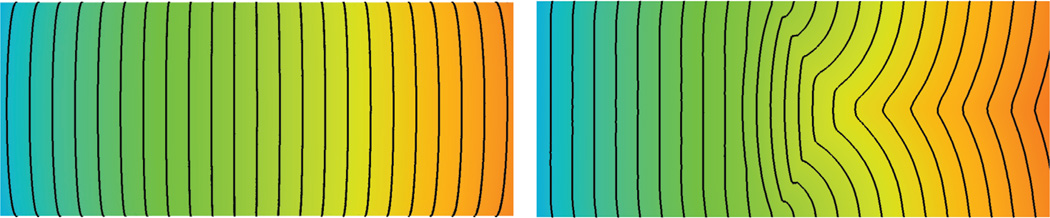
Fig. 4.3.
Color maps and level curves of the solutions on the lens model with boundary as given by the figure on the left.
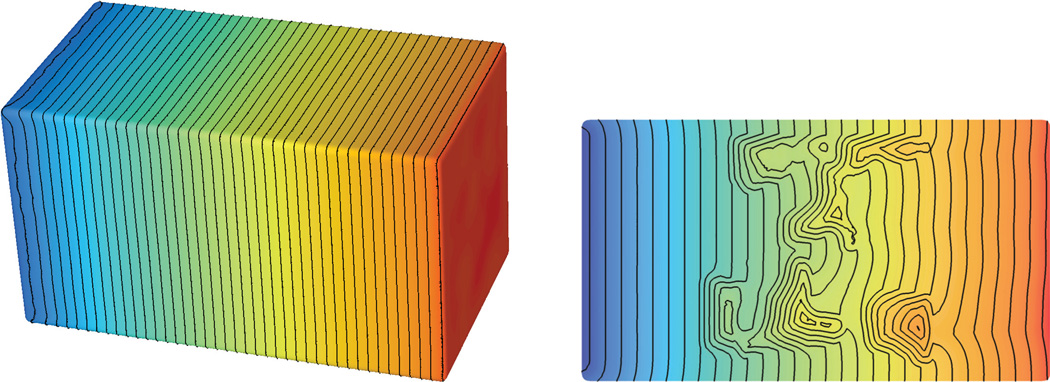
Fig. 4.4.
Color maps and level curves of the solutions on the blobs model with boundary as given by the figure on the left.
Table 4.8.
Run time (in seconds) of all methods on Meshes 4 and 5. The “Speedup VS. FMM” column lists the speedup of all methods compared to FMM with negative numbers denoting that the method is slower than FMM.
| Mesh 4 | Speedup VS. FMM | Mesh 5 | Speedup VS. FMM | |
|---|---|---|---|---|
| FMM | 43 | 1 | 51 | 1 |
| FSM | 378 | −8.8 | 517 | −10.1 |
| tetFIM-ST | 74 | −1.7 | 62 | −1.2 |
| tetFIM-MT | 22 | 2.0 | 21 | 2.4 |
| tetFIM-A-ORS | 2.372 | 18.1 | 2.032 | 25.1 |
| tetFIM-A-CA | 1.801 | 23.9 | 1.538 | 33.2 |
4.5. Analysis of results
In this section, we discuss the analysis of our results in terms of asymptotic cost and parameter optimization choices.
4.5.1. Asymptotic cost analysis
We performed an asymptotic cost analysis that measured the number of iterations and number of updates per vertex for our proposed serial CPU version tetFIM-ST and GPU version tetFIM-A. We used four meshes with different sizes to show that our method scales very well against mesh size for a given speed function (see Table 4.9).
Table 4.9.
Asymptotic cost analysis: # iter is the number of iterations needed to converge and # up is the average number of updates per vertex.
| tetFIM-ST | tetFIM-A | |||||||
|---|---|---|---|---|---|---|---|---|
| Speed 2 | Speed 3 | Speed 2 | Speed 3 | |||||
| Mesh sizes | # iter | # up | # iter | # up | # iter | # up | # iter | # up |
| 17 | 37 | 11 | 44 | 13 | 48 | 29 | 69 | 51 |
| 33 | 70 | 12 | 81 | 15 | 103 | 29 | 119 | 49 |
| 65 | 139 | 12 | 170 | 16 | 206 | 32 | 265 | 51 |
| 129 | 276 | 11 | 326 | 15 | 403 | 31 | 510 | 50 |
4.5.2. Parameter optimization
In tetFIM-A, there are two parameters that need to be specified: the agglomerate size and the internal iteration number. The agglomeration scheme provides fine-grained parallelism that is suitable for SIMD architectures by partitioning the mesh into agglomerates that are mapped to different computational blocks. During the internal iterations on the agglomerate accomplished per block, the boundary conditions are lagged. Hence taking an excessive number of internal iterations is wasteful as it merely drives the local solution to an incorrect fixed point (in the absence of boundary condition updates). For this reason, it may seem ideal to have smaller agglomerate sizes which tend to need fewer internal iterations for the agglomerate to converge (and thus less computation is wasted). However, smaller agglomerates result in large boundary and more global communication among blocks. In addition, we need also take into account the size of the limited hardware resources, e.g., GPU shared memory and registers. We want to fit the agglomerate into the fast on-chip (shared) memory space to increase the computational density. Based upon our experiments, the best agglomerate size is around 64 vertices. For the internal iteration number, our experiments show that the ideal number is approximately three when agglomerates are of this size.
5. Conclusions
In this paper, we have presented a variant of the FIM appropriate for solving the inhomogeneous anisotropic eikonal equation over fully unstructured tetrahedral meshes. Two building blocks are required for such an extension: the design and implementation of a local solver appropriate for tetrahedra with anisotropic speed information, and algorithmic extensions that allow for rapid updating of the active list used within the FIM method in the presence of the increased data footprint generated when attempting to solve PDEs on 3D domains. After describing these two building blocks, we make the following computational contributions. First, we introduce our tetFIM algorithms for both single processor and shared memory parallel processors and perform a careful empirical analysis by comparing them to two widely used CPU-based methods, the state-of-the-art FMM and the FSM, in order to understand the benefits and limitations of each method. Second, we propose an agglomeration-based tetFIM solver, specifically for more efficient implementation of the proposed method on massively parallel SIMD architectures. We then describe the detailed data structures and algorithms, present the experimental results of the agglomeration-based tetFIM and compare them to the results of the CPU-based methods to illustrate how well the proposed method scales on state-of-the-art SIMD architectures. In comparison to [7], we have demonstrated that careful management of data allows us to maintain high computational density on streaming SIMD architectures—yielding significantly greater speedup factors than seen when solving 2D eikonal problems on GPUs.
In future work, we envisage extending this technique to time-dependent Hamilton–Jacobi problems in two and three dimensions. Specifically, we will seek to address how one might solve the level-set equations over unstructured meshes on current streaming GPU hardware.
Acknowledgment
The authors would like to thank Dr. Won-Ki Jeong for helpful discussions on the material of this paper.
This work was funded by NIH/NCRR Center for Integrative Biomedical Computing (P41-RR12553-10) and Department of Energy (DOE NETL DE-EE0004449).
Footnotes
Files containing the mesh and speed function definitions can be found at: http://www.sci.utah.edu/people/zhisong.html
Contributor Information
Zhisong Fu, Email: zhisong@sci.utah.edu.
Robert M. Kirby, Email: kirby@sci.utah.edu.
Ross T. Whitaker, Email: whitaker@sci.utah.edu.
REFERENCES
- 1.Adalsteinsson D, Sethian JA. A fast level set method for propagating interfaces. J. Comput. Phys. 1995;118:269–277. [Google Scholar]
- 2.Adalsteinsson D, Sethian JA. Transport and diffusion of material quantities on propagating interfaces via level set. J. Comput. Phys. 2003;185:271–288. [Google Scholar]
- 3.Barth TJ, Sethian JA. Numerical schemes for the Hamilton–Jacobi and level set equations on triangulated domains. J. Comput. Phys. 1998;145:1–40. [Google Scholar]
- 4.Cecil TC, Osher SJ, Qian J. Simplex free adaptive tree fast sweeping and evolution methods for solving level set equations in arbitrary dimension. J. Comput. Phys. 2006;213:458–473. [Google Scholar]
- 5.Cockburn B, Qian J, Reitich F, Wang J. An accurate spectral/discontinuous finite-element formulation of a phase-space-based level set approach to geometrical optics. J. Comput. Phys. 2005;208:175–195. [Google Scholar]
- 6.Colli-Franzone P, Guerri L. Spreading of excitation in 3-D models of the anisotropic cardiac tissue I. Validation of the eikonal model. Math. Biosci. 1993;113:145–209. doi: 10.1016/0025-5564(93)90001-q. [DOI] [PubMed] [Google Scholar]
- 7.Fu Z, Jeong W-K, Pan Y, Kirby RM, Whitaker RT. A fast iterative method for solving the eikonal equation on triangulated surfaces. SIAM J. Sci. Comput. 2011;33:2468–2488. doi: 10.1137/100788951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Greivenkamp JE. Field Guide to Geometrical Optics. Bellingham, WA: SPIE; 2003. [Google Scholar]
- 9.Herrmann M. Center for Turbulence Research Annual Research Briefs. 2003. A domain decomposition parallelization of the fast marching method; pp. 213–225. http://handle.dtic.mil/100.2/ADA420749 (2003) [Google Scholar]
- 10.Holm DD. Geometric Mechanics: Part I: Dynamics and Symmetry. 2nd ed. London, UK: Imperial College London Press; 2011. [Google Scholar]
- 11.Jeong W-K, Fletcher PT, Tao R, Whitaker R. Interactive visualization of volumetric white matter connectivity in DT-MRI using a parallel-hardware Hamilton–Jacobi solver. IEEE Trans. Visualization Comput. Graph. 2007;13:1480–1487. doi: 10.1109/TVCG.2007.70571. [DOI] [PubMed] [Google Scholar]
- 12.Jeong W-K, Whitaker RT. A fast iterative method for eikonal equations. SIAM J. Sci. Comput. 2008;30:2512–2534. doi: 10.1137/100788951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Karypis G, Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1998;20:359–392. [Google Scholar]
- 14.Keener JP. An eikonal equation for action potential propagation in myocardium. J. Math. Biol. 1991;29:629–651. doi: 10.1007/BF00163916. [DOI] [PubMed] [Google Scholar]
- 15.Kimmel R, Sethian JA. Computing geodesic paths on manifolds. Proc. Natl. Acad. Sci. USA. 1998;95:8431–8435. doi: 10.1073/pnas.95.15.8431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.NVIDIA. NVIDIA Developer Zone. https://developer.nvidia.com/thrust.
- 17.NVIDIA. Cuda Programming Guide. http://www.nvidia.com/object/cuda.html.
- 18.Open Access Review Board et al. OpenGL(R) Programming Guide: The Official Guide to Learning OpenGL(R), Version 2. Boston: Addison Wesley; 2005. [Google Scholar]
- 19.Osher S, Cheng L-T, Kang M, Shim H, Tsai Y-H. Geometric optics in a phase-space-based level set and Eulerian framework. J. Comput. Phy. 2002;179:622–648. [Google Scholar]
- 20.Otani NF. Computer modeling in cardiac electrophysiology. J. Comput. Phys. 2010;161:21–34. [Google Scholar]
- 21.Pharr M, Fernando R, editors. GPU Gems 2: Programming Techniques for High-Performance Graphics and General-Purpose Computation. Boston: Addison-Wesley; 2005. [Google Scholar]
- 22.Qian J, Zhang Y-T, Zhao H-K. Fast sweeping methods for eikonal equations on triangulated meshes. SIAM J. Numer. Anal. 2007;45:83–107. [Google Scholar]
- 23.Rawlinson N, Sambridge M. The fast marching method: an effective tool for tomographics imaging and tracking multiple phases in complex layered media. Exploration Geophys. 2005;36:C341–C350. [Google Scholar]
- 24.Rawlinson R, Sambridge M. Wave front evolution in strongly heterogeneous layered media using the fast marching method. Geophys. J. Internat. 2004;156:631–647. [Google Scholar]
- 25.Sethian J. Evolution, implementation, and application of level set and fast marching methods for advancing fronts. J. Comput. Phys. 2001;169:503–555. [Google Scholar]
- 26.Sethian JA. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA. 1996;93:1591–1595. doi: 10.1073/pnas.93.4.1591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sethian JA, Vladimirsky A. Ordered upwind methods for static Hamilton–Jacobi equations: Theory and algorithms. SIAM J. Numer. Anal. 2003;41:325–363. doi: 10.1073/pnas.201222998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Smith B, Bjorstad P, Gropp W. Domain Decomposition: Parallel Multilevel Methods for Elliptic Partial Differential Equations. New York: Cambridge University Press; 1996. [Google Scholar]
- 29.Tsai Y-HR, Cheng L-T, Osher S, Zhao H-K. Fast sweeping algorithms for a class of Hamilton–Jacobi equations. SIAM J. Numer. Anal. 2003;41:673–694. [Google Scholar]
- 30.Tugurlan MC. Fast Marching Methods-Parallel Implementation and Analysis, Ph.D. thesis. Baton Rouge, LA: Louisiana State University; 2008. [Google Scholar]
- 31.Zhao H. A fast sweeping method for eikonal equations. Math. Comp. 2005;74:603–627. [Google Scholar]
- 32.Zhao H. Parallel implementations of the fast sweeping method. J. Comput. Math. 2007;25:421–429. [Google Scholar]