Abstract
One key factor that limits resolution of single-molecule superresolution microscopy relates to the localization accuracy of the activated emitters, which is usually deteriorated by two factors. One originates from the background noise due to out-of-focus signals, sample auto-fluorescence, and camera acquisition noise; and the other is due to the low photon count of emitters at a single frame. With fast acquisition rate, the activated emitters can last multiple frames before they transiently switch off or permanently bleach. Effectively incorporating the temporal information of these emitters is critical to improve the spatial resolution. However, majority of the existing reconstruction algorithms locate the emitters frame by frame, discarding or underusing the temporal information. Here we present a new image reconstruction algorithm based on tracklets, short trajectories of the same objects. We improve the localization accuracy by associating the same emitters from multiple frames to form tracklets and by aggregating signals to enhance the signal to noise ratio. We also introduce a weighted mean-shift algorithm (WMS) to automatically detect the number of modes (emitters) in overlapping regions of tracklets so that not only well-separated single emitters but also individual emitters within multi-emitter groups can be identified and tracked. In combination with a maximum likelihood estimator method (MLE), we are able to resolve low to medium density of overlapping emitters with improved localization accuracy. We evaluate the performance of our method with both synthetic and experimental data, and show that the tracklet-based reconstruction is superior in localization accuracy, particularly for weak signals embedded in a strong background. Using this method, for the first time, we resolve the transverse tubule structure of the mammalian skeletal muscle.
OCIS codes: (100.0100) Image processing, (180.0180) Microscopy, (000.1430) Biology and medicine, (100.6640) Superresolution, (110.4155) Multiframe image processing
1. Introduction
The spatial resolution of conventional fluorescence microscopy is limited by the Abbe diffraction limit to , where is the wavelength of the emission light and is the numerical aperture of the objective [1–5]. In the past few years, a number of breakthroughs have been made in far-field microscopy to improve the spatial resolution by over an order of magnitude both in the lateral and axial direction [6–14]. Among them is the widely used single-molecule localization microscopy, which relies on the precise localization of the activated single emitters. Stochastic optical reconstruction microscopy (STORM) [10], direct STORM [11, 12], photo-activated localization microscopy (PALM) [13], and fluorescence photoactivation localization microscopy (fPALM) [14] all belong to this category, and hold superior capability achieving a typical lateral resolution of ~20 nm [15–17].
In single molecule localization microscopy, a random subset of fluorophores (emitters) are activated, imaged, and localized to nanometer resolution. This procedure is repeated to allow different subsets of emitters to be switched on and localized. A final superresolution image is reconstructed from a large number of emitter localizations so that adjacent localization points can be closer than one-half of the desired spatial resolution (Nyquist criterion) [18]. Due to the iterative nature of the procedure, single molecule localization microscopy has poor temporal resolution. For example, to achieve a superresolution image with resolution of 20 to 50-nm, the image acquisition can take tens of thousands of frames, requiring lengthy acquisition time. This greatly limits the application of superresolution techniques from the fast dynamics process.
To improve the temporal resolution of single molecule localization microscopy, two different strategies have been proposed. One is by controlling the photophysical properties of the fluorescence probes. In a seminal work by Zhuang et al [19], a temporal resolution as high as 0.5 second was achieved in live cell imaging by using engineered bright emitters with a strong activation laser and a sensitive low light detector. Another approach involves increasing the density of activated emitters in each frame so the total number of frames could be significantly reduced to locate the same number of emitters. However, a strong excitation laser can induce phototoxicity to cells; and a high density of activated molecules causes the signals to overlap, which invalidates the widely used single molecule localization methods. One way to reduce the probability of spatially overlapping emitters is to use faster acquisition rates to increase the temporal separability of neighboring fluorophores. However, with faster acquisition rates, an activated emitter usually lasts multiple frames with reduced number of photons at each frame. This results in a low signal noise ratio and reduced localization accuracy. To improve the resolution, it is important to associate the signals of the same emitters from multiple frames without losing their temporal separability.
In this paper we apply a spatio-temporal object association algorithm along with a multi-emitter mode detection scheme to identify and link the same emitters in time, forming tracklets (short trajectories of the same objects) of the emitters. A superresolution image is reconstructed on the basis of these tracklets instead of identifying individual disjoint objects at each frame. By aggregating the signals from the same tracklet, we are able to significantly increase the signal noise ratio and improve the localization accuracy by integrating temporal information. We also use a generalized weighted mean shift algorithm (WMS) to detect the number of modes in an overlapping region of tracklets together with the Maximum-Likelihood Estimation (MLE) to determine the centers of the emitters. We test our method using both synthetic data and experimental STORM images of microtubules in HeLa cells. We show that our method improves localization accuracy particularly for low signals in strong background and is able to identify low to medium density of emitters with improved accuracy. We also apply the tracklet-based reconstruction method to resolve the T-tubule structure in skeletal muscle. To our knowledge, this is the first time that the fine T-tubule structure in skeletal muscle has been resolved with an optical microscopy technique.
2. The imaging model and simulation
The point spread function (PSF) of a microscope can be well approximated by a Gaussian function [20, 21]:
| (1) |
where is the standard deviation of the Gaussian. This continuous distribution of the PSF is integrated over a square pixel to account for the finite pixel size of CCD based detectors. On an individual pixel located at a position , the expected number of photons from independent emitters located at is given by [22]:
| (2) |
where is the total emitted photon counts from a single emitter. Due to photon shot noise, the actual number of photons detected by the pixel is selected from a Poisson distribution with a mean given by . Camera readout noise and a general background noise are combined and modeled as a Gaussian noise , where is the mean and is the standard deviation. Thus, the realization of the photon count at pixel at position is [23]
| (3) |
In the simulation, the pixel size is set to 75 nm and the standard deviation of the PSF is 1.7 pixels (127.5 nm), matching the one in our microscope system. To emulate the photophysical properties of the uniformly distributed emitters on a 256x256 pixel grid of camera pixels (19.2 x19.2 ), we define (number of emitters/ ) and the density and inactivation probability (from bright to dark) of the emitters respectively. In this case the activation probability of the emitters is given by , where is the average number of emitters in a single frame and is the predefined total number of emitters. By tuning and we are able to simulate either low-density well-separated emitters or high-density emitters with significant overlap between neighboring images of emitters. The average distance between activated emitters is given by .
3. Overview of the analysis procedure
Figure 1 shows the overview of our analysis procedure. We divide our image sequence to groups of N frames (N equals 1000 in our analysis), which can be analyzed in parallel. For each frame, potential 2D emitter blobs corresponding to single emitters or overlapping multi-emitters are detected using a Laplacian of Gaussian (LoG) filter [Fig. 1(b)]. These detected emitter blobs are tracked in time using area overlap criteria and the linked 2D blobs are assigned with unique labels [Fig. 1(c)]. Modes of the 2D emitter blobs are decomposed using WMS, and the estimated centers of the individual emitters are tracked in time using spatial proximity and nearest neighbor match strategy to form tracklets [Fig. 1(d)]. We assign different scores to the tracklets according to the spatial separability [Fig. 1(e)]. Image information within the support regions of the tracklets are temporally integrated to construct image chips, small images obtained by summing the local regions of interest around the centroids of a tracklet, with increased signal noise ratio and photon counts. Individual emitter centers are re-estimated from these integrated image chips using MLE [Fig. 1(f)]. In the following sections, we provide details for each step.
Fig. 1.
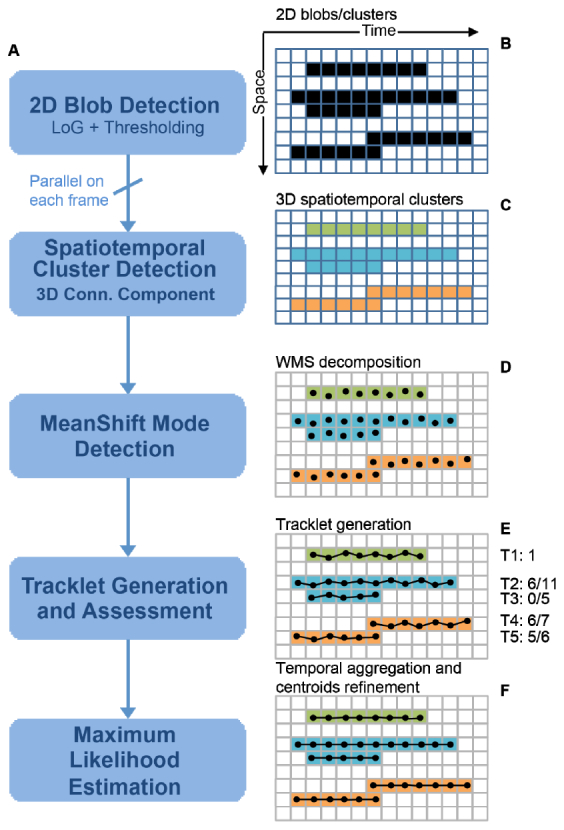
Illustration of the tracklet-based superresolution microscope image reconstruction algorithm. (a). Flowchart of the analysis procedure. (b). 2D blob detection with LoG filter. Masks of the candidate emitters, both disjoint single emitters and the overlapping multi-emitters, are identified through the LoG filter. (c). 3D spatiotemporal labeling through coarse tracking. (d). WMS decomposition of the emitter candidates. (e). Tracklet generation through the fine tracking processing. Tracklets are scored according to the percentage of the overlap regions with neighboring tracklets. (f). Re-estimation of the positions through MLE. The final positions of the emitters are refined by MLE fitting of the integrated image through combining of the frames belonging to the same tracklets.
3.1 Image segmentation
The acquired intensity images are first converted to photon count images by a factor determined by the electron multiplier (EM) gain and the calibration factor provided by the camera manufacturer. Then, 2D Laplacian of Gaussian (LoG) filter
| (4) |
with standard deviation is applied to the images to detect bright regions of interests (ROI) that are candidates corresponding to well separated single emitters as well as groups of overlapping multi-emitters. The filter kernel is chosen to match the imaging system PSF. Signals that have strong spatial correlation are enhanced and the random background noise is suppressed. To expedite the calculation, we use a separable version of the LoG filter [24]. The binary mask images are obtained using hard threshold technique [25]. Unlike previous studies, we do not define a fixed size region of interest (ROI) around a local maximum. Instead, we threshold the filtered images to obtain binary masks. These masks are used to define the ROIs. Application of the LoG filter significantly reduces noise and enhances the real signal, making the mask generation more reliable and less sensitive to background noise. This is particularly important for associating objects from multiple frames, in which case there may be disappearance of old emitters or appearance of new emitters across different frames, resulting in change of the mask size.
Mode detection and emitter center estimation using weighted mean shift procedure (WMS)
Blobs detected during image segmentation can correspond to single emitters or multiple emitters overlapping in space. This step aims to estimate the number of emitters and their centers within the detected masks from the previous step. Mean shift procedure is a non-parametric density estimation method that does not need a-priori knowledge of the number of clusters in the data set and is not constrained by the shape of the clusters. This method was first proposed by Fukunaga and Hostetler [26], and then developed and generalized by Cheng [27]. Let be a kernel with . The weighted kernel density estimate is then given by:
| (5) |
where represents the index of a pixel, is the total number of pixels, and is a weight function. In our case it is the photon count of each pixel. The gradient of the density estimate is given by:
| (6) |
where , is a constant. Taking the gradient to be zero, we get the mode estimator as
| (7) |
In our analysis, we use a generalized Gaussian kernel that is defined as
| (8) |
where is defined as a stabilization parameter [28], and is the bandwidth that is fixed to the standard deviation of the physical PSF (1.7 pixels, 127.5 nm). In WMS, a random point from the masked region is chosen as the starting point; then it is updated through Eq. (7) until it converges. The converged corresponds to the coordinate of a detected mode. The procedure of choosing a different initial starting point and updating until it converges is repeated until all the points in the masked region have been traversed. This will result in multiple coordinates ( ), which may coincide. The total number of different (coordinates) is the number of modes. To speed up the process, for each iteration a data point is labeled if it is traversed; and the initial starting point for the next iteration is chosen only from the non-labeled data points.
Selecting the right bandwidth is critical for the performance of our WMS procedure. Here we applied the method described by Wu et al. [28] who introduced the concept of stabilization factor . The reason for selecting this method is because we used the generalized Gaussian kernel , which has a well-defined , the standard deviation of the PSF. Instead of changing , we use the stabilization parameter to adjust the bandwidth. The density estimate with a stabilization parameter can be calculated by:
| (9) |
where and are the indices of the pixels and is the total number of pixels. The values of the estimated density at each pixel are . If a suitable is chosen, a satisfactory density estimate will be achieved and WMS gives the correct number of modes. When changes to where , if the two estimated densities and are similar, the correlation of the two estimated densities should be close to 1. Figure 2(e) illustrates the relationship between the value and the correlation coefficient, which allows justification of stabilization parameter with a set correlation coefficient [28]. In practice, a value that corresponds to correlation coefficient of 0.95 to 0.97 gives a robust result for the mean shift algorithm.
Fig. 2.
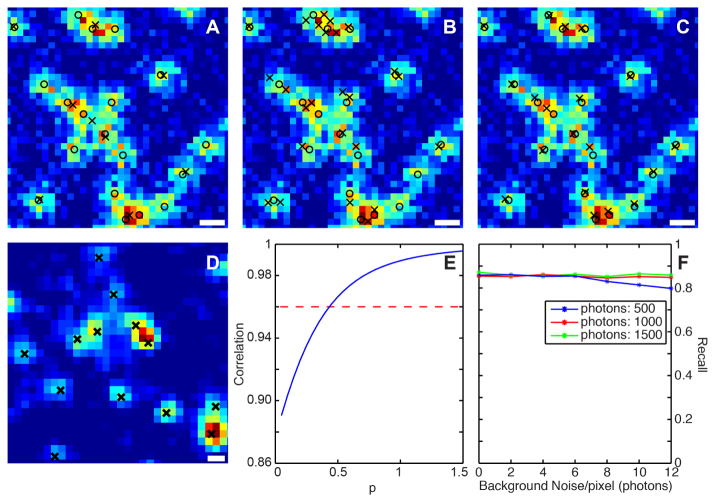
Effect of the stabilization factor in the Gaussian kernel. (a) WMS decomposition with a small stabilization factor underestimates the number of emitters. True positions of the emitters are labeled with circles and the estimated positions are labeled with crosses. (b) WMS decomposition with a large stabilization factor overestimates the number of modes. (c) WMS decomposition with the right stabilization factor renders the right number of emitters. (d) Mode detection using WMS on an image acquired via a 60x objective yields good match with raw data. Scale bars: 300 nm. (e) The stabilization factor is determined using the correlation method (Eq. (9), section 3.1). (f) The recall (percentage of detected modes) does not change significantly with the background noise or the photon levels as tested via simulation. At each condition, the value of the stabilization parameter was adjusted accordingly so that the correlation coefficient is 0.95.
3.2 Tracklet generation
The goal of this analysis step is to infer tracklets that link individual emitters over an interval of frames through spot tracking. While spot tracking has intrinsic challenges, originating from low SNR, variable number of emitters, and segmentation issues [29–33], there are several features that can facilitate the tracking process: (1) emitters turns on or off but do not have large displacements, making proximity-based correspondence reliable; (2) emitters do not stay on for too long, long-term tracking is not needed, and more importantly (3) because the same emitter lasts for multiple frames emitter localization is robust to few possible tracking errors. We developed an algorithm based on our earlier work on cell tracking [34, 35] with modifications that take advantage of these features to speed up the computation process.
The algorithm contains two tracking steps: a coarse tracking step to associate single or multi-emitter blobs in time, and a fine tracking step to associate individual emitter centers in time. Coarse tracking is achieved using an area overlap criteria. As the spatial shift of the same emitters in consecutive frames is minimum even in the presence of segmentation error, it is guaranteed that there will be overlap between the masks of the same emitters in successive frames. This process results in labeled 3D connected regions that are later used to constrain and speed up the finer tracking step [Fig. 1(c)].
The fine tracking step involves decomposition of individual blobs through the generalized WMS, which results in estimation of the number of modes in the group and their corresponding centers. A subsequent centroid-tracking step is applied to associate the estimated centers of the individual emitters in time [Fig. 1(d)]. We use a simplified version of our earlier tracker [34, 35] with a nearest neighbor match strategy based on spatial proximity to associate the positions. A gating function accounting for the centroid localization error is used to eliminate invalid/infeasible associations. We compute the likeliness of two modes as:
| (10) |
where is the mode in previous frame and is the mode in current frame. is the position vector of the estimated modes; and is the characteristic distance for the associated objects (75 nm in our case). Pairwise likeliness is only computed for centers within the same 3D connected component to reduce the computational complexity.
It is not unusual that the numbers of detected modes are different for two consecutive frames. For example, there may be M emitters at frame t and N emitters at frame t + 1. When N is bigger than M, suggesting newly appearing emitters. If assignments of the N emitters to the existing M tracklets can be done without ambiguity, we extend the existing M tracklet from frame t to frame t + 1 and initialize the newly appeared (N-M) emitters. If there is assignment ambiguity, for example tracklet at frame t does not have a matched emitter at frame t + 1, we then terminate tracklet . Non-assigned emitters from frame t + 1 are used to initialize new tracklets. When N is smaller than M, indicating disappearance of emitters. If assignment of the N emitters at frame t + 1 to the existing M tracklets can be done, then we extend existing tracklets from frame t to frame t + 1, and terminate the non-matching (M-N) tracklets. If there is assignment ambiguity, we terminate the ambiguous tracklet and initiate new tracklets if needed.
3.3 Center re-estimation using spatiotemporal information
This step aims to increase center localization accuracy by integrating spatiotemporal image information in a selective and controlled way using the tracklets obtained in the previous section. First tracklets are scored according to their spatial separability from the other tracklets [Fig. 1(e)]. Then individual support regions within the same tracklet are aggregated to increase the SNR and photon count. Finally individual emitter centroids are re-estimated from these integrated image chips using MLE [Fig. 1(f)].
We assign scores for each tracklet according to the percentage of non-overlapping regions. For example, as shown in Fig. 1(e), tracklet T1 is assigned a score of 1 since it is a disjoint track with no spatial overlapping with other tracklets; tracklet T2 is assigned 0.55 due to the 55% of non-overlapping region. T3 is assigned a score of zero since the whole tracklet overlaps with T2. We process the tracklets sequentially from the highest to the lowest scores. For tracklets that are scored 1.0 (no overlapping regions), we sum all the support regions as defined by the union of a 7x7 region centered at the position of the mode and the corresponding mask. The summed image is then fitted to get the emitter position using the MLE. For tracklets with scores higher than a threshold value (0.6), for example tracklet T4 and T5, we only add up the support regions of non-overlapping frames, ignoring the overlapping frames. For other tracklets that have low scores, such as T3 (0.0), we aggregate the support regions of all the emitters with overlapping (the overlapping regions from both T2 and T3). The support regions are defined as the union of all the 7x7 regions centered at each estimated emitter locations and the corresponding labeled masks. We then fit the summed signal with the known number of modes (2 in this case for T2 and T3) and with the estimated positions from WMS as the initial values. The position of the involved emitters that have already been processed due to their higher scores will be used as prior information in the multi-emitter maximum likelihood estimation.
4. Experimental methods
4.1 Microscopy and data acquisition
Our home-built STORM system is based on an inverted microscope (IX71, Olympus America Inc.) with 1.49 NA 100x oil immersion TIRF objective. Four lasers–405 nm, 488 nm, and 647 nm diode lasers (Vortran Laser Technology Inc.) and 561 nm DPSS laser (CrystaLaser) cover the spectrum of the most commonly used fluorophores. The filter set consists of a multi-band dichroic mirror (FF405/496/593/649, Semrock) and an emission filter (692/40, Semrock). An electron multiplying CCD camera (iXon Ultra 897, Andor Technologies PLC.) is used for imaging with EM gain set to 255. The sample holder is mounted on a 3D piezo stage (Nano-LPS, Mad City Lab). An infrared 980 nm laser is used in combination with the piezo stage for the axial Zero Drift Correction (ZDC) [36].
4.2 Cell culture and immunofluorescence staining
HeLa cells are cultured on 35-mm petri dishes with a No. 1.5 glass coverslip window (MatTek Corp) at 37 °C with 5% CO2. The Dulbecco’s modified Eagle’s medium (DMEM, Invitrogen) is supplemented with 10% FBS, 100 U/mL penicillin and 100 µg/ml streptomycin. For the immunofluorescence staining, cells are fixed at room temperature in the fixation buffer (3% paraformaldehyde and 0.1% glutaraldehyde in PBS) for 10 minutes, and then rinsed 3 times with PBS. To reduce the background induced by glutaraldehyde, cells are quenched in 0.1% NaBH4 water solution for 7 minutes. After rinsing quickly 3 times with PBS, cells are blocked in blocking buffer (3% bovine serum albumin (BSA) and 0.2% Triton X-100) for 1 hour at room temperature. Primary antibody to α-tubulin (Sigma Aldrich) is diluted in blocking buffer and added to cells for 1 hour. Cells are then washed 3 times in PBS on a rocking platform and then treated with secondary antibody conjugated to AlexaFluor647 for 30 minutes. Antibodies are “locked” in place with a post-fixation using the same fixation buffer for 5 minutes. Cells are imaged in the imaging buffer (10% glucose, 50 mM Tris pH 8.5, 10mM NaCl, 14mg Glucose Oxidase, 50uL 20mg/mL catalase, and 1X B-mercaptoethanol (Sigma Aldrich)) [37].
4.3 FDB isolation and immunofluorescence staining
Adult male Sprague-Dawley rats are euthanized, following The Ohio State University Animal IACUC protocol, via CO2 asphyxiation and the flexor digitorum brevis muscles (FDB) are dissected. The muscles are digested in type I collagenase (Sigma Aldrich, 2 mg/mL) and placed in a 37°C orbital shaker for approximately 1 hour. Samples are then washed in minimal calcium Tyrode solution, and sequentially triturated using 1 ml pipette tips with incrementally smaller diameters. Once muscle bundles are frayed, and individual fibers could be visualized, the fibers are allowed to gravity settle in an Eppendorf tube and fixed in 4% Para-Formaldehyde for 20 min. Fibers are quickly washed 3 times using minimal calcium Tyrode, and suspended in blocking buffer and placed on a rocking platform for 1 hour at room temperature. Primary antibody to MG29 [38] is diluted in blocking buffer, and added to fibers for overnight incubation at 4°C. Samples are then washed 3 times in washing buffer. Mouse IgG antibody is conjugated to Alexa 647 fluorophore (Life Technology, USA), diluted in blocking buffer, and fibers are allowed to incubate for 1.5 hours at room temperature. Samples are washed 3 times with washing buffer, and post-fixed in 4% paraformaldehyde for 10 minutes. After quickly washing 3 times in PBS, fibers can be transferred to a 35 mm dish, and collected using a 10 µl pipette under a microscope. Individual fibers are placed upon an agarose pad (1% m/v) atop a microscope slide, and allowed 10 minutes to adhere. A coverslip is placed atop after applying 2 µl imaging buffer, and is sealed carefully with nail polish.
5. Results and discussion
5.1 Mode detection and tracklet generation
One of the difficulties caused by combining multiple frames is that temporally separated emitters may overlap. It is critical to resolve these multiple emitters without losing resolution. A number of algorithms have been developed [22, 39–46], and majority of these methods require prior knowledge on the number of modes within the cluster. Here we introduce a generalized weighted mean shift method to automatically detect the number of modes and estimate the positions of the decomposed modes. By integrating temporal information, we increase the photon counts of the signal and increase the localization accuracy [23].
Mean shift procedure is a non-parametric density estimation method, and it is critical to choose the right parameters (stabilization parameter and bandwidth) for the performance of the WMS. In our analysis, we used a generalized Gaussian kernel as defined in Eq. (8). We test different values of the stabilization parameter with the bandwidth fixed to the standard deviation of the PSF. When the value of is too small or too big, the WMS either underestimates or overestimates the number of modes respectively [Fig. 2(a) and 2(b)]. To choose the right value of the stabilization parameter, we graph the correlation coefficient versus different values of as described in Eq. (9) [Fig. 2(e)], and find that when the correlation value is in the range [0.95, 0.97], the corresponding value of works well to identify the right number of modes [Fig. 2(c)].
We perform simulation with different photon levels (500, 1000, and 1500) and background noises to test the mode detection efficiency using our algorithm. As shown in Fig. 2 (f), the recall (percentage of detected modes) does not show significant change with different background noise level or different photon levels. In another test, we used a different objective (60x oil immersion, N.A 1.3) to check how the method works on real experimental data. In this case, in Eq. (8) is set to the standard deviation of the 60x objective PSF. We choose a value corresponding to the correlation coefficient of 0.95 for mode detection and localization. Figure 2(d) shows detected modes marked with black crosses matched well with the raw experimental data.
We also test the capability of WMS in resolving emitter pairs with various distances. We simulate a pair of emitters in a 12x12 region. In our simulation we fix the Gaussian background noise to 3.2 photons/pixel and the signal to 1000 photons/emitter/frame. WMS can correctly identify the number of modes when the two emitters are as close as 200 nm [Fig. 3(A) ]. As another measure to evaluate the performance of WMS on resolving multi-emitters, we vary the density of activated emitters from 0.1 molecules to 5 molecules per micron meter squares. We also change the number of photons of an emitter from 500 to 1500 photons/emitter/frame, with the background Gaussian noise fixed to 10 photons/pixel. We apply WMS to estimate the locations of the emitters, and calculate the distance between the estimated positions and the true emitter positions. We match the estimated emitter with the corresponding true emitter, and we make sure there is a one-to-one correspondence. The measured density is defined as the number of correctly detected emitters per micron meter square. Figure 4 shows that WMS can reliably provide the correct number of modes when the emitter density is up to 3 emitters .
Fig. 3.
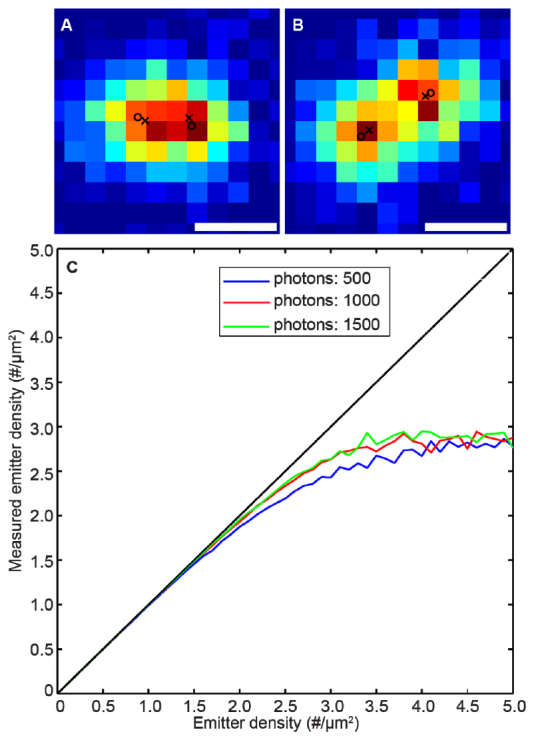
Performance of WMS on resolving emitter pairs and high density of emitters with overlapping. (a) and (b), WMS is able to resolve an emitter pair when the distances between them are 200 nm and 300 nm respectively. True positions of the emitters are labeled with circles and the estimated positions are labeled with crosses. (c). WMS is able to resolve the right number of emitters when the emitter density is as high as 3 emitters per micrometer square. Scale bars: 300 nm.
Fig. 4.
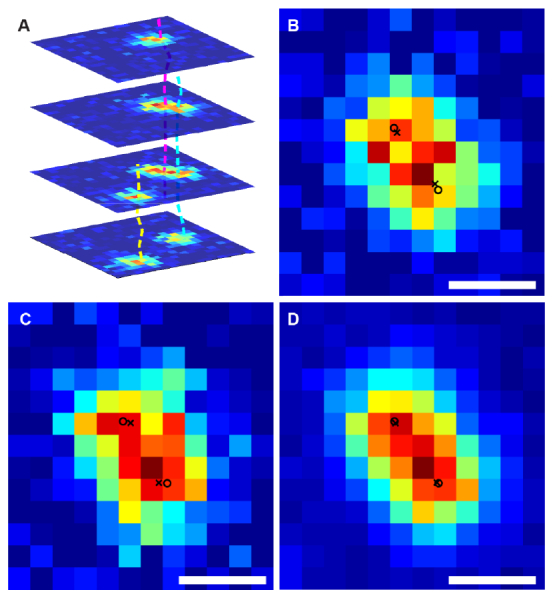
(a). Illustration of three tracklets generated from the simulation. The yellow one is an isolated tracklet while the other two have significant overlapping in time. (b, c). Two individual frames from the two overlapping tracklets as shown in (a). The true positions of the emitters are labeled with circles and the estimates are labeled as crosses. Due to the low signal noise ratio, the estimates deviate from the true positions. (d). By aggregating all the support regions of the tracklets, the signal is significantly increased. Now the estimate positions (crosses) overlap with the true locations of the emitters. Scale bars: 300 nm.
We note that the accuracy of the estimated positions from the WMS calculation is not sufficient for single molecule localization microscopy. Instead, we use the estimates to form tracklets for further MLE analysis.
Figure 4(a) demonstrates three tracklets from our simulation. One (yellow) is an isolated tracklet, and the other two temporally overlap for most of the sequence. Figure 4(b) and 4(c) are two frames of the overlapping emitters. Due to the low signal noise ratio, the localization accuracy is low even with the MLE method [Fig. 4(b) and 4(c)]. In contrast, after we integrate the supporting regions of all the frames, the photon count of the signal is significantly increased [Fig. 4(d)]. We then apply the MLE fitting to get positions that are of much higher accuracy.
5.2 Resolving overlapping multi-emitters and improving localization accuracy
The proposed method is able to resolve overlapping multi-emitters using WMS and to improve the localization accuracy with the tracklet method. Figure 5 demonstrates the advantages of the method. We simulate a cross of four lines with a constant line density of emitters. Due to the higher density of the emitters at the center, the probability of the appearance of overlapping multi-emitters at the center is much higher. As shown in Fig. 5(a), single molecule analysis (SA) [10] fails to locate these emitters, resulting in very low number of detected emitters at the center; while the proposed method is able to resolve these emitters and precisely locate them [Fig. 5(b)]. We also compare the localization accuracy of the two methods. Figure 5(d) shows the line profiles of the selected regions from the two reconstructed images. The width of the line constructed using the tracklet method is much thinner, demonstrating the increased localization accuracy [Fig. 5(b)].
Fig. 5.
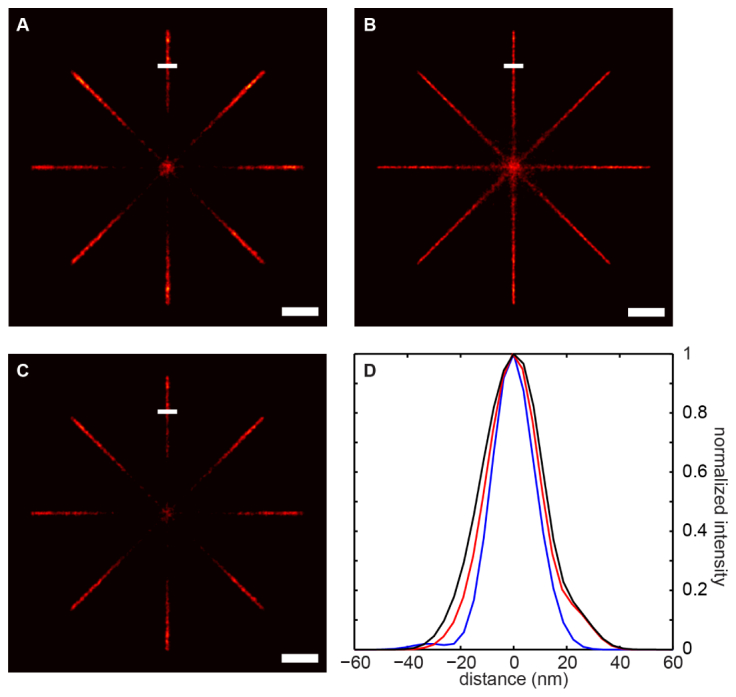
Tracklet based reconstruction is able to resolve overlapping multi-emitters with improved localization accuracy. (a). Reconstructed image using the SA method. Due to the high density of emitters at the central part of the image, SA is not able to resolve the overlapping emitters, which results in very low number of detected emitters. (b). Tracklet-based reconstruction of the same image. Comparing with (a), the central part of the image is well reconstructed. (c). Image reconstructed with the combined SA method as defined in the main text. (d). Line profiles of the selected regions as shown in (a), (b), and (c). The black curve represents the line profile of the selected region in (A), and the blue curve is from (b), and red is from (c). The blue curve has smaller width, demonstrating the smaller localization uncertainty with the tracklet-based method. Scale bar: 300 nm.
We note that another approach that has been used in previous studies [10, 37] is that one can locate the emitters at each frame, after which all the located centers that are within a preset threshold region (usually 1 pixel) are averaged, and the averaged center is used as the final estimation of the emitter (combined SA method). Figure 5(c) shows the reconstructed image using the combined SA method. As shown in Fig. 5(d), our tracklet-based method provides better localization accuracy than the combined SA (the blue curve vs. the red curve). Our method differs from it in the following aspects. First, our method is able to resolve overlapping multi-emitters, while the SA method in [10, 37] only works for sparse, disjoint single emitters. Second, SA discards emitters when the fitting does not meet the criteria that assure the detected signal is from a single emitter instead of overlapping multi-emitters. This usually results in loss of frames, particularly when the signal is weak and the background is high. Third, in our method, we fully utilize the temporal information of the signals. For example, if a tracklet partially overlaps with other tracklets, instead of discarding the overlapping region, we use the estimated locations from the non-overlapping region to help the decomposition and localization of the positions at the overlapping regions, fully integrating all the temporal information.
5.3 Analysis of HeLa cell microtubule structure
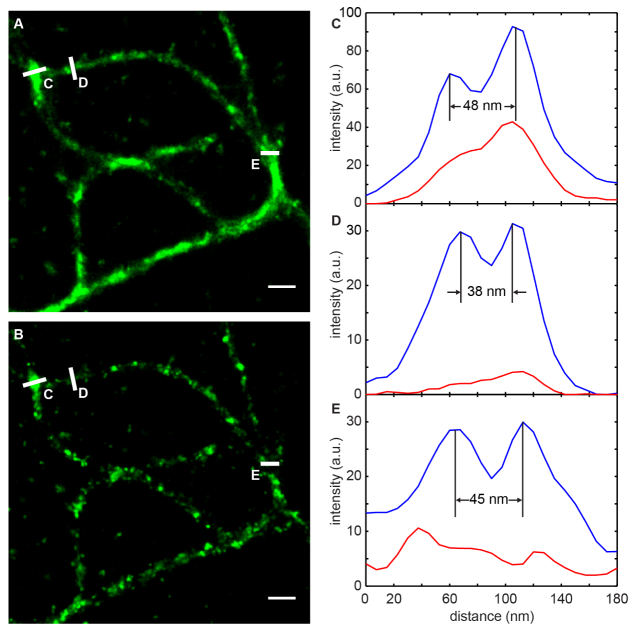
Figure 6(a) , and 6(b) show reconstructed microtubule images with the proposed method and the SA method [10] respectively. These images are reconstructed from 50,000 frames. Since all the overlapping signals are discarded by the SA method, the reconstructed microtubule filaments are discontinuous [Fig. 6(b)]. In contrast, Fig. 6(a) is reconstruction from the same data set with the proposed method. With the proposed method, the filaments are more continuous since we are able to resolve both overlapping multi-emitters and weak emitters that are discarded by SA method. The difference is more significant at locations with high emitter density, such as the region labeled with E in Fig. 6(a) and Fig. 6(b). Second, as shown in Fig. 6(c)-6(e), the proposed method is able to resolve the two adjacent microtubules as close as 38 nm, which are completely missed with the SA method [Fig. 6(d)].
Fig. 6.
Microtubule images in HeLa cells. (a). Image reconstructed using the tracklet-based method from 50,000 frames. (b). Image reconstructed using the same data set as in (a) but with the SA method. Structures are discontinuous, particularly at crossing regions where emitter density is high. Scale bars: 300 nm. (c, d, e). Line profiles of the selected regions in (a) and (b). The tracklet-based method is able to resolve two structures as close as 38 nm, which is not resolvable with the SA method due to insufficient localization of emitters.
5.4 Resolving the T-tubule structure in skeletal muscle cells
In skeletal muscle, the transverse (T)-tubular invagination of the sarcolemmal membrane touches the terminal cisternae of the junctional sarcoplasmic reticulum to form a triad junction structure that provides the structural framework for excitation-contraction (EC) coupling [47]. Most of the ultrastructural analyses of the triad junction involves electron microscopy [47]. Recently, T-tubule structure in cardiomyocytes has been investigated using the stimulated emission depletion (STED) microscopy with a resolution of ~50 nm [48]. However, T-tubule structures in skeletal muscle cells have never been studied optically.
We use the antibody to mitsugumin29 (MG29), a skeletal muscle-specific protein, to label the T-tubule structure in the rat FDB fiber [38, 49, 50]. Different from adherent cells, FDB fibers do not attach well to the glass coverslips, which makes it difficult to apply total internal reflective fluorescence (TIRF) illumination during the image acquisition. We applied oblique illumination method to acquire the MG29-labelled fluorescence images in order to resolve the T-tubule structure. Compared with TIRF, the oblique-illumination method produces high background noises that will require the implementation of our tracklet-based reconstruction algorithm for data processing. To eliminate out-of-focus emitters, we apply a threshold to the fitted Gaussian at the end of the image reconstruction. We discard all emitters with fitted bigger than 190 nm (~1.5 times of the standard deviation of the PSF). This allows us to partially remove out-of-focus emitters.
As shown in Fig. 7(a) , the traditional epifluorescence microscopy produced striated pattern of MG29-labelled T-tubule network, with doublet pattern that resembles the typical membrane structure in rat skeletal muscle. Within each of the doublets, there are two T-tubule membranes running in parallel that could not be resolved in traditional optical imaging. With the proposed method, we are able to reconstruct the images, clearly showing the two sides of the T-tubule membrane within a single doublet. Figure 7(b) shows the overlay of the superresolution image (green) and the conventional epi-fluorescence image (red). Figure 7(c) shows the line profiles of the selected region. The epi-fluorescence image does not show any fine structures of the T-tubule, while the superresolution image shows the two sides clearly [Fig. 7(b)]. To our knowledge, this is the first time that the T-tubule structure in skeletal muscle cells is resolved optically. One of our future studies is to investigate the remodeling of the T-tubule structures in different disease models.
Fig. 7.
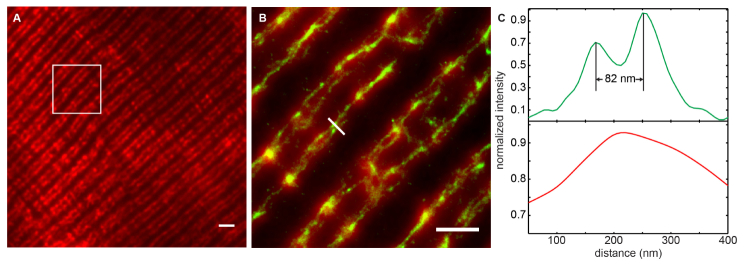
T-tubule structures in rat FDB fiber. (a) Epifluorescence image of MG29-labelled T-tubule network in rat skeletal muscle. Scale bar: 2 μm. (b) Overlay of the epifluorescence image (red) of the T-tubule and the corresponding superresolution image (green). Scale bar: 1 μm. (c). The line profiles of the selected region in (b). The green curve corresponds to the line profile from the superresolution image, which shows clearly the distance between the two T-tubule membranes is about 82 nm. The conventional epifluorescence image completely misses the fine structure (red curve).
6. Conclusion and future work
In this paper, we describe a tracklet based image reconstruction algorithm for localization based superresolution microscopy imaging, which enables us to resolve overlapping multi-emitters (low to medium emitter density) and to fully integrate the temporal information of the emitters to achieve improved localization accuracy. Because our image analysis routine contains the WMS and tracklet features, it provides a better way to dissect the spatial and temporal relationship of overlapping emitters for broader application in biological imaging.
In a typical single molecule localization microscope experiment, it is not unusual to have tens of thousands frames. Effectively incorporating temporal information is critical to improve the spatial resolution. By forming different reliable tracklets of emitters and analyzing these tracklets separately, we are able to incorporate temporal information of different emitters, and increase the localization accuracy by increasing the photon counts of the signal. When two tracklets have spatiotemporal overlapping regions, instead of discarding the information, we apply the MLE method to locate these multiple emitters simultaneously. One required input of our MLE method is the number of the modes in the data set. Here we introduce a weighted mean-shift (WMS) method for the mode detection. Our analysis shows that WMS is robust to the background noise, and is able to reliably provide the right number of modes for the MLE.
In summary, our progressive superresolution microscope image reconstruction system uses and integrates reliable information at multiple stages resulting in improvement of the localization accuracy. A previous study by Cox et al. [51] introduced a Bayesian analysis of the blinking and bleaching (3B analysis) method that also incorporates temporal information to analyze high-density superresolution data. However, since the 3B method incorporates temporal information by modeling the entire data set using a factorial hidden Markov model, the data processing requires extensive computation resources and analysis takes a long time, making it hard to handle by conventional desktop computers. Our method integrates temporal information with single molecule tracking to form tracklets, and significantly reduces the need of expensive computation resources and shortens the computation time. For example, in the original paper by Cox et al. [51] and a recent publication by Rosten et al. [52], they showed that analyzing an image stack of 200 frames 15 pixels x 15 pixels took 6 hours using a single core i7 (3.33 GHz) computer. Another publication by Hu et al. [53] using the 3B approach showed that with 300 instances of 600 virtual cores using the commercial (paid service) Amazon EC2 cloud server, it took 210 minutes to analyze 150 pixels x 100 pixels x 1,500 frames, while analyzing the same data set using 3B on a state-of-the-art desktop computer would take ~9 days. With a similar data set, our algorithm will take a few min to complete the data processing process using a desktop personal computer.
Our method is also of particular advantage for high frame rate image acquisition. By increasing the frame rate, there is a better chance to temporally separate two adjacent emitters, a prerequisite for superresolution imaging. However, high frame rates usually result in low signals. By associating these weak signals through the tracklet, we are able to increase the localization accuracy. Another potential usage of our method is molecule counting. Knowing the blinking (switching) dynamics of the emitters, we can do a global association of the tracklets to get more precise counting of the molecules. For example, Alexa 647 labeled molecules can reversibly turn on and off for many times, resulting in multiple tracklets. By associating these tracklets with the proper modeling of the switching dynamics, we can associate these tracklet to eliminate the multi-appearance of the emitter, which is critical for precise counting of molecules.
Our method is implemented using Matlab 2013b (The Mathworks, USA). Most of the analysis procedures can be parallelized, or to be distributed to the graphic processing unit (GPU). By converting the program to C/C + + and combine with parallel and GPU programming, we expect significant improvement of computation speed that can lead to potential application in live cell superresolution imaging.
Acknowledgments
This work was supported by NIH grants R01-AR061385 and R01-HL069000 to J.M. The study was supported in part by an allocation of computing time from the Ohio Supercomputer Center. The authors would like to thank Dr. David Hudak for the technical support and the inspiring discussion.
Acknowledgments display corrected in full-text HTML display.
References and links
- 1.Born M., Wolf E., Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed. (Cambridge University, 1975). [Google Scholar]
- 2.Hell S. W., “Far-field optical nanoscopy,” Science 316(5828), 1153–1158 (2007). 10.1126/science.1137395 [DOI] [PubMed] [Google Scholar]
- 3.Huang B., Bates M., Zhuang X., “Super-resolution fluorescence microscopy,” Annu. Rev. Biochem. 78(1), 993–1016 (2009). 10.1146/annurev.biochem.77.061906.092014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Patterson G., Davidson M., Manley S., Lippincott-Schwartz J., “Superresolution imaging using single-molecule localization,” Annu. Rev. Phys. Chem. 61(1), 345–367 (2010). 10.1146/annurev.physchem.012809.103444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chi K. R., “Microscopy: Ever-increasing resolution,” Nature 462(7273), 675–678 (2009). 10.1038/462675a [DOI] [PubMed] [Google Scholar]
- 6.Hell S. W., Wichmann J., “Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy,” Opt. Lett. 19(11), 780–782 (1994). 10.1364/OL.19.000780 [DOI] [PubMed] [Google Scholar]
- 7.Gustafsson M. G., “Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy,” J. Microsc. 198(2), 82–87 (2000). 10.1046/j.1365-2818.2000.00710.x [DOI] [PubMed] [Google Scholar]
- 8.Fölling J., Bossi M., Bock H., Medda R., Wurm C. A., Hein B., Jakobs S., Eggeling C., Hell S. W., “Fluorescence nanoscopy by ground-state depletion and single-molecule return,” Nat. Methods 5(11), 943–945 (2008). 10.1038/nmeth.1257 [DOI] [PubMed] [Google Scholar]
- 9.Dertinger T., Colyer R., Iyer G., Weiss S., Enderlein J., “Fast, background-free, 3D super-resolution optical fluctuation imaging (SOFI),” Proc. Natl. Acad. Sci. U.S.A. 106(52), 22287–22292 (2009). 10.1073/pnas.0907866106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rust M. J., Bates M., Zhuang X., “Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM),” Nat. Methods 3(10), 793–796 (2006). 10.1038/nmeth929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Heilemann M., van de Linde S., Schuttpelz M., Kasper R., Seefeldt B., Mukherjee A., Tinnefeld P., Sauer M., “Subdiffraction-resolution fluorescence imaging with conventional fluorescent probes,” Angew. Chem-Ger. Edit. 47(33), 6172–6176 (2008). 10.1002/anie.200802376 [DOI] [PubMed] [Google Scholar]
- 12.Heilemann M., van de Linde S., Mukherjee A., Sauer M., “Super-resolution imaging with small organic fluorophores,” Angew. Chem. Int. Ed. Engl. 48(37), 6903–6908 (2009). 10.1002/anie.200902073 [DOI] [PubMed] [Google Scholar]
- 13.Betzig E., Patterson G. H., Sougrat R., Lindwasser O. W., Olenych S., Bonifacino J. S., Davidson M. W., Lippincott-Schwartz J., Hess H. F., “Imaging intracellular fluorescent proteins at nanometer resolution,” Science 313(5793), 1642–1645 (2006). 10.1126/science.1127344 [DOI] [PubMed] [Google Scholar]
- 14.Hess S. T., Girirajan T. P. K., Mason M. D., “Ultra-high resolution imaging by fluorescence photoactivation localization microscopy,” Biophys. J. 91(11), 4258–4272 (2006). 10.1529/biophysj.106.091116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vaughan J. C., Jia S., Zhuang X., “Ultrabright photoactivatable fluorophores created by reductive caging,” Nat. Methods 9(12), 1181–1184 (2012). 10.1038/nmeth.2214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pertsinidis A., Mukherjee K., Sharma M., Pang Z. P., Park S. R., Zhang Y., Brunger A. T., Südhof T. C., Chu S., “Ultrahigh-resolution imaging reveals formation of neuronal SNARE/Munc18 complexes in situ,” Proc. Natl. Acad. Sci. U.S.A. 110(30), E2812–E2820 (2013). 10.1073/pnas.1310654110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pertsinidis A., Zhang Y., Chu S., “Subnanometre single-molecule localization, registration and distance measurements,” Nature 466(7306), 647–651 (2010). 10.1038/nature09163 [DOI] [PubMed] [Google Scholar]
- 18.Shroff H., Galbraith C. G., Galbraith J. A., Betzig E., “Live-cell photoactivated localization microscopy of nanoscale adhesion dynamics,” Nat. Methods 5(5), 417–423 (2008). 10.1038/nmeth.1202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jones S. A., Shim S. H., He J., Zhuang X., “Fast, three-dimensional super-resolution imaging of live cells,” Nat. Methods 8(6), 499–505 (2011). 10.1038/nmeth.1605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang B., Zerubia J., Olivo-Marin J. C., “Gaussian approximations of fluorescence microscope point-spread function models,” Appl. Opt. 46(10), 1819–1829 (2007). 10.1364/AO.46.001819 [DOI] [PubMed] [Google Scholar]
- 21.Stallinga S., Rieger B., “Accuracy of the gaussian point spread function model in 2D localization microscopy,” Opt. Express 18(24), 24461–24476 (2010). 10.1364/OE.18.024461 [DOI] [PubMed] [Google Scholar]
- 22.Huang F., Schwartz S. L., Byars J. M., Lidke K. A., “Simultaneous multiple-emitter fitting for single molecule super-resolution imaging,” Biomed. Opt. Express 2(5), 1377–1393 (2011). 10.1364/BOE.2.001377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thompson R. E., Larson D. R., Webb W. W., “Precise nanometer localization analysis for individual fluorescent probes,” Biophys. J. 82(5), 2775–2783 (2002). 10.1016/S0006-3495(02)75618-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sage D., Neumann F. R., Hediger F., Gasser S. M., Unser M., “Automatic tracking of individual fluorescence particles: application to the study of chromosome dynamics,” IEEE Trans. Image Process. 14(9), 1372–1383 (2005). 10.1109/TIP.2005.852787 [DOI] [PubMed] [Google Scholar]
- 25.Starck J. L., Murtagh F., Bijaoui A., “Multiresolution support applied to image filtering and restoration,” Graph Model Im. Pro. C. 57(5), 420–431 (1995). 10.1006/gmip.1995.1036 [DOI] [Google Scholar]
- 26.Fukunaga K., Hostetler L., “The estimation of the gradient of a density function, with applications in pattern recognition,” IEEE Trans. Inf. Theory 21(1), 32–40 (1975). 10.1109/TIT.1975.1055330 [DOI] [Google Scholar]
- 27.Cheng Y., “Mean shift, mode seeking, and clustering,” IEEE T. Pattern Anal. 17(8), 790–799 (1995). 10.1109/34.400568 [DOI] [Google Scholar]
- 28.Wu K. L., Yang M. S., “Mean shift-based clustering,” Pattern Recognit. 40(11), 3035–3052 (2007). 10.1016/j.patcog.2007.02.006 [DOI] [Google Scholar]
- 29.E. Meijering, I. Smal, O. Dzyubachyk, and J.-C. Olivo-Marin, “Time-lapse imaging,” Microsc. Img. Proc. 401-440 (2008). [Google Scholar]
- 30.Meijering E., Dzyubachyk O., Smal I., “Methods for cell and particle tracking,” Methods Enzymol. 504, 183–200 (2012). 10.1016/B978-0-12-391857-4.00009-4 [DOI] [PubMed] [Google Scholar]
- 31.Jaqaman K., Loerke D., Mettlen M., Kuwata H., Grinstein S., Schmid S. L., Danuser G., “Robust single-particle tracking in live-cell time-lapse sequences,” Nat. Methods 5(8), 695–702 (2008). 10.1038/nmeth.1237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li F. H., Zhou X. B., Ma J. W., Wong S. T. C., “Multiple nuclei tracking using integer programming for quantitative cancer cell cycle analysis,” IEEE Trans. Med. Imaging 29(1), 96–105 (2010). 10.1109/TMI.2009.2027813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kanade T., Yin Z., Bise R., Huh S., Eom S., “Cell image analysis: algorithms, system and applications,” IEEE Work. App. Comp. (2011).
- 34.F. Bunyak, K. Palaniappan, S. K. Nath, T. L. Baskin, and G. Dong, “Quantitative cell motility for in vitro wound healing using level set-based active contour tracking,” I. S. Biomed. Imaging 1040–1043 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Palaniappan K., Bunyak F., Nath S., Goffeney J., “Parallel Processing Strategies for Cell Motility and Shape Analysis,” High-Throughput Image Reconstruction and Analysis, Artech House Publisher, 39–87 (2009). [Google Scholar]
- 36.Huang B., Wang W., Bates M., Zhuang X., “Three-Dimensional super-resolution imaging by stochastic optical reconstruction microscopy,” Science 319(5864), 810–813 (2008). 10.1126/science.1153529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bates M., Jones S. A., Zhuang X., “Stochastic optical reconstruction microscopy (STORM): a method for superresolution fluorescence imaging,” Cold Spring Harb Protoc 2013(6), 498–520 (2013). 10.1101/pdb.top075143 [DOI] [PubMed] [Google Scholar]
- 38.Takeshima H., Shimuta M., Komazaki S., Ohmi K., Nishi M., Iino M., Miyata A., Kangawa K., “Mitsugumin29, a novel synaptophysin family member from the triad junction in skeletal muscle,” Biochem. J. 331(Pt 1), 317–322 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Holden S. J., Uphoff S., Kapanidis A. N., “DAOSTORM: an algorithm for high- density super-resolution microscopy,” Nat. Methods 8(4), 279–280 (2011). 10.1038/nmeth0411-279 [DOI] [PubMed] [Google Scholar]
- 40.Zhu L., Zhang W., Elnatan D., Huang B., “Faster STORM using compressed sensing,” Nat. Methods 9(7), 721–723 (2012). 10.1038/nmeth.1978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Quan T., Zhu H., Liu X., Liu Y., Ding J., Zeng S., Huang Z. L., “High-density localization of active molecules using Structured Sparse Model and Bayesian Information Criterion,” Opt. Express 19(18), 16963–16974 (2011). 10.1364/OE.19.016963 [DOI] [PubMed] [Google Scholar]
- 42.Wang Y., Quan T., Zeng S., Huang Z. L., “PALMER: a method capable of parallel localization of multiple emitters for high-density localization microscopy,” Opt. Express 20(14), 16039–16049 (2012). 10.1364/OE.20.016039 [DOI] [PubMed] [Google Scholar]
- 43.Babcock H. P., Moffitt J. R., Cao Y., Zhuang X., “Fast compressed sensing analysis for super-resolution imaging using L1-homotopy,” Opt. Express 21(23), 28583–28596 (2013). 10.1364/OE.21.028583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mukamel E. A., Babcock H., Zhuang X., “Statistical deconvolution for superresolution fluorescence microscopy,” Biophys. J. 102(10), 2391–2400 (2012). 10.1016/j.bpj.2012.03.070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Deng Y., Coen P., Sun M., Shaevitz J. W., “Efficient multiple object tracking using mutually repulsive active membranes,” PLoS ONE 8(6), e65769 (2013). 10.1371/journal.pone.0065769 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dedecker P., Duwé S., Neely R. K., Zhang J., “Localizer: fast, accurate, open-source, and modular software package for superresolution microscopy,” J. Biomed. Opt. 17(12), 126008 (2012). 10.1117/1.JBO.17.12.126008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Franzini-Armstrong C., Heuser J. E., Reese T. S., Somlyo A. P., Somlyo A. V., “T-tubule swelling in hypertonic solutions: a freeze substitution study,” J. Physiol. 283, 133–140 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wagner E., Lauterbach M. A., Kohl T., Westphal V., Williams G. S. B., Steinbrecher J. H., Streich J. H., Korff B., Tuan H. T. M., Hagen B., Luther S., Hasenfuss G., Parlitz U., Jafri M. S., Hell S. W., Lederer W. J., Lehnart S. E., “Stimulated emission depletion live-cell super-resolution imaging shows proliferative remodeling of T-tubule membrane structures after myocardial infarction,” Circ. Res. 111(4), 402–414 (2012). 10.1161/CIRCRESAHA.112.274530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Komazaki S., Nishi M., Kangawa K., Takeshima H., “Immunolocalization of mitsugumin29 in developing skeletal muscle and effects of the protein expressed in amphibian embryonic cells,” Dev. Dyn. 215(2), 87–95 (1999). [DOI] [PubMed] [Google Scholar]
- 50.Pan Z., Yang D., Nagaraj R. Y., Nosek T. A., Nishi M., Takeshima H., Cheng H., Ma J., “Dysfunction of store-operated calcium channel in muscle cells lacking mg29,” Nat. Cell Biol. 4(5), 379–383 (2002). 10.1038/ncb788 [DOI] [PubMed] [Google Scholar]
- 51.Cox S., Rosten E., Monypenny J., Jovanovic-Talisman T., Burnette D. T., Lippincott-Schwartz J., Jones G. E., Heintzmann R., “Bayesian localization microscopy reveals nanoscale podosome dynamics,” Nat. Methods 9(2), 195–200 (2011). 10.1038/nmeth.1812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rosten E., Jones G. E., Cox S., “ImageJ plug-in for Bayesian analysis of blinking and bleaching,” Nat. Methods 10(2), 97–98 (2013). 10.1038/nmeth.2342 [DOI] [PubMed] [Google Scholar]
- 53.Hu Y. S., Nan X., Sengupta P., Lippincott-Schwartz J., Cang H., “Accelerating 3B single-molecule super-resolution microscopy with cloud computing,” Nat. Methods 10(2), 96–97 (2013). 10.1038/nmeth.2335 [DOI] [PMC free article] [PubMed] [Google Scholar]