Stability in computed optical interferometric tomography (Part I): Stability requirements

Abstract

As imaging systems become more advanced and acquire data at faster rates, increasingly dynamic samples can be imaged without concern of motion artifacts. For optical interferometric techniques such as optical coherence tomography, it often follows that initially, only amplitude-based data are utilized due to unstable or unreliable phase measurements. As systems progress, stable phase maps can also be acquired, enabling more advanced, phase-dependent post-processing techniques. Here we report an investigation of the stability requirements for a class of phase-dependent post-processing techniques – numerical defocus and aberration correction with further extensions to techniques such as Doppler, phase-variance, and optical coherence elastography. Mathematical analyses and numerical simulations over a variety of instabilities are supported by experimental investigations.

1. Introduction

High-resolution volumetric tomography in biological tissue is of great importance to both basic science and medicine. Reaching high-resolutions and approaching the cellular level in volumetric imaging, though, often incurs fundamental barriers imposed by the divergent nature of light. The difficulty of confining light to a small area in tissue, and the complexity of designing aberration-free optical systems, means that truly diffraction-limited volumetric tomography is rarely achieved.

Computed imaging has a long history of enhancing the overall utility of different imaging modalities and has the potential to solve these challenges. Techniques such as x-ray computed tomography [1, 2] and synthetic aperture radar (SAR) [3] enhance their respective underlying imaging modalities through a better understanding the basic physics involved. More recently, interferometric detection of optical frequencies has enabled high-resolution imaging of biological samples through holography and optical coherence tomography (OCT) [4–6]. These techniques, while useful in their own right, have also benefitted from the introduction of various computed optical interferometric techniques [7–10]. The ability for these techniques to exactly correct defocus and optical aberrations means that near diffraction-limited imaging over larger depth ranges and with simpler optical designs is possible.

Computationally correcting defocus and aberrations brings with it some tradeoffs. Possibly the most severe tradeoff, and the one focused on in this article, is the increased need of stability. As a general rule, computed optical interferometric techniques rely on the retrieved phase of collected light. Utilizing the phase is preferable, as it has the ability to exactly reconstruct images convolved with phase-only masks. The sensitivity of the retrieved phase to motion, though, is typically orders of magnitude greater than the retrieved amplitude as is traditionally used in blind deconvolution [11, 12] or other techniques for OCT [13]. The impact of motion has until recently [14] limited computed optical interferometric techniques to fresh or fixed ex vivo biological samples, greatly reducing the potential for clinical applications. Reconstructions in SAR also suffer from undesired motion where position feedback can be greatly beneficial [15].

The side effects of motion in OCT, such as image distortion and fringe washout [16], have previously been investigated. This article investigates the additional impact of sample motion or system fluctuations on data reconstructions in computed optical interferometric imaging techniques. Specifically we investigate two such techniques. The first is interferometric synthetic aperture microscopy (ISAM) which solves an inverse problem for OCT and corrects for defocus due to a Gaussian beam. The second is computational adaptive optics (CAO) which corrects for more general optical aberrations. Extensions of this work to holoscopy [17] or other computed optical interferometric techniques [18] which acquire many data points over disjoint intervals of time should also be possible.

This article is separated into two parts. This part (Part I) focuses on the impact of motion on computed optical interferometric techniques and the stability requirements which should be met for successful reconstructions. The second part [19], following this article, is dedicated to assessing the stability of OCT systems for in vivo computed imaging. The stability assessment in the second part is then related back to this part to validate the stability requirements set forth.

2. Theory

This section lays the theoretical groundwork to be used throughout the rest of this article. Such a theoretical framework will provide the necessary intuition to approach and understand the stability results presented in the other sections.

2.1 Complex-valued deconvolution

Traditionally, ISAM takes advantage of a Fourier-domain coordinate warping to remove defocus due to a Gaussian beam in a single step [8] similar to SAR [20]. Equivalently, ISAM could be performed as many sequential 3-D deconvolutions – one for each depth [17]. Thus, ISAM can be viewed as an aberration correction technique where the aberration is defocus. As such, both ISAM and CAO can be analyzed in the same way when it comes to stability. A simplified inverse process is given below.

$$S_{\text{AC}}(x,y,z)={ℱ}^{-1}\left\{ℱ\left\{S_{\text{OCT}}(x,y,z_{\text{ref}.},z_f,z)\right\}{H}^{-1}(q_x,q_y,k)\right\}$$ (1)

In Eq. (1), $S_{\text{AC}}$ is the aberration-corrected complex signal, $S_{\text{OCT}}$ is the complex signal obtained from standard OCT processing, $(x,y,z)$are standard Cartesian coordinates, $z_{\text{ref}.}$ is the position of equal path length relative to the optical focus, $z_f$is the location of the optical focus, $(q_x,q_y)$ are the transverse spatial frequencies of the measured data, $k$is the optical wavenumber, $ℱ$is a forward Fourier transform, and $H$is a phase-only filter which models the aberration/defocus. For defocus, $H(q_x,q_y,k)=\exp \left(2i{z}_0\sqrt{k^2-q_x^2-q_y^2}\right)$ where $z_0$ is the amount of defocus. The implementations of ISAM and CAO we consider here are to correct for the phase-only filter, $H$. This is in contrast to the complete inverse problem which involves amplitude filters as well [8]. Finally, let the operator ${\mathcal{A}}_H{}^{-1}$ represent Eq. (1) in a compact way such that ${\mathcal{A}}_H{}^{-1}\left\{S_{\text{OCT}}\right\}=S_{\text{AC}}$.

2.2 Motion Model

In this article, we focus on analyzing bulk sample motion, galvanometer jitter, and reference arm fluctuations. For these types of motion (and even for more generalized motion), the first Born approximation model remains linear in the scattering potential. To demonstrate this, let

$$\begin{array}{c}{\tilde{S}}_{OCT}(x_s,y_s,z_{\text{ref}.},z_f,k)\propto \int \int \int dxdydz\eta (x,y,z-z_{\text{ref}.}){\mathrm{e}}^{i2k(z-z_{\text{ref}.})}\\ \times g^2(x-x_s,y-y_s,z-z_{\text{ref}.}-z_f,k)\end{array}$$ (2)

be the signal measured from a point-scanned spectral domain (SD) OCT system (extended from [17]) where $\eta$is the scattering potential of the object, $x_s$ and $y_s$ represent the transverse scanning positions, $g$ is the 3-D complex optical field, and the tilde $\tilde{}$is used to reinforce that ${\tilde{S}}_{\text{OCT}}$ is a function of $(x,y,k)$. Since ${\tilde{S}}_{\text{OCT}}$ is measured over time, then $x_s$, $y_s$ and $z_{\text{ref}.}$ are actually functions of time. For a raster-scanned system with no undesired fluctuations,

$$\begin{array}{c}{x}_s(t)=v_{\text{fast}}\left(t-\lfloor t/\Delta t_{\text{fast}}\rfloor \Delta t_{\text{fast}}\right)\\ y_s(t)=v_{\text{slow}}\lfloor t/\Delta t_{\text{fast}}\rfloor \Delta t_{\text{fast}}\\ z_{\text{ref}.}(t)=z_0\end{array}$$ (3)

where $v_{\text{fast}}$ is the velocity of the beam along the fast axis, $\Delta t_{\text{fast}}$ is the length of time it takes to scan a single fast-axis frame, $v_{\text{slow}}$ is the velocity of the beam along the slow axis, $\lfloor \cdot \rfloor$is the floor operator, and $z_0$ is a fixed value. Bulk motion of the sample, improper beam scanning, or fluctuations in the reference arm can be modeled as time-varying fluctuations added onto $x_s$, $y_s$ and $z_{\text{ref}.}$.

Now consider a fluctuating reference arm or equivalently, small axial motion of the sample. This can be modeled as, $z_{\text{ref}.}(t)=z_0+f_z(t)$ for some function $f_z(t)$. As seen from Eq. (2), this will affect the measured signal in two ways. First, the object and the optical beam waist appear to move together since $z_{\text{ref}.}$ appears in both $\eta$ and $g$. This will produce fluctuations in the amplitude and phase of the measured signal which vary only as rapidly as the object and beam structures. The second influence of a time-varying reference arm directly influences the phase through the $\exp \left(i2k(z-z_{\text{ref}.})\right)$ term. This term can produce very rapid fluctuations in the phase and only depends on the wavelengths of light used. This is why many techniques in OCT/phase imaging can measure very small displacements in the axial dimension [21–23].

Alternatively, motion along the transverse dimension and/or jitter in the beam scanners can be modeled as arbitrary functions of time, $x_s(t)=v_{\text{fast}}\left(t-\lfloor t/t_{\text{fast}}\rfloor t_{\text{fast}}\right)+f_x(t)$ and $y_s(t)=v_{\text{slow}}\lfloor t/t_{\text{fast}}\rfloor +f_y(t)$. When measuring a flat sample, motion introduced in this manner only affects the measured signal through $\eta$ and $g$. Thus, the effect of transverse motion on the final data depends only on the object structure and the shape of the imaging beam. For a moderate numerical aperture (NA) Gaussian beam (0.1 – 0.2), the transverse resolution is much greater than the wavelength of light. This suggests that motion along the transverse dimension at these NAs is much less significant than axial motion. As the NA of the imaging system increases, the structure of $g$ along the transverse dimensions scales inversely proportional and approaches the wavelength of light. Thus, at high NAs, the sensitivity to motion along the transverse dimension can become comparable to the axial dimension.

Finally, Eq. (2) shows that even with bulk sample motion, reference arm fluctuations, and galvanometer jitter, the measured signal (assuming a single scattered, first Born model) is still linear in the scattering potential, $\eta$. As a result, the simulations and experiments performed in the rest of this article will focus on point scatterers. Note, though, that the measured signal is non-linear with respect to the motion functions $f_x,f_y,f_z$ since, for example, $\eta (x,y,z-z_0+f_1+f_2)\ne \eta (x,y,z-z_0+f_1)+\eta (x,y,z-z_0+f_2)$. This is even when assuming a linear scattering model. Thus, characterizing the impulse response will not suffice and various classes of motion will be separately investigated.

Moving beyond the first Born approximation (introducing multiple scattering) will make the resulting model non-linear in the scattering potential, and will surely influence the stability requirements. We argue, though, that the effect is not severe. First, consider axial motion of a highly-scattering tissue. Similar to Eq. (2), movement in the axial dimension with multiple scattering influences the phase directly through the interferometric term and, in addition, the multiple scattering structure (speckle) will only vary in phase and amplitude on the order of the axial resolution. Thus the sensitivity to axial motion will remain similar with and without multiple scattering. In addition, the structure in the transverse dimension resulting from multiple scattering also scales with the NA of the imaging beam [24]. Thus, the fluctuations in the measured signal due to transverse motion with and without multiple scattering should also not significantly change.

2.3 Interrogation time

The stability requirements for phase-sensitive techniques are also governed by a quantity we refer to as the ‘interrogation time’. The interrogation time is defined as the union of time intervals during imaging over which signal is collected from a point in the sample. This quantity is often dependent on spatial location and imaging modality. For telecentrically scanned systems, raster scanning is often performed to measure the full sample space and the scan lines of the raster scan define a ‘fast axis’ while the transverse direction orthogonal to the fast axis defines the ‘slow axis’. When using a Gaussian beam, a point is said to be interrogated by the beam when the point is within the 1/e² boundary. Although the interrogation time is often separated into many disjoint intervals (one for each fast axis scan), it is a good approximation to suppose that the interrogation time is a single interval defined by its interval span (the interval span of a set of numbers, A, is the unique interval which contains A and no other interval which contains A except itself). This becomes the interval of time the point is interrogated along the slow axis. Thus, the length of the interrogation time is defined by a quantity τ which is directly proportional to the 1/e² width of the Gaussian beam at that depth. Figures 1(a) –1(c) depict the interrogation times for such a system. Interestingly, an aberrated beam can result in a non-circular PSF such as with astigmatism [9]. Thus, if the PSF is elongated along the fast axis but not the slow axis, the interrogation length could be shorter than a purely defocused Gaussian beam.

Fig. 1.

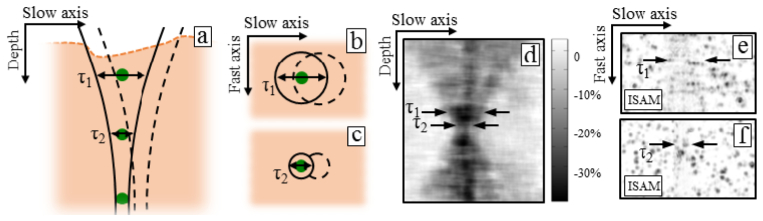
A graphical depiction and experimental validation of the interrogation time. (a-c) As the Gaussian beam performs a raster scan in a telecentric setup, particles further from the focus see a longer interrogation time (the length of which is indicated by τ) than particles at the focus. This means that stability is required over a longer period of time further from focus. (d-f) Experimentally, a short, impulse-like disturbance to the sample results in a degradation of the ISAM reconstruction. (d) Points in the sample being interrogated during the disturbance will not be reconstructed properly leading to a higher loss in contrast (black) while points not being interrogated experience little to no loss in contrast (white). (e) An en face plane away from the focus experiences signal degradation over a large area (indicated by black arrows), while an en face near the focus (f) is disrupted over only a small area (indicated by black arrows).

If bulk displacement of the sample (such as a Heaviside step function along some direction) occurs during imaging, then a phase sensitive imaging technique will be corrupted in a region of the imaged volume if the motion occurred during the interrogation time of that region. Furthermore, if a point is not being interrogated during the motion, the reconstruction will not be disturbed in that region. Figures 1(d)–1(f) demonstrates this in a tissue-mimicking phantom consisting of sub-resolution TiO₂ particles in a clear silicone substrate. When imaged with moderately high NA (0.1), appreciable defocus due to the Gaussian beam is present away from the focus (data not shown). Using ISAM, the defocus is corrected. The sample was imaged with and without a short, impulse-like disturbance applied to the sample stage. Figure 1d plots the change in local contrast obtained with and without the disturbance. Points in the sample not being interrogated during the disturbance showed no change in contrast and appear as white. Points in the sample being interrogated during the disturbance present as a reduction in contrast. The boundary of these areas trace out the shape of the Gaussian beam used for imaging and demonstrate the depth dependency of the interrogation time and thus of the stability requirements. Figures 1(e) and 1(f) shows en face planes from the ISAM reconstruction with the impulse-like disturbance. Away from the focus [Fig. 1(e)], the extent of the disturbance is large (as indicated by the black arrows), while near the focus [Fig. 1(f)], the disturbance is small (again indicated by the black arrows). This means that for ISAM with a telecentric scanning system, as higher NAs are used and/or reconstructions further from the focus are desired, stability must be met over longer periods of time.

2.4 Motion as fluctuations on spatial frequencies

An interesting, and possibly more intuitive, way to think of the influence of motion on aberration correction in point-scanned systems involves the concept of sequentially measured spatial frequencies. First consider a particle near the focus. The interrogation length for this particle is very short, and all the spatial frequencies contributing to the in-focus image are measured simultaneously. Away from the focus, though, due to the confocal gating, as the defocused beam scans over a particle, the particle is sequentially interrogated and measured with waves from varying directions. This can be seen schematically in Fig. 3 of [8] and also discussed in [25]. This means that far from focus, the spatial frequencies are measured as a function of time. Thus, any motion which occurs during scanning will result in fluctuations superimposed on the spatial frequency content of that defocused particle and result in poor reconstructions.

3. Determining thresholds for stability

For telecentrically scanned systems, Section 2.2 laid out a mathematical framework showing how strongly motion in different directions should influence the phase and thus the ISAM/CAO reconstructions, and Section 2.3 explained that only instabilities during the interrogation time of a particular point will corrupt the reconstruction of that point. This section explores various types of instabilities and, through simulations, determines thresholds for successful reconstructions. The end goal is to determine, for a given stability measurement, either how fast one must scan to accurately reconstruct sample structure imaged with a given aberration, or the magnitude of an aberration that can be tolerated at a fixed speed.

3.1 Optical coherence tomography simulation

The OCT simulation used in this article is based around the first Born approximation and wave propagation. Beginning at the fiber tip, a Gaussian beam is numerically calculated utilizing the specified wavelengths of 1,230 – 1,430 nm and the 1/e² mode-field diameter of the fiber (defined on the intensity profile) of 8.9 µm. Supposing that the Gaussian beam is perfectly imaged to the focus inside the sample, the beam is copied to the focal position. For each wavelength, the beam is then numerically propagated to the specified point scatterer using the propagation kernel $\exp \left(-i{k}_z{z}_0\right)$, where $k_z=\sqrt{k^2-q_x^2-q_y^2}$, $k$ is the wavenumber of a particular wavelength of light, and $z_0$ is the distance propagated in the axial dimension. At the plane of the point scatterer, the field is scaled by the scattering potential (1 where the point is, and 0 everywhere else) then propagated back to the focus. The beam at the focus is then copied back to the fiber core (again assuming a perfect imaging system) and summed in the complex field to determine the amplitude and phase of the light propagating in the fiber. Interference was then simulated by adding $\exp \left(ik{z}_{\text{ref}.}\right)$ to the field in the fiber where $z_{\text{ref}.}$ is the position of the reference arm with respect to the focus. Detection was finally simulated by instantaneously taking the magnitude of the field at each wavelength. Standard processing for OCT (except k-linearization since the field was simulated linear in k) and ISAM could then be used.

We note that in the simulations, specific wavelengths and transverse resolution (the mode-field diameter of the fiber) were used. From the theory in Section 2.2, though, we know that the sensitivity to motion in the axial dimension is predominantly dependent on wavelength and in the transverse dimension, is dependent on the transverse resolution. In addition, these relationships are direct proportionalities. For example, the theory tells us that halving the transverse resolution is the same as scaling the disturbance in that dimension by 2. Thus, although the simulations were performed with absolute quantities (µm), the plots in the following section have normalized axes. For plots involving axial motion, the quantities are measured in radians (thus normalized by the wavelength λ₀ = 1.33 µm), and for plots involving transverse motion, the quantities have been normalized by the transverse resolution at 1/e² (8.9 µm).

Finally, it is important to note the amount of spatial oversampling used. An unusually high amount of oversampling could artificially inflate the sensitivity of these techniques to motion and undersampled data could result in poor reconstructions. We chose our simulations and experiments to spatially sample the data at 2 µm per step. This results in a bit more than 4 times oversampling (at 1/e²).

3.2 Types of disturbances

Discussed briefly in [26], fluctuations in the reference arm can have a detrimental impact on image reconstructions for ISAM. In addition, several other types of disturbances are common. For instance, bulk sample motion can lead to arbitrary transverse and axial disturbances, electrical noise (e.g. 50/60 Hz) or other spurious signals bleeding into driving waveforms can lead to periodic disturbances to the galvanometer scanners, and also low SNR can lead to increased ‘phase-noise’ [27, 28]. This section provides simulation results which investigate each of these classes of disturbances.

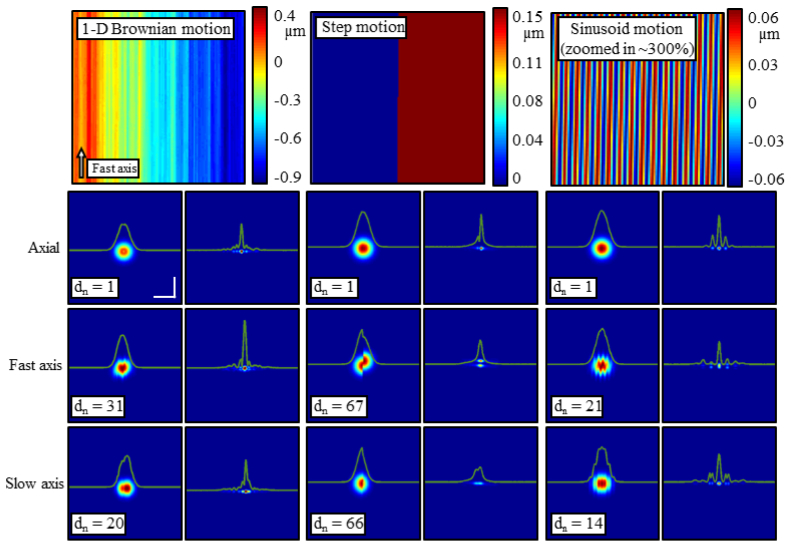
To begin, Figs. 2(a) –2(g) show simulation results of how increasing levels of 1-D Brownian motion included in the reference arm impacts the ISAM reconstruction. Across time, the 1-D Brownian motion is defined as independent increments following a mean-zero Gaussian distribution with a specified variance. Figure 2h shows a map of the realization of Brownian motion, $f_z(t)=S_{\text{B}}(t)$, used as a disturbance for Figs. 2(a)–2(g). A simple scaling, $f_z(t)=d_n{S}_{\text{B}}(t)$, was used to control the strength of the disturbance. Figure 2a shows an en face section through a single point scatterer from the original, defocused, undisturbed OCT tomogram. Figures 2(b)–2(g) then show the same en face sections after the ISAM reconstructions.

Fig. 2.

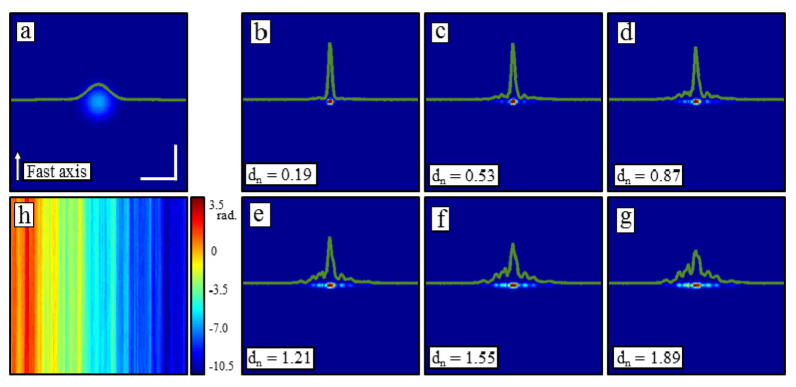
Reconstructions of a simulated point scatterer in the presence of reference arm fluctuations. (a) An OCT en face plane through a point scatterer. (b-g) ISAM reconstructions with varying levels of 1-D Brownian motion added to the reference arm. A scaling factor $d_n$ was used to control the strength of the random process (h). As the reconstruction fails, the main peak remains narrow, but decreases in intensity while side lobes rise to both sides. Scale bars represent 50 µm.

We note the manner in which the reconstruction fails as it is a common result seen throughout the other disturbances. As $d_n$ is increased, rather than broadening the central peak in both transverse dimensions, the central peak remains narrow but drops in intensity, ultimately reducing the Strehl ratio of the computed imaging system. Furthermore, side lobes begin to rise predominantly along the slow axis. Justification for this can be seen from Fig. 2(h) where, along the fast axis, the variance of the disturbance is very low, and along the slow axis, the disturbance varies much more rapidly. This is a side effect of the timescale difference between the fast and slow axes. Thus, for these examples, and most of the others later, effects of the instability are seen predominantly along the slow axis. These are also similar to the artifacts found previously in SAR [15].

Figure 3 outlines the typical responses seen by adding 1-D Brownian motion, step functions, or sinusoidal motion along each axial ( $f_z(t)$), fast ( $f_x(t)$), and slow ( $f_y(t)$) axis. These types of motion were chosen to appropriately model motions in experimental systems. For instance, the 1-D Brownian motion represents small, but rapid bulk movements of the sample or scanning optics, the step function represents larger, but very brief motion, and the sinusoid motion could represent a repetitive disturbance from a moving part such as a fan. The figure is organized in 3 main columns, one for each type of motion. The top row of each column gives a map of the disturbance at each point as the simulation scans over the sample. The next 3 rows of each column show OCT (left) and ISAM (right) results with a particular amount of motion applied in the specified direction. The magnitude of the motion is scaled by the value of $d_n$ which were chosen here to show representative artifacts from each type of motion. In all responses, as discussed previously, artifacts arise along the slow axis. In addition, though, when motion of the sample occur along the fast axis, smearing or other artifacts are present along the fast axis as well. This is seen most strongly with the step function. The smearing occurs in a similar manner as in standard OCT imaging [16]. The sinusoidal motion is also interesting because narrow and equally spaced side lobes appear along the slow axis - the location and strength of which are determined by the period of oscillations along the slow axis. This is in contrast to the 1-D Brownian motion where the motion is much less structured and thus the side lobes are much broader and random [Figs. 2(e)–2(g)].

Fig. 3.

The impact of various classes of disturbances. Organized in 3 main columns, the effects of 1-D Brownian motion, step functions, and sinusoidal motion are summarized here. The top row in each column shows the type of motion which is applied and the lower 3 rows specify in which direction this disturbance is applied (axial, fast, or slow axis). Finally, within each column, the left side shows the OCT processed en face plane and the right shows the corrected plane. The magnitude of the motion applied is scaled by $d_n$. The central wavelength simulated is λ₀ = 1.33 µm. The scale bars represent 50 µm.

Finally, low SNR adds noise in the recovered phase and requires special treatment. Shot, excess, receiver, and flicker noise [29, 30], can be partially modeled as Gaussian white noise added to the measured interferogram [31]. Thus, variations in phase will occur isotropically. It may then seem reasonable that the high-frequency oscillations in the phase will result in large side lobes surrounding the central peak in all directions. The aberration correction algorithms considered here, though, are linear phase operators. Therefore, if the noisy signal is written as $S_{\text{OCT}}(x,y,k)+n(x,y,k)$ for $n(x,y,k)$ being white noise, then applying the aberration correction expressed in Eq. (1) gives $S_{AC}(x,y,k)+{\mathcal{A}}^{-1}\left\{n\right\}$. Here, $S_{AC}(x,y,k)$ is the noise-free reconstructed image and ${\mathcal{A}}^{-1}\left\{n\right\}(x,y,k)$ has the same power spectrum as $n(x,y,k)$. Therefore, the reconstruction is simply the noise-free reconstruction with the same power spectrum of noise in the background as was present before aberration correction. Simulations and experimental results are provided later in Section 4.

3.3 Reconstruction thresholds

With an understanding of how these various classes of disturbances affect defocus/aberration correction, this section will determine the strength of each disturbance which can be tolerated. A specified quality measurement will be used to determine whether or not a reconstruction is considered successful.

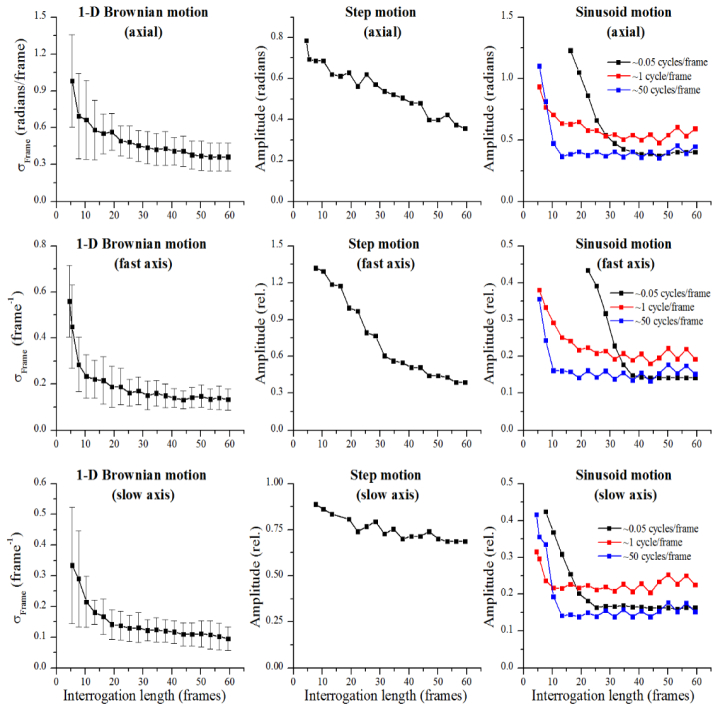
As is understood from the above theory and experiments, the robustness of aberration correction depends on the interrogation length. Thus, the results in this section will be shown as a function of interrogation length. Figure 4 outlines the results. These plots show thresholds beyond which the defocus correction is deemed unsuitable. The area below the threshold line will result in acceptable reconstructions while the area above the threshold line will result in unsuccessful reconstructions. A reconstruction is considered successful if the mean intensity projection of it along the fast and slow axes separately meet all of the following three criteria:

Fig. 4.

Thresholds for successful defocus correction with various types of motion. Organized in a similar manner to Fig. 3, the three main columns separate the type of motion (1-D Brownian, step, sinusoidal), and the rows list the direction in which the motion was applied (reference arm, fast axis, slow axis). The independent variable in each case is the interrogation length measured to the 1/e² boundary. The dependent axes have been normalized. For transverse motion, normalization was to the transverse resolution (8.9 µm).

• •The maximum peak is within 3 dB of the non-disturbed reconstruction.
• •The central peak decreases monotonically down to 7 dB below the maximum and all points outside the central peak remain below this 7 dB line.
• •The 3 dB full width of the central peak is less than twice the 3 dB full width of the non-disturbed reconstruction.

The motivation behind the first two criteria follow from the results shown in Fig. 2 where it was noted that with increasing disturbances, while the central peak remains narrow, the intensity drops and side lobes increase. The third criteria then follows from Fig. 3 where a step function or 1-D Brownian motion along the slow axis can lead to an overall broadening of the central peak without strong side lobes. Finally, these criteria are required to be satisfied along both the fast and slow axes because motion along the fast axis can lead to smearing along the fast axis (as can be seen in Fig. 3) while motion in the other directions lead to smearing and side lobes along the slow axis. In terms of Strehl ratios, violations of the first and third criteria independently would result in a Strehl ratio of less than 0.5 and severely impact the imaging systems. The Strehl ratio resulting from a violation of the second criteria is difficult to clearly define as it more directly affects contrast rather than resolution. The resulting Michelson contrast (or modulation [32]) of a single particle would be less than 0.66. Here we considered the central peak of the reconstruction to be the signal maximum and the maximum of the side lobes to be noise and, thus, the signal minimum.

By running simulations along each of the three dimensions for many realizations of 1-D Brownian motion (n = 20 for each interrogation length), multiple sinusoidal frequencies, and step functions, we determined thresholds beyond which one of the above three criteria fail. Figure 4 is organized into 3 columns to mimic the layout of Fig. 3. The far left column provides the thresholds for 1-D Brownian motion, the middle column shows the thresholds for a step disturbance, and the far right column provides results for various frequency sinusoid disturbances. The rows organize the results from top to bottom for reference arm, fast axis, and slow axis fluctuations, respectively. The strength of the 1-D Brownian motion is measured using the standard deviation of the process between frames, ${\sigma }_{\text{frame}}$, and the strength of the step and sinusoid disturbances were then measured using the amplitudes. In general, the plots show a trend of decreasing threshold (stricter stability requirement) with increasing interrogation length. These plots also show, as was predicted from the analysis of Eq. (2), that reconstructions at moderate transverse resolutions are much more susceptible to motion in the reference arm than to transverse motion. This is reflected in the much lower threshold values for the reference arm disturbances. Specifically considering 1-D Brownian motion, the threshold for axial motion with an interrogation length of 60 frames is approximately $0.3{\lambda }_0/(2\pi ){\text{frame}}^{-1}$while for transverse motion, the threshold for the same interrogation length is approximately $0.05w_0{\text{frame}}^{-1}$ where w₀ is the transverse resolution at 1/e². Supposing that λ₀ = 1.33 µm and w₀ = 8.9 µm, the thresholds differ by a factor of 7. The thresholds in Fig. 4 also show a clear dependence on interrogation length, again validating that the stability requirements for image reconstructions become stricter with larger interrogation lengths.

To further explore Fig. 4, consider a system where the standard deviation of the fluctuations in the reference arm were measured (perhaps with a static mirror in the sample arm) to be 0.1 µm/frame. Normalizing this value to the central wavelength of λ₀ = 1.33 µm, we obtain 0.5 radians/frame. In addition, by analyzing the temporal dynamics of the fluctuations, it was found that the dynamics are well approximated by 1-D Brownian motion. Then, using the plot in the top left corner of Fig. 4, we approximate that reconstructions can be performed with an interrogation length up to about 20 frames. Further supposing that the diameter of the Gaussian beam is 8.9 µm at the waist, and that about 2 µm spatial sampling is used, this interrogation length corresponds to ~280 µm (optical) above the focus, or ~4 Rayleigh ranges. Reconstructions further from the focus could be possible with a stabilized system by, for example, scanning faster, better stabilization of the reference arm, or utilizing a phase reference [26]. The use of these thresholds will be explored in more detail in the second part of this article [19].

3.4 Time-domain, spectral-domain, and swept-source OCT systems

Although this article focuses mostly on data acquired with SD-OCT, over the years, a number of OCT scanning and acquisition methods have been developed, each with a set of advantages and disadvantages such as imaging speed, imaging depth, peak SNR, depth-dependent SNR, and phase stability. Initially, time domain (TD) OCT systems utilized a moving reference arm to obtain depth information [6]. Subsequently, it was realized that the depth information could be determined by directly measuring the spectrum. This resulted in both SD-OCT systems, which measure the entire spectrum simultaneously, and swept-source (SS) OCT systems, which measure the spectrum across time [33]. The tradeoffs between these methods have been thoroughly investigated elsewhere [16, 29, 34], though it is worth mentioning how the stability of these methods relates to the material presented here.

Among point-scanned TD-, SD-, and SS-OCT systems, SD-OCT is known to be the most stable due to the absence of moving parts or time-varying (on the time scale of a single A-scan) optical sources. The second most stable is SS-OCT, which can match SD-OCT at tissue-level SNR values with the addition of a phase reference [35] or a Mach-Zehnder interferometer (MZI) [36]. Finally, TD-OCT is typically the least stable OCT modality due to slow imaging speeds and moving parts included in the reference arm.

Although the stability of each OCT system varies, SD-OCT and SS-OCT systems are known to reach the theoretical SNR limits of phase stability for the SNR levels achieved in biological samples. Thus, these measurements give an upper bound on the actual stability of the system. As discussed in Section 3.2 and later in Section 4, phase-noise resulting from SNR does not significantly affect the reconstructions considered here. From [35], for an SNR of ~45 dB, the measured phase noise met the theoretical phase noise, which was <0.01 radians. Furthermore, from [36], a SS-OCT system with a MZI measured phase noise <0.011 radians, which nearly meets the theoretical limit at an SNR of 48.1 dB. Supposing that a tomogram with 512 A-scans/frame is measured, and that the phase noise quoted above is 1-D Brownian motion, this corresponds to <0.25 radians/frame, which meets the stability thresholds presented in the top left corner of Fig. 4 for even the longest interrogation length of 60 frames. This suggests that, with additional hardware for phase stabilization, SS-OCT is sufficiently stable for the defocus and aberration correction techniques considered in this article.

4. Experimental results

The above sections provide many results using a simulation of an idealized OCT system. In this section, results are provided from an experimental laboratory system to validate some of the simulated results. The experimental system used is the one after which the simulation was modeled and is the same system as was used in [14]. Briefly, the system is a 1300 nm SD-OCT system using a superluminescent diode with a bandwidth of 170 nm (LS2000B, Thorlabs). The measured axial resolution was 6.0 µm (full width at half max) in air. The fiber core was imaged with two 30 mm focal length doublets (AC254-030-C, Thorlabs) resulting in an NA of 0.1 (at 1/e²). A 1024-pixel InGaAs line-scan camera (SU-LDH2, Goodrich) was used in the spectrometer. Finally, real-time processing of both OCT and ISAM [15] was provided for visualization during imaging sessions with a graphics processing unit (GPU) (GeForce GTX 580, NVIDIA) programed with the compute unified device architecture (CUDA). Although the real-time processing provides good results, the experimental data was reprocessed offline to ensure minimal rounding and processing errors due to the single precision processing and 16-bit precision data saving. Offline processing on the CPU was performed with double precision in MATLAB and the data was analyzed with single-precision floats.

Figure 5 compares simulated and experimental reconstructions of a single defocused particle with varying levels of SNR. The far left column in Fig. 5 shows simulated data in the presence of additive Gaussian white noise before and after ISAM. The right three columns show experimental data where the SNR of the acquired data was experimentally changed using a variable neutral density (ND) filter in the sample arm. The OCT and ISAM data labeled as 0 dB shows the images acquired with the ND filter set to 0 (effectively removed). The other two columns show OCT and ISAM data where the peak signal-to-noise ratio decreased by 11 and 18 dB, respectively. The relative SNR values in the experiments were calculated by assuming that the background noise statistics will remain the same and the reduction in SNR was measured off the peak of the ISAM reconstructions. In all examples, even if the OCT signal appears to be overwhelmed with noise (especially in the −18 dB image), the reconstructed peak remains narrow and clear. This validates the predicted results from the end of Section 3.2 where, even with low SNR, the reconstructed peak will remain narrow with a noisy background. The OCT and ISAM images are all normalized to the peak values of the corresponding ISAM reconstructions, and displayed on the same scale between 0 and 1.

Fig. 5.

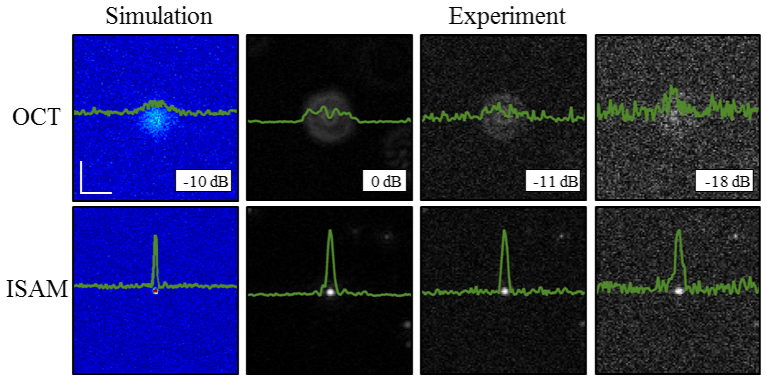
Impact of varying SNR on reconstructions. Simulations (far left column) and experiments (right 3 columns) show the impact of lowering SNR on defocus correction. Validating the predictions provided from the theory, the narrow peak and the background noise remain the same before and after reconstructions. The scale bars represent 50 µm.

Next, an experiment with sample motion is matched to simulations. The results are shown in Fig. 6 . The top row of simulations show from left to right, the OCT data, an ISAM reconstruction with no disturbance, and ISAM reconstruction with 1-D Brownian motion in the reference arm. The strength of the disturbance was ~0.3 radians/frame which is close to the threshold level for this interrogation length of ~25 frames found in the top left corner of Fig. 4. The middle row shows the corresponding experiments with the same particle distribution and the same amount of disturbances. In the experiment, the sample was mounted on a 3-axis piezoelectric stage (Thorlabs) and was vibrated appropriately in the axial dimension. Since the scale of these vibrations is very low, axial motion of the sample well approximates a displacement of the reference arm. The side lobes present in the simulation and experiment approximately match. Differences could be explained by aberrations present in the experimental beam (the ring-shaped point spread function is indicative of spherical aberration), and also by an imperfect movement of the piezoelectric stage at high frequencies. In order to see the details of weak scatterers in the OCT data, all images in Fig. 6 are viewed on a normalized scale. Finally, traces through the scatterers indicated by the white arrows are shown at the bottom of Fig. 6. Before normalization, the ISAM reconstructions showed a reduction in peak intensity by a factor of 0.70 in simulation and 0.88 in experiment.

Fig. 6.

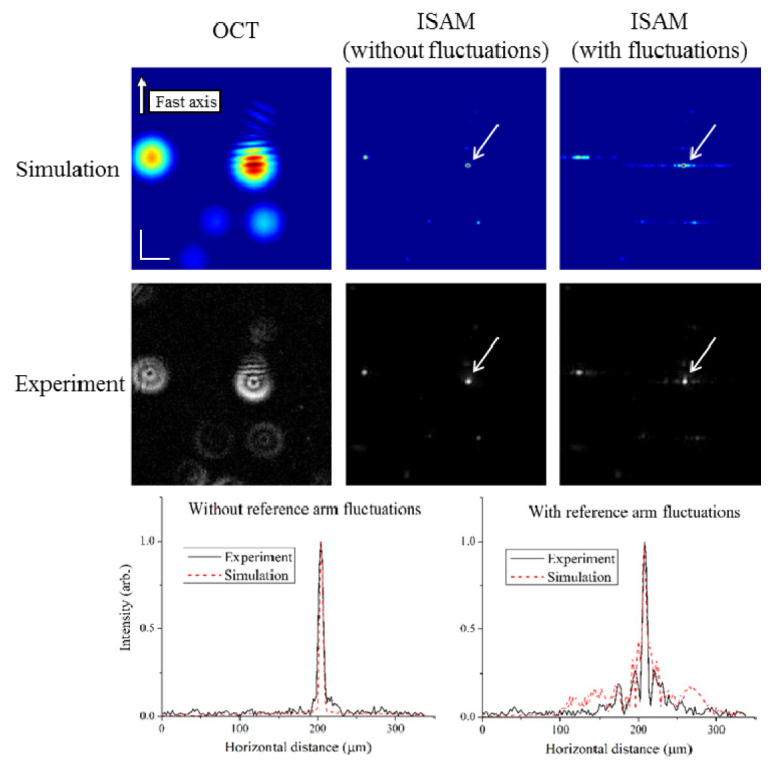
A comparison of an experiment and simulation with and without motion. The top row shows a simulation with point scatterers placed to match the experiment in the second row. Shown are the OCT (left column), ISAM without fluctuations (middle column), and ISAM with fluctuations. In both reconstructions with fluctuations, side lobes appear along the slow axis in similar ways. The bottom row shows traces along the slow axis through the center of the scatterers indicated by the white arrows. Intensities in all images are viewed on a normalized scale. The scale bars represent 50 µm.

5. Conclusion

Throughout this article, we have shown the effects of various types of motion on defocus and aberration correction that would be encountered in phase-sensitive optical computed imaging techniques. Although all simulations and experiments focused on defocus correction, the same principles apply for phase aberrations as well. The investigations were aimed at quantitatively establishing guidelines for how much motion a particular phase-sensitive reconstruction technique can withstand. We found that although the corrupted reconstruction is linear in the scattering potential (hence experiments and simulations carried out were with point scatterers), it can be nonlinear with respect to the motion. This nonlinearity required a systematic investigation of some common instabilities: 1-D Brownian motion, step functions, and sinusoidal motion. A clear and relatively predictable dependence on the interrogation length of a particle was found. In addition, for moderate NAs, a high-sensitivity to motion in the axial dimension when compared to motion in the transverse dimensions was found. The results can be used to assist in the optimal design of systems implementing these and other phase-sensitive techniques, in addition to better identifying the possibilities for imaging of in vivo or dynamic samples.

In the second part to this article [19], techniques to measure the stability of systems for in vivo imaging will be discussed and directly related back to the quantitative thresholds derived here.

08/01/2014--Acknowledgments revised. 08/08/2014--Reference 19, initially in-press, has been published; reference updated with current information.