Changes in velocity profile according to blood viscosity in a microchannel

Abstract

Red blood cells (RBCs) are important to dictate hemorheological properties of blood. The shear-thinning effect of blood is mainly attributed to the characteristics of the RBCs. Variations in hemorheological properties alter flow resistance and wall shear stress in blood vessels. Therefore, detailed understanding of the relationship between the hemorheological and hemodynamic properties is of great importance. In this study, blood viscosity and blood flow were simultaneously measured in the same microfluidic device by monitoring the flow-switching phenomenon. To investigate blood flows according to hemorheological variations, the flow rate of blood samples (RBCs suspended in autologous plasma, dextran-treated plasma, and in phosphate buffered saline solution) was precisely controlled with a syringe pump. Velocity profiles of blood flows were measured by using a micro-particle image velocimetry technique. The shape of velocity profiles was quantified by using a curve-fitting equation. It is found that the shape of the velocity profiles is highly correlated with blood viscosity. To demonstrate the relationship under ex vivo conditions, biophysical properties and velocity profiles were measured in an extracorporeal rat bypass loop. Experimental results show that increased blood viscosity seems to induce blunt velocity profile with high velocity component at the wall of the microchannel. Simultaneous measurement of blood viscosity and velocity profile would be useful for understanding the effects of hemorheological features on the hemodynamic characteristics in capillary blood vessels.

I. INTRODUCTION

Blood is a two-phase fluid composed of red blood cells (RBCs), leukocytes, and platelets suspended in plasma. Among suspended cells, RBCs mainly dictate the hemorheological properties of the blood. RBCs tend to form rouleaux through aggregating each other under low-shear rate conditions, because proteins contained in plasma enhance the attractive force between RBCs. By contrast, dispersion, deformation, and rotation of RBCs are induced at high-shear rate conditions.^1,2 The shear-thinning effect of blood viscosity is mainly attributed to these hemorheological characteristics of RBCs in plasma. Blood viscosity varies according to physiological and pathological conditions.^3–5 The increase in blood viscosity augments the flow resistance and wall shear stress which mechanically stimulates the endothelial cells of blood vessels. For these reasons, the accurate measurement of blood viscosity is necessary for early detection of cardiovascular disease (CVDs) and microcirculation diseases.⁶

For the measurement of blood viscosity, two types of viscometer, such as cone-and-plate type⁷ and capillary type,⁸ are widely used. However, the cone-and-plate viscometers suffer from drawbacks, including large amount of sample consumptions due to repetitive tests, tedious, and time-consuming procedures.⁹ The capillary viscometers need to measure a pressure and flow rate in a capillary tube. Routine calibrations should be required for the reliability. In order to overcome these technical limitations of conventional viscometers, several microfluidic devices have been proposed.^10–13 Nevertheless, these microfluidic platforms also require calibration procedures using a standard fluid as a reference. Moreover, additional procedures with intricate mathematical models are required to measure the viscosity of non-Newtonian fluids.¹⁴ To resolve these problems, a new viscosity measurement technique with label-free operation was proposed based on a flow-switching phenomenon in the bridge channel, which depends on hydrodynamic balancing in a H-shaped microfluidic device.¹⁵ This method is capable of measuring blood viscosity without flow-rate measurement, contamination, and tedious calibration procedures.

It has been known that variations in hemodynamic characteristics are associated with variation of hemorheological properties^16,17 under pathological conditions such as diabetes¹⁸ and malaria.^19,20 Therefore, the relationship between the hemorheological and hemodynamic properties is of great importance for early diagnosis of such diseases. It is reported that increase in hematocrit^21,22 and aggregation²³ tends to make velocity profile blunt. However, these previous studies measured hemorheological properties and velocity profiles by using different devices. Because the hemodynamic and hemorheological properties can be varied according to experiment conditions, blood viscosity and velocity profile should be simultaneously measured using the same device for getting more keen insight into the effects of blood viscosity on the hemodynamic characteristics of microvascular blood flows.

In the present study, the viscosity of rat blood was measured by monitoring the flow-switching phenomenon in the bridge channel of a microfluidic device under various flow conditions. To change the hemorheological properties, RBCs suspended in autologous plasma, dextran-treated plasma, and phosphate buffered saline (PBS) solution were used as test samples. In addition to the viscosity measurement, velocity fields of blood flows in the microfluidic channel were simultaneously measured by using a micro-particle image velocimetry (micro-PIV) technique based on cross-correlation algorithm. The shape of velocity profiles was quantified using a curve-fitting equation. It is found to be highly correlated with blood viscosity. To demonstrate the relationship between hemorheological properties and velocity profile under ex vivo condition, biophysical properties and velocity profiles were measured by using an extracorporeal rat bypass loop.^24,25 A complex fluidic network was connected between the abdominal aorta and jugular vein in a rat. The temporal variations in viscosity, flow rate, and pressure in the rat bypass model were measured with the lapse of the time, and results were compared with the shape of velocity profiles.

II. MATERIALS AND METHODS

A. Experimental setup with a light-emitting diode (LED) system

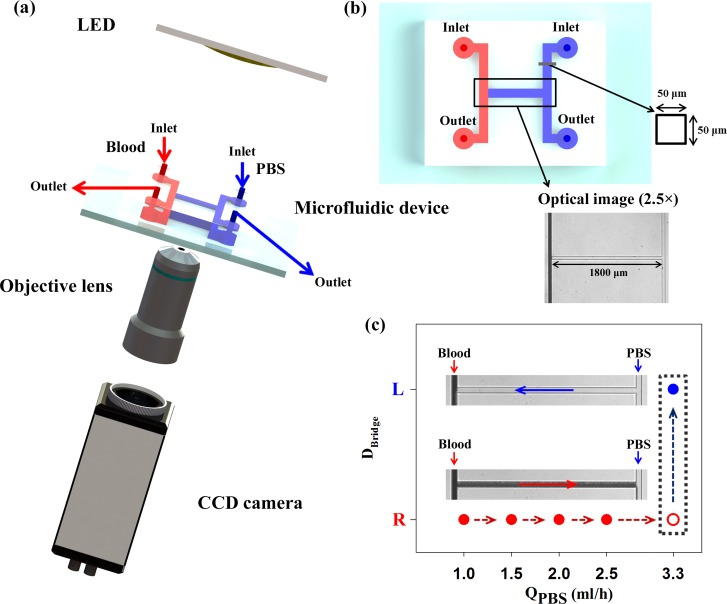
The experimental setup for optical imaging is shown in Fig. 1(a). A microfluidic device was mounted on an inverted optical microscope (Zeiss, Germany) equipped with a Sensi-Cam charged coupled device (CCD) camera (PCO, Germany). Optical images of the microfluidic device were captured by using a 2.5× objective lens (numerical aperture (NA) of 0.075). The camera has a resolution of 1280 × 1024 pixels, with a corresponding spatial resolution of 4.167 μm/pixel. An array-type, high-powered LED (BXRA-50C2600-B-00, Bridgelux) was employed as an illumination source. The CCD camera and LED pulses were synchronized by using a delay generator (model 555, BNC, USA). Blood sample was supplied into the left-side of a microchannel by a syringe pump (neMESYS, Centoni Gmbh, Germany) with 1 ml plastic syringe (BD) at different flow rates ranging from 0.01 ml/h to 1 ml/h. To stabilize blood flows in the channel, optical images of blood flow were acquired after 5 min from the instant of changing the flow rate of blood. In the right-side of a microchannel, PBS solution (pH 7.4, Bio Solution, Korea) was delivered as a reference fluid by the syringe pump. The flow rates of PBS solution were adjusted according to the flow condition of blood samples. All experiments were conducted at constant room temperature (25 °C).

FIG. 1.

(a) Schematics of the experiment setup composed of a LED system, a microfluidic device, an objective lens, and a CCD camera. A delay generator transmits trigger signals to the LED system and CCD camera for the synchronization. 8 bit gray images captured by using the CCD camera were saved in the personal computer. (b) The microfluidic device with two identical side channels and a connecting bridge channel. The channel has a width and depth of 50 μm. Blood and PBS solution are delivered into left and right side channels, respectively. Optical images of the bridge channel are captured by using a 2.5× objective lens. (c) Variation of the flow direction in the bridge channel (D_Bridge) at the blood flow rate of 1 ml/h according to the flow rate of PBS solution (Q_PBS). Microscopic images showing flow direction; L and R indicate that blood in the bridge channel moves to the left and right directions. At the PBS flow rate of 3.3 ml/h, the flow direction of blood is reversed.

B. Fabrication of the microfluidic device

For fabrication of the microfluidic device based on soft lithography process and deep reactive-ion etching, a master replica molder with a rectangular shape was made by using MEMS technologies. As shown in Fig. 1(b), the microfluidic device has two identical side channels (width = 50 μm, length = 3.6 mm) connected by a bridge channel (width = 50 μm, length = 1.8 mm). The depth of those channels is fixed at 50 μm. After polydimethylsiloxane (PDMS) (Sylgard 184, Dow Corning, USA) was poured on the silicon molder and cured at 80 °C for 3 h, a PDMS block was peeled off from the silicon molder. Two side channels have their own inlet and outlet made with a 1 mm diameter puncher. After oxygen plasma treatment, the microfluidic device was finally prepared by bonding the PDMS block on a glass substrate.

C. Sample preparation

Blood was collected from male Sprague–Dawley rats with body weight in the range of 370–410 g through abdominal aortic puncture under intramuscular ketamine (100 mg/kg) and xylazine (10 mg/kg) anesthesia. The blood samples were anticoagulated with ethylenediaminetetraacetic acid (EDTA) dipotassium salt (1.5 mg of EDTA per 1 ml of blood). Rat blood was separated into RBCs and plasma by centrifugation. The buffy layer, composed of leukocytes and platelets, was removed. The separated RBCs were carefully remixed with the autologous plasma to have 40% hematocrit. To evaluate the blood flows attributed to hemorheological variations, rat blood samples were treated. The aggregability of rat blood was elevated by mixing Dextran 500 (molecular mass 450–550 kDa; Sigma) in PBS (6%) with plasma to archive a plasma-dextran concentration of 0.6%. On the contrary, RBC suspension in PBS solution was prepared for dispersing RBCs. The hematocrit of dextran-treated blood and RBC suspension was precisely adjusted to be 40% by carefully mixing RBCs with plasma-dextran mixture or PBS solution. The each group (normal, dextran-treated blood and RBC suspension) has three samples. Each experiment was finished in 3 h from the collection of blood to prevent noticeable variation of hemorheological properties. All procedures performed on the animals were approved by the Animal Care and Ethics Committee of POSTECH.

D. Measurement of blood viscosity

Blood viscosity was measured by monitoring flow-switching phenomenon in the bridge channel of the microfluidic device. The flow-switching phenomenon occurs based on hydrodynamic force balancing between two parallel side channels. When the pressure at the left-side end of the bridge channel is larger than the pressure at right-side end, the fluid starts to move from the left-side to the right-side in the bridge channel. If the pressures at both ends reach to the hydrodynamic balancing state, the direction of flow in the bridge channel (D_Bridge) is reversed because of the flow instability in the junction. The blood viscosity (μ_Blood) is simply derived based on the formula proposed in our previous studies:^15,26

$${\mu }_{\mathit{B}\mathit{l}\mathit{o}\mathit{o}\mathit{d}}={\mu }_{\mathit{P}\mathit{B}\mathit{S}}\frac{{Q_{\mathit{P}\mathit{B}\mathit{S}}}^B}{{Q_{\mathit{B}\mathit{l}\mathit{o}\mathit{o}\mathit{d}}}^B}.$$ (1)

In here, Q_Blood^B and Q_PBS^B denote the flow rate of blood and PBS solution at the hydrodynamic balancing state. μ_PBS is viscosity of the PBS solution.

For an explanation, Fig. 1(c) shows variations of the flow direction in the bridge channel (D_Bridge) at blood flow rate of 1 ml/h according to the flow rate of PBS solution. Considering the transient responses of the syringe pump, the flow direction was monitored for 45 s after increasing the flow rate of PBS solution. Until the flow rate of PBS solution increases up to 3.3 ml/h, the blood in the left-side channel moves to the right direction. When the flow rate of PBS solution is set to be 3.3 ml/h, flow-switching phenomenon occurs. Given that the viscosity of the PBS solution is approximately 1.00 ± 0.05 cP measured by a commercial viscometer (DV-II, Brookfield, USA) in advance,¹⁵ the blood viscosity estimated with Eq. (1) at flow rate of 1 ml/h is about 3.3 cP.

E. Micro-PIV technique

LED illumination is capable of directly using RBCs as tracer particles. Blood images magnified by a 100× objective lens (NA of 1.3) were captured at the upper part of the left-side channel by using a double shutter mode of the Sensi-Cam camera. The double shutter mode can record two separate images with full resolution. Time intervals between two consecutive images were controlled from 5 μs to 995 μs by adjusting the input signals transmitted to the LED-driver. The duration time for a single LED pulse was set to 5 μs. A total of 450 image pairs were acquired for PIV analysis.

Before applying the PIV technique to each image pair, the captured optical images of blood flows were cropped into the images of 992 × 480 pixels in size. To enhance the signal-to-noise ratio of the cross-correlation map, the captured flow images were processed by using digital image-processing techniques.^27,28 The background image which was obtained by averaging total image pairs was subtracted from original images. Then, a contrast-limited adaptive histogram equalization (CLAHE) technique was applied to the subtracted images.²⁹ After applying some image-processing techniques to RBC images, an in-house PIV code based on cross-correlation algorithm divided each image into many interrogation windows. A recursive cross-correlation algorithm was employed to enhance the measurement accuracy of the PIV technique. The displacement vector of each interrogation window was determined by searching the location of a dominant peak in the cross-correlation plane. Because the time interval was adjusted to make the maximum displacements for different flow rates similar, the size of each interrogation window was fixed to 64 × 64 pixels with 50% overlapping for all experimental conditions. The obtained velocity vectors were filtered by using a 3 × 3 Median kernel to minimize errors.

F. Preparation of a rat extracorporeal loop

A male Sprague−Dawley rat (14 weeks old, body weight of 419.4 g) was anesthetized with intramuscular injection of ketamine (100 mg/kg) and xylazine (10 mg/kg). A 1500 IU/ml/kg of heparin was injected into the tail vein to prevent blood clotting in vascular conduits. After 10 min of heparin injection, the bypass loop was connected to a rat sample. Prior to the connection of microchannel to the bypass loop, channel surfaces were incubated with 2% bovine serum albumin (BSA, Sigma, MO) for 1 h at room temperature to block platelet adhesion. A PE-50 (ID = 0.58 mm, polyethylene tube) tube at one end of the heparin-filled (10 IU/ml) bypass loop was cannulated into the right jugular vein. The silicon tube (ID = 0.8 mm) at the other end of the loop was inserted into the abdominal aorta by using a 22 G catheter. A flow stabilizer with an air cavity of 0.5 ml was connected between the silicon tube and the inlet of the left-side microchannel to supply blood to the microchannel stably.³⁰ The supplied blood was returned to the jugular vein of the test rat by connecting the outlet of microchannel with the PE-50 tube. All experimental procedures were approved by the Animal Care and Ethics Committee of POSTECH.

III. RESULTS

A. Variations of blood viscosity

Variations in blood viscosity were measured by varying the flow rate of blood and observing the flow rate of PBS solution at the hydrodynamic balancing condition. Because the blood viscosity is strongly dependent on shear rate, the viscosity is depicted with respect to the shear rate (Fig. 2(a)). The shear rate ($\dot{\gamma }$) of a blood flow is approximately estimated as

$$\dot{\gamma }=\frac{32Q_{\mathit{B}\mathit{l}\mathit{o}\mathit{o}\mathit{d}}}{\pi D^3}.$$ (2)

Here, D denotes the hydraulic diameter for a rectangular channel. In the present analysis, the hydraulic diameter of the microfluidic device is 50 μm. It was reported that when the hydraulic diameter of the microfluidic device is less than of 95 μm, the measured blood viscosity is somewhat reduced due to the presence of cell-free layer in the narrow-scale channels.²⁶ Therefore, the blood viscosity measured by the present microfluidic device may be relatively smaller than that measured by other fluidic devices with larger hydraulic diameter.

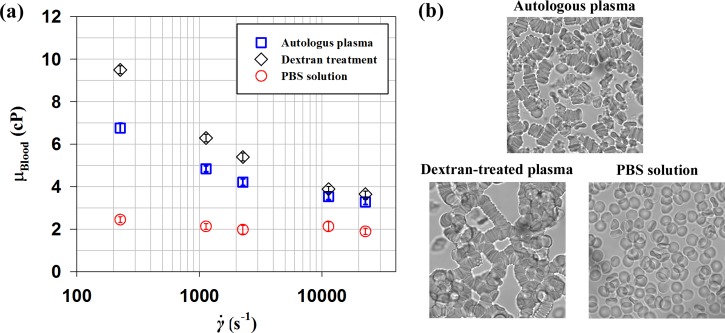
FIG. 2.

(a) Variations of blood viscosity (μ_Blood) with respect to shear rate ($\dot{\gamma }$) for RBC suspension in plasma, dextran-treated plasma, and PBS solution with a hematocrit of 40% are compared. (b) Microscopic images of rat blood samples anticoagulated with ethylenediaminetetraacetic acid (EDTA). (Top) RBCs suspended in plasma. (Bottom-left) RBCs suspended in plasma-dextran suspension. (Bottom-right) RBCs suspended in PBS. The total measurement uncertainty of viscosity was estimated to be less 5%. Error bars indicate 95% confidence interval (n = 3).

The viscosity of RBC suspension in autologous plasma largely increases as shear rate decreases. This result indicates that RBC suspension in plasma behaves as a non-Newtonian fluid. The viscosities of samples treated by dextran and suspended in PBS are compared with that of RBC suspension in plasma. As shown in the optical images of blood samples (Fig. 2(b)), RBC suspension in plasma exhibits some rouleaux and separated RBCs. The dextran-treated plasma induces larger rouleaux compared with RBC suspension in plasma. However, RBCs in PBS are completely dispersed. The enhanced aggregability of dextran-treated blood results in higher viscosity than RBC suspension in plasma. This tendency becomes more pronounced at lower shear rate conditions. This high viscosity of dextran-treated samples is also affected by elevated viscosity of the solution (autologous plasma: 1.49 ± 0.02 cP, dextran-treated plasma: 1.88 ± 0.02 cP). On the contrary, the RBC suspension has relatively low viscosity values.

B. Comparison of velocity profiles

A typical 3D analytical velocity distribution of Poiseuille flow in the rectangular micro-channel with a width and depth of 50 μm in is depicted in Fig. 3(a). Since micro-PIV measurement utilizes volume illumination on the entire depth of a microfluidic device, the measurement plane has a certain thickness which is determined by the optics of the imaging system.³¹ Some factors, such as particle size, Brownian motion, and the out-of-plane motion, have an influence on the thickness of the measurement volume.³² The depth of correlation (DOC, δ_C), which expresses the depth over which particles contribute to the cross-correlation analysis, is defined as^33,34

$${\delta }_C=2{\left\{\frac{(1-\sqrt{\epsilon })}{\sqrt{\epsilon }}\left[\frac{{n_0}^2{d_p}^2}{4N{A}^2}+\frac{5.95{(M+1)}^2{\lambda }^2{n_0}^4}{16M^{2}N{A}^4}\right]\right\}}^{1/2},$$ (3)

where d_p is the particle diameter, λ is the wavelength of illumination light, M is the image magnification, n₀ is the refractive index of the lens immersion liquid, and NA is the numerical aperture of the lens. ε denotes the relative threshold over which particles no longer contribute to the evaluation of displacement-correlation peak and is normally set to be 0.01.³³ In the present study, the DOC is about δ_C = 14.16 μm. This value was calculated by using the peak wavelength of LED light (λ = 440 nm) and size of RBCs (d_p = 4 μm), evaluated based on the assumption that RBCs are aligned with the angle of 30° from tube center.³⁵ However, the size of RBC aggregates depends on hemodynamic and hemorheological conditions.

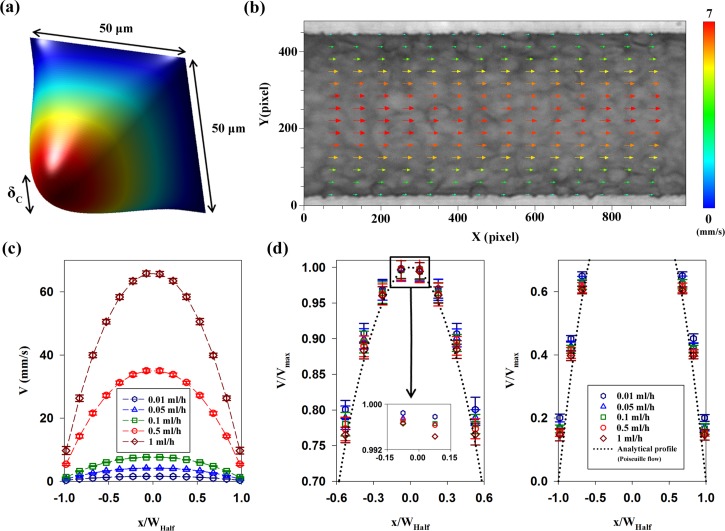
FIG. 3.

(a) 3D analytical velocity distribution of Poiseuille flow in the rectangular channel and the depth of correlation (DOC, δ_C) at the channel center. (b) Instantaneous velocity field in the center plane of the microchannel at a flow rate of 0.1 ml/h. The corresponding flow image is superimposed on the velocity field. (c) Variations of the axial velocity profile (V) according to flow rates of RBC suspension in plasma. The mean velocity profiles are ensemble-averaged. Normalized position (x/W_Half) depicts the lateral position in the channel. (d) (Left) Normalized velocity profiles (V/V_max) in the range of 0.7–1. The magnified velocity profiles in the center are included for easy comparison. (Right) Normalized velocity profiles (V/V_max) in the range of 0–0.7. The analytical velocity profile of Poiseuille flow averaged over the DOC is included as a reference. Error bars indicate s.d. (n = 450).

Figure 3(b) shows a representative velocity field superimposed on the corresponding optical image in the microchannel at the flow rate of 0.1 ml/h. The velocity field is symmetric with respect to the center of the channel. In order to improve the measurement accuracy in the near-wall region, a binary mask was applied to the channel wall region in the captured images. The mask avoids the calculation of cross-correlation in the masked region.³⁶ Although the measured velocity fields have the minimum value in the near-wall region, slow movement of RBCs is observed near the channel wall due to Fåhraeus-Lindqvist effect.

Velocity profiles were obtained by averaging velocity fields along the axial direction. Figure 3(c) shows velocity profiles of RBCs suspended in plasma along with normalized lateral position at five different flow rates. The velocity profiles were normalized with the centerline velocity (V_max) to compare their shapes (Fig. 3(d)). Because the measured velocity profiles do not show highly noticeable differences, the upper and lower velocity profiles are separately represented and the center region is magnified. The analytical velocity profile of Poiseuille flow in a rectangular channel, which was averaged over the DOC, is included as a reference. All measured velocity profiles are located above the analytical profile. The shape of the normalized profiles is slightly different. Specifically, the normalized velocity at a lower flow rate has larger values than those at relatively high flow rate conditions. This trend is accentuated as the lateral position approaches the channel wall. This shape change in the measure velocity profiles is mainly caused by hemorheological characteristics, but the change in the DOC might contribute somewhat to the results.

C. Curve-fitting of velocity profiles

The different shape of velocity profiles was depicted with respect to the flow rate in Sec. III B. The shape can be expressed by using the following fitting equation:³⁷

$$V(x)=V_{\text{Max}}\left(1-(1-\alpha ){\left|\frac{x}{W_{\mathit{H}\mathit{a}\mathit{l}\mathit{f}}}\right|}^{\beta }\right).$$ (4)

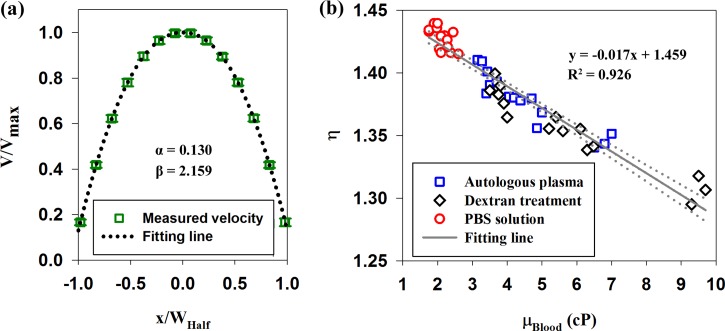
In here, V(x) is the velocity at lateral position x, V_Max is the maximum velocity at the center, and W_Half is the half of the channel width. α and β represent scale factor and bluntness index, respectively. The scale factor (α) expresses the velocity component at the edge of the vessel, by ignoring the cell-free layer. The bluntness index (β) describes the flatness of velocity profile. Table I shows variations of the scale factor and bluntness index according to the flow rate for the three blood samples. As an example, a normalized velocity profile at the flow rate of 0.1 ml/h for the RBC suspension in plasma condition and its fitting curve (α = 0.130 and β = 2.159) are depicted in the right top of Fig. 4(a). In cases of normal and dextran-treated blood samples, the scale factor and bluntness index are increased as the flow rate decreases. However, the scale factor and bluntness index of RBC suspension are similar, irrespective of flow rate.

Table I.

Fitting parameters α and β for the velocity profiles of three test samples. ^{a, b}

	0.01 ml/h	0.05 ml/h	0.1 ml/h	0.5 ml/h	1 ml/h
RBCs in autologous plasma
α	0.167 ± 0.011	0.135 ± 0.011	0.131 ± 0.009	0.124 ± 0.006	0.107 ± 0.004
β	2.253 ± 0.034	2.217 ± 0.029	2.157 ± 0.025	2.130 ± 0.029	2.089 ± 0.031
RBCs in dextran-treated plasma
α	0.203 ± 0.011	0.158 ± 0.018	0.150 ± 0.005	0.132 ± 0.006	0.123 ± 0.008
β	2.398 ± 0.043	2.284 ± 0.019	2.225 ± 0.023	2.188 ± 0.031	2.116 ± 0.036
RBCs in PBS
α	0.094 ± 0.009	0.093 ± 0.008	0.090 ± 0.003	0.095 ± 0.009	0.092 ± 0.006
β	2.049 ± 0.014	2.009 ± 0.014	2.012 ± 0.012	2.040 ± 0.032	2.023 ± 0.026

^aα and β indicate the scale factor and bluntness index, respectively.

^bEach value represents mean ±95% confidence interval (n = 3).

FIG. 4.

(a) Velocity profile at the flow rate of 0.1 ml/h for RBCs in autologous plasma and a fitting curve obtained by Eq. (4). (b) Relationship between the velocity ratio (η) and blood viscosity (μ_Blood). Solid line depicts the linear-curve fitting with respect to blood viscosity. R² values and the corresponding fitting equations are included. Dotted lines indicate 95% confidence intervals.

The scale factor and bluntness index are not independent each other. To express the shape of a velocity profile with fitting parameters, a velocity ratio (η) between the maximum velocity (V_max) and average velocity (V_average) in the measurement plane is defined as

$$\eta =\frac{V_{\max }}{V_{\text{average}\hspace{0.17em}}}=\frac{\beta +1}{\beta +\alpha }.$$ (5)

Here, α and β are the scale factor and bluntness index, respectively. It was reported that velocity profiles become blunt with respect to decrease of velocity ratio.³⁷ In order to further investigate the relationship between the shape of velocity profile and blood viscosity, variations of the velocity ratio according to blood viscosity were analyzed. As depicted in Fig. 4(b), the velocity ratios decrease as blood viscosity increases. To find general trend, a linear curve-fitting method was applied to all data. R² value of the fitting lines is 0.926. This implies that the velocity ratio is highly correlated with blood viscosity, regardless of blood treatment. It signifies that the shape of velocity profiles is significantly affected by blood viscosity.

D. Variations of hemodynamic and hemorheological parameters in the rat extracorporeal loop

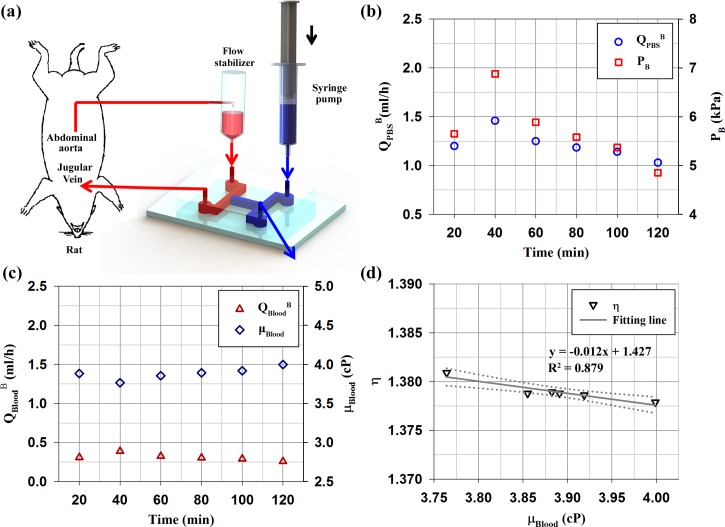
To monitor the temporal variations of biophysical properties of blood flow and investigate relationship between them under ex vivo condition, a microfluidic device was connected to an extracorporeal rat bypass model as illustrated in Fig. 5(a). Like above procedure under in vitro conditions, the blood viscosity is measured by monitoring the flow-switching phenomenon in the bridge channel. The biophysical properties of blood flow and the velocity profiles were measured at intervals of 20 min for a total of 2 h after streaming blood flow though the microchannel. The detailed explanation on the experimental procedure was described in our previous study.²⁵

FIG. 5.

(a) Schematic of the microfluidic device for monitoring the temporal variations of biophysical properties of rat blood circulating in a complex fluidic network. The fluidic network is established by connecting the abdominal aorta and jugular vein in an extracorporeal rat bypass model. The extracorporeal rat bypass loop consists of a flow stabilizer (air cavity = 0.5 ml) and microfluidic channel. To measure biophysical properties (viscosity, flow rate, pressure), PBS solution is supplied as a reference fluid by using a syringe pump. (b) Temporal variations of the flow rate of PBS solution at the hydrodynamic balancing state (Q_PBS^B) and the balancing pressure (P_B) of rat blood circulating within the complex fluidic network. (c) Temporal variations of flow rate of blood at the hydrodynamic balancing state (Q_Blood^B) and rat blood viscosity (μ_Blood) measured by using Eq. (1). (d) Relationship between the velocity ratio (η) and blood viscosity (μ_Blood). Solid line depicts the linear-curve fitting with respect to blood viscosity. R² values and the corresponding fitting equations are included. Dotted lines indicate 95% confidence intervals.

Figure 5(b) shows temporal variations in the balancing flow rate of PBS solution (Q_PBS^B) and pressure at the end of the bridge channel (P_B). The equilibrium pressure was estimated by using linear relation between the fluidic resistance and flow rate. During the measurements, these values are increased up to 40 min and then slightly decreased. By measuring the balancing flow rate of rat blood (Q_Blood^B), the blood viscosity (μ_Blood) in the rat extracorporeal network was estimated (Fig. 5(c)). The temporal variation of blood viscosity exhibits an inverse relationship with the balancing flow rate of rat blood. The viscosity of whole blood with a relatively high hematocrit (47%) has slightly higher value compared with the in vitro results. Figure 5(d) shows variation of the velocity ratio (η) evaluated based on the scale factor (α) and the bluntness index (β) according to blood viscosity under ex vivo condition. As expected, the fitting line exhibits a high negative correlation with R² value of 0.879. This result is similar with that of in vitro experiments. However, some points are not exactly matched with the variation trend of blood viscosity. This means that it is not easy to distinguish the scale factors and bluntness indices in the similar range of the flow rate, because fitting parameters are very sensitive to deviations.

IV. DISCUSSION

In previous studies, RBC aggregation was revealed to make velocity profiles blunt under in vivo and ex vivo conditions.^23,38 The velocity profile of plasma was varied according to hemodilution.³⁹ In addition, the increase of hematocrit induces blunt velocity profile under in vitro condition.²¹ Considering the influence of these hemorheological factors on the blood viscosity, the shape of velocity profiles may also be associated with blood viscosity.

In this study, the relationship between the velocity profile and blood viscosity was investigated under in vitro and ex vivo conditions by using a micro-PIV technique and a microfluidic device capable of measuring the blood viscosity. As shown in Figs. 4 and 5 and Table I, the velocity ratio has negative correlation with blood viscosity. Specifically, the increase of blood viscosity augments the two fitting parameters of scale factor and bluntness index. This tendency implies that the increase in blood viscosity makes the velocity profile of blood flow have blunt shape with relatively high velocity component at the vessel wall. Because the increase of blood viscosity is mainly caused by RBC aggregation, the linear relationship between the bluntness index and the blood viscosity is accounted for enhanced RBC aggregation in the center region of the channel. However, the relation between the scale factor and blood viscosity cannot be thoroughly explained by RBC aggregation only. Given that the cell-free layer adjacent to the wall reduces the estimated value of blood viscosity,^26,40 the scale factor is also closely related with thickness of the cell-free layer.

The presence of cell-free layer is attributed to the tendency of RBCs and aggregates to migrate away from the vessel wall. This migration is dependent on deformability, shape of RBC, and cell–cell interactions.^40,41 Some in vitro and in vivo studies reported that the elevated RBC aggregation gives rise to increase the thickness of cell-free layer.^42,43 This increase in the thickness of cell-free layer may contribute to the variation of the scale factor, because the moving speed of RBCs rapidly decreases as RBCs approach to the wall. However, the cell-free layer was not clearly observed under the present experimental condition. It may be attributed to the quadrate microfluidic channel, relatively high hematocrit, and aggregability of rat blood. Rat blood has smaller RBC aggregability, compared to the human blood.⁴⁴ Dextran treatment in this procedure elevates the level of aggregation up to that of humans.²³

In light of the distribution of shear rate in a rectangular channel, various RBC behaviours, such as RBC aggregation, deformations, and erratic rotations of RBCs, occur at different positions of the channel.^1,45 In the high-shear region around the channel wall, the dissociation of RBC aggregates with deformation and erratic rotation may reduce the axial movement and later migration of RBCs due to energy dissipation. This tendency is accentuated with increasing flow rate and decreasing intercellular interaction of RBCs. The variation of profile shape may be resulted from such RBCs behaviours at different positions in the channel. These variations in velocity profile and blood viscosity significantly alter the flow resistance in the blood vessel. Some in vivo studies reported increase in the flow resistance according to change of profile shape and infusion of dextran.^46–48 Simultaneous measurements of blood viscosity and flows have a strong potential for understanding the relationship between blood flows and hemorheological properties. In addition, their relation can be used to quantify the biophysical properties of blood which circulates within CVD animal models.

V. CONCLUSION

The blood viscosity and velocity profiles of blood flows were simultaneously measured in the same microfluidic channel by observing the flow-switching phenomenon in the bridge channel. In order to investigate the variations according to hemorheological properties, results obtained by RBC suspension in plasma, dextran-treated plasma and PBS solution were compared. In addition, the rat extracorporeal model was employed to verify the relationship between the shape of velocity profile and blood viscosity under ex vivo condition. The shape of velocity profiles in a rectangular channel, expressed by the fitting parameters of scale factor (α), bluntness index (β), and velocity ratio (η), varies according to the flow condition and sample treatment. The relationships between the fitting parameters of velocity profiles and blood viscosity have high values of R². This implies that the velocity profiles are significantly influenced by the variation of blood viscosity due to aggregation and deformations of RBCs and dispersion of rouleaux. The blunt velocity profile with relatively high speed at the vessel wall, induced by increase of blood viscosity, may increase flow resistance in the capillaries. The present results would be beneficial in understanding the relationships between the velocity profiles in blood vessels and blood viscosity under various flow conditions.