Dean flow-coupled inertial focusing in curved channels

Abstract

Passive particle focusing based on inertial microfluidics was recently introduced as a high-throughput alternative to active focusing methods that require an external force field to manipulate particles. In inertial microfluidics, dominant inertial forces cause particles to move across streamlines and occupy equilibrium positions along the faces of walls in flows through straight micro channels. In this study, we systematically analyzed the addition of secondary Dean forces by introducing curvature and show how randomly distributed particles entering a simple u-shaped curved channel are focused to a fixed lateral position exiting the curvature. We found the lateral particle focusing position to be fixed and largely independent of radius of curvature and whether particles entering the curvature are pre-focused (at equilibrium) or randomly distributed. Unlike focusing in straight channels, where focusing typically is limited to channel cross-sections in the range of particle size to create single focusing point, we report here particle focusing in a large cross-section area (channel aspect ratio 1:10). Furthermore, we describe a simple u-shaped curved channel, with single inlet and four outlets, for filtration applications. We demonstrate continuous focusing and filtration of 10 μm particles (with >90% filtration efficiency) from a suspension mixture at throughputs several orders of magnitude higher than flow through straight channels (volume flow rate of 4.25 ml/min). Finally, as an example of high throughput cell processing application, white blood cells were continuously processed with a filtration efficiency of 78% with maintained high viability. We expect the study will aid in the fundamental understanding of flow through curved channels and open the door for the development of a whole set of bio-analytical applications.

I. INTRODUCTION

The enrichment of particles is an essential technique for sample pre-treatment for downstream bio-analyses. Microfluidics has the potential to overcome the shortcomings associated with large-scale equipment through the reduction of analyte and reagent volumes, as well as favorable scaling properties of several important instrument processes. Microfluidics is particularly amenable to gentle and high throughput cell handling. Historically, microfluidic-based particle focusing has been implemented using various different techniques. Continuous flow techniques based on active manipulation of particles, such as dielectrophoresis,¹ magnetophoresis,² acoustic waves,³ and optical forces⁴ have been described on the microscale. Although these systems are generally sensitive and accurate, for instance differentiation between live and dead cells using dielectrophoresis, throughput is limited since sufficient time is required for force fields to act upon particles to achieve the necessary deflection. In addition, the requirement of external forces, on-chip integration of interfacing components, such as mechanical moving parts, electrodes, or heaters often complicates fabrication procedures and increases the complexity of resulting devices. Passive continuous-flow techniques based on filtering through sieving structures^5–7 or by differential interaction of particles with local flow profiles^8–11 (such as pinch flow fractionation, deterministic lateral displacement) have proven to be relatively simple to operate. However, the need for narrow channel geometries makes these systems less versatile and may lead to channel clogging and particle–particle interactions.

Very recently, techniques utilising inertia-induced forces developed in microchannels have been proposed by us and others as a promising approach for particle focusing, filtration, and separation.^12–19 Segré and Silberberg first described lateral migration of particles across streamlines due to inertial forces.²⁰ Di Carlo et al. showed that particles could be focused in four points along the centre of wall faces for flow through straight square (50 × 50 μm) microchannels.¹² The focusing position can be reduced to two positions located centrally along the longer channel dimension in straight rectangular channels, and have been used to continuously focus and filter particles based on size.^15,21,22 Different curved geometries have been explored to reduce the focusing points, including asymmetrically repetitive curves,¹² spirals,^16,17 and contraction-expansion microchannels.²³ In flow through curved channel geometries, curvature amplifies a lateral instability that drives a secondary cross-sectional flow field (Dean flow) characterized by the presence of two counter-rotating vortices located above and below the horizontal plane of symmetry of the channel.

While the physics of inertial focusing in flows through straight channels is relatively well understood,^24,25 the effect of curvature on particle equilibrium positions is yet to be fully understood. This is partly due to the fact that particles experience a more complicated interplay of forces. In flow through repetitive asymmetric curved channels, Di Carlo et al. showed how the particle focusing positions could be reduced from four to a single position focused at the center point in z-direction.¹² In spiral microchannels, the direction of the Dean flow is unidirectional and will act on particles to quickly find the equilibrium positions. While there is a consensus that the ratio of inertial lift to drag forces from the secondary flow is one of the underlying players for the reduction of focusing positions, there are some conflicting descriptions on how curvature changes the equilibrium positions of particles along the z-position (the height) of the channel. The luck of consistency in the experimental designs has made it difficult to predict focusing behaviour in other spiral devices. For instance, using a spiral microchannel, Papautsky et al. suggested the particle equilibrium position to be at the center z-position.¹⁶ In contrast, we have previously reported the emergence of two focusing points along the height of the channel in flows through low aspect ratio (AR) spiral channels.¹⁷ Recently, Martel et al. showed that depending on the aspect ratio, particles can occupy a single or two focusing points along the height of the channel.²⁶ Finally, using a u-shaped channel, Gossett et al. showed how pre-focused particle migration followed the pattern of the Dean vortices.²⁷ Using a high-speed camera, the authors could follow the trajectory of the pre-focused particles indicating the strong influence of the Dean vortex on particles.

Recent studies using spiral geometries have focused on cell sorting applications, such as the separation of white blood cells^28,29 and circulating tumor cells^30,31 from diluted whole blood. The lack of general design rules has put constraint, such that designs had to be optimized for individual applications. Martel et al. recently showed that particles first tend to migrate towards the inner wall followed by an inner-to-outer wall transition independent of the channel width of the spiral.²⁶ Previous studies have shown that an increase of channel height and flow rate tend to shift particle focusing position away from the inner wall.^16,17 More recently, Sun et al. showed that increasing the length of the spiral microchannel by designing a double spiral channel when compared with a single spiral channel significantly improved the separation between 5 μm and 15 μm particles.³² They showed a separation efficiency of 90% of spiked HeLa cells spiked in 20× diluted whole blood using the optimized spiral geometry. Although these sets of previous work have shed some light on the complex particle behaviour in curved channels, as well as practical cell-based applications, to date there has not been a systematic study on the effect of curvature on the focusing of particles.

In this work, we have performed a systematic study of the influence of curvature on particle focusing using a single curved “u-shaped” and a double curved “s-shaped” channel. We show that a simple u-shaped curved microchannel geometry effectively focuses randomly distributed particles entering the curvature into a deterministic single lateral position exiting the 180° curvature. As a proof of principle, continuous focusing and filtration of 10 μm particles from 2 μm particles is demonstrated at extremely high flow rates (channel Reynolds numbers Re_c ∼ 325, corresponding volume flow rate of Q = 4.25 ml/min). Finally, we used the u-shaped microchannel to continuously filter leukocytes for cell-based applications.

II. THEORETICAL BACKGROUND

In Poiseuille flow, the parabolic velocity profile results in a shear-gradient-induced lift force (F_LS) that is directed down the shear gradient toward the wall and a wall-induced lift force (F_LW) directed away from a stationary wall pushing particles to an equilibrium position. Assuming point-particles (Rp ≪ 1), a balancing lift force, F_L, has been shown to scale with the particle Reynolds number squared (Rp²) and a lift coefficient (fc):³³ F_L = Rp²fcμ²/ρ. Rp (=Re (a/D_h)²), the particle Reynolds number, depends on intrinsic properties of the fluid, described by the channel Reynolds number, Re (=ρU_mD_h/μ), particle diameter (a) and the hydraulic diameter (D_h) (defined as D_h = 2wh/(w + h)), where w and h are the width and height of the channel. U_m is the maximum channel velocity; μ and ρ are the viscosity and density of the fluid, respectively. At intermediate Re, inertial effects cause particles to move across streamlines and occupy equilibrium positions along the faces of microchannel walls.¹²

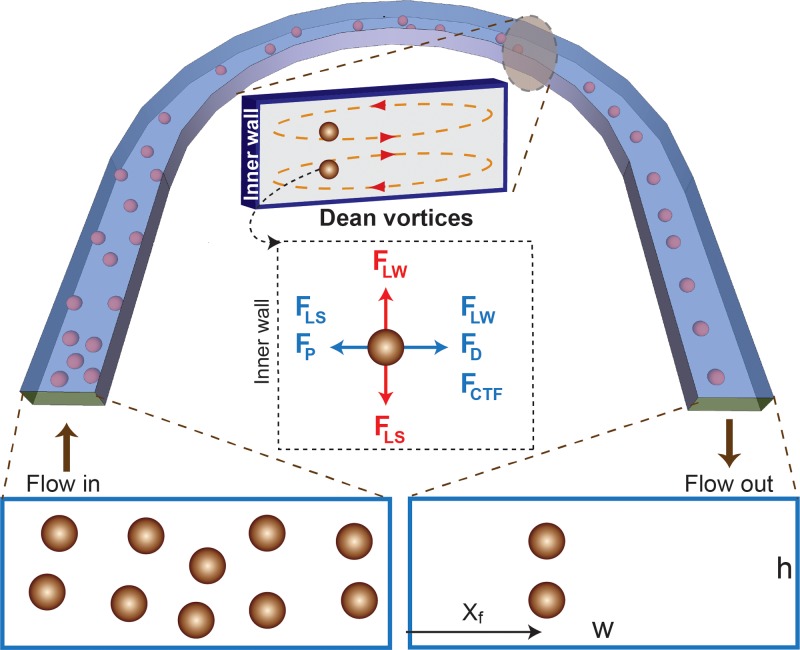
In flows through curved channel geometries, in addition to F_L, secondary flows (i.e., Dean flow^34,35) due to centrifugal effects on the fluid act on particles and affect the particle equilibrium positions. The secondary flow is characterized by counter rotating vortices, located above and below the horizontal plane of symmetry of the channel, such that the flow at the midline is directed outward to the outer wall, while fluid at the top and bottom are directed inward as seen in Fig. 1.

FIG. 1.

Schematic illustration of particle focusing in flow through curved channels. Randomly distributed particles are first affected by dominant lift forces in the straight channel. In this section, the particles start to focus vertically along the height of the channel. When the particles enter the curvature, counter rotating Dean vortices will force the particles to occupy a single lateral focusing point (xf) when exiting the curvature. Inset: Cross-section of the channel showing the presence of Dean vortices and how the dominant forces acting on a particle forcing it to focus in a distinct lateral position exiting the curved channel. Among the lift forces in flow through low aspect ratio, the vertical lift forces dominate and will tend to focus particles vertically on top and bottom while the Dean forces then move participles towards the lateral focusing position.

The magnitude of the secondary flow is represented by the Dean number, De (defined as De = Re(D_h/2r)^1/2); and the curvature ratio, δ (defined as δ = D_h/(2r)), where r is the radius of curvature. The Dean flow results in a drag force (F_D) that scales with De² (from Stokes drag (F_D ∼ ρUm² aD_h²/r)). In addition to F_D, particles in curved channels experience pressure forces, F_P (F_P ≈ (π/6) a³(−(dp/dr)ŕ – (dp/dz)ź)), and centrifugal forces, F_CTF (F_CTF = ρ_p(π/6)a³(U_p²/r) ŕ).¹⁷ Here, ρ_p, U_p, and ŕ are particle density, downstream velocity, and the radius at which a particle is focused.

Fig. 1 shows a schematic illustration of how the different lateral forces (F_D, F_P, and F_CTF,) can interplay with dominant lift forces to trap particles at a single lateral position (X_f) as they exit the curved channel. Among the lateral forces, the Dean force (F_D) dominates, influencing particles to flow in the direction of the vortices flow. This means particles at the top and bottom move laterally towards the inner wall, while particles closer to the mid-plane are pushed towards the outer wall. Although more study is required to obtain the full picture, depending on where the particles are in the vertical z-direction, pressure drag (F_p) due to curvature can be an additional force of significance in that it can counteract Dean forces. It should be noted that pressure drag is less important for smaller particles (F_p ∝ a³ while F_D ∝ a).

III. MATERIALS AND METHODS

A. Device micro fabrication

The microfluidic device was fabricated using standard poly-dimethylsiloxane (PDMS) replica molding process described previously. Briefly, the microfluidic device was fabricated by casting PDMS (Dow Corning) polymer on a resist-structured silicon wafer according to standard soft lithographic techniques. Structures in SU-8 resist (MicroChem) were produced according to the supplier's recipe using standard MEMS technology. The PDMS was mixed (10:1(wt/wt)) with a cross linker, poured on top of the silicon wafer, degassed, and cured at 65 °C for 6 h. The PDMS with the replicated channels was peeled off from the master, and channel access holes were punched with a 22-gauge needle. The PDMS replica was bonded to a glass slide via oxygen plasma. Access tubing (Tygon; Small Parts) of slightly larger diameter was press-fitted into the holes. (The designs of the u-shaped and s-shaped microchannels are shown in Figure S1 of the supplementary material.³⁷)

B. Flow experiments

Internally dyed green and red fluorescent polystyrene microspheres (Thermo Scientific.) were diluted to 0.1%–0.5% vol. with deionized water with 0.1% Tween 80 (Fisher Chemical). The solutions were pumped by a syringe pump (Harvard Apparatus PHD 2000) connected by tubing to the channel inlet. The device was mounted onto the stage of an inverted fluorescent microscope (Nikon TE2000-U) and fluorescent streak images were obtained. The image streaks were analyzed using tools from ImageJ software (Rasband, W.S., ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, http://rsb.info.nih.gov/ij/, 1997–2009.). For the filtration application, a suspension mixture of 10 μm (green) and 2 μm (red) were pumped together through the device and collected in four fractions. The output fractions were quantified using a Coulter counter.

C. Blood experiments

Blood samples from anonymous healthy blood were used (Blodcentralen, Stockholm, Sweden). For experiments with cell filtration from buffer, the leukocytes were separated by ficoll gradient solution. Briefly, 5 ml of blood was carefully pipetted onto the top of ficoll gradient solution, centrifuged at RT for 30 min, the middle layer was separated carefully. The cells were suspended in Phosphate buffer saline (PBS) and flown through the channel. The fractions from the four outlets were counted using Coulter counter. For diluted blood experiments, aliquots of dilute blood (0.5%) were run through device. Samples collected at four different outlets were analyzed by flow cytometry. The samples were centrifuged and re-suspended in 1× PBS. Multicolor Human T cell marker panel (CD3-FITC, CD8-APC, and CD45-PE/Cy7^®) (Abcam) was used to stain different population of blood cells and cancer cells were stained with anti-EpCAM-PE monoclonal antibodies (Thermoscientifc) incubated for 15 min for flow cytometry analysis. Beckman coulter flow cytometer used for Fluorescence-activated cell sorting (FACS) analysis and data obtained from the flow cytometry was analyzed using Kaluza software.

IV. RESULTS AND DISCUSSION

A. Flow through curved channels

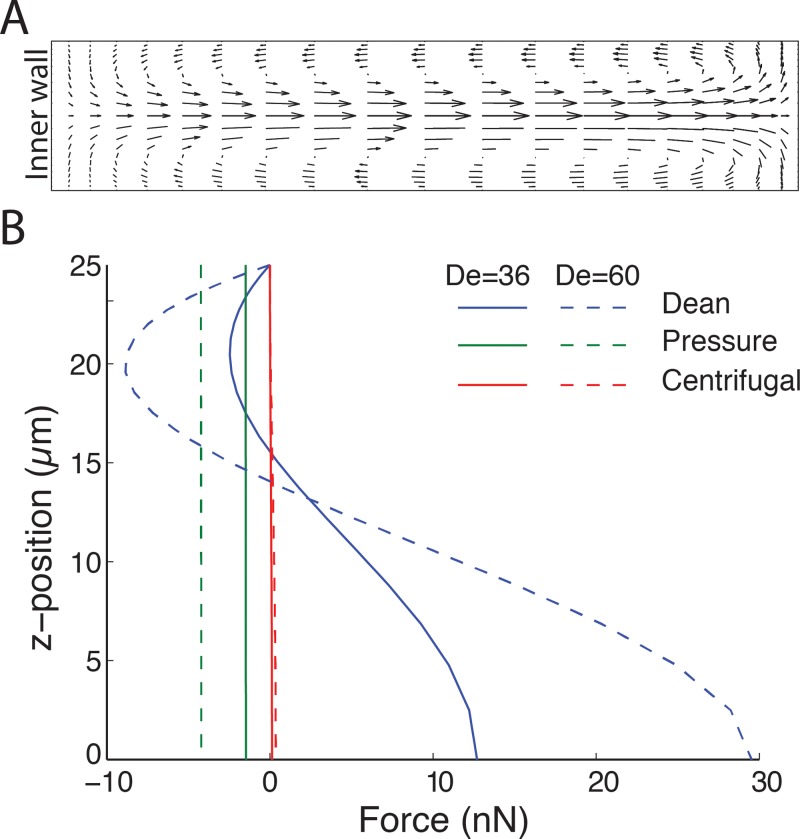
Using COMSOL Multiphysics, we first modeled the influence of the Dean flows in perturbation of the fluid flow (Fig. 2). We examined the extent of fluid perturbation at different fluid velocities for various channel geometries. Fig. 2(a) shows secondary Dean flow due to curvature in flow through channel AR of 1:5 (h = 50 μm and w = 250 μm).

FIG. 2.

Computational analysis of the flow through curved channel. (A) Velocity profile of the transverse Dean flow at De = 36 for channel aspect ratio of 1:5 (h = 50 μm and w = 250 μm) and radius of curvature of 2 mm. The arrows indicate the magnitude and direction of the flow. (B) The influence of the lateral forces acting on a 10 μm particle due to curvature. The figure shows the secondary forces along the 50 μm channel height from the horizontal mid-plane to top (0 → H/2) at the lateral centre position (x = w/2), with the positive sign indicating direction towards the outer wall and negative sign towards inner wall. The centrifugal force (F_cft) directed towards the outer wall and is relatively small irrespective of De. The average Dean drag to pressure forces is about 4:1 for De = 36, and increases for De = 60. Note the Dean drag is directed towards the outer wall at the channel midpoint and changes sign as it approaches the channel top, while the pressure force is unidirectional toward the inner wall and constant.

At lower Dean numbers, the fluid is not perturbed notably, presumably due to insufficient Dean forces developed at these flow rates. As De is increased, an apparent fluid movement following the direction of the Dean vortices with increasing magnitude is observed due to the increased centrifugal force acting on the fluid (supplementary videos,³⁷ movies S1 and S2, show fluid movement as a function of channel angle). The secondary fluid flow suggests that the lateral forces may initially act to “speed up” the focusing by acting on particles to quickly find their lateral equilibrium position, but with increased velocity mixing (defocusing behavior) is expected due to particle entrainment in the Dean vortices. For the given channel geometry in Fig. 2, De = 36 resulted in the two liquids switching positions (half turn) by the time the flow reaches 180° of the u-shape channel.

Next, we evaluated the influence of the lateral forces of significance in comparison to the lift forces. Fig. 2(b) shows the individual lateral forces acting on a 10 μm particle, depicted as a function of z-position along the height at x = 0.5w. The centrifugal force is an order of magnitude smaller than the pressure force and Dean force. In addition, due to the parabolic flow profile (F_CTF ∝ U_p²), the centrifugal force has even less effect on focused particles. The ratio of average F_D to F_P is around 4:1 indicating that pressure drag can play a significant role in the focusing of large particles. These findings suggest that focusing is largely independent of centrifugal forces acting on particles, in agreement with previous reports.¹⁷ The pressure force pushing particles towards the inner wall is largely the same across the height of the channel, while particles closer to the top and bottom will feel smaller Dean drag (Fig. 2(b)). Hence, the influence of the unidirectional pressure forces could be key to understanding the focusing phenomenon in flows through curved channels. This would mean that wall effects would balance the excess pressure force near the inner wall for a given De. Note that F_P scales with a³ while F_D scales with a. This means pressure force due to curvature will have less influence on smaller particles compared to larger. As the bulk flow velocity increases, F_D increases faster than F_P (Fig. 2(b)). Hence, while the influence of pressure drag is significant for particle focusing, Dean drag is the dominant lateral force acting on particles.

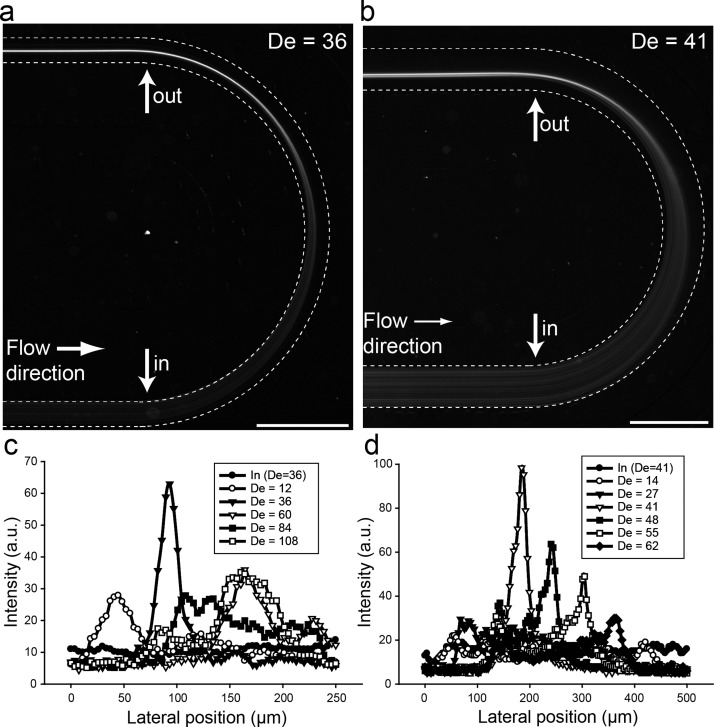
Experimentally, we tested a wide range of flow rates, 2 < De < 80, using several u-shaped, single-turn devices (supplementary Figure S1³⁷), where we systematically varied the radius of curvature and AR. The height of the channels was kept constant (50 μm), while the width of the channels was varied to obtain different ARs (1:1; 1:2; 1:5; 1:10; and 1:20). All devices had a channel length of 20 mm before the 180° curvature. Using 10 μm particles, we obtained single stream focusing for AR 1:1 to 1:10, while AR 1:20 (channel width = 1 mm) did not result in any focusing. For AR 1:1 and 1:2, the particles are pre-focused entering the curvature while for AR 1:5 and 1:10 the particles are randomly distributed entering the curvature. This is in agreement with our previous work in flow through straight channels up to AR 1:3.²² In both cases, the particles are focused into a single lateral focusing position when exiting the curvature. In flow through straight, square, and rectangular channels, the absence of particles in the corners in AR ∼ 1:1 suggests that additional lateral migration effects take place near channel walls. However, for AR ∼ 1:5 and above, a length of 2 cm is not enough to observe the additional lateral migration. Following the initial experiments, we went on to fully characterize particle behaviour in flow through the low aspect ratio devices (AR 1:5 and 1:10, Figs. 3 and 4). Fig. 3 shows fluorescence image of 10 μm particles, initially well distributed entering the curved channel, focused into a single stream exiting the 180° u-shaped channel for AR 1:5 (a) and 1:10 (b).

FIG. 3.

Flow through curved u-shaped channel. (a) and (b) Fluorescence image of 10 μm particle flowing through the 180° u-shaped channel with channel widths 250 μm (a) and 500 μm (b). The radius of curvature, r, was 2 mm in both cases. (c) and (d) Cross-sectional intensity of the particles at the entrance and exiting points (see arrows in Figs. 2(a) and 2(b)) for channel widths 250 μm (c) and 500 μm (d) over a range of flow rates. Scale bar: 1 mm.

FIG. 4.

Fluorescence image of 10 μm particle flowing through the u-shaped channel at different flow rates. The radius of curvature, r, was 1.5 mm and the channel width 500 μm. Particles start to move laterally when entering the curved section, in a motion that follows the Dean vortices.

Several observations can be made from the fluorescence streak images. First, the particles, well distributed across the channel width entering the channel, are focused into a single lateral focusing point exiting the curved section of the channel. Second, there is an asymmetry in the motion, such that particles move more inward than outward, indicating that the particles are entrained in the Dean vortices and transported towards the inner wall and quickly find their lateral focusing positions when exiting the curved section of the channel. We analyzed the De dependence of particle entrainment in the Dean vortices in detail (Figs. 3(c) and 3(d). The cross sectional intensity of the particles at the entrance and exiting points (see arrows in Figs. 3(a) and 3(b)) of the curved section is shown in Fig. 3(c) (AR 1:5) and Fig. 3(d) (AR 1:10). At low De, the 10 μm particles were not focused, but rather distributed across the width of the channel exiting the u-shaped curved channel due to the weak secondary forces developed at these velocities. When the flow was increased to De = 36 for AR 1:5 (Fig. 3(c)) and De = 41 for AR 1:10 (Fig. 3(d)), particles are entrained in the Dean vortices and migrate across streamlines towards a single lateral focusing point. When the fluid velocity is increased, the particles are pushed further away from the inner wall resulting in defocusing, visualized as broadening of the intensity streaks away from the inner wall in comparison to the single stream focusing point. A further increase in flow rate results in particles being pushed further away to the outer walls.

We found that the particles did not focus exiting the curvature if the straight channel prior the curved section was removed (data not shown). This is presumable due to the lack of dominant lift forces developed in the straight section of the channels. This would mean that there are two distinguished particle movement patterns: first, dominant lift forces initiate the particle focusing in all directions towards the faces of the channel cross-section, and then the Dean vortices quickly move the particles towards the lateral focusing position. Hence, for the low aspect ratio microchannels, the particles are expected to be pre-focused along the height of the channel (on top and bottom) while laterally well distributed before entering the curved section. Figure 4 shows the particle movement behaviour at the curvature at different flow rates for low aspect ratio channel (AR 1:10).

Here, the radius of curvature, r, is 1.5 mm while the height and width are 50 μm and 500 μm, respectively. Depending on the balance between the lift force (F_L) and Dean force (F_D), particles are focused or defocused after the exit of the curved section. Initially, only lateral movement is observed indicating that the vertically pre-focused (on top and bottom) start to move inward towards the laterally equilibrium position. At this stage, F_L and F_D are in balance. With increased flow rate, F_D increases faster than F_L.¹⁷ This results in particle movement towards the outer wall, away from the lateral focusing. Furthermore, the particles are moving in the direction of the Dean vortices (see Fig. 4 for De = 63, and supplementary movie S3³⁷).

B. Deterministic lateral focusing position

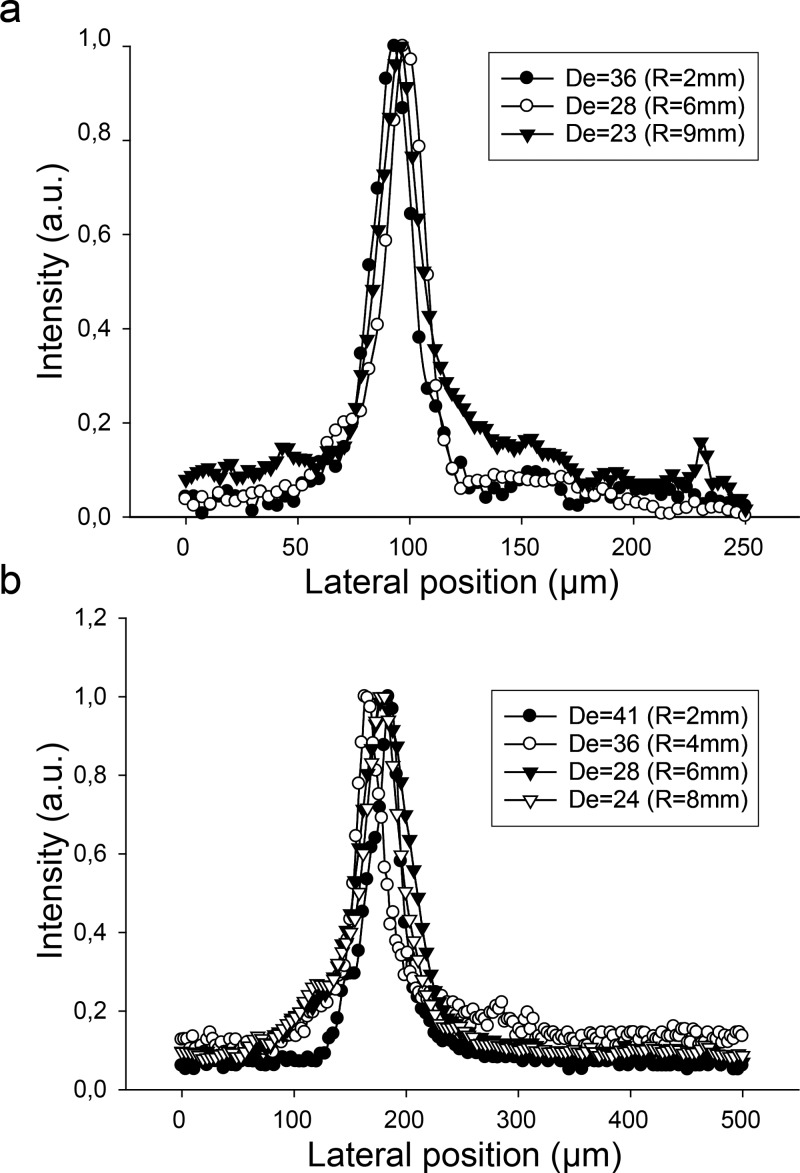
Next, we investigated the influence of the radius of curvature. Interestingly, we found the lateral particle focusing position (x_f) to be fixed and largely independent of the radius of curvature (Fig. 5). Despite the large variation in radius of curvature (2 mm–9 mm), the particles were focused at a fixed lateral position (x_f = 0.30w and 0.35w for channel width of 250 and 500 μm, respectively). The particles focus at lower De with increased radius of curvature (De proportional to 1/r,^1/2 or De = Re(D_h/2r)^1/2). In other words, particles migrate to lateral focusing position faster (i.e., at shorted channel length) with increased curvature. Supplementary Figure S2³⁷ shows how the lateral particle position is affected by the flow rate and radius of curvature for the different radius shown in Fig. 5.

FIG. 5.

Cross-sectional intensity of 10 μm particles at the exiting points of the curved section for channel widths 250 μm (a) and 500 μm (b) over a range of radius of curvature. The lateral focusing position was fixed and independent of radius of curvature.

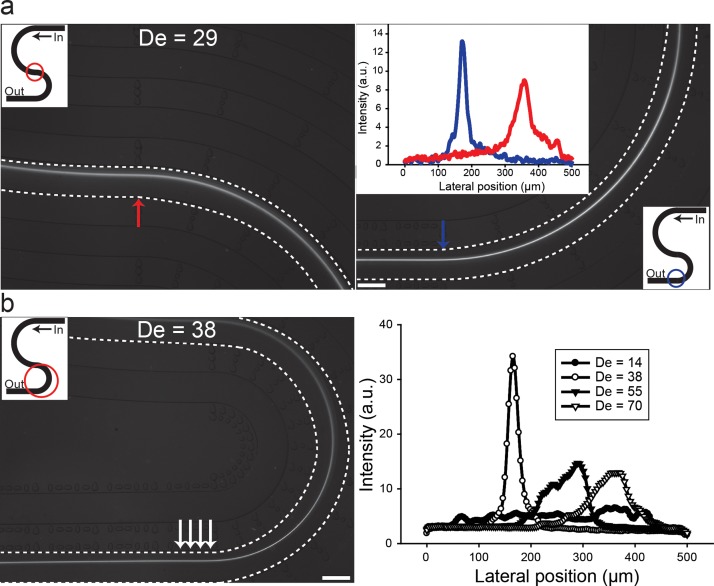
Using the low AR u-shaped channels, it was possible to investigate the influence of curvature on laterally unfocused particles. To investigate the lateral focusing position in more detail we designed and designed new sets of “s-shaped” curved channels and evaluated the flow (Fig. 6).

FIG. 6.

Summary of flow through “s-shaped” double curved channels. (a) Particles, pre-focused in the first curvature of the s-shaped channel (left panel), are maintained focused exiting the second curvature (right panel) with radius of curvature of 4 mm. Inset (right panel), the cross section intensities of particles entering and exiting the second curvature (red and blue arrow) is shown. (b) Intensity of particles flowing through the second curvature with radius of curvature of 2 mm (right panel) and average intensity of the area marked with arrows (left panel). The lateral focusing position was fixed (see Fig. 3(b) for comparison). Scale bar: 500 μm.

The unique geometry allows for “priming” the particle entering position to the second curvature without “cross-talk” of the secondary forces from previous curvature, since the flow field changes direction. As a comparison, in flow through spiral channels, the radius of curvature changes at each infliction point and the secondary forces remain unidirectional. In the s-shaped channel, the length of the straight channel leading to the first curvature was maintained at 2 cm to enable particle focusing (see supplementary Figure S1(b)). As can be seen in Fig. 6, the particles pre-focused in the first curvature remained focused as they exit the second curvature at a fixed lateral focusing position. The lateral focusing position is in agreement with results in flows through single curved channels (see Fig. 3(b)). Evidently, the lateral focusing position is deterministic irrespective of particles being in equilibrium or randomly distributed entering the curved channel.

Using simple u-shaped and s-shaped channel structures, we show in this study that it is possible to focus particles to a single lateral position in channel aspect ratios not possible in flow through straight channels. Importantly, particle focusing in curved channel depends on the relative magnitude of F_L and F_D. Re, De, and the channel aspect ratio influence the competition dynamics these forces. Although the radius will influence the intensity of the main and secondary flows, it contributes nothing to break the balance between the F_L and F_D.³⁶ This might partly explain our experimental observation of the deterministic fixed lateral focusing position. Although more investigation is required, we speculate that in addition to the balance between F_L and F_D, the unidirectional pressure forces (F_P) might also to some extent affect the lateral focusing position. Finally, our findings reiterate the fact that, while the simple u-shaped and s-shaped channel geometries are useful in designing experiments to measure the influence of curvature, it is also possible to use these simple devices for high throughput particle focusing, separation and filtration applications.

C. High throughput particle and cell filtration

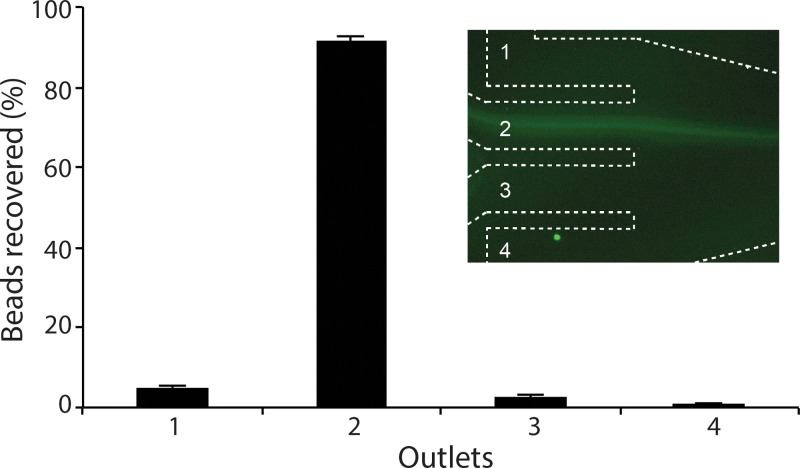
To demonstrate the u-shaped microfluidic device for filtration applications, a mixture of 10 μm and 2 μm particles was pumped through a device with a channel width of 500 μm with four outlets. We used the fact that particles focus at a deterministic and fixed lateral position to design the u-shaped device with a single inlet and four outlets. As expected, the 2 μm particles were unfocused and scattered throughout the device, while the 10 μm particles were focused. The Coulter Counter result reveals filtration efficiency, defined as the fraction of 10 μm particles collected through outlet nr 2, of 92% for the focused 10 μm beads at a flow rate of 4.25 ml/min (Fig. 7).

FIG. 7.

Ultra high-throughput filtration. 10 μm particles are successfully focused and filtered through outlet two (see inset) at flow rate of 4.25 ml/min. The filtration efficiency was 92%.

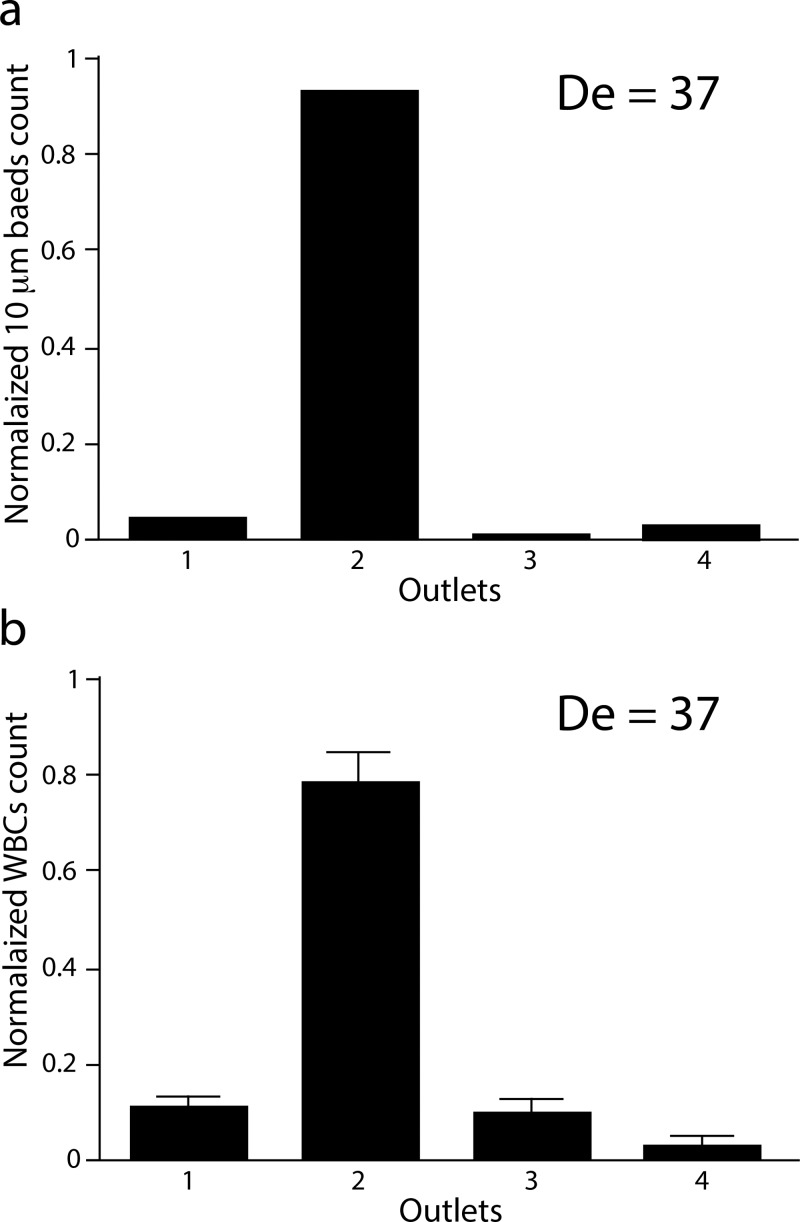
For cell-based applications, we tested the filtration of leukocytes from a buffer solution and then from diluted whole blood. Leukocytes comprise only ∼1% of the cells in total blood and must first be enriched for further downstream analysis. We designed a new single inlet and four-outlet u-shaped channel, with a width of 250 μm, height of 50 μm, and radius of curvature of 4 mm. First, 10 μm particles were used to find the optimal flow conditions (Fig. 8(a)). Following, the leukocyte population pre-isolated from whole blood were processed under the (for 10 μm particles) optimal flow rate (Fig. 8(b)). The filtration efficiency for the 10 μm particles was 96%, while a filtration efficiency of 78% was obtained for the leukocyte. The lower filtration efficiency for the leukocyte population compared to the 10 μm particles reflects the fact that the size of the leukocyte population is quite heterogeneous. The size of leukocyte population is typically between 7 and 15 μm. Moreover, the cell elasticity and deformability compared to rigid spherical particles is also likely to contribute to different behaviours. Finally, we performed preliminary filtration experiments of leukocytes from diluted (0.5%) blood (supplementary Figure S3³⁷). We observed a similar trend as for rigid particles: at low flow rates, the leukocytes were predominantly recovered through outlets 1 and 2, and with increased flow rate the cells were pushed further away from the inner wall. The filtration efficiency at outlet 2 for De = 37 was around 72%. The slightly reduced filtration efficiency for diluted blood compared to pure buffer is likely due to interference with red blood cells. The cell viability was very high (>97%), comparable to control cells.

FIG. 8.

Filtration of leukocytes. (a) 10 μm particles focused and filtered through the u-shaped device. The filtration efficiency, defined as fraction of the particles recovered through outlet 2, was 96%. (b) Filtration of leukocytes. The filtration efficiency was 78% (n = 3). The flow rate was 2.2 ml/min (De = 37) in both cases.

The vast majority of miniaturized systems deal with the analysis and quantification of cells and rely on off-the-chip sample preparation via conventional centrifugation. This is mainly because it is very difficult to integrate sample preparation while maintaining the volumes required for practical applications. Hence, despite the many promising advances made in microscale cell separation technologies, most microfluidic devices are limited by their incompatibility with complex, heterogeneous biological fluids such as whole blood and their extensive sample preparation requirements. In general, there is a trade-off between speed of separation and performance when non-inertial forces are used. Towards this goal, the use of label-free inertial microfluidics elegantly addresses the throughput without compromising with performance.

Several different inertial microfluidic devices have been proposed over the past few years, including high aspect ratio straight channels and different curved geometries, such as sigmoidal repetitive curved channels, and spirals. While maintaining the design simplicity of straight channels, the u-shaped device presented in this work has comparative filtration efficiency to the spiral channels for particles. However, for cell-based assays the use of spiral devices is very attractive compared to the u-shaped geometry since one can differentially focus cells at different lateral position based on size and easily collect at different outlets. The fact that the Dean vortices act during a larger channel length in spirals is the main contributor for improved separation performance. For improved cell separation in the u-shaped channel, the radius of curvature of the microchannel could be increased from the current 4 mm. Alternatively, the s-shaped channel might also offer a better separation performance since the total channel length is increased.

For fundamental fluid flow behaviour studies, the u-shaped and s-shaped channels have added value compared to spiral. This is because the curvature introduces complex focusing behaviour, and the u-shaped and s-shaped channels allow for constant channel curvature throughout the curvature (and consequently constant De), which is not possible in spiral microchannels. Hence, we expect these devices, combined with computational analysis, will offer improved understanding of Dean-coupled inertial particle focusing behaviour. For particle focusing and filtration applications, the simple u-shaped channel has several advantages compared to flow through straight channels. In flow through straight channels, particles are focused along the face of the longer channel sidewalls generating two symmetric focusing points. This puts limitation of throughput. All together, the reported straight channel aspect ratio has been limited to 1:3, with the largest side channel being 100 μm and a maximum flow rate of 200 μl/min.^15,21,22 In this work, we introduce flow through u-shaped channels and demonstrate particle focusing into a single and deterministic lateral position that enables effective extraction of the focused stream at more than 20 times higher flow rate compared to straight channels.

V. CONCLUSIONS

In summary, we report particle focusing in curved channels using u-shaped and s-shaped channels we analysed the effect of curvature on particle focusing at various channel aspect ratios (AR 1:1–1:20). The particle focusing position exiting the curved channels was found to be independent of radius of curvature. The lateral focusing position is fixed and independent whether particles entering the curvature are pre-focused (at equilibrium) or randomly distributed. Using the u-shaped channel geometry with one inlet and four outlets, we successfully demonstrated a continuous particle filtration application, with extremely high throughput. As an example of cell-based application, leukocytes were successfully filtered through the u-shaped microchannel. The simple device requiring neither external force fields nor mechanical parts to operate is readily applicable for low cost particle focusing and filtration applications.