Red blood cell as a universal optoacoustic sensor for non-invasive temperature monitoring

Abstract

Optoacoustic (photoacoustic) temperature imaging could provide improved spatial resolution and temperature sensitivity as compared to other techniques of non-invasive thermometry used during thermal therapies for safe and efficient treatment of lesions. However, accuracy of the reported optoacoustic methods is compromised by biological variability and heterogeneous composition of tissues. We report our findings on the universal character of the normalized temperature dependent optoacoustic response (ThOR) in blood, which is invariant with respect to hematocrit at the isosbestic point of hemoglobin. The phenomenon is caused by the unique homeostatic compartmentalization of blood hemoglobin exclusively inside erythrocytes. On the contrary, the normalized ThOR in aqueous solutions of hemoglobin showed linear variation with respect to its concentration and was identical to that of blood when extrapolated to the hemoglobin concentration inside erythrocytes. To substantiate the conclusions, we analyzed optoacoustic images acquired from the samples of whole and diluted blood as well as hemoglobin solutions during gradual cooling from +37 to −15 °C. Our experimental methodology allowed direct observation and accurate measurement of the temperature of zero optoacoustic response, manifested as the sample's image faded into background and then reappeared in the reversed (negative) contrast. These findings provide a framework necessary for accurate correlation of measured normalized optoacoustic image intensity and local temperature in vascularized tissues independent of tissue composition.

Temperature monitoring of live tissue is an important technique that provides feedback information needed for guidance of thermal therapies, such as laser interstitial thermotherapy, high-intensity focused ultrasound, radio frequency ablation, and cryoablation.^1–3 Temperature readings collected in real time around the treated areas help warranting safety and efficiency of the therapeutic procedure.⁴ Non-invasive temperature monitoring is unanimously preferred among the clinicians, especially when there are crucial requirements to minimize collateral thermal damage to the adjacent normal tissues and zones of innervation. Several imaging and sensing modalities have been proposed for non-invasive temperature monitoring during thermal therapies, including ultrasound imaging, magnetic resonance imaging, and optoacoustic (photoacoustic) imaging and sensing.^5–7 The potential advantages of optoacoustic temperature imaging techniques reside in enhanced spatial resolution, temperature sensitivity, and faster data acquisition.^8–10

During the past decade, optoacoustic imaging has attracted significant attention from researchers and clinicians due to its success in a variety of biomedical applications that involve high resolution deep tissue imaging of optical absorbers (blood, water, and near infrared contrast agents) unattainable with other modalities.^11–13 The premium quality of optoacoustic images, as compared to other imaging modalities based on tissue optical contrast, comes from the fact that optoacoustic energy conversion allows for tissue-specific information being encoded in and carried by acoustic rather than optical waves. Since optoacoustic detection is technologically implemented in a manner very similar to detection in ultrasonic imaging, it yields the same benefits of high spatial resolution.^11,12 It is well known that the magnitude of optoacoustic response is sensitive to the local temperature, the phenomenon attributed to temperature dependent behavior of thermodynamic and mechanical properties, which comprise thermoelastic efficiency of the tissue, also known as Grüneisen parameter.^14–16 The presence of temperature dependent optoacoustic response (ThOR) measured from biological solutions, cells, and tissues provided the foundation for pioneering efforts in non-invasive temperature monitoring since over a decade ago.^17,18 Recent progress in this field of science demonstrated close correlation between local optoacoustic image intensity and temperature in tissue mimicking phantoms,^7–10,15,19 possibility to enhance the technique by combining laser optoacoustic and thermoacoustic sensing,²⁰ and optoacoustic temperature measurements in microscopy mode.^21,22 However, when considering in vivo applications, sample-to-sample and spatial variations of Grüneisen parameter for different tissues negate all the advantages of the current methods, including high precision of the obtained temperature calibration curves. Each calibration remains valid as long as it is applied to the temperature measurements made on the same particular tissue/phantom, which is practically unacceptable. When a population of biological subjects is studied, it becomes obvious that the measured temperature accuracy is no better than several degrees Celsius.²³ Below we report a discovery of universal behavior of normalized ThOR in blood near isosbestic point of hemoglobin (805 nm). We use the finding to propose a laser optoacoustic temperature imaging technique which ultimately solves the problems of tissue variability.

Our working hypothesis in these studies is that the normalized ThOR in blood at 805 nm should be independent of the erythrocyte volume fraction (hematocrit). In live organisms, the hemoglobin, which under normal physiological conditions is exclusively compartmentalized inside red blood cells (RBCs), is the only chemical tissue component with significant optical absorption at 805 nm (Ref. 24), which was also reported to be independent of oxygenation status²⁵ and temperature.^26,27 The intracellular concentration of hemoglobin is a part of broad homeostasis and is relatively constant for individual species. For example, for adult humans, it varies in the range of 330–360 mg/ml or 5.1–5.6 mM.²⁸ Therefore, we can expect that in spite of significant spatial variations of hemoglobin concentrations caused by hematocrit differences between major blood vessels and capillaries and tissue-specific density of vascularization, in vivo normalized ThOR at 805 nm will be defined by physical properties of intracellular hemoglobin.

The experimental setup was upgraded from the one previously used to study optoacoustic response of solutions as a function of temperature.¹⁵ It utilizes a real-time two-dimensional laser optoacoustic imaging system (LOIS, TomoWave Laboratories, Houston, TX) with a linear ultrasound probe. The laser unit (SpectraWave, TomoWave Laboratories, Houston, TX) was tuned to 805 nm near the isosbestic point of hemoglobin. Detailed description of the experimental setup can be found in supplementary material.⁴⁵

Our test unit contained seven tubes placed at two levels of 15 and 22 mm from the detection end of the ultrasound probe. The tubes were positioned orthogonally to the imaging plane, so that their cross-sections could be observed on reconstructed optoacoustic images. Polytetrafluoroethylene (PTFE) tubes (Sub-Lite-Wall Tubing, Zeus, Orangeburg, SC) of inner diameter 0.635 mm and wall thickness of 0.051 mm were filled by liquid samples.

Preparation of samples is described in detail in supplementary material.⁴⁵ Briefly, we used porcine blood with anticoagulating agent and powdered human hemoglobin diluted in phosphate buffered saline (PBS) (pH 7.4).

We employed a chest freezer (CF-1510, Avanti, Miami, FL) providing 0.1–0.2 °C/min cooling rate of a thermostat tank with the test unit. The 1.5 l tank was filled with 23 wt. % aqueous sodium chloride solution with freezing temperature at about −21 °C. The solution served as an acoustically coupling medium necessary to transmit the generated optoacoustic pressure signals to the ultrasound probe. Prior to the experiment, the solution was heated to 42 °C, the test unit was assembled, and placed into the chest freezer. Data collection was initiated when temperature dropped to about 37–38 °C. The temperature was measured with 5 s intervals using fine gauge thermocouples placed both inside and outside of the tubes and logged by multiple channel acquisition module (OM-DAQ-USB-2401, Omega, Stamford, CT) with precision of 0.01 °C. Optoacoustic data (averaged over 6.4 s or 64 laser pulses) were acquired with 30 s intervals and synchronized with temperature readings using internal clock of the computer.

Each optoacoustic frame was reconstructed using 2D filtered backprojection of measured integrated signals.²⁹ Detailed description of the signal processing can be found in supplementary material.⁴⁵ To obtain a quantitative metric of the optoacoustic response, we evaluated the median intensity inside a region of interest (ROI) manually selected on the first reconstructed frame of the tube's cross-section. The selected ROI contained information on optoacoustic response only from the sample inside the tube. Using median estimate of the optoacoustic image intensity made our measurements less sensitive to the ROI tracking. Since speed of sound in the coupling medium was changing with temperature, we implemented an automatic adjustment algorithm based on locating the maximum of cross-correlation function for the sample images.

In the previous publication, we showed that the intensity-normalized 2D optoacoustic imaging (a metric of normalized ThOR) could be reliably used for remote temperature monitoring inside optically absorbing solutions, if a solution- and concentration-specific parameter T₀ is known.¹⁵ The material parameter T₀ was extracted from linear fit of the measured data as a temperature at zero optoacoustic response. The implemented normalization of the optoacoustic image intensity at initial temperature provided spatial confinement of optical fluence and absorption, which is necessary for potential in vivo applications. Here, we used the same imaging approach to study ThOR in whole and diluted porcine blood contained inside ultrathin-wall plastic tubes. Blood dilution was implemented in order to simulate conditions of physiological variability of hematocrit across systemic vasculature and capillary networks.³⁰ PBS (pH 7.4) was used to dilute the whole blood while preserving the integrity of red blood cells. Optoacoustic imaging was performed while slowly decreasing the temperature from +37 to −15 °C. As an acoustically coupling medium, we used aqueous solution of sodium chloride at its eutectic concentration (23 wt. %) with freezing temperature at about −21 °C.³¹

Image intensity of a blood sample was gradually decreasing by following the local temperature trend and eventually became indistinguishable from background. Further cooling resulted in re-appearance and growth of the optoacoustic response from the sample but now registered as the image with opposite (negative) polarity. Fig. 1 provides the first direct observation of the change in polarity of optoacoustic image which, for the presented blood sample, manifested itself at the temperature T₀ = −12.9 °C. Such a positive-negative transition of optoacoustic intensity is expected from aqueous compounds due to nil volumetric thermal expansion coefficient achieved at the extremum of the compound's density. For example, such an effect is predicted for water with maximum density at 3.98 °C. In supplementary material,⁴⁵ we provide an example showing direct experimental evidence that optoacoustic response completely disappears at the temperature of maximum density.

FIG. 1.

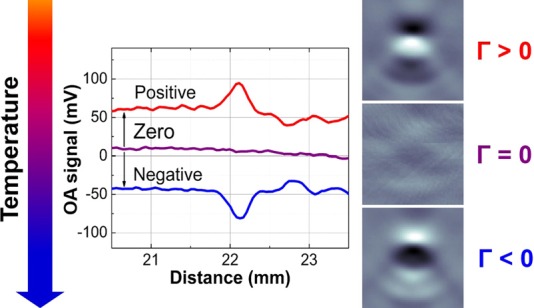
Transition through the temperature of zero optoacoustic response visualized in blood samples. Processed optoacoustic signals (central graph) and reconstructed 3 × 3 mm² images (right panel) illustrate change of the polarity in optoacoustic response observed during cooling of blood samples at the temperature where Grüneisen parameter Γ = 0. “Positive” and “negative” optoacoustic signals are shown offset by ±50 mV for illustrative purposes.

Figure 2(b) shows optoacoustic response from diluted blood samples simulating physiological range of hematocrit across the entire vasculature (from systemic blood vessels down to capillaries,³² Fig. 2(a)). While dilution of blood samples resulted in proportional decrease of the optoacoustic intensity measured at a particular temperature, the entire data ensemble still intersected in the same point of zero optoacoustic response at T₀ = −13.1 ± 0.3 °C (N = 4). Here and anywhere else below, if not explicitly stated, statistical data are presented as average ± standard deviation with number of samples indicated in parenthesis. After normalization at physiological 37 °C, the graphs merge into a universal calibration curve (Fig. 2(c)), which can be accurately approximated by a second order polynomial (see supplementary material⁴⁵). The second order approximation is consistent with thermal behavior of Grüneisen parameter for water³³ and optoacoustic response measured from in vitro retina tissue²³ and turkey breast²⁰ in a wide range of temperatures. We analyzed data from whole blood samples obtained from eight animals and estimated the temperature of zero optoacoustic response for the porcine blood T₀ = −12.8 ± 0.5 °C. We believe that the thermal expansion coefficient of erythrocyte's cytoplasm is the factor dominating in the observed ThOR of blood samples. The functional trend and the measured temperature of zero optoacoustic response are in agreement with those of thermal expansion coefficient estimated for erythrocyte concentrates in the temperature range from 4 to 48 °C.³⁴ However, T₀ extrapolated from the data reported on plasma ultrafiltrate³⁴ is much higher and is rather close to the one we measured in pure PBS (see Fig. 3 and supplementary material⁴⁵).

FIG. 2.

(a) Schematic showing that volumetric fraction of erythrocytes (hematocrit or Ht) significantly varies through the entire vascular network, decreasing from systemic blood vessels down to capillaries. (b) Experiments with whole and diluted blood show that the temperature dependent optoacoustic response is scaled proportionally to hematocrit. (c) However, when normalized at 37 °C, it becomes invariant as the curves representing whole and diluted blood coincide. Curves labeled Ht 40 represent whole porcine blood. Curves with reduced Ht indicate that the blood sample was diluted, for example, Ht 20 represents a sample with dilution fraction of ½. Dashed-dotted line marks zero optoacoustic response. Yellow dashed line on the panel (c) shows the universal blood calibration curve $\overline{\mathit{O}\mathit{A}}=-\frac{4\Delta T_{\mathit{m}\mathit{a}\mathit{x}}}{{\left(T_1-T_0\right)}^3}\left(T-T_0\right)\left(T-T_1\right)+\frac{T-T_0}{T_1-T_0}$ with parameters: T₁ = 37 °C—fixed normalization temperature, where normalized optoacoustic intensity $\overline{\mathit{O}\mathit{A}}=1$; T₀ = −12.8 ± 0.5 °C—temperature of zero optoacoustic response estimated directly from the image (N = 8 animal samples); and ΔT_max = 10.8 ± 0.2 °C—maximum nonlinear temperature deviation in the temperature range [T₀ T₁]. If ΔT_max = 0, the calibration is linear. For comparison, normalized Grüneisen parameter of water has maximum nonlinear temperature deviation ΔT_max = 1.9 °C in the range of 4–37 °C. For more details on ΔT_max, see supplementary material.⁴⁵

FIG. 3.

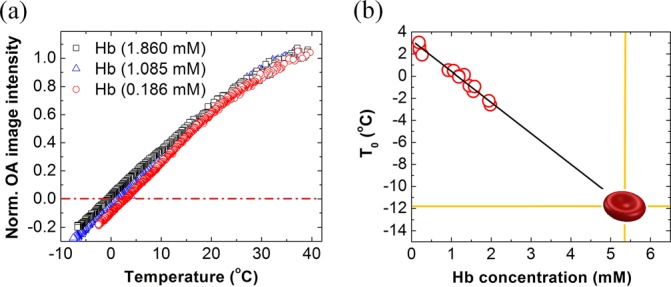
(a) Optoacoustic image intensity normalized at 37 °C as a function of temperature for three different concentrations of hemoglobin. Dashed dotted line marks zero optoacoustic response. (b) Temperature T₀ of zero optoacoustic response as a function of hemoglobin concentration. Linear fit results in equation: T₀ = −2.8·[Hb] + 3.1, where [Hb] is the molar concentration of hemoglobin. The fit line intercepts the ordinate at about 3 °C, which represents the properties of used PBS solvent (see supplementary material⁴⁵ for experimental proof). Extrapolation of the fit function to the typical concentration of hemoglobin inside red blood cells [Hb] ≈ 5.3 mM results in T₀ = −11.7 °C, which is close to the experimentally measured value of −12.8 °C.

To prove that the universal normalized ThOR observed in blood is confined within the stable internal environment of erythrocytes, we performed control imaging of hemoglobin solutions. The hemoglobin powder was dissolved in PBS to keep physical and chemical properties of hemoglobin within physiological range. The solutions were prepared at different concentrations from highly diluted 12 mg/ml or 0.186 mM to the concentration mimicking whole blood at average hematocrit (120 mg/ml or 1.860 mM). It was found that in contrast to blood, there is a linear decrease of parameter T₀ with hemoglobin concentration from about +3 °C at low concentrations to about −3 °C for 1.86 mM solutions (Figure 3(b)). Similar negative trend was observed in our previous studies of cupric sulfate solutions.¹⁵ When extrapolated to a typical physiological concentration of hemoglobin found inside red blood cells (about 5.3 mM for humans), the estimated value T₀ = −11.7 °C was close to that experimentally measured for the blood samples, supporting the hypothesis that explains universal temperature dependent behavior of normalized optoacoustic response in blood by intracellular compartmentalization of hemoglobin. The 1.1 °C mismatch in average temperatures of zero optoacoustic response measured for blood and estimated for hemoglobin solution could be caused by the fact that cytoplasm solvent of erythrocytes represents a more complex mixture than the employed PBS and includes multiple protein components. Also, deviation from the linear regression model used to fit the T₀ data for hemoglobin could happen at very high concentrations observed inside red blood cells and not achievable while using PBS as a solvent.

The hemoglobin molecule has much more complex interaction with solvent than simple ionic salts. Amphipathic nature of the protein results in a multilayer local aqueous environment with significant differences in physical properties, especially molecular mobility, of individual shells.³⁵ Due to large size of the protein, significant amount of water is pulled out of bulk and immobilized near the protein's surface, probably via the formation of stronger hydrogen-bonded network.³⁶ The ions of inorganic salts, which are present in the solvent, also affect molecular structure of water shells surrounding the dissolved proteins.³⁷ In the case of hemoglobin compartmentalized inside red blood cells, the effect could be further augmented by other components of the erythrocyte's cytoplasm. Reduced molecular mobility of water depresses the maximum solution density, and therefore also the point of zero optoacoustic response, towards lower temperatures, the phenomenon known as the Despretz's law.³⁸ This effect is also similar to lowering of freezing temperatures of solutions in comparison with pure liquids—the cryoscopic effect.³⁶ It is still remarkable that the relationship experimentally found between temperature of zero optoacoustic response and concentration of the solute has the same basic linearity for simple salts and complex molecules of hemoglobin. Similar relations have been observed in the cryoscopic effect, but more investigations are needed in order to make connections between these fundamental phenomena.

Despite multiple publications in the area of optoacoustic temperature monitoring, the phenomenon of a universal ThOR in blood was not previously described. It could be only observed while comparing the normalized ThOR in whole and diluted blood and hemoglobin solutions, which has never been studied before. It is also crucial that the measured optoacoustic response comes solely from the native optical absorption of hemoglobin compartmentalized inside red blood cells rather than external contrast agents.^7,8 Also, if optically absorbing substance is not forming chemical bonds with solvent, its ThOR would replicate the one of the pure solvent. The examples of such situations include suspensions of carbon microparticles⁴⁵ and gold nanospheres.³⁹ Finally, using a laser wavelength different from the isosbestic point of hemoglobin provides data that are biased by temperature dependent behavior of the oxygen dissociation curve.²⁸ Temperature changes affect the equilibrium between oxygenated/deoxygenated forms of hemoglobin, leading to changes in optical absorption coefficient everywhere but around its isosbestic wavelengths.^26,27 The isosbestic point of hemoglobin at 805 nm is the only one acceptable for deep live tissue temperature monitoring applications, since it is located within the near-infrared spectral transparency window.

Based on the reported findings, we propose the following procedure for non-invasive monitoring of temperature using 2D optoacoustic imaging at 805 nm laser wavelength: (1) Prior to any thermal intervention record optoacoustic image from the vascularized tissue regions of interest at a normal local physiological temperature, e.g., 37 °C; and (2) at any subsequent moment, obtain intensity-normalized optoacoustic response and convert it to the local temperature via the universal blood calibration curve measured for a particular biological population. Since in vivo optoacoustic response is generated predominantly within blood vessels and normalization makes it independent of hematocrit and local fluence, the calibration should remain valid across the entire field of view.

One particularly promising clinical application of the proposed technique could be temperature monitoring during cryoablation of prostate cancer.^3,40 Cryoablation involves rapid localized temperature decrease, and there is a crucial requirement to minimize collateral thermal damage in the innervation areas near rectal wall, which cannot be addressed by direct invasive temperature measurements with the needle probes.⁴¹ On the other hand, two-dimensional optoacoustic imaging of temperature could be implemented in this case using a modified transrectal linear ultrasound probe,⁴² which has imaging characteristics similar to the general-purpose clinical probe used in our studies. We expect that the normalized optoacoustic imaging technique will show better accuracy when monitoring lower temperatures due to non-linearity of the temperature calibration curve, which decreases sensitivity for higher temperatures (Fig. 2(c)).

There are still many questions to be answered before the proposed technique could be translated into a robust and reliable clinical modality for non-invasive temperature mapping. Full applicable range of temperatures is not yet determined and is at least constrained by thermal stability of hemoglobin with intact near-infrared spectral features. Another critical requirement of the technique is hemoglobin compartmentalization inside erythrocytes. Thermal hemolysis was reported at high temperatures (45–50 °C).⁴³ However, at the extremely slow rate (fraction of % per hour), it would not be noticeable in the measured ThOR during typical times of thermotherapy (minutes). We examined blood samples that underwent our cooling procedure down to −15 °C using two techniques. (1) We did not find any morphological changes in red blood cells under 40× light microscope with additional digital zoom. (2) Optical absorption spectra of supernatant in the centrifuged samples of blood did not reveal any spectroscopic features of released hemoglobin. The observations suggest that the hemoglobin compartmentalization was maintained during our experiments. However, cryoablation is known to produce disruptive effects within cell membranes, caused by repetitive cycles of fast freezing followed by slow thawing,⁴⁰ an indication that the rate of temperature change could be another important factor to consider in development of the optoacoustic temperature mapping technology. It is prudent to stress that the proposed technique still relies on assumptions of temperature-invariant fluence and acoustic attenuation of the background tissues, and careful studies must be performed to validate those for each particular case of temperature monitoring. For example, blood flow in the interrogated area of tissue could change with time as a part of physiological response resulting in reduced accuracy of the technique. Although acoustic attenuation in water is small for low-megahertz frequency range,⁴⁴ it may become a significant factor if measurements are performed in live tissues with high-frequency transducers. Statistical variance of T₀ is another important characteristic that will affect accuracy of the technique and should be estimated for the entire clinical population. As far as we know, subject-to-subject variations in T₀ could be caused by differences in cytoplasmic composition including hemoglobin concentration inside red blood cells.²⁸ In this work, T₀ of blood samples from 8 animals was measured with standard deviation of 0.5 °C. Depending on the clinical application, the variance of the T₀ could be further minimized by categorizing subjects based on sex, age, etc.

Optoacoustic imaging of blood samples was performed while temperature was gradually decreased from 37 °C to −15 °C allowing direct observations of samples' transition through zero optoacoustic response. The temperature of zero optoacoustic response was invariant with dilution of blood but decreased linearly with respect to concentration of control hemoglobin solutions as it had been found for ionic salts. The phenomenon was explained by a unique compartmentalization of the dominant near-infrared absorber, hemoglobin, inside a stable cytoplasmic environment of red blood cells and allowed for accurate hematocrit-independent calibration of optoacoustic response vs temperature in blood by normalizing it at physiological 37 °C. The reported findings present a strong background and open an avenue for using intensity-normalized optoacoustic imaging of blood vessels and vascularized tissue as a universal in vivo temperature monitoring technique. Providing good image quality (high signal-to-noise ratio in the region of interest), the proposed procedure can allow real-time temperature mapping, which would help to improve efficacy of thermal therapies and reduce undesired damage to surrounding healthy tissues.