Abstract
Missing data are common in studies that rely on multiple informant data to evaluate relationships among variables for distinguishable individuals clustered within groups. Estimation of structural equation models using raw data allows for incomplete data, and so all groups may be retained even if only one member of a group contributes data. Statistical inference is based on the assumption that data are missing completely at random or missing at random. Importantly, whether or not data are missing is assumed to be independent of the missing data. A saturated correlates model that incorporates correlates of the missingness or the missing data into an analysis and multiple imputation that may also use such correlates offer advantages over the standard implementation of SEM when data are not missing at random because these approaches may result in a data analysis problem for which the missingness is ignorable. This paper considers these approaches in an analysis of family data to assess the sensitivity of parameter estimates to assumptions about missing data, a strategy that may be easily implemented using SEM software.
Missing data in a multiple informant analysis are commonplace. The measurement battery for any single individual may be incomplete, for instance, when an individual does not respond to all assessment tools or their subcomponents, such as subscales or scale items. This is often the case in longitudinal studies, for example, in which missing data arise when participants drop from a study or miss planned assessments but return for subsequent interviews. The reasons for non-response can vary, from an individual’s refusal to participate at the onset of a study to an inability on the part of the researcher to arrange an interview. Other reasons for missing data include problems in the data collection process, such as data entry errors. Although these sources of missing data are common to behavioral studies in general, studies that rely on multiple informants to provide information about a target individual or context potentially have the added challenge of dealing with missing data for one or more informants. Family studies that rely on reports from the mother, father, and child, for instance, often report difficulties in obtaining data from all individuals (Kazak, Segal-Andrews, & Johnson, 1995; Phares, 1992).
Obtaining data from multiple informants is important in many behavioral studies. Information about a target individual, such as a child, is often obtained through interviews with key individuals, such as parents and teachers, to provide a rich assessment of the environment of the targeted child. Data from multiple informants may also serve as proxies for information that cannot be obtained directly from the targeted individual, such as a child who is too young to provide responses to survey questions. Data from multiple individuals are often considered necessary to give a full accounting of an environment and related experiences. Thus, loss of data from key individuals can be a source of concern for researchers.
Structural equation models estimated by full information maximum likelihood (FIML) are often applied in the analysis of multiple informant data when some data are missing (e.g., Cui, Durtschi, Donnellan, Lorenz, & Conger, 2010). Multivariate analysis using FIML allows a group to be included even if data are partially complete for the group. Data are assumed to be missing completely at random (MCAR) such that the missingness (i.e., whether or not data are missing) is independent of the observed and the missing data or to be missing at random (MAR) such that the missingness is independent of the missing data. For MAR, the missingness may depend on the observed data (Little & Rubin, 2002). The estimation of models using FIML is a tremendous improvement over complete-case approaches that require that data are MCAR, an assumption that is more difficult to satisfy in practice. The assumption of MAR is not, however, routinely evaluated in practice. If data are not missing at random (NMAR), such that the missingness is dependent on the missing data, and this relationship is ignored in an analysis, the resulting parameter estimates may be biased (Little & Rubin, 2002). When data are NMAR, the source of the missing data is considered non-ignorable and should be addressed in an analysis to avoid possible biases in parameter estimates and statistical inferences (Little & Rubin, 2002).
This paper considers missing data methods for multiple informant studies when data may be NMAR. Although data from such studies are often analyzed using methods that provide valid statistical inference if data are MCAR or MAR, the assumptions are not often evaluated. In fact, it is not possible to empirically test assumptions about missingness (unless, for example, data are simulated from a known distribution). It may be possible, however, to study the sensitivity of parameter estimates and statistical inferences to assumptions about the missing data (Little & Rubin, 2002). Indeed, sensitivity analysis is a widely recommended procedure for evaluating assumptions about missing data. Extending an analysis of data on the adoption process from an adoption study (Ge et al., 2008) in which data are missing primarily for the birth father, multiple approaches to the data analysis are taken to conduct a sensitivity analysis of the parameter estimates and statistical inferences to assumptions about the missing data and to potentially provide information about the parameters of a model if data are NMAR.
The remainder of this paper is organized as follows: First, three type of data are reviewed. These descriptions of data types are necessary because statistical methods can differ in their assumptions about the relationship between the missingness and the data. Major missing data methods are briefly reviewed, including complete-case techniques and methods based on advanced statistical theory. The adoption study is described and a model based on data from multiple family members is presented as an example of how missing data methods may be applied. Applications of different methods to the sample data highlight benefits and shortcomings of each method, providing insight into the planning of multiple informant studies where missing data may be anticipated.
Types of Data When Some Data Are Missing
Little and Rubin (2002) classify data according to three types with each type involving an assumption about missingness. The data refer collectively to the observed and the missing values. Missingness is represented by an indicator variable, such as one that denotes whether or not an individual completed a study. First, data are MCAR if the missingness is independent of the observed and the missing data. In a family study in which data for fathers are missing, data are MCAR if the missingness is independent of the fathers’ missing data and all observed data, such as when missing data are planned by design (Graham, Taylor, Olchowski, & Cumsille, 2006). Second, data are MAR if the missingness is independent of the missing data but is dependent on the observed data. In a study of father reports of marital satisfaction, for instance, where some satisfaction scores are missing, data are MAR if fathers with low levels of self-esteem are less likely to report their marital satisfaction. Here, the missingness depends on self-esteem level and not the missing satisfaction data. Lastly, data are NMAR when the missingness is related to the missing data even after accounting for dependencies of the missingness on the observed data. In the example presented in the current study that uses birth father reports of openness in the adoption process, data are NMAR if birth fathers with low levels of openness during the adoption process are less likely to report their level of openness. In this case, the missingness depends on the missing openness data.
Data Analysis with Missing Data
Applications of statistical procedures such as regression analysis generally require complete data and so are considered valid when data are MCAR. In a study that defines a family unit by a mother, father and target child or considers specific dyads (e.g., mother and child), for instance, missing data on any one variable for any one family member will result in an exclusion of the entire family from analysis when only complete data are considered (see, e.g., Kenny & Ledermann, 2010). Longitudinal studies in which only individuals with complete data for all measurement waves are considered in an analysis will also result in an exclusion of some individuals from an analysis (see, e.g., Rhoades, Stanley, & Markman, 2010). If data are MCAR, parameter estimates will not be biased as a result of the excluded cases. A complete-case analysis will, however, reduce the effective sample size, and thus, reduce statistical power.
Problems may arise when data are not MCAR and only complete cases are studied. If multiple models based on different variables are to be estimated, for example, a complete-case approach may result in different, albeit possibly overlapping, samples (e.g., Helms, Walls, Crouter, & McHale, 2010). This can make comparisons among different models difficult and statistical inference complicated if data are not MCAR. More generally, analyses based on only complete cases are not likely to generalize well to the targeted population if data are not MCAR.
Strategies have been proposed for dealing with missing data in family studies so that statistical procedures requiring complete data may be used. One approach is to conduct analyses separately for individual reporters or specific dyads, such as mother and child (e.g., Baumann, Kuhlberg, & Zayas, 2010). Research questions are then limited to relationships among measures for specific family members (e.g., mother and child), potentially neglecting important relationships between measures for key family members (e.g., mother, father and child).
Various methods have been proposed to deal with missing data in multivariate analyses. Single imputation methods, such as mean substitution in which missing values are replaced by the mean of the observed scores (e.g., Hughes & Gullone, 2010) and regression substitution in which scores predicted by the observed data replace missing values were once routinely employed. Research has shown that such methods can result in biased estimates and errors in statistical inference. Readers are referred to Schafer (1997) and Schafer and Graham (2002) for comprehensive reviews of these and similar procedures and the problems associated with them.
It is well known that advances in statistical methodology and computer software have provided alternative methods for dealing with missing data in multivariate data analysis. Multivariate analysis using FIML and multiple imputation (MI) methods that generate complete data are available through major software programs, such as SAS, and software programs for SEM, such as LISREL (Jöreskog & Sörbom, 2006) and Mplus (Muthén & Muthén, 1998-2010). FIML and MI are generally superior to single imputation methods because they provide a more appropriate representation of the data (see Little & Rubin, 2002). These methods rely on information across multiple variables in a dataset, and so they do not suffer from the limitations of ad hoc methods.
A multivariate analysis using incomplete data is commonly handled with methods that rely on FIML, a method of estimation in which a likelihood function for a model is defined by the raw data as opposed to sufficient statistics, such as the means, variances and covariances of the data. A benefit of SEM is that data need not be complete for all variables in a model if FIML is used for estimation. Using FIML in an analysis of family data, each family contributes data as available. A family may be included in an analysis, for instance, although data may be missing for one or more members (e.g., Fulkerson, Pasch, Stigler, Farbakhsh, Perry, & Komro, 2010).
MI, although not as commonly implemented in practice as FIML, is an alternative procedure for dealing with missing data. Relative to an analysis that relies on FIML, an analysis based on MI can be computationally intensive. Unlike FIML in which a single analysis is performed directly on the observed data, MI results in multiple complete data sets with the analysis carried out on each imputed data set. MI proceeds in three steps (see Allison, 2001). First, based on a set of data that includes missing values, multiple imputed data sets are generated in which missing values are replaced by random draws of scores from assumed distributions. Second, a data model is fitted separately to each imputed data set. Finally, a single set of parameter estimates is obtained by averaging estimates across the multiple sets, and standard errors are produced that take into account that the missing values were imputed. Assuming a sufficient number of imputed data sets have been generated, comparable results between MI and FIML procedures have been reported (Schafer, 1997). Oftentimes, 10 to 20 imputed datasets yield satisfactory results (see Schafer & Graham, 2002). Problems involving a high rate of missing information may, however, require additional imputations. Graham, Olchowski, and Gilreath (2007), for instance, recommend a minimum of 40 imputed datasets for problems involving data with 50% missing information.
A key advantage to using MI over the standard implementation of FIML is that MI can make use of auxiliary variables in the imputation process. Auxiliary variables, distinct from the variables that define a data model, are variables that may be correlated with variables of the data model. Auxiliary variables may help to provide needed information about the missingness or the missing data so that the missingness is then ignorable (Rubin, 1996). Daniels and Hogan (2008, Definition 5.11) refer to this as auxiliary variable MAR (or A-MAR). Using an SEM framework, Graham (2003) and Graham, Hofer, Donaldson, MacKinnon, and Schafer (1997) proposed a model in which auxiliary variables are included in a model with estimation carried out using FIML. The relationships between the auxiliary variables and those of the data model are specified so that the added variables do not impact parameters estimates of the data model other than to potentially provide information about the missingness or the relationships between variables that may have missing data, an approach that is comparable to MI. Relative to the computational burden imposed by MI methods, computing time is reduced because the method does not require the generation and subsequent analysis of multiple data sets.
While relatively more complex, models that assume that the missing data process is not ignorable may be used to incorporate into the data model a separate model for the missing data process (Little & Rubin, 2002). The two models, the data model and the missing data model, are estimated simultaneously. Modeling frameworks that assume data are NMAR and include an explicit missing data model include selection models and pattern-mixture models. In a selection model for longitudinal data, for instance, the missingness may depend on the observed or missing data up to and at the time of dropout. In a pattern-mixture model, the data depend on indicators of missing data patterns. A pattern-mixture random-effects model, for example, is a model for longitudinal data that allows for differences in longitudinal responses according to patterns of missing data (Little, 1995; see, e.g., Atkins, 2005).Many variations of a selection model and pattern-mixture model have been proposed.
Despite the availability of methods that allow for different types of missing data, challenges arise in evaluating assumptions about missing data. Although a given analysis may be appropriate when data are MAR, for instance, the assumption of MAR and its impact on parameter estimates is rarely evaluated in practice. Each of the three types of data makes a specific assumption about the relationship between the missingness and the missing data. As the missing data in an empirical study are not available, it is not ever possible to test an assumption about their relationship (Little & Rubin, 2002). Importantly, examination of the relationships between indicators of missing data and the observed study variables does not provide the evidence necessary to evaluate the relationship between the missingness and the missing data, although this approach has nevertheless been applied with conclusive remarks about the source of the missing data (see, e.g., Leung, Stewart, Wong, Ho, Fong, & Lam, 2009, p. 639). As statistical inference of a model depends in part on the assumption about the relationship between the missingness and the missing data, this presents an analytic challenge for researchers.
Sensitivity Analysis
A strategy for the problem of evaluating missing data assumptions comes from a general procedure known as sensitivity analysis. Although used for various purposes, the primary function of sensitivity analysis is to study how changes in data or a model lead to changes in a parameter estimate or statistical inference. In the context of missing data, sensitivity analysis can used to study how different assumptions about missing data may impact parameter estimates and statistical inferences (Little & Rubin, 2002). Here, sensitivity analysis is considered when fitting a model to data from an adoption study that involves missing data, where most missing data are due to missing responses for the birth father. The model is studied under different assumptions about the missing data process to see how treatments of the missing data impact the parameter estimates and statistical inferences of the specified model. It is important to note that the sensitivity analysis involves only those variables of the data model and different conclusions about sensitivity may be reached given a different model or set of variables.
The Early Growth and Development Study (EGDS)
The EGDS is a prospective adoption study designed to examine mechanisms of geneenvironment interplay in child development. A more detailed description of the study aims is provided in Leve et al. (2007). For this study, a large proportion of the families (nearly 2/3 of the sample) had missing data for the birth father. Given that birth fathers help to bring a more complete picture of a family linked through adoption, it is important to develop strategies to deal with problems relating to their missing data.
Recruitment procedure and sample
All procedures were approved by the Institutional Review Board of the institutions involved in the data collection. The recruitment procedures are detailed in Leve et al. (2007) and so are not repeated here. This study uses data collected when children were between 3-9 months old. The sample consisted of 361 families linked through adoption. Each family unit included the adopted child (207 males, 154 females), the adoptive parent(s), and the birth parent(s). At the time of this report, 34% of eligible birth fathers were participating. The mean age of children at adoption placement was 7 days (SD = 13 days). The mean ages of the birth mothers and fathers and the adoptive mothers and fathers at the birth of the child were 25.45 (SD = 7.20), 24.12 (SD = 5.89), 37.75 (SD= 5.46), and 38.39 (SD = 5.82), respectively. The median annual household income was more than $100,000 for adoptive parents and below $20,000 for the birth parents. The majority of adoptive parents (90% for adoptive fathers and 91% for adoptive mothers) were Caucasian. The birth parent sample was more ethnically diverse, with 73% and 71% Caucasian for birth fathers and mothers, respectively.
A model of openness
Based on data from a published report using this sample, a model of openness in the adoption process and post-adoption psychosocial adjustment and satisfaction for birth mothers and fathers were simultaneously studied. Similar relationships were studied in Ge et al. (2008), but the birth mother and birth father variables were tested separately. As in Ge et al., indicators of a latent measure of openness, Openness, were the measured responses by the birth mother, adoptive mother, and adoptive father, denoted by BMOpen, AMOpen and AFOpen, respectively. Birth father’s measure of openness, BFOpen, was treated as a separate predictor as it had relatively poor correlations with the other three openness measures. Birth mother and birth father adjustment and satisfaction measures were regressed on openness measures. A path diagram of the hypothesized relationships is given in Figure 1.
Figure 1.
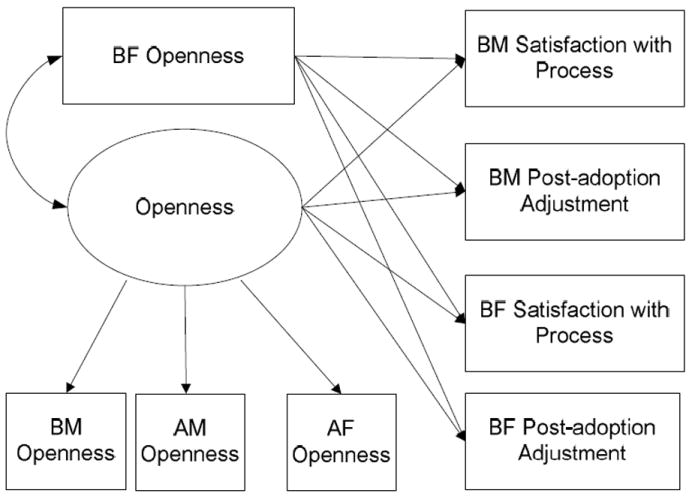
Prediction of birth parent’s adoption satisfaction and post-adoption adjustment excluding auxiliary variables.
Missing data
A total of n = 359 of the 361 yoked families had observed data for at least one of the eight variables of the model. Of these families, 93 had complete data on all eight measures, with most of the missing data due to missing reports from the birth father. There are two possible sources for the missing responses from the birth father. First, data would be missing for those birth fathers who did not participate in the study but did participate in the adoption process. In this case, data would be MAR if, for example, birth father participation was related to the observed data considered in the model, such as observed measures provided by the birth mother and adoptive parents, but independent of the missing values, such as missing measures of birth father openness, satisfaction or adjustment. Data would be NMAR if the missingness depended on the missing data, such as if birth fathers with low openness levels, low satisfaction levels, or relatively poor adjustment levels tended not to participate in the study. In this case, the missingness would depend on the missing data. Second, data would be missing for those birth fathers who did not participate in the adoption process, such as fathers who did not know about the pregnancy and so did not participate in the study. These data are not actually missing because the survey questions were not applicable to fathers who did not participate in the adoption. Although it was not known with certainty as to which of either was the source of missing data for the birth fathers, this study makes use of variables that may be related to the birth father’s participation in the adoption process, as well as the birth father variables studied in the model. These particular variables are described later.
Data analysis
The model of openness was first fitted to the data of the 93 families with complete data. Inference from this analysis may be valid if data are MCAR. While limiting an analysis to only those participants with complete data is decreasing in its application in the analysis of family data, some studies continue to rely on this approach (e.g., Meltzer & McNulty, 2010). In a second approach, the model was estimated using FIML with all 359 families contributing to the analysis assuming the data were multivariate normal and MAR. This is the standard approach taken in many multiple informant studies. A comparison of results obtained from the complete-data approach and those from FIML may provide insight into how a limited sample size may influence the parameter estimates and statistical inference or how a difference in the treatment of the source of the missing data as either MCAR or MAR may impact results.
A third approach relied on MI to generate multiple imputed data sets for analysis using the eight variables of the data model and assuming the data to be multivariate normal and MAR. Results from analyses using FIML and MI tend to provide comparable results (Allison, 2001; Schafer, 1997). Thus, estimates from this analysis were expected to agree generally with those using FIML, although some differences are to be expected given that MI is based on random draws from assumed distributions (see Allison, 2001). In a fourth approach, MI was employed using the variables of the data model in addition to a set of auxiliary variables. After generating the imputed data using the auxiliary variables, the model of openness was estimated using the imputed data. Based on recommendations in Graham, Olchowski, and Gilreath (2007), analyses using MI were based on 40 imputed data sets.
Auxiliary Variables
As the missing data problem primarily involved reports by the birth father, auxiliary variables were chosen if they had relatively little missing data and moderate to high correlations with the birth father’s observed data (specifically for the birth father variables specified in the model) or conceptually were thought to correlate with the birth fathers’ missing data or participation in the adoption process. Using these criteria, variables based primarily on reports from the birth mother, the adoptive parents, and the interviewer were selected, although a few birth father variables were also included as they had moderately strong correlations with the observed birth father variables of the data model. Variables were included to account for possible dependencies of the birth father’s participation in the adoption process on study variables, such as measures of the extent to which the adoptive parents had contact with the birth father and the birth mother’s report of how well she knew the birth father. Table 1 provides the zero-order correlations based on the observed data between the birth father variables of the data model and the selected correlates.
Table 1. Sample sizes for study and auxiliary variables and correlations between observed BF and other variables.
| Variable | N | Variable description | Correlation with BF Variable | ||
|---|---|---|---|---|---|
| BFOpen | BFSatisf | BFAdjust | |||
| BMOPEN | 356 | BM report of degree of openness | 0.33 | -0.08 | 0.09 |
| BFOPEN | 107 | BF report of degree of openness | 1.00 | 0.41 | 0.24 |
| AMOPEN | 349 | Extent to which AM believes the openness of adoption | 0.21 | -0.21 | 0.04 |
| AFOPEN | 335 | Extent to which AF believes the openness of adoption | 0.24 | -0.19 | 0.01 |
| BMSATISF | 357 | BM’s overall satisfaction with the adoption process | 0.13 | 0.59 | 0.06 |
| BMADJUST | 355 | Extent of effect on adjustment for BM | 0.16 | 0.13 | 0.29 |
| BFSATISF | 107 | BM’s overall satisfaction with the adoption process | 0.41 | 1.00 | 0.24 |
| BFADJUST | 103 | Extent of effect on adjustment for BF | 0.24 | 0.24 | 1.00 |
| A1 | 331 | Frequency of AF talking on the phone with BF (AF report) | 0.54 | 0.20 | 0.15 |
| A2 | 332 | Frequency of face-to-face contact between AF and BF (AF report) | 0.54 | 0.17 | 0.10 |
| A3 | 331 | Frequency of BF sending presents to the child (AF report) | 0.41 | 0.15 | 0.12 |
| A4 | 323 | Extent to which AF plans to talk to BF on the phone (AF report) | 0.43 | 0.10 | 0.09 |
| A5 | 333 | Extent to which AF knows about BF (AF report) | 0.43 | 0.29 | 0.01 |
| A6 | 332 | Extent to which AF had actual contact with BF (AF report) | 0.65 | 0.28 | 0.14 |
| A7 | 342 | Extent to which AM knows about BF (AM report) | 0.40 | 0.27 | 0.04 |
| A8 | 356 | Adoptive Family Composition | -0.09 | -0.47 | 0.04 |
| A9 | 99 | Interviewer report on BF’s participation in adoption decision and process | -0.41 | -0.36 | -0.23 |
| A10 | 104 | Interviewer’s impression of BF’s relationship with the adoptive family | -0.62 | -0.39 | -0.27 |
| A11 | 86 | BF’s satisfaction with the amount of contact with the adoptive families | -0.34 | -0.35 | -0.33 |
| A12 | 86 | Preferred level of adoption openness if BF could change it (BF report) | -0.15 | -0.48 | -0.31 |
| A13 | 166 | Serious mental health and behavioral problems of BF’s mother (BM report) | 0.21 | 0.40 | 0.12 |
| A14 | 286 | How well BM knows BF (BM report) | -0.37 | -0.24 | -0.35 |
| A15 | 234 | How supportive was BF of the adoption plan | 0.40 | -0.07 | 0.31 |
Notes. AF= adoptive father. AM=adoptive mother. BF=birth father. BM=birth mother. Sample sizes in the second column are for the individual variables and may not correspond to sample sizes for the reported correlations.
In a fifth approach, the data model shown in Figure 1 was extended to include the auxiliary variables listed in Table 1 to form a saturated correlates model (see Graham, 2003). In a saturated correlates model, auxiliary variables are allowed to correlate with all fully exogenous variables, the residuals of all manifest variables that are dependent variables in a model (including the residuals of indicators of latent variables) and with each other. For the model of openness, a saturated correlates model is depicted in Figure 2. As shown, BFOpen and the residuals that correspond to the three indicators of openness (BMOpen, AMOpen and AFOpen) and those that correspond to the four outcome measures of birth mother and father satisfaction and adjustment were allowed to correlate with each auxiliary variable, as denoted by the two-headed arrows between these variables. Additionally, the double-headed arrow on the auxiliary variables denotes that these variables may be correlated with each other.
Figure 2.
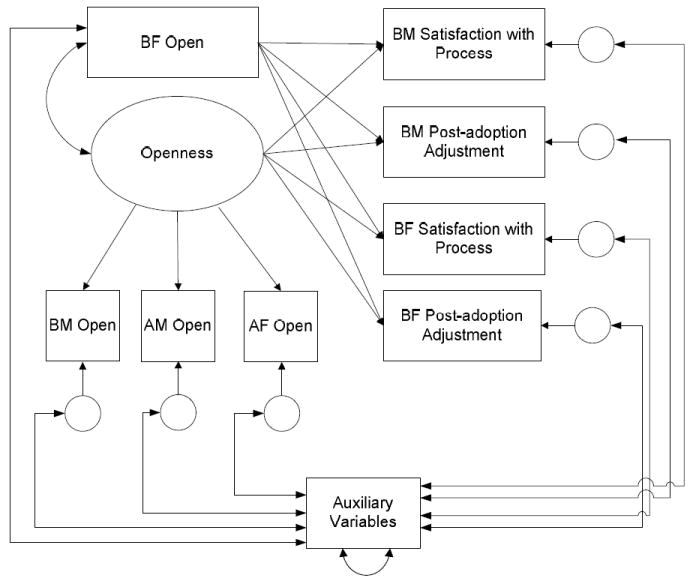
Prediction of birth parent’s adoption satisfaction and post-adoption adjustment including auxiliary variables.
Statistical Software and Estimation
Maximum likelihood (ML) estimates of a structural equation model may be obtained using sufficient statistics, such as a set of sample means and a covariance matrix generated from complete data. FIML may be implemented to obtain ML estimates by supplying raw data. SAS PROC MI may be used to implement MI and then SAS or another program may be used to fit a model to the imputed data sets. PROC MIANALYZE may be used to generate a summary of results based on an analysis of the imputed data. Beginning with LISREL version 8.5 and Mplus version 6, MI may be performed, a model fitted to the imputed data, and a single set of parameter estimates with adjusted standard errors obtained across the multiple sets of results. Here, SAS PROC MI was used to generate the imputed data sets, and Mplus was used to fit the model to the imputed data and obtain parameter estimates.
Results
ML estimates with robust standard errors and 95% confidence intervals (CI) are provided in Table 2. Overall, the estimates, standard errors and statistical inferences drawn from the interval estimates were comparable within missing data methods, such as those results produced by MI and FIML when auxiliary variables were not included in the analysis and by MI and FIML when these variables were not included in the analysis. These findings are consistent with other reports (Schafer, 1997; Graham, 2003).
Table 2. Maximum Likelihood Estimates of the Openness Model using Different Missing Data Methods.
| Effect | Complete dataa | FIMLbc | MIbc | MIbd | FIMLbd |
|---|---|---|---|---|---|
|
| |||||
| Openness on BMOpen | 1.00* | 1.00* | 1.00* | 1.00* | 1.00* |
|
| |||||
| Openness on AMOpen | 1.24 (0.11) | 1.14 (0.06) | 1.13 (0.06) | 1.14 (0.06) | 1.14 (0.06) |
| (1.02, 1.46) | (1.03, 1.25) | (1.01, 1.25) | (1.02, 1.26) | (1.03, 1.25) | |
|
| |||||
| Openness on AFOpen | 1.16 (0.11) | 1.09 (0.06) | 1.08 (0.06) | 1.08 (0.06) | 1.09 (0.06) |
| (0.94, 1.38) | (0.98, 1.20) | (0.97, 1.19) | (0.97, 1.19) | (0.97, 1.20) | |
|
| |||||
| Openness on BMSatis | -0.12 (0.29) | 0.28 (0.17) | 0.29 (0.15) | 0.31(0.15) | 0.32 (0.15) |
| (-0.69, 0.44) | (-0.04, 0.61) | (-0.01, 0.59) | (0.01, 0.60) | (0.02, 0.62) | |
|
| |||||
| Openness on BMAdjust | 1.37 (0.70) | 0.80 (0.36) | 0.78 (0.35) | 0.88 (0.34) | 0.87 (0.34) |
| (-.01, 2.74) | (0.11, 1.50) | (0.09, 1.47) | (0.21, 1.55) | (0.20, 1.54) | |
|
| |||||
| BFOpen on BMSatis | 0.17 (0.18) | 0.22 (0.17) | 0.18 (0.16) | 0.16 (0.13) | 0.16 (0.16) |
| (-0.19, 0.52) | (-0.12, 0.55) | (-0.15, 0.50) | (-0.09, 0.40) | (-0.15, 0.46) | |
|
| |||||
| BFOpen on BMAdjust | 0.61 (0.43) | 0.42 (0.37) | 0.47 (0.31) | 0.27 (0.29) | 0.29 (0.31) |
| (-0.23, 1.45) | (-0.30, 1.13) | (-0.14, 1.08) | (-0.31, 0.84) | (-0.33, 0.90) | |
|
| |||||
| Openness on BFSatisf | -1.12 (0.31) | -0.84 (0.26) | -0.84 (0.28) | -0.89 (0.32) | -0.82(0.30) |
| (-1.73, -0.50) | (-1.36, -0.33) | (-1.38, -0.30) | (-1.52, -0.26) | (-1.40, -0.23) | |
|
| |||||
| Openness on BFAdjust | 0.03 (0.63) | -0.17 (0.57) | -0.11 (0.59) | -0.16 (0.66) | -0.24 (0.63) |
| (-1.21, 1.27) | (-1.29, 0.95) | (-1.25, 1.04) | (-1.46, 1.13) | (-1.47, 1.00) | |
|
| |||||
| BFOpen on BFSatisf | 1.01 (0.19) | 1.07 (0.22) | 1.02 (0.20) | 1.18 (0.19) | 1.20 (0.26) |
| (-0.19, 0.52) | (0.65, 1.49) | (0.62, 1.42) | (0.81, 1.55) | (0.69, 1.72) | |
|
| |||||
| BFOpen on BFAdjust | 0.96 (0.40) | 0.93 (0.31) | 0.85 (0.35) | 1.18 (0.42) | 1.11 (0.34) |
| (0.18, 1.74) | (0.31, 1.54) | (0.16, 1.54) | (0.36, 2.00) | (0.45, 1.78) | |
Notes: Robust standard errors for maximum likelihood estimates are in parentheses following the estimates. Estimated 95% confidence intervals appear directly below and assume normality.
Factor loading was set equal to 1.
n = 93;
n= 359;
model excludes auxiliary variables.
model includes auxiliary variables.
A sensitivity analysis was conducted by comparing the estimates and their standard errors, as well as the statistical inferences that may be drawn from each model using a significance level of .05. A comparison of estimates relating to the measurement model for Openness showed the greatest differences between the results based on data for families with complete data and the remaining four sets of results regardless of whether auxiliary variables were included in the analysis or not. The estimated loadings and their standard errors were slightly larger when only the complete data were considered. These differences may reflect the impact of the reduced sample size when using only complete cases. These differences may also suggest a sensitivity of estimates to the treatment of the data as MCAR versus MAR but not MAR versus NMAR given that the estimates and standard errors, as well as the statistical inferences were comparable across the four models that relax the assumption of MCAR but differed slightly from the results produced by the complete-case analysis that assumes MCAR.
A comparison of estimates for the regression of birth mother’s satisfaction and adjustment, BMSatisf and BMAdjust, respectively, on Openness and BFOpen suggested differences between the analysis based on complete data only, the analyses that excluded auxiliary variables, and the analyses that included auxiliary variables. Relative to the results produced by the methods that made use of all available data, the effect of Openness on BMSatis was opposite in sign, and the effect of Openness on BMAdjust was nearly double in size, as were the standard errors of both of these effects. Neither effect from the complete data analysis was statistically significant. Differences were also notable between results based on methods that involved auxiliary variables and those that did not. In particular, the 95% confidence intervals (CI) for the effect of Openness on BMSatis included zero when the data were assumed to be MAR and auxiliary variables were excluded from the analysis and did not include zero when the data were assumed to be NMAR and auxiliary variables were included (albeit the lower bound value of the intervals based on the models that included auxiliary variables were close to zero). These results may suggest a sensitivity of statistical inference involving these effects to these particular assumptions made about the missing data. The estimated effects and standard errors for the regressions of BMSatis and BMAdjust on BFOpen were relatively more comparable across methods and none were statistically significant. Thus, these results do not seem to suggest a sensitivity of statistical inference for these effects to these particular assumptions made about the missing data.
Across all methods, the estimated confidence intervals did not suggest a relationship between Open and the two birth father outcomes, BFSatis and BFAdjust, suggesting that statistical inference of these effects was not sensitive to the assumptions made about the missing data. The estimated effect of BFOpen on BFSatis was not statistically significant when only the complete data were analyzed but was statistically significant under all other data treatments, possibly suggesting an effect of the reduced sample size or a sensitivity of statistical inference to the assumptions made about the missing data. Also concerning the estimated effect of BFOpen on BFSatis, the estimated effect was somewhat larger when the auxiliary variables were included in the analysis relative to when the auxiliary variables were excluded, suggesting a sensitivity of the estimated effect to the assumption that data were MAR versus NMAR. The estimated effect of BFOpen on BFAdjust was also somewhat larger when the auxiliary variables were included in the analysis relative to when the auxiliary variables were excluded, suggesting a sensitivity of the estimated effect to the assumption that data were MAR versus NMAR.
Discussion
A major source of missing data in multiple informant studies is that due to individual members who do not participate in a study, such as a father in a family study. Many of the approaches still in use to deal with the loss of data, however, can result in a loss of information from particular individuals or a loss in the total sample size, such as in a family study that relies on only complete data and excludes all families with missing data. Ad hoc methods developed to circumvent these problems, such as mean substitution, can result in biased parameter estimates and standard errors.
Multivariate statistical procedures developed to handle missing data are superior to ad hoc methods and are available through many commercial statistical software programs and specialized programs for estimation of structural equation models. Among the methods now often considered in the estimation of multivariate models are those based on SEM using FIML. The advantage of using SEM with FIML is that data need not be complete for each unit of analysis (e.g., family). Not as widely used are MI procedures in which missing values are imputed through a process that generates multiple imputed data sets. In either approach, data are required to be MCAR or MAR for valid statistical inference.
When data are NMAR, information about the missing data process should be incorporated into an analysis to avoid biased parameter estimates (Little & Rubin, 2002). Strategies for dealing with data that are NMAR may rely on known analytic procedures, including mean and covariance structure analysis, but may also include a model for the missingness. Major frameworks in this area include selection models and pattern-mixture models (Demirtas & Schafer, 2003; Kenward, 1998; Little, 1995; Xu & Blozis, 2010). A major complication in the estimation of NMAR models concerns the identification of parameters that correspondence to the dependence of the missingness on the missing data (Little & Rubin, 2002).These models also require that a model for the missing data process be explicitly defined, an added challenge as the process that generated the missing data in a given problem is not likely to be known.
One approach developed to address these challenges is one in which variables that are correlated with the missingness or the missing data are included in an analysis (Ibrahim, Lipsitz, & Horton, 2001). Specifically, a model is specified that allows for associations between variables of a data model and correlates of the missingness or missing data. When these correlates are included in an analysis, the data are A-MAR (Daniels & Hogan, 2008, Definition 5.11). Under A-MAR, the data are MAR under the condition that the missingness is no longer dependent on the missing data after accounting for dependencies of the missingness on the observed data, any covariates, and the auxiliary variables. In this way, the source of the missing data may be ignorable (Ibrahim, Lipsitz, & Horton, 2001). Essentially, auxiliary variables help by providing important information about the relationships among variables that have missing data. In the case of multiple informant data, information provided by informants with complete data may also help, similar to auxiliary variables, in providing the needed information for about the data that are missing for other informants. In any case, the specific reasons for the missing data need not be known and the auxiliary variables need not correlate with the missingness (Collins, Schafer, & Kam, 2001).
An important aspect of using auxiliary variables is that variables that are correlated with the missingness or missing data may provide the needed information so that an explicit model for the missing data process need not be incorporated into the data model (Ibrahim, Lipsitz, & Horton, 2001). Auxiliary variables may be used in MI procedures and in SEM in what are called added-variables models (Graham, 2003; Graham, Hofer, Donaldson, MacKinnon, & Schafer, 1997). Under a saturated correlates model, for instance, the relationships between auxiliary variables and the variables of the data model are specified such that the data model retains its hypothesized structure. Thus, a saturated correlates model is a viable alternative to MI methods because it does not require the creation of multiple data sets but does take advantage of the added information that may be provided by auxiliary variables.
Given that assumptions of missing data that explicitly involve the missing data cannot be empirically tested, a sensitivity analysis of parameter estimates and statistical inference to missing data assumptions is a recommended strategy for understanding a missing data process. Here, a model of openness in an adoption process was studied under different assumptions about the missing data. This analysis extends previous consideration of these data (see Ge et al., 2008) to address a major problem of missing data for the birth father. For the adoption data, some of the parameter estimates and statistical conclusions drawn from the results were sensitive to the assumptions made about the missing data, suggesting that for some of the effects, it may not be reasonable to assume the data were MAR. Although it is not possible to know which set of results best represents the true parameter values, the sensitivity analysis did suggest that the results were in some cases dependent on the assumptions made about the missing data and that the missingness may need to be taken into account in drawing inferences from the data. Finally, although the auxiliary variables used in the current analysis were thoughtfully selected, the findings reported here may be sensitive to the particular auxiliary variables used and a different set may have produced different results.
Advances in missing data methods make it possible to plan for missing data. In planning studies, it may be helpful to identify in advance variables that may be correlated with variables that may be anticipated to have missing data or to be related to the likeliness that an individual will participate in a study. In this way, correlates of the missingness or missing data may be used in a statistical analysis as a means of addressing data that may be NMAR. It is not essential to know the causes of the missing data. Rather, it may be sufficient to identify correlates of the missingness or missing data and include them in a data analysis (Collins et al, 2001). A sensitivity analysis may then be conducted using FIML or MI with and without auxiliary variables. Differences in estimates or statistical conclusions across methods might suggest data are sensitivity to assumptions about missing data and that auxiliary variables may be needed to make valid statistical inference. Such analyses may also help researchers to better understand the possible sources and mechanisms underlying missing data.
Acknowledgments
This project was supported by grant R01 HD042608 from the National Institute of Child Health and Human Development and the National Institute on Drug Abuse, NIH, U.S. PHS (PI Years 1–5: David Reiss, MD; PI Years 6–10: Leslie Leve, PhD). The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver National Institute of Child Health and Human Development or the National Institutes of Health.
References
- Allison PD. Missing data. Thousand Oaks, CA: Sage; 2001. [Google Scholar]
- Atkins DC. Using multilevel models to analyze couple and family treatment data: Basic and advanced issues. Journal of Family Psychology. 2005;19:98–110. doi: 10.1037/0893-3200.19.1.98. [DOI] [PubMed] [Google Scholar]
- Baumann AA, Kuhlberg JA, Zayas LH. Familism, mother-daughter mutuality, and suicide attempts of adolescent Latinas. Journal of Family Psychology. 2010;24:616–624. doi: 10.1037/a0020584. [DOI] [PubMed] [Google Scholar]
- Collins LM, Schafer JL, Kam CM. A comparison of inclusive and restrictive strategies in modern missing data procedures. Psychological Methods. 2001;6:330–351. [PubMed] [Google Scholar]
- Cui M, Durtschi JA, Donnellan MB, Lorenz FO, Conger RD. Intergenerational transmission of relationship aggression: A prospective longitudinal study. Journal of Family Psychology. 2010;24:688–697. doi: 10.1037/a0021675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniels MJ, Hogan JW. Missing data in longitudinal studies: Strategies for Bayesian modeling and sensitivity analysis. Chapman & Hall/CRC; 2008. [Google Scholar]
- Demirtas H, Schafer JL. On the performance of random-coefficient pattern-mixture models for non-ignorable dropout. Statistics in Medicine. 2003;22:2553–2575. doi: 10.1002/sim.1475. [DOI] [PubMed] [Google Scholar]
- Fulkerson JA, Pasch KE, Stigler MH, Farbakhsh, Perry CL, Komro KA. Longitudinal associations between family dinner and adolescent perceptions of parent-child communication among racially diverse urban youth. Journal of Family Psychology. 2010;24:261–270. doi: 10.1037/a0019311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge X, Natsuaki MN, Martin DM, Leve LD, Neiderhiser JM, Shaw DS, et al. Bridging the divide: Openness in adoption and postadoption psychosocial adjustment among birth and adoptive parents. Journal of Family Psychology. 2008;22:529–540. doi: 10.1037/a0012817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham JW. Adding missing-data-relevant variables to FIML-based structural equation models. Structural Equation Modeling. 2003;10:80–100. [Google Scholar]
- Graham JW, Hofer SM, Donaldson SI, MacKinnon DP, Schafer JL. Analysis with missing data in prevention research. In: Bryant K, Windle M, West S, editors. The science of prevention: Methodological advances from alcohol and substance abuse research. Washington, DC: American Psychological Association; 1997. pp. 325–366. [Google Scholar]
- Graham JW, Olchowski AE, Gilreath TD. How many imputations are really needed? Some practical clarifications of multiple imputation theory. Preventative Science. 2007;8:208–213. doi: 10.1007/s11121-007-0070-9. [DOI] [PubMed] [Google Scholar]
- Graham JW, Taylor BJ, Olchowski AE, Cumsille PE. Planned missing data designs in psychological research. Psychological Methods. 2006;11:323–343. doi: 10.1037/1082-989X.11.4.323. [DOI] [PubMed] [Google Scholar]
- Helms HM, Walls JK, Crouter AC, McHale SM. Provide role attitudes, marital satisfaction, role overload, and housework: A dyadic approach. Journal of Family Psychology. 2010;24:568–577. doi: 10.1037/a0020637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes EK, Gullone E. Reciprocal relationships between parent and adolescent internalizing symptoms. Journal of Family Psychology. 2010;24:115–124. doi: 10.1037/a0018788. [DOI] [PubMed] [Google Scholar]
- Ibrahim JG, Lipsitz SR, Horton N. Using auxiliary data for parameter estimation with non-ignorably missing outcomes. Applied Statistics. 2001;50:361–373. [Google Scholar]
- Jöreskog KG, Sörbom D. LISREL 8.8 for Windows [Computer software] Lincolnwood, IL: Scientific Software International, Inc.; 2006. [Google Scholar]
- Kazak A, Segal-Andrews A, Johnson K. The role of families and other systems in pediatric psychology research and practice. In: Roberts M, editor. Handbook of pediatric psychology. 2. New York: Guilford; 1995. pp. 84–104. [Google Scholar]
- Kenny DA, Ledermann T. Detecting, measuring, and testing dyadic patterns in the actor-partner interdependence model. Journal of Family Psychology. 2010;24:359–366. doi: 10.1037/a0019651. [DOI] [PubMed] [Google Scholar]
- Kenward MG. Selection models for repeated measurements for nonrandom dropout: An illustration of sensitivity. Statistics in Medicine. 1998;17:2723–2732. doi: 10.1002/(sici)1097-0258(19981215)17:23<2723::aid-sim38>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Leung SSK, Stewart SM, Wong JPS, Ho DSY, Fong DYT, Lam TH. The association between adolescents’ depressive symptoms, maternal negative affect, and family relationships in Hong Kong: Cross-sectional and longitudinal findings. Journal of Family Psychology. 2009;23:636–645. doi: 10.1037/a0016379. [DOI] [PubMed] [Google Scholar]
- Leve LD, Neiderhiser JM, Ge X, Scaramella L, Conger RD, Reid JB, et al. The Early Growth and Development Study: A prospective adoption design. Twin Research and Human Genetics. 2007;10:84–95. doi: 10.1375/twin.10.1.84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little RJA. Modeling the dropout mechanism in repeated-measures studies. Journal of the American Statistical Association. 1995;90:1112–1121. [Google Scholar]
- Little RJA, Rubin DB. Statistical analysis with missing data. 2. New York: Wiley; 2002. [Google Scholar]
- Meltzer AL, McNulty JK. Body image and marital satisfaction: Evidence for the mediating role of sexual frequency and sexual satisfaction. Journal of Family Psychology. 2010;24:156–164. doi: 10.1037/a0019063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. 6. Los Angeles, CA: Muthén & Muthén; 1998-2010. [Google Scholar]
- Phares V. Where’s Poppa? The relative lack of attention to the role of fathers in child and adolescent psychopathology. American Psychologist. 1992;47:656–664. doi: 10.1037//0003-066x.47.5.656. [DOI] [PubMed] [Google Scholar]
- Rhoades GK, Stanley SM, Markman HJ. Should I stay or should I go? Predicting dating relationship stability from four aspects of commitment. Journal of Family Psychology. 2010;24:543–550. doi: 10.1037/a0021008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB. Multiple imputation after 18+ years. Journal of the American Statistical Association. 1996;91:473–489. [Google Scholar]
- Schafer JL. Analysis of incomplete multivariate data. London: Chapman & Hall; 1997. [Google Scholar]
- Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychological Methods. 2002;7:147–177. [PubMed] [Google Scholar]
- Xu S, Blozis SA. Sensitivity Analysis of a Mixed Model for Incomplete Longitudinal Data. Journal of Educational and Behavioral Statistics. 2010 Dec 16; doi: 10.3102/1076998610375836. [DOI] [Google Scholar]


