Simultaneous and Consistent Labeling of Longitudinal Dynamic Developing Cortical Surfaces in Infants

Abstract

The human cerebral cortex develops extremely dynamically in the first two years of life. Accurate and consistent parcellation of longitudinal dynamic cortical surfaces during this critical stage is essential to understand the early development of cortical structure and function in both normal and high-risk infant brains. However, directly applying the existing methods developed for the cross-sectional studies often generates longitudinally-inconsistent results, thus leading to inaccurate measurements of the cortex development. In this paper, we propose a new method for accurate, consistent, and simultaneous labeling of longitudinal cortical surfaces in the serial infant brain MR images. The proposed method is explicitly formulated as a minimization problem with an energy function that includes a data fitting term, a spatial smoothness term, and a temporal consistency term. Specifically, inspired by multi-atlas based label fusion, the data fitting term is designed to integrate the contributions from multi-atlas surfaces adaptively, according to the similarities of their local cortical folding with that of the subject cortical surface. The spatial smoothness term is then designed to adaptively encourage label smoothness based on the local cortical folding geometries, i.e. allowing label discontinuity at sulcal bottoms (which often are the boundaries of cytoarchitecturally and functionally distinct regions). The temporal consistency term is to adaptively encourage the label consistency among the temporally-corresponding vertices, based on their similarity of local cortical folding. Finally, the entire energy function is efficiently minimized by a graph cuts method. The proposed method has been applied to the parcellation of longitudinal cortical surfaces of 13 healthy infants, each with 6 serial MRI scans acquired at 0, 3, 6, 9, 12 and 18 months of age. Qualitative and quantitative evaluations demonstrated both accuracy and longitudinal consistency of the proposed method. By using our method, for the first time, we reveal several hitherto unseen properties of the dynamic and regionally heterogeneous development of the cortical surface area in the first 18 months of life.

1. Introduction

The human cerebral cortex develops dynamically in both structure and function in first years of life (Lyall et al., 2014; Nie et al., 2013a; Nie et al., 2012). At term birth, all primary and secondary cortical folding are present (Hill et al., 2010), resembling the morphology of the adult brain, and are then well preserved during the dynamic postnatal cortex development (Li et al., 2013a). For example, in the first year of life, the cortical gray matter volume doubles (Gilmore et al., 2012) and the cortical surface area expands 1.8 times (Li et al., 2013a). Increasing evidences suggest that many neurodevelopmental disorders are likely the results of abnormal development in this critical stage of rapid cortex growth (Gilmore et al., 2012; Lyall et al., 2014). Thus, studying the dynamic cortex development during this stage using MR images would greatly increase our limited knowledge on normal early brain development and also provide important insights into neurodevelopmental disorders (Gilmore et al., 2012; Li et al., 2014c; Lyall et al., 2014).

Cortical surface-based analysis is particularly suitable for studying the dynamic development of the highly-folded and thin cortex, as these methods respect the topology of the cortex and facilitate the alignment, analysis, functional mapping and visualization of buried sulcal regions (Dale et al., 1999; Van Essen et al., 2001). Moreover, cortical surface-based measurements, such as the surface area, cortical thickness, sulcal depth, cortical folding, and cortical gyrification, provide a very detailed picture on how the cortex develops (Li et al., 2014a). Parcellation of cortical surfaces into a set of Regions of Interest (ROIs) is of fundamental importance in localizing structural/functional regions and mapping regional cortex development. However, manual parcellation of the highly-folded cortical surface is extremely tedious, time-consuming, and subject to inter-rater variation. Accordingly, many methods have been proposed for cortical surface parcellation in the cross-sectional adult studies, based on the sulcal-gyral folding geometries from structural MR images (Cachia et al., 2003; Desikan et al., 2006; Destrieux et al., 2010; Fischl et al., 2004; Hu et al., 2010; Joshi et al., 2012; Klein and Hirsch, 2005; Klein and Tourville, 2012; Li et al., 2009; Li et al., 2013c; Liu et al., 2004; Lohmann and von Cramon, 2000; Nie et al., 2007; Rettmann et al., 2002; Shi et al., 2013; Van Essen et al., 2012; Wan et al., 2008; Yang and Kruggel, 2008; Yeo et al., 2008; Zhang et al., 2010).

Recently, longitudinal neuroimaging studies of the dynamic brain development in the first years of life have received increasing attention (Almli et al., 2007; Fan et al., 2011; Gilmore et al., 2012; Li et al., 2013a; Li et al., 2014b; Nie et al., 2013b; Shi et al., 2010; Shi et al., 2011). Because these longitudinal studies can uniquely capture the dynamic developmental trajectory of each individual and are also less influenced by the confounding effects of inter-subject variation, compared with the cross-sectional studies (Bernal-Rusiel et al., 2012; Li et al., 2014a). Due to the highly convoluted and variable cortical folding (Li et al., 2010b; Nie et al., 2010; Zhang et al., 2009), cortical surface parcellation often involves the highly complex nonlinear optimization, thus subtle changes of the cortical folding could lead to significantly different parcellation results. Hence, applying existing cross-sectional methods to each longitudinal infant cortical surface independently is likely to generate the longitudinally-inconsistent surface parcellation, especially for those small-sized cortical regions and ambiguous cortical regions. This will eventually lead to inaccurate measurements of longitudinal cortex development in infants. Therefore, a method for accurate and consistent parcellation of longitudinal dynamic infant cortical surfaces is essential to understand the early brain development in both healthy and high-risk infant populations.

To ensure the longitudinal consistency of cortical surface parcellation, one can first parcellate the cortical surface of a selected time point (e.g., typically the first or the last time point) by using an existing cross-sectional method, and then propagate its parcellation result onto the cortical surfaces of other time points. However, this type of parcellation results would be biased by the selected time point, in addition to the propagation of potential labeling errors. Accordingly, efforts have been made recently towards unbiased and temporally consistent parcellation of longitudinal cortical surfaces from adult serial MR images (Reuter et al., 2012). For example, in the longitudinal pipeline of FreeSurfer (Reuter et al., 2012), a within-subject template is first built by rigidly aligning all longitudinal images of a subject to its median time-point image. Then the cortical surfaces of the within-subject template are reconstructed and parcellated using the conventional cross-sectional method (Fischl et al., 2004). Next, the parcellated cortical surfaces of the within-subject template are rigidly transformed back to the space of each longitudinal image as the initialization. Finally, the initialized cortical surface parcellation is further refined independently for each time point to achieve the longitudinal consistency (Reuter et al., 2012). Although this independent refinement of each longitudinal surface might be suitable for the adult brains with small longitudinal changes (Reuter et al., 2012), it becomes problematic when applied to the infant brains with dynamic longitudinal development.

In this paper, we present a new method for accurate, consistent, and simultaneous parcellation of longitudinal dynamic cortical surfaces from serial infant brain MR images. The proposed method is explicitly formulated as a minimization problem of an energy function, which includes a data fitting term, a spatial smoothness term, and a temporal consistency term. Inspired by the recent success of multi-atlas based labeling, the data fitting term is designed to integrate the contributions from multiple atlas surfaces adaptively, according to the similarities of their local cortical folding with that of the subject cortical surface. The spatial smoothness term is designed to adaptively encourage the label smoothness based on the local cortical folding geometries. The temporal consistency term is further designed to adaptively encourage longitudinal label consistency based on the temporal similarities of local cortical folding. The energy function is efficiently minimized by the alpha-expansion graph cuts method (Boykov and Kolmogorov, 2004). In our method, all longitudinal cortical surfaces of the same infant are treated equally and labeled jointly, thus the longitudinal surface parcellation results are unbiased (not dominated by any specific time-point). Since adaptive temporal constraints are imposed in our method, the longitudinal surface parcellation results are temporally consistent, with no temporally-unrealistic (bumpy) changes. The proposed method has been applied to label the longitudinal cortical surfaces of 13 healthy infants, each with 6 serial MRI scans at 0, 3, 6, 9, 12 and 18 months of age. Both qualitative and quantitative evaluation results demonstrate the accuracy and consistency of the proposed method.

A preliminary version of this work was presented at the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) (Li et al., 2013b). This paper significantly extends the preliminary version with more details on introduction of methodology and also more extensive validations and discussions. Moreover, by using the proposed method, this paper presents several hitherto unseen properties of the dynamic, age-related, and regionally heterogeneous development of the cortical surface area in the first 18 months of life.

2. Materials and Methods

2.1 Subjects and MR Image Acquisition

This study was approved by the Institutional Review Board of the University of North Carolina (UNC) School of Medicine. Pregnant mothers were recruited during the second trimester of pregnancy from the UNC hospitals. Informed consent was obtained from both parents. Exclusion criteria included abnormalities on fetal ultrasound, or major medical or psychotic illness in the mother. Infants in the study cohort were free of congenital anomalies, metabolic disease, and focal lesions. No sedation was employed and all infants were imaged during natural sleep. A physician or nurse was present during each scan, and a pulse oximeter was used to monitor heart rate and oxygen saturation. More information on subjects can be found in (Li et al., 2014a; Nie et al., 2012; Wang et al., 2012b). Each infant was planned to be scanned every 3 months from birth till year 1 and again at 18 months. 13 healthy infants (9 males/4 females), each with 6 serial MRI scans (acquired at 2 weeks, 3, 6, 9, 12 and 18 months of age, respectively), were used in this study.

Serial T1-, T2-, and diffusion-weighted MR images of each infant were acquired using a Siemens 3T head-only MR scanner with a 32 channel head coil. T1 images (144 sagittal slices) were acquired with the following imaging parameters: TR = 1900 ms, TE = 4.38 ms, flip angle = 7, acquisition matrix = 256 × 192, and voxel resolution = 1 × 1 × 1 mm³. T2 images (64 axial slices) were acquired with the imaging parameters: TR/TE = 7380/119 ms, flip angle = 150, acquisition matrix = 256 × 128, and voxel resolution =1.25 × 1.25 × 1.95 mm³. Diffusion-weighted images (DWI) (60 axial slices) were acquired with the parameters: TR/TE = 7680/82 ms, acquisition matrix = 128 × 96, voxel resolution = 2 × 2 × 2mm³, 42 non-collinear diffusion gradients, and diffusion weighting b =1000s/mm². More information on image acquisition can be found in (Nie et al., 2012; Wang et al., 2012b).

2.2 Image Preprocessing

Distortion correction of DWI was performed and the respective fractional anisotropy (FA) images were then computed (Wang et al., 2012b; Yap et al., 2011). T2 and FA images were rigidly aligned onto their T1 image and further resampled to 1 × 1 × 1 mm³ using FLIRT in FSL (Smith et al., 2004). For each set of aligned T1, T2, and FA images, non-cerebral tissues, such as the skull, brain stem and cerebellum, were removed. Specifically, the skull was removed by an infant-specific learning-based method (Shi et al., 2012). The brain stem and cerebellum were removed by propagation of their masks from the atlas images to the subject image by using in-house developed registration methods (Shen and Davatzikos, 2002; Wu et al., 2006; Xue et al., 2006; Zacharaki et al., 2008). Intensity inhomogeneity correction was performed by N3 (Sled et al., 1998). All longitudinal images of the same infant were then rigidly aligned using FLIRT in FSL (Smith et al., 2004). Longitudinally-consistent tissue segmentation was performed by an infant-specific 4D level-set method (Wang et al., 2014a; Wang et al., 2011; Wang et al., 2012b). It integrates the prior information from infant brain atlases built by groupwise registration (Jia et al., 2010; Tang et al., 2009), the longitudinal information by 4D image registration (Shen and Davatzikos, 2004) and also the complementary information from T1, T2 and FA images. After tissue segmentation, non-cortical structures were masked and filled, and each brain was separated into left and right hemispheres (Li et al., 2013a; Li et al., 2014b).

2.3 Cortical Surface Reconstruction and Registration

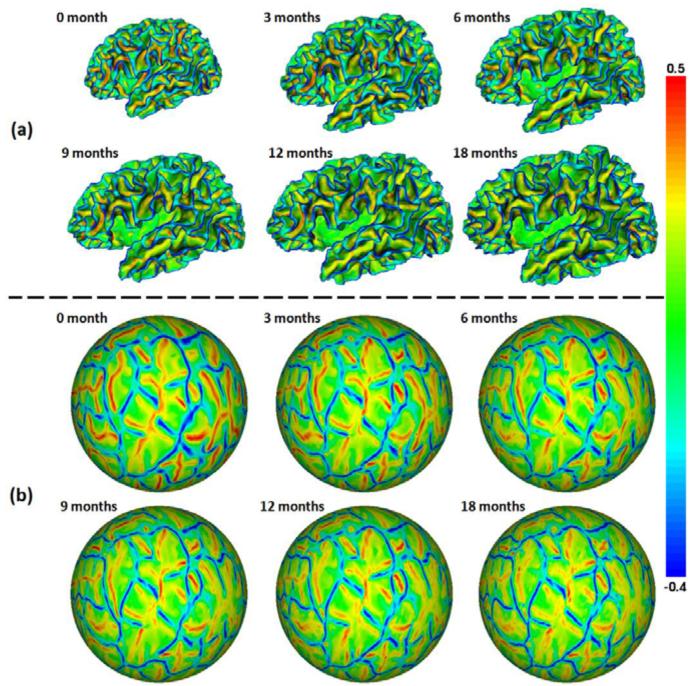
Based on the tissue segmentation results, the inner cortical surface (the interface between white matter (WM) and gray matter (GM)) of each hemisphere was reconstructed by tessellating the topology-corrected WM as a triangular mesh (Li et al., 2013a; Li et al., 2012). The inner cortical surface was then deformed by preserving its initial topology for reconstruction of the central and outer cortical surfaces (Li et al., 2012). The inner cortical surface was further inflated and mapped to a standard sphere by minimizing the metric distortion between the original surface and its spherical representation (Fischl et al., 1999). For each hemisphere, all longitudinal cortical surfaces of the same infant were group-wisely aligned to establish the within-subject longitudinal correspondences by using Spherical Demons (Yeo et al., 2010), based on their cortical folding patterns. Fig. 1(a) shows the longitudinal inner surfaces of the left hemisphere of a representative infant, color-coded by the mean curvatures. Fig. 1(b) shows the group-wisely aligned longitudinal spherical surfaces of the left hemisphere of the infant, again color-coded by the mean curvatures. As can be seen, all primary and secondary cortical folding are well established at term birth. Moreover, primary and secondary cortical folding is quite stable during the dynamic postnatal cortex development, and thus is well aligned by the group-wise surface registration.

Fig. 1.

(a) Longitudinal inner cortical surfaces of the left hemisphere of a representative infant from 0 to 18 months of age, color-coded by the mean curvatures. (b) Group-wisely aligned longitudinal spherical surfaces of the left hemisphere of the infant, color-coded again by the mean curvatures. Red colors indicate sulci, and blue colors indicate gyri.

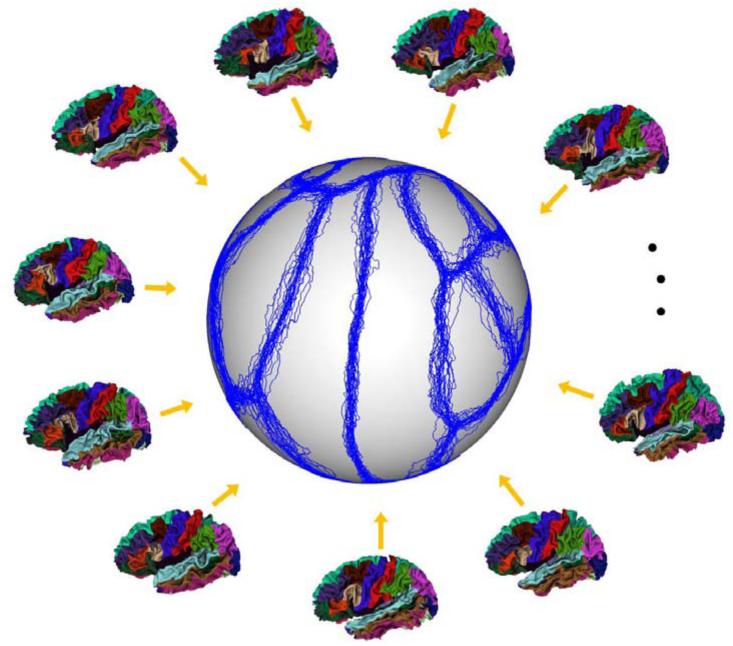
We adopted our multi-atlas surfaces from the publically available 39 cortical surfaces with manual parcellation based on sulcal bottoms by experts (Desikan et al., 2006; Yeo et al., 2010). This dataset has been used for training the classifiers for cortical surface parcellation in FreeSurfer (Fischl, 2012). In these atlases, cortical surfaces were reconstructed by using FreeSurfer (Fischl, 2012), and each cortical surface was labeled as 35 ROIs, with the structures listed in Table 1. More information on image acquisition, image processing, and demographics can be found in (Desikan et al., 2006; Yeo et al., 2010). To align all these atlas surfaces to a subject surface, one strategy is to perform pairwise registration between each atlas surface and the subject surface. However, this strategy is computationally expensive, as for each subject surface we have to repeat this procedure. Herein, we adopted another efficient strategy. First, we groupwisely aligned all atlas surfaces by using Spherical Demons (Yeo et al., 2010). Fig. 2 shows the exemplars of atlas surfaces manually labeled by experts and also the aligned boundaries (blue curves) of their labeled ROIs after group-wise spherical registration of atlas surfaces, overlaid on the standard spherical surface. As can be seen, most of the boundaries of ROIs in atlas surfaces are approximately aligned together, indicating reasonable group-wise registration results. Then, each longitudinal surface of an infant was aligned with the group-wisely aligned atlas surfaces based on their group-mean and variations of cortical folding geometries by using Spherical Demons (Yeo et al., 2010). Finally, the deformation field from each atlas surface to each subject surface was computed by concatenating the deformation field from this atlas surface to its group-wisely aligned atlas surface and that from its group-wisely aligned atlas surface to the subject surface. Accordingly, each atlas surface can be warped onto each subject surface. Note that the group-wise registration of all atlas surfaces was performed only for one time, and then used for all subjects. Note, this is computationally much more efficient than the conventional way of pair-wisely registering each atlas surface with each longitudinal surface of a subject. On the other hand, due to the considerable inter-subject variability of the cortical folding and also the regularization constraints imposed in the surface registration method, a subject surface and each warped atlas surface might not reach the best matching of their local cortical folding. This issue will be taken care in our longitudinal surface parcellation method, which will be introduced in Section 2.4.

Table 1.

List of structures on the cortical surface atlases.

1. Sylvian fissure/unknown	2. Banks of superior temporal sulcus	3. Caudal anterior cingulate cortex
4. Caudal middle frontal gyrus	5. Corpus callosum	6. Cuneus cortex
7. Entorhinal cortex	8. Fusiform gyrus	9. Inferior parietal cortex
10. Inferior temporal gyrus	11. Isthmus cingulate cortex	12. Lateral occipital cortex
13. Lateral orbital frontal cortex	14. Lingual gyrus	15. Medial orbital frontal cortex
16. Middle temporal gyrus	17. Parahippocampal gyrus	18. Paracentral lobule
19. Pars opercularis	20. Pars orbitalis	21. Pars triangularis
22. Pericalcarine cortex	23. Postcentral gyrus	24. Posterior cingulate cortex
25. Precentral gyrus	26. Precuneus cortex	27. Rostral anterior cingulate cortex
28. Rostral middle frontal gyrus	29. Superior frontal gyrus	30. Superior parietal cortex
31. Superior temporal gyrus	32. Supramarginal gyrus	33. Frontal pole
34. Temporal pole	35. Transverse temporal cortex

Fig. 2.

Exemplars of atlas surfaces manually labeled by experts, and the aligned boundaries (blue curves) of their labeled ROIs after group-wise registration of atlas surfaces, overlaid on the standard spherical surface.

2.4 Simultaneous and Consistent Parcellation of Longitudinal Infant Surfaces

After warping multi-atlas surfaces into the spherical spaces of infant surfaces, the proposed method for consistent and simultaneous labeling of all longitudinal dynamic cortical surfaces of an infant is explicitly formulated as the following energy minimization problem:

$$E=E_d+{\alpha }_s{E}_s+{\alpha }_t{E}_t$$ (1)

where E_d is the data fitting term, E_s is the spatial smoothness term, and E_t is the temporal consistency term. α_s and α_t are the weighting parameters for the spatial smoothness term and temporal consistency term, respectively. Each term is carefully designed to be responsible for one specific aspect of the longitudinal surface parcellation, as will be detailed in the following sections.

Data Fitting Term

Inspired by the recent success of multi-atlas based labeling methods (Artaechevarria et al., 2009; Heckemann et al., 2006; Langerak et al., 2010; Sabuncu et al., 2010; Wang et al., 2012a; Wang et al., 2014b; Warfield et al., 2004; Wu et al., 2013), to define the data fitting term, we take advantage of multiple atlas surfaces to account for considerable variability of the cortical folding between subjects and atlases. In general, the data fitting term encourages to propagate the labels from those atlas surfaces with similar cortical folding as the subject surface. Specifically, given K atlas surfaces with each having labels defined by experts, the data fitting term is defined as:

$$E_d={\Sigma }_x-log{P}_x\left(l_x\right)$$ (2)

where P_x(l_x) indicates the probability of assigning a label l_x ∈ {1, …, L} to a vertex x in a subject surface. The label probability at a vertex is computed based on the shape information of labels in the atlas surfaces, as well as the differences of local cortical folding between the subject surface and the atlas surfaces. The latter is defined based on the average absolute difference of their mean curvatures in local surface patches:

$$D\left(S\right(x),S(x_k\left)\right)=\frac{1}{\mid {\Omega }_s\mid }{\Sigma }_{y\in {\Omega }_s}\mid H\left(y\right)-H\left(y_k\right)\mid$$ (3)

where D(·,·) is the cortical folding difference between two surface patches, and S(·) is a local surface patch, defined as a circular region Ω_s with the radius of 2.5 mm (which was set experimentally) surrounding a center vertex (such as x or x_k) on the spherical surface, as illustrated by small red circles in Fig. 3. |Ω_s| is the number of vertices in the surface patch. For the vertex x in a subject surface, x_k is its corresponding point in the atlas surface k. y is a vertex in the subject surface patch, and y_k is its corresponding point in the atlas surface k. H(·) is the mean curvature. Note that other cortical folding measures could also be potentially used for defining the differences of local cortical folding between the subject surface and the atlas surfaces.

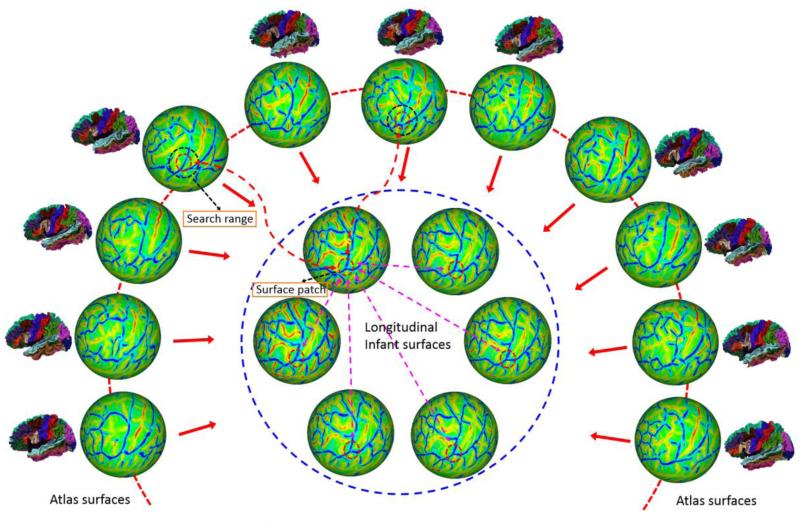
Fig. 3.

An illustration of the proposed method for consistent parcellation of longitudinal infant cortical surfaces. All longitudinal cortical surfaces of the same infant (enclosed by the blue dashed circle) are consistently and simultaneously labeled based on: 1) the subject-atlas similarities of their local cortical folding (represented by the surface patches enclosed by small red dashed circles) in a search range (represented by the dark dashed circles on atlas surfaces) for labeling accuracy; 2) the within-subject temporal similarities of local cortical folding for temporal labeling consistency; and 3) the local cortical folding geometry for adaptive spatial labeling smoothness, as will be illustrated in Fig. 4.

In multi-atlas based labeling, shape-based methods have been demonstrated to achieve more reasonable results than voxel-based methods (Rohlfing and Maurer, 2007; Sabuncu et al., 2010). To use shape information of labels in atlas surfaces, we adopt the logarithm of odds model (Pohl et al., 2006; Sabuncu et al., 2010) based on the signed geodesic distance map on the original cortical surface, computed by the fast marching method on triangular meshes (Kimmel and Sethian, 1998; Li et al., 2010a; Li et al., 2008). For the vertex x in a subject surface, denote d_k,lx(·) as the signed geodesic distance map of the label l_x in the atlas surface k that has been warped onto the subject surface. By setting the inside of the label as positive values, the label probability of the vertex x is defined as:

$$P_x\left(l_x\right)=\frac{1}{K}{\Sigma }_{k=1}^K\exp \left(-\gamma D\left(S\right(x),S(x_k^{\prime }\left)\right)\right)\ast \frac{1}{Z_k\left(x_k^{\prime }\right)}\exp \left(\beta d_{k,l_x}\right(x_k^{\prime }\left)\right)$$ (4)

where $Z_k\left(x_k^{\prime }\right)={\Sigma }_{l=1}^L\exp \left(\beta d_{k,l}\right(x_k^{\prime }\left)\right)$ is the partition function for atlas surface k. The first term in Eq. (4) is the weight of the atlas surface k, and the second term in Eq. (4) is the probability of observing label l_x at subject vertex x based on the atlas surface k. Positive parameters β and γ are experimentally set as 1.0 and 2.0, respectively. $x_k^{\prime }$ could be the corresponding point x_k in the atlas surface k for the subject vertex x, determined by surface registration in Section 2.3. However, it might not achieve the maximum similarity of local cortical folding due to the possible registration errors and smoothness constraints in the surface registration method. Therefore, after surface registration, a better corresponding point $x_k^{\prime }$ in the atlas surface k for the subject vertex x can be further determined by local search for the most similar surface patch: $x_k^{\prime }=\arg \min D\left(S\right(x),S(x_k^{\ast }\left)\right),x_k^{\ast }\in N^{\prime }\left(x\right)$. Herein, N′(·) is a search range on the atlas surfaces, defined as a circular region with the radius of 2.5mm surrounding the vertex x on the spherical surface. The dark circle in Fig. 3 illustrates the cortical regions covered by the surface patch when performing the local search.

Spatial Smoothness Term

The spatial smoothness term adaptively encourages the label smoothness on the subject surfaces based on its local cortical folding geometry. It represents the sum of the costs of labeling of a pair of spatial neighboring vertices on the subject surfaces:

$$E_s={\Sigma }_{\{x,y\}\in N_s}{V}_{x,y}^s(l_x,l_y)$$ (5)

where N_s is the set of the one-ring neighboring vertex pairs in the subject surfaces. $V_{x,y}^s$ indicates the cost of labeling a pair of spatial neighboring vertices x and y as l_x and l_y, respectively. The costs of discontinuous labeling are set as small values at highly-bended cortical regions, e.g., the sulcal bottoms. This is because the cytoarchitecturally and functionally distinct cortical regions are often divided by the sulcal bottoms, and the manual parcellation in atlas surfaces by experts are also based on the sulcal bottoms (Desikan et al., 2006). The costs of discontinuous labeling are set as large value at other regions, such as the flat cortical regions. $V_{x,y}^s(l_x,l_y)$ is thus defined as:

$$V_{x,y}^s(l_x,l_y)=\frac{(1+\mathbf{n}(x)\cdot \mathbf{n}(y\left)\right)}{2}\ast \frac{(e^{-\mid H\left(x\right)\mid }+e^{-\mid H\left(y\right)\mid })}{2}\ast (1-\delta (\mid l_x-l_y\mid \left)\right)$$ (6)

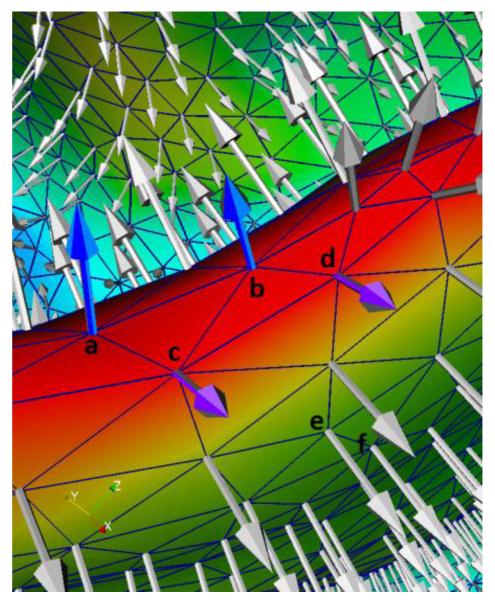
where n is the unit normal direction and δ is the Dirac delta function. If l_x = l_y, δ(|l_x − l_y|) = 1; otherwise, δ(|l_x − l_y|). Therefore, if l_x = l_y, which means that the neighboring vertices x and y have the same label, the cost $V_{x,y}^s(l_x,l_y)$ is 0. At the highly-bended cortical regions, e.g., the sulcal bottoms, x and y belonging to different cortical regions (such as illustrated by the neighboring vertices a and c (or b and d) in Fig. 4) generally have quite different normal directions and also large magnitudes of mean curvatures. Therefore, both the first and second terms in Eq. (6) are small values. On the other hand, if x and y are in the same region (such as illustrated by vertices a and b (or c and d) in Fig. 4), they generally have similar normal direction, but large magnitudes of mean curvatures. In this situation, only the second term in Eq. (6) is a small value. If x and y are at other cortical regions, i.e., the flat cortical regions (as illustrated by the neighboring vertices e and f in Fig. 4), their normal directions will be quite similar and their magnitudes of mean curvatures are close to 0. Hence, both the first and the second terms in Eq. (6) are close to 1.

Fig. 4.

An illustration of the mean curvatures and normal directions at different cortical regions. Note that this cortical region is viewed from the inside to the outside of the brain for convenience of inspection. The red color region indicates the sulcal bottom, and the green color region indicates the flat cortical region. Vertices a and b are in the same cortical region, and c and d are in another cortical region.

Temporal Consistency Term

The temporal consistency term adaptively encourages label consistency of temporal corresponding regions. It represents the sum of costs of labeling pairs of temporal corresponding vertices in longitudinal surfaces:

$$E_t={\Sigma }_{\{x,y\}\in N_t}{V}_{x,y}^t(l_x,l_y)={\Sigma }_{\{x,y\}\in N_t}\exp \left(-\gamma D\left(S\right(x),S(y\left)\right)\right)(1-\delta (\mid l_x-l_y\mid \left)\right)$$ (7)

where N_t is the set of temporal corresponding vertex pairs, and is defined in any two longitudinal surfaces of a subject, as illustrated by purple arrows in Fig. 3. $V_{x,y}^t$ indicates the cost of labeling a pair of temporal corresponding vertices x and y as l_x and l_y, respectively. The cost of discontinuous labeling of temporal corresponding vertices is set based on the similarity of their local cortical folding. To avoid bias and reduce the computational cost in the conventional pair-wise registration of longitudinal cortical surfaces, temporal correspondences are determined by group-wise registration of all longitudinal surfaces of the same infant as mentioned in Section 2.3.

Energy Function Minimization

Finally, the multi-label alpha-expansion graph cuts method (Boykov and Kolmogorov, 2004) is adopted to minimize the above defined energy function. Specifically, all longitudinal cortical surfaces of an infant are represented as an undirected weighted graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$. Herein, V is the set of nodes, including all vertices on the longitudinal surfaces and the terminals represented by all labels. $\mathcal{E}={\mathcal{E}}_N\cup {\mathcal{E}}_{\mathcal{T}}$ is the collection of edges, where ${\mathcal{E}}_{\mathcal{N}}$ is the set of edges formed by both spatial neighboring vertices and temporal corresponding vertices, called n-links, and ${\mathcal{E}}_{\mathcal{T}}$ is the set of edges formed by vertices to terminals, called t-links. In this graph, −logP_x describes the edge weight of t-links, and $V_{x,y}^s$ and $V_{x,y}^t$ describe the edge weights of n-links. For more details of the graph cuts method, please refer to (Boykov and Kolmogorov, 2004).

3. Results

The proposed method has been applied to parcellation of longitudinal dynamic cortical surfaces of 13 healthy infants, each with serial MRI scans acquired at 0, 3, 6, 9, 12 and 18 months of age. Parameters α_s and α_t in Eq. (1) were both set as 0.15 in all experiments. After cortical surface registration, our method took around 10 minutes (for both energy computation and minimization) to label all longitudinal cortical surfaces of each infant, on a standard PC with Intel Xeon 2.26GHz CPU and 4GB memory.

3.1 Qualitative Validation

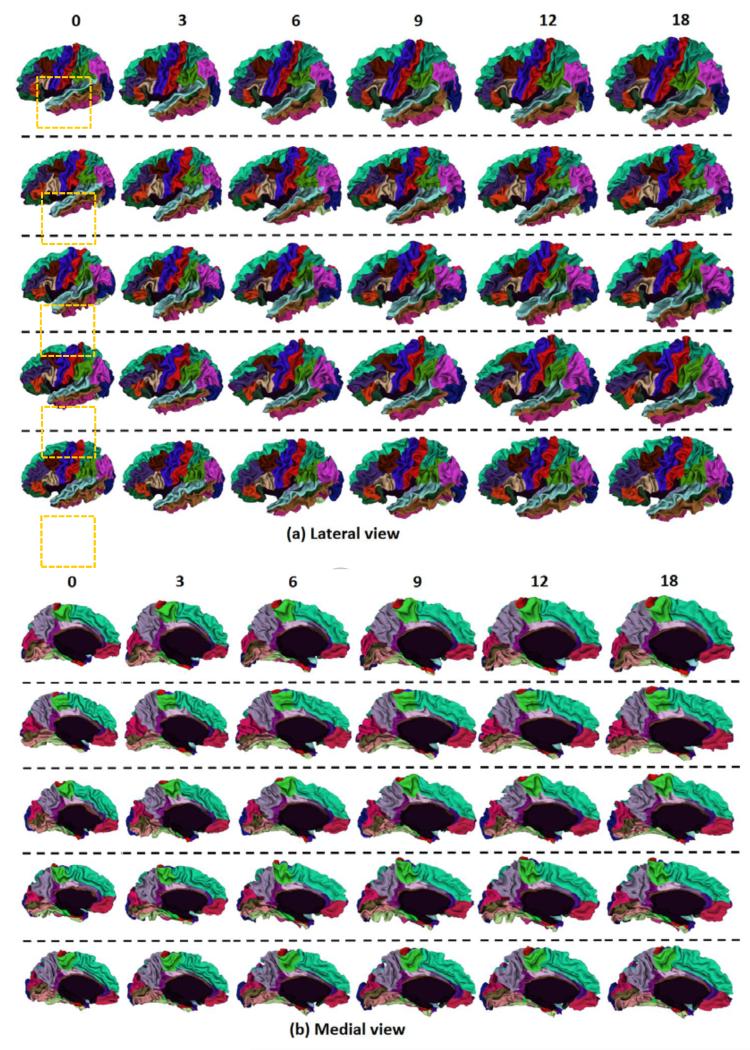
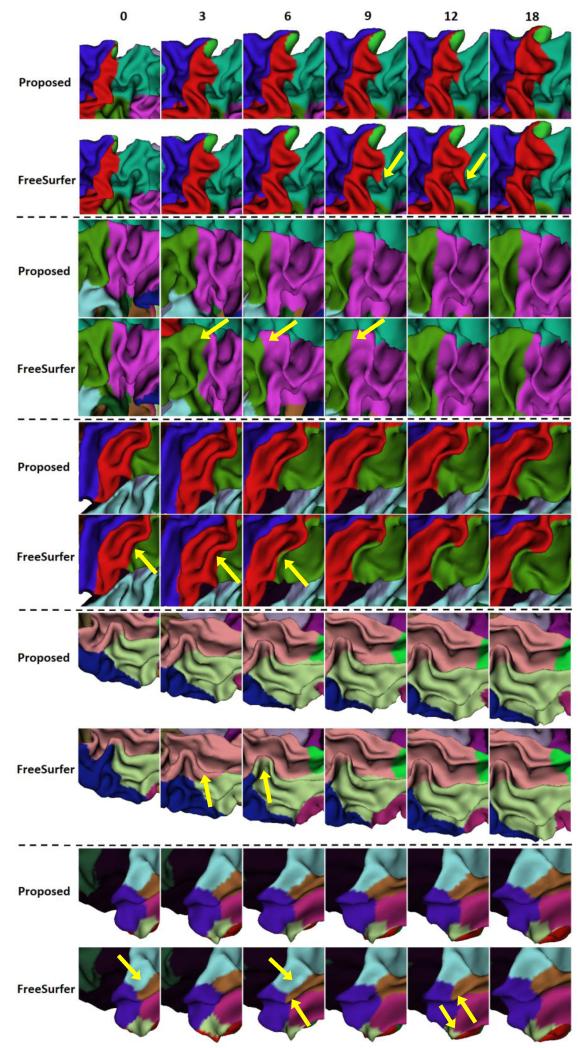
To visually demonstrate the proposed method, Fig. 5 showed the longitudinal cortical surface parcellation results on the left hemisphere of 5 randomly selected infants by the proposed method, with each color indicating a cortical region. For convenience of inspection of the longitudinal surface parcellation in sulci, Fig. 6 provided the close-up views of results in Fig. 5. As can be seen, the surface parcellation results were visually quite reasonable and temporally consistent, with many ROIs divided by sulcal bottoms. To further demonstrate the temporal consistency, Fig. 7 showed close-up comparisons of representative longitudinal infant surface labeling results by the proposed method and by FreeSurfer (Desikan et al., 2006; Reuter et al., 2012). For a fair comparison with FreeSurfer, by following the strategy in longitudinal pipeline in FreeSurfer, we first aligned the within-subject mean surface of the longitudinal infant cortical surfaces to the FreeSurfer atlas and parcellated this mean surface using FreeSurfer classifier. Then, we initialized the registration and parcellation of each longitudinal surface by using their within-subject mean surface. At last, each longitudinal cortical surface was further refined to achieve the final parcellation. As can be observed in Fig. 7, the proposed method achieved longitudinally more reasonable and consistent results than the longitudinal FreeSurfer.

Fig. 5.

Longitudinal cortical surface parcellation results of the left hemisphere on 5 randomly selected infants, each with 6 longitudinal surfaces at 0, 3, 6, 9, 12 and 18 months of age, by the proposed method. Each row indicates one infant.

Fig. 6.

Close-up views of longitudinal infant cortical surface parcellation results from 0 to 18 months of age in the dash orange rectangular regions in Fig. 5. Each row indicates one infant.

Fig. 7.

Close-up views of representative results of longitudinal infant cortical surface parcellation by the proposed method and the longitudinal FreeSurfer. Yellow arrows indicate several regions with longitudinally-inconsistent labeling by the longitudinal FreeSurfer.

3.2 Quantitative Validation of Accuracy

Since there is no ground truth on longitudinal infant surface parcellation, to quantitatively validate the accuracy, we manually annotated three representative cortical regions: precentral gyrus (in frontal lobe), postcentral gyrus (in parietal lobe), and superior temporal gyrus (in temporal lobe), in both the first and last time-point cortical surfaces of the left hemisphere in each of the 13 infants. Manual annotation was conducted according to the mean-curvature based cortical surface labeling protocol in (Desikan et al., 2006). These three ROIs were selected due to their relatively unambiguous anatomical boundaries and important functional roles in the brain. We calculated the Dice coefficients between automatically and manually labeled ROIs. Fig. 8 showed the Dice coefficients of precentral gyrus, postcentral gyrus and superior temporal gyrus on the 13 infants by the proposed method. For comparison, we also provided the results by the proposed method without temporal constraint (by setting α_t as 0) and also the longitudinal FreeSurfer in Fig. 8. For precentral gyrus, the average Dice coefficients were 0.941±0.008 by the proposed method, 0.932±0.009 by the proposed method without temporal constraint, and 0.918±0.010 by the longitudinal FreeSurfer, respectively. For postcentral gyrus, the average Dice coefficients were 0.944±0.007 by the proposed method, 0.934±0.010 by the proposed method without temporal constraint, and 0.916±0.012 by the longitudinal FreeSurfer, respectively. For superior temporal gyrus, the average Dice coefficients were 0.939±0.013 by the proposed method, 0.930±0.013 by the proposed method without temporal constraint, and 0.914±0.015 by the longitudinal FreeSurfer, respectively. As can be seen, the proposed method consistently achieved higher Dice coefficients than any other two methods.

Fig. 8.

Dice coefficients of precentral gyrus, postcentral gyrus, and superior temporal gyrus at 0 month and 18 months of age by the proposed method, the proposed method without temporal constraint, and longitudinal FreeSurfer on 13 infants.

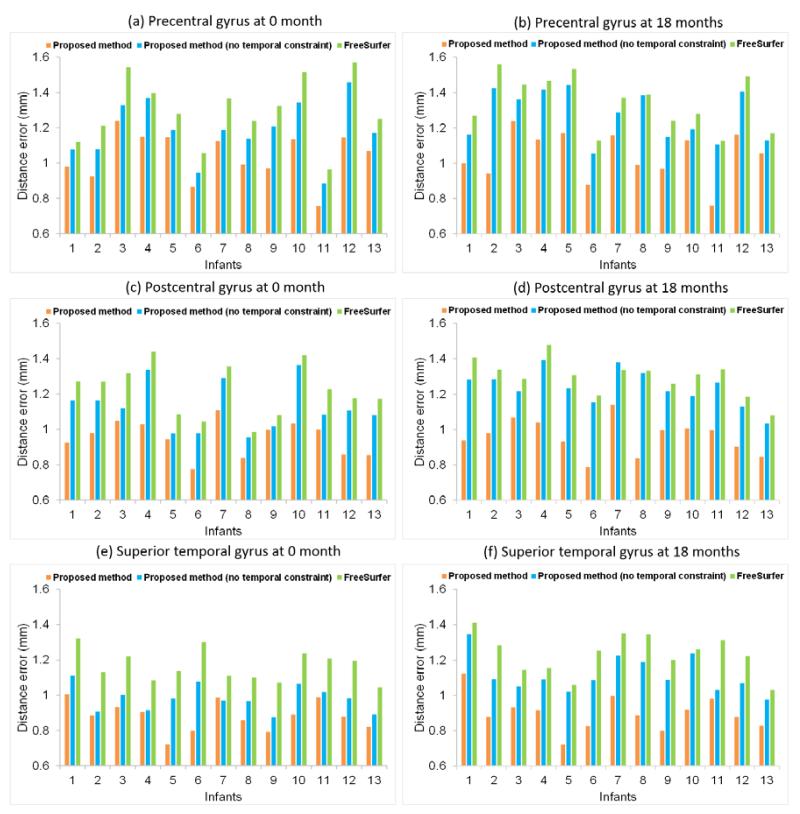
To further validate the accuracy, we also computed the average bidirectional boundary distance errors (Li et al., 2010a) between manually-annotated ROIs and automatically-parcellated ROIs by different methods, as shown in Fig. 9. Note that the distance was measured as the geodesic distance on the cortical surface manifold (Li et al., 2010a). For precentral gyrus, the average distance errors were 1.04±0.14 mm by the proposed method, 1.23±0.15 mm by the proposed method without temporal constraint, and 1.31±0.17 mm by the longitudinal FreeSurfer, respectively. For postcentral gyrus, these values were 0.96±0.10 mm by the proposed method, 1.18±0.12 mm by the proposed method without temporal constraint, and 1.25±0.12 mm by the longitudinal FreeSurfer, respectively. For superior temporal gyrus, these values were 0.89±0.09 mm by the proposed method, 1.05±0.09 mm by the proposed method without temporal constraint, and 1.20±0.10 mm by the longitudinal FreeSurfer, respectively. Again, the proposed method consistently achieved lower boundary distance errors than any other two methods.

Fig. 9.

Average bidirectional distance errors of boundaries of precentral gyrus, postcentral gyrus, and superior temporal gyrus at 0 month and 18 months of age by the proposed method, the proposed method without temporal constraint, and longitudinal FreeSurfer on 13 infants.

3.3 Quantitative Validation of Consistency

To quantitatively validate the consistency of the longitudinal infant surface parcellation, we defined a consistency measure for each cortical ROI as:

$$C\left(i\right)=\frac{{\Sigma }_{x\in ROI\left(i\right)}\left(1\frac{a(i,x)}{N-1}\right)}{{\Sigma }_{x\in ROI\left(i\right)}1}$$ (8)

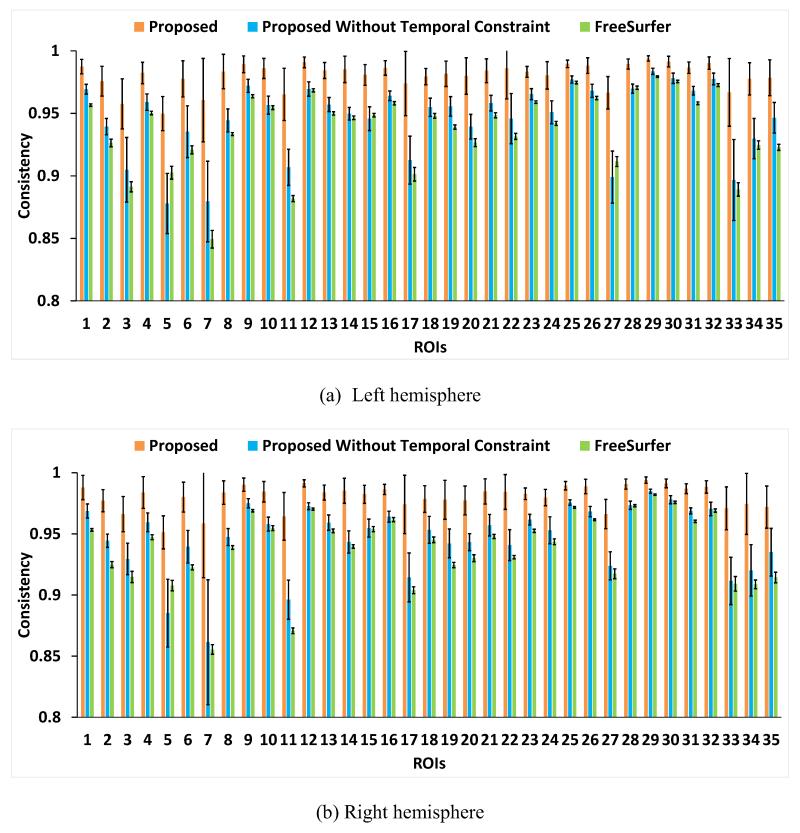
where a(i,x) is the accumulated time of label changes between each pair of temporally neighboring time points at vertex x in ROI _i, on the aligned longitudinal cortical surfaces. N is the total number of time points of an infant, which is set as 6 in our application. Thus, a(i,x) is in a range between 0 and 5. Ideally, C(i) should be close to 1, and larger values of C(i) indicate better consistency of the longitudinal surface parcellation results. Fig. 10 showed the consistency measures in each of the 35 cortical ROIs of the 13 infants by the proposed method, the proposed method without temporal constraint, and longitudinal FreeSurfer. As we can see, the proposed method is longitudinally much more consistent than the other two methods in each ROI. Specifically, the average consistency measures for all ROIs by 3 methods were: 0.980±0.010 (the proposed method), 0.946±0.030 (the proposed method without temporal constraint), and 0.938±0.030 (longitudinal FreeSurfer), respectively. Fig. 11 showed the improvement of the consistency measure in each of the 35 cortical ROIs by the proposed method, compared with both the proposed method without temporal constraint and the longitudinal FreeSurfer. As can be seen, the improvement is particularly pronounced in those small-sized ROIs without distinctive boundaries, e.g., frontal pole, temporal pole, entorhinal cortex, and isthmus cingulate cortex. Thus, for those small-sized regions, the inconsistent labeling of longitudinal cortical surfaces would seriously affect the accurate measurement of the infant cortex development.

Fig. 10.

The longitudinal label consistency in each of 35 cortical ROIs of 13 infants by the proposed method, the proposed method without temporal constraint, and longitudinal FreeSurfer.

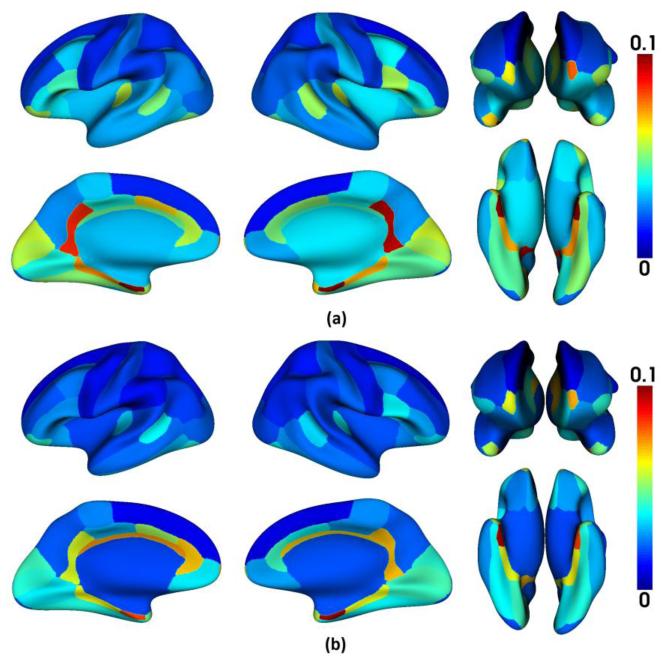
Fig. 11.

The average improvement of the consistency measure in each of 35 cortical ROIs of 13 infants by the proposed method over other comparison methods. (a) Compared with longitudinal FreeSurfer; (b) Compared with the proposed method without temporal constraint. The improvement is particularly pronounced in those small-sized ROIs without distinctive boundaries.

3.4 Application to Study of Dynamic Cortical Surface Expansion in Infants

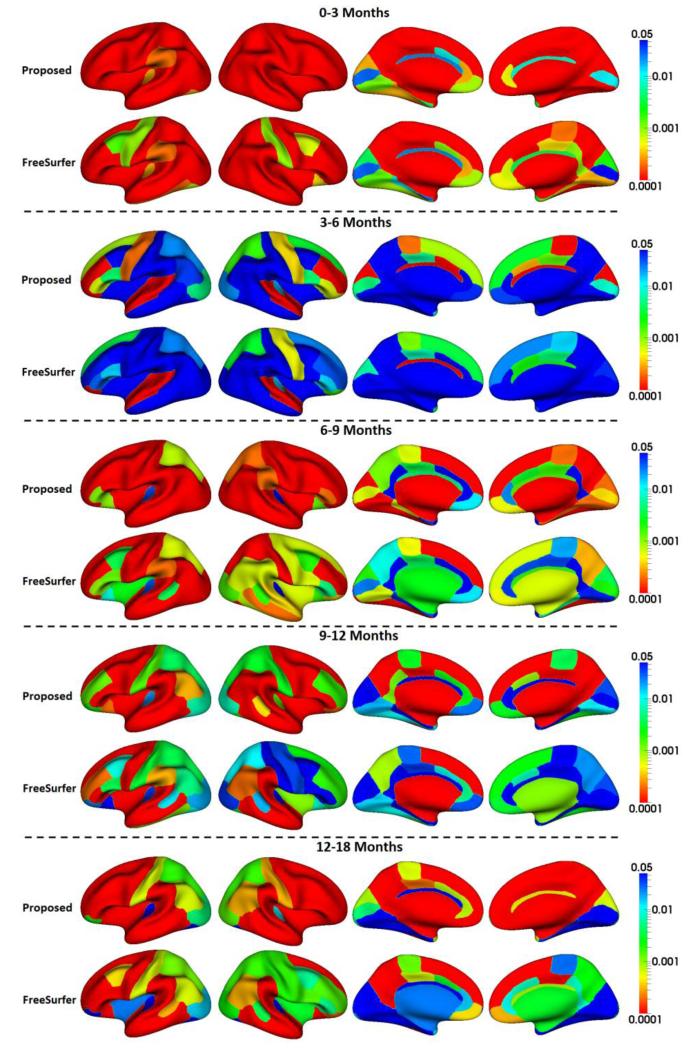
In this section, we applied the proposed method to study the dynamic, region-specific cortical surface area expansion in multiple stages from 0 to 18 months of age, based on the 13 infants. For each pair of neighboring time points, the growth percentage of the cortical surface area of each ROI was computed, as shown in Fig. 12. Meanwhile, we also preformed statistical significance testing of the regional cortical surface changes by using 5000 permutation tests, with the p-values (after multiple comparisons correction (Blair and Karniski, 1993)) shown in Fig. 13. For comparison, in Fig. 13, we also provided the p-values of the results obtained by longitudinal FreeSurfer. As we can see, the proposed method achieved more significant p-values than longitudinal FreeSurfer for the majority of cortical regions at all developmental stages.

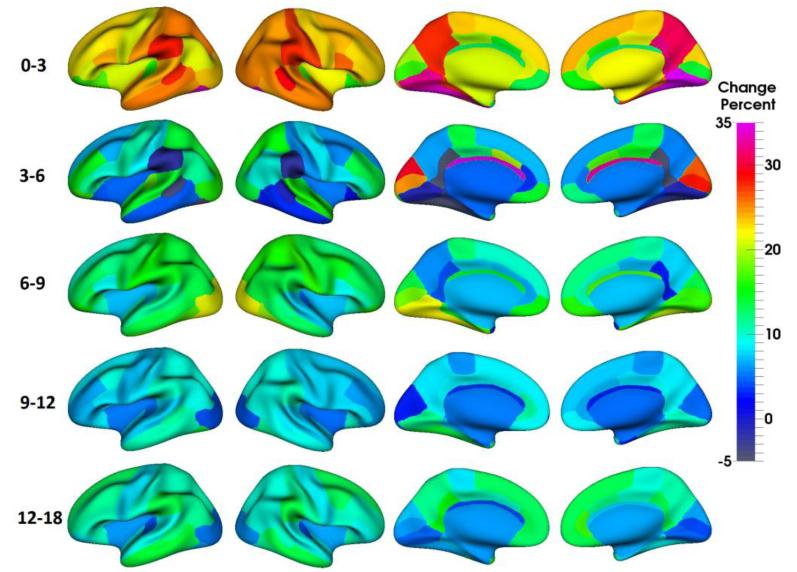
Fig. 12.

Change percentage of regional cortical surface area from 0 to 3, 3 to 6, 6 to 9, 9 to 12 and 12 to 18 months of age, on the 13 infants, obtained by the proposed method. Age-specific and regionally-heterogeneous patterns of the cortical surface area growth can be observed.

Fig. 13.

P-values (multiple comparisons corrected) of regional cortical surface area changes from 0 to 3, 3 to 6, 6 to 9, 9 to 12, and 12 to 18 months of age by the proposed method and the longitudinal FreeSurfer, respectively.

During the first 18 months of life, the cortical surface area growth was highly dynamic, age-related, and regionally heterogeneous. Overall, the regional cortical surface area increased most dynamically from birth to 3 months (23.2%), followed by an extremely regionally heterogeneous increase from 3 to 6 months (8.3%) and a substantial increase from 6 to 9 months (13.1%), then exhibited a moderate increase from 9 to 12 months (7.9%) and finally another substantial increase from 12 to 18 months (9.7%).

• In the first 3 months, the postcentral gyrus (somatosensory cortex), supramarginal gyrus, precuneus cortex, lingual gyrus, and fusiform gyrus grew most dynamically; while the transverse temporal gyrus (primary auditory cortex) and orbitofrontal cortex grew slowest.

• From 3 to 6 months, the lateral occipital cortex (primary visual cortex), cuneus cortex, pericalcarine cortex, transverse temporal gyrus, superior temporal gyrus, paracentral lobule, superior parietal cortex and rostral middle frontal cortex developed faster than other regions. Interestingly, several regions even exhibited decreased surface area, including supramarginal gyrus, banks of the superior temporal sulcus, isthmus cingulate cortex, and fusiform gyrus. However, none of these decreasing regions was statistically significant, as shown in Fig. 13.

• From 6 to 9 months, the somatosensory cortex and vision related regions (including the lateral occipital cortex, inferior temporal gyrus, fusiform cortex, lingual gyrus and pericalcarine cortex) exhibited larger growth rates than other regions.

• From 9 to 12 months, the supramarginal gyrus, fusiform gyrus, lingual gyrus, middle and inferior temporal gyri exhibited the largest growth; while the lateral occipital cortex, cuneus cortex and pericalcarine cortex showed the smallest growth.

• From 12 to 18 months, the association cortex (including the superior frontal gyrus, medial orbitofrontal cortex, middle temporal gyrus and supramarginal gyrus) underwent the largest growth; while the primary auditory cortex and the vision related regions underwent the smallest growth.

4. Discussion and Conclusion

This paper presents an original and novel method for consistent and simultaneous parcellation of longitudinal dynamic developing infant cortical surface by using multi-atlas surfaces. Previous methods for longitudinal surface parcellation are mainly developed for the adult brains with subtle longitudinal changes, thus not suitable for the longitudinal dynamic infant cortical surfaces (Li and Shen, 2011; Reuter et al., 2012). The main contributions of the proposed method are threefold. First, we propose a data fitting term, which is adaptively derived from multi-atlas surfaces and is based on the shape information of manual labels by experts, to ensure the accuracy of the longitudinal surface parcellation results. Second, we propose a spatial smoothness term adaptive to the local cortical folding geometries, to ensure the smooth boundaries of the longitudinal surface parcellation results. Third, we propose a temporal consistency term to explicitly incorporate temporal consistency into the longitudinal surface parcellation results.

Note that too high values of the temporal consistency coefficient could lead to longitudinal consistent but incorrect results. To impose adaptive longitudinal constraints, in our method, the temporal consistency coefficient is modulated by the temporal similarity of local cortical folding. Therefore, the regions with the high temporal similarity of local cortical folding will be strongly encouraged to have consistent parcellation, while the regions with the low temporal similarity of local cortical folding (due to possible errors in surface registration) will be more allowed to have inconsistent parcellation. Compared with the case of setting the longitudinal consistency coefficient as 0 and the longitudinal FreeSurfer, our current setting has led to better accuracy and consistency, although it might not be the optimal setting. Of note, the accuracy in the regions with distinct boundaries might be higher than the regions with ambiguous boundaries, where the temporal consistency is actually more important in longitudinal analysis.

In the previous imaging studies of the infant cortex development, Gilmore et al. (2012) investigated the development of regional cortical volume from 0 to 1 and from 1 to 2 years of age. In fact, the cortical volume development is jo intly determined by the growth of the cortical thickness and the expansion of the surface area, with distinct cellular and genetic mechanisms (Chen et al., 2013; Panizzon et al., 2009). Therefore, Li et al. (2013a) further investigated the region-specific expansion of cortical surface area from 0 to 1 and 1 to 2 years of age. Meanwhile, Nie et al. (2012) studied the development of regional cortical folding in the first year of life.

For the first time, in this paper, we have applied the proposed method to study the regional cortical surface area development in multiple stages of the first 18 months of life. Our results indicate that the cortical surface area development is highly age-related and regionally heterogeneous during this critical period of rapid cortex development. Importantly, we revealed several hitherto unseen properties of cortical surface area development in the first 18 months of life, as detailed below. 1) The regional cortical surface area increases most dynamically from 0 to 3 months; 2) The regional cortical surface area increases regionally most heterogeneously from 3 to 6 months, with many regions exhibiting insignificant changes; 3) The primary visual cortex exhibits a high growth from 0 to 9 months compared with other regions, followed by a low growth from 9 to 18 months; 4) The primary auditory cortex shows a high growth from 3 to 6 months compared with other regions, but a low growth at other developmental stages; 5) The somatosensory cortex exhibits a high growth from 0 to 3 months and from 6 to 9 months compared with other regions, but a median growth at other developmental stages; 6) The motor cortex exhibits a median growth at all stages from 0 to 18 months. In our previous study of the region-specific cortical surface area expansion between birth and 1 year of age, the visual cortex, auditory cortex, and sensory cortex expanded more rapidly than the motor cortex and association cortex (Li et al., 2013a). Compared with our previous study, our current work further provide much more detailed pattern for cortical surface area development in the first 18 months of life by using 6 scanning time points, which greatly advances our understandings on the normal developmental trajectories of cortical surface area in infants.

There still exist several limitations in our current method. First, in the proposed method, we adopt the manually annotated cortical surfaces of adults, used in FreeSurfer software, as our multi-atlas surfaces for longitudinal infant cortical surface parcellation. The rationale is that all the primary and second cortical folding are established at term birth (Hill et al., 2010), and are well preserved during the postnatal cortex development (Li et al., 2013a). Although these adult atlas surfaces have led to reasonable results, using age-matched infant atlas surfaces would further improve the accuracy of longitudinal infant surface parcellation. As more longitudinal infant dataset is being collected in our institute, we plan to apply our current method to this increasing infant dataset and then manually edit and correct longitudinal cortical surface parcellation results on at least 20 representative infants. In this way, we can significantly reduce the time for manually annotating the longitudinal infant cortical surfaces, and directly use these error-corrected infant surface parcellation as infant-specific atlas surfaces to further improve the results. Second, the parameters in the proposed method are set experimentally, thus cannot guarantee to generate the optimal results. With the above-mentioned manually annotated infant cortical surfaces, we will be able to further optimize these parameters, although the current parameter setting has already led to reasonable results. Finally, the proposed energy function could also be optimized by other methods, such as tree-reweighted message passing (Kolmogorov, 2006) and fast primal-dual scheme (Komodakis et al., 2011), which will be investigated in our further work.

With the further optimized method and the availability of larger-scale longitudinal infant dataset, we plan to comprehensively investigate the regional developmental trajectories of the cortical surface area, cortical thickness, and cortical folding, as well as their correlation networks in both healthy and high-risk infants. This would greatly advance our current understanding on normal cortical developmental trajectories during this critical period of brain development, and thus provide important insights into neurodevelopmental disorders.

Highlights.

• ➢We propose a method for consistent labeling of longitudinal dynamic infant surfaces;
• ➢The method ensures accuracy, spatial smoothness and temporal consistency;
• ➢We apply the method to reveal dynamic regional surface area development in infants;