Quantifying the effects of the division of labor in metabolic pathways

Abstract

Division of labor is commonly observed in nature. There are several theories that suggest diversification in a microbial community may enhance stability and robustness, decrease concentration of inhibitory intermediates, and increase efficiency. Theoretical studies to date have focused on proving when the stable co-existence of multiple strains occurs, but have not investigated the productivity or biomass production of these systems when compared to a single ‘super microbe’ which has the same metabolic capacity. In this work we prove that if there is no change in the growth kinetics or yield of the metabolic pathways when the metabolism is specialized into two separate microbes, the biomass (and productivity) of a binary consortia system is always less than that of the equivalent monoculture. Using a specific example of Escherichia coli growing on a glucose substrate, we find that increasing the growth rates or substrate affinities of the pathways is not sufficient to explain the experimentally observed productivity increase in a community. An increase in pathway efficiency (yield) in specialized organisms provides the best explanation of the observed increase in productivity.

1. Introduction

From the earliest observations of microbial organisms, it has been apparent that microbial consortia are ubiquitous in nature. In fact, naturally occurring ecosystems are almost exclusively organized as consortia. Recent metagenomic studies from the soil (Fierer and Jackson, 2006), to the ocean (Venter et al., 2004), to the human gut (Gill et al., 2006), have found that microbial communities are incredibly diverse, often consisting of thousands of interacting species. Subsets of these communities form consortia that act together to enhance their capabilities and survival (Eiteman et al., 2008).

Early theoretical ecology studies led to the development of the competitive exclusion principle (CEP), which states that the maximum number of species that can coexist in a system is equal to the total number of limiting (essential) resources (Hardin, 1960; MacArthur and Levins, 1964; Rescigno and Richardson, 1965). However, in nature we see many examples of multiple microbial species stably coexisting. Frequent explanations for coexistence in a natural population can be categorized into three main types: the development of multiple niches due to spatial heterogeneity or self-organized segregation, the system not being in equilibrium due to environmental fluctuations or external forcing, and the presence of inter- and intra-species interactions. Despite the limited direct applicability of CEP to natural systems, the clear mathematical formulation of CEP allows for significant insight by identifying which conditions of the CEP have been violated to lead to the observed coexistence of species. For example, by applying the CEP to the dynamics in a chemostat, we see that due to the consistent flow of nutrients and continuous mixing, the environment is kept constant and the development of different niches due to spatial heterogeneity is not possible; therefore, it must be some form of inter- or intra-species interactions such as crowding, chemical signaling, cooperativity, or mutual inhibition that lead to any observed coexistence. Studying these interactions in simple chemostat systems gives us a better understanding of the factors that maintain the diversity in naturally occurring microbial consortia.

Natural consortia are often found to form syntrophic systems, where the microbes depend on each other for survival, either by the production of required metabolic substrates or by the maintenance of chemically advantageous conditions (Schink, 2002). It is often observed that this syntrophic cooperation within microbial consortia increases their productivity and can allow the consortia to perform advanced functions that the microbial species are not capable of individually. These microbial interactions are known to be important in diverse areas including chronic medical infections (e.g. diabetic ulcers, Gardner et al., 2013; James et al., 2008), biofuel synthesis (e.g. biodiesel production, Peralta-Yahya et al., 2012; Zuroff and Curtis, 2012), environmental nutrient cycling (e.g. CO₂ sequestering, nitrification, Costa et al., 2006), bioprocessing (Shong et al., 2012), and wastewater treatment (Schink, 1997; Seitz et al., 1990a, 1990).

A frequently observed syntrophic system is a cross-feeding chain where microbes work together to perform the sequential degradation of complex compounds like lingocellulosic material (Schink, 2002). In these syntrophic cross-feeding systems a single substrate must be broken down in many steps, with one species catabolizing the available substrate and oxidizing it to produce a byproduct that the next species in the chain can consume. The intermediate byproducts in these systems are often found to be inhibitory. In this work we will consider the case where the intermediate byproduct inhibits growth. However, this more complicated system can be reduced to the case where there is no inhibition by taking the appropriate limit.

It has been observed experimentally that these syntrophic chain systems where the metabolic pathways are split among separate organisms (known as ‘microbial specialization’ or a ‘division of labor’) are more productive than a single organism with the equivalent metabolic capabilities (Bernstein et al., 2012; Wintermute and Silver, 2010). For example, if we compare a single organism that metabolizes A → B → C to a pair of organisms that metabolize A → B (organism 1) and B → C (organism 2), experimental observation has found the pair of organisms to be more productive than the single organism. Productivity is defined here as total biomass production per unit of input A.

An example of this division of labor that has been found to evolve repeatedly in different experiments occurs when E. coli is grown on a glucose substrate. The original population of E. coli can fully metabolize glucose (glucose → acetate → CO₂ (TCA cycle)), but when grown on glucose for many generations the population splits into two main subpopulations: microbes that preferentially consume glucose and produce acetate (glucose → acetate) and microbes that preferentially consume acetate (acetate → CO₂) (Rosenzweig et al., 1994; Rozen and Lenski, 2000; Treves et al., 1998).

In this paper we use standard chemostat modeling techniques to investigate whether the division of labor (splitting the pathways into two separate organisms) alone is sufficient to explain the observed increase in biomass, and if not, what other changes may be required. It is important to note that in contrast to the past work which has investigated the evolution of such cross-feeding systems, we will not consider the two systems in direct competition, instead comparing the maximum biomass (productivity) of the systems in isolation. This is motivated by industrial applications where the total productivity of the consortia, which is usually proportional to the biomass, is of primary interest.

This type of system has been studied mathematically, and it can be shown that for n species in a simple syntrophic cross-feeding chain, there is a stable coexistence steady state (Kreikenbohm and Bohl, 1986; Powell, 1985, 1986; Reilly, 1974). This simple system has been modified to include other forms of inhibition, external toxins, multiple substrates, and other forms of mutualism; in all cases, a stable, stationary, coexistence steady state is found (Aota and Nakajima, 2001; Burchard, 1994; Elkhader, 1991; Katsuyama et al., 2009; Sari et al., 2012). Previous research has focused on proving the existence and stability of coexistence steady-states. There has been no investigation of the productivity of these syntrophic chain systems. Some recent work (Doebeli, 2002; Estrela and Gudejl, 2010; Pfeiffer and Bonhoeffer, 2004) investigated the evolution of cross-feeding in microbial populations and found that there are a wide range of parameter values for which cross-feeding is seen to evolve. The aim of these evolution studies was to identify conditions for stable coexisting syntrophic chain systems to evolve and outcompete equivalent monocultures. They did not explicitly investigate the productivity of the systems that are found to evolve.

In our initial model, we assume that the metabolic dynamics of the pathways do not change when being split into separate microbes. In addition, we initially assume that the growth rate for the monoculture is a linear combination of the growth rates of the two pathways. This formulation allows us to obtain theoretical results and is effectively an upper bound on the growth rate of the monoculture microbe. Realistically, there are costs to utilizing both pathways at once for the monoculture, and there are changes that are known to occur to the metabolic pathway dynamics when the microbes specialize to a single substrate. For example, Pfeiffer and Bonhoeffer (2004) theorize that the evolution of cross-feeding could be due to the system minimizing the concentration of inhibitory intermediates and minimizing the concentration of enzymes it must produce, while maximizing the rate of ATP-production. Another explanation comes from Johnson et al. (2012) who find, by considering the biochemical conflicts which constrain the relationships between two metabolic processes that the division of metabolic pathways could be advantageous as it allows microbes to focus on producing a smaller number of enzymes and optimizing a smaller subset of pathways.

By starting with the assumption of no adaptation for the specialists and the maximal growth rate for the monoculture, we get a strong theoretical result. Then, by varying the growth kinetics (growth rates and substrate affinities) and yields between the monoculture and the binary culture systems, we are able to use our model to test possible explanations for the observed increase in productivity and to quantitatively investigate what changes are required for the division of labor to be advantageous (increased biomass). Considering the specific example of E. coli grown on a glucose substrate (Rosenzweig et al., 1994; Rozen and Lenski, 2000; Treves et al., 1998), we use standard Monod kinetics and measured experimental parameters to determine the conditions under which the model results match the experimentally observed increase in biomass.

The main result of this work is a comparison of the biomass production of a single microbe with full metabolic capacity to a syntrophic consortium of two specialized microbes each with a unique subset of the full metabolic chain, where the intermediate byproduct may be inhibitory. We prove that the monoculture system will always have higher biomass production (i.e., higher productivity) if there are no changes to the growth kinetics or yield of the pathways between the two systems. In a specific example, we show that increasing the growth rates or substrate affinities of the consortial pathways, a change that might be expected due to specialization, is not sufficient to generate the observed higher biomass production in the binary consortia. However, by varying the yields for the consortial pathways, higher biomass production can be achieved for the binary consortia relative to the monoculture. Yield changes are an expected result of microbial specialization because utilizing a smaller number of specialized pathways leads to reduced energy requirements. This result provides evidence for the argument that an increase in efficiency (yields) is a key factor underlying the observed productivity benefit of microbial consortia. Additionally, the finding that changing yields can lead to higher biomass production through specialization has important implications for industrial settings where higher biomass production is often highly desirable.

2. Model construction

To investigate the effects of separating metabolic pathways, we will analyze the simplest case of a syntrophic chain where there are only two microbial species. For clarity we will use a specific example in developing our notation, in this case the metabolism of glucose by E. coli. To construct the model we assume that the metabolism of a single provided substrate (glucose, G) can be split into two pathways. The first step (pathway) takes substrate G and produces an intermediate by-product A (acetate), creating new biomass at a growth rate μ₁(G, A). The intermediate by-product acetate A serves as a substrate for the second step (pathway), which has a growth rate μ₂(A). As well as being a substrate, acetate lowers the pH and is detrimental to both metabolism pathways in the cell, which slows the growth rates μ_i and thus slows the uptake of substrate. The lower pH caused by acetate production could also increase the energy required for cell homeostasis, which would affect the yield parameters. We do not consider this effect here, as if yield did decrease at higher A values, this would further disadvantage the binary consortia, and thus would not qualitatively affect our results but would greatly complicate the analysis.

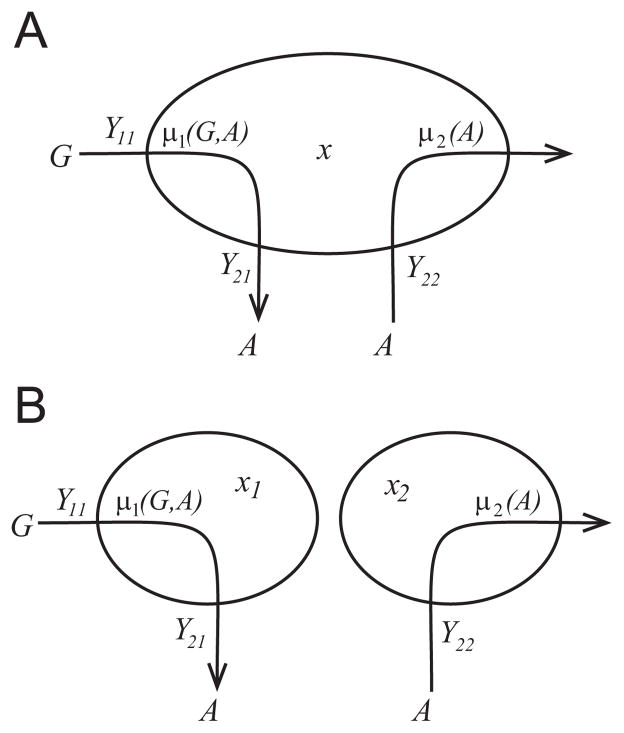
We will consider the situation where the microbes are grown in continuous culture (chemostat). We compare the total biomass produced in two different systems: a binary culture system where the two pathways are in two separate microbes, and a monoculture system where the pathways are combined into a single microbe. These two systems are shown in Fig. 1. For the monoculture system, acetate that is produced through the first pathway is then available to be consumed through the second pathway. If the acetate consumption rate is lower than the acetate production rate, acetate will accumulate in the system, see Eqs. (4) and (7). In our model of the monoculture, we consider the case where acetate is consumed (metabolized) by the individual microbial cell that produced it, and the case where acetate is released from that microbe into the environment and then consumed by distinct microbes, to be equivalent. This is possible because this model does not include any cost involved in transporting acetate into or out of the cell. Including a cost for transporting acetate would disadvantage the binary consortia compared to the monoculture, and thus it would not qualitatively affect our results.

Fig. 1.

Diagram showing the metabolic pathways in (a) the monoculture system with the microbes x and (b) the binary culture system with the primary (glucose) consumer x₁ and the scavenger (acetate consumer) x₂, where G is the primary substrate (glucose) and A is the inhibitory intermediate substrate (acetate). The yields Y₁₁ and Y₂₂ fix the rates of biomass production per gram of substrate consumed, the yield Y₂₁ is the ratio of biomass production to byproduct production, and the growth rates are given by the functions μ₁(G, A) and μ₂(A).

2.1. Model formulation

To model the dynamics in a chemostat we construct a system of ordinary differential equations (ODEs), following standard techniques (Smith and Waltman, 1995), that describe the evolution over time of the microbial biomass and substrate concentrations. In both systems we will track the concentration of primary substrate, G and the concentration of the intermediate by-product, A.

In binary culture, the biomass of a microbe that consumes G and produces A to grow at rate μ₁(G, A) will be denoted by x₁, and the biomass of the second microbe that consumes A and grows at rate μ₂(A) will be x₂. For the binary chemostat this situation can be described by the following system of ordinary differential equations:

$$\frac{{dx}_1}{dt}=({\mu }_1(G,A)-D)x_1,$$ (1)

$$\frac{{dx}_2}{dt}=({\mu }_2(A)-D)x_2,$$ (2)

$$\frac{dG}{dt}=(G_{in}-G)D-\frac{{\mu }_1(G,A)}{Y_{11}}{x}_1,$$ (3)

$$\frac{dA}{dt}=-AD+\frac{{\mu }_1(G,A)}{Y_{21}}{x}_1-\frac{{\mu }_2(A)}{Y_{22}}{x}_2,$$ (4)

where D > 0 is the dilution rate (with units 1/h, and D = V/Q where V is the volume and Q is the volumetric flow rate) and G_in > 0 is the input concentration of primary substrate. The parameters D and G_in are set by experimental conditions. The yields, constants Y_ij, are determined by the stoichiometry of the metabolic pathways involved, which dictates the energy produced per unit of substrate consumed, and the proportion of energy produced that goes towards biomass production, which depends on additional factors including the energy required for cell homeostasis and for the production of enzymes. In this work we have chosen to define the yield terms Y₁₁ and Y₂₂ as the amount of biomass made by one unit of substrate, G and A respectively, and Y₂₁ is the amount of biomass produced when one unit of intermediate substrate A is produced through the G-metabolism pathway. The parameter, r = Y₁₁/Y₂₁ defines the grams of the inhibitory intermediate substrate A produced per gram of primary substrate A consumed, and is fixed for a specific metabolic pathway.

To model the monoculture system, we assume that the two pathways are combined in a single microbe, whose biomass is represented by the variable x. The growth rate is assumed to be the sum of the metabolic pathways of the two microbes (μ_WT = μ₁(G, A) + μ₂(A)). This provides the maximal possible growth rate for the monoculture, without making further assumptions on whether monoculture can actually use this potential. In reality, using both pathways concurrently comes at a cost, as microbes have finite resources for the transport of nutrients into the cell, and the production of enzymes. We will later (Section 4.3) consider modeling the monoculture growth rate as a convex combination of the pathways (μ̄_WT = βf(G)I(A) + (1 − β)m(A)). However, we start the linear combination (μ_WT = μ₁(G, A) + μ₂(A)), which is the upper bound for the wildtype growth rate, in order to be able to obtain theoretical results. This gives the system of rate equations for the monoculture system:

$$x^{\prime }=[{\mu }_1(G,A)+{\mu }_2(A)-D]x,$$ (5)

$$G^{\prime }=(G_{in}-G)D-\frac{{\mu }_1(G,A)}{Y_{11}}x,$$ (6)

$$A^{\prime }=-AD+\left[\frac{{\mu }_1(G,A)}{Y_{21}}-\frac{{\mu }_2(A)}{Y_{22}}\right]x.$$ (7)

In this formulation we assume that there is no change in pathway efficiency (yield), growth rate, substrate affinity, or inhibition when the pathways are split into two separate microbes, thus the functions and parameters for the monoculture system (5)–(7) are identical to those in the binary culture system (1)–(4).

In this work we will assume that the inhibition by A on the first pathway is non-competitive, so that the growth rate of pathway 1 can be described by μ₁(G, A) = f(G)I(A), where the function f(G) describes the growth of x₁ on G and the function I(A) describes the inhibition of x₁ by A. The growth of x₂ due to the consumption of A we describe by the function μ₂(A) = m(A), where m(A) increases at low A values but decreases when A gets too high.

2.2. Model non-dimensionalization

In order to simplify the calculations, we non-dimensionalize the original system using the scalings:

$$\begin{array}{l}\widehat{x}=\frac{x}{G_{in}{Y}_{11}},\widehat{x_1}=\frac{x_1}{G_{in}{Y}_{11}},\widehat{x_2}=\frac{x_2}{G_{in}{Y}_{11}},\\ \widehat{G}=\frac{G}{G_{in}},\widehat{A}=\frac{A{Y}_{21}}{G_{in}{Y}_{11}},\widehat{t}=tD,\gamma =\frac{Y_{21}}{Y_{22}}.\end{array}$$ (8)

This gives us the dimensionless variables ( $\widehat{x_1},\widehat{x_2}$, Ĝ, Â) for the binary culture and (x̂, Ĝ, Â) for the monoculture. Both systems of equations depend upon the new dimensionless time variable t̂, and the only remaining parameter in the system is the dimensionless parameter γ.

Removing the hats for convenience and making the substitution μ₁(G, A) = f(G)I(A), μ₂(A) = m(A), gives us a dimensionless version of the binary culture system (Eqs. (1)–(4))

$$\begin{array}{l}{x}_1^{\prime }=(f(G)I(A)-1)x_1,\\ x_2^{\prime }=(m(A)-1)x_2,\\ G^{\prime }=1-G-f(G)I(A)x_1,\\ A^{\prime }=-A+f(G)I(A)x_1-\gamma m(A)x_2,\end{array}$$ (9)

and a dimensionless version monoculture system (Eqs. (5)–(7))

$$\begin{array}{l}{x}^{\prime }=[f(G)I(A)+m(A)-1]x,\\ G^{\prime }=1-G-f(G)I(A)x,\\ A^{\prime }=-A+[f(G)I(A)-\gamma m(A)]x.\end{array}$$ (10)

2.3. Model assumptions

Before we describe our main result, it is important to specify our assumptions on the functions and parameters in the model (in the dimensionless setting).

• A1The functions f(G), I(A) and m(A) are the same in both models, i.e. that the separation of the pathways does not modify the metabolic dynamics.
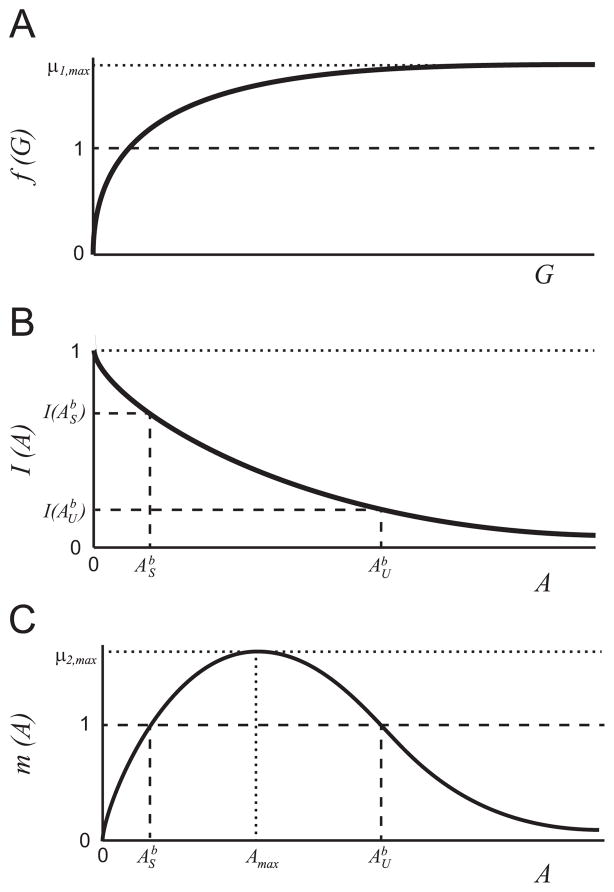
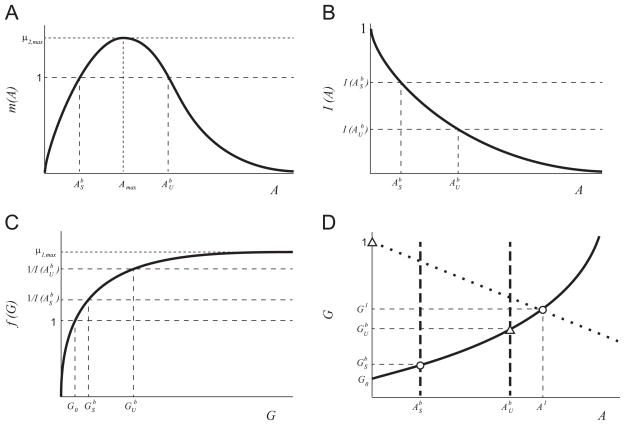
• A2
  The function f(G) is a monotonically increasing function of substrate concentration, G, with limiting rate, μ_1,max (see Fig. 2(a)). The properties of f(G) are

  $$\begin{array}{l}f(0)=0,\\ \underset{G\to \infty }{lim}f(G)={\mu }_{1,\mathit{max}},\\ \frac{df(G)}{dG}>0\text{for}G\ge 0,\\ \underset{G\to \infty }{lim}\frac{df(G)}{dG}=0.\end{array}$$ (11)

  These conditions on f(G) are readily satisfied by an increasing Hill function μ_1,maxGⁿ/(kⁿ + Gⁿ) for any n.

• A3
  The function I describes the inhibition of the G-metabolism pathway by the intermediate substrate A (see Fig. 2(b)). The properties of I(A) are:

  $$\begin{array}{l}I(0)=1,\\ I(A)>0\text{for}A\ge 0,\\ {\mathit{lim}}_{A\to \infty }I(A)=0,\\ \frac{\partial I(A)}{\partial A}<0\text{for}A>0.\end{array}$$ (12)

  These conditions on I(A) are satisfied by a decreasing Hill function kⁿ/(kⁿ + Aⁿ) for any n.

• A4
  The function m(A) describes the growth rate on the inhibitory substrate (A) (see Fig. 2(c)). m(A) has the following properties:

  $$\begin{array}{l}m(0)=0,\\ \underset{A\to \infty }{lim}m(A)=0,\\ \mathit{max}(m(A))=m(A_{\mathit{max}})={\mu }_{2,\mathit{max}},\\ \frac{dm(A)}{dA}>0\text{for}0\le A\le A_{\mathit{max}},\\ \frac{dm(A)}{dA}=0\text{at}A=A_{\mathit{max}},\\ \frac{dm(A)}{dA}\le 0\text{for}{A}_{\mathit{max}}\le A,\\ \underset{A\to \infty }{lim}\frac{dm(A)}{dA}=0.\end{array}$$ (13)

  These conditions on m(A) are satisfied by commonly used substrate-inhibition functions (Han and Levenspiel, 1988).

• A5
  We consider the case where the growth rates of each microbe are sufficiently large that they can survive at the chosen dilution rate; i.e.,

  $$\begin{array}{l}{\mu }_{1,\mathit{max}}>1,\\ {\mu }_{2,\mathit{max}}>1.\end{array}$$

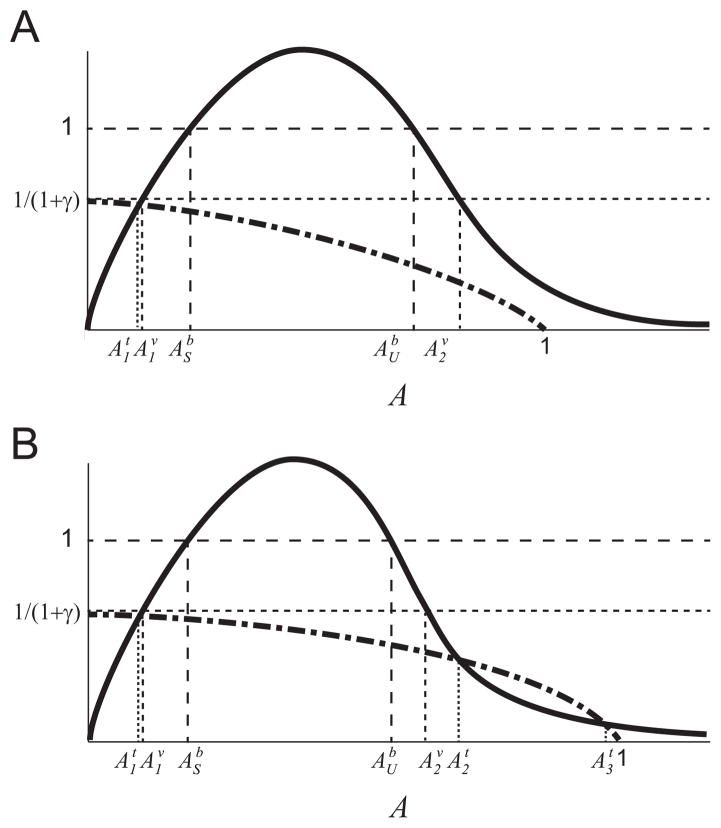
  For μ_2,max > 1 the equation m(A) = 1 has two solutions, which we define as $A_S^b$ and $A_U^b$, where $A_S^b<A_U^b$.

• A6We consider the case where the substrate inflow is in excess, by which we mean f(G_in) ≈ μ_1,max and consequently, f(G_in) > D (in the original variables). These conditions correspond to f(1) ≈ μ_1,max and f(1) > 1 in the dimensionless setting.

Fig. 2.

Qualitative sketch of the growth and inhibition functions: (a) f(G), (b) I(A), and (c) m(A) in nondimensional variables. The solutions to the equation m(A) = 1, $A_S^b$ and $A_U^b$, are shown in panels (b) and (c).

We use the product form of the function μ₁(G, A) = f(G)I(A) since it captures the growth and non-competitive inhibition of pathway 1 and simplifies the analysis. However, a more general function μ₁(G, A) with the properties (∂μ₁(G, A)/∂G > 0) for all G > 0 and (∂μ₁(G, A)/∂A) < 0 for all A > 0 may be used if inhibition is known to be competitive.

3. Main results

In this section we present our main result, the proof of which can be found in the Appendix. The implications of this technical result are then demonstrated with an example from a realistic situation in the following sections.

3.1. Binary culture system equilibria and stability

For the binary culture (9) we differentiate between three different types of equilibrium points: trivial equilibria where x₁ = 0, x₂ = 0, boundary equilibria where x₁ ≠ 0, x₂ = 0 (note there are no x₁ = 0, x₂ ≠ 0 equilibria, as G is the only substrate provided to the chemostat system), and co-existence equilibria where x₁ ≠ 0, x₂ ≠ 0. We consider only equilibria in the positive cone $(x_1,x_2,G,A)\in {ℝ}_{+}^4$.

Theorem 1

Given Assumptions [A 1]–[A 6] in Section 2.3, the binary culture system (9) has the following equilibria:

1. There exists a trivial equilibrium when there are no microbes in the system at (x₁, x₂, G, A) = (0, 0, 1, 0), for all functions satisfying [A 2]–[A 4]. This trivial equilibrium point is an unstable saddle for all parameter values satisfying [A 5]–[A 6].

2. There exists a boundary equilibrium point, where only x₁ survives, at $(x_1^1,x_2^1,G^1,A^1)=(1-G^1,0,G^1,1-G^1)$, where G¹ is implicitly defined by f(G¹)I(1 − G¹) = 1. The stability depends on the specific functions and parameters.

3. We define a value $A=A_{\text{crit}}^b$, where $A_{\text{crit}}^b$ is implicitly defined by $I(A_{\text{crit}}^b)=1/{\mu }_{1,\mathit{max}}$.

   1. If $A_{\text{crit}}^b<A_S^b$, or if $A_S^b<A_{\text{crit}}^b$ but $G_S^b+A_S^b>1$, there are no co-existence equilibria. The boundary equilibrium point is a stable node.

   2. If $A_S^b<A_{\text{crit}}^b<A_U^b$, and $G_S^b+A_S^b<1$, or if $A_U^b<A_{\text{crit}}^b$, and $G_S^b+A_S^b<1$, but $1<G_U^b+A_U^b$, there is a single, stable, co-existence equilibrium point $S:=(x_{1,S}^b,x_{2,S}^b,G_S^b,A_S^b)$. The boundary equilibrium point is an unstable saddle.

   3. If $A_U^b<A_{\text{crit}}^b$, and $G_U^b+A_U^b<1$, there are two co-existence (x₁ ≠ 0, x₂ ≠ 0) equilibria, $S:=(x_{1,S}^b,x_{2,S}^b,G_S^b,A_S^b)$ and $U:=(x_{1,U}^b,x_{2,U}^b,G_U^b,A_U^b)$. The point U is an unstable saddle, and the point S is a stable node. The boundary equilibrium point is a stable node.

Proof

Appendix A

Remark 1

The conditions related to $A_{\text{crit}}^b$ ensure that the equation f(G)I(A) = 1 has a solution for the given A^b value. The conditions G^b + A^b < 1 ensure that the equilibrium biomass values (x₁ and x₂) are strictly positive; if G^b + A^b > 1 then $x_{2,U}^b<0$ and the equilibrium point is non-physical.

Remark 2

Note that in case (iii) of Theorem 1c the system is bistable, with the stable manifold of the saddle point U forming a separatrix that separates the basins of attraction of the two stable equilibria, S and the boundary equilibrium point.

3.2. Monoculture system equilibria and stability

For the monoculture system (10), there are two types of equilibria: trivial equilibria where x = 0 and non-trivial equilibria where x ≠ 0.

Theorem 2

Given Assumptions [A 1]–[A 6] in Section 2.3, the monoculture system (10) has the following equilibria:

1. There exists a trivial equilibrium point at (x, G, A) = (0, 1, 0), which is an unstable saddle.

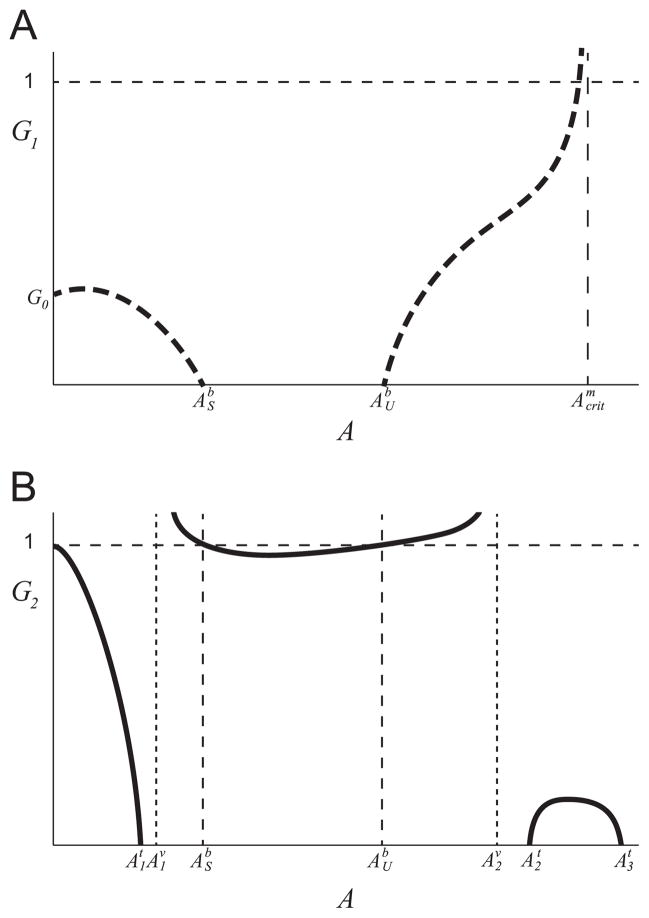
2. There are 2n + 1 non-trivial (x ≠ 0) equilibria $E_i:=(x_i^m,G_i^m,A_i^m)$ in the region $A<A_S^b$, where n ≥ 0, ordered by increasing $A_i^m$. If there is a unique internal equilibrium (n = 0) this equilibrium point is a stable node. If there are multiple internal equilibria, the odd equilibria (i = 1, 3, …, 2n + 1) are stable nodes, and the even equilibria (i = 2, 4, …, 2n) are unstable saddles.

3. If the curve G = 1 − A/(1 + γ − γ/(1 − m(A))) intersects the curve f(G)I(A) + m(A) = 1, in the region $A>A_U^b$, then there is an even number of equilibria K_j, j = 1, …, 2m. If we order these equilibria by increasing value of A, then the odd equilibria are saddles and even equilibria are nodes.

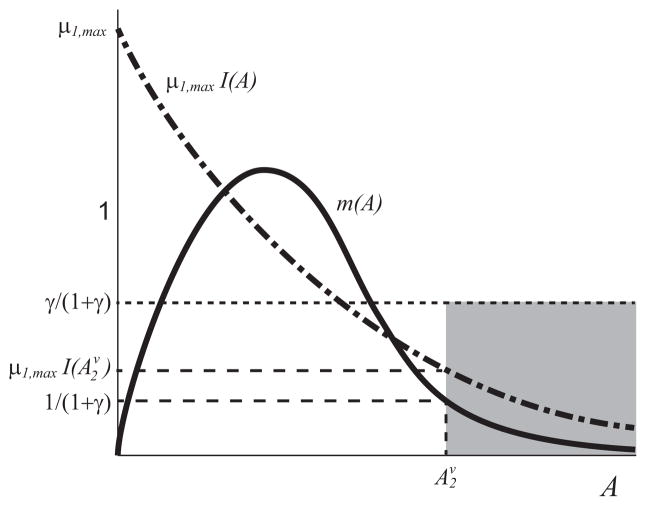
   These curves can only intersect if m(A) = 1 − γ/(1 + γ − A) has more than one solution. This condition is illustrated in Fig. B3. If

   $${\mu }_{1,\mathit{max}}I(A_2^v)<\frac{\gamma }{1+\gamma },$$ (14)

   these equilibria do not exist, where $A_2^v$ is the upper solution of m(A) = 1/(1 + γ). This condition is illustrated in Fig. 3.

Fig. 3.

Qualitative sketch of the curves m(A) (solid black curve) and μ_1,maxI(A) (dot-dash black curve) that satisfy the sufficient condition in Theorem 2c ruling out the upper monoculture equilibria. The curve μ_1,maxI(A) lies in the shaded region defined by the value $m(A_2^v)$, where $A_2^v$ is the upper solution of m(A) = 1/(1 + γ).

Proof

Appendix B

Remark 3

The equilibria K_j only exist in specific circumstances when the monoculture growth is less inhibited by acetate than the acetate consuming specialist (see (14) for exact statement), while at least one lower equilibrium E_i exists for all parameter values satisfying [A1]–[A6]. The high A (low biomass) stable equilibria, when they exist, have a small basin of attraction, which is characterized by high levels of acetate and low levels of glucose. Only initial conditions with high initial acetate and low glucose can lead to a monoculture that evolves to such stable equilibrium. For this reason, we do not consider these equilibria in the results below.

3.3. Biomass comparison

We wish to compare the productivity of the binary culture and monoculture systems, using their total biomass as a measure of productivity.

The biomass for the binary system is largest at the stable coexistence equilibrium point S, since it can be easily shown that $x_{1,S}^b+x_{2,S}^b>x_1^1$ (see Appendix C). The monoculture system has (at least) one stable non-trivial equilibrium point E_i, with high biomass. Since we do not consider the possible upper equilibria K_j with low biomass to be physical, we will compare the biomass at the binary system equilibrium S with an arbitrary monoculture equilibrium E_i.

Theorem 3

Given Assumptions [A 1]–[A 6] in Section 2.3, and the existence of at least one (stable) co-existence equilibrium point, S, in the binary system (conditions in Theorem 1c). Then the biomass of the monoculture, $x_i^m$, at any of the stable non-trivial equilibrium points E_i for i = 1, 3, …2n + 1 is always higher than the total biomass of the binary culture system $x_{1,S}^b+x_{2,S}^b$ at its stable co-existence equilibrium point S:

$$x_i^m>x_{1,S}^b+x_{2,S}^b.$$

Proof

Appendix C

Outline of the proof

We show in Appendix C that the monoculture biomass is given by

$$x^m=\left(1+\frac{1}{\gamma }\right)(1-G^m)-\frac{A^m}{\gamma },$$ (15)

and the combined biomass of the binary culture is

$$x_{\mathit{tot}}^b=x_{1,S}^b+x_{2,S}^b=\left(1+\frac{1}{\gamma }\right)(1-G_S^b)-\frac{A_S^b}{\gamma }.$$ (16)

We can also show that for all E_i monoculture equilibria:

$$G_S^b>G_i^m\text{and}{A}_S^b>A_i^m.$$ (17)

Thus,

$$\left(1+\frac{1}{\gamma }\right)(1-G_S^b)-\frac{A_S^b}{\gamma }<\left(1+\frac{1}{\gamma }\right)(1-G^m)-\frac{A^m}{\gamma }$$

and the biomass of the binary culture is always less than the biomass of the monoculture:

$$x_{1,S}^b+x_{2,S}^b<x^m.$$

Remark 4

If there are no upper equilibria in the monoculture, E_i for i = 1, 3, …2n + 1 are the only stable equilibrium points of the system, and the monoculture biomass will always be higher than the total biomass of the binary culture, for all initial conditions $(G,A)\in {ℝ}_{+}^2$.

4. Effect of modifications to the model on relative biomass

In chemostat experiments, a binary culture of the type analyzed here shows a biomass increase of around 20% over a wild-type monoculture system (Bernstein et al., 2012). As we have shown in Theorem 3, under our assumptions the monoculture system always has a higher biomass. Clearly this means that one or more of the assumptions that we make in Section 2 are incorrect. This is useful, as by examining the assumptions we made, we can investigate which of the effects that we did not include are most relevant.

One of the assumptions we made in formulating the initial model is that there is no change in the growth dynamics or yields of the metabolic pathways when the microbes specialize to a single substrate. However, as discussed already, there is evidence that the growth dynamics and pathway efficiencies will change, and we will investigate the effects of incorporating these changes in this section.

4.1. Increasing the growth rates in the binary culture system

Experiments have observed that growing E. coli on a single nutrient source can increase its growth rate ~15–20% (Edwards et al., 2001; Ibarra et al., 2002; Bernstein et al., 2012), as the microbe adapts to the single nutrient and can up regulate the transport for that substrate (Oh et al., 2002) and down regulate the transport for the pathways it is not using (catabolite repression, Egli et al., 1993; Lendenmann and Egli, 1922). We can incorporate the effect of increasing the growth rate of the species in the binary culture system by introducing multiplicative parameters α₁ and α₂ in front of growth rates f(G) and m(A), thus making the replacements:

$$f(G)\to {\alpha }_{1}f(G),m(A)\to {\alpha }_{2}m(A).$$ (18)

Note that this increases the growth rates at all concentrations of G and A, not just for high growth regions of G or A. For the original systems (with no change in growth rate) we have α₁ = 1, α₂ = 1. To simulate an increase in growth rate when the metabolic pathways are split up we simply choose α₁, α₂ > 1 in the binary culture system.

Increasing α₁ decreases $G_S^b\to 0$, while increasing α₂ in the binary culture moves $A_S^b\to 0$, which in turn decreases $G_S^b$ (bounded below by G₀). We find that it is always possible to get higher biomass for the binary culture than the monoculture ( $G_S^b<G^m,A_S^b<A^m$) if there are no bounds on the increases for both α₁ and α₂. If we can only vary one pathway’s growth rate, i.e., keeping α₁ = 1 or α₂ = 1, then it is not always possible to get higher biomass in the binary culture. Whether or not it is possible to surpass the monoculture biomass, and the increases in growth rate required, will depend on the specific functions and parameters for the system of interest.

4.2. Increasing the substrate affinity in the binary culture system

When growing on a single carbon source, it has been found that some microbes, including E. coli, can increase their affinity when the concentration of the substrate remains low for an extended period of time (Helling et al., 1987; Senn et al., 1994). This is thought to be achieved through up-regulating higher affinity transporters (Ferenci, 1996). Decreasing K_G, moves $G_S^b\to 0$, while decreasing K_A moves $A_S^b\to 0$, which in turn decreases $G_S^b$ (bounded below by G₀). This matches the effects of increasing the growth rates by a factor α₁ or α₂ in Section 4.1. We can explain this mathematically as follows: in the region where G (or A) is low, increasing the substrate affinity acts to increase the growth rate for that G (or A) value. By considering f(G) at low G, we find that f(G) ≈ (μ_1,max/K_G)G for small G, so increasing μ_1,max or decreasing K_G by the same factor should have the same effect.

4.3. Varying the form of the monoculture growth rate

It could be argued that the monoculture out-performs the binary culture in our formulation due to the way we have described the monoculture growth rate (μ_WT(G, A) = f(G)I(A) + m(A)). In this formulation we are assuming that the microbe can use both pathways concurrently, with both functioning at their maximal rates for the specific G and A. This acts as an upper bound on the maximal possible growth rate for the monoculture. In reality, there are limitations due to the transport of nutrients into the cell and the energy required for the synthesis and maintenance of metabolic enzymes. It has been observed experimentally that often a microbe preferentially consumes the substrate sustaining the higher growth rate (catabolite repression). In this process, the synthesis of enzymes required for alternate pathway is down-regulated, which would decrease the maximal growth rate of these other pathways. If we assume that the cell must choose to allocate resources between the two pathways, we can incorporate this into our model by making the monoculture’s growth rate a convex combination of the two pathways’ growth rates:

$${\overline{\mu }}_{WT}=\beta f(G)I(A)+(1-\beta )m(A).$$ (19)

where β could be some function of the relative growth rates of the two pathways at the given G and A concentrations, following (Abrams, 1987; Egli et al., 1993; Lendenmann and Egli, 1922).

According to catabolite repression the microbe will only consume the preferred substrate. However, if the intermediate substrate is inhibitory there is often a ‘switch’ that overrides this effect at high A to consume the excess intermediate substrate and decrease the inhibitory effects (Wolfe, 2005). In our model, we could incorporate this by using (19), with β being a function of A, switching to low β (increased A consumption) when A reached a critical value, even in the presence of high G.

Using μ̄_WT, we cannot get theoretical results for the relative productivity of the monoculture and binary culture systems in general, as the biomass will depend on the specific situation and the β values (or functions) chosen. However, we can easily show that for sufficiently high or low β the binary culture system would now out-perform the monoculture system:

• At β = 1, the monoculture growth rate is given solely by f(G)I(A), which is the equivalent of the binary culture system with x₂ = 0. In Appendix C we showed that this x₁-only equilibrium point has a lower biomass than the binary culture system coexistence equilibrium point, thus the binary culture outperforms the monoculture.

• As β → 0, the monoculture growth rate is increasingly dependent on the second pathway, m(A), which consumes exclusively acetate A. Since glucose G is the only substrate provided to the chemostat, we expect that the monoculture will not survive.

Based on optimal foraging theory and experiments, it is reasonable to assume that E. coli feeding on multiple substrates would allocate resources to pathways such that the growth rate is maximized (Abrams, 1987; Egli et al., 1993; Lendenmann and Egli, 1922), and this is indeed what is found with catabolite repression. In a chemostat at equilibrium, the growth rate is always fixed to the dilution rate D, so we cannot determine the optimum β value at equilibrium. One option could be to first find the β values required for the monoculture system to have lower biomass (for a given system), then to use the optimal foraging arguments to determine whether these β values are realistic by looking at the ratio of μ₁–μ₂ for the given G and A values. Another option would be to look at what β value maximizes biomass, and consider whether this leads to higher biomass in the monoculture than the binary culture, and whether this is a reasonable β value. We will consider both in Section 5.2.3 for the specific example of E. coli growing on glucose.

4.4. Increasing the efficiencies (yields) in the binary culture system

The yield terms Y₁₁ and Y₂₂ describe the amount of biomass produced per unit of substrate consumed, and are a measure of the microbe’s efficiency. The yields are determined by only two factors: how much energy the pathway can produce (given by the stoichiometry of the pathway), and how much of the energy produced is allocated to biomass production.

There are many ways that microbes can adapt to optimize their productivity, but only some of these will increase the yield terms in our formulation. For example, it is observed that when provided with multiple substrates, cells will consume the most productive substrate preferentially (also known as catabolite repression). In this way, the microbes are utilizing the most efficient pathways and thus increasing their efficiency. In our model the binary culture microbes only have one substrate, and thus catabolite repression will not affect their dynamics. In the monoculture, catabolite repression would lead to the most efficient pathways being prioritized. This increase in resources would increase the substrate uptake and growth rate of the preferred pathway, and could be incorporated into our model through changing the parameter β as described above, where β = 1 describes consumption of the primary substrate only. However, as the stoichiometry of the pathways does not change, this effect would not directly change Y₁₁ or Y₂₂ in our model.

In order to increase the yield, a microbe must reduce the energy that is required for functions other than biomass production, such as cell homeostasis and enzyme production. Microbes growing on a single source are thought to down-regulate the production of enzymes for the metabolism of other substrates (Johnson et al., 2012). Since the synthesis and maintenance of metabolic enzymes requires energy, if a microbe can reduce its net enzyme production in this way, this would reduce the energy required and its yield would increase. Thus it is possible that by specializing to a single substrate, the yields Y₁₁ and Y₂₂ would increase.

Another factor that could affect the energy requirements, is the cost of transporting substrates into the cell. So far we have not included this cost. If we were to include the cost of transporting the primary substrate G into the cell, this would decrease the term Y₁₁ in both binary and monoculture systems equally. Including the cost of transporting the inhibitory intermediate substrate A into the cell, would decrease Y₂₂. The binary culture needs to transport all of the consumed A into the scavenger specialist x₂, whereas the monoculture can metabolize intracellular A as it is produced, as well as transporting A into the cell, thus deflecting some of this cost. Therefore, Y₂₂ would decrease more in the binary culture than in the monoculture system.

Examining the equations for steady-state biomass we find that changing Y₁₁ does not affect the nondimensionalized binary biomass, but from Eq. (8) it will affect the actual (dimensional) biomass. The total biomass of the binary culture increases when Y₁₁ increases (the G-metabolism pathway becomes more efficient). When Y₂₂ increases (the A-metabolism pathway becomes more efficient), or when Y₂₁ decreases (the amount of inhibitory metabolite produced increases), γ decreases, which will increase the total biomass of the binary culture. As discussed in Section 2.1, the ratio r = Y₁₁/Y₂₁, which describes the grams of the inhibitory intermediate substrate produced per gram of primary substrate consumed, is fixed for a specific metabolic pathway. Therefore, varying Y₂₁ or Y₁₁ independently is not realistic, and in the latter analysis we will vary Y₁₁ and Y₂₁ together, keeping r constant. When making increases to Y₁₁ or Y₂₂ we must keep in mind that there is an upper bound on the yield terms that given by the stoichiometry of the utilized metabolic pathway. Whether the yield increase required to match the observed increase in biomass for the binary culture is above that bound will depend on the system of interest.

4.5. Varying G_in and D

Some earlier work has found that the binary culture is favored over a monoculture for certain substrate inflow concentrations G_in or dilution rates D (Doebeli, 2002; Pfeiffer and Bonhoeffer, 2004). However, we find that for all G_in and D, satisfying assumptions [A5] and [A6], the monoculture has higher biomass than the binary culture. That being said, the difference in total biomass between the two systems will vary as G_in and D change, so there may be some experimental conditions where the binary culture is less disadvantaged, and where the aforementioned modifications would be more effective.

5. Specific example using Monod kinetics and typical values for E. coli

In this section, the results of this paper will be applied to the specific example of E. coli growing on glucose as the sole carbon source. Experimentally observed parameters for E. coli growth on glucose or acetate are summarized in Table 1. In the majority of the literature, E. coli were grown in aerobic conditions in which both pathways would be utilized. This will lead to overestimation of the parameters: μ_1,max, Y₁₁, Y₂₁, K_IP, and underestimation of the parameter r.

Table 1.

Typical parameter values for E. coli grown on glucose or acetate as the carbon source. See Table D1 for further details of the strains used and the specific experimental conditions.

Parameter	Experimental values
Maximum growth rate on glucosea (h−1)	0.43–0.49b (Bernstein et al., 2012), 0.57 (Chen et al., 1997), 0.43 (anaerobic) (Chen et al., 1997), 0.76 (Dykhuizen, 1978), 0.53 (Farmer and Liao, 1997), 0.39 (Fuhrer et al., 2005), 1.12 (Guardia and Calvo, 2001), 0.91 (Kleman and Strohl, 1994), 0.77 (Natarajan and Srienc, 2000), 0.57 (Paalme et al., 1997), 0.92 (Senn et al., 1994), 0.55–1.23 (Senn et al., 1994), 0.68 (Varma and Palsson, 1994), 0.43 (anaerobic) (Varma and Palsson, 1994), 0.54–0.55 (Xu et al., 1999)
Half-saturation glucose concentrationa (mg/L)	7.2 (Dykhuizen, 1978), 0.04–180 (Ferenci, 1996), 100 (Guardia and Calvo, 2001), 4 (Kleman and Strohl, 1994), 0.68 (Natarajan and Srienc, 2000), 0.0072 (Senn et al., 1994), 0.0053–99 (Senn et al., 1994), 50 (Xu et al., 1999)
Acetate product inhibition constanta (g/L)	4 (Guardia and Calvo, 2001), 4–5 (Xu et al., 1999), 9 (Xu et al., 1999)
Maximum growth rate on acetate (h−1)	0.11–0.15c (Bernstein et al., 2012), 0.31 (Edwards et al., 2001), 0.19 (Guardia and Calvo, 2001), 0.33 (Oh et al., 2002), 0.22 (Paalme et al., 1997), 0.05 (Xu et al., 1999), 0.06–0.08 (Xu et al., 1999)
Half-saturation acetate concentration (g/L)	0.4 (Guardia and Calvo, 2001), 0.05 (Xu et al., 1999)
Acetate substrate inhibition constant (g/L)	3.8 (Guardia and Calvo, 2001)
Biomass yield (gBiomass/gGlucose consumed)a	0.23 (Bernstein et al., 2012), 0.26 (Chen et al., 1997), 0.18 (anaerobic) (Chen et al., 1997), 0.3 (Farmer and Liao, 1997), 0.30 (Fuhrer et al., 2005), 0.43 (Kleman and Strohl, 1994), 0.50 (Paalme et al., 1997), 0.36 (Varma and Palsson, 1994), 0.13 (anaerobic) (Varma and Palsson, 1994), 0.52 (Xu et al., 1999), 0.49–0.51 (Xu et al., 1999), 0.15 (anaerobic) (Xu et al., 1999)
Acetate yield (gBiomass/gAcetate produced)a	0.4 (Guardia and Calvo, 2001), 0.3–0.9 (Kleman and Strohl, 1994)
Ratio (gAcetate produced/gGlucose consumed)a	0.25 (Farmer and Liao, 1997), 0.38 (Kleman and Strohl, 1994)
Biomass yield (gBiomass/gAcetate consumed)	0.38 (Edwards et al., 2001), 0.21–0.30 (Paalme et al., 1997), 0.4 (Xu et al., 1999)

^athe growth and yield of wildtype E. coli on glucose includes contributions from the acetate metabolism pathway, except in anaerobic conditions.

^bgrowth rate of mutant with acetate consumption pathway knocked out.

^cgrowth rate of mutant with glucose consumption pathway knocked out.

We can quantify the discrepancy between the actual yield of each pathway and the reported yield in wild-type aerobic conditions. If we assume that the growth rate from the first (anaerobic) pathway is given by μ₁ and the growth from the aerobic metabolism of acetate (acetyl CoA) is given by μ₂, then the discrepancy between the actual yield of each pathway and the reported yield in wild-type aerobic conditions will be

• The reported yield ${\mathrm{Y}}_{11}^{WT}$ (gBiomass/gGlucose consumed) will be overestimated by $Y_{11}^{WT}=Y_{11}({\mu }_1+{\mu }_2)/{\mu }_1$.

• The reported acetate production yield ${\mathrm{Y}}_{21}^{WT}$ (gBiomass/gAcetate produced) will be overestimated by $Y_{21}^{WT}=Y_{21}({\mu }_1+{\mu }_2)/({\mu }_1-\gamma {\mu }_2)$.

• The observed ratio r^WT (gAcetate produced/gGlucose consumed) will be underestimated by r^WT = r(1 − γμ₂/μ₁).

From the equation for ${\mathrm{Y}}_{11}^{WT}$ it can be seen that if μ₂ = 0 (i.e. there is no metabolism of acetate, which occurs in anaerobic conditions), then $Y_{11}^{WT}=Y_{11}$. Thus, in order to estimate the parameters of just the first pathway (max f(G) and Y₁₁), we use the yield and growth parameters from anaerobic experiments (Chen et al., 1997; Varma and Palsson, 1994; Xu et al., 1999). To estimate Y₂₁ we use the ratio r = 0.667 determined by the reaction stoichiometry and calculate Y₂₁ = Y₁₁/r. Substituting reasonable values for growth rates, we find that our choice of parameters leads to observed ${\mathrm{Y}}_{21}^{WT}{r}^{WT}$ that match experimental data (Table 1). The observed growth and yield parameters for E. coli grown on acetate as the sole carbon source provide good estimates for max (m(A)) and Y₂₂. The chosen yields are given in Table 2.

Table 2.

Selected yield values for monoculture and binary culture systems.

Parameter	Selected value	Notes
Y11	0.152	from anaerobic growth experiments reaction stoichiometry calculated, Y21 = Y11/r
r = Y11/Y21	0.667
Y21	0.227
Y22	0.400

It is important to note that for the yield terms Y₁₁ and Y₂₂, which are the grams of biomass produced when one gram of substrate is consumed, only some of the energy from the substrate metabolism will go towards biomass synthesis. Depending on the efficiency of the pathway, the energy produced per gram of substrate will vary, and the energy required for cell homeostasis (i.e. not available for biomass production) also varies. Estimates for the ratio of energy produced that goes towards biomass production and the efficiencies of the pathways used vary depending on the E. coli strain and the environmental conditions (Carlson and Srienc, 2004; Han et al., 1992). We choose to use measured values for the total yield from the literature. These yields could vary with strain and condition, and we will consider this in Section 5.2.3. In all cases the yields are bounded above by the stoichiometry of the most efficient biomass production pathways assuming zero energy required for cell homeostasis, and our choices for yield parameters are below this bound and consistent with experimental findings.

To fit growth parameters, we must choose specific functions for f(G), I(A), and m(A). Here we select Monod type kinetics for the growth and inhibition functions:

$$f(G)={\mu }_{1,\mathit{max}}\frac{G}{G+K_{\mathrm{G}}},$$ (20)

$$I(A)=\frac{K_{\text{IP}}}{K_{\text{IP}}+A},$$ (21)

$$m(A)={\mu }_{2,\mathit{max}}\frac{A}{A+K_{\mathrm{A}}+\frac{A^2}{K_{\text{IS}}}}.$$ (22)

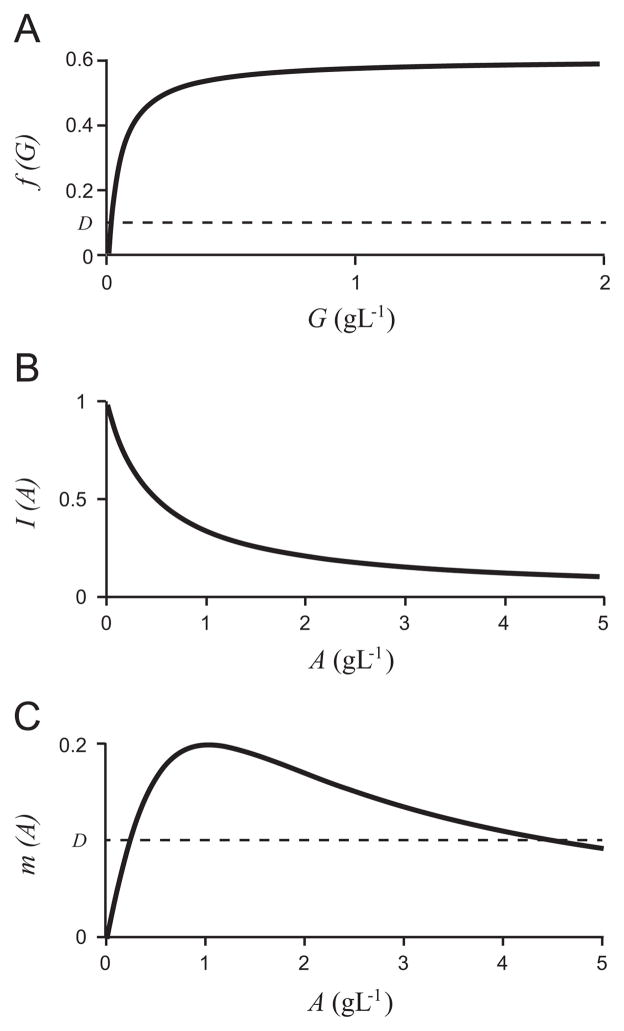
which satisfy assumptions [A2]–[A4] and are found to be appropriate for describing growth and inhibition rates of E. coli in chemostats or batch growth. With the exception of the half-saturation of glucose, K_G, experimental findings (Table 1) are reasonably consistent and the chosen parameters for these functions are given in Table 3.

Table 3.

Selected parameter values for growth and inhibition functions given in Eqs. (20), (21), (22), dilution rates, and substrate inflow concentrations.

Parameter	Selected value	Notes
μ1,max	0.6 h−1	max (f(G)) = 0.6 h−1
KG	0.05 g/L
KIP	0.5 g/L
μ2,max	0.8 h−1	max (m(A)) = 0.2 h−1
KA	1.5 g/L	half-saturation at A=0.23 g/L
KIS	0.7 g/L	inhibited to half maximum at A=4.6 g/L
D	0.1 h−1	chosen to prevent wash-out
Gin	10 g/L	chosen to ensure excess substrate

At low glucose concentrations it is known that glucose affinity increases (Ferenci, 1996; Helling et al., 1987), and the parameter K_G varies from O(0.01) to O(100) mg/L (Table D1) through the upregulation of higher affinity (and often slower or more energy intensive) pathways. In our model, K_G is a fixed parameter, and to demonstrate the results of this paper we choose an intermediate K_G value (see Table 3). This choice does not affect our result, as for equal substrate affinities the monoculture will outperform the binary culture for any choice of K_G (Theorem 3). We will investigate the effect of varying the glucose affinities between the monoculture and the binary culture in Section 5.2.2. However, as increases in glucose affinity are found to depend mostly on the growth conditions, we would expect any increase in glucose affinity (K_G) to affect both the monoculture and the binary culture similarly.

In E. coli there are two pathways for acetate assimilation: the phosphotransacetylase-acetate kinase (PTA-ACKA) pathway and the acetyl-CoA synthetase (acs) pathway. The PTA-ACKA pathway has lower substrate affinity, with K_m ≈ 0.4 – −0.6 g/L (Brown et al., 1977; Wolfe, 2005), but is more efficient requiring only one ATP for acetate assimilation. The PTA-ACKA pathway is found to be active until acetate gets to low concentrations (A « 0.15 g/L) (Kumari et al., 1995). In contrast, the acs pathway has higher substrate affinity, with K_m ≈ 0.01 g/L (Brown et al., 1977; Wolfe, 2005), but is more energy intensive, requiring two ATP for acetate assimilation. Kumari et al. (1995) find that both pathways are required for optimal growth on acetate across a range of concentrations, with the acs pathway being required for A < 0.6 g/L and the PTA-ACKA pathway being required for A > 1.5 g/L.

In our model, we use a single function m(A) and single yield term Y₂₂ to describe the growth kinetics and efficiency of growth on acetate; we do not include the two pathways separately. We choose growth parameters μ_2,max, K_A, and K_IS that match the experimentally observed growth in chemostat cultures which are utilizing both pathways. For example, the combined growth kinetics has a substrate affinity of K_m = 0.23 g/L which is midway between the K_m values of each pathway. We will investigate the effect of varying the acetate affinities between the monoculture and the binary culture in Section 5.2.2.

The yield parameter Y₂₂ is fixed, so we have chosen Y₂₂ = 0.4 which is at the lower end of the yields observed across a range of growth conditions (Kleman and Strohl, 1994). This is because we find that in our model acetate concentrations stay low and the yield will be determined predominantly by the lower efficiency, higher affinity acs pathway.

The dilution rate D and the glucose inflow concentration G_in are set by experimental conditions. We must select a dilution rate that satisfies non-wash-out conditions (from assumption [A6]: max(m(A)) > D, μ_1,max > D). This leads to a low dilution rate (D = 0.1) due to the low value of max(m(A)) > D seen experimentally. We also choose a high substrate inflow G_in » G₀, so that the system is in glucose-excess conditions (assumption [A5]).

For the selected functions and parameter values, the growth and inhibition curves are depicted in Fig. 4. We graph them in terms of the original variables, glucose concentration, G (g/L), and acetate concentration, A (g/L), for ease of comparison to the experimental literature (Table 1). However, for the remainder of the analysis we will use the dimensionless variables and parameter values unless otherwise stated. We use the nondimensionalization in Eqs. (8) and the parameter scalings:

$$\begin{array}{l}{\widehat{\mu }}_{1,\mathit{max}}=\frac{{\mu }_{1,\mathit{max}}}{D},{\widehat{\mu }}_{2,\mathit{max}}=\frac{{\mu }_{2,\mathit{max}}}{D},\widehat{K_G}=\frac{K_G}{G_{in}},\\ \widehat{K_A}=\frac{K_A}{{rG}_{in}},\widehat{K_{\text{IS}}}=\frac{K_{\text{IS}}}{{rG}_{in}},\widehat{K_{\text{IP}}}=\frac{K_{\text{IP}}}{{rG}_{in}}.\end{array}$$ (23)

where r = Y₁₁/Y₂₁.

Fig. 4.

The functions f(G), I(A), and m(A) (20, 21, and (22), respectively), in the original (dimensional) variables, for the chosen parameter values.

5.1. Monoculture and binary culture with no changes

In the monoculture system (10), for growth and inhibition functions (20)–(22) and parameter values in Tables 2 and 3, we find a unique non-trivial equilibrium at

$$(x_1^m,G_1^m,A_1^m)=(2.72,0.000418,0.0197).$$

In the binary culture system (9), there is one stable coexistence equilibrium point

$$(x_{1,S}^b,x_{2,S}^b,G_S^b,A_S^b)=(0.998,1.70,0.00159,0.0337),$$

with x̄_S = 2.70. There is also a stable equilibrium point where only x₁ survives at

$$(x_1^b,x_2^b,G^b,A^b)=(0.371,0,0.629,0.371).$$

The biomass of the monoculture, x = 2.72, is greater than the total biomass in the binary culture at the stable co-existence equilibrium, x̄ = x₁ + x₂ = 2.70, as given by Theorem 3.

5.2. Quantitative investigation of how to increase the binary culture’s relative productivity

In chemostat experiments, a binary culture of this type shows a biomass increase of around 20% over the wild-type monoculture system (Bernstein et al., 2012). In Fig. 5 we plot the curves that determine the equilibrium points of the systems. The biomass is determined by the values of G and A, given in Eqs. (15) and (16), thus in the (A,G)-plane, the curves G = c − A/(1 + γ), for a constant c = 1 − γx_c/(γ + 1), are the lines of constant biomass, x_c. In order for the binary culture biomass to exceed that of the monoculture, the binary culture system must be modified such that the point (A^b, G^b) crosses the dashed line in Fig. 5, or, alternatively, the monoculture system must be modified such that the point (A^m, G^m) crossed the dotted line in Fig. 5. (The only exception to this is if Y₁₁ or G_in are varied between the two systems, as these parameters appear in the non-dimensionalization of the biomass variables.)

Fig. 5.

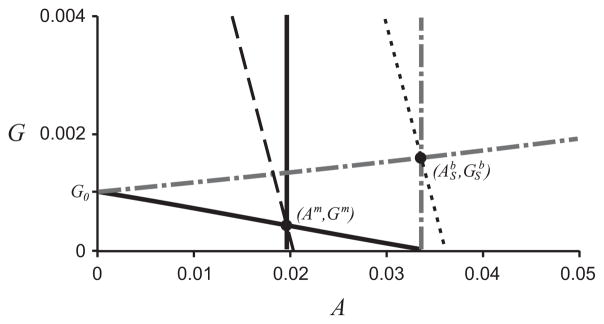
The curves G₁ and G₂, which determine the position of the monoculture equilibrium point(s) in the nondimensionalized system are shown in black solid lines, with the intersection labeled (A^m, G^m). The curves f(G)I(A) = 1 and m(A) = 1, which determine the position of the binary culture equilibrium point(s) are shown in gray dot-dash lines, with the intersection labeled ( $A_S^b,G_S^b$). The lines of constant biomass for the monoculture and binary culture are black dashed and dotted lines, respectively.

5.2.1. Varying growth rates independently

When microbes specialize to grow on a single substrate they are found to increase their growth rate. One explanation for this is that they are able to allocate more resources to synthesizing transporters that increase the substrate uptake rate. By making the substitutions in Eq. (18), we can use parameters, α₁ and α₂ to modify the growth rates independently and perform a more general investigation.

To increase the growth rate of the microbes in the binary culture compared to monoculture we set α₁ > 1, or α₂ > 1, or both. It is important to note that increasing α_i will increase the growth rate of the pathway i by the factor α_i across all substrate concentrations.

• If we only increase the maximal growth rate of the glucose metabolism, α₁, we cannot increase the total biomass of the binary culture to match that of the monoculture, even if α₁ → ∞.

• If we only increase the maximal growth rate of the acetate metabolism, α₂, the binary culture has the same biomass of the monoculture at α₂ = 1.69, i.e., the growth rate has to increase 69%.

• Finally, we allow both α₁ and α₂ to increase then we find multiple combinations of α₁, α₂ where the biomass has the same or larger mass than the monoculture. The combination of multipliers with minimal value of the sum α₁ + α₂ for which the total biomass of the binary culture matches that of monoculture is when we only increase the second pathway, so α₁ = 1 and α₂ = 1.69.

Increases of around 15–20% have been seen experimentally when microbes have been grown on a single substrate. The increases of 70% that are required here are not realistic. Moreover, Bernstein et al. (2012) observed a biomass increase of 20% in chemostat experiments. Even increasing α₂ → ∞ the binary culture biomass never reaches 20% more than the monoculture

5.2.2. Increasing the substrate affinity in the binary culture

In E. coli the experimentally observed glucose affinity varies by orders of magnitude in different experimental conditions (K_m = 0.0053–99 g/L Senn et al., 1994). This is because the bacteria have many different systems to transport and metabolize glucose as a substrate, that all have differing speeds and affinities. If we predict that the glucose specialist (x₁) in the binary system has an increasing substrate (glucose) affinity, we can investigate the effect this would have on biomass production by decreasing K_G in our model.

• Varying K_G we find that there is no decrease in K_G that will lead to the binary system having a higher biomass than the monoculture system. This is expected from our results in Section 5.2.1, since f(G) ≈ μ_1,maxG/K_G at low G, and there is no α₁ that leads to the binary system biomass exceeding that of the monoculture.

Additionally, the phenomenon whereby E. coli in low glucose conditions uses higher affinity transporters would be predicted to occur in both the monoculture and primary microbe in the binary culture, as this depends mostly on growth conditions. If glucose affinities increase but remain equal, the monoculture will still outperform the binary culture by Theorem 3.

If the acetate scavenger specialist (x₂) in the binary culture has an increased acetate substrate affinity, relative to the monoculture, we can investigate the effect this would have on biomass production by decreasing K_A and K_IS in our model.

• Varying K_A (and K_IS) we find that the binary culture has higher biomass when K_A and K_IS decrease to 54% of the monoculture values i.e. an increase in substrate affinity of 85%. This is to be expected from our results in Section 5.2.1, as increasing m(A) by 69% gave a higher biomass for the binary culture, and thus decreasing K_A (which increases the growth rate at low A values) should have a similar effect.

Note: we decrease K_IS concurrently with K_A in order to keep max (m(A)) constant, however, if we only decrease K_A and allow max(m(A)) to increase we see similar results (55% decrease cf. 54% decrease).

A twofold increase in the acetate affinity (halving the K_m value) is within realistic realms, and brings the K_m value of acetate metabolism to 0.12 g/L. However, the higher-affinity acs pathway, that would be required for an increased acetate affinity, is more energy intensive (lower yield); this means that although the increased substrate affinity would act to increase the biomass, the consequent decrease in yield would counteract this increase. In our model formulation, we cannot directly account for the use of different acetate assimilation pathways between the binary culture system and the monoculture in the comparison, as we do not include the two pathways separately. Furthermore, up-regulation of the higher affinity acs pathway has been observed in vivo in wild-type E. coli (Wolfe, 2005) growing on acetate as well, so we consider it difficult to justify a change that increases the binary culture acetate affinity by 85% more than that of the monoculture.

If we take our analysis one step further and attempt to match the observed biomass increase of 20% in the binary culture (Bernstein et al., 2012), we find that there is no increase in substrate affinity (K_m → 0) which can produce the required increase in biomass.

5.2.3. Varying form of the monoculture growth rate

When there is glucose available, E. coli will preferentially consume glucose due to catabolite repression until the acetate concentration gets too high, at which point the E. coli will switch to consuming acetate (Nicolaou et al., 2010; Wolfe, 2005). This effect is incorporated implicitly into our model, as for high G, low A, f(G)I(A) > m(A) and μ_WT ≈ μ₁. Whereas, for high A we find m(A) > f(G)I(A), and μ_WT → μ₂. However, there may be some additional trade-off in the ability of the cell to produce the enzymes required for each pathway, so the increased utilization of one pathway may decrease the growth rate of the other (Oh et al., 2002). We can incorporate this into the model by using the modified growth function for the monoculture system in Eq. (19).

In experiments it is observed that the utilization of the two pathways, and thus the value of the parameter β, depends on the concentration of acetate A (Wolfe, 2005). We will not assume a form for the dependence of β on A, however, by considering the existing experimental evidence we can determine whether the equilibrium acetate concentration and pathway utilization for a given β value is a realistic scenario.

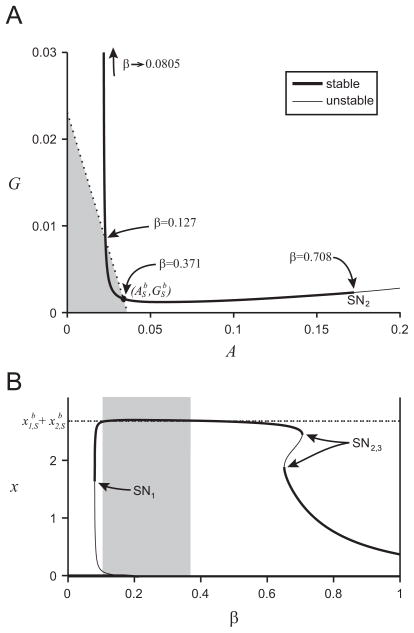
The position in the (A,G)-plane of the equilibrium point for the modified monoculture system as β varies is shown in Fig. 6(a). For β values (0.127 < β < 0.371) the monoculture equilibrium point is to the left of the dotted line (binary culture biomass equivalence), and thus has a higher biomass. As β decreases below β = 0.127 the monoculture equilibrium G value increases, until the monoculture does metabolize enough glucose to survive and the equilibrium point disappears in a saddle-node bifurcation at β = 0.0805 (SN₁). As β increases from β = 0.371, the monoculture equilibrium point disappears in a saddle-node bifurcation at β = 0.708 (SN₂). The system becomes bi-stable at β = 0.653 (SN₃), shown in Fig. 6(b). The lower biomass equilibrium point persists and reaches the x₁-only equilibrium point of the binary culture (A₁, G₁) at β = 1.

Fig. 6.

Panel (a) shows the position of the monoculture equilibrium point in the (A, G)-plane as β varies as a solid black line. The coexistence equilibrium point of the binary culture ( $A_S^b,G_S^b$) is shown as a filled black circle. The dotted line shows the line of constant biomass for the binary culture at the coexistence equilibrium point, equilibrium points to the left of the curve (the shaded area) have a higher biomass than the binary culture. Important β values are labeled in the figure. Saddle-node bifurcations are labeled SN_1,2,3, but only SN₂ is within the range of this figure. Panel (b) shows the biomass (x value) of the monoculture equilibrium point as β varies which is shown as a solid black line; thick where it is stable, thin where it is unstable. The dashed line shows the biomass of the comparative binary culture system, $x_{1,S}^b+x_{2,S}^b$, and the shaded region represents the β values where the monoculture has higher biomass than the binary culture system.

At β = 1 the monoculture is the equivalent of the binary culture system with x₂ = 0, which means it has a lower biomass than the binary culture system coexistence equilibrium point (not shown in Fig. 6). As β decreases from 1, the advantage of being able to consume the acetate increases the monoculture’s biomass. We find that the binary culture only has higher biomass than the monoculture for β > 0.371. However, for β > 0.371 the monoculture reaches an equilibrium point with high acetate concentration, but E. coli are observed to switch to consuming more acetate when the acetate concentration increases (Wolfe, 2005), which means that these high β values (a higher utilization of the glucose consumption pathway f(G)I(A) over the acetate consumption pathway m(A)) are unrealistic.

As β→ 0, the monoculture growth rate is increasingly dependent on the second pathway, m(A), which consumes exclusively acetate A. Since glucose G is the only substrate provided to the chemostat, we expect that the monoculture will not survive. Indeed, for β<0.0805 the monoculture washes out and the biomass of monoculture (x=0) will be less than the biomass of the binary culture.

The optimal β value (to maximize growth rate Abrams, 1987; Egli et al., 1993; Lendenmann and Egli, 1922) will depend on the concentration of G and A. However, for monoculture equilibrium values as β varies the growth rate is set to D by the chemostat dynamics. If we instead predict that the optimal β value would lead to a higher biomass, we find peak monoculture biomass at β = 0.208 (x^m=2.71), and we reach the conclusion that the monoculture would be expected to have a higher biomass than the binary culture.

5.2.4. Varying yields

In this section we examine the effect of varying yields in our model of E. coli growing on glucose. If the microbes in the binary culture are able to reduce their energy requirements when they specialize to a single substrate, the yields Y₁₁ and Y₂₂ would increase. If we include the effect of the cost of transporting acetate into the cell, this would decrease Y₂₂. Here we will assume that the metabolic pathway stoichiometry is fixed, i.e., the ratio r = Y ₁₁/Y₂₁ (grams of acetate produced per gram of glucose consumed) is fixed. The effects of varying the yields are as follows:

• By increasing Y₁₁ (and Y₂₁ as r is fixed) in the binary culture system, that is, reducing the amount of glucose G the primary consumer microbe requires to make one g of biomass x₁, the total biomass of the binary culture can exceed the monoculture biomass. In this example we find that the two systems have equal biomass when Ȳ₁₁ = 1.03 Y₁₁ (and Ȳ₂₁ = 1.03 Y₂₁), which represents an increase in glucose pathway efficiency of 3%.

• By increasing Y₂₂ in the binary culture system, which corresponds to a reduction in the amount of acetate A the secondary scavenger microbe requires to make one gram of biomass x₂, the total biomass of the binary culture can exceed the monoculture biomass. In this example we find that the two systems have equal biomass with Ȳ₂₂ = 1.02 Y₂₂. This represents an increase in acetate pathway efficiency of 2%.

If the ratio r = Y₂₁/Y₁₁ is not fixed, we find that increasing Y₁₁ independently of Y₂₁, we can get the same total biomass with Ȳ₁₁ = 1.01 Y₁₁, and decreasing Y₂₁ independently of Y₁₁ we find that Ȳ₂₁ = 0.98 Y₂₁ gives the same total biomass in both systems. However, in order for Y₂₁ to decrease without Y₁₁ decreasing (or Y₁₁ to increase without Y₂₁ increasing), the glucose consuming microbe would have to utilize different metabolic pathways, with different stoichiometry, that produce more A per G consumed. In experiments, it is observed that wild-type E. coli can modify their metabolic strategies depending on the environmental conditions, specifically, in excess acetate the monoculture is seen to increase the flux through the acetate-metabolism pathway m(A) (Wolfe, 2005). This would be equivalent to varying β in our modified monoculture system (Eq. (19)); the stoichiometry of the pathways would not change. In this application, we argue that it is unrealistic to modify Y₂₁ independently of Y₁₁.

Finally, we can generate the 20% increase in biomass observed in Bernstein et al. (2012) if we increase by the efficiency of the glucose-metabolism pathway (Y₁₁ and Y₂₁) by 57%, or increase the efficiency of acetate-metabolism pathway, Y₂₂, by 34%.

6. Discussion

In this paper we describe a minimal model of a syntrophic chain system in which the metabolism of a substrate is divided into two distinct organisms. We compare this to a monoculture, which is able to completely metabolize the substrate. Under very general assumptions we show that the monoculture will always produce larger biomass than the equivalent binary syntrophic chain system. This finding does not agree with experimental findings from microbial consortial systems, which show higher biomass for consortial systems (Bernstein et al., 2012). Two key assumptions in the creation of our minimal model are that there are no metabolic advantages to dividing the metabolic steps into separate organisms, and that there is no cost to the monoculture for using multiple substrates concurrently. Since the model under these assumptions does not reproduce the increased biomass in the consortium that is observed experimentally, this leads us to conclude that one (or both) of these assumptions is incorrect and allows us to investigate the effect of making these assumptions more realistic. By modifying the minimal model we are able to test hypotheses and investigate the effects of adaptations that can develop in a syntrophic chain system, clarifying the mechanisms that contribute to the experimentally observed advantage. We find that the division of metabolic pathways must have an effect on both the growth and yield of the system.

If we assume that in the binary culture the pathways are able to metabolize the substrate faster (increasing the growth rate), we find that it is sometimes possible to have a higher biomass in the binary culture system. However, considering a specific example from E. coli using typical parameters, the growth rate increases required are much larger than those observed experimentally when an organism adapts to a single food source. Considering instead the possibility of increases in substrate affinity, we find that, for the specific example of E. coli, a twofold decrease in the acetate K_m value for the binary culture relative to the monoculture would lead to higher biomass. However, in similar low substrate conditions acetate affinity increases would be seen in both the monoculture and binary culture, and even if the acetate specialist in the binary culture could increase its substrate affinity, this would not necessarily increase the productivity, as the higher affinity acetate assimilation pathway has a lower yield.

We also test a hypothesis that the efficiencies of the metabolic pathways in the binary culture are increased, as the specialists do not have to produce the enzymes related to the other pathways, reducing the amount of energy required for enzyme synthesis and maintenance, and thereby increasing the proportion of energy that can go towards biomass production (Oh et al., 2002). By varying the yield, it is possible to increase the binary culture’s biomass to match that of the monoculture with an increase of only 2–3% in the parameters Y₁₁ or Y₂₂. This magnitude of yield change is within the range of what is observed experimentally, and we consider this to be the most likely cause of the observed productivity increase in the binary culture.

Comparing our results to past work on the question of whether organisms maximize growth rates or efficiency, we find that two main theories are the Maximum Power Principle (MPP) (DeLong, 2008; Lotka, 1922; Sciubba, 2011) and the Resource Ratio Theory (RRT) (de Mazancourt and Schwartz, 2010; Miller et al., 2005; Tilman, 1982, 1988). The MPP states that systems strive to increase ‘power’ within the system constraints. This has been used to successfully predict the outcome of two species competition experiments (DeLong, 2008). The RRT states that the system/species that can use as much as possible of the resources available (have the lowest amount of ‘wasted’ substrate) will win in a competition experiment (or will evolve) (de Mazancourt and Schwartz, 2010). In summary, MPP argues for maximizing substrate uptake rate, whereas RRT argues for optimizing the growth at low substrate concentrations. In a chemostat with fixed yield, the highest substrate uptake will correspond to the highest growth rate, and these two will be consistent. Thus, in evolution (or competition) in a chemostat, maximizing growth rate or maximizing substrate uptake rate may be advantageous strategies in order to survive.

In this work we are motivated by the observation of increased biomass in a division of labor system (Bernstein et al., 2012), which has important implications for industrial settings. We find that yield maximization should be the advantageous strategy for increasing the biomass production of a chemostat system. In all our work we consider the binary and monoculture systems in isolation, and investigate and compare the optimal productivity (biomass production) of these systems. We are not considering the evolution of these division of labor systems, as there is much work already investigating this and it is not the focus of our work. We are also not considering competition of these two systems, thus the arguments from RRT and MPP are not directly applicable to this situation. Some work has found that evolutionary advantage depends on the stress conditions, with some papers even finding that the ‘optimal’ robust state has lower biomass (Pfeiffer and Bonhoeffer, 2004). This is not unexpected as up-regulating pathways with higher substrate affinities is often more costly (decreased yield), but this enables survival at lower substrate concentrations and thus resistance to invasion.

For E. coli communities, the cross-feeding syntrophic chain system studied in Section 5 has been seen to evolve repeatedly (Rosenzweig et al., 1994; Rozen and Lenski, 2000; Treves et al., 1998). This suggests that there must be some increase in growth rate or substrate affinity following specialization in order for the system to out-compete the original monoculture. When synthetically engineered, this cross-feeding system has been found to have higher productivity (Bernstein et al., 2012). Our model shows that increases in growth rate or substrate affinity are not sufficient to explain this observed increase in productivity, and that an increase in the efficiency (yield) of the syntrophic system must have occurred.

An interesting contradiction that remains is that in the unmodified model $A_S^b>A^m$ for all parameters and growth functions, but in experiments the concentration of the inhibitory intermediate A is observed to be lower in a syntrophic chain system than in a monoculture. If we assume that an increase in efficiency when organisms specialize to a single substrate is sufficient to explain the observed increase in biomass, we find that there is no decrease in $A_S^b$ in the binary culture when we increase the yield Y₂₂ and only a small decrease when we increase the yield Y₁₁. However, increasing the growth rates in the binary system does decrease $A_S^b$. This suggests that increases in both yield (increased efficiency) and growth kinetics play a role in metabolic specialization. By applying our model to experimental data, we will be able to investigate these factors in future work.

HIGHLIGHTS.

• We investigate the division of labor (metabolic function) in microbial systems.

• We compare a syntrophic consortia to a monoculture with equivalent metabolic capability.

• Consortia biomass is always lower than a monoculture with the same metabolic dynamics.

• Increasing the growth rate or substrate affinity does not explain the observed consortial advantage.

• Increased metabolic pathway efficiency (yield) provides the observed increase in productivity.

Appendix A. Binary culture equilibrium points existence and stability

In this appendix we prove Theorem 1.

A.1. Existence of equilibrium points

Equilibrium points in the binary system (9) must satisfy

$$(f(G)I(A)-1)x_1=0,$$ (24)

$$(m(A)-1)x_2=0,$$ (25)

$$1-G-f(G)I(A)x_1=0,$$ (26)

$$-A+f(G)I(A)x_1-\gamma m(A)x_2=0,$$ (27)

1. A trivial equilibrium point, where x₁ = 0, x₂ = 0, must satisfy 1− G = 0 from Eq. (26) and − A = 0 from equation (27). This exists for all functions and parameter values at (x₁, x₂, G, A) = (0, 0, 1, 0).

2. A boundary equilibrium point where only x₁ survives (x₁ ≠ 0) must satisfy:

   $$\begin{array}{l}f(G)I(A)-1=0\text{from}\text{Eq}.(24),\\ 1-G-f(G)I(A)x_1=0\text{from}\text{Eq}.(26),\\ -A+f(G)I(A)x_1=0\text{from}\text{Eq}.(27).\end{array}$$
   A single boundary equilibrium point exists at

   $$(x_1^1,x_2^1,G^1,A^1)=(1-G^1,0,G^1,1-G^1),$$

   where G¹ is the solution to f (G¹)I(1− G¹) = 1.

3. Co-existence equilibrium points, where both x₁ and x₂ survive, are positive solutions $(x_1,x_2,G,A)\in {ℝ}_{+}^4$ that satisfy

   $$f(G)I(A)-1=0\text{from}\text{Eq}.(24),$$ (28)

   $$m(A)-1=0\text{from}\text{Eq}.(25),$$ (29)

   and Eqs. (26) and (27). The co-existence equilibria take the form $1-G_i^b,(1-G_i^b-A_i^b)/\gamma ,G_i^b,A_i^b$ for i = S, U, where $A_i^b$ are the solutions of m(A) = 1 (see Fig. A1(a)), and $G_i^b$ are the solutions to $f(G)I(A_i^b)=1$ (see Fig. A1(b) and (c)).

Given Assumption [A5] in Section 2.3, Eq. (29) has two positive solutions $A_S^b$ and $A_U^b$, where $A_S^b<A_U^b$ (Fig. A1(a)).

For each of these A^b values, Eq. (28) has a unique positive solution for G^b, if and only if 1/I(A^b)<μ_1,max (as shown in Fig. A1 (b) and (c)). Thus, we define the critical A value by $I(A_{\text{crit}}^b)=1/{\mu }_{1,\mathit{max}}$. For $A^b<A_{\text{crit}}^b$ there is a unique positive G^b.

From Eqs. (26) and (27) the biomass at equilibrium is given by $x_1^b=1-G^b$ and $x_2^b=(1-G^b-A^b)/\gamma$. Thus, the biomass of x₂ is only positive if 1− G^b − A^b >0.

The co-existence equilibrium points are the intersections of the curves implicitly defined by f(G)I(A) = 1 and m(A) = 1. The equation m(A) = 1 defines two vertical lines $A=A_S^b$ and $A=A_U^b$ in the (A, G) plane. The slope of the curve $h:=\{(A,G)\in {ℝ}_{+}^2\mid f(G)I(A)=1\}$ is given by

$$\frac{dh}{dA}=\frac{-f\frac{\partial I}{\partial A}}{\frac{\partial f}{\partial G}I}$$ (30)

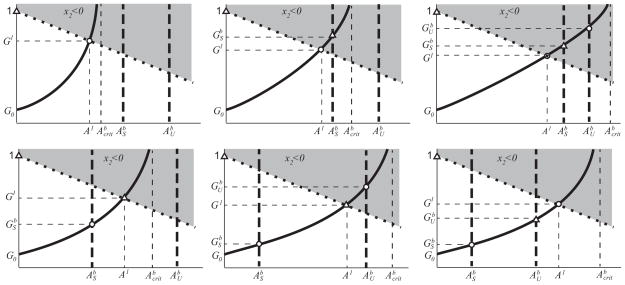
From assumptions [A2] and [A3] this gives dh/dA>0 for all (A, G). The curve has a vertical asymptote at ${\mathrm{A}}_{\mathit{crit}}^b$. As $A\to A_{\mathit{crit}}^b$, we find that f(G)→ μ_1,max, I(A)→1/μ_1,max, G→∞, ∂f/∂G→0, and ∂I/∂A<0. Combining this information, the numerator of dh/dA is positive and bounded away from zero, while the denominator of dh/dA goes to zero, thus dh/dA→∞ as $A\to A_{\mathit{crit}}^b$ from below. The assumptions [A1]–[A6] give six possible cases for the intersections of these curves (shown in Fig. A2). Their intersection is the projection of the co-existence equilibrium points to (A, G) plane.

• There are no co-existence equilibria in the following three cases:

  1. If $A_{\text{crit}}^b<A_S^b$, then $1/I(A_S^b)>{\mu }_{1,\mathit{max}}$ and there are no solutions to Eq. (29) for $A=A_S^b$ or $A=A_U^b$. Thus, there are no co-existence equilibria.

  2. If $A_S^b<A_{\text{crit}}^b<A_U^b$ and $G_S^b+A_S^b>1$. Then $1/I(A_S^b)<{\mu }_{1,\mathit{max}}$ and Eq. (29) with $A=A_S^b$ has solution $G=G_S^b$, but $1/I(A_U^b)>{\mu }_{1,\mathit{max}}$ and there are no solutions to Eq. (29) with $A=A_U^b$. However, as $1-G_S^b-A_S^b<0,x_{2,S}^b<0$ and there are no (positive) co-existence equilibria.

  3. If $A_U^b<A_{\text{crit}}^b$ and $G_S^b+A_S^b>1$. Then $1/I(A_S^b)<{\mu }_{1,\mathit{max}}$ and Eq. (29) with $A=A_S^b$ has solution $G=G_S^b$, and $1/I(A_U^b)<{\mu }_{1,\mathit{max}}$ Eq. (29) with $A=A_U^b$ has solution $G=G_U^b$. However, as $1-G_S^b-A_S^b<0,x_{2,S}^b<0$ and since $G_U^b>G_S^b$ and $A_U^b>A_S^{b}1-G_U^b-A_U^b<1-G_S^b-A_S^b<0$ so $x_{2,U}^b<0$, and there are no (positive) co-existence equilibria.

• There is a single co-existence equilibrium point in the following two cases:

  1. If $A_S^b<A_{\text{crit}}^b<A_U^b$, then $1/I(A_S^b)<{\mu }_{1,\mathit{max}}$ and Eq. (29) with $A=A_S^b$ has solution $G=G_S^b$, but $1/I(A_U^b)>{\mu }_{1,\mathit{max}}$ and there are no solutions to Eq. (29) with $A=A_U^b$. If $1-G_S^b-A_S^b>0$, then $x_{1,S}^b>0$ and $x_{2,S}^b>0$ and there is one co-existence equilibrium point $S:=(x_{1,S}^b,x_{2,S}^b,G_S^b,A_S^b)$.
  2. If $A_U^b<A_{\text{crit}}^b$, then Eq. (29) with $A=A_S^b$ and $A=A_U^b$ has corresponding solutions $G=G_S^b$ and $G=G_U^b$, where $G_S^b<G_U^b$ (see Fig. A1(d)). If $1-G_U^b-A_U^b<0<1-G_S^b-A_S^b$, then co-existence equilibrium point $S:=(x_{1,S}^b,x_{2,S}^b,G_S^b,A_S^b)$ exists, but $x_{2,U}^b<0$ so S is the only co-existence equilibrium point.
• There are two co-existence equilibria in the following case:

  1. If $A_U^b<A_{\text{crit}}^b$, then Eq. (29) with $A=A_S^b$ and $A=A_U^b$ has corresponding solutions $G=G_S^b$ and $G=G_U^b$, where $G_S^b<G_U^b$ (see Fig. A1(d)). If $1-G_U^b-A_U^b>0$, then $1-G_S^b-A_S^b>0$ and $x_{1,S}^b>0,x_{2,S}^b>0,x_{1,U}^b>0$, and $x_{2,U}^b>0$. Therefore there are two co-existence equilibrium point $S:=(x_{1,S}^b,x_{2,S}^b,G_S^b,A_S^b)$ and $U:=(x_{1,U}^b,x_{2,U}^b,G_U^b,A_U^b)$.

A.2. Stability of equilibrium points

We introduce the following variables:

$$w_1(t)=G(t)+x_1(t),$$ (31)

$$w_2(t)=G(t)+\gamma x_2(t)+A(t).$$ (32)

Note that the system obeys a conservation law of material consumed to biomass produced. The rate equations for these new variables are

$${\stackrel{.}{w}}_1=1-w_1$$ (33)

$${\stackrel{.}{w}}_2=1-w_2.$$ (34)

which means that the set ${\mathit{\Omega }}^b:=\{(x_1,x_2,G,A)\in {ℝ}_{+}^4:x_1=1-G,\gamma x_2=1-G-A\}$ is an exponentially attracting two-dimensional invariant subspace of the full ℝ⁴ phase space. The asymptotic behavior of the system is determined by the dynamics on Ω^b, given by

$$\stackrel{.}{G}=1-G-f(G)I(A)x_1(G),$$ (35)

$$\stackrel{.}{A}=-A+f(G)I(A)x_1(G)-\gamma m(A)x_2(G,A),$$ (36)

with x₁(G) = 1 −G, x₂(A, G) = (1 −G −A)/γ. In this reduced system, we consider the region where x₁ ≥0, x₂ ≥0, given by G ≤1 − A in the positive quadrant. The Jacobian of this reduced system is

$$J(G,A)=\left[\begin{array}{cc}-1+fI-\frac{\partial f}{\partial G}{Ix}_1& -f\frac{\partial I}{\partial A}{x}_1\\ -fI+\frac{\partial f}{\partial G}{Ix}_1+m& -1+f\frac{\partial I}{\partial A}{x}_1-\gamma \frac{\partial m}{\partial A}{x}_2+m\end{array}\right],$$ (37)

where x₁ = 1−G, x₂ = (1−G−A)/γ. The trivial equilibrium point (x₁, x₂, G, A) = (0, 0, 1, 0), I(0) = 1 and m(0) = 0 (from Assumptions [A3] and [A4]) and the Jacobian becomes

$$J(G,A)=\left[\begin{array}{cc}-1+f(1)& 0\\ -f(1)& -1\end{array}\right],$$ (38)

which has eigenvalues λ = , −1, f (1) −1. From Assumption [A2] in Section 2.3 we know that 0<f (1)< μ_1,max. When f (1)>1 the trivial equilibrium will have three negative eigenvalues (two from the components normal to Ω^b and one from the 2D reduced subsystem) and one positive eigenvalue, thus it is an unstable saddle. The condition f (1)>1, which corresponds to f (G_in) >D in the original dimensions, is ensured by assumption [A6]: the trivial equilibrium point will be unstable as long as the substrate inflow is in excess.

The boundary equilibrium point (fI=1, x₂ = 0) has the Jacobian

$$J(G^1,A^1)=\left[\begin{array}{cc}-\frac{\partial f}{\partial G}{Ix}_1& -f\frac{\partial I}{\partial A}{x}_1\\ -1+\frac{\partial f}{\partial G}{Ix}_1+m& -1+f\frac{\partial I}{\partial A}{x}_1+m\end{array}\right].$$ (39)

From this we find

$$\text{Tr}(J)=-\left[\left(\frac{\partial f}{\partial G}I-f\frac{\partial I}{\partial A}\right)x_1+(1-m)\right]$$

and

$$\text{Det}(J)=(1-m)\left[\frac{\partial f}{\partial G}I-f\frac{\partial I}{\partial A}\right]x_1(G).$$

The boundary equilibrium point undergoes transcritical bifurcations when m(A) = 1, i.e., when $A^1=A_S^b$ and $A^1=A_U^b$. For $A^1<A_S^b$, m(A¹)<1, Det (J)>0, Tr (J)<0, and (Tr² −4 · Det)>0 and the equilibrium point is a stable node. For $A_S^b<A^1<A_U^b$, m(A¹)>1, Det (J)<0 and the equilibrium point is an unstable saddle. For $A_U^b<A^1$, m(A¹)<1, Det (J)>0, Tr (J)<0, and (Tr² −4 · Det)>0 and the equilibrium point is a stable node again. The vector (A, G) = (1, −1) is a stable eigenvector which lies on the x₂ = 0 invariant line: G = 1−A.

For the co-existence equilibria (fI=1, m=1) the Jacobian becomes

$$J(G,A)=\left[\begin{array}{cc}-\frac{\partial f}{\partial G}{Ix}_1& -f\frac{\partial I}{\partial A}{x}_1\\ -\frac{\partial f}{\partial G}{Ix}_1& f\frac{\partial I}{\partial A}{x}_1-\gamma \frac{\partial m}{\partial A}{x}_2\end{array}\right],$$ (40)

with

$$\text{Tr}(J)=-\left[\left(\frac{\partial f}{\partial G}I-f\frac{\partial I}{\partial A}\right)x_1(G)+\gamma \frac{\partial m}{\partial A}{x}_2(G,A)\right]$$

and

$$\text{Det}(J)=\frac{\partial f}{\partial G}{Ix}_1(G)\gamma \frac{\partial m}{\partial A}{x}_2(G,A).$$

For ( $A_S^b,G_S^b$) in the region x₂ >0, Tr (J)<0 and Det (J)>0, and (Tr² −4 · Det)>0 so the equilibrium point is a stable node. For ( $A_U^b,G_U^b$) in the region x₂ >0, Det (J)<0 and the equilibrium point is an unstable saddle. These equilibrium points go through transcritical bifurcations at x₂ = 0 when they pass through the boundary equilibrium point. Details are shown in Fig. A2.

Fig. A1.

Qualitative sketches of the growth and inhibition curves and positions of equilibria for the case where there are two co-existence equilibrium points. Panel (a) shows the function m(A) showing A_max and the relative positions of $A_S^b$ and $A_U^b$. Panel (b) shows the function I(A) with the relative positions of $A_S^b$ and $A_U^b$. Panel (c) shows function f(G) and the relative positions of $G_S^b$ and $G_U^b$. The position of G₀ defined by f(G) = 1 is shown as well. Panel (d) shows the curves f(G)I(A) = 1 (solid black curve) and m(A) = 1 (dashed black lines). The co-existence equilibrium points projected to (A, G) plane are at the two intersections of these curves. The dotted black line G = 1−A (together with the solid black curve f (G)I(A) = 1) determines the position of the boundary (x₂ = 0) equilibrium point projected into the (A, G) plane. The position of G₀ defined by f(G) = 1 is shown as well.

Fig. A2.

Qualitative sketches of the six possible cases based on assumptions [A1]–[A4] in Section 2.3. Equilibrium points are marked with a circle for stable equilibria and a triangle for unstable equilibria. In the shaded gray region (G>1−A) any solutions are physically unrealistic as x₂ <0. The trivial (x₁ = 0, x₂ = 0) equilibrium point at (0,1) is shown. For all cases, there is a boundary (x₂ = 0) equilibrium point (A¹, G¹) which, when projected into the (A, G) plane, lies at the intersection of the dotted black line G = 1−A together with the solid black curve f (G)I(A) = 1. The curves f (G)I(A) = 1 (solid black curve) and m(A) = 1 (dashed black lines) are shown, the position of co-existence equilibrium points projected to (A, G) plane is at the intersections of these curves. The vertical asymptote of the curve f (G)I(A) = 1 is labeled $A_{\text{crit}}^b$. The position of G₀ defined by f (G) = 1 is shown as well.

Appendix B. Monoculture equilibrium points

In this appendix we prove Theorem 2.

B.1. Existence

Given assumptions [A1]–[A6]

1. The monoculture system (10) has a trivial equilibrium point with x=0, which must satisfy 1−G = 0 and −A = 0. This equilibrium point lies at (x, G, A) = (0, 1, 0) for all functions and parameters.

2. Any non-trivial, x≠0, equilibrium points must satisfy

   $$f(G)I(A)+m(A)-1=0,$$ (41)

   $$1-G-f(G)I(A)x=0,$$ (42)

   $$-A+(f(G)I(A)-\gamma m(A))x=0,$$ (43)

Eliminating f(G), I(A), and m(A) from Eqs. (41)–(43) yields the equation for equilibrium biomass

$$x=\left(1+\frac{1}{\gamma }\right)(1-G^m)-\frac{A^m}{\gamma },$$ (44)

where G^m and A^m lie in the intersection of the curves

$$G_1:=\{(x,G,A)\in {ℝ}_{+}^3:f(G)I(A)+m(A)=1\},$$ (45)

and

$$G_2:=\left\{(x,G,A)\in {ℝ}_{+}^3:G=1-\frac{A}{1+\gamma -\frac{\gamma }{1-m(A)}}\right\}.$$ (46)

To determine the number of non-trivial equilibrium points, we must consider the shape and position of the curves G₁ and G₂ to find intersection points.

B.1.1. Shape and position of G₁

The curve G₁ has the following properties:

• The intersection of the curve G₁ with G-axis (A = 0) satisfies f (G) = 1. Note that this equation has a unique solution since f is monotonically increasing and has μ_1,max >1. We label this intersection G₀.

• The intersection of the curve G₁ with A-axis (G = 0) satisfies m(A) = 1, which has two solutions, $A_S^b$ and $A_U^b$. We note for future reference that these values correspond to the equilibrium acetate concentration solutions for the binary system.

• Since D_G(f(G)I(A)+m(A) −1)≠ 0 for all G>0, A>0 by the implicit function theorem, there is a scalar function h such that

  $$f(h(A))I(A)+m(A)=1$$

  and thus the points on G₁ satisfy G = h(A).

• Implicitly differentiating equation (45) we get an expression for the slope of this curve in (G,A) space:

  $$\begin{array}{l}\frac{\partial }{\partial A}(f(h(A))I(A)+m(A)-1)=0\\ \frac{\partial (fI)}{\partial h}·\frac{dh}{dA}+\frac{\partial (fI)}{\partial A}+\frac{\partial m}{\partial A}=0,\end{array}$$
  which we can rearrange to give the expression for the derivative of the function G = h(A)

  $$\frac{dh}{dA}=\frac{-\left(\frac{\partial (fI)}{\partial A}+\frac{\partial m}{\partial A}\right)}{\frac{\partial (fI)}{\partial G}}.$$ (47)

We now try to determine the sign of this derivative from Assumptions [A2]–[A4] in Section 2.3. First we note that

$$\begin{array}{l}\frac{\partial (fI)}{\partial G}>0\text{for}\text{all}(G,A),\frac{\partial (fI)}{\partial A}<0\text{for}\text{all}(G,A),\\ \frac{\partial m}{\partial A}>0\text{for}A<A_{\mathit{max}},\frac{\partial m}{\partial A}<0\text{for}A>A_{\mathit{max}}.\end{array}$$

The discussion that follows is illustrated in Fig. B1 (a).

• For the lower branch of the curve (A<A_max), (∂(fI)/∂A)<0 but (∂m/∂A)>0, so the sign of dh/dA is not determined by our assumptions. However, since the lower branch intersects G-axis in a point (0, G₀) and the A-axis at ( $A_S^b$, 0), the derivative dh/dA must become negative for some interval (A, $A_S^b$).

• For the upper branch of the curve (A>A_max) we know that dh/dA>0 and that the curve intersects the A-axis at $A=A_U^b$. As A increases, f (G)I(A)→0 and m(A)→0. At a critical A value, implicitly defined by μ_1,maxI(A)+m(A) = 1, the curve reaches a vertical asymptote, ${\mathrm{A}}_{\mathit{crit}}^m$, and for $A_{\mathit{crit}}^m<A$ there is no solution to f (G)I(A)+m(A) = 1.

B.1.2. Shape and position of G₂

We rewrite Eq. (46) as G₂ = 1 −H(A), where

$$H(A)=\frac{A}{1+\gamma -\frac{\gamma }{1-m(A)}}.$$

We summarize our observations about curve G₂ = G₂(A).

• When A=0, H(A) = 0 and so the curve G₂ intersects the G-axis at G=1.

• The intersection of the curve G₂ = 1 −H(A) with A-axis satisfies H(A) = 1. This solution, which we denote A^t satisfies 1+γ − γ/(1 −m(A^t)) = A^t, or rewritten, m(A^t) = (1 − γ)/(1+γ−A^t). This equation always has one solution, in the region $0<A^t<A_S^b$, and in some cases can have two more solutions for high $A_U^b<A^t<1$, as shown in Fig. B3. The intersections with the A-axis will be ordered by increasing A with subscripts $A_1^t$ and $A_2^t,A_3^t$ (if applicable).

• The curve G₂ = 1 −H(A) has vertical asymptotes when 1+ γ − γ/(1 −m(A)) = 0, which correspond to the value A satisfying 1+ γ = γ/(1 −m(A)). There is one asymptote in the region $A<A_S^b(m(A)<1)$, which follows from the fact that the left hand side is bounded and the right hand side grows without bound as $A\to A_S^b$, since $m(A_S^b)=1$ by definition. In the region $A>A_U^b(m(A)<1)$, there is one asymptote, as the left hand side is bounded and the right hand side grows without bound as $A\to A_U^b$ from above, since $m(A_U^b)=1$ by definition. We denote the asymptotic values of A by $A_1^v$ and $A_2^v$, which satisfy $m(A_i^v)=1/(1+\gamma )$, shown in Fig. B3.

• For $A_1^v$ and $A_1^t$, which are both in the region $A<A_S^b$ we wish to determine their relative positions. Consider equations 1+ γ = γ/(1 −m(A^v)) and 1+ γ = A^t + γ/(1 −m(A^t)). It follows that

  $$A^t+\frac{\gamma }{1-m(A^t)}=\frac{\gamma }{1-m(A^v)}.$$
  and since 0<A^t <1 this means that

  $$\frac{\gamma }{1-m(A^t)}<\frac{\gamma }{1-m(A^v)},$$

  In the region $A<A_S^b$ the function γ/(1−m(A)) is increasing as A increases, thus $A_1^t<A_1^v$. In the region $A>A_U^b$ the function γ/(1 −m(A)) is now decreasing as A increases, thus (if ${\mathrm{A}}_2^t$ and ${\mathrm{A}}_3^t$ exist) $A_2^v<A_2^t<A_3^t$.

• The slope of the curve is given by

  $$\begin{array}{l}\frac{{dG}_2}{dA}=-\frac{dH(A)}{dA}\\ =-1·\frac{\left(1+\gamma -\frac{\gamma }{1-m(A)}\right)-A\frac{d}{dA}\left(\frac{-\gamma }{1-m(A)}\right)}{{\left(1+\gamma -\frac{\gamma }{1-m(A)}\right)}^2}\\ =-1·\frac{\left(1+\gamma -\frac{\gamma }{1-m(A)}\right)+\frac{dm(A)}{dA}\frac{\gamma A}{{(1-m(A))}^2}}{{\left(1+\gamma -\frac{\gamma }{1-m(A)}\right)}^2}\end{array}$$ (48)

  For $0<A<A_1^v$, 1 + γ − γ/(1 −m(A))>0 and dm(A)/dA>0, thus dG₂/dA <0.

• The function H(A) has a removable singularity at $A_S^b$ and $A_U^b$, with the limit value at these points lim_A→AS,AUH(A) = 0. Thus, G₂ = 1 at $A_S^b$ and $A_U^b$.

• For $A_1^v<A<A_S^b$ the slope of G₂ is negative, and for $A_U^b<A<A_2^v$ the slope of G₂ is positive. As A approaches $A_S^b$ and $A_U^b$, 1−m(A)≪1 and the second term in the numerator of (48) dominates. Near $A_S^b:dm(A)/dA>0$ and 1+ γ − γ/(1−m(A))<0, therefore dG₂/dA <0. Near $A_U^b:dm(A)/dA<0$, 1+γ − γ/(1−m(A))<0, and thus dG₂/dA <0. As A increases from $A=A_U^b$, dG₂/dA remains positive, and m(A) decreases until the curve G₂ reaches an asymptote at $A_2^v$.

We summarize this information in Fig. B1(b) which shows a qualitative sketch of the curve G₂.

B.1.3. Intersections of G₁ and G₂

Equilibrium points are at intersections between the curves G₁ (45) and G₂ (46). The curve G₁ is in the region G >0 for $A<A_S^b$ and $A_U^b<A<A_{\mathit{crit}}^m$. We will call the region $A<A_S^b$ the lower region and $A_U^b<A$ the upper region.

For $A_1^v<A<A_S^b$ and $A_U^b<A<A_2^v$, curve G₂ is above G = 1, thus there can be no intersections with curve G₁ in physically relevant (x>0) regions of phase space.

Intersections between the curves can only occur in the region $A<A_1^v$ and the region $A_2^v<A<1$.

B.1.3.1. Intersections in the lower region

The lower branch of G₁ (see Eq. 45) is a continuous curve connecting the point (0, G₀) and the point (A_S, b, 0), while G₂ is a continuous curve that connects (0, 1) and (A^t, 0). Since 1>G₀ to $A_1^t<A_S^b$, thus these curves must intersect at 2n+1 points, where n≥0. These correspond to equilibria of the system and we can order them based on their A value by E₁, E₂, …E_{2n + 1}. In particular, there is at least one non-trivial equilibrium point between $0<A<A_1^t$ and $0<G<\text{max}(G_1(A\in (0,A_1^t)))$.

B.1.3.2. Intersections in the upper region

The upper branch of G₁ is a smooth curve that increases from G=0 at $A_U^b$ until it reaches an asymptote at A defined by μ_1,maxI(A)+m(A) = 1. If the curve 1− γ/(1+ γ −A) intersects m(A) in the upper region, the curve G₂ will cross the A-axis to lie in the G>0 region for $A_2^t<A<A_3^t$, where $A_U^b<A_2^v<A_2^t<A_3^t<1$. In this case it is possible for the upper branch of the curve G₂ to intersect G₁, thus creating equilibrium points. If these curves do intersect in the upper region, these new upper equilibria, K_j for j = 1…2m, would appear in pairs at saddle-node bifurcations.

Fig. B2 shows the situation when there is an upper branch of G₂, but it does not intersect G₁. For there to be equilibrium points in the upper region the upper branch of the curve G₂ must cross the A-axis, and it also must reach high enough G values to intersect with the curve G₁ before G₁ reaches its asymptote at ${\mathrm{A}}_{\mathit{crit}}^m$.

As was mentioned in the introduction we do not consider these equilibria to represent biologically plausible state of the monoculture. The high stable equilibria only exist in specific circumstances when the acetate growth curve m(A) decreases rapidly for high acetate levels, while the lower stable equilibrium exists for all parameter values. The high stable equilibria, when they exist, have a small basin of attraction, which is characterized by high levels of acetate and low levels of glucose. So only initial conditions with high initial acetate and low glucose can lead to the monoculture that is positioned at such equilibrium. Below we provide some sufficient conditions under which the curves G₁ and G₂ do not intersect in the upper region and thus there are no equilibria in this region.

1. We expect that the acetate consumer in the binary culture is better adapted to growth on acetate that the monoculture for large value of A. Our fist condition states that the maximal growth rate of monoculture is not greater than a multiple of the growth rate of acetate consumer

   $${\mu }_{1,\mathit{max}}I(A_2^v)<\gamma m(A_2^v)$$ (49)

   where the inequality is evaluated at $A_2^v$ defined implicitly by $m(A_2^v)=1/(1+\gamma )$. This assumption is summarized in Fig. 3. Monotonicity implies that the curve μ_1,maxI(A) is in the shaded region for $A>A_2^v$. The condition (49) comes from the observation that if $I(A_2^v)<\gamma /({\mu }_{1,\mathit{max}}(1+\gamma ))$, then $A_{\mathit{crit}}^m<A_2^v$ and the curve G₁ reaches its asymptote before G₂ can enter the region G >0. Therefore there can be no upper equilibria.

2. The second condition which rules out the upper equilibria asks that the function m(A) does not decrease too rapidly for large values of A. Note that if the curve G₂ does not cross the A-axis into the G>0 region for upper A values, there can be no upper equilibria. This is equivalent to situation a condition that m(A) = 1 − γ/(1+ γ − A) has no solutions ${\mathrm{A}}_2^t$ and ${\mathrm{A}}_3^t$, see Fig. B3. Finally, observe if

   $$m(1)>1/(1+\gamma )$$ (50)
   then $1<A_2^v$ which implies that m(1 − γ/(1+γ − A) has only one solution $A_1^t$. The condition (50) is equivalent to

   $$\frac{m\left(\frac{G_{in}{Y}_{21}}{Y_{11}}\right)}{D}>\frac{Y_{21}}{Y_{21}+Y_{22}}.$$

   in terms of the original parameters and variables.

B.2. Stability of equilibrium points

We define a new variable in the monoculture system

$$z(t)=\gamma x(t)+(1+\gamma )G(t)+A(t).$$

It is each to show that

$$\frac{dz}{dt}=(1+\gamma )-z$$

which means that the plane

$$\gamma x+(1+\gamma )G+A=(1+\gamma )$$

is an attracting (exponentially at a rate of e^−t) invariant subspace of the phase space ${ℝ}_{+}^3$.

The long term behavior of the system is determined by the dynamics on this attracting plane, which is given by

$$\frac{dA}{dt}=-A+[f(G)I(A)-\gamma m(A)]x(A,G)$$ (51)

$$\frac{dG}{dt}=1-G-f(G)I(A)x(A,G)$$ (52)

$$x(A,G)=\left(1+\frac{1}{\gamma }\right)(1-G)-\frac{A}{\gamma }$$ (53)

This system has the Jacobian

$$J(A,G)=\left[\begin{array}{cc}-1+(f\frac{\partial I}{\partial A}-\gamma \frac{\partial m}{\partial A})x-\frac{1}{\gamma }(fI-\gamma m)& \frac{\partial f}{\partial G}Ix-\left(1+\frac{1}{\gamma }\right)(fI-\gamma m)\\ -f\frac{\partial I}{\partial A}x+\frac{1}{\gamma }fI& -1-\frac{\partial f}{\partial G}Ix+\left(1+\frac{1}{\gamma }\right)fI\end{array}\right].$$

For any 2D system, Tr(J) = λ₁ + λ₂ and Det(J) = λ₁ · λ₂. The conditions Det(J)>0 and Tr(J)<0 are necessary and sufficient conditions to show that an equilibrium point is stable. The condition Det(J)<0 is necessary and sufficient to show that an equilibrium point is an unstable saddle.

At the trivial equilibrium point, (A, G) = (0, 1) where x=0, I(0) = 1, and m(0) = 0, the Jacobian becomes

$$J(0,1)=\left[\begin{array}{cc}-1-\left(\frac{1}{\gamma }\right)f(1)& -\left(1+\frac{1}{\gamma }\right)f(1)\\ \left(\frac{1}{\gamma }\right)f(1)& -1+\left(1+\frac{1}{\gamma }\right)f(1)\end{array}\right].$$

The characteristic equation: λ² + λ (2−f (1))+(1 −f(1)) has roots λ₁= −1<0, λ₂ = f(1)−1. We know that f(1)≈μ_1,max >1 from assumption [A6], so λ₂ >0, which means that (0, 1) is a saddle, with two negative (stable) eigendirections (one from the reduction to the 2D reduced system and the other from the dynamics of reduced flow) and one unstable eigendirection.

The corresponding eigenvectors are

$$v_1=\left(\begin{array}{c}(1+\gamma )\\ -1\end{array}\right),v_2=\left(\begin{array}{c}1\\ -1\end{array}\right).$$

An important observation to make here is that the stable manifold of the trivial equilibrium point in reduced system is an invariant line G = 1 −A/(1+ γ) which corresponds to x=0.

Now we analyze the stability of the non-trivial equilibria E_i and K_j. At these equilibria we have fI + m = 1, (fI − γm)x = A, and fIx = 1 −G, with x(A, G) = (1+1/γ)(1 −G) −A/γ. The Jacobian becomes

$$J(A^m,G^m)=\left[\begin{array}{cc}(f\frac{\partial I}{\partial A}-\gamma \frac{\partial m}{\partial A})x-\left(1+\frac{1}{\gamma }\right)fI& \frac{\partial f}{\partial G}Ix+(1+\gamma )\left(1-\left(1+\frac{1}{\gamma }\right)fI\right)\\ -f\frac{\partial I}{\partial A}x+\frac{1}{\gamma }fI& -1-\frac{\partial f}{\partial G}Ix+\left(1+\frac{1}{\gamma }\right)fI\end{array}\right].$$

The determinant of this Jacobian can (after lengthy rearrangement) be reduced to:

$$\text{Det}(J(A^m,G^m))=c_0=\frac{\partial f}{\partial G}I\left(\frac{\partial m}{\partial A}\gamma x^2+\mathit{fIx}\right)-A\left(\frac{\partial m}{\partial A}+f\frac{\partial I}{\partial A}\right).$$

And the trace of the Jacobian is

$$\text{Tr}(J(A^m,G^m))=-c_1=-1-x\left(\frac{\partial f}{\partial G}I-f\frac{\partial I}{\partial A}+\gamma \frac{\partial m}{\partial A}\right).$$

To determine the sign of c₀ and thus the stability of any monoculture equilibrium point, we consider the relative slopes of the curves G₁ and G₂ and their intersections in the region $A<A_S^b$. We will show that the stability is determined by the relative slope of the curves G₁ and G₂. Note that at any odd lower equilibrium point E_i, i = 1, 3, 5, …, 2n+1 and at any even upper equilibrium point K_j, j = 2, 4, …2m, we have ∂G₂/∂A< ∂G₁/∂A, whereas at any even lower equilibrium points E_i, i = 2, 4, 6, …, 2n, and any odd upper equilibrium points K_j, j = 1, 3, …2m−1, we have ∂G₂/∂A> ∂G₁/∂A.

Taking the expressions for the slopes from Eqs. (47) and (48), with some rearranging we can show that at non-trivial equilibria

$$A\frac{{dG}_2}{dA}=-\frac{\partial m}{\partial A}\gamma x^2-\mathit{fIx}$$

and

$$\frac{\partial f}{\partial G}I\frac{{dG}_1}{dA}=-\left(\frac{\partial m}{\partial A}+f\frac{\partial I}{\partial A}\right)$$

thus

$$c_0=\frac{\partial f}{\partial G}I\left(\frac{\partial m}{\partial A}\gamma x^2+\mathit{fIx}+A\frac{{dG}_1}{dA}\right)$$ (54)

$$=A\frac{\partial f}{\partial G}I\left(\frac{{dG}_1}{dA}-\frac{{dG}_2}{dA}\right)$$ (55)

• At even lower equilibrium points and odd upper equilibrium points, dG₂/dA > dG₁/dA, c₀ <0 and the equilibrium point is an unstable saddle.

• At points where the curves G₁ and G₂ are tangent, c₀ = 0 and bifurcations occur.

• At any odd lower equilibrium point and at any even upper equilibrium point dG₁/dA >dG₂/dA and c₀ >0. The equilibrium point in the 2D system is a stable or unstable node, depending on the sign of Tr(J(A^m, G^m)), which would correspond to a stable node or an unstable saddle in the full system.

For lower even equilibrium points, Tr(J(A^m, G^m))<0 and c₀ >0, so the equilibrium point is a stable node. We can show that these stable equilibria do not undergo Hopf bifurcations (where Re(λ) = 0) since Tr(J(A^m, G^m)) = λ₁+ λ₂ ≠0.

For upper odd equilibrium points, c₀ >0 but ∂m/∂A<, so the stability depends on the sign of Tr(J(A^m, G^m). If Tr(J(A^m, G^m))<0, then the equilibrium point in the 2D system is a stable node, which corresponds to a stable node in the full system, however, if Tr(J(A^m, G^m))>0, then the equilibrium point in the 2D system is an unstable node, which corresponds to an unstable saddle in the full system.

Fig. B1.

(a) Qualitative sketch of the curve G₁ implicitly defined by (45). (b) Qualitative sketch of the curve G₂ defined by (46).

Fig. B2.

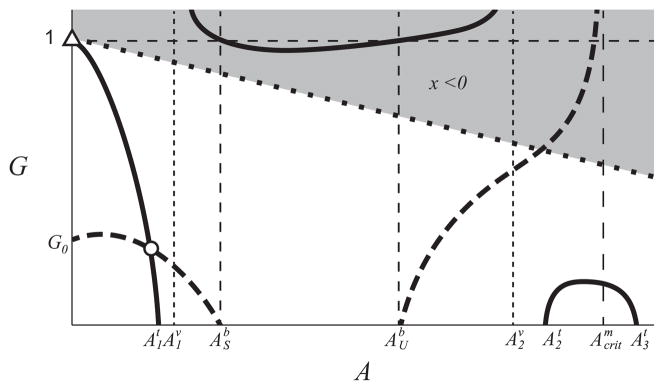
Qualitative sketch of the curves G₁ (dashed black curve) and G₂ (solid black curve). The position of non-trivial equilibrium points projected to (A, G) plane is at the intersections of these curves. Equilibria are marked with a circle for a stable equilibrium point and a triangle for an unstable saddle. The trivial (x=0) equilibrium point at (0,1) is shown. In the shaded gray region (G>1−A/(1+γ)) any solutions are physically unrealistic as x<0. The vertical asymptote of the curve f(G)I(A)+m(A) = 1 is labeled $A_{\text{crit}}^m$.

Fig. B3.

Qualitative sketch of the curves m(A) (solid black curve) and 1 − γ/(1+ γ −A) (dot-dashed black curve). The case with only one intersection $A_1^t$ is shown in panel (a). In panel (b) the case with three intersections is shown. The $A_1^v$ and $A_2^v$ values which are solutions to m(A) = 1/(1+ γ) are also shown.

Appendix C. Biomass of monoculture and the binary system

In this section we will prove Theorem 3.

C.1. Comparison of binary culture and monoculture biomass

It can be shown that the biomass ${\overline{x}}^1=x_1^1+x_2^1=x_1^1+0$ for the boundary equilibrium point in the binary system (Eqs. (9)) is always less than the total biomass of the stable co-existence equilibrium point, S: Since x₁ = 1 −G at both equilibria for the binary system, and $G_i^b<G^1$, where $G_i^b$ is the equilibrium glucose concentration for the co-existence equilibria defined below. Thus ${\overline{x}}^1<x_{1,i}^b<{\overline{x}}_i^b$. In order to compare the maximum biomass in the two systems, we must compare the stable co-existence equilibrium point (x₁ ≠0, x₂ ≠0) for the binary system with the nontrivial equilibria E₁, …, E_2n+1 with x ≠0 for the monoculture.

The biomass of the monoculture at equilibrium is given by

$$x^m=\left(1+\frac{1}{\gamma }\right)(1-G_i^m)-\frac{A_i^m}{\gamma }.$$ (C.1)

The total biomass of the binary system at its stable equilibrium point ${\overline{x}}_S^b=x_{1,S}^b+x_{2,S}^b$:

$${\overline{x}}_S^b=\left(1+\frac{1}{\gamma }\right)(1-G_S^b)-\frac{A_S^b}{\gamma }.$$ (C.2)

As shown in Appendix B, $A_i^m<A_t<A_S^b$ for all monoculture equilibria in the region (on the lower $A<A_b^S$ branch).

The slope of curve implicitly defined by f(G)I(A) = 1, on which $G_S^b$ lies, is given by Eq. (30). The curve G₁, on which $G_i^m$ lies, has slope given by Eq. (47). Both curves intersect the G-axis at G = G₀. The slope for the binary culture curve (Eq. (30)) is always larger than the slope of the monoculture curve (Eq. (47)) in the region A<A_max, as ∂m/∂A>0. Thus, in the region A<A_t, the monoculture curve G₁ lies below the binary culture curve implicitly defined by f(G)I(A) = 1 and $G_i^m<G_S^b$.

As $A_i^m<A_S^b$ and $G_i^m<G_S^b$, from Eqs. (C.1) and (C.2) we know that $x^m>{\overline{x}}_S^b$. In other words, given these assumptions, the monoculture will always have greater biomass than the binary culture (division of labor system).

Appendix D. Experimental values for E. coli growth

Table D1 details the experimental conditions and strains used for the parameters listed in Table 1. When the reported constants were obtained by fitting data to a specific model, we report the equivalent observable values. The maximum growth rates are the maximum values of the growth function on that substrate, assuming zero inhibitory products. The half-saturation values are the substrate concentration at which the growth has reached half its maximum value. The acetate product inhibition constant we define as the acetate concentration at which the growth rate has decreased to half its maximum value, in excess glucose (G » K_G). The acetate substrate inhibition constant we define as the acetate concentration at which the growth rate has decreased to half its maximum value.

Table D1.

Typical parameter values for E. coli growth.

Source	Strain	Experimental conditions	Parameter	Value
Bernstein et al. (2012)	E. coli MG1655 WT	Aerobic batch growth, 37 °C, M9 minimal media, acetate consumption deletion	Biomass yield (CDW[g]/g of glucose)	0.23
	mutant 307		Maximum growth rate on 4 g/L glucose (h−1)	0.43–0.49a
	mutant 403	glucose consumption deletion	Maximum growth rate on 1.5 g/L acetate (h−1)	0.11–0.15a
Chen et al. (1997)	E. coli K-12 MG1655	Aerobic batch growth, complex medium, 37 °C	Maximum growth rate on glucose (h−1)	0.57
			Biomass yield (CDW[g]/g of glucose)	0.255
Chen et al. (1997)	E. coli K-12 MG1655	Anaerobic batch growth, complex medium, 37 °C	Maximum growth rate on glucose (h−1)	0.43
			Biomass yield (CDW[g]/g of glucose)	0.175
Dykhuizen (1978)	E. coli K-12 W3110	Aerobic batch growth, Davis salts, 37 °C	Maximum growth rate on glucose (h−1)	0.76
Dykhuizen (1978)	E. coli K-12 W3110	Chemostat growth, Davis salts, 37 °C	Glucose half-saturation constant (mg/L)	7.2
Edwards et al. (2001)	E. coli K-12 MG1655	Aerobic batch growth, M9 minimal media 27.5–37 °C, 0.05–4 g/L acetate	Maximum growth rate on acetate (h−1)	0.31
			Biomass yield (CDW[g]/g of acetate)	0.38
Farmer and Liao (1997)	E coli K-12 VJS632	Aerobic batch growth, 37 °C, M9 minimal media, 0.5% glucose	Maximum growth rate on glucose(h−1)	0.52
			Biomass yield (CDW[g]/g of glucose)	0.30
			Acetate yield (g of acetate/g of glucose)	0.25
Review paper	E. coli various	various	Glucose half-saturation constant (mg/L)	0.04–180
Fuhrer et al. (2005)	E. coli K-12 MG1655	Aerobic batch growth, 30 °C, M9 minimal media, 3 g/L glucose	Maximum growth rate on glucose (h−1)	0.39
			Biomass yield (CDW[g]/g of glucose)	0.30
Guardia and Calvo (2001)	E. coli ATCC 8789	Aerobic batch and chemostat growth, 37 °C, complex medium including 5 g/L yeast extract, varying 1–19 g/L glucose, parameter fits to model	Maximum growth rate on glucose (h−1)	1.12
			Glucose half-saturation constant (mg/L)	100
			Acetate product inhibition constant (g/L)	4
			Maximum growth rate on acetate (h−1)	0.19
			Acetate half-saturation constant (g/L)	0.4
			Acetate substrate inhibition constant (g/L)	3.8
			Acetate yield (g acetate produced/CDW[g])	0.4
Kleman and Strohl (1994)	E. coli K-12 W3110	Aerobic fed-batch with target 0.5 g/L glucose, mineral medium, 35 °C	Maximum growth rate on glucose (h−1)	0.91
			Glucose half-saturation constant (mg/L)	4
			Biomass yield (CDW[g]/g of glucose)	0.43
			Acetate yield (g of acetate/g of glucose)	0.38
			Acetate yield (g acetate produced/CDW[g])	0.3–0.9
Natarajan and Srienc (2000)	E. coli BL21	Chemostat, 30 °C, dilution rate 0.12–0.40 h−1 inflow: M9 minimal media, 0.25 g/L glucose	Maximum growth rate on glucose (h−1)	0.768
			Glucose half-saturation constant (mg/L)	0.68
Oh et al. (2002)	E. coli MC4100	Aerobic batch growth, M9 minimal media	Maximum growth rate on 0.25% acetate (h−1)	0.33
Paalme et al. (1997)	E. coli K-12 W3350	A-stat, 37 °C, mineral medium, 10 g/L glucose	Maximum growth rate on glucose (h−1)	0.57
			Biomass yield (CDW[g]/g of glucose)	0.50
Paalme et al. (1997)	E. coli K-12 W3350	A-stat, 37 °C, mineral medium, 5 g/L acetate	Maximum growth rate on acetate (h−1)	0.22
			Biomass yield (CDW[g]/g of acetate) max/min	0.30/0.21
Senn et al. (1994)	E. coli ML30	Chemostat growth, mineral medium, 37 °C	Maximum growth rate on glucose (h−1)	0.92
			Glucose half-saturation constant (mg/L)	0.0072
Literature review Senn et al. (1994)	E. coli various	various	Maximum growth rate on glucose (h−1)	0.55–1.23
			Glucose half-saturation constant (mg/L)	0.0053–99
Varma and Palsson (1994)	E. coli K-12 W3110	Aerobic batch growth, 38 °C, M9 minimal media, 2 g/L glucose	Maximum growth rate on glucose (h−1)	0.68
			Biomass yield (CDW[g]/g of glucose)	0.36
Varma and Palsson (1994)	E. coli K-12 W3110	Anaerobic batch growth, 38 °C, M9 minimal media, 2 g/L glucose	Maximum growth rate on glucose (h−1)	0.43
			Biomass yield (CDW[g]/g of glucose)	0.13
Xu et al. (1999)	E. coli K-12 W3110	Aerobic batch growth, 35 °C, mineral medium, 4–14 g/L glucose	Maximum growth rate on glucose (h−1)	0.55
			Biomass yield (CDW[g]/g of glucose)	0.52
			Maximum growth rate on acetate (h−1)	0.05
Xu et al. (1999)	E. coli K-12 W3110	Aerobic batch growth, 35 °C, mineral medium, 5 g/L glucose, 0–8 g/L acetate	Acetate product inhibition constant (g/L)	9
			Biomass yield (CDW[g]/g of acetate)	0.4
Xu et al. (1999)	E. coli K-12 W3110	Aerobic fed-batch (exponential feeding rate) with target μ = 0:3 h−1, mineral medium, 35 °C	Maximum growth rate on glucose (h−1)	0.54
			Glucose half-saturation constant (mg/L)	50
			Acetate product inhibition constant (g/L)	4, 5
			Aerobic biomass yield (CDW[g]/g of glucose)	0.49, 0.51
			Anaerobic biomass yield (CDW[g]/g of glucose)	0.15
			Maximum growth rate on acetate (h−1)	0.06, 0.08
			Acetate half-saturation constant (g/L)	0.05
			Biomass yield (CDW[g]/g of acetate)	0.4

Note: When parameters were from the fit to a specific inhibition model, the parameters reported in are the ‘effective’ parameters, i.e., the reported ‘inhibition constants’ are the concentration at which growth rate has decreased to half its maximum. Similarly, the ‘half-saturation constants’ are the concentrations at which growth has increased to half its maximum, and the ‘maximum growth rates’ are the maximum possible growth rates.

^a(before - after) adaptation to a single carbon source.