Effects of truncating van der Waals interactions in lipid bilayer simulations

Abstract

In membrane simulations, it is known that truncating electrostatic interactions results in artificial ordering of lipids at the truncation distance. However, less attention has been paid to the effect of truncating van der Waals (VDW) interactions. Since the VDW potential decays as r⁻⁶, it is frequently neglected beyond a cutoff of around 1 nm. In some cases, analytical dispersion corrections appropriate for isotropic systems are applied to the pressure and the potential energy. In this work, we systematically study the effect of truncating VDW interactions at different cutoffs in 1,2-Dipalmitoyl-sn-glycero-3-phosphocholine bilayers with the Berger force field. We show that the area per lipid decreases systematically when the VDW cutoff (r_c) increases. This dependence persists even when dispersion corrections are applied. Since the analytical form of the dispersion correction is only appropriate for isotropic systems, we suggest that a long VDW cutoff should be used in preference over a short VDW cutoff. To determine the appropriate cutoff, we simulate liquid pentadecane with the Berger parameters and find that r_c ≥ 1.4 nm is sufficient to reproduce the density and the heat of vaporization of pentadecane. Bilayers simulated with r_c ≥ 1.4 nm show an improved agreement with experiments in both the form factors and the deuterium order parameters. Finally, we report that the VDW cutoff has a significant impact on the lipid flip-flop energetics and an inappropriate short VDW cutoff results in a bilayer that is prone to form water defects across the bilayer.

I. INTRODUCTION

In molecular dynamics simulations, electrostatic and van der Waals (VDW) interactions constitute the nonbonded interactions and their treatments dominate the total simulation runtime as well as the simulation accuracy. In early days, restrained by computational resources, simple cutoff schemes were used for both the electrostatic and VDW interactions. However, truncating electrostatic interactions introduces major artifacts in simulations, such as the artificial ordering of lipids.^1–3 Therefore methods such as particle-mesh Ewald (PME),^4,5 reaction field (RF),⁶ and particle-particle-particle-mesh (P3M)⁷ were developed to solve this problem. These approaches introduce fewer artifacts than even very long direct electrostatic cutoffs and have now become the standard methods for treating electrostatics in biomolecular simulations.

In contrast, very little attention has been paid to the treatment of VDW interactions. The VDW interactions, which decay as r⁻⁶, are much smaller in magnitude than electrostatic interactions beyond a short distance. Therefore a simple cutoff scheme is often used. The cutoff length is usually around 1 nm and interactions beyond the cutoff are neglected. In some cases, analytical dispersion corrections that are appropriate for isotropic systems are applied to the pressure and the potential energy.

In this work, we systematically explore the effects of truncating VDW interactions in simulating lipid bilayers using the Berger force field.⁸ This force field, which was developed by Berger et al. in 1997, is widely used by the simulation community. A key contribution of Berger et al. was to optimize the VDW parameters of the methyl and methene groups in lipid acyl tails. They obtained the parameters by reproducing the correct condensed phase properties (density and heat of vaporization) of liquid pentadecane. Although Berger et al. optimized the VDW parameters with a 1.0 nm cutoff and applied dispersion correction, various VDW cutoffs, with/without dispersion correction, have been used in the literature, such as 0.9 nm,^9–13 1.0 nm,^8,14–16 1.2 nm,^17,18 1.4 nm,^19,20 and 1.8 nm.²¹ The most common choice for the cutoff is 1.0 nm, similar to the value used when the force field was developed.

In this work, we show that the bilayer properties are very sensitive to the choice of VDW cutoffs. The application of the dispersion correction does not eliminate the problem. With the dispersion correction applied, the area per lipid in 1,2-Dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) bilayers decreases from 67 ± 0.3 to 60.5 ± 0.12 Ų, when the VDW cutoff increases from 0.9 to 1.4 nm. This indicates that the dispersion correction works poorly for lipid bilayers and we argue that a long VDW cutoff should be used instead of a short cutoff with a dispersion correction. We determine the appropriate cutoff value by simulating liquid pentadecane without the dispersion correction (unlike Berger's approach where he applied dispersion correction), and find that a 1.4 nm cutoff is sufficient to produce the density and heat of vaporization of pentadecane. Lipid bilayers simulated with this cutoff showed an improved agreement with experimental form factors and deuterium order parameters. Furthermore, we report that the VDW cutoff has a significant impact on lipid flip-flop energetics and an inappropriate VDW cutoff (including the most common choice of 1.0 nm) can result in a bilayer that is prone to form water defects. We also discuss this effect in the context of other lipid force fields.

II. MATERIALS AND METHODS

A. Simulation systems

The system we studied consisted of 64 DPPC molecules and 3846 water molecules (corresponding to a ratio of 60 waters per lipid) to ensure a fully hydrated bilayer.²² The initial configuration that was downloaded from Tieleman's website has an area per lipid of 62.4 nm², which is consistent with a DPPC bilayer in the L_α phase.²³

The bilayer's structural properties under different VDW cutoff lengths were explored by seven molecular dynamics simulations, labeled A to G in Table I, with each simulation extended for 80 ns. The free energy of lipid flip-flop in the bilayer was calculated from three independent sets of umbrella sampling molecular dynamics simulations, which are listed in Table II. Finally, the spontaneous water pore formation associated with lipid flip-flop was explored by eight independent molecular dynamics simulations (labeled cA to cH in Table III) with the phosphate atom of a DPPC molecule restrained by a harmonic potential at the bilayer center. Three force fields besides the Berger force field were also tested, including 43a1-s3,²⁴ 53a6 Poger,²⁵ 53a6 Kukol.²⁶ Each simulation in Table III was simulated for 80 ns, except for cE, which was extended to 160 ns.

Table I.

Area per lipid of DPPC bilayers simulated with different VDW cutoffs.

		LJ cutoff (nm)
	Parameter	Short	Long	Dispersion
Label	set	range	range	correction	${\overline{A}}_L({\AA }^2$)
A	Berger	0.9	0.9	No	69.5 ± 0.2
B	Berger	0.9	0.9	Yes	67.0 ± 0.3
C	Berger	1.0	1.0	Yes	64.3 ± 0.3
D	Berger	1.0	1.2	Yes	62.9 ± 0.5
E	Berger	1.0	1.4	Yes	60.5 ± 0.1
F	Berger	1.0	1.4	No	61.0 ± 0.2
G	Berger	1.0	1.6	No	60.5 ± 0.5

Table II.

Simulation details of umbrella sampling simulations of lipid flip-flops.

		LJ cutoff (nm)
	Parameter	Short	Long	Dispersion
Label	set	range	range	correction
umb0.9c	Berger	0.9	0.9	Yes
umb1.4	Berger	1.0	1.4	No
umb1.6	Berger	1.0	1.6	No

Table III.

Summary of spontaneous pore formation in lipid bilayers with one lipid molecule restrained at the bilayer center.

		LJ cutoff (nm)
	Parameter	Short	Long	Dispersion	Pore
Label	set	range	range	correction	formation
cA	Berger	0.9	0.9	Yes	Yes
cB	Berger	1.0	1.0	Yes	Yes
cC	Berger	1.0	1.2	Yes	No
cD	Berger	1.0	1.4	Yes	No
cE	Berger	1.0	1.4	No	No
cF	43A1-S3 (SPCE)	1.0	1.6	No	No
cG	53A6 Poger	1.0	1.4	No	No
cH	53A6 Kukol	1.0	1.4	No	No

B. Simulation parameters

All molecular dynamics simulations were performed using Gromacs 4.5.4 software package.^27,28 Systems were simulated under periodic boundary conditions, at constant temperature and pressure. For temperature coupling, lipid and water molecules were coupled as separated groups. Each group was kept at 323 K using the V-rescale algorithm.²⁹ We used the Berendsen barostat³⁰ at 1 atm, with the pressure in the plane of the bilayer coupled separately from the pressure normal to the bilayer. The temperature and pressure time constants of coupling were 0.1 and 1.0 ps, respectively. A 2 fs time integration step was used. The Simple Point Charge (SPC/E) water model³¹ was used with the 43A1-S3 force field and the SPC water model³² was used with other force fields. The SETTLE algorithm³³ was used to constrain water molecules and the Linear Constraint Solver (LINCS)³⁴ was used to constrain all other bond lengths in the system. In general, simulation parameters for non-bonded interactions were chosen to be the same as those used by the workers who created the force fields. The VDW cutoff length was varied systematically for the Berger force field. The VDW interactions were evaluated with a twin-range cutoff scheme (for details, refer to Tables I–III): interactions within the short range cutoff were calculated every step, whereas interactions within the long range cutoff were updated every 10 steps, together with the pair list. The direct term for electrostatics in each simulation was chosen to be the same as the short range VDW cutoff, and the Fourier space electrostatic interactions were treated with the PME method.⁴ A fourth order interpolation of charges on a 0.12 nm Fourier spacing was used. For the 43A1-S3 force field, a sixth order interpolation on a 0.15 nm Fourier spacing was used, as it was used in the original paper describing this force field.²⁴

C. Umbrella sampling and free energy calculations

Three sets of umbrella sampling simulations were carried out to estimate the free energy of lipid flip-flop in a DPPC bilayer under different VDW cutoffs (see Table II). We define the Z axis as the bilayer normal and refer to values of Z > 0 nm and Z < 0 nm as the “upper” and “lower” monolayer, respectively.

In umbrella samplings, a lipid chosen at random from the upper monolayer was restrained with an umbrella potential. The umbrella potential was applied to the order parameter, which is defined as the vertical distance between the phosphate atom of the restrained lipid and the center of mass (COM) of the bilayer. This lipid was then pulled successively into the bilayer with a 3000 kJ/mol/nm² force constant at the rate of 0.1 nm/ns. From the pulling simulations, configurations of the lipid at desired depths were selected and were used as starting configurations for each umbrella window. Ten umbrella windows were used and they were separated by 0.2 nm in the Z direction. Each umbrella window was equilibrated for 20 ns and run for 80 ns for production. In the production run, a 750 kJ/mol/nm² force constant was used.

The free energy of each umbrella sampling simulations was calculated using the Weighted Histogram Analysis Method (WHAM).^35,36 The g_wham utility³⁷ provided by Gromacs was used to calculate the free energy and 200 bootstraps were used to estimate the error bars.

D. Liquid pentadecane

To find out the appropriate VDW cutoff to simulate lipid bilayers without dispersion correction, we calculated the density and heat of vaporization of pentadecane under various VDW cutoffs. We constructed a system of 128 chains of pentadecane. Initially, pentadecane was randomly distributed in the simulation box. The force field parameters for pentadecane were extracted from the Berger parameters. The system was then simulated under a constant temperature of 323 K and a constant pressure of 1 atm. The VDW cutoff was varied systematically from 0.9 nm to 1.6 nm with a 0.1 nm interval. When the VDW cutoff was longer than 1.0 nm, a twin-range cutoff scheme was used with the short range cutoff at 1.0 nm. The system was simulated with and without the dispersion correction at each cutoff length for comparison. Each system was simulated for 10 ns and the last 5 ns data were used for analysis. The volume follows directly from the size of the simulation box. Assuming the molar volume of the molecule in the gas phase is much larger than in the liquid phase, the heat of vaporization ΔH_vap can be calculated from

$$\Delta H_{\text{vap}}=E\left(gas\right)-E\left(liquid\right)+NKT,$$ (1)

where E(gas) and E(liquid) are the potential energies of N molecules in the gas and the liquid phase, respectively. To determine E(gas), we simulated a single pentadecane molecule in a 6.4 nm cubic box under a constant volume. To confirm that our box size is big enough to prevent the intermolecular interactions between monomers in the gas phase, we doubled the box length and found negligible change in E(gas).

III. RESULTS AND DISCUSSIONS

A. Area per lipid under different VDW cutoffs

The area per lipid (A_L) is defined as the projected area of the bilayer in the x-y plane divided by the number of lipids in a monolayer. Fig. 1 shows the time evolution of the area per lipid from simulations (B,C,E) selected from Table I. Each simulation started from the same initial configuration and the area per lipid stabilized in our simulation timescale. Statistics of A_L simulated under different VDW cutoffs are summarized in Table I. The Block average method was used to estimate the mean and standard error of A_L.³⁸

FIG. 1.

Time evolution of the area per lipid in simulations B, C, and E. The first 20 ns were used for equilibration.

The values of A_L reported in Table I indicate that VDW cutoffs have a significant effect on bilayer properties. Simulations A, F, and G show that without the dispersion correction, the area per lipid decreases from 69.5 to 60.5 Ų when the VDW cutoff increases from 0.9 to 1.6 nm. The application of dispersion correction does not eliminate this dependence, as shown from simulations B–E. The A_L of 69.5 Ų simulated with a 0.9 nm VDW cutoff, without dispersion correction, agrees with the result reported in a recent work by Tieleman and co-workers.¹¹ To understand the failure of dispersion correction in lipid bilayers, we briefly review how the analytical dispersion correction is conducted. For further detail, refer to the GROMACS²⁸ manual.

The dispersion energy between particle i, j is written as

$$V\left(r_{ij}\right)=-C_6(i,j)r_{ij}^{-6}.$$ (2)

For system with N particles, we define the average dispersion constant as

$$⟨C_6⟩=\frac{2}{N(N-1)}\sum _i^N\sum _{j>i}^N{C}_6(i,j).$$ (3)

The long-range dispersion correction V_lc to the energy beyond the cutoff r_c with the particle density ρ = N/V can be approximated by

$$V_{lc}=\frac{1}{2}N\rho {\int }_{r_c}^{\infty }g\left(r\right)4\pi r^2(-⟨C_6⟩r^{-6})dr,$$ (4)

where g(r) is the radial distribution function. Assuming g(r) is 1 beyond r_c, the above equation can be integrated as

$$V_{lc}=-\frac{2}{3}\pi N\rho ⟨C_6⟩r_c^{-3}.$$ (5)

Using the average dispersion constant requires the system to be reasonably isotropic. However, this assumption is not valid for interfacial systems, as particles with very different dispersion coefficients could be partitioned into different regions. Therefore, we suggest that a long VDW cutoff should be used instead.

Since the VDW cutoff affects the area per lipid greatly, we want to determine which cutoff length should be used. Although the area per lipid is commonly used to validate simulations of lipid bilayers, it cannot be measured from experiments directly. The area per lipid is usually derived from models based on experimental measure and varies in a range.²³ Therefore it is more useful to rule out simulations that are extreme outliers. This was also pointed out by Anézo et al.³

B. Determination of an appropriate VDW cutoff

From Sec. III A, we learned that the VDW cutoff can affect the area per lipid greatly. The application of the dispersion correction does not eliminate the problem. The issue of keeping the same VDW cutoff as Berger et al. used is that Berger et al. optimized the VDW parameters with a dispersion correction but the dispersion correction works poorly in lipid bilayers. Therefore, the simplest approach to determine the cutoff is to simulate liquid pentadecane without dispersion correction and choose the cutoff that can reproduce the experimental properties of liquid pentadecane.

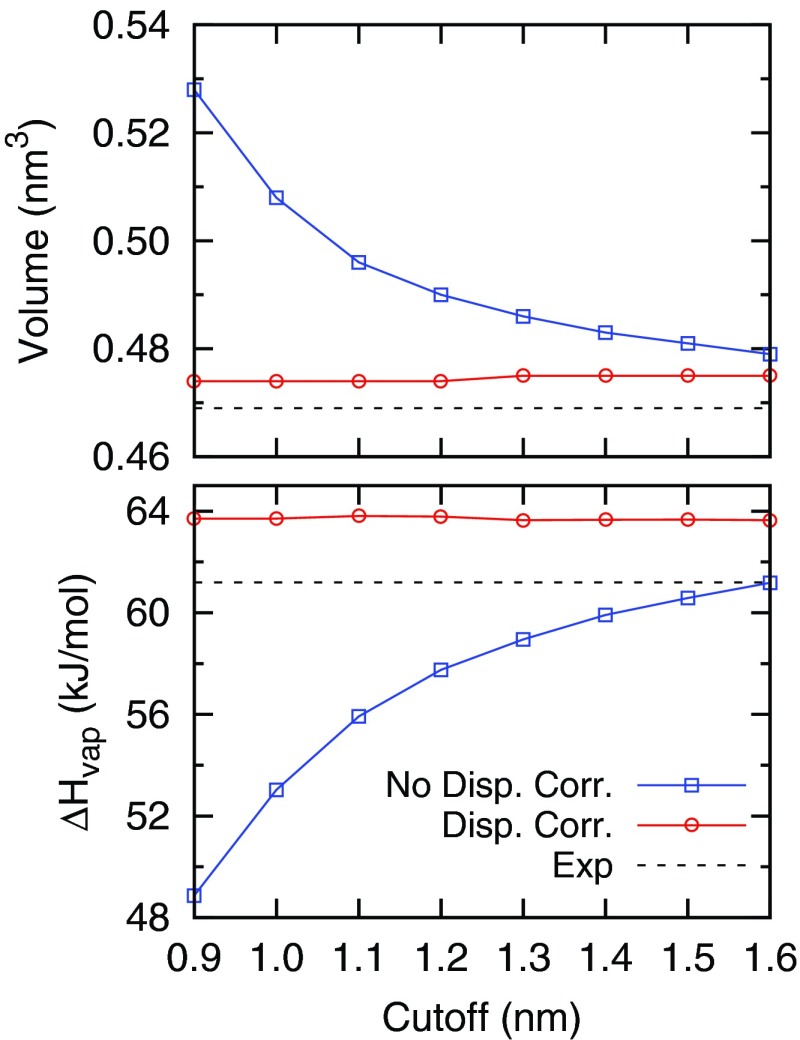
Fig. 2 shows the volume and heat of vaporization (ΔH_vap) of liquid pentadecane calculated from simulations with different VDW cutoffs, with and without dispersion correction. Experimental values for the volume and ΔH_vap are 0.469 nm³ and 61.2 kJ/mol, respectively.³⁹ With the dispersion correction applied, it is clear that simulations are almost independent of cutoffs, which means that the dispersion correction works well for the pentadecane fluid. For simulations without the dispersion correction, a 0.9 nm cutoff can result a 12.6% error in the volume and a 20.1% error in the ΔH_vap. A 1.4 nm VDW cutoff should suffice as it reduces the error to 3%. We note that further improvement in force field parameters is possible as the volume and ΔH_vap from simulations do not match with experiments exactly. To quantitatively measure the amount of dispersion energy lost in lipid bilayers when short VDW cutoffs are used, we took the system from simulation E and calculated the VDW interactions under different cutoffs using the Gromacs energy rerun option. Results are shown in Fig. S1 of the supplementary material.⁵⁹ The VDW energy decreases when the cutoff increases as the long range VDW interactions are attractive. Fig. S1 of the supplementary material⁵⁹ shows that short cutoffs significantly overestimate the amount of dispersion energy in the system and the VDW energy gradually converges at large cutoffs.

FIG. 2.

The molecular volume and heat of vaporization of pentadecane calculated from different VDW cutoff lengths using Berger parameters, with and without dispersion correction. The experimental values are 0.469 nm³ and 61.2 kJ/mol, respectively.

C. Improved bilayer structural properties with an appropriate VDW cutoff

In this session, we calculated the form factors and deuterium order parameters of lipid bilayers. In contrast to the area per lipid, both the form factors and deuterium order parameters can be measured from experiments directly.

1. Form factors

The form factors of lipid bilayers can be measured by x-ray and neutron scattering and can be calculated from MD simulations by⁴⁰

$$F\left(q\right)={\int }_{-D/2}^{D/2}(\rho \left(z\right)-{\rho }_{water})cos\left(qz\right)dz,$$ (6)

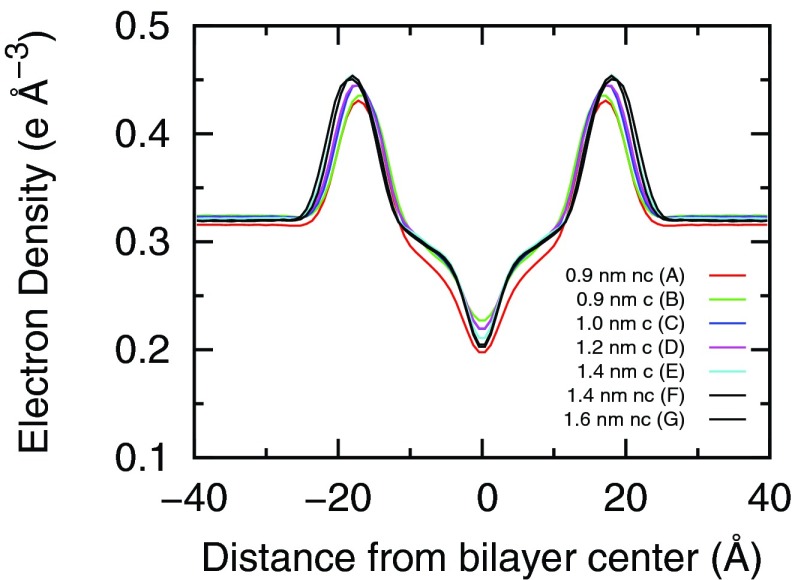
where D is the repeat z-spacing (along the bilayer normal) of the simulation box, ρ(z) is the system electron density at a distance of z away from the bilayer center, and ρ_water is the bulk water density. The electron density was calculated by binning the number of electrons of the system projected in the z direction with a 0.1 nm binsize. The center of the bilayer was set to z = 0 at each time frame. The electron density profiles calculated from simulations A–F are shown in Fig. 3. The two peaks in the profile indicate the bilayer and water interface. The distance between the two peaks indicates the thickness of the bilayer. Fig. 3 shows that as the VDW cutoff increases, the bilayer becomes thicker.

FIG. 3.

Electron density profiles across a hydrated DPPC bilayer calculated from simulations A–G. In the figure legend, c/nc means with/without the dispersion correction.

Fig. 4 shows the form factors computed from MD simulations. We used the Pearson's chi-squared test χ² to compare the agreement between the simulated and experimental form factors. The χ² is defined as follows:⁴¹

$${\chi }^2=\sqrt{\frac{{\sum }_{i=1}^{N_q}\left(\right|F_s\left(q_i\right)|-|F_e\left(q_i\right){\left|\right)}^2/{\left(\Delta F_e\left(q_i\right)\right)}^2}{N_q-1}},$$ (7)

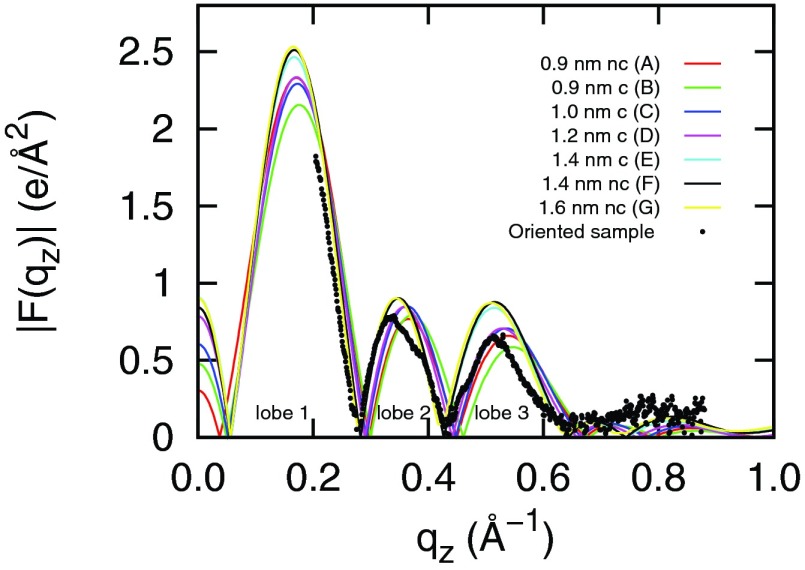
where N_q is the number of experimental data points, F_s(q_i) and F_e(q_i) are simulated and experimental form factors, and ΔF_e(q_i) is the experimental uncertainty at each data point. Experimental data were obtained from Kučerka et al.^40,42 The experimental form factors (black dots shown in Fig. 4) in lobe 1 and 2 have better accuracy than in lobe 3 and the χ² test takes this inaccuracy into account. The smaller the χ² value, the better the agreement between the simulation and experiment. The χ² values for simulations A–G are 2.02, 2.17, 1.81, 1.53, 1.25, 1.28, 1.26, respectively. We can see that simulations with r_c ≥ 1.4 nm (E, F, and G) have smaller χ² values than simulations with shorter cutoffs, indicating a better agreement with experiments.

FIG. 4.

Simulated and experimental form factors for DPPC bilayers at 323 K. In the figure legend, c/nc means with/without the dispersion correction. The experimental data were obtained from Kučerka et al.^40,42

2. Ordering of lipids

An important characteristic of the bilayer liquid crystalline phase is that the acyl tails of the phospholipids are disordered. The degree of order can be probed experimentally using ²H-NMR. Specifically, the deuterium order parameter, S_cd, provides a measure of the relative orientation of individual C-D bonds with respect to the bilayer normal. The order parameter of a methylene at position i is defined as

$$S_{cd}^i=\frac{1}{2}⟨3co{s}^2{\theta }_i-1⟩,$$ (8)

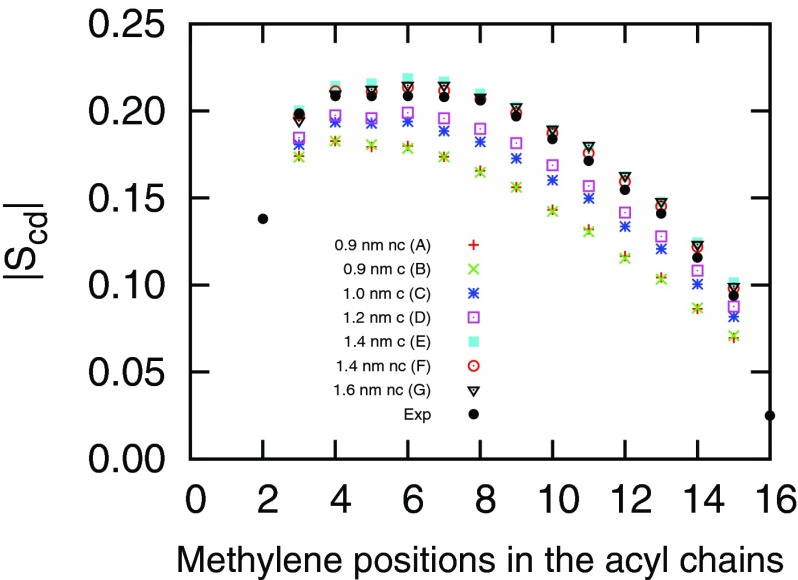
where θ_i is the angle between a C-D vector of the ith methylene in an acyl chain and the normal of the bilayer (z axis). The angular brackets indicate an ensemble average. Fig. 5 shows the |S_cd| profiles of the sn-2 chains of DPPC lipids calculated from simulations A–F. The experimental data were obtained from Douliez et al.⁴³ When the VDW cutoff increases, the |S_cd| of lipid tails increases. This indicates the increase of ordering in lipid acyl tails. The increase in order parameters is associated with the corresponding decrease of area per lipid. When the A_L decreases, the bilayer becomes more compact. This results in more rigid acyl tails. From Fig. 5 we conclude that the deuterium order parameters computed from simulations with r_c ≥ 1.4 nm have the closest agreement with the experimental data. Simulations with shorter VDW cutoffs resulted in bilayers with tails that were more disordered than the experimental measure. Similar to the form factors, bilayers simulated with a 1.4 nm and 1.6 nm cutoff have similar deuterium order parameters, indicating a convergence in terms of cutoff length. In Fig. S2 of the supplementary material,⁵⁹ we show the probability distributions of the angle between the lipid headgroup P → N dipole and the bilayer normal pointing away from the bilayer under different VDW cutoffs. In all simulations, the average P → N vectors are parallel to the bilayer surface. The change of VDW cutoff has little effect on the distribution of this angle. The broad peak in the angle distribution indicates a high degree of disorder in the lipid headgroup region and all bilayers in our simulations are in the liquid-disordered phase.⁴⁴

FIG. 5.

Deuterium order parameters |S_cd| of sn-2 palmitoyl chain of hydrated DPPC at 323 K. In the figure legend, c/nc means with/without the dispersion correction. The experimental data were obtained from Douliez et al.⁴³

D. Free energy of lipid flip-flop under different VDW cutoffs

In Secs. III A–III C we demonstrated that dispersion correction works poorly with lipid bilayers. By studying the density and heat of vaporization of pentadecane under different cutoffs, we determined that 1.4 nm would be sufficient to simulate bilayers without a dispersion correction. Bilayers simulated with this cutoff showed an improved agreement with the experimental form factors and deuterium order parameters. Here, we report another important bilayer related phenomenon, lipid flip-flop. We show the VDW cutoff effect on lipid flip-flop energetics.

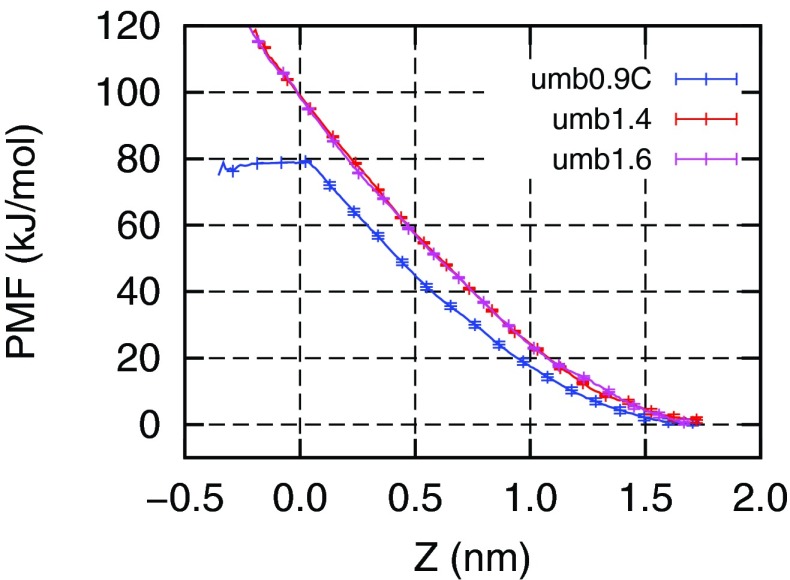
Fig. 6 shows the potential of mean force (PMF) free energy of lipid flip-flop calculated from umbrella sampling simulations. Simulation details are described in Table II. The blue line PMF in Fig. 6 was calculated from simulations with a 0.9 nm VDW cutoff. This cutoff has been reported several times in lipid flip-flop free energy calculations.^9–11 In our simulations, we used a force constant of 750 kJ/mol/nm² per umbrella. This force constant enables us to separate each umbrella window by 0.2 nm, yet still maintains a good histogram overlap with neighboring umbrella windows. The free energy barrier to transfer a lipid from its equilibrium position to the bilayer center is about 80 kJ/mol, which agrees with the work by Tieleman et al.⁹ The blue line PMF is flattened at the position close to the bilayer center, due to the spontaneous formation of a water pore, which transfers the lipid into a hydrophilic environment. A snapshot of the water pore is shown in Fig. 7(a).

FIG. 6.

Free energy of lipid flip-flop in DPPC bilayer calculated from umbrella sampling simulations. Z is the vertical distance between the restrained phosphate to the bilayer center.

FIG. 7.

Snapshots of lipid flip-flop configurations obtained from constrained MD simulations. A phosphate atom of a DPPC was restrained in the bilayer center by a harmonic potential. (a)–(e) are snapshots taken from simulations cA, cE, cF, cG, and cH.

The red and purple lines in Fig. 6 were calculated from simulations with the 1.4 nm and 1.6 nm cutoffs, respectively. The free energy profiles are very similar to each other, indicating a convergence in the cutoff length. More importantly, we did not observe a spontaneous pore formation when the lipid is restrained at the bilayer center. In both cases, the free energy barrier of transferring a lipid into the bilayer center is about 100 kJ/mol, which is 20 kJ/mol more than the barrier with a 0.9 nm VDW cutoff. Longer VDW cutoff reduces the area per lipid, which results in a more compact bilayer, that is less prone to form water defects.

In Fig. 6, the PMF profiles are not symmetric around the bilayer center. The lack of symmetry is due to the hysteresis in sampling in the umbrella windows which are close to the bilayer center. The error bars shown in Fig. 6 only represent the statistical errors in our simulations but do not include the systematic errors. The hysteresis in umb0.9c (0.9 nm with dispersion correction) is slightly different from the hysteresis in umb1.4 and umb1.6. In all umbrella simulations, the initial configurations were obtained by successively pulling a restrained lipid from the upper monolayer towards the lower monolayer. This resulted in an invagination in the upper monolayer. This invagination formed since forming the defect and keeping the lipid head groups solvated is energetically more favorable than immersing the head groups in bilayer's hydrophobic tails. When the lipid passed the bilayer center, the invagination should form from the lower side as the restrained lipid was closer the lower leaflet. However, due to the hysteresis this did not happen in our simulation. Therefore, the PMFs for umb1.4 and umb1.6 kept increasing and lost symmetry around the bilayer center. For umb0.9c, when the lipid was close to the bilayer center we observed the formation of a pore formation. The water pore kept the lipid head group solvated, therefore we observed a flattened PMF after the water pore was formed. After the lipid passed the bilayer center to a certain distance, the water pore may close but the timescale for closing may be longer than our simulation timescale. Therefore, we have an asymmetric PMF in umb0.9c and the hysteresis is due to the formation and closing of a water pore. The asymmetry in PMF related to umbrella sampling in lipid bilayers has also been observed in previously^45–47 and recently Neale et al. has proposed a replica exchange among umbrellas method to reduce this hysteresis.⁴⁸

To further evaluate the force field dependence of spontaneous water pore formation associated with lipid flip-flop, we performed a series of simulations with the phosphate atom of a DPPC restrained at the bilayer center (cA-cH) with different VDW cutoffs and different force fields. Simulation details are described in Table III. As listed in Table III, we found that the spontaneous pore formation was only observed in simulations with the Berger force field using short VDW cutoffs (≤1.0 nm). It was not observed in bilayers simulated with the Berger forcefield using the suggested cutoffs or other Groningen Molecular Simulation (GROMOS) based force fields (43A1-S3,²⁴ 53A6 Poger,²⁵ 53A6 Kukol²⁶). Snapshots of some selected simulations (cA, cE, cF, cG, and cH) are shown in Fig. 7.

To make a statistical argument that the spontaneous water pore formation associated with the lipid flip-flop is indeed due to the use of a short VDW cutoff, we randomly chose ten configurations out of simulation cE (Berger force field with a 1.4 nm VDW cutoff) as starting configurations and simulated under a 0.9 nm VDW cutoff. The water pore formed in all simulations. The time to form a water pore in each simulation were 4.0, 7.6, 14.4, 20.8, 32.1, 44.0, 46.4, 57.2, 69.0, and 76.8 ns (referred as t₁, t₂ … t₁₀), respectively. Wohlert et al. suggest that the formation of a water pore is due to the random fluctuation of “holes” in bilayers,⁴⁹ thus can be modeled as a Poisson process. The probability distribution of the time to form pores can therefore be modeled as the exponential distribution,

$$f\left(t\right|\beta )=\left\{\begin{array}{cc}\hfill \beta e^{-\beta t},& \hfill \text{for}t>0\\ \hfill 0,& \hfill \text{for}t\le 0,\end{array}\right.$$ (9)

where $\frac{1}{\beta }$ is the expected timescale. Given n independent observations, the maximum likelihood estimator (MLE) of $\widehat{\beta }$ is⁵⁰

$$\begin{array}{ccc}\hfill {\left.\frac{dP\left(\beta \right)}{d\beta }\right|}_{\beta =\widehat{\beta }}& =& {\left.\frac{d[f\left(t_1\right|\beta )f\left(t_2\right|\beta )...f\left(t_n\right|\beta )]}{d\beta }\right|}_{\beta =\widehat{\beta }}=0\hfill \\ \hfill \Rightarrow \widehat{\beta }& =& \frac{n}{t_1+t_2+...+t_n}.\hfill \end{array}$$ (10)

From the simulations above, the expected time to form pores with a lipid restrained at the bilayer center with a 0.9 nm VDW cutoff is 37.2 ± 2.7 ns. Error bars were estimated from the Jackknife method.⁵¹ To test whether there is a statistical difference to form water pores between bilayers simulated with a 0.9 nm VDW cutoff and a 1.4 nm VDW cutoff, we extended the simulation cE to 160 ns. Still we did not observe a water pore formation. If the two systems simulated with different cutoffs have the same probability distribution to form pores, the likelihood that the pore forming at a time later than 160 ns is less than $Pr(t\ge 160\text{ns})={\int }_{160\text{ns}}^{+\infty }\beta e^{-\beta t}dt$, which is 2%. Therefore, we are confident that there is a statistical difference of the timescale to form water pores between the systems simulated with different VDW cutoffs.

IV. CONCLUSIONS

In this work, we systematically investigated the effects of VDW cutoffs in simulating DPPC bilayer using the Berger force field. The Berger forcefield is one of the most used force field to simulate lipids. A wide range of VDW treatments have been found in literature, with a VDW cutoff varying from 0.9 to 1.8 nm with or without a dispersion correction. However, we found that the VDW cutoff has a distinct effect on lipid bilayers. The area per lipid decreases significantly with the increase of VDW cutoff and the application of dispersion correction does not eliminate this dependency.

The key issue of using the cutoff the same as what Berger et al. used in their original development is that Berger et al. optimized the force field parameters with a dispersion correction. However, the analytical correction is only appropriate for isotropic systems and fails for bilayers. To determine the appropriate cutoff, we followed Berger's original intention, but decided to choose a cutoff that could reproduce the density and heat of vaporization of pentadecane liquid without the dispersion correction. We found that a 1.4 nm cutoff was sufficient for this purpose.

Bilayers simulated with a 1.4 nm cutoff show an improved agreement with experiments in terms of form factors and deuterium order parameters. Bilayers simulated with shorter cutoffs are more flexible in the lipid tail region than the experiments suggest. Although in this work we took a straight cutoff approach to handle VDW interactions in heterogeneous systems, other approaches could be taken. One direction is to develop a dispersion correction that is suitable for semi-isotropic systems, such as the Isotropic Periodic Sum (IPS) method^52–54 and the pressure based long range correction method⁵⁵ that are developed in Chemistry at Harvard Molecular Mechanics (CHARMM).⁵⁶ Another direction is to calculate VDW interactions more accurately. Recently, Wennberg et al. developed the Lennard-Jones (LJ)-PME method⁵⁷ that applies the PME method to VDW interactions. Although the LJ-PME looks like a very promising way to treat VDW interactions, it is computationally costly, especially for force fields that follow the Lorentz-Berthelot combination rule.⁵⁸

Finally, we reported that the free energy of a lipid flip-flop increased from 80 kJ/mol to 100 kJ/mol when the VDW cutoff increased from 0.9 nm to 1.6 nm. The difference between a 1.4 nm and 1.6 nm cutoff is small indicating the convergence in terms of the cutoff length. More importantly, within our simulation timescale, the spontaneous formation of a water pore associated with the lipid flip-flop could only be observed when the applied VDW cutoff was no longer than 1.0 nm. Statistically, we showed that the rate of forming water pores in bilayers simulated with a short cutoff is much faster than the rate in bilayers simulated with an appropriate cutoff. This indicates that previous reports on water pore mediated lipid flip-flop mechanism could be caused by the use of inappropriate short VDW cutoff.^9,11

This work emphasizes the importance of an appropriate and consistent treatment of VDW interactions in lipid bilayers and we recommend the 1.4 nm VDW cutoff for the Berger force field in future simulation studies.