Computational Simulations of Flow Dynamics and Blood Damage Through a Bileaflet Mechanical Heart Valve Scaled to Pediatric Size and Flow

Abstract

Despite pressing needs, there are currently no FDA approved prosthetic valves available for use in the pediatric population. This study is performed for predictive assessment of blood damage in bileaflet mechanical heart valves (BMHVs) with pediatric sizing and flow conditions. A model of an adult-sized 23mm St. Jude Medical (SJM) Regent™ valve is selected for use in simulations, which is scaled in size for a 5-year old child and 6-month old infant. A previously validated lattice-Boltzmann method (LBM) is used to simulate pulsatile flow with thousands of suspended platelets for cases of adult, child, and infant BMHV flows. Adult BMHV flows demonstrate more disorganized small-scale flow features, but pediatric flows are associated with higher fluid shear stresses. Platelet damage in the pediatric cases is higher than in adult flow, highlighting thrombus complication dangers of pediatric BMHV flows. This does not necessarily suggest clinically important differences in thromboembolic potential. Highly damaged platelets in pediatric flows are primarily found far downstream of the valve, as there is less flow recirculation in pediatric flows. In addition, damage levels are well below expected thresholds for platelet activation. The extent of differences here documented between the pediatric and adult cases is of concern, demanding particular attention when pediatric valves are designed and manufactured. However, the differences between the pediatric and adult cases are not such that development of pediatric sized valves is untenable. This study may push for eventual approval of prosthetic valves resized for the pediatric population. Further studies will be necessary to determine the validity and potential thrombotic and clinical implications of these findings.

INTRODUCTION

Heart valve defects are among the most common congenital cardiovascular anomalies. Although prosthetic heart valves are widely used for adults with valve disease and can be implanted in children in some circumstances (Black 1994; Yoganathan 2003), and custom-sized valves are available for special patients in the form of the Humanitarian Device Exemption, there are currently no FDA approved prosthetic heart valves available for use in children. In studies of pediatric patients treated with aortic or mitral valve replacement, repeat surgery to implant a larger valve was common (Selamet T. 2008; Brown 2012). In a study of children aged < 5 years undergoing mechanical mitral valve replacement, prosthesis size and valve size mismatch were indicators of shorter prosthesis survival (Raghuveer 2003), demonstrating the need for appropriately sized prosthetic valves designed and approved for use in the pediatric population (Yoganathan 2013).

Thrombotic dysfunction is a serious potential complication of mechanical heart valves, and necessitates chronic systemic anticoagulation after valve replacement (Giersiepen 1990; Grunkemeier 1998). In one pediatric study, prosthetic valve thrombosis was found to be the second most common complication of mechanical valves in children (Raghuveer 2003). Damage to blood elements due to complex flow through valves has been connected to thrombosis related outcomes (Ellis 1996; Ellis 2000; Lu 2001). One of the important complications in prostheses designed for pediatric applications may be increased blood damage profile due to smaller valves and different fluid dynamic conditions.

Many clinical studies on prosthetic valve performance have been conducted in adults, but have typically excluded pediatric patients for reasons such as limited patient pool, complex health histories, and limited valve sizes. It has been recommended that pediatric valves take adult-sized designs and scale them to fit pediatric patients (Yoganathan 2013). Understanding the hemodynamics and blood damage performance of potential re-sized valves may help to facilitate their approval for use in children.

Computational fluid dynamics (CFD) simulations can model three-dimensional bileaflet mechanical heart valve (BMHV) flows with high spatiotemporal resolution where the smallest scales of fluid motion can be resolved. Computational studies have employed particle tracking to assess damage potential, but have mostly been limited to point particle tracking in prostheses flows (Alemu 2007; Dumont 2007; Simon 2010). The use of suspended particles has been performed in BMHV hinge and hinge-like flows, in which modeling of platelets with meshed surfaces and finite volumes was shown to differ in damage assessment from point particle methods (Wu 2011; Yun 2012). This platelet modeling has also been employed for bulk BMHV flows (Yun 2014). However, these various studies have not modeled pediatric prosthetic valve flows.

This study was performed to model pulsatile BMHV flows with adult and pediatric sized valves and flow conditions, with the use of a suspension flow solver that has been validated for modeling bulk BMHV flows (Yun 2014) and for accurately quantifying platelet damage (Wu 2011). The aim of this preliminary predictive assessment was to help to understand the hemodynamics and blood damage profile of potential pediatric-sized mechanical heart valves.

METHODS

Numerical solver and setup

The lattice-Boltzmann method (LBM) was used for fluid flow modeling, with an entropic LBM employed for higher Reynolds number flows. Fluid-solid interaction (FSI) for the solid domain was based on the standard bounce-back method, whereas FSI with suspended platelets was based on the External Boundary Force (EBF) method. Detailed descriptions and validations of these methods were reported previously (Aidun 1998; Keating 2007; Aidun 2010; Wu and Aidun 2010). These methods are validated for modeling BMHV pulsatile flows (Yun 2014) and modeling suspended platelets to quantify damage in BMHV flows (Wu 2011).

The St. Jude Medical (SJM) valve has been shown to perform best among mechanical valve designs when implanted in patients < 5 years old (Raghuveer 2003). Particle Image Velocimetry (PIV) experiments were performed of pulsatile flow through a 23mm SJM valve (Figure 1a) in the aortic position. The experimental setup was recreated computationally for use in simulations (Figure 2). The ventricular and aortic chambers were rigid tubes of diameter 25.4mm. Total domain length was 16 diameters, with ventricular chamber length of 4 diameters. Downstream of the valve was a sudden axisymmetric expansion to a diameter of 31.75mm representing an idealized aortic sinus. Details of the experimental setup have been published (Dasi 2007).

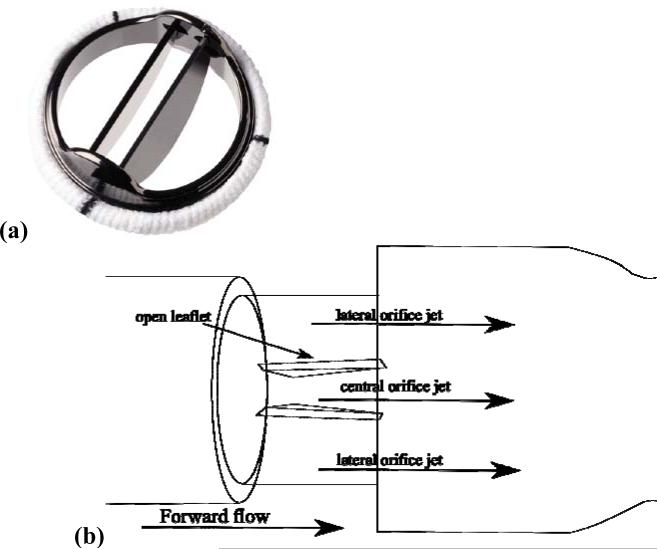
Figure 1.

(a) St. Jude Medical 23mm Regent valve, (b) Diagram of BMHV in forward flow phase with three orifices

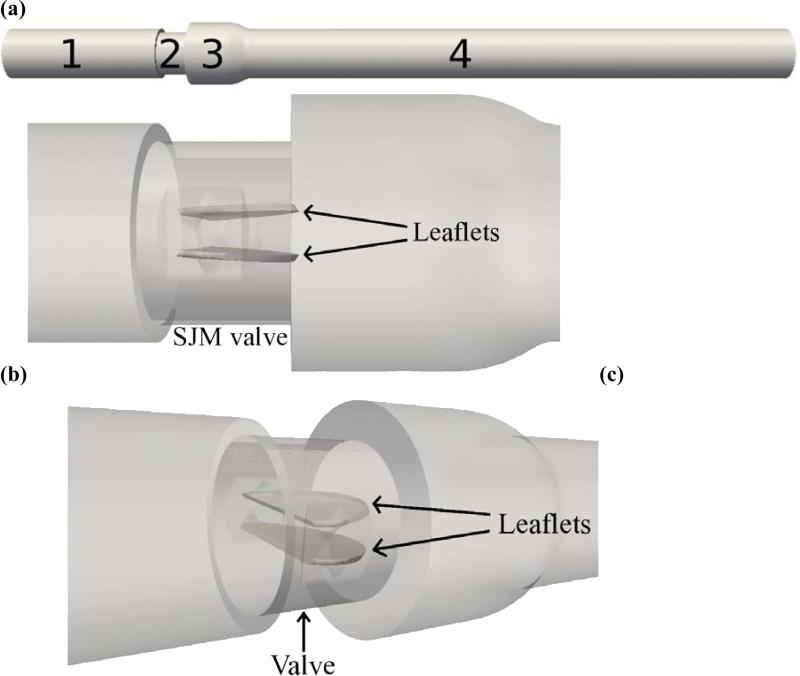
Figure 2.

Computational setup of SJM valve in aortic position, (a) Domain split into regions: (1) ventricular side chamber, (2) valve, (3) sinus expansion, (4) aortic side chamber, (b) zoomed view showing fully open leaflets in valve region, (c) angled view.

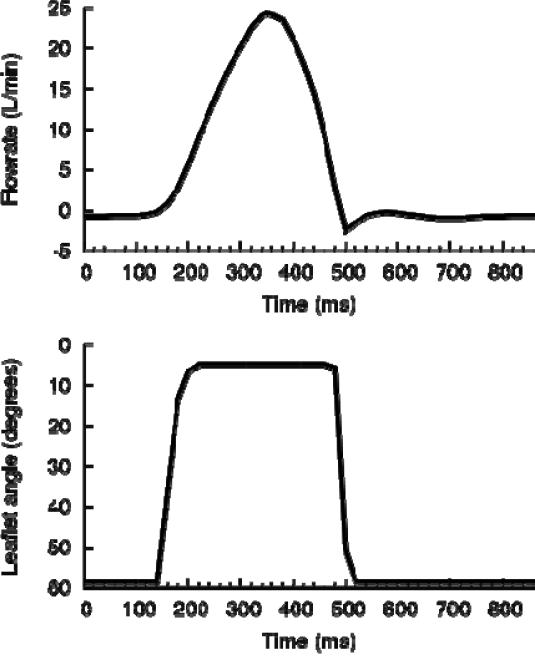
Reynolds number is defined by Re = U_avgD/ν, where U_avg is average inlet velocity. Flowrate was prescribed at the inlet from experimental data (Figure 3), with plug flow chosen due to high Womersley number (Wn = 18 for adults). At the outlet, a stress-free boundary condition was applied. These conditions were used in validation against experiments (Yun 2014). Details of the numerical setup for BMHV flow simulations and the PIV experiments can be found in literature (Dasi 2007; Yun 2014).

Figure 3.

(a) Prescribed flowrate and (b) leaflet motion throughout one cardiac cycle of 860ms from experimental data, based on adult flow conditions

Blood modeling

Blood was modeled as an incompressible Newtonian fluid with the same kinematic viscosity as whole human blood (3.5 cSt). Suspended platelets were modeled with the same shape (3D ellipsoid), size (3μm major axis diameter), and surface mesh (292 triangular elements).

Platelet damage was quantified as accumulated damage using a simple linear shear stress-exposure time damage accumulation blood damage index (BDI) model with no threshold level. The BDI was defined for each platelet as

$$BDI=\sum _{t=0}^{t=end}{\tau }_{\max }•\Delta t$$ Equation 1

where τ_max is the maximum instantaneous surface shear stress experienced by the platelet, and Δt is the numerical timestep. Platelet damage was accumulated upon platelet release until simulation end. This methodology was used in validation against blood damage experiments (Wu 2011). Platelet damage was averaged in small cubic regions of the flow domain to present “Eulerian views” of blood damage.

For all cases, 300 representative platelets were released at regular intervals during the systolic phase for a total of 5400 released platelets. Platelets were released in adult flow every 20ms at a position 1D upstream of the valve with randomized cross-sectional position. Damage was tracked in adult flow for 460ms of the 860ms cardiac cycle, representing all of systole, leaflet closing, and early diastole. As the platelet suspension is dilute, no contact modeling between platelets was required.

Instantaneous plots of viscous fluid shear stress magnitude are displayed, with the viscous fluid stress tensor defined as

$${\tau }_{ij}=\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$$ Equation 2

For a plane defined by unit normal vector n̂, the magnitude of shear stress τ_{shear stress} projected on the plane is defined as

$${\tau }_{shearstress}=\mid \widehat{t}•\underset{̱}{\underset{¯}{\tau }}•\widehat{n}\mid$$ Equation 3

where t̂ is a unit vector tangential to the plane. Shear stresses are projected onto planes perpendicular to the leaflets and quantified in units of dynes/cm².

Flow conditions

For the adult case, physiologic conditions were used matching conditions of the experiments (Dasi 2007). Figure 3 shows prescribed flow rate and leaflet angle for one cardiac cycle taken from experiments (Dasi 2007). The fluid domain employed uniform 3D grid spacing with spatiotemporal resolution of 80μm and 2.4μs per numerical timestep. The flow through the hinges cannot be resolved at this resolution. However, use of this spatiotemporal resolution was shown to result in good matching with experimental PIV data, and is high enough to resolve the smallest scales of BMHV flow (Yun 2014). Good matching was also shown with a lower spatial resolution of 160μm, demonstrating that 80μm resolution of this study is suitable for accurate modeling of BMHV flow. Translational motion of the leaflets was restricted, and only rotational motion was allowed.

Conditions for pediatric patients were based on published normative data (Sluysmans 2005; Zilberman 2005; Kaldararova 2006; Pettersen 2008; Pees 2013; Yoganathan 2013) and consultation with Dr. Doff McElhinney of NYU Langone Medical Center. Additional input was received from clinicians from Children's Healthcare of Atlanta and Children's Hospital Boston. Flow conditions and sizing were chosen for a representative 5 year-old child and 6 month-old infant. Although children are defined as 5 to 12 years of age (Yoganathan 2013), the age of 5 years was chosen to perform simulations of a case that is markedly different than a physiologic adult. Infants are defined clinically as 1 month to 1 year of age, during which there is a large period of growth. The age of 6 months was chosen for modeling, although valve implantation at this age is not common, to demonstrate more “extreme” scenarios for valve implantation.

Simple scaling is performed of adult data to match relevant parameters for pediatric cases (valve size, systolic duration, cardiac output, heart rate). Flow conditions for all cases are given in table 1. Flowrate and leaflet motion curves were modified from adult conditions to match appropriate conditions of the pediatric cases. This included stretching of systolic flow period for the infant case to match systolic duration %. The flowrate curves were then scaled in length and magnitude to match heart rate and cardiac output for both pediatric cases.

Table 1.

Conditions for adult, 5 year-old child, 6 month-old infant. Value size refers to the internal diameter of value and not sewing cuff diameter.

Age	Valve Size (mm)	Systolic %	Heart rate (bpm)	Cardiac output (L/min)	Peak flowrate (L/min)	Peak Re #
18– years	21.4	40%	70	5.0	25.0	5780
5 years	14	40%	90	2.5	12.5	4418
6 months	9	50%	120	1.25	4.8	2725

As with the adult case, 5400 platelets were released during systolic flow for the pediatric simulations, with 300 platelets released every 15.5ms for child flow and every 13ms for infant flow. The same fraction of the cardiac cycle was modeled for adult, child, and infant flows. The platelets were released slightly further upstream (1.25D) of the valve for pediatric flows. The number of “waves” of release (18 total) was maintained equal for all simulations for consistency and to capture all parts of forward systolic flow.

The spatiotemporal resolution of the child simulation was 51.6μm and 1.52μs, with a simulation time of 360ms. For the infant case, the simulation time was 317ms, with spatiotemporal resolution of 33.6μm and 1.08μs. The pediatric flows are of lower peak Reynolds numbers, and thus the smallest flow scales will be even larger than for adult flows (approximately 60μm for child flows, 90μm for infant flows using simplified scaling). Thus, the higher resolutions of the pediatric flow simulations are certainly high enough to resolve the smallest features of those flows. As the domain was smaller, some platelets exited the domain during the infant flow simulation. These platelets retained their final accumulated damage value upon leaving the domain.

RESULTS

Final platelet distributions at the end of all three simulations are shown in figure 4. For the infant case, 1403 platelets exited the domain.

Figure 4.

(a) 5400 platelets at end of adult flow simulation, (b) 5400 platelets at end of child flow simulation, (c) 3997 platelets at end of infant flow simulation.

Flow fields

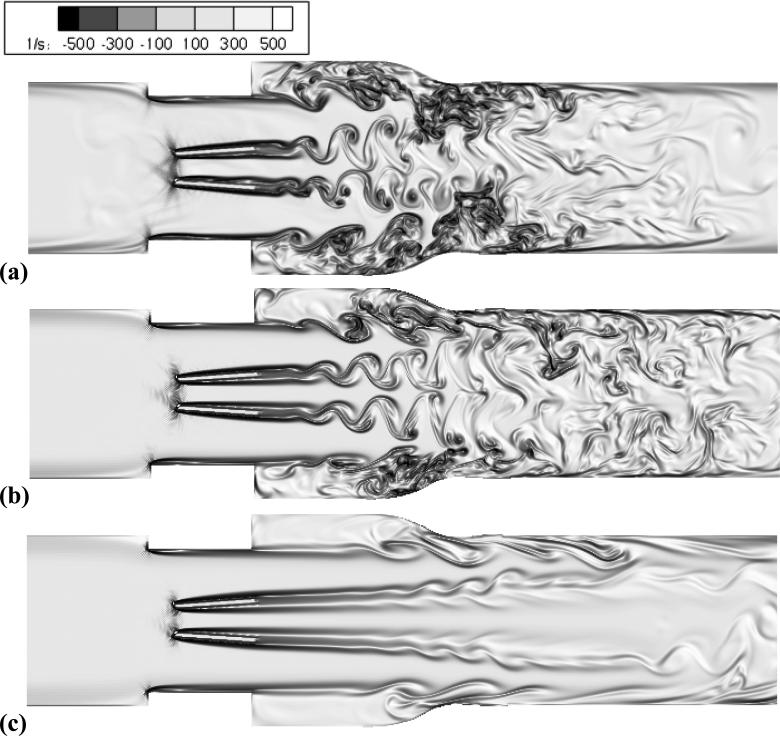
During leaflet opening and early acceleration, the flow fields were qualitatively similar due to low Reynolds numbers in all cases. For peak flow, adult flows (Re = 5780) showed many small-scale eddies and disorganized flow downstream of the valve (figure 5a). At the sinus, adult flow showed a strong recirculation region, which frequently mixed with leaflet vortex wakes. Peak flow for child flow (Re = 4418) demonstrated vortex wakes past the leaflets, but these vortices were large, coherent, and did not break into smaller eddies (figure 5b). There was less mixing between leaflet wakes and sinus recirculation regions in child flow, and weaker overall recirculation. Infant peak flow (Re = 2725) did not demonstrate any vortex wakes, but triple jet-like flow (figure 5c). This flow field did not show any small-scale structures, and showed little recirculation.

Figure 5.

Peak flow visualizations of vorticity for (a) adult – Re = 5780, (b) child – Re = 4418, (c) infant – Re = 2725.

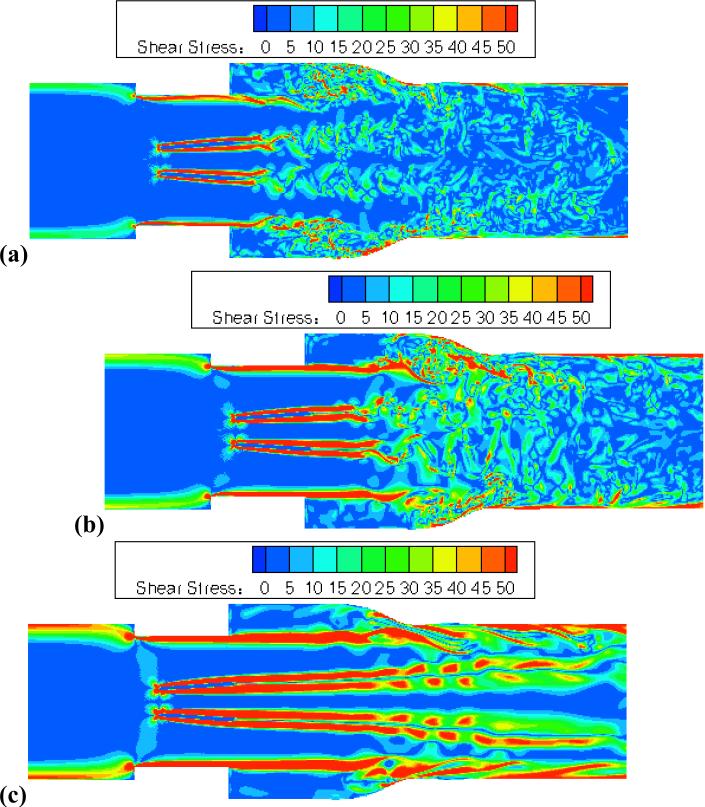
Shear stress fields are plotted at peak flow for the three cases (figure 6). This comparison shows moderate shear stresses in leaflet wake vortices for adult and child cases. Child flow showed stronger shear stresses, particularly immediately downstream of the valve (figure 6b). Although peak Reynolds number of child flow was lower than adult flow, peak inlet velocity was 17% higher. In infant flow, peak shear stresses in the flow field were much higher than for adult flows (figure 6c). Peak inlet velocity was 41% higher for infant flow than adult flow. The coherent forward jets were associated with high shear stresses, located in shear layers past the leaflets and valve housing. Thus, fluid shear stresses associated with small-scale eddies in adult flows were much lower than for the more coherent flows in pediatric cases, despite the small-scale eddies appearing more unstable and chaotic.

Figure 6.

Peak flow viscous shear stress visualizations for (a) adult – Re = 5780, (b) child – Re = 4418, (c) infant – Re = 2725.

Blood damage

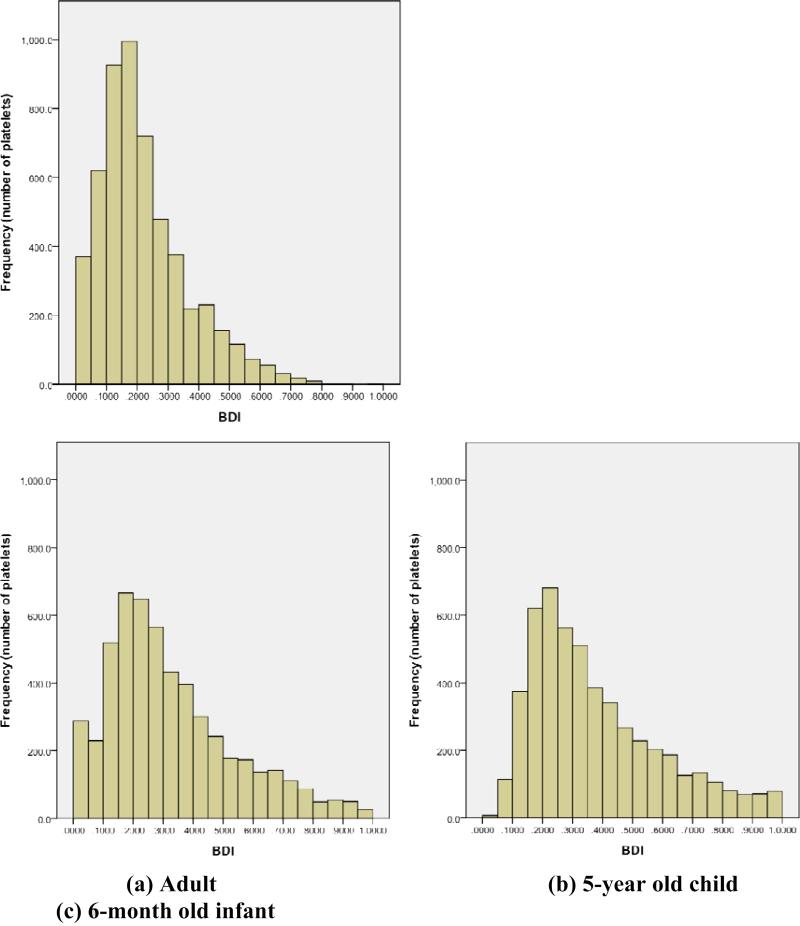
Analysis of blood damage for adult flow was reported previously (Yun 2014), and a histogram of the distribution is presented in Figure 7a. The average BDI for adult flow was 0.224±0.154 dynes•s/cm². Only four platelets out of 5400 (0.07%) had damage accumulation larger than 1.0 dynes•s/cm², with maximum BDI of 3.6 dynes•s/cm². Platelet damage after 460ms of simulation is listed by domain region in table 2.

Figure 7.

BDI histograms of 5400 platelets after (a) 460ms of damage accumulation for adult, (b) 360ms of damage accumulation for 5-year old child, (c) 317ms of damage accumulation for 6-month old infant. Histogram interval: 0.05 dynes*s/cm², with BDI values over 1.0 dynes*s/cm² not shown.

Table 2.

Platelet and BDI distribution by region – physiologic adult

	Overall		Top 10%		Top 1%
Region	# platelets	BDI average (dynes s / cm2)	# platelets	BDI average (dynes s / cm2)	# platelets	BDI average (dynes s / cm2)
Overall	5400	0.2248	540	0.5509	54	0.8355
Ventricular side	732	0.0739	10	0.5421	2	0.7325
Valve	302	0.1988	27	0.7173	5	1.586
Sinus expansion	951	0.3227	214	0.5633	29	0.7891
Aortic side	3415	0.2322	289	0.5265	18	0.7131

After 360ms of simulation, average BDI for all 5400 platelets of child flow was 0.342±0.238 dynes•s/cm². Higher heart rate for child flow results in shorter exposure time for platelets. Nevertheless, average accumulated damage was 53% higher than for adult flow. The BDI distribution for child flow was qualitatively similar to adult flow, where distribution was skewed to lesser damage (figure 7b). Compared to adult flow, child flow showed more platelets with higher accumulated damage, with BDI above 1.0 dynes•s/cm² in 99 of 5400 platelets (1.83%). However, maximum platelet damage was 1.77 dynes•s/cm², lower than the maximum for adult flow (3.6 dynes•s/cm²). 72% of platelets advected to the aortic chamber, which was more than adult flows (63%). In adult flows, the sinus had average damage 62% higher than in the valve, whereas for child flow the average damage in the sinus was only 1.5% higher than for the valve, suggesting more even damage distribution by region. Although damage values were higher for child flow than adult flow, a large majority of highly damaged platelets were found in the aortic chamber.

For infant flow, only 3997 (74%) of seeded platelets remained in the domain (figure 4c). BDI distribution (figure 7c) was still skewed towards lesser damage. Average BDI for all 5400 platelets was 0.419±0.287 dynes•s/cm², higher than both adult and child flows despite shortest overall exposure time for platelets (317ms vs. 360ms child / 460ms adult), and the fact that platelets (26%) did not accumulate damage upon exiting the domain. 248 of 5400 platelets (4.6%) have damage higher than 1.0 dynes•s/cm², more than both child and adult flows. Maximum platelet damage of 2.29 dynes•s/cm² was lower than the maximum for adult flow but higher than for child flow. Overall, 81% of platelets advected downstream to the aortic chamber (table 4). In infant flow, 81% of the top 10% damaged platelets and 85% of the top 1% were located in the aortic chamber.

Table 4.

Platelet and BDI distribution by region – 6-month old infant

	Overall		Top 10%		Top 1%
Region	# platelets	BDI average (dynes s / cm2)	# platelets	BDI average (dynes s / cm2)	# platelets	BDI average (dynes s / cm2)
Overall	5400	0.4186	540	1.070	54	1.698
Ventricular side	278	0.2239	8	1.059	1	1.479
Valve	174	0.3363	13	1.078	1	1.435
Sinus expansion	568	0.5059	81	1.034	6	1.739
Aortic side	4380	0.4229	438	1.076	46	1.703

Eulerian view

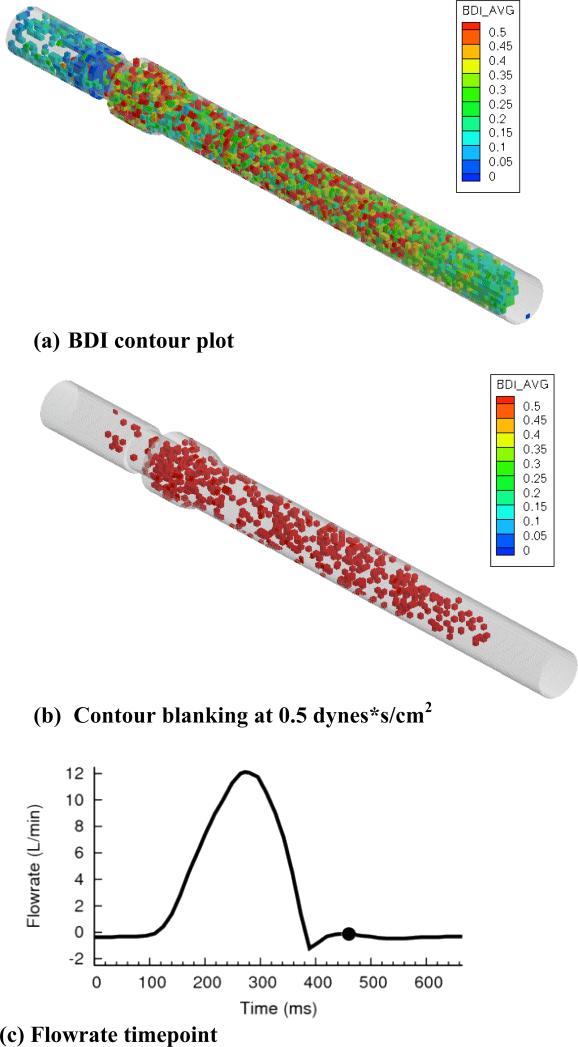
For child flow (figure 8a), high damage regions existed primarily in the sinus expansion and aortic chamber. As shown in figure 8b, high damage regions were clustered in the sinus and aortic chamber. The same viewpoint is shown for infant flows (figure 9a), with qualitative similarity to child flow. For blanking plots (figure 9b), a larger number of high damage regions were observed throughout the entire domain. High damage regions filled the entire aortic chamber, extending to the outlet.

Figure 8.

(a) BDI contour plot, (b) regions blanked if damage less than 0.5 dynes*s/cm², and (c) flowrate curve for child flow, 5400 released platelets

Figure 9.

(a) BDI contour plot, (b) regions blanked if damage less than 0.5 dynes*s/cm², and (c) flowrate curve for infant flow, 5400 released platelets

The Eulerian view comparison among the three cases is shown in figure 10 with blanking performed at 0.5 dynes•s/cm². These plots clearly show larger number of high damage regions in pediatric cases than in adult flow. Though there is clustering in the sinus for all cases, there were more high damage regions in the aortic chamber for pediatric flows.

Figure 10.

BDI contour plot at end simulation timepoints, 5400 released platelets. Contours blanked if damage less than 0.5 dynes*s/cm² for (a) adult, (b) child, (c) infant cases.

DISCUSSION

Flow fields

The three simulations (adult, child, infant) produced very different flow fields at peak flow. Adult flow was characterized by a large number of small-scale eddies that were not present in pediatric cases. Simulations also showed strong recirculation in the sinus for adult flows, weaker recirculation in child flow, and no recirculation in infant flow. This may explain why more highly damaged platelets for pediatric flows were found in the aortic chamber. Platelets that experienced high levels of damage near the sinus region for pediatric flows had a higher likelihood of being swept out of the sinus due to low recirculation. In adult flows, however, highly damaged platelets caught in the sinus region did not get swept out of recirculation zones and remained in the sinus.

Shear stress fields at peak flow showed relatively moderate shear stresses in leaflet shedding vortices for adult and child flows. Infant flow showed very high shear stresses in flow past the leaflets and sinus step, but with no recirculation zones. Although peak Reynolds number for infant flows was lowest, bulk average velocities were highest. The more laminar infant flows resulted in higher velocity gradients for flow past the leaflets and valve housing. As velocity gradient is directly related to viscous shear stresses, this led to higher viscous shear stresses. This was found in infant flow, where high shear stresses were observed near the leaflet and valve housing surface and in jets downstream of the valve in the form of shear layers. The aortic sinus showed high shear stresses in thin layers downstream of the leaflet and valve housing, but low shear stress values in the middle of each orifice flow and within the sinus. This is in contrast to adult flow, where shear stresses were lower but the entire sinus was filled with moderate levels of viscous shear stress from disorganized and mixing flow.

The coherent shear layers in infant flow are associated with high shear stresses, but are not associated with flow recirculation. This explains why platelet damage is highest in infant flows, but highly damaged platelets are found far downstream of the valve. A larger number of platelets are damaged while flowing in shear layers for infant flow, as they are associated with coherent triple forward flow jets. However, lack of recirculation caused platelets to advect downstream far from the valve, where they may be less likely to form thrombi.

Blood damage

Although adult flow had highest maximum damage for an individual platelet, the average blood damage was lower than in pediatric flows. In all three cases, platelet damage was skewed towards lesser degrees of damage, due to low exposure time of platelets that are seeded later in simulations. However, with decreasing patient age, the distribution became less skewed towards lower damage values. For the infant case in particular, a high number of platelets experienced damage greater than 1.0 dynes•s/cm². Very few cases in the simulations exhibited damage above 2.0 dynes•s/cm² and none were above 4.0 dynes•s/cm².

For these one pass simulations, no platelets were in danger of reaching activation thresholds of 10.0 – 35.0 dynes•s/cm² (Hellums 1977; Alemu 2007). However, infant flow did have 248 (4.6%) platelets that exceeded a damage value of 1.0 dynes•s/cm², compared with 4 platelets (0.07%) for adult flow and 99 platelets (1.8%) for child flow. Although platelet activation is not a danger for one pass through the valve, blood damage values are elevated on average and a larger number of highly damaged platelets exist for pediatric cases.

For average blood damage and top 1% and 10% damage values across flow conditions, infant flow had highest damage for all simulated cases. For the top 1% of damaged platelets, infant flow had average damage 103.2% higher than adult flow. However, as patient age decreased, more platelets overall were found in the aortic chamber due to lower recirculation. The top damaged platelets were found with increasing frequency in the aortic chamber and less in the ventricular chamber and valve for pediatric cases. The potential clinical significance of these differences is unknown.

Thromboembolic potential

Vorticity fields appear qualitatively more unstable and disorganized for adult flows, but this does not translate directly to higher platelet damage values. This implies that observing instantaneous flow fields for disorganized flow alone is not sufficient to make implications to thromboembolic potential of a valve.

Pediatric flows may have higher platelet damage average and higher number of highly damaged platelets. However, platelets are not close to activation thresholds, and are easily advected into the aortic chamber. After traversing downstream, damaged platelets are widely dispersed and would flow through the aorta in the next systolic phase. This may be of lesser concern for potential platelet activation and thrombus formation in the valve, the most important type of thrombotic complication for prosthetic valves. Adult flows have larger recirculation due to higher Reynolds number at peak flow, which leads to highly damaged platelets remaining near the valve, where they could potentially become activated and initiate thrombosis. Although elevated damage values of pediatric BMHV flows are of concern and should be examined in more detail, these results cannot conclusively determine the thromboembolic potential of pediatric sized valves due to the final location of highly damaged platelets.

The more laminar nature of pediatric flows is simply a product of lower Reynolds number conditions for pediatric cases. However, the presence of the two BMHV leaflets leads to generation of more shear layers than in native valve flows. These shear layers are associated with higher shear stresses and platelet damage, and may lead to increased thromboembolic complications for pediatric BMHV flows. The simulations of a previous study demonstrated the danger of recirculation for inducing platelet damage (Yun 2014), and thus pediatric BMHV designs may focus on reducing recirculation zones for pediatric flows. This would ensure that elevated platelet damage for pediatric BMHV flows are not exacerbated by formation of dangerous recirculation zones near valves. This could be accomplished by creating smoother geometries throughout the valve design, though further investigation is warranted. The potential thromboembolic implications of pediatric BMHV flows in other parts of the cardiovascular system are uncertain. Further studies are necessary to determine validity and potential thrombotic and clinical implications of these findings.

Table 3.

Platelet and BDI distribution by region – 5 year-old child

	Overall		Top 10%		Top 1%
Region	# platelets	BDI average (dynes s / cm2)	# platelets	BDI average (dynes s / cm2)	# platelets	BDI average (dynes s / cm2)
Overall	5400	0.3416	540	0.8662	54	1.286
Ventricular side	710	0.1066	13	0.9259	3	1.197
Valve	114	0.4441	22	0.8727	2	1.315
Sinus expansion	697	0.4512	128	0.9056	18	1.343
Aortic side	3879	0.3619	376	0.8526	31	1.260