Noise Propagation in Region Of Interest Measurements

Abstract

Purpose

The purpose of this work was to develop and validate a technique for predicting the standard deviation associated with thermal noise propagation in region of interest measurements.

Theory and Methods

Standard methods for error propagation estimation were used to derive equations for the standard deviations of linear combinations of complex, magnitude, or phase pixel values. The equations were applied to common imaging scenarios where the image pixels were correlated due to anisotropic pixel resolutions and parallel imaging. All standard deviation estimates were evaluated efficiently using only vector-vector multiplications and Fourier transforms. The estimated standard deviations were compared to standard deviations obtained using repeated experiments and pseudo replica reconstructions.

Results

The proposed method was able to predict region of interest standard deviations in all the tested analysis scenarios. Positive and negative noise correlations caused by different parallel imaging aliasing point spread functions were accurately predicted and the method predicted the confidence intervals of time-intensity curves for in vivo cardiac perfusion measurements.

Conclusions

An intuitive technique for region of interest confidence intervals was developed and validated using phantom experiments and in vivo data.

Introduction

Diagnostic interpretation of MR images frequently involves Region Of Interest (ROI) measurements. An important component of ROI analysis is to determine the average (or sum) pixel intensity in specific area of the image, e.g. to compare signal intensities in a suspected lesion with signal intensities in normal tissue. More generally the objective is to determine the value of some linear combination of the pixel values in an image region. For such an analysis it is desirable to know the variability of the estimate caused by thermal noise. The standard deviation (σ) or variance (σ²) of each individual pixel can be estimated directly from the raw data and noise samples for most Cartesian linear reconstructions using the techniques developed for Signal To Noise (SNR) scaled reconstruction (1,2). An alternative method to obtain pixel-wise noise variance estimates is the pseudo replica technique proposed by Robson et al. (3) or the faster approximation based on only a few pseudo replicas introduced by Weins et al. (4). If the pixels are assumed to be uncorrelated, the variance of the sum of the pixels in an ROI is simply the sum of the variances of each of the individual pixels in the ROI. In most practical imaging experiments, the pixels are correlated, which makes it more challenging to determine standard deviation of the average pixel intensity in an ROI. In some simple cases, it may be possible to determine the effective number of independent pixels in the region of interest and calculate a factor to scale an estimate of the ROI standard deviation accordingly. However, in the general case, the pixel correlation in an ROI is affected by several interacting factors such as reduced phase encoding resolution, partial Fourier acquisition, raw data filtering, and parallel imaging (5–7). Moreover, the orientation of the ROI also plays a role, i.e. a given ROI may have a different standard deviation if oriented along the phase encoding direction as opposed to along the frequency encoding direction. This latter point makes it difficult to use a global pixel correlation factor to scale standard deviation estimates.

The standard deviation of an ROI measurement can, in general, be determined using the pseudo replica technique (3). With this technique multiple reconstructions (replicas) are obtained by adding noise to the original raw data and repeating the reconstruction. The standard deviation in each pixel is obtained as the standard deviation across the replicas and similarly one can determine the standard deviation for an ROI measurement (sum or average) by repeating the ROI measurement on each replica and calculating the standard deviation of the results. While this technique has many advantages in terms of generally applicability and simplicity, it is time consuming and difficult to integrate with an image analysis workflow. The faster method for pixel-wise noise estimation (4) employs averaging of a neighborhood of pixels to improve precision of noise variance estimates. This approach does not capture the noise correlation between pixels within an ROI and in this article the original pseudo replica method has been used as reference standard.

The purpose of this article is to demonstrate a practical technique for calculating the standard deviation of any linear combination of the pixels in an MR image without the need for repeated reconstructions. The techniques can be applied to most Cartesian, linear reconstructions and it can be used to determine standard deviations for ROI measurements of real, imaginary, magnitude, and phase components of the complex images.

Theory

The goal of the ROI measurement is to obtain some linear combination of the pixels in the image. If ρ is a column vector containing all the pixels of the image and m is a column vector containing linear weighting coefficients corresponding to each pixel, then the result r (scalar) of an ROI measurement can be written as:

$$r={\mathbf{m}}^{\mathrm{H}}\mathbf{\rho }$$ [1]

In general the variance of r is:

$${\sigma }_r^2={\mathbf{m}}^{\mathrm{H}}{\mathbf{\sum }}_{\mathbf{\rho }}\mathbf{m}$$ [2]

Where Σ_ρ; is the covariance matrix of the pixel noise. In the rare case where the pixels are uncorrelated, Σ_ρ; is a diagonal matrix with the noise variance of each pixel along the diagonal. In most ROI measurements, m would be a vector with entries of either ‘1’ (for pixels within the ROI) or ‘0’ (for pixels outside the ROI). However, it need not be a binary mask. If a certain region of the image should be weighted differently in the analysis, the coefficients can be adjusted accordingly. The covariance matrix Σ_ρ; is a large matrix which would be impractical to form directly for most real experiments, but it is possible to obtain an expression for it using the knowledge that if covariance matrix of some vector x is Σ_x then the covariance matrix of the linear transform Ax is AΣ_xA^H. This is the general form used to obtain eq. [2]. If the covariance matrix of the noise in the acquired k-space samples is denoted Σ_k and the linear image reconstruction (image formation) process is defined by the matrix F then eq. [2] can be written as:

$${\sigma }_r^2={\mathbf{m}}^{\mathrm{H}}\mathbf{F}{\mathbf{\sum }}_{\mathbf{k}}{\mathbf{F}}^{\mathrm{H}}\mathbf{m}$$ [3]

In general, it is straightforward to ensure that Σ_k is diagonal or even identity. Specifically, if noise pre-whitening is performed as described in (1,8) and any oversampling in the readout direction is removed by Fourier-transform to image space, field of view reduction, and Fourier transform back to k-space, the k-space noise covariance matrix, Σ_k, will be diagonal or identity in the case of uniform k-space sampling. For Cartesian acquisitions using phased array coils, the image formation matrix F can be split into a set of operations that are either vector-vector multiplications or Fourier transform operations. Specifically, F would consist of a) a k-space masking operation, which would account for any undersampled areas (reduced resolution or parallel imaging) and raw data filtering, b) Fourier transform to image space, c) pixel-wise, linear combination of data from multiple receive channels. The latter operation would take the form:

$$\mathrm{\rho }(x)=\sum _{i=1}^{\mathrm{\Gamma }}{u}_i(x)a_i(x)$$ [4]

Where ρ(x) is the reconstructed image pixel at location x, u_i(x) is the phased array combining (or unmixing) coefficient for coil i at location x, a_i(x) is the pixel value (after Fourier transform) in coil i at location x, and Γ is the number of coils. The coil pixel values, a_i(x), could contain aliasing in the case of parallel imaging and u_i(x) will be the set of coefficients that produce unaliased and SNR optimal images (in some sense defined by the parallel imaging approach). Both SENSE (6) and GRAPPA (7) type parallel reconstruction algorithms can be expressed as unmixing with a phased array combiner. The multiplication with F^H would be a) multiplication of the image with the conjugate of the unmixing coefficients u_i (this generates multiple image channels from a single image), b) Fourier transform to k-space, and c) k-space masking. Based on the operations described above, it is possible to obtain the variance of a linear combination of pixels in a complex image.

It is common to perform the ROI measurements on a magnitude or phase image. The magnitude or phase operators are not linear operations and consequently, eq. [3] cannot be applied directly. The method presented in this article employs a linear approximation of this non-linear operation, which is valid in the case of moderate and high SNR ratios. The approximation follows commonly used principles uncertainty propagation, e.g. (9,10). Let T(x) be a function (linear or non-linear) such that y = T(x), then y can be approximated by:

$$\mathbf{y}\approx \mathrm{T}({\mathbf{x}}_0)+\mathbf{J}(\mathbf{x}-{\mathbf{x}}_0)$$ [5]

Where J is the Jacobian of T at x₀. Using this, the covariance matrix of y, Σ_y, can be approximated:

$${\mathbf{\sum }}_{\mathbf{y}}\approx \mathrm{E}\{(\mathbf{y}-{\mathbf{y}}_0){(\mathbf{y}-{\mathbf{y}}_0)}^{\mathrm{H}}\}$$ [6]

$$\approx \mathrm{E}\left\{\left(\mathbf{J}(\mathbf{x}-{\mathbf{x}}_0)\right){\left(\mathbf{J}(\mathbf{x}-{\mathbf{x}}_0)\right)}^{\mathrm{H}}\right\}$$ [7]

$$\approx \mathbf{J}{\mathbf{\sum }}_{\mathbf{x}}{\mathbf{J}}^{\mathrm{H}}$$ [8]

Where E{·} denotes the expected value. Equation [8] allows an approximation of the variance even in the case of non-linear transformations as long as an estimate of the Jacobian is known. If the operation of taking the magnitude is approximated as a pixel-wise phase change to rotate the complex pixel signal to be oriented along the real axis, the variance of a linear combination of the magnitude image pixels can be approximated as:

$${\mathrm{\sigma }}_{\mathit{mag}\mathit{roi}}^2={\mathbf{m}}^{\mathrm{H}}{\mathbf{\theta }}^{\mathrm{H}}\mathbf{F}{\mathbf{\sum }}_{\mathbf{k}}{\mathbf{F}}^{\mathrm{H}}\mathbf{\theta }m$$ [9]

Where θ is a diagonal matrix with complex numbers along the diagonal with magnitude 1 and phase equal to some estimate of the image phase when the image has a well-defined phase (there is some signal) and zero otherwise. This is equivalent to a transformation of the covariance matrix to an in-phase/quadrature covariance matrix (11). Since the standard deviation of the phase is approximately inversely proportional to the SNR (at moderate to high SNR), an expression of the uncertainty of the phase can be found to be:

$${\mathrm{\sigma }}_{\mathit{phase}\mathit{roi}}^2={\mathbf{m}}^{\mathrm{H}}{\mathbf{\theta }}^{\mathrm{H}}\mathbf{MF}{\mathbf{\sum }}_{\mathbf{k}}{\mathbf{F}}^{\mathrm{H}}\mathbf{M}\mathbf{\theta }\mathbf{m}$$ [10]

Where M is a diagonal matrix with $\frac{1}{\mid \mathrm{\rho }\mid }$ (the reciprocal of the signal magnitude) along the diagonal. Clearly this will not be well defined in regions of very low signal.

The results in Eqs. [9] and [10] can be obtained through other simpler analyses than the formalism outlined in Eqs. [6]-[8], which applies in general for any non-linear approach to pixel estimation. Since the Jacobian can be used for cases where the pixel intensities have obtained through more complicated non-linear estimation procedures (e.g. parametric mapping), it is included here for completeness.

Equations [3], [9], and [10] provide a way to obtain the variance or standard deviation of an ROI measurement. Equation [3] can be used to estimate the variance when analyzing complex images and equations [9] and [10] would be used to analyze magnitude or phase images respectively. The variances can be calculated directly without the need to form pseudo replicas. Moreover, the evaluation of those equations can be done using vector-vector multiplications and Fourier transforms alone and the large covariance matrices need not to be formed or stored explicitly. In the following sections practical methods for working with the proposed solution will be outlined and the methods will be demonstrated on phantom and in vivo data.

Methods

Image Reconstruction and Analysis

The methodology outlined in this article does not rely on a particular reconstruction procedure as long as the operations contained in the image formation matrix F are known. However, the reconstruction used in the experiments is outlined here for clarity. Figure 1 illustrates an overview of the reconstruction pipeline. For all experiments, noise samples were acquired and used to calculate a noise pre-whitening matrix, which was applies to all acquired data (1). Any readout oversampling was then removed from the data by Fourier transform to image space, field of view reduction and Fourier transform back to k-space. After these first two steps the k-space data was considered to have unit noise variance and the noise was considered uncorrelated between channels and also between sample locations in k-space. The data was then Fourier transformed from k-space to image space to form individual channel images. These individual channel images were combined with a set of channel combination or unmixing coefficients as described in eq. [4]. These coefficients were calculated from calibration data, which were either acquired inline with the data or obtained as a time average of the data (12). A GRAPPA calibration was used to calculate k-space convolution kernels. These kernels were zero-padded to the full matrix size and Fourier transformed to image space where the image space kernels for each individual channel were combined using coil sensitivity maps estimated from the calibration data using the method outlined by Walsh et al. (13). To enable validation of the method outlined in this article, multiple pseudo replicas were also generated by adding noise with unit variance to the data and repeating the reconstruction. In all image reconstruction steps, scaling was applied to ensure that unit noise variance was maintained (1). Specifically, scale factors were applied to account for the number of independent samples in the Fourier transforms and scale factors were applied to account for raw data filters, etc. As a result the reconstructed images had noise variance equal to one in each pixel except in the cases where parallel imaging was employed (see below); here the noise variance in in each pixel was scaled according to the g-factor (6).

Figure 1.

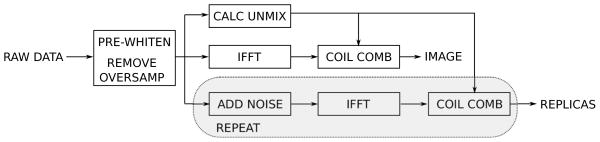
Reconstruction pipeline. Data is first pre-whitened to ensure unit noise variance and that noise is uncorrelated between receive channels. Any readout oversampling is also removed from the data. Calibration data is processed to calculate unmixing coefficients and the remaining data is Fourier transformed to image space where the channel images are combined using the unmixing coefficients. In a parallel pipeline, noise with unit variances is repeatedly added to the raw data and pseudo replicas are reconstructed.

With such a noise scaled reconstruction, the standard deviation of the sum or the mean of an ROI has a predictable behavior in reconstructions where the noise is uniformly distributed in the image (no parallel imaging) and there is no correlation between the image pixels. This is illustrated in Fig. 2 for a reconstruction where all the pixels are independent and no parallel imaging is used. The left panel shows a plot of the standard deviation of the sum of the pixel magnitudes in an ROI as a function of the square root of the number of pixels. It is a linear function with slope 1 for both the standard deviation predicted by eq. [9] and the result of a pseudo replica experiment. The right panel is a more familiar illustration of the same point; a plot of the standard deviation of the mean of an ROI against the number of pixels is a straight line on a log-log plot (i.e., the standard deviation decreases proportionally to the square root of the number of pixels). In reconstructions where the pixels are correlated, these plots could deviate from a straight line and/or the slope would be different. The following experiments are intended to illustrate these deviations due to pixel correlations and the proposed methods ability to predict them.

Figure 2.

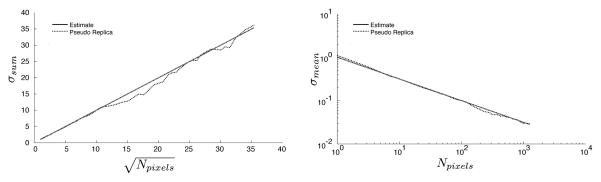
An illustration of the relationship between the standard deviation of a magnitude ROI and the number of pixels for a reconstruction where all pixels are independent and no parallel imaging was employed. The left plot shows the sum of the pixel magnitudes as a function of the square root of the number of pixels in a linear coordinate system and the right plot shows the mean of the pixel magnitudes as a function of the number of pixels in a log-log coordinate system.

Phantom Experiments

A spherical, oil-filled phantom was scanned with an RF spoiled gradient echo sequence with the following parameters: matrix 128×128, field of view 300×300 mm, TR 3.0ms, TE 1.5ms. Twenty receive coils were used. The acquired k-space was fully sampled and 100 repetitions (with a 10s pause between each repetition) were acquired. The phantom data was used to probe the proposed techniques ability to predict ROI standard deviations for two commonly used imaging techniques.

First, a reduced phase encoding direction resolution of 50% (effective sampled matrix 128×64) was simulated. An ROI with a fixed width of 10 pixels and increasing length from 1 to 80 (to fit inside the spherical phantom) was defined and placed with the length direction either along the frequency encoding direction or along the phase encoding direction. Figure 3 is an illustration of the spherical phantom image (fully sampled) with the maximum length ROI placed along the phase encoding direction. The gray scale on the image is in units of SNR, the average SNR in the depicted ROI is ~15 for the fully sampled image. For each length of the ROI, the standard deviation of the sum and the mean of the ROI was calculated based on a) the proposed technique, b) pseudo replica technique (100 replicas), and c) the 100 actual repetitions of the experiment. The results of were plotted for the analysis of the magnitude or the phase of the image.

Figure 3.

Illustration of the spherical phantom used in the phantom experiments. The reconstruction depicted is for fully sampled data and the dotted line outlines the largest ROI analyzed. The ROI is oriented along the phase encoding direction. The grey scale is in units of SNR and the average SNR in the depicted ROI is ~15.

The purpose of the second experiment was to investigate the effects of parallel imaging. The acquired phantom data was undersampled by a factor of 4 in the phase encoding direction. Two different undersampling patterns were investigated, in one undersampling pattern, lines 1, 5, 9, 13, … were “acquired”, in another undersampling pattern, lines 3, 7, 11, 15, … were acquired. The purpose of this experiment was to illustrate the effects of different point spread functions due to sampling phase on the noise correlation in an ROI. For the parallel imaging experiments, the phase encoding direction resolution was 100% and the same ROI sizes and orientations were the same as in the phase encoding resolution experiment.

In Vivo Experiments

To demonstrate the proposed techniques ability to predict standard deviations of ROI measurements on in vivo images, an example from myocardial stress perfusion measurements was chosen. A patient with a transmural septal perfusion defect was imaged during infusion of a bolus of Gd based contrast agent. The local Institutional Review Board (IRB) approved the study protocol and the patient gave written informed consent. A combination of a spine array coil and a surface array coil was used for signal reception. A total of 30 coil elements were used. A short axis slice through the heart was imaged with a saturation recovery (SR) prepared single shot steady state free precession perfusion sequence. The acquired matrix size was 192×110 and the field of view was 360×270 mm. Partial Fourier (asymmetric echo, 75%) was used in the readout direction and a parallel imaging acceleration (rate 2) was used with a time interleaved sampling pattern (14) to enable calibration from a time average of the data. The phase encoding direction was anterior-posterior. Echo time was 1.03 ms and repetition time was 3.03 ms. Total acquisition time per frame was 167 ms including saturation recovery time and a total of 60 time frames were acquired, one every heartbeat for 60 heartbeats. The initial 2 frames had a with proton density weighting acquired at a lower excitation flip angle without SR prep in order to correct for spatial variation in surface coil intensity. The proton density images were used to calculate the average proton density signal in the ROIs used in the image analysis. The proton density ratio between the analyzed ROIs was used to scale the ROI weights, i.e. it was used to modify m in Eq. [9] to correct for surface coil sensitivity variations between ROIs.

The images for each frame were reconstructed as outlined in Fig. 1. In the in vivo case, it was not practical to repeat the actual experiment 100 times, but 100 pseudo replicas were reconstructed. Two ROIs were drawn on the short axis image. One ROI covered the septum with the perfusion defect and the other covered the healthy left ventricular muscle. Each ROI took up about half of the left ventricle. The position of the ROIs was adjusted manually for respiratory motion on each of the 60 frames. The standard deviation of the signal intensities on both normal and ischemic regions was predicted with the proposed method and calculated based on the 100 pseudo replica reconstructions.

Results

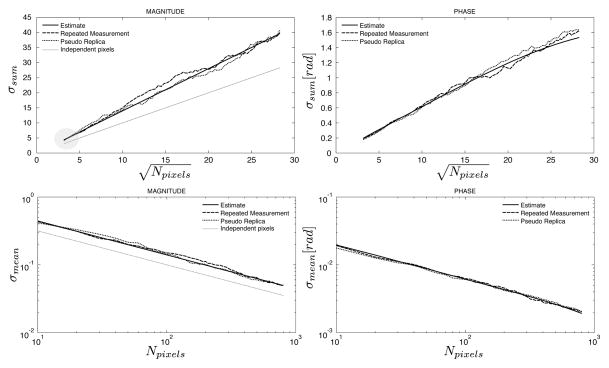
Figures 4 and 5 show the results of the phantom experiment with reduced phase encoding resolution. In Fig. 4, an ROI with width of 10 pixels was increased in length along the frequency encoding direction from 1 pixel up to 80 pixels. It can be seen that for the ROI with length of 1 pixel, there is already a discrepancy between the standard deviation predicted by the pixel-wise standard deviation and the combined standard deviation for the ROI. This is caused by the correlation between pixels in the phase encoding direction resulting from the inherent use of interpolation to create square pixels although the true resolution is reduced in the phase encoding direction. As the length of the ROI increases, the standard deviation of the sum increases linearly with the square root of the number of pixels. In Fig. 5, the ROI is placed orthogonal to the ROI used in Fig. 4. Consequently, the prediction of the standard deviation based on the pixel-wise standard deviation is in agreement with the predicted and measured standard deviations when the ROI is only 1 pixel long (since all pixels are independent in the frequency encode direction). As the ROI grows, the standard deviation of the sum goes up linearly with the square root of the number of pixels, but it grows faster than it would if the pixels were independent. In all cases, the predicted standard deviation and the measured by repeated experiments or pseudo replicas are in good agreement.

Figure 4.

Measured and predicted standard deviations of the sum (top row) and mean (bottom row) of an ROI as a function of the number of pixels in the ROI as it grows along the readout direction in an image with reduced effective resolution in the phase encoding direction. The solid line is the predicted standard deviation from the proposed method, the dashed line is the calculated standard deviation from 100 repeated experiments, and the dotted line is the calculated standard deviation from 100 pseudo replica reconstructions. The gray dotted line on the magnitude plots indicates the predicted standard deviation when assuming that all pixels are independent. The gray circle highlights the initial region of the curve where the actual standard deviations deviate from the gray line since even an ROI with length 1 has dependencies between the pixels. This should be compared to Fig. 5 where the pixels of an ROI with length 1 are actually independent.

Figure 5.

Measured and predicted standard deviations of the sum (top row) and mean (bottom row) of an ROI as a function of the number of pixels in the ROI as it grows along the phase encoding direction in an image with reduced effective resolution in the phase encoding direction. The solid line is the predicted standard deviation from the proposed method, the dashed line is the calculated standard deviation from 100 repeated experiments, and the dotted line is the calculated standard deviation from 100 pseudo replica reconstructions. The gray dotted line on the magnitude plots indicated the predicted standard deviation when assuming that all pixels are independent. Compared to Fig. 4, the actual standard deviations and the gray line are in agreement for an ROI with length 1 but deviates as the ROI increases in length.

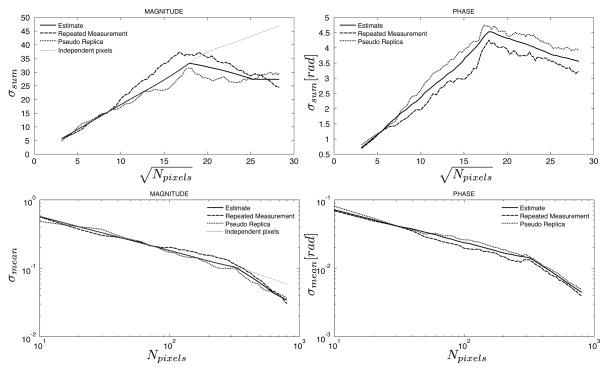
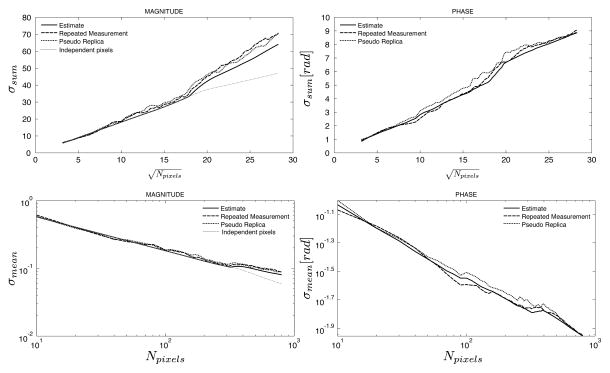
Figures 6 and 7 show the results of applying parallel imaging (rate 4) to the phantom experiment. Two different sampling patterns were used to illustrate the effects of the different resulting aliasing point spread functions. In both cases the ROI increased in size along the phase encoding direction and when the ROI reached a size, which is larger than FOV/4, the correlation in the noise cause by the aliasing point spread function takes effect. In both cases, the standard deviation of the ROI starts to deviate from what would be predicted by the g-factor alone but in one case (Fig. 7) the noise actually decreases because pixels with negatively correlated noise are included in the ROI and in the other case (Fig. 8) the standard deviation is elevated from what would be expected due to positively correlated noise in pixels in the ROI. In all cases, the standard deviations predicted by the proposed method and the actual measurements are in good agreement.

Figure 6.

Comparison of predicted and measured standard deviations of the sum (top row) and mean (bottom row) of an ROI as it grows along the phase encoding direction in an image with parallel imaging factor 4. The sampling pattern used here sampled lines 1,5,9,…, etc. The solid line is the predicted standard deviation from the proposed method, the dashed line is the calculated standard deviation from 100 repeated experiments, and the dotted line is the calculated standard deviation from 100 pseudo replica reconstructions. The gray dotted line on the magnitude plots indicated the predicted standard deviation when assuming that all pixels are independent, i.e. the standard deviation is calculated based on the g-factor taking parallel imaging associated noise enhancement into consideration.

Figure 7.

Comparison of predicted and measured standard deviations of the sum (top row) and mean (bottom row) of an ROI as it grows along the phase encoding direction in an image with parallel imaging factor 4. Plot is similar to Fig. 6, but the sampling pattern used here sampled lines 3, 7, 11, …, i.e. the sampling pattern was still undersampled by a factor of 4, but the sampled lines were shifted by 2 lines in k-space.

Figure 8.

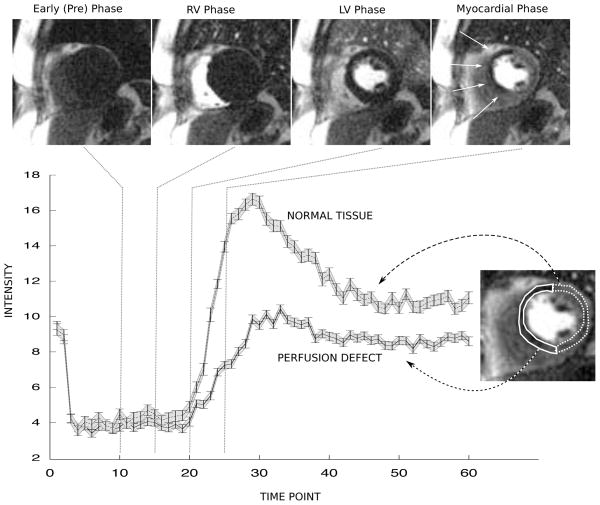
Example of standard deviation analysis on a stress perfusion MRI examination. The top row shows example real-time frames acquired during injection of a bolus of Gd contrast agent. The last frame shows a hypo-intense region in the septal wall marked by arrow. The plot on the bottom row shows time-intensity curves of the average signal in the ROIs drawn on the frame to the right of the curves. The solid line ROI contained the tissue with the perfusion defect and the dotted line ROI contained the healthy tissue. The 95% limits of agreement (±1.96 * σ) predicted by the proposed method are shown as the shaded grey area around the curve and the 95% limits of agreement measured from 100 pseudo replicas are shown as the error bars on the curves.

The results of from the in vivo perfusion example are shown in Fig. 8. The top row shows example frames from the series of real-time images acquired during infusion of a bolus of Gd contrast agent. A clear perfusion defect is present in the septal wall. The plot shows the individual time intensity curves of the hypoperfused and the healthy myocardium. The gray shaded areas indicate the 95% limits of agreement (±1.96*σ) predicted by the proposed method and the actual error bars represent the 95% limits of agreement calculated from 100 pseudo replica experiments. There is no practical way of measuring the 95% limits of agreement from repeated measurements in the in vivo case, but the limits predicted by the proposed method and the ones obtained from the pseudo replica reconstructions are in good agreement. Fluctuations in the time intensity curves due to uncorrected respiratory motion are apparent; they are not caused by thermal noise.

Discussion

Region of interest analysis is an important part of many MRI exams. Often signal intensities of healthy and diseased tissues are compared. In such analysis it is advantageous to have an estimate of the standard deviation of the sum or the mean of a given ROI caused by thermal noise propagation. In cases where the pixels in the reconstructed image are independent, it is trivial to obtain such an estimate. Even in cases where there is some easily predicted correlation between the pixels it is fairly straightforward to predict the actual standard deviation of ROI measurements as illustrated in the experiment with reduced phase encoding direction resolution (Figures 4 and 5), but some care must still be taken since the orientation of the ROI can affect the correlation between the pixels. In other cases, such as the parallel imaging example presented here (Fig. 6 and 7), the noise behavior is less intuitive and is influenced by things like the parallel imaging undersampling pattern, the actual phase of the signal in the images, and orientation of the ROI. This is especially true if the ROI covers a region of the field of view, which is larger than the FOV divided by the acceleration factor. Although it may be unusual to have ROIs that are large enough individually for these effects to become visible, it could have an effect on an ROI measurement where two more distant regions of the image are compared.

The method described here provides a general way of calculating the standard deviation of any linear combination of the pixels in an image. The method uses information about the reconstruction process to predict what the noise correlation of a linear transform of the k-space samples (where the noise is uncorrelated) would be. The method is intuitive in the sense that eqs. [3], [9], and [10] can be though of as assuming the pixels are uncorrelated in the image and convolving them with the point spread function caused by the sampling and reconstruction. We have demonstrated that the method can be used to predict the standard deviation in ROI measurements for both magnitude and phase measurements even in the fairly complicated case of noise correlation caused by parallel imaging. A number of experimental and reconstruction parameters such as sampling pattern, calibration scheme, and GRAPPA kernel configuration (size) have an effect on the ROI noise propagation. The proposed method can be used to investigate the optimal settings of such parameters although that was not explored here. The method is also able to predict standard deviation in ROI measurements of real and imaginary parts of the signal (using eq. [3]), but the plots were left out here due to their repetitive nature. The method uses some approximations for the non-linear steps of extracting the magnitude and the phase during image reconstruction. These approximations rely on estimates of the image signal and phase, which may not be reliable in the case of low SNR. In the phantom experiments conducted here, the base SNR was on the order of 15 for the fully sampled case and considerably lower in the parallel imaging case and the method was still able to predict the ROI noise behavior. In the case of lower SNR, it may be necessary to replace the approximation used for the estimation of phase standard deviation ( ${\mathrm{\sigma }}_{\mathit{phase}}~\frac{1}{\mathit{SNR}}$) with a lookup table that takes the non-linear increase in σ_phase at low SNR into account. In the studies conducted here, it was not found to be necessary, but the ultimate SNR limits of the proposed method were not explored in detail.

The method was compared here to both pseudo replica experiments and actual repeated measurements in the case of the phantom study. The repeated measurements are rarely practical to perform (even in the case of phantom experiments), but the pseudo replica method is often an available option. Compared to the pseudo replica method, the proposed method is orders of magnitude faster and has a much smaller memory footprint, but it is only really practical for Cartesian measurements. Furthermore, the method requires detailed knowledge of the reconstruction process, which is not needed by the pseudo replica method, where the reconstruction can be treated as a black box. For non-Cartesian methods and when the reconstruction details are unknown, the pseudo replica method may be the only available option. In principle, the formulas in Eqs. [3], [9], and [10] are valid for non-Cartesian methods, but since pixel-wise unmixing coefficients are not generally obtained with non-Cartesian parallel imaging reconstructions, they would be so computationally inefficient that the pseudo replica method would the method of choice. The alternative to the pseudo replica method proposed by Wiens et al. (4) offers computational efficiency and is related to the method proposed in this paper in that a region of the image is used to obtain a standard deviation estimate. That method could be modified to obtain an ROI standard deviation estimate if the image region used for smoothing was adapted to fit the ROI of interest, but the precision of the ROI standard deviation estimate would suffer since only two (or a few) pseudo replicas would form the basis of the estimate.

In practice, ROI measurements are often done using an image analysis workstation operating on reconstructed images (in DICOM format). The proposed method and the pseudo replica method require access to the acquisition raw data and the reconstruction process. Consequently, there are some hurdles to the integration of such an analyses in a clinical workflow. However, the proposed method can potentially be integrated into an image analysis workstation if infrastructure is available to store the image formation matrix (F in the equations above), the sampling pattern, and the complex images. The image formation matrix need not be stored in matrix form; it can be stored as a compiled function or script. If that information is available, the technique is fast enough that it can be applied on the fly during image analysis and it does not require storage of multiple pseudo replica images.

Conclusions

This article proposes a method for calculation of the standard deviation of any linear combination the image pixels of a Cartesian MRI acquisition. The method accurately predicts standard deviations of region of interest measurements of complex, magnitude, and phase images.