On-the-fly machine-learning for high-throughput experiments: search for rare-earth-free permanent magnets

Abstract

Advanced materials characterization techniques with ever-growing data acquisition speed and storage capabilities represent a challenge in modern materials science, and new procedures to quickly assess and analyze the data are needed. Machine learning approaches are effective in reducing the complexity of data and rapidly homing in on the underlying trend in multi-dimensional data. Here, we show that by employing an algorithm called the mean shift theory to a large amount of diffraction data in high-throughput experimentation, one can streamline the process of delineating the structural evolution across compositional variations mapped on combinatorial libraries with minimal computational cost. Data collected at a synchrotron beamline are analyzed on the fly, and by integrating experimental data with the inorganic crystal structure database (ICSD), we can substantially enhance the accuracy in classifying the structural phases across ternary phase spaces. We have used this approach to identify a novel magnetic phase with enhanced magnetic anisotropy which is a candidate for rare-earth free permanent magnet.

Recent explosion of activities in computational materials design is rapidly changing the landscape of materials science, and massive databases of predicted materials properties are now generated out of high-throughput thermodynamic and electronic-structure calculations¹,²,³,⁴,⁵. To truly harness the benefits of potential gold mines contained in the large number of such materials “blue prints”, however, it is still necessary to complete the materials exploration cycle by experimentally verifying the computed results. To establish such a cycle with steady feedback to predictions, it is often desirable to also carry out experiments in a high-throughput manner.

High-throughput and combinatorial experimental methods have indeed become mainstream techniques in many arenas of materials science in recent years owing in part to development of sophisticated materials synthesis and rapid characterization techniques. Depending on the physical property, measurement and data acquisition speed are now matching or in some instances outpacing the library synthesis speed. In many cases, one can now collect the data faster than they can be analyzed. This disparity in data collection and analysis time is fueling interest in expanding the high-throughput materials science to include accelerated data analysis through the use of new machine learning algorithms.

In the past, machine learning techniques have been implemented to computed materials properties such as electronic structures⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷. Recent applications in materials science include texture analysis in micrographs¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴. However, compared to the widespread use in other domains such as medical diagnostics²⁵,²⁶, computational finances²⁷,²⁸, and natural language processing²⁹, by and large, applications of machine learning in materials science are in their infancy. This is particularly true for exploratory learning from experimental data, which has been mostly limited to simple latent variable analysis techniques such as principle component analysis. More effective data mining techniques are especially in dire need when a large amount of data are being generated in a turn-key manner and individual data sometimes takes on non-trivial, high-dimensional forms such as spectra or images, and thus data from combinatorial experimentation represents an ideal platform to carry out machine learning based analysis.

One demonstrated application of machine learning in data from combinatorial libraries is to employ algorithms to quickly separate different parts of libraries into groups. When this is performed on a large number of x-ray diffraction patterns taken across a composition spread, the algorithms can be used to guide and delineate structural phase boundaries leading to rapid construction of a composition-structure relationship, often an end goal of many materials science experiments³⁰,³¹,³². The learned composition-structure relationship from diffraction data can also be extrapolated to relationships between structure and functional properties such as magnetostriction or piezoelectricity³³,³⁴, with structural phase boundaries indicating potential regions of significant change in functional properties. Here, we have devised an efficient and computationally-inexpensive new algorithm based on mean shift theory (MST) which overcomes shortcomings of previous methods we had used (hierarchical clustering and non-negative matrix factorization), including the inability to handle diffraction peak shifting.

Equipping the data analysis platform with a means of accessing and utilizing data entries from existing archival databases can provide significant benefits: analyzing experimental data in rapid cross-referencing mode with verified/archived data entries can substantially increase reliability and one's confidence in analysis performance. To this end, for studying a large number of x-ray diffraction data, we have developed a technique to mix and guide clustering of experimental diffraction patterns with simulated diffraction patterns using entries from the Inorganic Crystal Structure Database (ICSD), containing over 166,000 known compounds.

Further integrating the analysis platform with direct access to data as it is being collected by the characterization systems can provide the added benefits of live data analysis. For example, when instrument time or financial constraints limit the number of measurements to be performed, live data analysis can provide a means for guiding one to the optimal (number of) samples to characterize, maximizing knowledge of the overall set of samples with a minimum number of measurements. This is of great utility to experiments being carried out, for instance, at synchrotron beamlines.

We have developed a comprehensive algorithm which allows on-the-fly analysis of diffraction data from combinatorial libraries as they are collected and rapidly cross-referenced with pre-selected entries from the ICSD. Below, we describe how this strategy was used to study a series of Fe-Co-X ternary thin film composition spreads (where X is a transition metal element such as Mo, W, Ta, Zr, Hf, and V)³⁵,³⁶ to explore novel magnetic phases with enhanced magnetic anisotropy. Through the use of mean shift theory³⁷ as the machine-learning technique of choice on-the-fly separation and grouping of hundreds of diffraction patterns taken at a synchrotron beamline have led to the identification of a Mo substituted Fe-Co, whose tetragonally distorted structure is the origin of enhanced magnetic anisotropy.

Unsupervised learning as applied to data from combinatorial materials libraries

Previously, hierarchical cluster analysis (HCA) has been used to sort samples within combinatorial libraries into groups with similar characteristics using x-ray diffraction patterns, Raman spectra, and ferroelectric hysteresis loops³⁰,³⁴. In addition to separating the composition regions into groups with similar structural properties, comparison of clustering results from different measurement techniques has been effective in revealing hidden correlations between physical properties. It is important to recognize that however robust and automated such a procedure might become, the clustering results always require human inspection for consistency and agreement with physical rules, e.g. Gibb's phase rule. The high speed technique of principal component analysis and other multidimensional scaling methods have been used to take the high dimensional powder patterns, typically hundreds to thousands of dimensions long, and visualize them in a 2D or 3D space, allowing experts to quickly determine structural trends. The latent variable analysis tool of non-negative matrix factorization (NMF) has also been found to be useful for swiftly identifying different phase mixture regions through a rapid basis pattern deconvolution process³¹.

However, one problem these techniques have in common is that they do not perform as well in the presence of peak shifting (the movement of diffraction peaks as a function of continuously changing composition due to lattice constant change), and often cluster adjacent region with shifted lattice constants as different phases. Because shifting of peaks as a function of composition is also common in many other spectral data such as Raman and X-ray photoelectron spectroscopy, a robust algorithm which can keep track of moving peaks is needed for analysis of a variety of characterization techniques.

One solution to the peak shifting issue had been proposed in the method of dynamic time warping (DTW). This method provides a measure for identifying similarities between diffraction patterns despite the presence of peak shifts³⁸. LeBras, et al. incorporated the DTW measure into their clustering algorithm³⁹. The algorithm breaks down each diffraction pattern into a list of peaks and uses constraint programming to discover the constituent phases through hard constraints on the form of the constituent phases. This algorithm is resilient to peak shifting and enforces both phase region connectivity and the Gibbs' phase rule. However, it currently comes at a high computational cost. Evaluation time can run in the tens of hours, without additional data processing performed by the user – currently too slow for a turn-key operation of continuous measurement/analysis cycles.

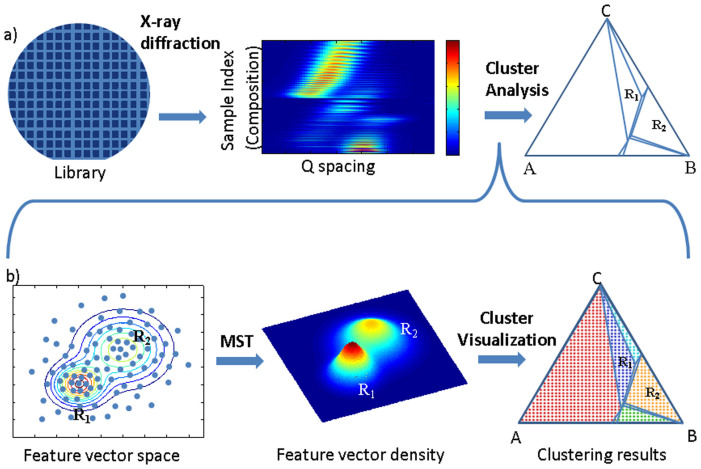
Out of a number of relatively new machine learning techniques we have looked at⁴⁰, we have elected to implement MST for the current work. We have found that MST is resilient to the presence of background noise in diffraction patterns and peak shifting and provides good cluster connectivity. MST is also fast and computationally inexpensive, taking less than ten seconds to analyze the material systems discussed here, and, as such, can be used for high-throughput analysis⁴⁰. MST is a non-parameteric density estimation based clustering method. While not a Bayesian method, MST's statistical framework provides a probabilistic perspective on cluster membership in a high speed algorithm. The density of samples in the sample feature space are assumed to be dictated by probability density functions (PDF) associated with underlying (and unknown) sample classifications. For the case of mapping a composition spread, the classifications are assumed to be phase mixture regions in the composition space. MST identifies the PDF modes and sorts samples into clusters associated with each mode. This method is robust and applicable to different phase distribution scenarios, i.e. the phase regions to be distinguished can be either phase pure or phase mixed regions. (Figure 1) The implementation of MST follows the work found in Ref 41.

Figure 1. Mean shift theory (MST) as applied to diffraction patterns taken from a composition spread wafer for rapid phase distribution analysis.

(a) X-ray diffraction data are taken from a thin-film composition spread wafer mapping a ternary (A-B-C) compositional phase diagram. The data are then analyzed using cluster analysis to produce a potential structural phase distribution diagram, identifying separated phase regions. (b) The MST process: 1) Feature vectors are produced for each sample on a combinatorial library. Each sample is projected into the feature vector space - shown here as 2 dimensional and unitless for ease of visualization, and the feature vector density is correlated to an underlying probability density function (PDF) for each ‘hidden' classification, which in this case are assumed to be two separated different phase regions R1 and R2. 2) PDF analysis is performed using MST-based mode detection, and all samples from the same PDF are clustered together.

The feature vectors used for this work are a concatenation of the relative ternary composition with x-ray diffraction pattern intensity in order of corresponding Q values. While only the two feature types of composition and x-ray diffraction patterns have been used for this analysis, the MST method in general is capable of clustering based on a larger set of features including scalar features such as coercive field and high dimensional features such as Raman spectra. We combine experimental sample vectors with simulated sample vectors derived from the ICSD to provide improved clustering results.

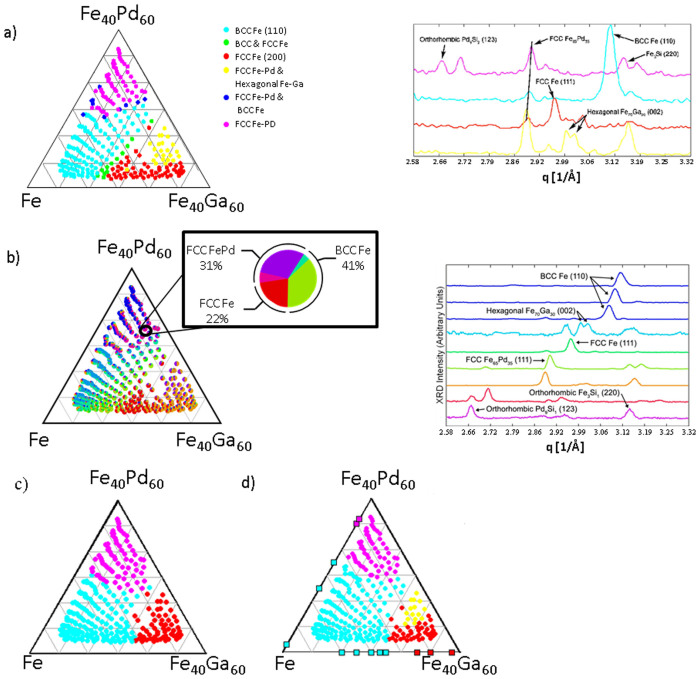
To validate the overall approach developed here, MST was applied to a set of diffraction data from a Fe-Ga-Pd composition spread³⁰, which were previously also analyzed with other clustering techniques in separating composition regions into groups with similar crystal structures (Figure 2).

Figure 2. Comparison of clustering results using different machine learning techniques applied to diffraction data taken from a Fe-Ga-Pd composition spread in the Fe-rich region.

(a) Hierarchical cluster analysis clustering of diffraction pattern data (left); representative diffraction patterns from major cluster groups are plotted on the right; Reproduced from Ref. [30]. (b) Non-negative matrix factorization (NMF) analysis provides the positive principle components of the diffraction patterns. NMF gives deconvolution of patterns into components corresponding to peaks from pure phases, and accordingly, pie-charts are obtained at each average composition spot (left); peaks from basis patterns are then identified (right); Reproduced from Ref [31]. (c) High-speed mean shift theory based structural phase distribution analysis of experimental data using a suboptimal choice of bandwidth parameters. (d) High-speed MST results for experimental diffraction pattern data (ternary data points) and simulated data based on ICSD entries (square points along the binary lines) using the same suboptimal choice of bandwidths as in (c). ICSD based simulated data provides improved cluster stability despite suboptimal bandwidth choice.

Compared to hierarchical clustering (Fig. 2a) and non-negative matrix factorization (Fig. 2b), MST (Fig. 2d) provides similar clustering results separating composition regions into different structural phases previously identified.

Inclusion of ICSD indeed leads to improved clustering results when using a suboptimal choice of bandwidths (Fig. 2c and 2d). We therefore incorporate ICSD data in analysis of all systems whenever data are available. Because most ICSD entries are for binary compounds, as is the case with most ternary composition phase diagram studies, this works in such a way so that the mapping of ternary composition spreads is guided by known binary phases.

High-throughput search of Fe-Co-X with enhanced magnetic anisotropy

The utility of the above mentioned method was demonstrated in the high-throughput experimental search of novel rare-earth-free permanent magnets. We are systematically exploring Fe-Co-X composition spreads, where X is one of the 3d, 4d or 5d transition-metal elements. The outstanding challenge in the permanent magnet materials community is to design a magnetic crystal with sufficient magnetization and a large magnetic anisotropy without the use of inherently large spin-orbit coupling present in rare-earth elements⁴². One avenue to pursue such compounds is to insert elements such as W, Mo, or V in small atomic percentage to Fe-Co, so that hybridization of electronic states due to the finite spin-orbit coupling of 4d or 5d electrons with those of Fe and Co would lead to magnetic anisotropy. Another possibility is that small atomic percentage of inserted X element in the unit cell of cubic Fe-Co leads to tetragonal distortion resulting in magnetocrystalline anisotropy⁴³,⁴⁴,⁴⁵.

Fe-Co-X thin film composition spreads encompassing large ternary composition variation were made by co-sputtering and annealed in vacuum at 700°C for X = Mo, W, Ta, Zr, Hf, and V³⁵. Their magnetic properties were initially screened by a scanning MOKE (magneto-optical Kerr effect) set up, followed by more detailed hysteresis measurements using vibrating sample magnetometry (VSM) once composition regions which display indication of enhanced out-of-plane anisotropy were identified. Based on the shapes of the hysteresis loops, we can separate the composition regions into different groups as shown in Fig. 3(a), where hysteresis loops are overlaid on their approximate positions on the composition spread wafer. Such a quick visualization scheme is effective in rapidly assessing the landscape of how magnetism evolves as a continuous function of composition³⁴.

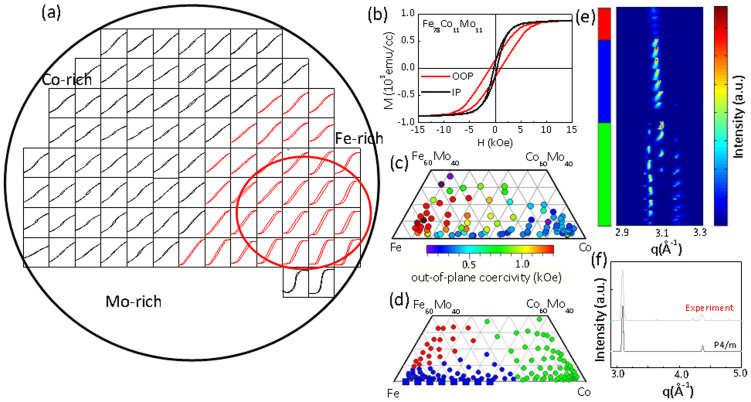
Figure 3.

Magnetic and structural property maps of Fe-Co-Mo composition spread: (a) out-of-plane hysteresis loops of Fe-Co-Mo samples for different compositions superimposed on the spread wafer positions; (b) typical out-of-plane (OOP, red) and in-plane (IP, black) hysteresis loops of Fe_78.4Co_10.8Mo_10.8 sample with perpendicular anisotropy (1 emu/cc = 10³ A/m, 1 Oe = 10³/(4π) A/m); (c) Out-of-plane coercive field map of Fe-Co-Mo ternary alloys. (d) Clustering results of diffraction data using MST of Fe-Co-Mo ternary; (e) Intensity plot of x-ray diffraction patterns grouped by the clustering result (same color clusters as Fig. 3(d)); (f) Synchrotron X-ray diffraction spectrum (red) of Fe₇₈Co₁₁Mo₁₁ and calculated X-ray diffraction spectrum (black) with P4/m tetragonal structure.

A composition region which consistently displays increased coercive field (which we take as the sign of anisotropy enhancement) in a single-phase-like out-of-plane hysteresis loop was observed in Fe-Co-Mo composition spreads (hysteresis loops plotted in red in Fig. 3(a)). This group of compositions was found to be centered around Fe₇₈Co₁₁Mo₁₁. Fig. 3(b) shows the typical out-of-plane and in-plane hysteresis loops of a Fe₇₈Co₁₁Mo₁₁ film. Other major characteristics seen in this visualization include 1) a broad composition region where two-phase-like out-of-plane hysteresis curves are observed indicating the presence of two co-existing magnetic phases (within each sample) with different coercive fields, and 2) a region with atom % concentration of Mo larger than 40%, where the films largely display paramagnetic behavior due to nanocrystalline and amorphous films.

The out-of-plane coercive field can also be mapped on the Fe-Co-Mo ternary spread as shown in Fig. 3(c). We see a clear transition of magnetization easy axis from out-of-plane to in-plane, and it is reflected in the out-of-plane coercive field map as a function of composition: the films of high Fe and low Mo concentration areas show higher perpendicular coercive field indicated by the red spots (corresponding to highest values in the coercive field measured here), and the films of high Co or high Mo concentration areas show minimal to no perpendicular coercive field from the blue spots where the magnetizations predominantly are lying in the film plane.

In order to streamline the process of determining the phase distribution and structural evolution across composition spreads, we carried out synchrotron x-ray diffraction at beam line 7-2 at Stanford Synchrotron Radiation Laboratory. An automated scanning stage is used to quickly step from spot to spot on the composition spread wafer, so that each diffraction image is acquired in 30 seconds per spot, and it takes roughly two hours to obtain mapping of the entire spread with approximately 200 spots using a Pilatus detector. The data were analyzed on-the-fly using a combination of software, WxWindows Diffraction Integration Tool for integration of diffraction images into diffraction patterns, and CombiDM-Live for live clustering analysis. The fast and computationally-inexpensive MST implemented in this manner enabled the live analysis in such a way so that as the diffraction images are acquired for a spread wafer, updated clustering results are available for human inspection after measurement of each spot. Because of the robustness of the MST results, no noise smoothing was required for the analysis.

A quick inspection of the clustering behavior of the diffraction patterns using MST (Fig. 3 (d)) on a Fe-Co-Mo spread revealed that a group of compositions with enhanced single-phase-like coercive field (in Fig. 3(c)) coincides with a clustered region which displays a broad diffraction peak observed at q = 3.06 ~ 3.09 Å⁻¹ (red cluster in Fig. 3(d)). Fig. 3 (e) shows the intensity plot of all the X-ray diffraction patterns, grouped by MST in a selected q-region from 2.9 and 3.3 Å⁻¹. From the top, they are: the region of interest with the broadened diffraction peak which coincides with the perpendicularly magnetized samples (red); the α-bcc Fe phase region with the sharp (110) peak (blue); the fcc Co phase, cubic Co-Mo or Fe-Mo phases (green). Because of the limited Mo solubility (at the annealing temperature of 700°C) and the non-equilibrium sputtering process, the mapping of the observed phases is a non-equilibrium one. Some clustered regions (red and green) stretch into the high average Mo concentration region due partly to segregation of Mo (which we have confirmed with transmission electron microscopy (not shown)).

The films with the composition in the vicinity of Fe₇₈Co₁₁Mo₁₁ show perpendicular magnetic anisotropy with coercive field of 1.2 kOe (95.5 kA/m) and magnetization of 850 emu/cc (850 kA/m) (Fig. 3(b)). From these numbers, one can estimate the perpendicular anisotropy K_U using 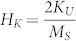assuming that the magnetization reversal is through coherent rotation. Here, M_S is the saturation magnetization, and H_K is the anisotropic field. The estimated perpendicular anisotropy K_U is typically around 3.6 × 10⁶ erg/cm³ (27.0 μeV/atom) for Fe_78.4Co_10.8Mo_10.8 which is of the same order as that of the Co-Pt alloy⁴⁶.

To understand the origin of the enhanced coercive field and the out-of-plane anisotropy of this compound, we have employed the genetic algorithm (GA) search approach⁴⁷,⁴⁸ using the composition Fe₈CoMo, and the Scherrer equation was used in simulating the XRD patterns to take into account the broadening of the peak with a typical grain size of 50 nm (observed with transmission electron microscopy, not shown). There is good agreement between the experimental XRD pattern and the simulated pattern for a relatively low energy tetragonal P4/m structure (Fig. S1) identified by the GA search (Fig. 3(f)).

The formation energy of the P4/m structure is positive (7.7 meV/atom), indicating that the structure may be a metastable one. However, the structure can be stabilized in non-equilibrium processes depending on synthesis conditions. We believe it is not unreasonable that our co-sputtered films have resulted in formation of this structure. The magnetic moment of 4j-site Fe, 4k-site Fe, Co and Mo atoms in the P4/m Fe₈CoMo structure are 2.11, 2.55, 1.67 and −0.61 μ_B, respectively, in our spin-polarized calculations. A non-collinear magnetic structure density function theory calculation including spin-orbit coupling interaction shows that P4/m Fe₈CoMo structure has a uniaxial easy axis along the (001) direction with magnetic anisotropy energy of 18.2 μeV/atom, which compares well with the experimental observed value of 27.0 μeV/atom.

Alternatively, the observed broadened bcc (110) peak can be taken as merging of two tetragonal peaks with a corresponding c/a ratio of approximately 1.04. We have also calculated the magnetocrystalline anisotropy energy (MAE) of Fe₈CoMo with a layered structure using this c/a ratio value using the full potential LMTO (linear muffin tin orbital) method. The calculation details can be found elsewhere⁴⁹. The calculated MAE is 28.0 μeV/atom, which is very close to the experimentally extracted anisotropy value. Our calculations also indicate that a similar distortion may be brought about by substitution of other elements such as W and V.

We have thus experimentally realized a sought-after tetragonally distorted Fe-Co⁴³,⁴⁴ by introducing a third element and identified its composition. While the increase in anisotropy is modest, the fact that such a structure can be realized in a thin film form indicates that this is potentially a viable path toward manufacturing rare-earth free permanent magnets.

We have shown the use of the MST machine learning algorithm for on-the-fly analysis of x-ray diffraction and composition data toward the discovery of a novel rare-earth-free permanent magnet. While the MST method was found to be resilient to noise in the data, specifically diffraction pattern noise, further algorithm developments should focus on Bayesian techniques that utilize data noise to quantify the uncertainty of cluster membership. Furthermore, an area of machine learning that may prove fruitful for high speed diffraction pattern analysis, including pure phase identification, is that of blind source separation: this is a research direction made popular by the famous cocktail party problem, where the goal is to identify individual speakers in a crowded room through the use of multiple simultaneous audio recordings, each recording containing a different mixture of the party goers' voices. For the case of the combinatorial library, the analogous goal is to identify pure phases from samples containing different phase mixtures. The diffraction patterns from the different phase mixture samples provide the multiple ‘recordings' of the mixed pure phases to be analyzed with blind source separation. A collection of simple clustering methods such as MST and hierarchical cluster analysis can also be used in combination with a collection of blind source separation methods through the use of an ensemble algorithm that capitalizes on each method's benefits to provide an optimized analysis result. For example, the ensemble method could select the clustering result with the greatest cluster stability and then utilize the cluster boundaries to inform the blind source separation method on potential phase boundaries.

Naturally, the methods presented here can be extended to a variety of other spectral and image data. As previously demonstrated³⁴, such clustering algorithms (as well as visualization) can be applied simultaneously to data from a number of different physical properties measured on the same composition spread in order to rapidly delineate correlations between them. An important next step in developing the rapid materials exploration cycle is to directly integrate computational results and experimental results, as some computational databases provide extensive information on predicted stable crystal structures with lattice constants⁵⁰. Carrying out various machine learning algorithms on merged diffraction data from high-throughput experiments together with simulated diffraction patterns from predicted structures would provide instant feedback on a number of computational results simultaneously. Such an integrated platform could thus truly speed up the process of materials discovery in the future.

Methods

For mean shift theory clustering, the concatenated sample vectors are first normalized by subtracting the vector mean. No noise smoothing is performed. The feature vectors in the composition space are assumed to be relatively uniformly distributed and the local density in both feature spaces is approximated using the normal kernel density estimator 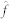given by:

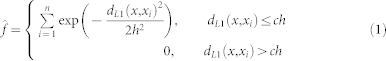where d_L1 is the L1 metric⁵¹, h is the bandwidth, and a symmetric kernel support of ch is used with c = 1. Two bandwidths are selected by the user, one for the diffraction data and one for the relative composition data, and these bandwidths determine the mode detection resolution. Choice of bandwidths impacts the number of clusters in the final clustering results, with suboptimal bandwidth choices resulting in either too many or too few clusters. The bandwidth selection heuristic used here and alternative methods for setting the bandwidths are discussed in the Supplementary Information.

The experimental sample vectors and the ICSD derived sample vectors are combined in the same feature space during clustering. The experimental samples are given a mass of 1 during MST mode detection, and all ICSD vectors are given the same user determined mass. Increasing the mass of the ICSD vectors increases local density in the feature space. In this way, the critically evaluated data from the ICSD can be given greater influence in guiding the clustering results than the experimentally obtained data. Cluster assignment is performed by associating each converged sample vector to the nearest original diffraction pattern, and all sample vectors that share the same associated diffraction pattern are assigned to the same cluster. Again, validation of clustering results against physical rules (e.g. Gibbs' phase rule for equilibrium systems) by a human expert is critical.

In incorporating data from the ICSD, the material structure data was exported in CIF format and then transformed into simulated diffraction patterns using Bruker's Topas software. Typical parameters were used and are listed in Table S1 in Supplementary Information. The simulated patterns from ICSD were then combined with their compositions to create simulated sample vectors. Most of the metallic film phases we are looking at deposited on Si/SiO₂ wafers predominantly grow with (110)/(101) texture (for α-Fe and related structures studied here), and therefore in generating the simulated patterns, (110) (and its family of) peaks were used as the main peaks.

The ternary composition spread films were deposited using magnetron co-sputtering on 3-inch diameter Si wafers (with 200 nm thick thermally oxidized SiO₂ layer) at room temperature. The details of the composition spread deposition technique are described elsewhere⁵². A physical shadow mask is used to separate the composition spread film into a grid of 4.5 mm × 4.5 mm regions in order to characterize the structural and magnetic properties. The room-temperature deposited samples were then post-annealed in vacuum at 700°C for 45 min. The average composition for both spreads of each thin film region is determined by wavelength dispersive spectroscopy (WDS). The synchrotron X-ray diffraction was performed with 16.5 keV energy at Beam line 7-2 at Stanford Synchrotron Radiation Laboratory (SSRL). Some of the Fe-Co-Mo wafers were cut into small pieces to characterize the magnetic and microstructural properties by vibrating sample magnetometry (VSM) and transmission electron microscopy (TEM).

The genetic algorithm (GA) searches were “from scratch” with only chemical compositions given. Structural optimizations during the GA searches were carried out by LAMMPS code⁵³ with Embedded Atom Method potential developed by Zhou et. al.⁵⁴. The low energy structures obtained from GA searches were then fully relaxed again by first-principles calculations for the final structures. The first-principle spin-polarized density functional theory calculations⁵⁵ were performed by Vienna Ab initio Simulation Package⁵⁶ with PAW pseudopotential method⁵⁷,⁵⁸ within generalized-gradient approximation⁵⁹. The energy cutoff was 370 eV and the Monkhorst-Pack's scheme⁶⁰ was used for Brillouin zone sampling. A high-quality k-point grid, which is corresponding to 14 × 14 × 14 for body-centered cubic (bcc) Fe, was used in all calculations. The references for formation energy calculations were bcc Fe, hexagonal closed-pack (hcp) Co and bcc Mo. The X-ray diffraction patterns were simulated with X-ray wavelength λ = 0.7517 Å and the Scherrer equation was used for the peak broadening with sample size of 50 nm.

The magnetocrystalline anisotropy of layered Fe₈CoMo was calculated by using the full potential (FP) LMTO method with smoothed generalizations of Hankel functions for the envelope functions. Spin-orbit coupling has been added into the Hamiltonian and self-consistent calculations have been performed with spin quantization direction along different directions. The integration over the Brillouin zone was performed using the tetrahedron method with the Blöch's correction. A dense k-mesh was used for integration to ensure a good accuracy of calculated MAE. Certain commercial equipment, instruments, or materials are identified in this publication for informational purposes only. Such identification is not intended to imply recommendation or endorsement by NIST, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.

Author Contributions

The on-the-fly machine learning procedure was conceived and developed by A.G.K. and I.T. T.G. made the combinatorial libraries and did the magnetic characterization. T.G., A.M., M.J.K. and I.T. carried out the synchrotron diffraction experiment. L.K. and V.A. performed the density functional theory calculations. The genetic algorithm calculations were carried out by M.C.N., C.Z.W. and K.M.H. C.L. performed the non-negative matrix factorization on the Fe-Ga-Pd data. A.G.K., T.G. and I.T. wrote the manuscript. All authors discussed and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information: On-the-fly machine-learning for high-throughput experiments: search for rare-earth-free permanent magnets