Functional Linear Models for Association Analysis of Quantitative Traits

Abstract

Functional linear models are developed in this paper for testing associations between quantitative traits and genetic variants, which can be rare variants or common variants or the combination of the two. By treating multiple genetic variants of an individual in a human population as a realization of a stochastic process, the genome of an individual in a chromosome region is a continuum of sequence data rather than discrete observations. The genome of an individual is viewed as a stochastic function that contains both linkage and linkage disequilibrium (LD) information of the genetic markers. By using techniques of functional data analysis, both fixed and mixed effect functional linear models are built to test the association between quantitative traits and genetic variants adjusting for covariates. After extensive simulation analysis, it is shown that the F-distributed tests of the proposed fixed effect functional linear models have higher power than that of sequence kernel association test (SKAT) and its optimal unified test (SKAT-O) for three scenarios in most cases: (1) the causal variants are all rare, (2) the causal variants are both rare and common, and (3) the causal variants are common. The superior performance of the fixed effect functional linear models is most likely due to its optimal utilization of both genetic linkage and LD information of multiple genetic variants in a genome and similarity among different individuals, while SKAT and SKAT-O only model the similarities and pairwise LD but do not model linkage and higher order LD information sufficiently. In addition, the proposed fixed effect models generate accurate type I error rates in simulation studies. We also show that the functional kernel score tests of the proposed mixed effect functional linear models are preferable in candidate gene analysis and small sample problems. The methods are applied to analyze three biochemical traits in data from the Trinity Students Study.

Introduction

In the last decades, the widespread availability of high-throughput genotyping technology has made large scale genome-wide association studies (GWAS) possible. Initially, the research focused on using common genetic variants to detect the association. In recent years, however, there has been increasing interest in using rare variants in the analysis [Gorlov et al., 2008; Lin and Tang, 2011; Schork et al., 2009]. The rare variants’ minor allele frequencies (MAFs) are less than 0.01 ~ 0.05. Much progress has been made in developing novel statistical methods for rare variant association analysis. According to the literature, the statistical methods for rare variant association studies are broadly classified as burden tests and kernel-based approaches [Bansal et al., 2010b; Lee et al., 2012a, b; Wu et al., 2011]. Burden tests are based on collapsing rare variants in a genetic region to be a single variable that is then used to test for the association with the phenotypes [Han and Pan, 2010; Li and Leal, 2008; Madsen and Browning, 2009; Morgenthaler and Thilly, 2007; Morris and Zeggini, 2010; Price et al., 2010; Zawistowski et al., 2010]. The kernel-based tests aggregate the association between variants and phenotypes via a kernel matrix, which measures the similarity between individuals [Kwee et al., 2008; Lee et al., 2012a, b; Lin and Schaid, 2009; Liu et al., 2008; Mukhopadhyay et al., 2010; Neale et al., 2011; Wessel and Schork, 2006; Wu et al., 2010, 2011]. In Wu et al. [2011] and Lee et al. [2012a], it was found that the sequence kernel association test (SKAT) and its optimal unified test (SKAT-O) have higher power than quite a few burden tests, such as the cohort allelic sums test [Morgenthaler and Thilly, 2007], the combined collapsing and multivariate method [Li and Leal, 2008], and the nonparametric weighted sum test [Madsen and Browning, 2009].

A limitation of the existing burden tests and kernel-based approaches is that they do not utilize the information of linkage and linkage disequilibrium (LD) or correlation of genetic variants sufficiently. SKAT and SKAT-O do model the similarity between individuals well and they also take pair-wise LD into account through their kernel matrix, but they do not model higher order LD among genetic markers. In burden tests, the LD pattern and information among the genetic variants may be missed/reduced after collapsing rare variants into a single variable and this can be another reason that the power of burden tests is lower than that of SKAT or SKAT-O in addition to the reasons reviewed by Wu et al. [2011] and Lee et al. [2012a].

Next-generation sequencing technologies will detect millions of novel rare variants [Bansal et al., 2010a; Clarke et al., 2009; Mardis, 2008; Metzker, 2010; Rusk and Kiermer, 2008; Shendure and Ji, 2008]. In the presence of very high density of genetic variants by high resolution genotyping and next-generation sequencing technologies, large numbers of genetic variants are expected to locate in very narrow regions and the LD levels among those variants can be very high. The next-generation sequencing data provide a unique opportunity for statisticians to develop novel models and tests to answer these new challenges. It is important to develop statistical models to use both GWAS and next-generation sequencing data in a unified analysis. It is a particularly high priority to develop novel statistical methods to simultaneously take into account the similarity between individuals, linkage, and LD or correlation information of genetic variants in order to build novel new-generation analytical tools [Kiezun et al., 2012; Mechanic et al., 2012].

In this article, we propose to use a functional data analysis (fda) approach to perform association tests between genetic variants and quantitative traits. The basic idea of the functional data analysis approach is different from those of either burden tests or kernel-based approaches [Luo et al., 2011, 2012a, b]. Instead of collapsing genetic variants as burden tests or building a kernel matrix as SKAT, multiple genetic variants of an individual in a human population are treated in our approach as a realization of a stochastic process in the functional data analysis [de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay and Silverman, 1996; Ramsay et al., 2009]. The genetic data of an individual in a region is a continuum of sequence data rather than discrete observations. The genome of an individual is viewed as a stochastic function that contains both linkage and LD or correlation information of the genetic markers.

The framework of considering genetic variant data as a stochastic process is not a strange idea. To understand this, let us look at one genetic variant case. Everyone agrees that the data of one genetic marker can be described by a single random variable, and one individual’s genotype of one genetic marker is one value of the random variable. Now look at multiple genetic variant data, it is basically a collection of random variables that is exactly a stochastic process from the textbook or literature, and one individual’s SNP data is a realization of the stochastic process [Ross, 1996, p41].

By using techniques of functional data analysis, both fixed and mixed effect functional linear models are built to test the association between quantitative traits and multiple genetic variants such as single nucleotide polymorphism (SNP) markers adjusting for covariates. Since we treat the genetic data as stochastic functions, the genetic effect of the genetic variants is modeled as a function. Hence, testing the association between genetic variants and quantitative traits is equivalent to test if the genetic effect function is 0. This forms the basis of building valid test statistics.

One important feature of the proposed approaches is that the models and tests can analyze rare variants or common variants or the combinations of the two. Interestingly, the kernel machine regression was first proposed to analyze common variants, which forms the basis of SKAT and SKAT-O to analyze only rare variants while it should be possible to use SKAT and SKAT-O to analyze the combinations of both rare and common variants [Kwee et al., 2008; Lee et al., 2012a; Liu et al., 2008; Wu et al., 2010, 2011]. Extensive simulation analysis was performed to evaluate the robustness and power performance of the proposed models and tests. The robustness was evaluated by empirical type I error calculation. The power performance is primarily based on the comparison with the performance of SKAT and SKAT-O, simply because SKAT and SKAT-O tend to outperform the burden tests [Lee et al., 2012a; Wu et al., 2011]. In our simulations, the same sequence data and strategy of Wu et al. [2011] and Lee et al. [2012a] were used to make the comparison valid. The methods were applied to analyze three biochemical traits using data from the Trinity Students Study.

Methods

Functional Linear Model

Consider n individuals who are sequenced in a genomic region that has m variants. We assume that the m variants are located in a region with ordered physical locations 0 ≤ t₁ <· · · < t_m = T. Here, we assume that each variant’s physical location t_j is known, e.g., in terms of the number of base pairs. To make the notation simpler, we normalized the region [t₁, T] to be [0, 1]. For the i-th individual, let y_i denote a quantitative trait, G_i = (g_i(t₁), …, g_i(t_m))′ denote the genotype of the m variants, and Z_i = (z_i1, …, z_ic)′ denote the covariates. Hereafter in this article, denotes the transpose of a vector or matrix. For the genotypes, we assume that g_i(t_j) (= 0, 1, 2) is the number of minor alleles of the individual at j-th variant located at the location t_j.

In addition to the quantitative traits and covariates, we denote the i-individual’s genetic variant function (GVF) as X_i (t), t ∈ [0, 1]. Notice that the sample includes n discrete realizations or observations G_i of the human genome. By using the genetic variant information G_i, we may estimate the related genetic variant function X_i(t), which will be discussed below. To relate the genetic variant function to the phenotype adjusting for covariates, we consider the following functional linear model

$$y_i={\alpha }_0+Z_i^{\prime }\alpha +{\int }_0^1{X}_i(t)\beta (t)dt+{\epsilon }_i,$$ (1)

where α₀ is the overall mean, α is a c × 1 vector of regression coefficients of covariates, β(t) is the genetic effect of genetic variant function X_i (t) at the location t, and ε_i is an error term that is normally distributed with a mean of zero and a variance of ${\sigma }_e^2$. Note that the genetic effect function β(t) is a function of the physical location t.

Estimation of Genetic Variant Function

To estimate the genetic variant functions X_i(t), t ∈ [0, 1], we consider the following three discrete realizations: (1) to model the additive effect of the minor alleles, define X_i(t_j) = g_i(t_j), (2) to model the dominant effect of the minor alleles, define X_i(t_j) = 1 when g_i(t_j) = 1, 2, and X_i(t_j) = 0 when g_i(t_j) = 0, (3) to model the recessive effect of the minor alleles, define X_i(t_j) = 1 when g_i(t_j) = 2, and X_i(t_j) = 0 when g_i(t_j) = 0, 1. Using the discrete realizations (X_i(t₁, …, X_i(t_m))′, we may estimate the genetic variant function X_i(t), t ∈ [0, 1], by ordinary linear square smoother [Ramsay and Silverman, 1996, Chapter 4]. Specifically, let ϕ_k (t), k = 1, …, K, be a series of basis functions. Denote the m by K matrix Φ as containing the values ϕ_k(t_j). Then, X_i(t) is estimated by

$${\widehat{X}}_i(t)=(X_i(t_1),\dots ,X_i(t_m))\mathrm{\Phi }{[{\mathrm{\Phi }}^{\prime }\mathrm{\Phi }]}^{-1}\varphi (t),$$ (2)

where ϕ(t) = (ϕ₁(t), …, ϕ_K(t))′ is a column vector of basis functions. Corresponding to the above three discrete realizations, the genetic variant functions are called additive, dominant, and recessive, respectively. In this article, we consider two types of basis functions: (1) the B-spline basis: B_k(t), k = 1, …, K, and (2) the Fourier basis: ϕ₀(t) = 1, ϕ_2r−1(t) = sin(2πrt), and ϕ_2r(t) = cos(2πrt), r = 1, …, (K − 1)/2. Here for Fourier basis, K is taken as a positive odd integer [de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay and Silverman, 1996; Ramsay et al., 2009].

The second approach to estimate the genetic variant functions is to utilize functional principal component analysis (FPCA) techniques [Goldsmith et al., 2011; Horváth and Kokoszka, 2012; Ramsay and Silverman, 1996; Ramsay et al., 2009]. To briefly introduce the main idea of FPCA, let Σ_X (s, t) be the covariance function of the genetic variant function. One may want to notice that the covariance function Σ_X (s, t) can be estimated by the observed genotype data G_i = (g_i(t₁), …, g_i (t_m))′, i = 1, 2 …, n [Horváth and Kokoszka, 2012; Ramsay and Silverman, 1996]. Let ${\sum }_{k=1}^{\infty }{\lambda }_k{\varphi }_k(s){\varphi }_k(t)$ be the spectral decomposition of Σ_X(s, t), where λ₁ = λ₂ = · · · are the non-increasing eigenvalues and ϕ_k (t), k = 1, 2, …, are the corresponding orthonormal eigenfunctions. An approximation for X_i (t), based on a truncated Karhunen–Loève expansion, is ${\widehat{X}}_i(t)={\sum }_{k=1}^K{c}_{ik}{\varphi }_k(t)=(c_{i1},\dots ,c_{iK})\varphi (t)$, where K is the truncation lag, $c_{ik}={\int }_0^1{X}_i(t){\varphi }_k(t)dt$ that can be estimated by the observed genotype data, and ϕ(t) = (ϕ₁(t), …, ϕ_K(t))′.

The third approach to deal with the genetic variant functions is to use the genotype data G_i = (g_i(t₁), …, g_i(t_m))′ directly. Then, the focus is to estimate the genetic effect function β(t), and we call this approach as beta-smooth only approach. The related revised models are presented below.

Revised Functional Linear Model

First, let us talk about the case of expanding X_i (t) by B-spline basis or Fourier basis functions. In a similar way to estimate the genetic variant function X_i(t), t ∈ [0, 1], we may expand the genetic effect β(t) by a series of basis functions ψ_k(t), k = 1, …, K_β as β(t) = (ψ₁(t), …, ψ_Kβ(t))(β₁, …, β_Kβ)′, where β = (β₁, …, β_Kβ)′ is a vector of coefficients β_k. Note that the basis functions to expand β(t) can be different from those to expand the genetic variant functions. Thus, ϕ(t) and ψ(t) can be different. Let θ(t) = (ψ₁(t), …, ψ_Kβ(t)′. Replacing X_i(t) in (1) by X̂_i(t) in (2) and β(t) by the expansion, we have a revised function linear model

$$\begin{array}{l}{y}_i={\alpha }_0+Z_i^{\prime }\alpha +\left[(X_i(t_1),\dots ,X_i(t_m))\mathrm{\Phi }{[{\mathrm{\Phi }}^{\prime }\mathrm{\Phi }]}^{-1}{\int }_0^1\varphi (t){\theta }^{\prime }(t)dt\right]\beta +{\epsilon }_i\\ ={\alpha }_0+Z_i^{\prime }\alpha +W_i^{\prime }\beta +{\epsilon }_i,\end{array}$$ (3)

where $W_i^{\prime }=(X_i(t_1),\dots ,X_i(t_m))\mathrm{\Phi }{[{\mathrm{\Phi }}^{\prime }\mathrm{\Phi }]}^{-1}{\int }_0^1\varphi (t){\theta }^{\prime }(t)dt$. In the above revised regression model, one needs to calculate Φ[Φ′Φ]⁻¹ and ${\int }_0^1\varphi (t){\theta }^{\prime }(t)dt$ in order to get W_i. In the statistical packages R or Matlab, there are readily available codes to calculate them [Ramsay et al., 2009]. Thus, the revised regression model (3) transforms the initial model (1) to be useful for practical data analysis.

In the case of FPCA, we expand the genetic effect β(t) by linear spline basis as $\beta (t)={\beta }_1+{\beta }_{2}t+{\sum }_{k=3}^{K_{\beta }}{\beta }_k{(t-{\kappa }_k)}_{+}$, where κ_k are knots in the interval [0, 1]; and (t − κ_k)₊ indicates if t is larger than κ_k, i.e., (t − κ_k)₊ = 0 if t ≤ κ_k and 1 if t > κ_k. Thus, θ(t) = (1, t, (t − κ₃)₊, …, (t − κ_Kβ)₊)′ is a column vector of linear spline basis. In addition, we denote $W_i=(c_{i1},\dots ,c_{iK}){\int }_0^1\varphi (t){\theta }^{\prime }(t)dt$. Then, the revised model in the case of FPCA is

$$y_i={\alpha }_0+Z_i^{\prime }\alpha +W_i^{\prime }\beta +{\epsilon }_i.$$ (4)

When we use B-spline (or Fourier) basis functions to estimate the genetic variant function in the model (3), the genetic effect function β(t) is expanded by B-spline (or Fourier) basis functions. In the model (4), β(t) is expanded by the linear spline basis. This provides a wide range of choices to make comparison.

In the beta-smooth only case, the model (1) is revised as

$$y_i={\alpha }_0+Z_i^{\prime }\alpha +\sum _{j=1}^m{X}_i(t_j)\beta (t_j)+{\epsilon }_i.$$ (5)

In the above model, the integration term ${\int }_0^1{X}_i(t)\beta (t)dt$ in model (1) is replaced by a summation term ${\sum }_{j=1}^{K_{\beta }}{X}_i(t_j)\beta (t_j)$, and we make no assumption about smoothness of the genetic variant functions X_i(t). The genetic effect function β(t) is assumed to be smooth and one may estimate it by B-spline or Fourier or linear spline basis functions. Replacing β(t) by the expansion β(t) = (ψ₁(t), …, ψ_Kβ(t))(β₁, …, β_Kβ)′, the model (5) can be revised as

$$\begin{array}{l}{y}_i={\alpha }_0+Z_i^{\prime }\alpha +\left(\sum _{j=1}^m{X}_i(t_j){\psi }_1(t_j),\dots ,\sum _{j=1}^m{X}_i(t_j){\psi }_{K_{\beta }}(t_j)\right)\times {({\beta }_1,\dots ,{\beta }_{K_{\beta }})}^{\prime }+{\epsilon }_i\\ ={\alpha }_0+Z_i^{\prime }\alpha +W_i^{\prime }\beta +{\epsilon }_i,\end{array}$$ (6)

where $W_i^{\prime }=({\sum }_{j=1}^m{X}_i(t_j){\psi }_1(t_j),\dots ,{\sum }_{j=1}^m{X}_i(t_j){\psi }_{K_{\beta }}(t_j))$. The revised model (6) is straightforward and less technical. It turns out that model (6) performs very similar to the corresponding model (3) in our real data analysis and simulation studies.

F-distributed Tests of Fixed Effect Functional Linear Models

We first consider the fixed effect models (3), (4), and (6), i.e., we treat the regression coefficients β as unknown constant parameters. Therefore, the revised regression models (3), (4), and (6) are treated as usual multiple linear regressions that model the genetic effect of genetic variant functions adjusted for covariates. To test the association between the m genetic variants and the quantitative trait, the null hypothesis is H₀ : β = (β₁, …, β_Kβ)′= 0. By using the standard statistical approach, we may test the null H₀ : β = 0 by a F_{Kβn−Kβ−1}-distributed statistic with degrees of freedom (K_β, n − K_β − 1) (Weisberg, 2005). An alternative approach is to use likelihood ratio tests (LRT) to test the association, which is χ²-distributed with K_β degrees of freedom. In Luo et al. (2012a, b), χ²-distributed score statistics were used to test the association without adjusting for covariates.

Functional Kernel Score Tests of Mixed Effect Functional Linear Models

In the second analysis, we treat the regression coefficients β as a random vector. We assume that each β_k follows a normal distribution with a mean of zero and a variance τ, and β₁, …, β_Kβ are identically independent. Therefore, models (3), (4), and (6) are treated as linear-mixed effect models with α₀ and α as fixed effect components, and β as a random component. Denote W = (W₁, …, W_n)′ the model matrix of the regression coefficients β. Then, models (3), (4), and (6) can be viewed as linear-square kernel machine regression with a kernel = WW′ proposed in Liu et al. [2007].

To test the association between the m genetic variants and the quantitative trait, one may test a null hypothesis H₀ : τ = 0. A variance-component functional kernel score test as follows can be used to test the association

$$S(\widehat{\mu },{\widehat{\sigma }}_e^2)={(Y-\widehat{\mu })}^{\prime }\mathcal{K}(Y-\widehat{\mu })/{\widehat{\sigma }}_e^2,$$ (7)

where Y = (y₁, …, y_n)′ is a vector of trait values, μ̂ is the prediction mean of Y under the null H₀, and ${\widehat{\sigma }}_e^2$ is the estimation of ${\sigma }_e^2$ under the null. That is, μ̂ = α̂₀ + Zα̂, where Z = (Z₁, …, Z_n)′ is the covariate matrix, and α̂₀ and α̂ are estimated under the null model by regressing Y on the covariate matrix Z. As pointed out by the authors of SKAT, an important advantage of the score test is that it only fits the null model and computationally it is simple and routine [Kwee et al., 2008; Lee et al., 2012a, b; Liu et al., 2008; Wu et al., 2010, 2011]. The test statistic $S(\widehat{\mu },{\widehat{\sigma }}_e^2)$ follows a mixture of ${\chi }_1^2$ distributions. To facilitate the inference, one can approximate the distribution of S by a scaled χ² distribution $\delta {\chi }_{\nu }^2$, where δ is scale parameter and ν is the degree of freedom [Davies, 1980; Duchesne and Lafaye De Micheaux, 2010; Lin, 1997; Liu et al., 2009]. It can be shown that the mean and variance of $S(\mu ,{\sigma }_e^2)$ are given by

$$\begin{array}{c}\mathrm{E}S(\mu ,{\sigma }_e^2)=tr(\mathcal{K})\\ \text{Var}(S(\mu ,{\sigma }_e^2))=2tr({\mathcal{K}}^2).\end{array}$$

Notice that μ and ${\sigma }_e^2$ are unknown in practice, and they are estimated/replaced by μ̂ and ${\widehat{\sigma }}_e^2$ to get $S(\widehat{\mu },{\widehat{\sigma }}_e^2)$. To account for this, we replace the mean $\mathrm{E}S(\mu ,{\sigma }_e^2)=tr(\mathcal{K})$ by ê = tr(P₀ ) by the same argument as Kwee et al. [2008], where P₀ = I_n – Z(Z′ Z)⁻¹ Z′ and I_n is the n × n identity matrix. In addition, the variance $\text{Var}(S(\mu ,{\sigma }_e^2))=2tr({\mathcal{K}}^2)$ is replaced by ${\widehat{I}}_{\tau \tau }=I_{\tau \tau }-I_{\tau {\sigma }_e^2}^2/I_{{\sigma }_e^2{\sigma }_e^2}$, where I_ττ = 2tr [(P₀ 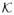)²], $I_{\tau {\sigma }_e^2}=2tr(P_0\mathcal{K}{P}_0)$, and $I_{{\sigma }_e^2{\sigma }_e^2}=2tr(P_0^2)$. Solving the equations δν = ê and 2δ²ν = Î_ττ gives the approximations of the scale parameter and the degree of freedom by

$$\begin{array}{l}\delta ={\widehat{I}}_{\tau \tau }/[2\widehat{e}],\\ \nu ={\widehat{I}}_{\tau \tau }/[2{\delta }^2]=2{\widehat{e}}^2/{\widehat{I}}_{\tau \tau }.\end{array}$$

Real Data Analysis of the Trinity Students Study

We analyzed the effect of 36 SNP variants in one enzyme gene region on three biochemical traits in a sample of 2,232 individuals from the Trinity Students Study (see below for a brief description of the study). Since the raw traits were not normally distributed, we transformed the three traits by inverse normal rank transformation. We adjusted for three factors: gender, a continuous covariate of another chemical compound known to affect these biochemical traits, and a dichotomous covariate to indicate if supplements containing these biochemical factors was used. We tested the association between the transformed individual traits and the 36 SNPs by F-test statistics of fixed effect models and variance-component functional kernel score tests of mixed effect models using both B-spline basis and Fourier basis. To make comparisons with the existing methods in the literature, we applied SKAT in R package to test the association by both SKAT and SKAT-O.

Details concerning the Trinity Student Study data collection, SNP genotyping, and quality control procedures are given in Stone et al. [2011] and Mills et al. [2011]. Briefly, this study enrolled a cohort of 2,524 healthy, ethnically Irish individuals, attending the University of Dublin, Trinity College during the academic year in 2003–2004. These students ranged in age from 18 to 28 years. Dietary and supplement questionnaires and blood samples were collected from participants. Ethical approval was obtained from the Dublin Federated Hospitals Research Ethics Committee (affiliated with the Trinity College), and reviewed by the Office of Human Subjects Research at the National Institutes of Health. Written informed consent was obtained from participants before recruitment. SNP genotyping was conducted at the Center for Inherited Disease Research (CIDR) (Baltimore, Maryland), using Illumina 1M HumanOmni1-Quad v1-0 B chips on DNA from 2,438 study samples, 14 blind duplicates, and 105 HapMap controls. The HapMap samples had a 99.71% concordance rate with their known genotypes and the blind duplicate sample pairs had a concordance rate of 99.997%. Samples were excluded based on: (1) incomplete phenotype information (n = 11), (2) gender discrepancy between self-report and genotypes (n = 7), (3) aberrant ploidy of sex chromosomes (n = 3, one XYY male and two XX/XO mosaic females), and (4) less than 95% call rate using all SNPs with at least 95% call rate. Further quality assessment was performed on 1,008,829 SNPs. SNPs were dropped that (1) had less than 98% call rate, (2) had any Mendelian errors using HapMap trios (n = 583), (3) had discordant genotypes using HapMap controls (n = 880), (4) had discordant genotypes from two or more pairs among the study duplicates (n = 1,765) allowing for one error, (5) were monomorphic or (6) had low minor allele frequency (MAF < 0.01). SNPs with deviation from Hardy–Weinberg equilibrium (P-value < 10E-4) were flagged for future reference but kept in the analysis. Thirty-six high-quality SNPs within one enzyme gene were chosen for the demonstration of the methods described in this paper.

Numerical Simulations

Two sets of simulations were performed to evaluate the performance of the proposed methods when sample sizes range from 250 to 2,000. The first one uses the sequence data used in Wu et al. [2011] and Lee et al. [2012a, b] for two scenarios in empirical power calculation: (1) the causal variants are all rare; (2) the causal variants are both rare and common. The sequence data are with European ancestry from 10,000 chromosomes covering 1 Mb regions using the calibrated coalescent model programed in COSI [Schaffner et al., 2005]. Using the same strategy of the simulations in Wu et al. [2011] and Lee et al. [2012a, b], genetic regions of 3 kb length were randomly selected in the simulations for type I error calculation and power calculations.

The second set of simulations is based on the GWAS data of the Trinity Students Study. We consider the enzyme gene used in the real data analysis. In the GWAS data of the Trinity Students Study, 36 SNPs are located in the region. The MAF of the 36 SNPs ranges from 0.05428 to 0.4108. Thus, the 36 SNPs can be treated as common variants if the same cutoff for rare variants is taken to be 0.03 as in literature of Wu et al. [2011] and Lee et al. [2012a, b].

Simulations Based on COSI Sequence Data

In this part of simulations, we used the same strategy as Wu et al. [2011] and Lee et al. [2012a, b] to generate phenotype data and the same COSI sequence data were used. This guarantees the comparison with SKAT and SKAT-O to be valid.

Type I error Simulations

To evaluate the robustness of the proposed models and tests, we generated phenotype datasets by using the model

$$y=0.5Z_1+0.5Z_2+\epsilon ,$$ (8)

where Z₁ is a dichotomous covariate taking values 0 and 1 with a probability of 0.5, Z₂ is a continuous covariate from a standard normal distribution N(0, 1), and ε follows a standard normal distribution N(0, 1). To obtain genotype data, 3 kb subregions were randomly selected in the 1 Mb region and the ordered genotypes were these SNPs in the 3 kb subregions. Notice that the trait values are not related to the genotypes, and so the null hypothesis holds. The sample size of the datasets were taken as 250, 500, 1,000, 1,500, 2,000, respectively. For each sample size case, 10⁶ phenotype-genotype datasets were generated to fit the proposed models and to calculate the test statistics and related P-values. Then, an empirical type I error rate was calculated as the proportion of 10⁶ P-values that were smaller than a given α level (i.e., 0.05, 0.01, and 0.001, 0.0001, respectively).

Empirical Power Simulations

To evaluate the power performance of the proposed models and tests, we simulated datasets under the alternative hypothesis by randomly selecting 3 kb subregions to obtain causal variants for the phenotype values as follows. Once a 3 kb subregion was selected from the 1 Mb region, a subset of P causal variants located in the 3 kb subregion was then randomly selected to obtain ordered genotypes (g(t₁), …, g(t_p)). Then, we generated the quantitative traits by

$$y=0.5Z_1+0.5Z_2+{\beta }_{1}g(t_1)+\cdots +{\beta }_{p}g(t_p)+\epsilon ,$$ (9)

where Z₁, Z₂, and ε are the same as in the type I error model (8), and the βs are additive effect for the causal variants defined as follows. We used |β_j | = c | log₁₀(MAF_j)|/2, where MAF_j was the MAF of the j-th variant. As in Wu et al. [2011] and Lee et al. [2012a], three different settings were considered: 10%, 20%, and 50% of variants in the 3 kb subregion are chosen as causal variants. When 10%, 20%, and 50% of the variants were causal, c = log(7), log(5), and log(2), respectively. For each setting, 2,000 datasets were simulated to calculate the empirical power as the proportion of P-values that are smaller than a given α level (i.e., 0.05, 0.01, and 0.001, respectively).

One may want to notice that only rare variants with MAF < 0.03 were used as causal variants in the simulations of Wu et al. [2011] and Lee et al. [2012a]. In our simulations, we considered two scenarios: (1) the causal variants are all rare, and (2) the causal variants are both rare and common. For each scenario, we performed power calculations by using two strategies: (1) only rare variants were used to calculate the empirical power levels, and (2) both rare and common variants were used.

Simulations Based on the SNP Data of the Trinity Students Study

Type I error Simulations

The 36 SNP genotype data in the enzyme gene region of the Trinity Students Study were used to evaluate the robustness of the proposed models and tests for the common variant case. We generated 10⁶ phenotype datasets by using the model

$$y=-0.5Z_1+0.002Z_2+0.5Z_3+\epsilon ,$$ (10)

where Z₁ is the gender of the individual in the dataset taking values 0 and 1, Z₂ is a continuous biochemical covariate from the dataset, Z₃ is a dichotomous covariate to indicate if supplement was used, and ε follows a standard normal distribution N(0, 1). The coefficients (−0.5, 0.002, 0.5) were chosen based on an empirical analysis of a trait of the Trinity Students Study data. Then, a sample of individuals was selected and the genotypes of 36 SNPs of these individuals were taken from the Trinity Students Study database. Notice that the simulated trait values are not related to the genotypes, and so it can be used to test the null. Using the genotypes and the simulated phenotype traits, we fitted the proposed models and calculated the tests to get related P-values. In addition, empirical type I error rates were calculated as the proportions of P-values which were smaller than a given α level (i.e., 0.05, 0.01, and 0.001, 0.0001, respectively).

Empirical Power Simulations

To evaluate the power performance of the proposed models and related tests for a single common variant as causal variant, we chose one SNP of the 36 SNPs as the causal variant. Based on the genotype G (=0, 1, 2, respectively) of the SNP, we defined X as follows: (1) for a mode of additive inheritance, X = G; (2) for a mode of dominant inheritance, X = 1 when G = 1, 2 and X = 0 when G = 0; (3) for a mode of recessive inheritance, X = 1 when G = 2 and X = 0 when G = 0, 1. We generated phenotype traits by using the model

$$y=-0.5Z_1+0.002Z_2+0.5Z_3+\beta X+\epsilon ,$$ (11)

where Z₁, Z₂, Z₃, and ε are the same as in the type I error model (10), and β = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5 is the genetic effect of the minor allele of the causal SNP (i.e., additive effect, dominant effect, and recessive effect for the three modes of inheritance, respectively).

For each value of genetic effect β = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, we considered five sample sizes of 250, 500, 1,000, 1,500, 2,000, respectively. For each combination of a genetic effect and a sample size, 2,000 datasets were simulated to calculate the empirical power as the proportion of P-values that were smaller than a given α level (i.e., 0.05, 0.01, and 0.001, respectively).

Parameters of Functional Data Analysis

In the data analysis and simulations, we used functional data analysis procedure in the statistical package R. We use two functions in library fda of R package as follows to create basis:

$$\begin{array}{l}\text{basis}=\text{create}.\text{bspline}.\text{basis}(\text{norder}=\text{order},\text{nbasis}=\text{bbasis})\\ \text{basis}=\text{create}.\text{fourier}.\text{basis}(\mathrm{c}(0,1),\text{nbasis}=\text{fbasis})\end{array}$$

The three parameters were taken as order = 4, bbasis = 15, fbasis = 25 in all data analysis and simulations to make sure that the type I error rates were properly controlled. Specifically, the order of B-spline basis was 4, and the number of basis functions of B-spline was K = K_β = 15; the number of Fourier basis functions was K = K_β = 25. In the data analysis and simulations of FPCA, the number of knots of linear spline basis was taken as 10. To make sure that the results are valid and stable, we tried a wide range of parameters that 10 ≤ K = K_β ≤ 25 and the results are very close to each other (data not shown).

Results

Application to the SNP Data of the Trinity Students Study

Table 1 presents the results of SNP data of the enzyme gene of the Trinity Students Study. We analyzed the data by three types of genetic variant functions: additive, dominant, and recessive. For all three traits, the results of fixed effect F-distributed tests are far better than those of SKAT and SKAT-O since the P-values of the fixed effect F-distributed test statistics in columns 3–7 of Table 1 were much smaller than those of SKAT and SKAT-O in columns 8 and 9 of Table 1 for most entries. The results of beta-smooth only are identical to those of smoothing both the genetic variant functions X_i(t) and the genetic effect function β(t) except for trait C using Fourier basis functions. Therefore, whether smoothing the genetic variant functions or not does not have much impact on the results.

Table 1.

Results of association analysis of three traits of the Trinity Students Study in the region of an enzyme gene

Type of GVF	Trait	P-values of the proposed F-tests					P-values
		Basis of both GVF and β(t)		FPCA	Basis of beta-smooth only
		B-spline basis	Fourier basis		B-spline basis	Fourier basis	SKAT	SKAT-O
Add	A	1.73E-13	7.89E-13	1.54E-15	1.73E-13	7.89E-13	7.13E-08	2.16E-10
	B	3.44E-13	1.80E-11	1.58E-13	3.44E-13	1.80E-11	4.34E-05	2.69E-05
	C	1.11E-11	9.91E-10	8.67E-11	1.11E-11	9.91E-10	5.80E-05	1.26E-05
Dom	A	1.83E-10	1.71E-10	3.68E-12	1.83E-10	1.71E-10	3.10E-07	4.23E-10
	B	4.66E-09	3.35E-07	3.62E-09	4.66E-09	3.35E-07	0.000152	0.000154
	C	1.54E-08	5.93E-07	9.52E-08	1.54E-08	5.93E-07	8.99E-05	1.84E-05
Rec	A	5.26E-11	9.92E-11	4.94E-13	5.26E-11	3.72E-10	7.28E-06	6.32E-06
	B	2.75E-06	4.38E-06	4.04E-06	2.75E-06	5.70E-06	0.063910	0.095384
	C	2.26E-07	5.19E-08	1.07E-07	2.26E-07	3.84E-07	0.075480	0.108617

The P-values of the proposed F-tests were based on the fixed effect models, and the P-values of SKAT and SKAT-O were based of R package SKAT. When type of GVF = Add, Dom, and Rec, the genetic variant function was taken as additive, dominant, and recessive, respectively. Abbreviation: GVF, genetic variant function.

The results of functional kernel score tests of mixed effect models are presented in the Table S1 of Supplementary Materials. The results of functional kernel score tests are somewhat mixed: for additive genetic variant function and Fourier basis, the functional kernel score tests perform better than SKAT. For dominant and recessive genetic variant functions and Fourier basis, the functional kernel score tests may perform poorer than SKAT. For B-spline basis, the functional kernel score tests may sometimes perform poorer, or sometimes better than SKAT.

Type I Error Simulation Results

The empirical type I error rates are reported in Tables 2 and 3 in the main text, and Tables S2, S3, and S4 in the Supplementary Materials. For each entry of empirical type I error rates, we generated 10⁶ datasets. Results of four different α = 0.05, 0.01, 0.001, and 0.0001 levels were reported. When additive genetic variant function was used, Tables 2 and 3 and supplementary Table S2 reported the results based on COSI sequence data and the enzyme gene SNP data of the Trinity Students Study, respectively. In Tables S3 and S4 of the Supplementary Materials, we used dominant and recessive genetic variant functions, respectively, based on the enzyme gene SNP data.

Table 2.

Simulation results of type I error rates of the proposed F-tests of the fixed effect models based on sequence data generated by COSI, when the genetic variant functions were taken as additive. The results of “Basis of both GVF and β(t)” were based on the model (3), the results of “FPCA” were based on the model (4), and the results of “Basis of beta-smooth only” were based on the model (6), respectively

Nominal level α	Sample size	Basis of both GVF and β(t)		FPCA	Basis of beta-smooth only
		B-sp basis	Fourier basis		B-sp basis	Fourier basis
0.05	250	0.049816	0.049839	0.049850	0.048148	0.046349
	500	0.049955	0.050035	0.049817	0.049779	0.046926
	1000	0.050112	0.050188	0.050266	0.050141	0.049293
	1500	0.050000	0.049933	0.050065	0.049967	0.049800
	2000	0.050211	0.050143	0.050370	0.050191	0.050163
0.01	250	0.009757	0.009925	0.009832	0.009458	0.009205
	500	0.009930	0.010094	0.010031	0.009900	0.009414
	1000	0.010164	0.010005	0.010058	0.010139	0.009794
	1500	0.010012	0.010058	0.010053	0.010003	0.009988
	2000	0.009926	0.010061	0.010129	0.009928	0.010064
0.001	250	0.000987	0.000995	0.001028	0.000968	0.000916
	500	0.001018	0.001007	0.000986	0.001012	0.000946
	1000	0.001037	0.000988	0.001018	0.001044	0.000965
	1500	0.000949	0.000998	0.000997	0.000943	0.000996
	2000	0.000931	0.000967	0.001054	0.000931	0.000961
0.0001	250	0.000102	0.000109	9.70E-05	9.20E-05	1.00E-04
	500	0.000106	9.80E-05	9.60E-05	0.000107	9.90E-05
	1000	0.000108	8.80E-05	9.30E-05	0.000108	8.60E-05
	1500	0.000110	8.60E-05	0.000101	0.000112	8.90E-05
	2000	9.40E-05	0.000106	0.000120	9.40E-05	0.000104

Table 3.

Simulation results of type I error rates of four tests based on 36 SNPs of the Trinity Students Study when the additive genetic variant functions were used

Nominal level α	Sample size	Basis of both GVF and β(t)		Basis of FKST
		B-spline basis	Fourier basis	B-spline basis	Fourier basis
0.05	250	0.049813	0.049989	0.049077	0.049759
	500	0.049970	0.049750	0.048870	0.048709
	1000	0.050406	0.049664	0.049154	0.049170
	1500	0.050334	0.050181	0.049428	0.049935
	2000	0.050218	0.049991	0.049077	0.050262
0.01	250	0.009906	0.010043	0.011951	0.010759
	500	0.010025	0.009932	0.011644	0.011102
	1000	0.010093	0.010030	0.011803	0.010734
	1500	0.009936	0.010024	0.012013	0.010522
	2000	0.010119	0.010067	0.011886	0.011785
0.001	250	0.001036	0.001017	0.001808	0.001216
	500	0.001030	0.001021	0.001632	0.001416
	1000	0.000996	0.001052	0.001634	0.001311
	1500	0.000916	0.001009	0.001674	0.001125
	2000	0.001016	0.000983	0.001672	0.001604
0.0001	250	0.000113	0.000117	0.000293	0.000143
	500	8.10E-05	0.000113	0.000234	0.000190
	1000	0.000102	0.000106	0.000241	0.000176
	1500	9.80E-05	9.50E-05	0.000245	0.000109
	2000	9.60E-05	7.20E-05	0.000260	0.000252

The results of “Basis of both GVF and β(t)” were based on the F-distributed test statistics of the fixed effect model (3) and the results of “Basis of FKST” were based on the variance-component functional kernel score test (7) of the mixed effect models, for B-spline basis and Fourier basis, respectively. FKST, functional Kernel score tests.

For the proposed F-distributed test statistics of the fixed effect functional linear models, all empirical type I error rates are around the nominal α levels (columns 3–7 of Table 2, columns 3 and 4 of Table 3 and supplementary Tables S2, S3, and S4). Therefore, the F-distributed test statistics of fixed effect functional linear models controlled type I error rates correctly over all sample sizes and all significance levels. For the variance-component functional kernel score tests of mixed effect functional linear models, the empirical type I error rates are around the nominal α = 0.05 and α = 0.01 levels, but are generally higher than the nominal α = 0.001 and α = 0.0001 levels (columns 5 and 6 of Table 3 supplementary Tables S2, S3, and S4). In addition to the results reported, we also calculated the type I error rates of LRT statistics of the fixed effect functional linear models. For large sample size cases (1,500 and 2,000), the type I error rates of LRT statistics are around all the nominal α = 0.05, 0.01, 0.001, and 0.0001 levels; when the sample sizes are 250, 500, and 1, 000, the type I error rates are around the α = 0.05, 0.01 nominal levels, but higher than the smaller nominal 0.001 and 0.0001 levels (data not shown).

Therefore, the fixed effect functional linear models and related F-tests are very robust and can be useful in the whole genome-wide and whole exome association studies, while the mixed effect functional linear models can be useful in candidate gene analysis. One may want to notice that the proposed methods are reasonably robust for small sample size cases. Interestingly, the variance-component functional kernel score tests of mixed effect models are counter-conservative at the nominal α = 0.001 and α = 0.0001 levels in Table 3 and supplementary Tables S2, S3, and S4, based on both the enzyme gene SNP and COSI sequence data, since large sample sizes can lead to higher type I error rates.

Statistical Power of the Proposed Tests and SKAT

We compared the power performance of the proposed tests with SKAT and SKAT-O based on both the simulated COSI sequence data and the SNP data of the Trinity Students Study. The proposed tests are those considered in the type I error simulations, i.e., the F-distributed test statistics of fixed effect functional linear models and two variance-component functional kernel score tests of mixed effect functional linear models, respectively. The empirical power levels are reported in the figures both in the main text and in the Supplementary Materials. In Figures 1–6, and supplementary Figures S1–S6, the results of the proposed F-tests of the fixed effect models are compared with those of SKAT and SKAT-O based on the COSI sequence data. Supplementary Figures S7–S11 compared the power performance of the proposed tests with single causal SNP regression, SKAT and SKAT-O based on the enzyme gene SNP data.

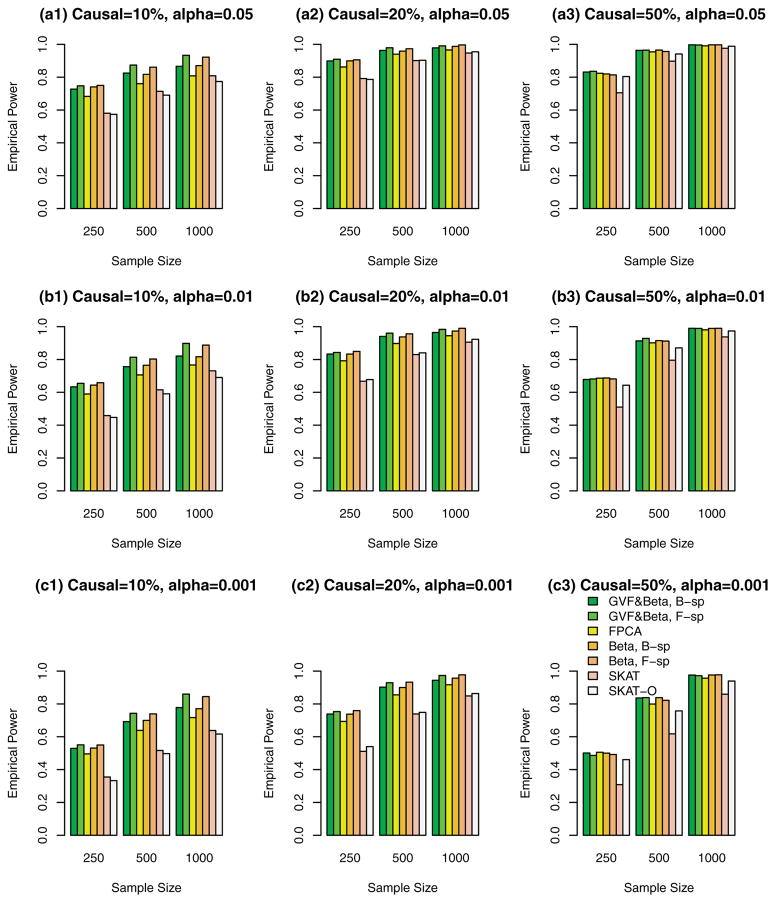
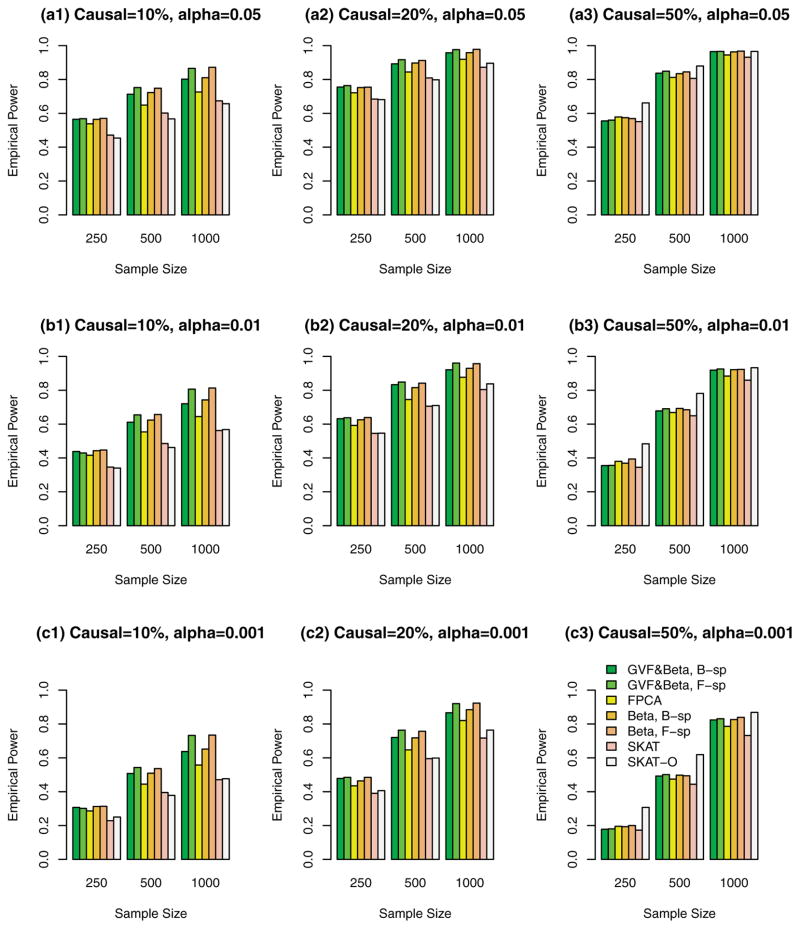
Figure 1.

The empirical power of the F-test statistics of the fixed effect models (3), (4), and (6), and SKAT and SKAT-O using both rare and common variants in analysis, when causal variants were both rare and common, and all causal variants had positive effects. The simulations were based on COSI sequence data.

Figure 6.

The empirical power of the F-test statistics of the fixed effect models (3), (4), and (6), and SKAT and SKAT-O using rare variants in analysis, when causal variants were only rare, and 50%/50% causal variants had negative/positive effects. The simulations were based on COSI sequence data.

In the legend of all the Figures, “GVF&Beta, B-sp” (or “GVF&Beta, F-sp”) means that both genetic variant function and genetic effect function β(t) were smoothed by B-spline (or Fourier) basis functions, “Beta, B-sp” (or “Beta, F-sp”) means that only the genetic effect function β(t) was smoothed by B-spline (or Fourier) basis functions (i.e., beta-smooth only), “FKST” means that functional kernel score tests were used to calculate the power level based on the mixed effect models, “B-sp” means B-spline basis was used, and “F-sp” means Fourier basis was used. In addition, the F-test statistics are used except for “FKST.”

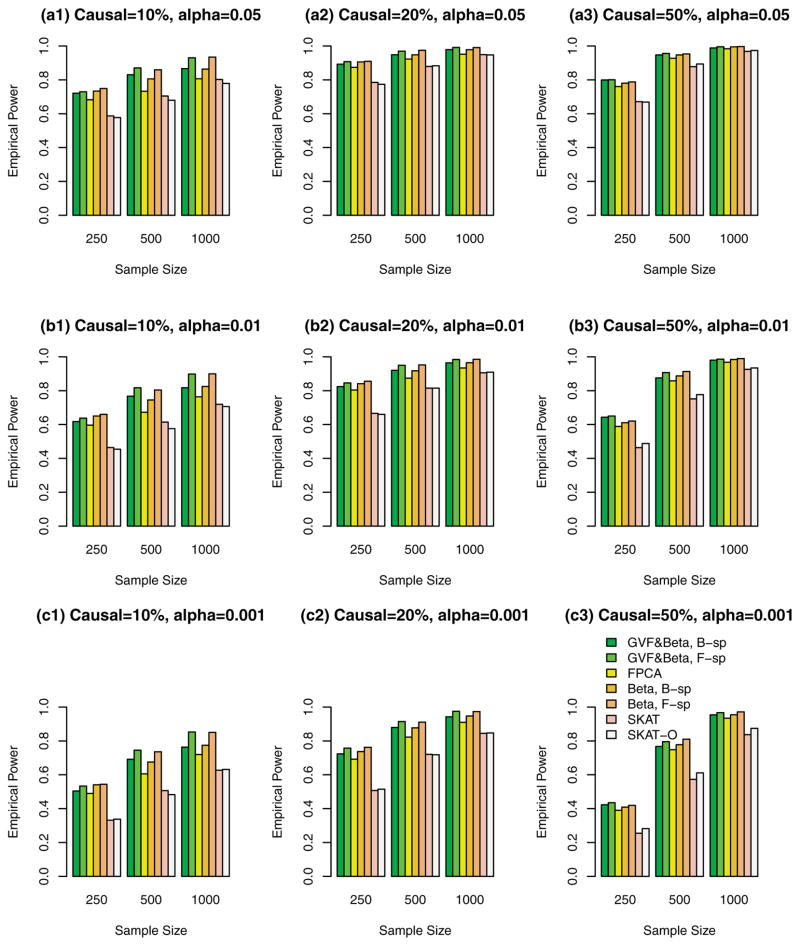
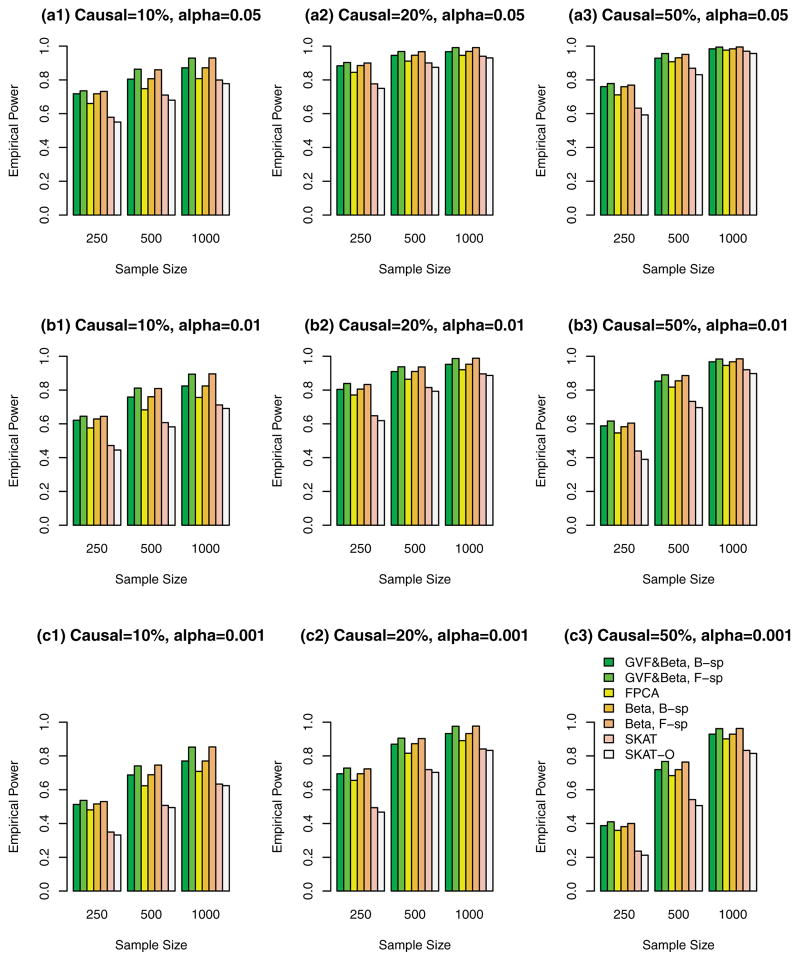
Simulation Results Based on COSI Sequence Data When the Causal Variants Can Be Both Rare and Common

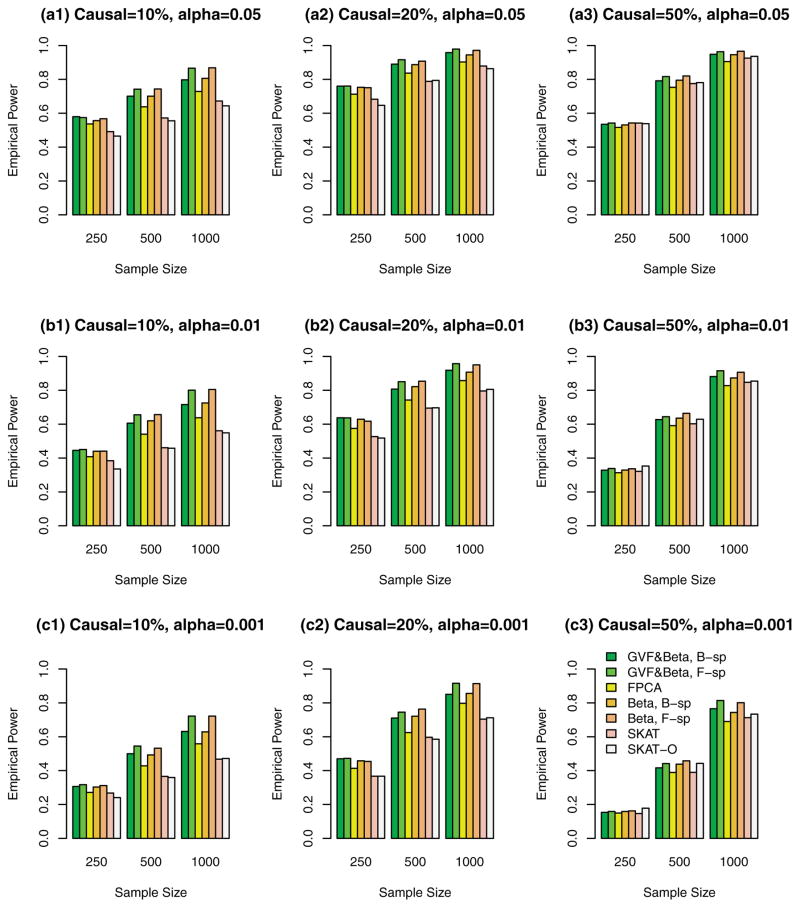
In Figures 1, 2, 3, and supplementary Figures S1, S2, and S3, the causal variants can be both rare and common. In Figures 1, 2, and 3, both rare and common variants were used in the analysis while only rare variants were used in the analysis in supplementary Figures S1, S2, and S3. In Figure 1 and supplementary Figure S1, all causal variants have positive effects; when 20%/80% causal variants have negative/positive effects, we present the results in the Figure 2 and supplementary Figure S2; when 50%/50% causal variants have negative/positive effects, the results are presented in the Figure 3 and supplementary Figure S3.

Figure 2.

The empirical power of the F-test statistics of the fixed effect models (3), (4), and (6), and SKAT and SKAT-O using both rare and common variants in analysis, when causal variants were both rare and common, and 20%/80% causal variants had negative/positive effects. The simulations were based on COSI sequence data.

Figure 3.

The empirical power of the F-test statistics of the fixed effect models (3), (4), and (6), and SKAT and SKAT-O using both rare and common variants in analysis, when causal variants were both rare and common, and 50%/50% causal variants had negative/positive effects. The simulations were based on COSI sequence data.

The proposed F-distributed test statistics of the fixed effect functional linear models have higher power than that of SKAT and SKAT-O, except that the SKAT-O has slightly higher power for small and moderate sample size cases of n = 250, 500 in plots (a3), (b3), and (c3) of a single supplementary Figure S1. When both rare and common variants were used in the analysis (Fig. 1, 2, and 3), the power of the proposed F-distributed test statistics of fixed effect functional linear models are usually much higher than that of SKAT and SKAT-O for small and moderate sample size cases of n = 250, 500. If only rare variants were used in the analysis, the power will be dramatically reduced. To see this, let us compare the corresponding power levels of Figure 1 and supplementary Figure S1 (or Fig. 2 and supplementary Fig. S2 or Fig. 3 and supplementary Fig. S3). Figure 1 (or Fig. 2 or Fig. 3) provides higher power levels than those of supplementary Figure S1 (or supplementary Fig. S2 or supplementary Fig. S3).

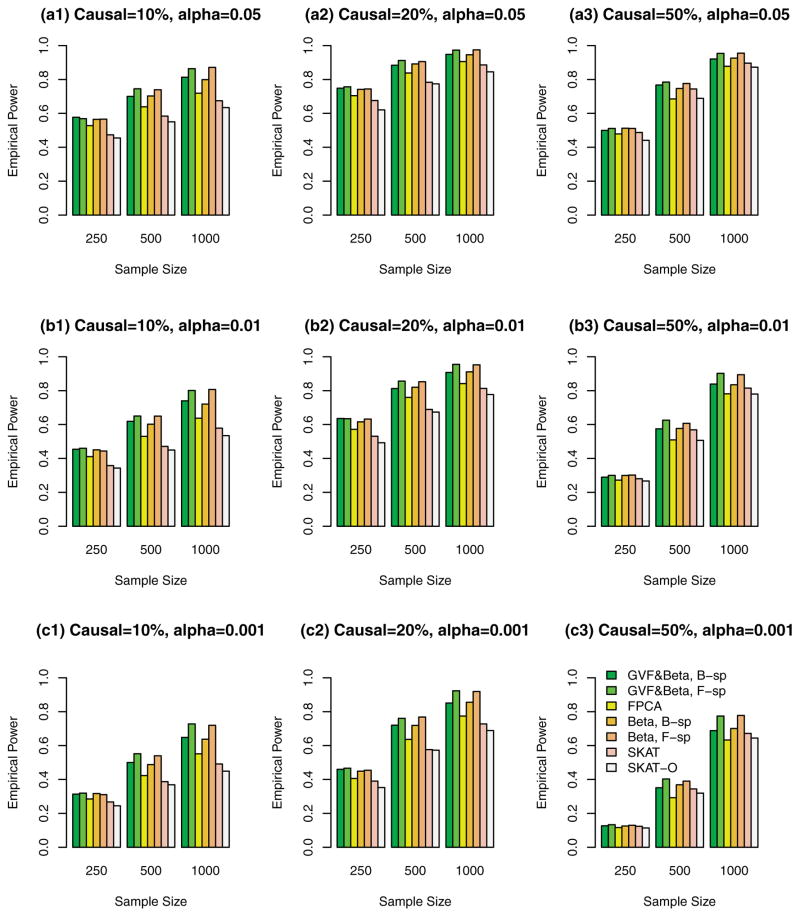
Simulation Results Based on COSI Sequence Data When the Causal Variants Are Only Rare Variants

In Figures 4, 5, 6 and supplementary Figures S4, S5, and S6, the causal variants are only rare variants. In Figures 4, 5, and 6, only rare variants were used in the analysis while both rare and common variants were used in supplementary Figures S4, S5, and S6. In Figure 4 and supplementary Figure S4, all causal variants have positive effects; when 20%/80% causal variants have negative/positive effects, we present the results in Figure 5 and supplementary Figure S5; when 50%/50% causal variants have negative/positive effects, the results are presented in Figure 6 and supplementary Figure S6.

Figure 4.

The empirical power of the F-test statistics of the fixed effect models (3), (4), and (6), and SKAT and SKAT-O using rare variants in analysis, when causal variants were only rare, and all causal variants had positive effects. The simulations were based on COSI sequence data.

Figure 5.

The empirical power of the F-test statistics of the fixed effect models (3), (4), and (6), and SKAT and SKAT-O using rare variants in analysis, when causal variants were only rare, and 20%/80% causal variants had negative/positive effects. The simulations were based on COSI sequence data.

The proposed F-distributed test statistics of fixed effect functional linear models have higher power than that of SKAT and SKAT-O, except that the SKAT-O has slightly higher power for small and moderate sample size cases of n = 250, 500 in some plots (a3), (b3), and (c3) of Figure 4 and supplementary Figure S4. When only rare variants are causal, if only rare variants were used in analysis, the tests have higher power levels in Figure 4 (or 5 or 6) than those in supplementary Figure S4 (or S5 or S6) if both rare and common variants in the analysis.

Statistical Power Based on the Enzyme Gene SNP Data of the Trinity Students Study

Supplementary Figures S7, S8, S9, S10, and S11 report the results of power simulations based on the enzyme gene SNP data of the Trinity Students Study and model (11), when one SNP is the only causal variant for the modes of additive, dominant, and recessive inheritance.

As expected, single causal SNP regression model provides the highest power compared with the proposed tests, and SKAT and SKAT-O. For the mode of additive inheritance, the proposed test statistics have substantially higher power than that of SKAT and SKAT-O except for small sample sizes n = 250. Interestingly, the functional kernel score test of B-spline offers the second highest power for small and moderate sample sizes of n = 250 and 500 as shown in graphs (a1), (a2), and (a3) of supplementary Figures S7 and S8. For the mode of dominant inheritance, the two F-distributed tests of the fixed effect models and the functional kernel score test of B-spline have higher power than that of SKAT and SKAT-O. For the mode of recessive inheritance, only the two F-distributed tests of fixed effect models offer good power when the sample size n ≥ 1, 000. Both the two functional kernel score tests of mixed effect models and SKAT/SKAT-O have minimal power.

General Observation

The results of the proposed F-tests are very similar in the Figures 1, 2, and 3 (or in the supplementary Figs. S1, S2, and S3, or in the Figs. 4, 5, and 6, or in the supplementary Figure S4, S5, and S6), when all causal variants have positive effect, 20%/80%, and 50%/50% causal variants have negative/positive effects, respectively. Therefore, the proposed tests are very robust to the proportion of causal variants that were positively/negatively related to the trait. Although SKAT-O has higher power than the proposed F-tests in some plots (a3), (b3), and (c3) of supplementary Figures S1 and S4 and Figure 4, the power levels of SKAT-O are not higher anymore in the other figures. This shows that the presence of both negative and positive effects of causal variants has little impact on the proposed F-tests, but can affect SKAT-O much more severely.

In total, we compared five F-test statistics of the fixed effect models: two are based on B-spline basis functions, two are based on Fourier basis functions, and one is based on FPCA. In the two F-tests to use B-spline (or Fourier) basis functions, one is to smooth both the genetic variant functions and the genetic effect function β(t), and the other is only to smooth the genetic effect function β(t) (i.e., beta-smooth only). Generally, the five F-test statistics of the fixed effect functional linear models have similar power, although the two tests of Fourier basis have slightly higher power and the test of FPCA has slightly lower power and the two tests of B-spline basis have power levels right in the middle. Such as in the real data analysis, the power levels of beta-smooth only are almost identical to those of smoothing both the genetic variant functions and genetic effect function β(t) by B-spline basis (or Fourier basis). Therefore, the proposed F-tests of the fixed effect models have superior performance, and the tests do not strongly depend on whether the genotype data are smoothed or not. In addition, the F-tests do not strongly depend on which basis functions are used.

For the fixed effect functional linear models, we calculated the empirical power levels of the LRT statistics, which provide very similar power levels as the F-tests (data not shown). We also explored the power performance of the variance-component functional kernel score tests of mixed effect functional linear models for COSI sequence data, and it was found that they have less power than the proposed F-tests and SKAT (data not shown).

Discussion

In this paper, we develop functional linear models to test association between a quantitative trait and rare variants or common variants or the combinations of the two. The basic philosophy is to treat the observed genetic variant data as single entities/functions, rather than as a sequence of discrete observations. Although the observed genetic data G_i = (g_i(t₁), …, g_i(t_m))′ (or their modified versions that we called dominant or recessive) are always discrete, we view them as realizations of continuous genetic variant functions X_i(t) at the location t. Here, t is simply the location of the genetic variant in the genome, which is a continuum, rather than discrete. We believe that the genetic variant functions have an intrinsic functional structure. By using modern state-of-the-art functional data analysis techniques, the observed high dimension genetic variant data can be used to estimate the genetic variant functions based on B-spline or Fourier basis functions or FPCA [de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay and Silverman, 1996; Ramsay et al., 2009]. Then, the estimated genetic variant functions are used in the functional linear regression models to connect to the phenotype adjusting for covariates.

To test the association, we proposed F-distributed test statistics of fixed effect functional linear models and functional kernel score tests of mixed effect functional linear models. The models and tests are very flexible and computationally efficient. Specifically, we have developed codes based on the procedure of functional data analysis in the statistical package R to facilitate data analysis and simulations. Since SKAT and SKAT-O were shown to be advantageous over several burden tests for a range of genetic models, we focused on comparing power performance of our tests with SKAT and SKAT-O [Lee et al., 2012a; Wu et al., 2011]. To make our comparison reasonable, we used exactly the same simulated COSI sequence data of Wu et al. [2011] and Lee et al. [2012a, b]. In addition, we performed simulations based on the SNP data of the Trinity Students Study to evaluate the performance of the proposed tests in the case of common variants. Before that, we evaluated the robustness of the proposed models and tests by empirical type I error calculations.

After extensive simulation analysis, it is shown that the proposed F-distributed tests of the fixed effect functional linear models have higher power than that of SKAT and SKAT-O for most cases of three scenarios: (1) the causal variants are all rare, (2) the causal variants are both rare and common, and (3) the causal variants are common. The superior performance of the fixed effect functional linear models is most likely due to its optimal utilization of both genetic linkage and LD information of multiple genetic variants in a region of the human genome and the similarity between different individuals, while SKAT and SKAT-O only model the similarities but they do not model linkage and LD information sufficiently. In addition, the proposed F-tests of the fixed effect models generate accurate type I errors in simulation studies. We also show that the functional kernel score tests of mixed effect models can be useful in candidate gene analysis and small sample problems. The methods are applied to analyze three biochemical traits in one enzyme gene region of the Trinity Students Study.

One question about the proposed approach is the accuracy of the estimation of the genetic variant functions, which can be relieved by fast moving next-generation sequencing technologies that will detect millions of novel rare variants and will have profound impacts on genetic studies. By adding more and more variants into the human genome including rare and common variants, the estimation of the genetic variant functions can be vastly improved and one may obtain almost the entire spectrum of DNA sequence of an individual.

Since the genotype data can only take 0, 1, and 2 values, one concern is that it may not make sense to smooth them. To investigate the issue, we explored two alternative approaches: FPCA and beta-smooth only. Neither FPCA nor beta-smooth only approach assumes any smoothness of the genotype data. In both real data analysis and simulation studies, we found that beta-smooth only approach offers identical or very similar results as the approach of smoothing both the genetic variant functions (or genotype data) and the genetic effect function β(t). Therefore, the performance of the proposed fixed effect models does not strongly depend on whether the genotype data are smoothed. In addition, the results do not strongly depend on which basis functions are used. Moreover, the results are similar and stable when the number of basis functions is in a range of 10 ≤ K = K_β ≤ 25.

Intuitively, beta-smooth only approach makes sense in genetic analysis. To understand this, assume that the trait is affected by one causal variant. Then, the variants around the causal variant can have impact on the trait due to the linkage disequilibrium. Thus, smoothing β(t) makes sense. The logic applies to the case of the existence of multiple causal variants of complex traits. If multiple causal variants exist, the variants around the causal variants may have impact on the trait, again, due to the linkage disequilibrium. Hence, there is less concern to smooth the genetic effect function β(t).

The basic idea of the proposed approaches is different from those of burden tests and kernel-based methods, which do not view the genetic variant data as single entities/functions or do not use their functional properties sufficiently. Although the proposed functional kernel score tests of the mixed effect models are statistically kernel-based, they are actually based on functional representation of the genetic variant data that includes information of linkage, LD, and similarity simultaneously. Basically, our approaches are functional, but burden tests and kernel-based methods are not.

In terms of practical applicability, the proposed tests can be used in both candidate gene analysis and genome-wide association analysis. Specifically, the proposed F-distributed tests of the fixed effect models are good for both since they control type I error rates accurately at all α = 0.05, 0.01, 0.001, and 0.0001 levels. The functional kernel score tests of the mixed effect models would be more appropriate for candidate gene analysis since they only control type I error rates accurately at α = 0.05 and 0.01 levels. The proposed models and tests can be used for analysis of rare variants or common variants or the combinations of the two, which makes the proposed approaches very attractive. It is our hope that the proposed research can help in the search of genetic variants that are responsible for complex diseases, and stimulate further interest and research in developing statistical methods for analysis of next-generation sequence data and GWAS data by using the fascinating functional data analysis techniques.

Computer Program

The methods proposed in this paper are implemented by using procedure of functional data analysis (fda) in the statistical package R. The R codes for data analysis and simulations are available from the web http://www.nichd.nih.gov/about/org/diphr/bbb/software/Pages/default.aspx