Viscoelastic Response (VisR) Imaging for Assessment of Viscoelasticity in Voigt Materials

Abstract

Viscoelastic response (VisR) imaging is presented as a new acoustic radiation force (ARF)-based elastographic imaging method. Exploiting the Voigt model, VisR imaging estimates displacement in only the ARF region of excitation from one or two successive ARF impulses to estimate τ_σ, the relaxation time for constant stress. Double-push VisR τ_σ estimates were not statistically significantly different (p < 0.02) from those of shearwave dispersion ultrasound vibrometry (SDUV) or monitored steady-state excitation recovery (MSSER) ultrasound in six homogeneous viscoelastic tissue mimicking phantoms with elastic moduli ranging from 3.92 to 15.34 kPa and coefficients of viscosity ranging from 0.87 to 14.06 Pa·s. In two-dimensional imaging, double-push VisR τ_σ images discriminated a viscous spherical inclusion in a structured phantom with higher CNR over a larger axial range than single-push VisR or conventional acoustic radiation force impulse (ARFI) ultrasound. Finally, 2-D in vivo double-push VisR images in normal canine semitendinosus muscle were compared with spatially matched histochemistry to corroborate lower double-push VisR τ_σ values in highly collagenated connective tissue than in muscle, suggesting double-push VisR’s in vivo relevance to diagnostic imaging, particularly in muscle. The key advantages and disadvantages to VisR, including lack of compensation for inertial terms, are discussed.

I. Introduction

Discrimination of the mechanical properties of tissues has been a subject of interest for the past two decades and has led to the development of many elastographic imaging methods. One established method for noninvasively interrogating the mechanical properties of tissue is acoustic radiation force impulse (ARFI) ultrasound [1]. In ARFI, a short duration, relatively high-intensity acoustic radiation force (ARF) impulse is used to generate localized, micrometer-scale displacements [1], [2]. The induced displacements, which are tracked in the region of excitation using conventional B-mode style pulses, qualitatively reflect the underlying tissue mechanical properties. The applied radiation force, however, is proportional to the acoustic intensity of the focused ultrasound beam, resulting in more applied force, and thus more displacement, at the focal depth. This gradient in displacement can be removed by applying focal gain displacement normalization; however, such normalization requires assuming an area of homogeneity to compute the mean depth-dependent displacement profile as well as assuming uniform acoustic attenuation in the region of interest [3]. Although ARFI has been demonstrated for a wide range of clinical uses [4]–[12], these applications have largely focused on the elastic properties of tissue. Because soft tissues naturally exhibit a time-dependent mechanical behavior, a viscoelastic description of the mechanical behavior may provide more information than a purely elastic one [13]. New approaches to ARF imaging that assess viscoelasticity have gained interest in the ultrasound imaging field.

Viscoelastic properties may be assessed by a variety of ARF methods. Some approaches relate viscoelastic properties to shear wave propagation characteristics. Tissue elasticity and viscosity are reconstructed using an inversion algorithm. Shearwave dispersion ultrasound vibrometry (SDUV) extracts the shear modulus and viscosity by generating ARF-induced shear waves at multiple frequencies and measuring the frequency dispersion of the shear-wave propagation speed [14], [15]. Another shear wave method, supersonic shear imaging (SSI), uses an ultrafast ultrasound scanner to generate a supersonic moving source as well as to image the resulting shear wave [16]. The ultrafast frame rate of the scanner is achieved by insonifying the medium with a single plane wave and allows for real-time visualization of transient shear waves propagating through tissue. From observed shear wave propagation, SSI solves for tissue elasticity and viscosity [16]–[18]. However, because these techniques rely on shear wave propagation, they assume tissue homogeneity over the millimeter-scale measurement region, and they lack the ability to access the viscoelastic properties directly in the region of excitation.

Other approaches to viscoelastic property assessment within the region of excitation apply sustained mechanical force to induce displacements and solve for elastic and viscous parameters using established viscoelastic models. Kinetic acoustic vitreoretinal examination (KAVE) [19] uses multiple successive ARF impulses to fully displace tissue to a steady-state level and qualitatively evaluates elasticity by fitting observed displacement to viscoelastic models. Like KAVE, monitored steady-state excitation and recovery (MSSER) ultrasound [20] also uses multiple successive ARF impulses to displace tissue to steady-state, but unlike KAVE, MSSER observes tissue creep and recovery to quantify mechanical parameters, including the relaxation time for constant stress. However, both KAVE and MSSER may suffer from slow frame rate and/or undesired bioeffects from the duration and amplitude of ARF excitations necessary to achieve steady-state displacement under physiologically relevant conditions.

This paper presents a faster alternative to MSSER, with more consistency through depth than conventional ARFI, which assesses the viscoelastic properties of tissue using two successive ARF impulses and monitoring induced displacements in only the region of ARF excitation. We call the approach viscoelastic response (VisR) imaging. VisR methods are mathematically derived using the Voigt viscoelastic model and demonstrated in viscoelastic tissue-mimicking materials as well as in canine muscle, in vivo, with spatially matched histochemical validation.

II. Background

Rather than pushing to steady-state, as in KAVE and MSSER, VisR assesses viscoelasticity by observing only three points along the viscoelastic creep profile predicted by the Voigt model. The Voigt model is a model that describes the response of a viscoelastic medium to external stimuli [13] and has been used extensively in literature to characterize the mechanical properties of soft tissue, including muscle tissue [15], [21]–[23]. The model consists of a linear spring with spring constant μ in parallel with a dashpot with coefficient of viscosity η. The differential equation describing the Voigt model is

$$\sigma (t)=E\epsilon (t)+E{\tau }_{\sigma }\frac{\mathrm{d}\epsilon (t)}{\mathrm{d}t},$$ (1)

where E is the relaxed modulus, τ_σ is the relaxation time constant for constant stress, σ(t) is the applied stress, and ε(t) is the measured creep strain. Given that ultrasound motion detection estimates displacement responses instead of strain response, (1) can be rewritten in terms of displacement [13]

$$F(t)=Ex(t)+E{\tau }_{\sigma }\frac{\mathrm{d}x(t)}{\mathrm{d}t},$$ (2)

where F(t) is the applied force magnitude in newtons and x(t) is axial displacement in meters. The constants from (2) can be described in terms of the spring and damper constants, where E = μ in newtons per meter and τ_σ = η/E in seconds. Acoustic radiation force can be used to apply a step-stress input that causes creep in a visco-elastic medium. If the ARF excitation is described as a temporal Heaviside function of force magnitude A and duration t_ARF, then displacement D₁ measured at time t₁, where t₁ > t_ARF, is the solution to (2) with the initial condition of x(0) = 0:

$$\begin{array}{l}{D}_1=\frac{A}{E}(1-e^{-t_{\text{ARF}}/{\tau }_{\sigma }})e^{-(t_1-t_{\text{ARF}})/{\tau }_{\sigma }}\\ =\frac{A}{E}{e}^{-(t_1-t_{\text{ARF}})/{\tau }_{\sigma }}-\frac{A}{E}{e}^{-t_1/{\tau }_{\sigma }}.\end{array}$$ (3)

After allowing time for partial recovery, the displacement remaining is D₂. A second ARF excitation of duration t_ARF is then administered at time t₂. The displacement D₃ measured at time t₄, where t₄ − t₂ = t₁, is the solution to (2) with the initial condition of x(0) = D₂:

$$\begin{array}{l}{D}_3=\left[\frac{A}{E}-\left(\frac{A}{E}-D_2\right)e^{-t_{\text{ARF}}/t_{\sigma }}\right]e^{-(t_1-t_{\text{ARF}})/t_{\sigma }}\\ =\frac{A}{E}{e}^{-(t_1-t_{\text{ARF}})/{\tau }_{\sigma }}-\frac{A}{E}{e}^{-t_1/t_{\sigma }}+D_2{e}^{-t_1/t_{\sigma }}.\end{array}$$ (4)

Subtracting (3) from (4) and solving for τ_σ yields:

$${\tau }_{\sigma }=\frac{-t_1}{ln\left(\frac{D_3-D_1}{D_2}\right)}=\frac{\eta }{E}.$$ (5)

Fig. 1 depicts the response of a massless Voigt material to the two ARF excitations and indicates where the three displacement measurements are obtained.

Fig. 1.

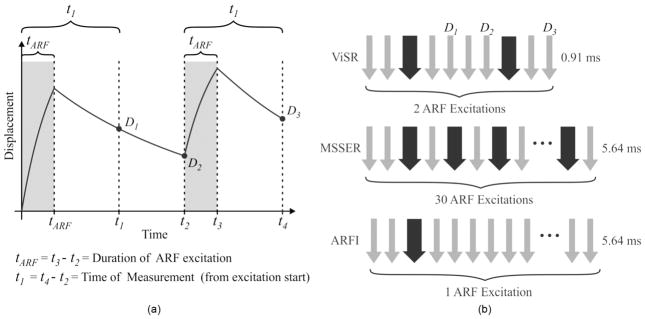
(a) The methods of VisR involve measuring displacement induced by a first ARF excitation, D₁, the level of displacement after allowing time for partial recovery, D₂, and the displacement caused by a second ARF excitation, D₃, and applying the Voigt biomechanical model to solve for the viscoelastic relaxation time constant for constant stress. (b) A VisR beam sequence is illustrated in comparison to MSSER and conventional ARFI beam sequences. The large black arrows represent ARF excitation pulses, the gray arrows represent tracking pulses, and the pulses are separated in time by the pulse repetition period. The total beam sequence duration is noted.

An alternative approach to assessing τ_σ exploits only one ARF excitation (as in ARFI) and measures two displacements D_1a and D_2a at two successive time points, t_1a and t_2a. Using (3), expressions for D_1a and D_2a at times t_1a and t_2a are derived, and dividing them and solving for τ_σ yields:

$${\tau }_{\sigma }=\frac{t_{1a}-t_{2a}}{ln\left(\frac{D_{2a}}{D_{1a}}\right)}.$$ (6)

Later, we will compare the performance of VisR using two pushes and (5) to estimate τ_σ versus using one push and (6) to estimate τ_σ.

VisR provides a facile estimate of τ_σ, the ratio of the viscosity coefficient to the relaxed elastic modulus. It is important to note that (5) and (6) suggest that τ_σ is independent of the applied force magnitude and of the time separation between successive ARF excitations, providing gains in image quality over conventional ARFI due to more consistent values through depth. Further, because the measurement is achieved by observing displacements in only the region of ARF excitation, it does not rely on shear wave propagation; so, local inhomogeneity is not corruptive. Finally, because it is neither necessary to push to a steady-state level of displacement nor to observe full recovery, its frame rate is high relative to KAVE and MS-SER methods and full 2-D imaging is supported.

III. Methods

Imaging was performed using a Siemens Acuson Antares imaging system (Siemens Medical Solutions USA Inc., Ultrasound Division, Mountain View, CA), which has been adapted to provide users with the ability to modify acoustic beam sequences, and a VF7-3 linear array transducer. ARF excitations were 300 cycles (t_ARF = 70 μs) in duration centered at 4.21 MHz with an F/1.5 focal configuration and 6.5 mm depth of field. Tracking pulses were conventional B-mode beams centered at 6.15 MHz with an F/1.5 focal configuration and 11 kHz pulse repetition frequency. Double-push VisR beam sequences consisted of two reference tracking lines preceding a first ARF excitation, then 4 tracking lines followed by a second ARF excitation and two additional tracking lines for a total of 10 pulses (0.91 ms). It is important to note that the first track lines immediately following the ARF excitations cannot be used because the probe is blinded by the reflected echoes of the pushing beam, therefore displacements D₁ and D₃ are measured from the second tracking line following the first and second ARF excitation, respectively. An additional two tracking beams are used following the first ARF excitation to allow for partial recovery of the tissue before the application of the second ARF excitation, for a total of 0.41 ms between ARF excitations. Referring to Fig. 1, D₁ is measured at time t₁ = 0.31 ms, D₂ is measured at time t₂ = 0.52 ms, and D₃ is measured at time t₄ = 0.83 ms.

For comparative purposes, MSSER, conventional ARFI, and single-push VisR imaging were also performed. The MSSER beam sequence consisted of two reference tracking pulses (as described for VisR) followed by 30 ten-cycle ARF excitations interspersed by 30 tracking pulses for a total of 62 pulses (5.64 ms). Conventional ARFI imaging was performed with a beam sequence that used the same excitation and tracking beams described for VisR, but with only one ARF excitation followed by an ensemble of 59 tracking lines for a total of 62 pulses (5.64 ms). Single-push VisR also used a single ARF excitation, as in the ARFI beam sequence, but with displacements D_1a measured at time t_1a = 0.26 ms and D_2a measured at time t_2a = 0.35 ms for τ_σ estimates at the focal depth. The measurement times t_1a and t_2a were shifted to align t_1a to the time of peak displacement for τ_σ estimates at depths above or below the focus. This was performed to account for the temporal spreading of the ARF excitation as it moved away from the focal position. Double-push VisR, MSSER, and ARFI beam sequences are illustrated in Fig. 1(b).

Two-dimensional imaging was achieved by administering the VisR, MSSER, or ARFI beam sequence in 40 lateral locations evenly spaced across a 2-cm lateral field of view. Frame rates for 2-D double-push VisR, MSSER, ARFI, and single-push VisR imaging were 27.3, 4.4, 4.4, and 31.2 frames per second, respectively. Immediately before each 2-D data acquisition, a B-mode frame was acquired. RF echo data were acquired at a 40 MHz sampling frequency and transferred to a computation workstation for processing and analysis. Displacement tracking in the region of excitation was performed using 1-D cross-correlation in the axial dimension between sequentially acquired tracking lines [24]. Each tracking line was up-sampled using cubic spline interpolation by a factor of 4 and divided into a series of 80-μm search regions; the location of the peak in the cross-correlation function between a 38-μm kernel in the first tracking line and a search region in the next tracking line was used to estimate axial tissue displacement in that region.

VisR and MSSER imaging were performed in six cylindrical (6.5 cm diameter × 6 cm height), homogeneous tissue-mimicking phantoms, and VisR and ARFI were performed in one structured (spherical inclusion) tissue-mimicking phantom (10 cm diameter × 6 cm height). The background and inclusion had comparable elasticities, but the inclusion had increased viscosity. Phantom gelatin and xantham gum concentrations were varied to alter elasticity and viscosity, respectively [25], and were prepared as follows: 200 mL of deionized water was heated to 60°C then gelatin (Type A, Acros Organics, Geel, Belgium) was added and stirred until clarified. 5.5 mL of surfactant (Photo-flo 200, Kodak, Rochester, NY), to minimize air bubbles, and 0.65 mL of N-propanol (Fisher Scientific, Waltham, MA), to increase sound speed, were added. When the mixture had cooled to 40°C, 2 g of agar powder (Fisher Scientific) for ultrasound scattering was added. At this point, 1 g of xanthan gum (Spectrum Chemicals & Laboratory Products, New Brunswick, NJ) was added to viscous phantoms and stirred until fully dispersed. The solution was then poured into a mold for cooling and congealing overnight to room temperature. Elasticity and viscosity were characterized using SDUV [15]. The SDUV sequence consisted of five 300-cycle ARF excitations, repeated with a pulse repetition of PRF_p, while tracking 3 mm lateral to the region of excitation between pulses. The pushes were then repeated in the same location while tracking 5 mm lateral to the region of excitation. Using the 1-D cross-correlation method described earlier, tissue displacements were estimated at the two lateral locations.

A 4.5-mm region just above the 24 mm focal depth was selected as the region of interest (ROI) and averaged along the axial dimension to increase the SNR of the data. A Fourier transform of the displacement data in the ROI in the time domain allows for calculation of the phase data of the shear wave in the frequency domain. Based on the measured phase difference, Δφ, at the two lateral locations at frequency PRF_p, the shear wave speed is then

$$c_{\mathrm{s}}(\omega )=\frac{\omega \mathrm{\Delta }r}{\mathrm{\Delta }\phi },$$ (7)

where ω is the angular frequency (2πPRF_p) and Δr is the distance between the lateral tracking beams, which in our experiment was 2 mm. This was repeated at various PRF_ps to compute shear wave speeds at several frequencies; the PRF_ps used ranged from 100 to 500 Hz, incrementing by 50 Hz. Assuming a homogeneous Voigt medium, shear wave speed is related to frequency by

$$c_{\mathrm{s}}(\omega )=\sqrt{\frac{2({\mu }^2+{\omega }^2{\eta }^2)}{\rho ({\mu }^2+\sqrt{{\mu }^2+{\omega }^2{\eta }^2})}},$$ (8)

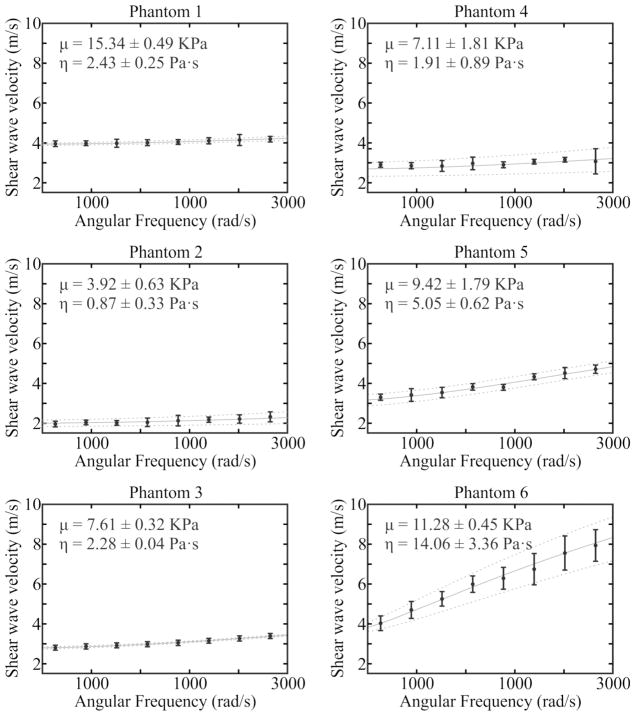
where ρ, μ, η and are the density, elasticity, and viscosity of the medium, respectively. The density of the phantoms was assumed to be 1000 kg/m³. Therefore, measured shear wave speed versus frequency were fit by (8) using nonlinear regression (nlinfit in Matlab, The MathWorks Inc., Natick, MA) to inversely solve for elasticity and viscosity. SDUV sequences were performed in 4 locations evenly spaced across the 2-cm lateral field of view, and mean and standard deviation of elasticity and viscosity were calculated. Phantom gelatin and xantham gum formulations and associated SDUV elasticity and viscosity measures are reported in Table I. Fig. 2 shows the nonlinear fits of shear wave velocity to angular frequency for SDUV calculation of elastic modulus and coefficient of viscosity.

TABLE I.

Phantom Formulations and Shearwave Dispersion Ultrasound Vibrometry (SDUV) Characterization.

Phantom number	Gelatin concentration (g/L)	Xanthan gum concentration (g/L)	μ (KPa) SDUV	η (Pa·s) SDUV
1	266	0	15.34 ± 0.49	2.43 ± 0.25
2	82	0	3.92 ± 0.63	0.87 ± 0.33
3	165	0	7.61 ± 0.32	2.28 ± 0.04
4	82	5	7.11 ± 1.81	1.91 ± 0.89
5	165	5	9.42 ± 1.79	5.05 ± 0.62
6	266	5	11.28 ± 0.45	14.06 ± 3.36

Fig. 2.

Nonlinear fits of shear wave velocity to angular frequency for shearwave dispersion ultrasound vibrometry (SDUV) calculation of elastic modulus and coefficient of viscosity. For each of the six evaluated homogeneous tissue mimicking phantoms, mean (black dots) and standard deviation (bars) of the measured shear wave velocity for repeated acquisitions is shown with the mean (solid gray line) and standard deviation (dashed gray lines) of the dispersion fit.

MSSER estimates of τ_σ were found by fitting MSSER displacement profiles to the equation for creep displacement [20]

$$x(t)=\frac{A}{E}(1-e^{-l/{\tau }_{\sigma }})$$ (9)

using nonlinear regression. Mean and standard deviations of MSSER τ_σ were measured in a 20 mm lateral by 4.5 mm axial region. In addition, a normalized mean displacement profile was found by averaging measured displacements in this region at each time point, and dividing by the maximum mean displacement.

For VisR imaging, τ_σ was estimated using double- and single-push pulse sequences from the measured axial displacement profiles using (5) and (6), respectively. Parametric images of τ_σ were rendered. In homogeneous phantoms, VisR τ_σ mean and standard deviation were calculated in a 20 mm laterally by 4.5 mm axially region positioned just above the focal depth (24 mm). The VisR τ_σ estimates were then statistically compared with the ratio of viscosity coefficient to elastic modulus from SDUV and MSSER-derived τ_σ using paired t-tests. In addition, predicted normalized creep displacement curves was generated from (9) using the VisR-dervived values of τ_σ and an A/E equal to 1. These VisR-predicted curves were compared with the MSSER-observed normalized mean displacement profiles by calculating an R² value.

In the structured phantom, parametric images of double-push VisR τ_σ, ARFI displacement (PD) and time to 67% recovery (RT), and single-push VisR τ_σ were generated. Contrast-to-noise ratio (CNR) for the spherical inclusion was calculated as

$$\text{CNR}=\frac{\mid {\mu }_{\mathrm{i}}-{\mu }_{\mathrm{b}}\mid }{\sqrt{{\sigma }_{\mathrm{i}}^2+{\sigma }_{\mathrm{b}}^2}},$$ (10)

where μ_i and μ_b denote the means and σ_i and σ_b denote the standard deviations of the parameter inside and outside the inclusion, respectively. CNR versus distance from the imaging focus (34 mm) resulting from single- and double-push VisR τ_σ versus ARFI PD and RT parameters were compared using 3 mm lateral by 1 mm axial kernels inside and outside the lesion at each depth.

Using the same imaging methods as in the phantom experiments, double-push VisR imaging was performed in vivo in the right semitendinosus (ST) muscle of an approximately 13-kg golden retriever cross-bred dog with no known musculoskeletal disorders. The Institutional Animal Care and Use Committee (IACUC) of the University of North Carolina at Chapel Hill approved all procedures. The dog was premedicated with acepromazine maleate (0.2 mg/kg), butorphanol (0.4 mg/kg), and atropine sulfate (0.04 mg/kg), masked, and then intubated and maintained with isoflurane. For imaging, the anesthetized dog was positioned in lateral recumbency. The muscle was imaged in a plane approximately transverse to the muscle fiber orientation, and the imaging plane was marked with methylene blue dye injected under B-mode image guidance [26]. The methylene blue dye was visible both macroscopically at necropsy and microscopically after sectioning and staining and did not interfere with histochemical processing. The marking was used to spatially align histological sections to the imaging plane. The extracted, marked sample was frozen, embedded, sectioned, and stained with hematoxylin and eosin, Oil Red O for fat, and Masson’s trichrome for collagen. Microscopy of the stained sections was performed using an Aperio Scanscope microscope (Vista, CA) at 20× magnification. Microscopy and parametric double-push VisR τ_σ images were aligned using the methylene blue dye as a fiducial marker and spatially compared.

IV. Results

Representative double-push VisR profiles of axial displacement versus time observed in viscoelastic phantoms are illustrated in Fig. 3. Fig. 3(a) shows profiles measured in phantoms with different elasticity but comparable viscosity (phantoms 3 and 1 in Table I), whereas Fig. 3(b) depicts profiles measured in phantoms with comparable elasticity but different viscosity (phantoms 3 and 6 in Table I). The associated double-push VisR τ_σ estimates for each profile are listed.

Fig. 3.

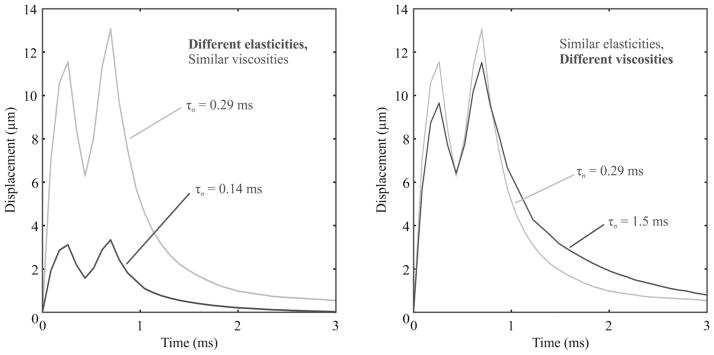
Representative double-push VisR one-dimensional axial displacement profiles measured in homogeneous tissue mimicking phantoms. In panel (a), phantoms have different elasticities (gray: 7.61 ± 0.32 kPa, black: 15.34 ± 0.49 kPa), but similar viscosities (gray: 2.28 ± 0.04 Pa·s, black: 2.43 ± 0.25 Pa·s). In panel (b), phantoms have similar elasticities (gray: 7.61 ± 0.32 kPa, black: 11.28 ± 0.45 kPa), but different viscosities (gray: 2.28 ± 0.04 Pa·s, black: 14.06 ± 3.36 Pa·s).

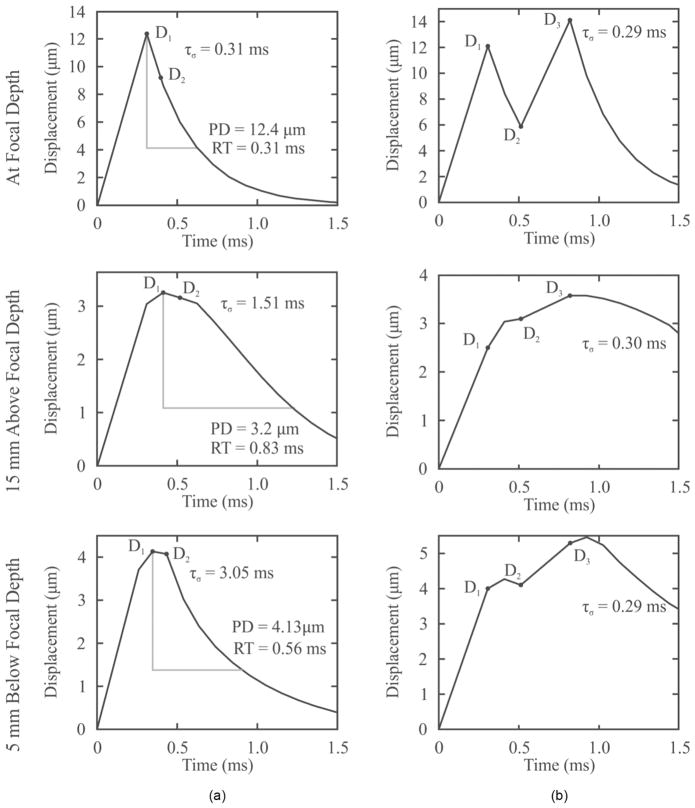
Representative profiles of axial displacement versus time for ARFI and VisR in a viscoelastic phantom (phantom 4 in Table I) are shown in Fig. 4. Fig. 4(a) shows ARFI and single-push VisR profiles taken at the focal depth (24 mm), profiles 15 mm above the focal depth, and 5 mm below the focal depth, whereas Fig. 4(b) shows the corresponding double-push VisR profiles at the three depths. The associated ARFI PD and RT as well as VisR τ_σ estimates are listed at each axial depth.

Fig. 4.

Representative (a) ARFI and single-push VisR and (b) double-push VisR one-dimensional axial displacement profiles measured in a homogeneous tissue mimicking phantom at the focal depth, 15 mm above and 5 mm below the focal depth. For each depth, ARFI peak displacement (PD) and recovery time (RT) measures (column a), single-push VisR D_1a and D_2a measures with associated τ_σ values (column a), and double-push VisR D₁, D₂, and D₃ measures with associated τ_σ values (column b) are shown. Although ARFI PD and RT and single-push VisR τ_σ values vary with depth, double-push VisR τ_σ values are more consistent.

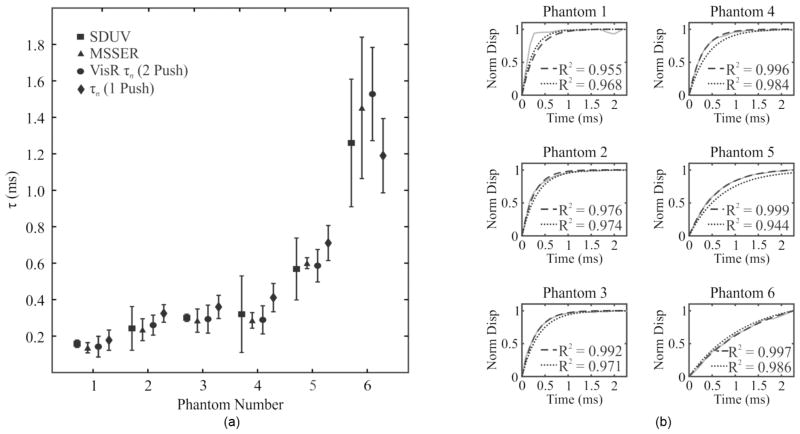
In Fig. 5(a), double- and single-push VisR τ_σ estimates (circles and diamonds, respectively) for all 6 homogeneous tissue-mimicking phantoms are plotted in comparison to corresponding SDUV ratios of viscosity to elastic modulus (squares) and MSSER τ_σ estimates (triangles). Double-push VisR τ_σ estimates are not statistically significantly different from those generated with SDUV or with MS-SER (p < 0.02). However, single-push VisR τ_σ values statistically differ from those of SDUV in phantoms 3 and 5 and from those of MSSER in phantoms 2 and 4. The agreement between VisR and MSSER τ_σ measurements is further illustrated in Fig. 5(b), in which VisR τ_σ values are used to predict creep displacement curves (black, dashed) and are plotted against the creep displacement curves observed experimentally (gray) using MSSER in each of the 6 phantoms. The accuracy of the VisR method is indicated by the closeness of fit between the experimental data and predicted data, given by the R² statistic. R² values ranged from 0.955 to 0.999 for the double-push method and from 0.944 to 0.986 for the single push method.

Fig. 5.

(a) Shearwave dispersion ultrasound vibrometry (SDUV; squares), monitored steady-state excitation recovery (MSSER; triangles), double-push VisR (circles) τ_σ values (mean ± standard deviation) estimated in the six examined homogeneous tissue phantoms at the focal depth are consistent (p < 0.02, paired t-test). Single-push VisR τ_σ values (diamonds) are statistically different from those of SDUV in phantoms 3 and 5 and from those of MSSER in phantoms 2 and 4. (b) Double- (black, dashed) and single-push (black, dotted) VisR τ_σ values predict viscoelastic creep profiles by the Voigt model that follow the creep profile experimentally observed during MSSER imaging (gray, solid) in the six homogeneous phantoms. Similarity between creep profiles predicted by single- and double-push VisR and experimentally observed by MSSER is indicated by the R² value included in the corresponding panels.

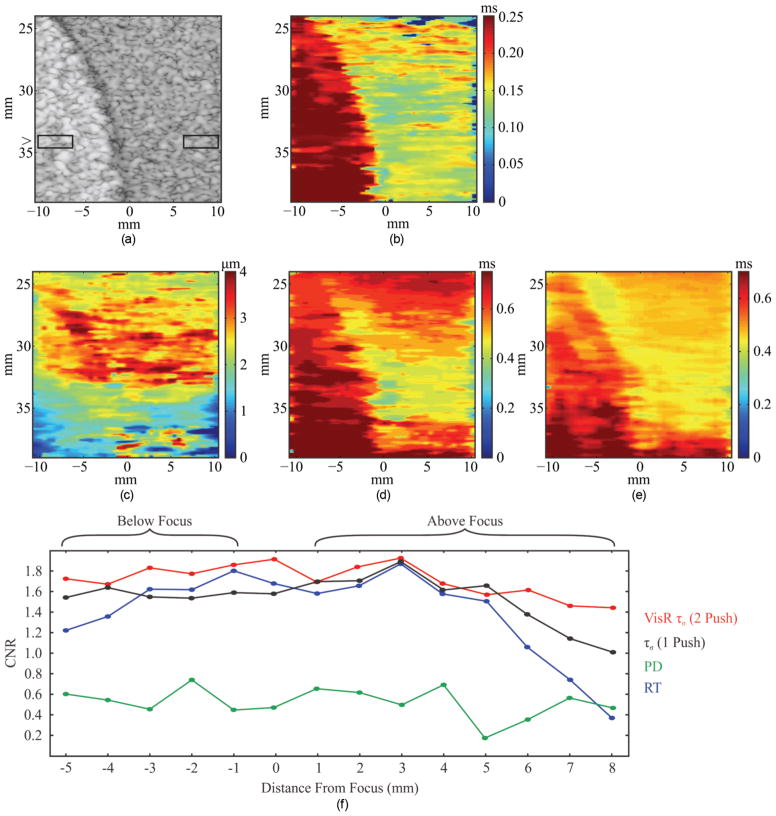
VisR, ARFI, and B-mode imaging results in the structured phantom are shown in Fig. 6. Recall that phantom background and spherical inclusion have comparable stiffness, but the background viscosity is lower than that of the inclusion (background is phantom formulation 1 and the inclusion is phantom formulation 6). For all three imaging methods, the focal depth was 34 mm. In the B-mode image [Fig. 6(a)], the spherical inclusion is evident as the hyperechoic spherical structure spanning 24 to 39 mm axially and −10 to −1 mm laterally. The two boxes represent the positions of the ROIs within and outside the inclusion for CNR calculations. The boxes were moved axially in 1-mm steps to evaluate CNR as a function of distance from the imaging focus. In the double-push VisR τ_σ image [Fig. 6(b)], the lesion is clearly delineated across its 24 to 39 mm axial range; however, the lesion is not well distinguished from background in the parametric ARFI peak displacement (PD) image [Fig. 6(c)]. The parametric ARFI recovery time (RT) image [Fig. 6(d)] delineates the spherical inclusion better than the ARFI PD image, but CNR diminishes with distance from the focal depth, as is described by the graph of CNR versus distance from focus in Fig. 6(f). Although ARFI RT yields comparable CNR to double-push VisR near the imaging focus, RT CNR drops beyond 5 mm above the focus and 4 mm below the focus. This is not the case for double-push VisR, which maintains generally constant CNR across the 14 mm axial range of the inclusion. The single-push VisR image [Fig. 6(e)] discriminates the inclusion with generally lower CNR than the double-push VisR method, but CNR is improved over that of RT alone from approximately 5 mm above the focus.

Fig. 6.

(a) B-mode, (b) double-push VisR τ_σ, (c) ARFI peak displacement (PD), (d) ARFI recovery time (RT), and (e) single-push VisR τ_σ images of a tissue-mimicking phantom with a spherical inclusion that is comparably stiff but more viscous than the background. The boxes in the B-mode image represent the 3 mm laterally by 1 mm axially ROIs used to calculate contrast-to-noise ratio (CNR). (f) CNR is plotted versus distance from the focus for the double-push VisR τ_σ (red), ARFI PD (green), RT (blue) images, and single-push VisR τ_σ (black).

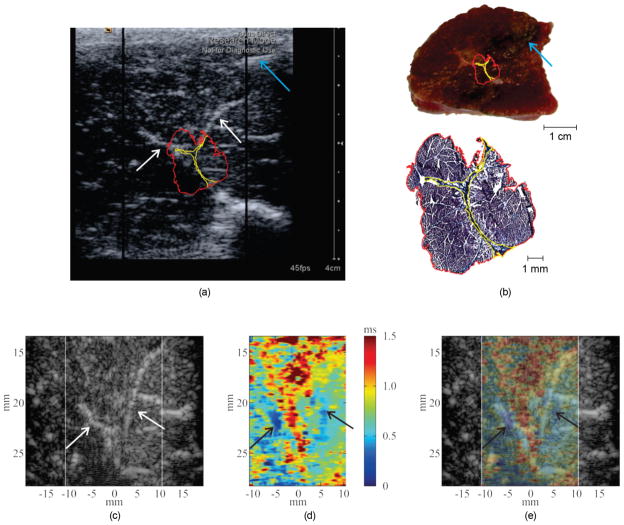
In vivo double-push VisR imaging in a canine semi-tendinosus (ST) muscle is shown with spatially-matched histochemistry in Fig. 7. Fig. 7(a) shows the B-Mode image acquired during injection of the methylene blue dye to mark the imaging plane. The needle is evident in the upper right portion of the B-mode image (blue arrow). The corresponding gross muscle is shown in the top of Fig. 7(b), with methylene blue dye macroscopically visible (blue arrow). Also observable are white anatomical features confirmed by Masson’s trichrome stain [Fig. 7(b) bottom] to be perimysial connective tissue outlining an area where three separate fascicles come into contact. This connective tissue is highly collagenated according to the Masson’s stain and hyperechoic in the B-mode image [Fig. 7(c)]. The connective tissue also yields low τ_σ values in the spatially matched VisR image [Fig. 7(d)]. The VisR image is superimposed with transparency on the B-mode image in Fig. 7(e) to highlight the spatial alignment of low VisR τ_σ estimates to the hyperechoic connective tissue in the B-mode image.

Fig. 7.

In vivo double-push VisR imaging in normal canine semitendinosis muscle: (a) The B-mode image captured from the system display shows the needle injecting methylene blue dye to mark the VisR imaging plane (blue arrow), and hyperechoic structures (white arrows). The hyperechoic structures and position of methylene blue injection are used to align the B-mode image to histology. The red polygon denotes the corresponding tissue in the histology section (panel b) with the hyperechoic structure contained within the histology section outlined in yellow. (b) In the gross image of the dissected muscle (top), the methylene blue mark is apparent (blue arrow). Also evident is white tissue spatially corresponding to the hyperechoic structures highlighted in the B-mode image, which are confirmed by Masson’s trichrome stain to be highly collagenated connective tissue (bottom). The red polygon on the gross image denotes corresponding tissue in the Masson’s stain, with the highly collagenated structure outlined in yellow. (c) The B-mode image rendered by envelope detection of the raw RF B-mode data acquired immediately before VisR imaging is shown with hyperechoic connective tissue structures again apparent (arrows). Note the injection needle was removed before VisR imaging to avoid disruption of ARF propagation beyond the needle. (d) The VisR τ_σ image shows low τ_σ spatially corresponding to the position of the connective tissue structures (arrows). (e) The spatial correspondence of low VisR τ_σ estimates to the connective tissue structures is further demonstrated by overlaying the VisR transparency on the B-mode.

V. Discussion

VisR is a novel approach to elastographic imaging that estimates τ_σ, the viscoelastic stress relaxation time constant in the Voigt biomechanical model, by delivering to the same region of excitation one or two successive ARF excitations. Although the single-push VisR approach yields τ_σ estimates that are similar to the double-push approach at the focal depth, the double-push approach supports a larger axial range over which τ_σ estimates are valid. Fig. 4 shows that in a homogeneous tissue-mimicking phantom, double-push τ_σ values remained relatively constant from 5 mm below the focus (0.29 ms) to the focus (0.29 ms) to 15 mm above the focus (0.30 ms). On the contrary, the single-push VisR τ_σ values varied from 3.05 ms below the focus to 0.31 ms at the focus to 1.51 ms 15 mm above the focus. This represents a 10-fold and 5-fold increase in single-push VisR τ_σ values 5 mm below and 15 mm above the focus, respectively. The impact of single-push VisR’s depth dependence on two-dimensional imaging is demonstrated in Fig. 6, which shows that double-push VisR yields higher CNR over a larger axial range than single-push VisR, although in the axial range of 1 to 5 mm above the focal depth, single- and double-push VisR perform comparably in terms of CNR. These data demonstrate an important advantage to double-push VisR, which is the extended axial range over which its τ_σ estimates are consistent. It could be possible to interrogate a 20 mm axial range using single-push VisR in the phantoms if an ARF excitation and tracking were performed every 4 mm axially. However, this would require a total of 6 ARF excitations and roughly 2.1 ms (6 ensembles × 0.35 ms/ensemble), as opposed to 2 ARF excitations and 0.9 ms for the double-push VisR approach, to interrogate the same axial range.

Both single- and double-push VisR τ_σ values estimated at the focal depth are compared with SDUV (which is considered as the gold standard) and MSSER (which measures τ_σ by pushing to steady-state displacement) in Fig. 5. Fig. 5(a) shows that single- and double-push VisR τ_σ estimates are generally similar to each other and to SDUV- and MSSER-derived τ_σ values in all phantoms. Double-push VisR τ_σ estimates were not statistically different (p <0.02) from SDUV or MSSER τ_σ values in any phantom. However, single-push VisR yielded τ_σ estimates that were statistically different from SDUV τ_σ estimates in phantoms 3 and 5 and from MSSER τ_σ estimates in phantoms 2 and 4. Moreover, single-push and double-push VisR τ_σ estimates were statistically different from each other in phantom 6. Overall, the differences between τ_σ estimated at the focal depth using single- or double-push VisR appear minor, which suggests that single-push VisR may be a useful tool if the desired axial range for imaging is limited to a few millimeters above the focal depth.

Note that although VisR and SDUV yielded similar τ_σ values, the methods of computing τ_σ differed substantially. SDUV calculations relied on tracking the dispersion of multiple shear wave frequencies over tens of milliseconds and across several millimeters beside the ARF region of excitation. In contrast, VisR τ_σ was estimated using only one or two 70-μs ARF excitations and tracking displacement over a total of 0.6 or 0.9 ms only in the region of ARF excitation.

Although the methods of VisR support important advantages, including fast frame rates and independence from tissue inhomogeneity surrounding the ARF region of excitation, the VisR approach is associated with a critical limitation as it pertains to imaging tissue. Specifically, the Voigt model, upon which the VisR method is based, does not account for material mass, and therefore, no inertial terms are associated with the observed displacements. However, tissue is not in fact massless, and neglecting contributions from inertia distorts VisR τ_σ estimates. The correlation between τ_σ values estimated using VisR and SDUV (Fig. 5) suggests that with the employed imaging parameters in the employed tissue-mimicking phantoms, the error from neglecting inertia in VisR τ_σ was not significant. However, it is important to note that under different imaging conditions (for example, using a larger focal configuration, which excites a larger volume and therefore mass of tissue) or in materials with higher density, neglecting the inertial term could result in meaningful error in τ_σ, and thus VisR implemented without compensation for the intertial terms cannot be considered quantitative.

Another limitation to VisR is that it does not isolate the viscosity coefficient from the elastic modulus as in SDUV. Rather, VisR estimates τ_σ, the ratio of viscosity coefficient to the elastic modulus. In this regard, VisR may be limited in scenarios in which discriminating changes in viscosity coefficient from changes in elastic modulus are diagnostically meaningful. For example, using VisR as described in this manuscript, it would not be possible to determine if a given tissue A has half the elastic modulus or twice the coefficient of viscosity of tissue B with a twofold difference in τ_σ.

The statistical sameness of double-push VisR and MS-SER imaging methods in Fig. 5 demonstrates that VisR, which exploits the Voigt biomechanical model in a manner similar to MSSER imaging but with far fewer ARF excitation and tracking pulses, achieves τ_σ estimation much more efficiently than MSSER. Moreover, independence from pushing to a steady-state level of displacement and from observing undisturbed progression to steady-state in VisR makes its clinical implementation lower energy and more tractable than that of MSSER.

Another advantage of VisR is its independence from the applied ARF magnitude and from the impulsive nature of the ARF excitation. This is not the case for conventional ARFI imaging, in which induced peak displacement is proportional to the applied force magnitude that diminishes with distance from the ARF region of excitation. Further, ARFI recovery time measures are distorted away from the region of ARF excitation where the propagating excitation is no longer impulsive. This phenomena is illustrated in Fig. 4. Fig. 4(a) shows that with conventional ARFI, a point 15 mm above the focal depth exhibited a PD that was 74% smaller and an RT that was 167% longer than a point at the focus; similarly, PD was 67% smaller and RT was 81% longer in a point 5 mm below the focal depth compared with the point at the focus. In double-push VisR [shown in Fig. 4(b)], despite decreases in D₁, D₂, and D₃, τ_σ estimates at 15 mm above the focus and 5 mm below the focal depth were 3% smaller and equal to τ_σ estimated at the focus, respectively.

Double-push VisR’s independence from the impulsive nature of the ARF excitation is further demonstrated in Fig. 6. Fig. 6(b) shows that double-push VisR τ_σ estimates are consistent over the 14-mm axial range of the inclusion despite diminishing ARF magnitude and impulsive excitation distortion (not shown) with distance from the focus. Accordingly, double-push VisR CNR values remain generally constant across the axial range of the inclusion, varying from 1.9 at the imaging focal depth to 1.45 at 8 mm above the focal depth and 1.75 at 5 mm below the focal depth [Fig. 6(f)]. The ARFI PD image in Fig. 6(c) does not discriminate the inclusion well, with a maximum CNR of 0.8. This result is expected given that the inclusion and the background were comparably stiff and that ARFI PD primary exploits tissue stiffness. The inclusion is discriminated in the ARF RT image and consistent over 8 mm, which is just wider than the depth of field of the ARFI excitation (6.5 mm); however, CNR drops substantially beyond 5 mm above the imaging focus and 4 mm below the focus, as expected with distortion of the impulsive excitation. Moreover, double-push VisR τ_σ is estimated using a beam sequence that was 6 times shorter than the ARFI RT beam sequence. Thus, Figs. 4 and 6 show that double-push VisR discriminates differences in viscosity over a larger axial range and faster than conventional ARFI RT measures. As with single-push VisR, ARFI RT could achieve the same axial range as double-push VisR in the examined phantoms if an ARFI impulse and tracking were implemented every 8 mm axially, which would require 3 ARF excitations and 16.9 ms (3 ARFI ensembles × 5.64 ms/ensemble) to interrogate the same axial range achieved using 2 ARF excitations and 0.91 ms in double-push VisR.

It is important to consider that double-push VisR assumes that the two successively applied ARF excitation impulses are identical in a given region of excitation. Although this assumption is generally reasonable, variations in system output and/or shear wave reflections that are immediately coincident with (and inconsistently augment) one of the two successive excitation impulses may corrupt VisR τ_σ estimates. In our preliminary experience to date, VisR τ_σ estimates were not statistically significantly different (p < 0.2) over 10 repeated measures in the examined tissue-mimicking phantoms (data not shown), but a more thorough analysis of repeatability with specific attention given to the potential impact of system variation in force output on VisR τ_σ estimates is warranted.

An additional consideration is that VisR estimates tissue displacements using speckle tracking methods, which are subject to errors from low SNR and decorrelation of the RF echo signals [27], [28]. The jitter in displacement estimation (observation noise) may mask some of the dynamics of the viscoelastic response. VisR can take advantage of its high frame rate and average over multiple acquisitions to improve SNR; however, repeated acquisitions would increase energy and could result in substantial transducer face and tissue heating [29]. Alternately, low displacement SNR could be overcome through the use of a specialized ARFI transducer [30].

Equations and numerical results in this manuscript are based on the approximation that an impulsive ARF excitation mimics constant stress over a time duration t_ARF. It is important to consider that t_ARF is 0.07 ms, whereas τ_σ values in the investigated materials range from 0.2 to 1.5 ms. Thus, each ARF excitation induces approximately 7% of the steady-state displacement, and the two successive excitations maximally achieve approximately 14% of the steady-state displacement. Although VisR observes only a small fraction of the full viscoelastic creep profile, consistency between τ_σ values estimated by VisR and those measured by MSSER (which are based on pushing to full steady-state displacement) suggests that the VisR push duration is sufficient for τ_σ approximation in our experimental context.

The relevance of double-push VisR as an in vivo imaging method is suggested in Fig. 7, which shows that double-push VisR τ_σ estimates are lower in regions of highly collagenated connective tissue than in surrounding normal muscle. Low τ_σ values are consistent with higher stiffness in the area of the connective tissue relative to the normal muscle, but it is important to consider that low τ_σ values could also be the result of stress relief along the collagen boundary of this complex media. Additional demonstration is need to establish that doube-push VisR is pertinent to discriminating focal differences in muscular viscoelasticity, which may be important to discriminating heterogeneous fatty and fibrous deposition with dystrophic muscle degeneration and other neurological and musculoskeletal disorders. Another important consideration in regard to in vivo imaging is the impact of gross and physiological motion. As in ARFI imaging, gross and physiological motion are rejected in VisR using established methods [31]–[33], but the potential for distortion of VisR creep and recovery responses after motion rejection should be evaluated further.

VI. Conclusion

VisR, a new ARF-based elastographic imaging method that estimates the relaxation time for constant stress (τ_σ) in viscoelastic materials, is presented with mathematical derivation based on the Voigt biomechanical model. Data acquired in tissue-mimicking phantoms highlight the key advantages to VisR. First, τ_σ is estimated using displacement tracked in only the ARF region of excitation, so VisR is faster, lower energy, and less susceptible to corruption from tissue inhomogeneity than approaches that rely on measuring shear wave propagation over a millimeter-scale lateral distance from the ARF region of excitation. Second, double-push VisR is relatively independent from the magnitude and impulsive nature of the ARF excitation, which results in a greater axial range than possible with conventional ARFI methods. Further, the equations for τ_σ suggest that VisR τ_σ estimates are independent from the duration of the applied ARF and from the time separation between the two ARF excitations. This will be the topic of future investigations. VisR’s facile 2-D implementation supports in vivo employment, and preliminary results in normal canine semitendinosus muscle suggest the clinical relevance of double-push VisR to muscle. Despite these significant advantages, disadvantages to VisR as implemented in this manuscript include that it does not consider inertial terms, and therefore cannot be considered quantitative, and it is not able to distinguish viscosity coefficient and elastic modulus. Further, gross or physiological motion may be corruptive if improperly rejected. Another potential shortcoming is VisR’s assumption that the two successively applied ARF excitations in a given region of excitation are identical. Future work will be directed toward investigating the impact of these possible drawbacks on VisR’s general clinical utility.

Biographies

Mallory R. Selzo was born in West Palm Beach, FL, in 1986. She received her B.S. degree in computer engineering in 2008 from the University of Washington. She is currently pursuing a Ph.D. degree in the joint Department of Biomedical Engineering at the University of North Carolina–Chapel Hill and North Carolina State University. Her research interests include acoustic radiation force imaging and neuromuscular disorders.

Caterina M. Gallippi earned a B.S.E. degree in electrical engineering and a certificate in engineering biology from Princeton University in 1998. She completed her Ph.D. degree in biomedical engineering at Duke University in 2003 with a focus on ultrasonic imaging. Dr. Gallippi is currently an Assistant Professor in the Joint Department of Biomedical Engineering at the University of North Carolina at Chapel Hill and North Carolina State University. Her research interests include radiation force imaging, adaptive signal filtering, multidimensional motion tracking, and magneto-motive ultrasound.