A computer model of unitary responses from associational/commissural and perforant path synapses in hippocampal CA3 pyramidal cells

Abstract

Despite the central position of CA3 pyramidal cells in the hippocampal circuit, the experimental investigation of their synaptic properties has been limited. Recent slice experiments from adult rats characterized AMPA and NMDA receptor unitary synaptic responses in CA3b pyramidal cells. Here, excitatory synaptic activation is modeled to infer biophysical parameters, aid analysis interpretation, explore mechanisms, and formulate predictions by contrasting simulated somatic recordings with experimental data. Reconstructed CA3b pyramidal cells from the public repository NeuroMorpho.Org were used to allow for cell-specific morphological variation. For each cell, synaptic responses were simulated for perforant pathway and associational/commissural synapses. Means and variability for peak amplitude, time-to-peak, and half-height width in these responses were compared with equivalent statistics from experimental recordings. Synaptic responses mediated by AMPA receptors are best fit with properties typical of previously characterized glutamatergic receptors where perforant path synapses have conductances twice that of associational/commissural synapses (0.9 vs. 0.5 nS) and more rapid peak times (1.0 vs. 3.3 ms). Reanalysis of passive-cell experimental traces using the model shows no evidence of a CA1-like increase of associational/commissural AMPA receptor conductance with increasing distance from the soma. Synaptic responses mediated by NMDA receptors are best fit with rapid kinetics, suggestive of NR2A subunits as expected in mature animals. Predictions were made for passive-cell current clamp recordings, combined AMPA and NMDA receptor responses, and local dendritic depolarization in response to unitary stimulations. Models of synaptic responses in active cells suggest altered axial resistivity and the presence of synaptically activated potassium channels in spines.

1 Introduction

Structure and function in the hippocampus have been extensively studied by neuroscientists. Since the experience of patient H.M. (Scoville and Milner 1957), we have known that the hippocampus plays a key role in learning and memory. Early anatomical studies noted extensive interconnections among pyramidal cells of the hippocampus (Ramón y Cajal 1995), particularly in area CA3 (Hjorth-Simonsen 1973; Swanson et al. 1978). Pioneering theories suggested a special role for the hippocampus in rapidly storing memories prior to their integration into the neocortex (Marr 1971). A series of more sophisticated models have addressed the role of CA3 as an autoassociative network supporting context-dependent memory (Rolls 1996), spatial navigation (Samsonovich and McNaughton 1997), and place field formation (Wallenstein and Hasselmo 1997; Káli and Dayan 2000), to name only a few.

Despite the long-term interest in CA3 and its unique aspects, a common limitation of models has been that, compared with CA1, there is much less experimental evidence upon which to base a biophysically realistic simulation. Even recently formulated biophysical models of CA3 pyramidal cells have, of necessity, drawn extensively from characterizations of CA1 pyramidal cells (Lazarewicz et al. 2002; Baker and Olds 2007; Hemond et al. 2008). Any model addressing functional or dysfunctional aspects of CA3 will necessarily concern itself with the question of synaptic integration. This requires an accurate characterization of the responses of individual synapses and their interaction with cell morphologies. CA3 pyramidal cells have a complex morphology and a large number of synaptic contacts in thin distal dendrites receiving inputs from multiple excitatory afferent pathways (Amaral and Witter 1989; Amaral et al. 1990). Of primary interest here are the divergent projections among CA3 pyramidal cells, the associational/commissural axons (A/C), and the projection from the entorhinal cortex to CA3, the perforant path (PP). Currently it is not feasible to record from the distal dendrites of CA3 pyramidal cells, limiting direct experimental characterizations of either synaptic properties or ion channels in these regions.

Within the limits of what can be measured, however, there are noteworthy studies characterizing CA3 pyramidal cells. Passive properties have been characterized both in purely experimental terms (Spruston and Johnston 1992) using cells from 4–8 week old guinea-pigs at 32°C, and in a combined experimental and modeling study (Major et al. 1994) using cells from 19–21 day old Wistar rats at room temperature. The latter study estimated passive properties through the use of detailed compartmental models based on reconstructions of the same cells from which the electrophysiological recordings were made. Transient current injections at the soma were used, this protocol being favorable for probing the electrotonic structure of the cells when only a single injection site is possible. As further discussed below, the finding by Major et al. (1994) of a somewhat larger than expected axial resistivity has a substantial effect on predicted synaptic responses and is a topic revisited in the current model.

Prior expectations regarding A/C and PP glutamatergic synaptic responses in CA3 pyramidal cells have generally relied upon experiments using either fast applications of glutamate to characterize glutamate receptor properties (Colquhoun et al. 1992; Jonas and Sakmann 1992; Spruston et al. 1995), unitary stimulations in cultured cells (Debanne et al. 1995), stimulation of mossy-fibers (Williams and Johnston 1991; Jonas et al. 1993), or methods not specifically intended to elicit unitary responses (Williams and Johnston 1991). An earlier study of synaptic responses in the guinea-pig (Miles and Wong 1986) used methods conceptually similar to those employed in the companion experimental work (Perez-Rosello et al. 2010). Antidromic stimulations were used to evoke minimal excitatory postsynaptic potentials (EPSP) in CA3b pyramidal cells, which were taken to be the result of unitary synaptic activations. In some cases, cesium solutions in the recording electrode were used to block potassium channels. Results were similar to those in the companion study except that minimal EPSPs were found to be larger in amplitude, possibly reflecting a difference in the recording conditions or neurotransmitter release properties of the different preparations. However, excitatory postsynaptic currents (EPSC) were not measured. Although PP synaptic responses in CA3 pyramidal cells have previously been described (Berzhanskaya et al. 1998), unitary PP responses have not previously been characterized.

The present work is the modeling component of a collaborative effort also involving the experimental characterization of unitary synaptic responses, described in the companion paper (Perez-Rosello et al. in press), and measurement of CA3 pyramidal cell electrophysiological properties (Hemond et al. 2008, 2009). A significant advantage of the experimental characterization of synaptic responses is that the CA3 pyramidal cells have been rendered electrically passive by blocking relevant ion channels prior to recording the results of minimal synaptic stimulations. This reduces the model to its simplest form, that of a passive cell whose responses are determined entirely by the interaction of synaptic receptors, cell morphology, and the experimental recording methods. The passive model removes many of the uncertainties associated with modeling CA3 pyramidal cells and permits the formulation of a well-constrained model implying synaptic properties that would otherwise be inaccessible to experimenters and modelers alike.

2 Methods

2.1 Software and hardware

Simulations of synaptic responses were conducted using the NEURON simulation environment (Carnevale and Hines 2005). Model files are available for public download under the ModelDB (Hines et al. 2004) section of the Senselab database (http://senselab.med.yale.edu). Postprocessing summarization was conducted using the statistical language R (R Development Core Team 2009). Simulations were conducted using a Dell Precision Workstation (Dell Computer Corp., Austin Texas) with dual Intel Xenon processors running 64-bit Fedora (http://fedoraproject.org).

2.2 Simulation methods

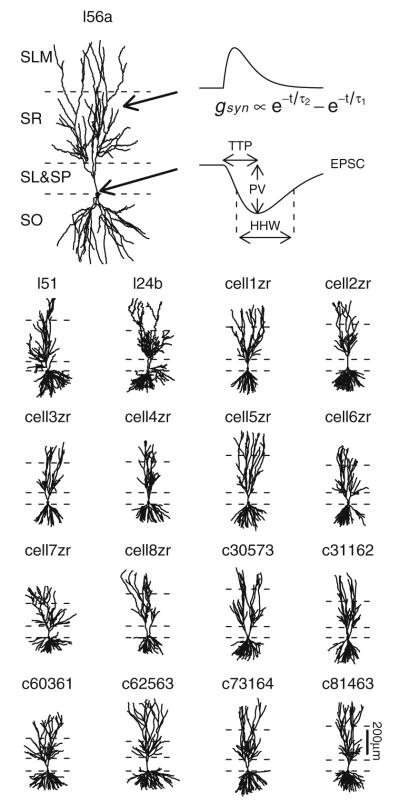
NeuroMorpho.Org (Ascoli et al. 2007), an archive of publicly accessible neuronal morphologies, was reviewed for reconstructed CA3b pyramidal cells. Seventeen neurons (Fig. 1) from three different sources (Ishizuka et al. 1995; Turner et al. 1995; Henze et al. 1996) were identified for use in these simulations. For consistency, any axonal segments present in the original reconstructions were removed and replaced with a common axon definition used in a previous CA3 pyramidal cell model (Hemond et al. 2008). As needed, each cell was reoriented so that its primary direction of extension was along the y-axis. Layer boundaries were identified either from fiducial marks provided as part of the reconstruction or else estimated based on overall cell morphology. Regions of each cell were categorized as stratum oriens (SO), soma, stratum lucidum (SL), stratum radiatum (SR), and stratum lacunosum-moleculare (SLM). Any dendritic segments having diameters of 5 μ or larger were treated as part of the soma. Synapses were then located along dendrites in SO, SR, and SLM by dividing dendritic sections into equal-sized segments of at most 10 μ each.

Fig. 1.

Model cell morphologies. Cells have been reoriented so that apical-basal direction is along the y-axis with layer boundaries as indicated. From top (most apical) to bottom (most basal), layers shown are stratum lacunosum-moleculare (SLM), stratum radiatum (SR), stratum lucidum and stratum pyramidale (SL+SP) together, and stratum oriens (SO). Axon segments are not shown. Cell l56a is shown at a larger size to facilitate illustration of an example time course for a synaptic receptor conductance (g_syn) and somatic EPSC along with extracted properties peak value (PV), time-to-peak (TTP), and half-height width (HHW)

For each individual synaptic location in a model cell, the appropriate clamp conditions were applied at the soma and a two second interval was simulated to allow membrane potentials to reach equilibrium, in line with experimental protocols. A synaptic response was then triggered and either voltage or current changes, as appropriate, were recorded at the soma. Response peak value (PV), time-to-peak (TTP), half-height width (HHW), local rest potential at the site of the synapse, and peak local dendritic depolarization at the site of the synapse were then extracted and written to an external file for post-simulation analysis (see Fig. 1). Selected examples of synaptic responses, current or voltage values, as appropriate, were separately saved to a file for subsequent plotting Figs. 2, 3.

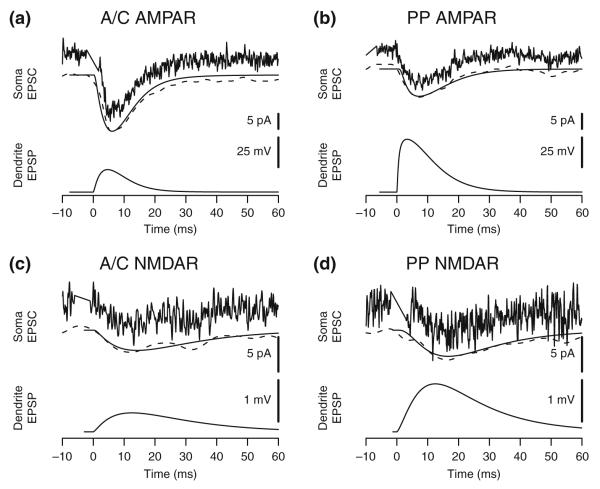
Fig. 2.

Typical response traces from model and experimental results. (a) AMPA receptor responses from A/C stimulations (experiment) and SR synapses (model). (b) AMPA receptor responses from PP stimulations (experiment) and SLM synapses (model). (c) NMDA receptor responses from A/C stimulations (experiment) and SR synapses (model). (d) NMDA receptor responses from PP stimulations (experiment) and SLM synapses (model). Typical experimental traces (noisy line above) from individual data sweeps are shown with smoothed data (dotted line below) from the same sweep overlaid with a comparable model response (solid line below) for comparison. Local dendritic EPSP at the site of the synapse is from the model. Time is relative to onset of synaptic activation. Stimulation artifacts have been removed from the experimental data

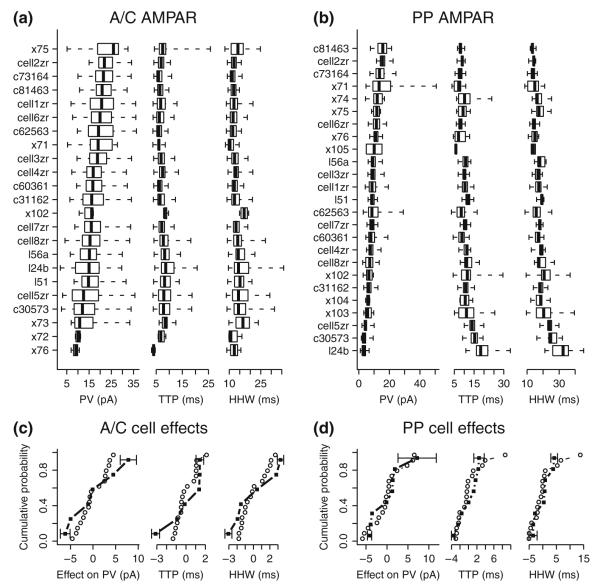
Fig. 3.

Distribution of model and experimental cell AMPA receptor responses. (a) Box-and-whiskers plots of A/C AMPA receptor synaptic responses from each simulated cell and each experimental cell showing PV, TTP, and HHW distributions. Cell names beginning with “x” indicate experimental cells. Whiskers indicate the range of response values, and boxes the second and third quartiles with the median indicated as a solid vertical line. Cells are ordered by PV median within each category of responses. (b) Box-and-whiskers plots of PP AMPA receptor synaptic responses, as above. (c) Cumulative distribution of cell effects on mean A/C AMPAR PV, TTP, and HHW for model cells (circles) and experimental cells (squares). Standard errors of the mean are shown as error bars for experimental cells with the minimum and maximum effects. For purposes of this analysis, each cell received equal weighting irrespective of the total number of unitary responses for the cell. Kolmogorov-Smirnov tests comparing model and experimental effects distributions do not show significant differences for PV, TTP, or HHW (p-values .58, .25, and .41, respectively). (d) Cumulative distribution of cell effects for PP AMPAR, as above. Distributions are not significantly different (p-values .78, .49, and .49, respectively)

AMPA receptor (AMPAR) synapse activation was modeled as point processes using the dual-exponential formulation implemented in the Exp2Syn object available in Neuron. Briefly, the dual-exponential models synaptic activation as a change in synaptic conductance with a time course given by:

$$g_{\mathit{syn}}\left(t\right)=g_{\max }\cdot a\left[\exp \right(-t∕{\tau }_2)-\exp (-t∕{\tau }_1\left)\right]$$ (1)

where g_syn(t) is the synaptic conductance at time t after the activation, a is chosen so that the maximum value of g_syn matches the maximum synaptic conductance parameter g_max, τ₁ is the rising time constant, and τ₂ is the falling time constant. Note that g_max is the combined conductance for all receptors of a given type in a synapse and should not be confused with the conductance of individual receptors. The Exp2Syn object automatically computes the appropriate value of a using the values of τ₁ and τ₂ available at model initialization (see Dayan and Abbott 2001, p. 182). When τ₁ and τ₂ are equal, g_syn(t) is an α-function, which Exp2Syn approximates by reducing the value of τ₁ by 0.01%. No consideration was given to possible effects of internal spine resistance on the responses of synapses, but prior estimates of such resistance (Svoboda et al. 1996; Palmer and Stuart 2009) suggest that the effect on synaptic responses would be minimal in the current model.

NMDA receptor (NMDAR) conductance is dependent on the local membrane potential and external Mg²⁺ concentration (Jahr and Stevens 1990). For these receptors, the standard Exp2Syn object was extended to take this dependency into account by using the following equation:

$$g_{\mathit{syn}}\left(t\right)=g_{\max }\cdot \frac{a\left[\exp \right(-t∕{\tau }_2)-\exp (-t∕{\tau }_1\left)\right]}{1+\frac{\mathit{Mg}}{3.57}\exp [-0.062V_m(t\left)\right]}$$ (2)

where Mg is the external Mg²⁺ concentration in mM, V_m(t) is the local membrane potential in mV, and other variables and parameters are as in eq. (1).

For simulations of experiments where AMPA receptors were blocked, external Mg²⁺ was set to 50 μM, consistent with the experimental protocol (Perez-Rosello et al. 2010), whereas when AMPA receptors were not blocked and both types of receptors contribute to the response, external Mg²⁺ was set to 1 mM, a value more typical of normal physiological conditions.

Model cell membrane resistivity (R_m) and capacitivity (C_m) were taken from CA3b pyramidal cell experimental results (Hemond et al. 2009). Without correction for spine membrane area, mean values from those earlier fittings were R_m=31,498 Ωcm² and C_m=1.44 μF cm⁻². In the current model, a spine membrane correction factor of two was used for layers SR and SO, resulting in a halving of membrane resistivity and a doubling of membrane capacitivity. Consequently, intrinsic R_m and C_m values were, in turn, doubled and halved to agree with the values from Hemond et al. (2009) giving values for the current model as R_m=62,996 Ωcm² and C_m=0.72 μF cm⁻². Spines densities are thought to be less in SLM (Ishizuka et al. 1995; Megías et al. 2001; Matsuda et al. 2004) and no spine correction was used in this layer. An upper bound for axial resistivity (R_a) was established based on the responses of fast AMPA receptor synapses located in SLM, as described below. The mean value of R_a=517 Ωcm from Hemond et al. (2009) was not used in the current model. A single set of passive cell parameter values was used for all simulated responses except as noted. Table 1 summarizes overall model parameters that were set prior to the fitting procedure.

Table 1.

Model parameters from prior data and experimental protocols

Model parameter	Value
Cell resting potential	−61 mV
VC soma holding potential	−80 mV
CC soma holding potential	−60 mV
Clamp settling interval	2 s
Membrane capacitivity (Cm)	0.72 μF cm−2
Membrane resistivity (Rm)	63 kΩ cm2
SR spine adjustment factor	2.0
SLM spine adjustment factor	1.0
Synapse sample rate (nominal)	1 per 10 μm
SLM-SR boundary location	Varies by cell
External Mg2+ (NMDAR responses)	50 μM
External Mg2+ (combined responses)	1 mM

2.3 Model fitting

Model parameters were fitted manually and are listed in Table 2. The objective of the fitting procedure was agreement with summary statistics of the experimental data such that, at a minimum, there are no statistically significant differences between model and experimental results. Experimentally measured mean values of PV, TTP, and HHW were sufficient to constrain the three free parameters defining synaptic responses: g_max, τ₁, and τ₂. Fitted model parameters are accurate to at most two significant digits, consistent with the perceived accuracy of experimental results used to constrain the model. Synapses in SO were modeled with the same parameters derived for SR, but were not used in the fitting procedures.

Table 2.

Model parameters constrained by current experimental results

Model parameter	Value
Axial resistivity (Ra)	140 Ωcm
SR AMPAR time constant (τ1=τ2)	3.3 ms
SR AMPAR peak conductance (gmax)	0.5 nS
SLM AMPAR rising time constant (τ1)	0.4 ms
SLM AMPAR falling time constant (τ2)	4.1 ms
SLM AMPAR peak conductance (gmax)	0.9 nS
NMDAR rising time constant (τ1)	5 ms
NMDAR falling time constant (τ2)	16 ms
SR NMDAR peak conductance (gmax)	0.16 nS
SLM NMDAR peak conductance (gmax)	0.18 nS

Model fitting was facilitated by several simple rules-of-thumb that apply to model voltage clamp (VC) responses. Within a given layer, changes in overall mean peak response values are approximately proportional to the common synapse g_max value. Similarly, a change in the time of peak synaptic conductance results in approximately the same change in mean response TTP. A change in the synaptic conductance area-under-curve integral results in approximately the same proportional change in mean response HHW. Use of these empirical rules significantly reduced the computational resources required for the fitting process.

Unless otherwise stated, model fitting was performed using data from the experimental characterizations at near physiological temperatures of synaptic responses in CA3b pyramidal cells where voltage-gated channels were blocked, as described in the companion paper (Perez-Rosello et al. 2010). Because experimental cell morphological reconstructions were not available, matching individual experimental data traces with model responses was not a factor in the fitting procedure.

In cases where additional variability is added to model responses (see Figs. 4, 5, and 6), zero-mean normally distributed random values were arithmetically added to model response TTP or HHW values, as appropriate. When negative values resulted for either TTP or HHW, the corresponding simulated synaptic response was removed from the sample. Depending on the circumstances, as described in the section 3, different methods were used to create randomly perturbed PVs. In the first case, a random value with normal distribution N(0,σ²) , that is, having a mean of zero and a variance of σ², was added to the PV giving a new perturbed PV. In the second case, a random value with distribution N(–δ ²/2, δ ²) was added to ln(PV) and the perturbed value of PV was found through exponentiation. This is equivalent to multiplying the original PV by a log normal random variable with an expected value of one, leaving the mean, but not the median or mode, of these values unchanged. In the third case, g_max values associated with individual synapses were multiplied by a log normal random variable with an expected value of one in much the same manner described above. Simulations of the resulting synaptic responses then yielded the perturbed PV. In all cases, perturbed PVs with values less than the minimum detectable experimental level (2 pA) were removed from the sample.

Fig. 4.

Fitting model and experimental response distributions. (a) Histogram of experimental A/C AMPA receptor response properties PV, TTP, and HHW overlaid with the corresponding distribution of model responses both with no additional variability (dotted lines) and with added variability to fit experimental response property distributions (solid lines). See section 2 for details of the fitting procedure. 0.5% of perturbed responses were eliminated based on limits on perturbed PV, TTP, or HHW. (b–d) Respectively, histograms and densities for PP AMPA, A/C NMDA, and PP NMDA receptor responses as above. Respectively, 2.7%, 8.5%, and 19.4% of the perturbed responses were eliminated from the sample. σ provides the standard distribution of a normally distributed variation and δ is the standard deviation of variability added to ln(PV). p-values are from a Kolmogorov-Smirnov test comparing experimental and model distributions. p₋ compares model and experiment without additional variability and p₊ compares model plus additional variability with experimental results. In panels (a) and (b), an experimental sweep was removed as an outlier prior to fitting and plotting

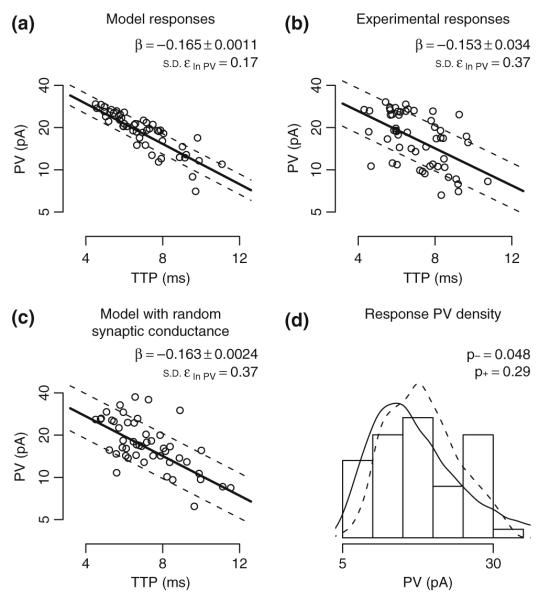
Fig. 5.

Effects of implied synaptic location on A/C AMPA receptor EPSC. Linear regression is used to fit ln(PV) as a function of TTP for A/C AMPAR responses. Fit coefficient β values are shown as mean ± SE. Deviation from the fit is summarized as the standard deviation of the residual (ε _{ln PV}). (a) Ideal model synaptic responses show an almost linear relationship between TTP and ln(PV). Prior to fitting, responses with TTP values outside the range of trimmed experimental values were removed, reducing the response sample size by 9%. (b) Experimental responses with the measurement error model fit. Responses in the top and bottom 4% of the distribution of TTP and PV were removed from the sample as outliers, reducing the sample of responses by 16%. (c) Simulated responses where peak synaptic conductance was multiplied by a unit mean log normal random variable with δ=0.4 (see section 2). Responses with TTP values outside the range of trimmed experimental values were removed, reducing the response sample size by 10%. The resulting random AMPAR conductance has a coefficient of variation of 40.6%. (d) Histogram of trimmed experimental PVs overlaid with PV densities from trimmed model responses corresponding to panels (a) (dotted lines) and (c) (solid line). A Kolmogorov-Smirnov test was used to compare experimental responses with model responses where p₋ is the p-value for the unperturbed model responses (panel A) and p₊ is for the model using a random synaptic conductance (panel c). For panels (a-c), the PV-axis is shown in log scale. Dotted lines indicate the regression fit ± 1 standard deviation of the ln(PV) residual. For panels (a) and (c), 50 representative points were plotted to illustrate distributions

Fig. 6.

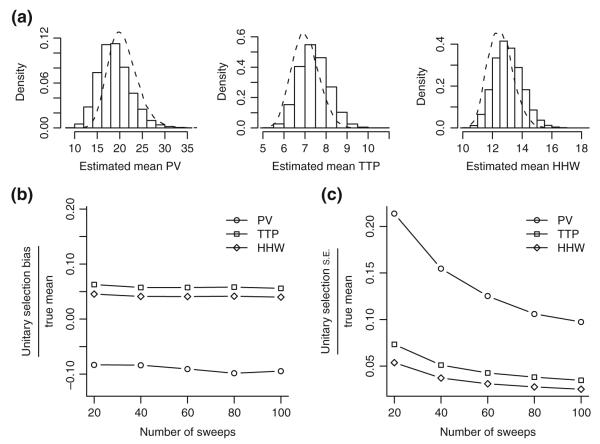
Post-hoc analysis of unitary selection methods. Effects of unitary selection are estimated using a probability model of failures and multiple responses. Responses were drawn from cell1zr model results with randomized synaptic conductance (Fig. 5(c)). Monte Carlo trials (N=10,000) were used to obtain the distribution of estimated mean unitary response properties (see section 2). (a) Density histograms of means estimated using the unitary selection method for PV, TTP, and HHW assuming 50 sweeps in the experiment and an observable failure rate of 30%. The density of ideal means that would have resulted if there were no errors in unitary selection is shown as dashed lines. (b) Bias in the unitary mean estimator as compared with the ideal mean estimator, i.e. the mean difference between the two, divided by the true cell mean for different numbers of sweeps in the experiment. True cell1zr means are 20.9 pA, 7.0 ms, and 12.5 ms for PV, TTP, and HHW, respectively. (c) Standard error of the unitary selection estimator as compared with the ideal estimator, i.e. the standard deviation of the difference between the two, divided by the true cell mean for different numbers of sweeps in the experiment

Active cell models were created using the same passive membrane properties and cell morphologies as for the passive model. For simulations containing only delayed rectifier (K_DR) and A-type potassium channels (K_A), ion channel models were adapted from an earlier CA1 pyramidal cell model (Migliore et al. 1999). Otherwise, ion channel models were adapted from a prior CA3b pyramidal cell model (Hemond et al. 2008) and placed in the various cell morphologies utilized for the passive model. In the model containing only delayed rectifier (K_DR) and A-type (K_A) potassium channels, non-uniform conductivity of K_A was modeled as:

$$g_{\max }\left(x\right)=g_{\mathit{soma}}\left(1+\frac{5.2}{350}x\right)$$ (3)

where x is the distance from the soma in μm, g_max(x) is the K_A conductivity at the given distance, g_soma is the K_A conductivity at the soma, and the fraction 5.2/350 indicates that distance-dependent conductance is increased by a factor of 5.2 at a distance of 350 μm. The proximal form of the K_A model was used at all locations. In a subset of the simulations, spines were modeled using two compartments, one for the head and one for the neck. The spine head was 0.9 μm² in area. For the spine associated with the activated synapse, passive membrane properties in the spine head were adjusted to reflect an unspecified K⁺ conductance that was tonically active during the synaptic response (E_K=−90 mV). The spine neck was modeled as a cylinder 1 μm in length and 0.06 μm in diameter giving a spine resistance of 500 MΩ, at the upper limit of experimental findings (Palmer and Stuart 2009).

2.4 Statistical methods

2.4.1 Analysis of model responses

Model synaptic responses are sampled from dendritic segments that are up to 10 μm in length. Within each dendritic section between branch points, a uniform segment size was used resulting in some variability of the dendrite length associated with individual synapses. For purposes of the model, synapses were assumed to be uniformly distributed along the length of the dendrites. To adjust for differences in sampling lengths, mean and standard deviation of response properties for a synaptic region (SR, SO, or SLM) within model cell i were determined by:

$$\begin{array}{cc}\hfill {\mu }_i& =\sum _j{x}_{\mathit{ij}}{y}_{\mathit{ij}}/\sum _j{x}_{\mathit{ij}}\hfill \\ \hfill {\sigma }_i^2& =\sum _j{x}_{\mathit{ij}}{(y_{\mathit{ij}}-{\mu }_i)}^2/\sum _j{x}_{\mathit{ij}}\hfill \end{array}$$ (4)

where μ_i is the mean response property value for the given region for cell i, σ_i is the standard deviation of the response property for cell i, y_ij is the response property (PV, TTP, or HHW) for synapse j in cell i, and x_ij is the length of the dendritic segment in the associated region. Because of the large number of synapses simulated per cell, sampling effects within each cell were negligible. The mean and standard error for all 17 cells was estimated by treating the individual cell statistics as those of a sample of cells drawn at random, that is:

$$\widehat{\mu }=\frac{1}{17}\sum _{i=1}^{17}{\mu }_i,\mathrm{var}\left(\widehat{\mu }\right)=\frac{\sum _{i=1}^{17}{({\mu }_i-\widehat{\mu })}^2}{16\cdot 17}$$ (5)

where $\widehat{\mu }$ is the estimated sample mean.

2.4.2 Further re-analysis of experimental results

A random effects one-way classification model (Miller 1998) was used to estimate the mean and standard error of experimental results described in the companion paper (Perez-Rosello et al. 2010). Briefly, the one-way classification model describes I cells, each with n_i measurements. The model has the form:

$$y_{\mathit{ij}}=\mu +a_i+e_{\mathit{ij}},i=1,\dots ,I,j=1,\dots ,n_i$$ (6)

where y_ij is the result j for cell i, a_i is the effect of cell i, and e_ij is the within-cell variability associated with y_ij. Random variables were assumed to be distributed with a_i independent N(0,σ_a²), e_ij independent N(0,σ_e²), and {a_i} independent of {e_ij}. Because the experimental designs are unbalanced, there are alternative consistent estimators of the population mean and standard error. The estimators used here were weighted by the n_i, as in:

$$\begin{array}{cc}\hfill \overline{y}..=\frac{1}{N}& \sum _{i=1}^I{n}_i{\overline{y}}_{j\cdot },\mathrm{var}(\overline{y}..)=\frac{1}{N^2}\sum _{i=1}^I{n}_i^2\left({\sigma }_e^2∕n_i+{\sigma }_a^2\right)\hfill \\ \hfill \text{where}& N=\sum _{i=1}^I{n}_i,{\overline{y}}_{i\cdot }=\frac{1}{n_i}\sum _{j=1}^{n_i}{y}_{\mathit{ij}}\hfill \end{array}$$ (7)

Estimates for σ_a and σ_e were found using the method of moments (Miller 1998) as:

$$\begin{array}{cc}\hfill & \mathit{MS}\left(E\right)=\frac{1}{N-1}\sum _{i=1}^I\sum _{j=1}^{n_i}{\left(y_{\mathit{ij}}-{\overline{y}}_i.\right)}^2,\mathit{MS}\left(A\right)=\frac{1}{I-1}\sum _{i=1}^I{n}_i{({\overline{y}}_{i.}-y..)}^2,\hfill \\ \hfill & {\widehat{\sigma }}_e^2=\mathit{MS}\left(E\right),{\widehat{\sigma }}_a^2=\frac{N(N-1)\cdot \left[\mathit{MS}\right(A)-\mathit{MA}(E\left)\right]}{N^2-\sum _{i=1}^I{n}_i^2}\hfill \end{array}$$ (8)

When the n_i are all equal, this reduces to the usual ANOVA formulas for balanced designs.

2.4.3 Testing for distance-dependent synaptic scaling

To test for systematic increases in synaptic conductance, TTP is used here as a proxy variable for distance of a synapse from the soma. For responses, both from the model and separately from passive-cell experiments, the relation between individual PV and TTP values was fit to the linear regression model:

$$\ln \left(\mathit{PV}\right)=\alpha +\beta \cdot \mathit{TTP}+{\epsilon }_{\ln \mathit{PV}}$$ (9)

where α and β are the usual linear regression coefficients and ε_{ln PV} is the residual term. To minimize the standard error of β, experimental responses were trimmed by removing responses with either TTP or PV in the top or bottom 4% of corresponding experimental values. When analyzing model results, only responses with TTP values within the limits for experimental responses were used. Model responses with PV below the experimentally detectable level of 2 pA were excluded from the analysis. Mean and standard error (SE) for β were estimated in the usual way as was the standard deviation (SD) of the residual ε_{ln PV} (Miller 1998). PV and TTP have units of pA and ms, respectively. Note that in this case, β has units of ms⁻¹ and ε_{ln PV} is non-dimensional.

2.4.4 Fitting of response distributions

Distributions of model and experimental response values were compared using the two-sample Kolmogorov-Smirnov (KS) test implemented in R. Because of discrete time step sizes used in the model, tie values are possible and in such cases the p-values are approximate. In addition to testing the unperturbed model results, variability was also added to model results prior to comparison with the experimental outcomes to better match the experimental distributions. Model results were replicated 100 times with different draws of random numbers used for generating the additional variability in individual responses. Perturbed model results were then tested for valid properties, that is, PV must be larger than the minimum detectable level (2 pA) and both TTP and HHW must be positive. Synaptic responses not meeting these conditions were discarded prior to applying the KS test. In fitting additional variability for the model, a manual search was used to find the additional variability yielding the largest p-value from the KS test.

2.4.5 Post-hoc validation of unitary selection methods

Model responses were used in a post-hoc validation of the unitary selection method used in the companion paper (Perez-Rosello et al. 2010) to analyze experimental data. An experiment simulated in the post hoc analysis potentially stimulated 20 AMPA receptor synapses in layer SR of cell1zr, each activated with equal probability. The ideal observable failure rate of the stimulations was fixed at 30% (typical of experiments in the companion paper) implying an individual failure rate of 94% for each synapse. Unitary response selection was simulated by probabilistically selecting sets of 20 synapses, and for each such set, responses from a series of stimulations. For responses where multiple synapses were activated, a combined response was formed by summing the PVs of responses from all activated synapses. TTP and HHW values for the combined response were the average of the corresponding values of activated synapses weighted by the individual PVs. Responses for individual synapses were the result of simulating the effect of a log normal random synaptic conductance as shown in Fig. 5(c) except that responses with PVs below 2 pA were not removed.

For each simulated experiment, the unitary selection method was then applied to the resulting stimulation responses, which consisted of a combination of failures, unitary synaptic responses, and multi-synaptic responses. A failure rate was estimated from the fraction of failure responses found in the simulated experiment, and from this, a Poisson probability model was applied to estimate the expected number of unitary responses. This number was used to select responses with the lowest PVs as unitary responses. Mean values of PV, TTP, and HHW for the selected unitary responses, if any, were then taken as the results of the experiment. For comparison with the ideal case, a separate set of mean values for PV, TTP, and HHW was computed from the responses that were truly unitary. The procedure of selecting the set of potentially activated synapses through unitary selection and summarization was repeated 10,000 times. The resulting empirical distribution of estimated mean values was compared with the distribution of ideal means to measure bias and standard error associated with the unitary selection process itself. Monte Carlo sampling errors were estimated as less than 3% for the mean values and less than 1% for the standard error values shown here.

3 Results

3.1 Biophysical properties of excitatory synapses in CA3b pyramidal cells

Synaptic parameters for SR and SLM were fit based on the experimental recordings of somatic responses to A/C and PP stimulation, respectively, in passive voltage clamp conditions from the companion study (Perez-Rosello et al. 2010). Values from prior AMPA receptor characterizations in CA3 pyramidal cells were used as a starting point in searching for best-fit model parameter values. Prior characterizations can be described as α-functions (Williams and Johnston 1991) and as fits with a rapid rise time and one or more decay time constants (Colquhoun et al. 1992; Jonas and Sakmann 1992; Jonas et al. 1993; Spruston et al. 1995). No common set of AMPA receptor parameters was found that provided acceptable fits to both A/C and PP experimental responses. A/C responses were well fit with an α-function (τ=3.3 ms) similar to that previously found by Williams and Johnston (1991), whereas fitting of PP responses required a rapidly rising response (τ₁=0.4 ms, τ₂=4.1 ms) to be consistent with experimental TTP values (Table 3). While AMPAR mediated A/C and PP synapse properties may appear quite different, the faster kinetics of the PP response are to some degree compensated for in a larger peak conductance resulting in similar charge transfer for A/C and PP unitary responses. The total integral of synaptic conductance is a metric proportional to charge transfer when postsynaptic membrane potentials are held fixed. For an AMPAR mediated unitary synaptic response these values are 4.5 nS ms for A/C synapses and 4.8 nS ms for PP synapses. Even with rapidly rising AMPA receptors, experimental constraints for PP AMPA receptor TTP values imposed an axial resistivity (R_a) value no larger than 140 Ω cm in the model, as described in more detail below. Multiple decay time constants were not resolvable within the limits of the experimental results and, in any case, were not consistent with the formulation of model synaptic responses assumed here. Experimental peak unitary AMPA receptor EPSCs were well fit with g_max values of 0.5 and 0.9 nS for A/C and PP AMPA receptor synaptic responses, respectively. An AMPA receptor reversal potential of 0 mV was used throughout.

Table 3.

Mean response properties in passive voltage clamp

Response type	I (cells)	N (sweeps)	Mean PV (pA) (mean ± SE)	Mean TTP (ms) (mean ± SE)	Mean HHW (ms) (mean ± SE)
AMPA receptor mediated responses
Associational/Commissural
Model	17	8334	17.92±0.70	7.51±0.25	13.62±0.37
Experiment	6	64	17.98±2.45	7.51±0.68	13.62±1.29
Perforant Path
Model	17	3984	9.12±0.87	10.97±0.73	18.58±1.17
Experiment	8	112	9.01±1.76	10.48±0.83	19.11±1.31
NMDA receptor mediated responses
Associational/Commissural
Model	17	8334	3.56±0.09	14.89±0.41	28.43±0.57
Experiment	6	93	3.48±0.66	16.02±2.21	28.60±2.64
Perforant Path
Model	17	3984	3.36±0.18	22.39±1.05	33.77±1.36
Experiment	4	76	3.46±0.20	21.76±3.20	37.72±6.32

NMDA receptors have multiple isoforms and subtypes with different kinetic properties (Vicini et al. 1998; Cull-Candy et al. 2001; Erreger et al. 2005). Models of NMDA receptors commonly use decay time constants in the 100–200 ms range (Destexhe et al. 1998) but typically do not take into account either temperature or developmental effects. In CA3 pyramidal cells, NMDA receptors have faster responses in older animals (Khazipov et al. 1995) and are much faster at physiological temperatures when compared with those at room temperatures (Chen et al. 2001; Cais et al. 2008). Relatively fast kinetics of NMDA receptor-mediated synaptic currents were found in several studies (Geiger et al. 1997; Feldmeyer et al. 2002; Diamond 2001).

Time constants for the NMDA receptor model were found by a search of plausible parameter settings to achieve an acceptable fit, that is, NMDA receptor model responses within the error tolerances of our experimental data. The resulting values (τ₁=5 ms, τ₂=16 ms) are similar to expected properties of NR2A receptors estimated based on results from dentate gyrus granule cells of mature rats measured at 34° (Dalby and Mody 2003) and in HEK transfections of receptors containing NR1 and NR2A subunits (Vicini et al. 1998). A single receptor model was sufficient for fitting mean NMDA receptor responses. Although more precise fits may be possible assuming PP and A/C NMDA receptors have different kinetic properties, detail in experimental data from the passive cell preparations was insufficient to justify and constrain a more complex model than the one presented here. Experimental peak unitary NMDA receptor EPSCs with low external Mg²⁺ were well fit by g_max values of 0.16 and 0.18 nS for A/C and PP NMDA receptor responses, respectively. An NMDA receptor reversal potential of 0 mV was used throughout.

Best-fit model parameters are summarized in Table 2. The fitting of axial resistivity is described below as part of the analysis of model parameter sensitivity.

3.2 Comparison of model and experimental results

One common criterion for comparing model and experimental results is that the model be able to reproduce experimental measurements, especially, in this case, voltage or current traces over time. Because the synaptic response model was calibrated based on mean response values over multiple experimental cells, individual data traces, as such, played only a minor and indirect role in model fitting. Thus, testing whether the model can reproduce typical experimental traces for each of the categories of simulated synaptic responses demonstrates a degree of plausibility beyond matching only mean response values. Figure 2 provides examples of typical experimental recordings with corresponding simulation responses that show similar response properties, that is, PV, TTP, and HHW. A correspondence between the smoothed experimental trace and the model can be used to qualitatively ascertain the degree of fit.

Mean response properties from the model and from experimental results can be interpreted as estimates of the expected values found in a response from a randomly selected synapse from a randomly selected CA3b pyramidal cell. Table 3 contains the estimated means for different types of synaptic responses comparing results from the model and from passive voltage clamp experiments. In all cases, the difference between model and experiment are well below the variability associated with the experimental estimates of the means.

3.3 Variability of synaptic responses

Cell morphology is a well-known contributor to variability in synaptic responses, even in the case of an ideal passive cell and uniform synaptic properties (Henze et al. 1996; Jaffe and Carnevale 1999). As shown in Fig. 3, AMPA receptor responses for both model and experimental cells are highly variable not only within cells but also across cells. There are general correlations between increasing median PV and decreasing median TTP and HHW for synapses in both SR and SLM. In addition, the variability of responses within the cell is correlated with the median PV so that cells with lowest median PV tend to have greater variability of responses. A similar pattern is also found in NMDA receptor responses (not shown).

A comparison of the relative rankings of model cells in Fig. 3 with their morphologies in Fig. 1 suggests a complex interrelation among the dendritic branching pattern found in the relevant morphological layer and the magnitude and variability of the mean response properties found in the electrophysiological simulations. One way to quantify the effect of cell morphology, at least for passive cells, is the effect of individual cell morphologies on the mean PV, TTP, and HHW associated with synaptic responses. Cell effects are estimated by the a_i terms of the one-way classification model (Eq. 6). Model cell morphologies are intended to be representative of the population of experimental cells used in fitting the model. A test of that proposition is a comparison of the overall distribution of cell effects from experimental cells with corresponding effects from model cells, as shown in Fig. 3 panels (c) and (d). No statistically significant differences were found between the experimental cell population and the model cell population, suggesting that the model cell morphologies are representative of the experimental cells, at least with regard to mean synaptic response properties.

The distribution of response properties in model cells can be further compared in terms of the empirical distributions of comparable properties found in model and experimental results. Overall, the variance of the experimental measures appears to be greater than that of the simulation results. This “excess” experimental variability can be quantified, even without explicitly simulating its sources, by introducing additional variability into model responses with the objective of matching the experimental and adjusted model distributions. Such best-match variability added to already existing model results is shown in Fig. 4. In the case of PV, variability was added either to the logarithm transformed PV (δ values in the figure) or directly to the untransformed value (σ values), with the best-fit case being shown. Differences between the distributions of adjusted model response properties and experimental properties were not statistically significant. The fit for PP NMDA receptor mean TTP may not reflect all sources of variability in the experimental data, but there is overall agreement in the empirical densities except possibly for outlier values in the tails of the experimental response distribution. In Fig. 4(d), the asymmetry seen in the fitted PV distribution suggests that some unitary PP NMDA receptor responses may have been too small to detect experimentally.

Two conceptually distinct components can contribute to the observed variability of somatic response to synaptic stimulation in excess of that resulting from morphological differences among cells and from synapse location within cells. The first is the intrinsic diversity of local synaptic properties. In particular, the peak conductance for a given receptor type (e.g. AMPA) might change from synapse to synapse independent of location within a dendritic layer (e.g. SR). The second component is ‘measurement noise’, which consists of all other contributions that cannot be explicitly accounted for in the model. An upper limit for the intrinsic diversity of local peak conductance can be computed under the assumption of zero ‘measurement noise’. This approach however requires accounting for the correlation between synaptic location and somatic peak value. Even though synapse location cannot be determined experimentally, response kinetics have previously been used to infer relative synaptic locations in passive cells (Rall et al. 1967; Iansek and Redman 1973). Specifically, the relationship between synapse location and TTP in a passive cell allows TTP to be used as a statistical proxy for location. The relationship between TTP and ln(PV) in the passive model for AMPA receptor synaptic responses originating in SR is approximately linear (Fig. 5(a)). Linear regression can be used to quantify additional variability in measured ln(PV) over that predicted by the passive model (Fig. 5(b)) as well as to test for distance-dependent synaptic scaling. A difference between the β value from passive model responses and the β value from experimental responses would have been indicative of the presence of a distance-dependent effect on synaptic conductance, but no significant difference was seen (Fig. 5(a) and (b)). As a more explicit test, model synaptic conductance values were allowed to randomly vary independent of location. Random synaptic conductance values were drawn from a log normal distribution with a ln(PV) standard deviation of 0.4, resulting in simulated g_max with a mean of 0.5 nS and a coefficient of variation of 40.6%. The β value from fitting these randomized model responses was statistically consistent with values from both the original model and the experimental responses (Fig. 5(c)), and the residual variability, as measured by the standard deviation of ln(PV), was the same for randomized model responses and for experimental responses (Fig. 5(c)). As shown above, adding additional variability to model responses can result in overall PV distributions that are not significantly different between model and experiment (Fig. 5(d)). The additional synaptic variability in the model necessary to match the experimental data dispersion suggests that the spread of somatic responses caused by the distribution of synaptic locations is not compensated by a distance-dependent increase in synaptic conductance, as in CA1 pyramidal cells (Andrásfalvy and Magee 2001), but rather is further increased by additional local diversity of receptor conductance.

3.4 Post-hoc analysis of the unitary sweep selection method

A potential source of error in the analysis of experimental responses is the procedure used to discriminate unitary responses from those caused by activating multiple synapses. In the process of analyzing experimental data recordings, responses that are truly unitary might be misclassified as originating from multiple synapses, or conversely, responses from multiple simultaneous synaptic activations might be classified as unitary. To evaluate the frequency and impact of such occurrences, we simulated probabilistic synaptic activation, applied the unitary selection method to the generated results, and compared the outcome with the known unitary response properties of the model. Because of the large number of Monte Carlo trials needed to estimate the distributions of estimated mean response properties, simplifying approximations are needed to reduce computational resource requirements. The outcomes should thus be considered as indicative only, and, in particular, the effects of multiple synaptic activations on TTP and HHW are approximate.

Our model simulated a hypothetical experiment measuring A/C AMPA receptor responses consisting of 50 consecutive sweeps with an intrinsic failure rate of 30%, in line with the average number of sweeps and failure rate for individual sets of experimental sweeps (Fig. 6(a)). Under ideal conditions, where only unitary sweeps were selected for analysis, mean values for this experiment were 20.7±3.2 pA, 7.0±0.6 ms, and 12.5±0.8 ms for PV, TTP, and HHW, respectively. When means were estimated using sweeps selected by the unitary selection method, values were 18.8±3.5 pA, 7.4±0.7 ms, and 13.1±0.9 ms, respectively. For the unitary selection method compared with the ideal case, there were a mean biases of −1.9 pA, 0.4 ms, and 0.5 ms, respectively, and standard errors of 2.7 pA, 0.3 ms, and 0.4 ms, respectively. Across all 526 simulated synapses, mean values were 20.7 (SD=10.2) pA, 7.0 (SD=2.0) ms, and 12.5 (SD=2.6) ms, respectively. Thus the unitary selection procedure itself can be a potential source of both additional variability and bias in experimental results.

The inherent bias, i.e. difference between estimated and ideal means, is relatively insensitive to the number of sweeps analyzed in the experiment (Fig. 6(b)). Bias for PV is especially sensitive to diversity in synaptic conductance values. In simulations where model AMPA receptor conductance does not vary, as shown in Fig. 5(a), the resulting bias for the unitary selection method was reduced to −0.5 pA or −2% of the actual mean PV for experiments with 50 sweeps. The relative standard error of the mean estimator associated with unitary selection is substantially greater for PV than for TTP and HHW (Fig. 6(c)). In particular, for experiments with 20 or fewer total sweeps, which in this instance would have only seven or fewer expected unitary sweeps, variability in the mean PV estimator induced by the unitary selection method could provide a significant contribution to variability of experimentally estimated means. Under the assumptions of the post hoc model, residual variability from unitary selection for even 100 total sweeps suggests a limiting accuracy that cannot be easily overcome when using the current unitary selection method. Across all categories of measurement described in the companion paper (Perez-Rosello et al. 2010), the mean number of non-rejected sweeps in a single experiment was 54 (median 34) and mean failure rate was 34% (median 32%). For the passive-cell experiments used in fitting the synaptic response model, the mean was 49 sweeps (median 31.5) with a mean failure rate of 28% (median 22%).

3.5 Model sensitivity

To test model robustness we explored the sensitivity of model results to parameter value choices and to underlying assumptions incorporated into the model. In particular, justifications for the choices of a relatively low axial resistivity and of pathway specific differences in AMPA receptor kinetics are examined here in further detail.

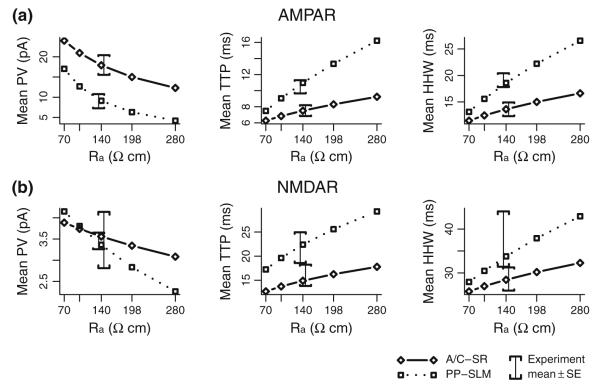
Experimental estimates of CA3 pyramidal cell axial resistivity (R_a) from somatic current injection have yielded values over relatively wide ranges, from 160 to 390 Ωcm (Major et al. 1994) and from 170 to 1,115 Ωcm (Hemond et al. 2009). For measures of synaptic responses, especially for distal dendritic locations and somatic voltage clamp, R_a is a more sensitive model parameter than it would be for fitting somatic current injection experiments. Measurements in CA1 pyramidal cells using simultaneous patch-electrode recordings from the soma and apical dendrite suggested R_a values in the range of 198–261 Ωcm if uniform membrane resistivity was assumed and 139–218 Ωcm if not (Golding et al. 2005). An experimental constraint for the present model is that PP AMPA receptor synapses have an experimentally estimated mean TTP of 10.5 ms, a value that limits R_a for even the fastest plausible AMPA receptors located in SLM. In addition, for synapses in SLM, receptor reversal potentials, when combined with a large value of R_a, would constrain the maximum possible peak response regardless of the synaptic conductance. For experimentally constrained values of R_m and C_m, an R_a value of 140 Ωcm was the largest that permitted fitting a passive model to experimental unitary AMPA receptor PP responses (Fig. 7). Within the limits of the precision of the experimental data, this value also permitted fitting of NMDA receptor PP responses as well as A/C responses for both receptor types. The current model does not include synaptic responses originating in the SL region near the soma nor does it consider any non-uniformity of axial resistivity in this region.

Fig. 7.

Sensitivity of model results to axial resistivity. (a) Model mean PV, TTP, and HHW for AMPA receptor synaptic responses are shown for axial resistivity values of 70, 99, 140, 198, and 280 Ωcm and for synapses located in SR (solid lines) and SLM (dotted lines). Comparable experimental means ± SE are shown as error brackets with PP offset to the left from A/C to reduce over plotting. (b) Model and experimental results for NMDA receptor synaptic responses, as above

Experimental estimates of R_m in CA3 pyramidal cells (Major et al. 1994; Hemond et al. 2009) suggest that R_m could vary considerably from cell to cell, Nevertheless, a single mean value of R_m is used in all cells simulated here. This simplification is justified based on the limited effect of R_m on synaptic responses (Jaffe and Carnevale 1999) resulting in a significantly reduced variability in synaptic response properties owing to variability in R_m. For example, the mean peak value of simulated voltage-clamp AMPA receptor mediated responses using cell1zr morphology changes by no more than 10% for PP responses and 3% for A/C responses even when the value of R_m is increased by 100%. The effect on response kinetics is similarly reduced, less than 6% of HHW in PP responses and 2% of HHW of A/C responses even though the cell time constant has doubled. In contrast, simulated cell input resistance is still quite variable even when using a uniform value for R_m, with a mean value of 172 MΩ and a range of 87 to 261 MΩ across the cell morphologies used here.

The intrinsic variability of C_m is less clear. Major et al. (1994) estimated passive parameters of CA3 pyramidal cells using reconstructed cell morphologies and carefully chosen stimulation protocols. Their estimated value of Cm was 0.75 μF cm⁻² in the mean, essentially the same as the value used here, with a range of 0.69 to 0.81 μF cm⁻². Gentet et al. (2000) directly measured C_m in nucleated patches drawn from a variety of cultured cell types and found a consistent value of 0.9 μF cm⁻². Employing a uniform C_m in simulations appears consistent with the underlying biophysics of lipid bilayers. In terms of parameter sensitivity, C_m is a more critical parameter than R_m. For AMPA receptor mediated responses in cell1zr, changing C_m from 0.72 to 0.9 μF cm⁻², a 25% change, resulted in a 10% change in mean peak value for PP responses and 5% for A/C responses. Changes in mean response HHW values were 15% and 7% for PP and A/C responses, respectively.

An additional passive property of cells potentially affects synaptic responses, the intrinsic cell resting potential. A wide range of values has been found among CA3 pyramidal cells (Hemond et al. 2009). The values used here is simulations, −61 mV, is typical of experimental measurements in CA3 pyramidal cells (Hemond et al. 2009; Spruston and Johnston 1992). Depending on the recording methods used, this value may be affected by experimental artifacts such as liquid junction potential. However, the experiments simulated here hyperpolarize the cell soma to a known potential, −80 mV in most cases, prior to recording synaptic response properties, specifically to minimize the effects of variable resting potential. The cell resting potential parameter used in simulations has a relatively small effect on simulated synaptic response properties. For example, hyperpolarizing the simulated resting potential in cell1zr by 10 mV results in an increase in the mean simulated peak value of AMPA receptor mediated responses of only 3% for PP synaptic responses and 1% for A/C synaptic response. Any change in simulated response kinetics is negligible for both cases.

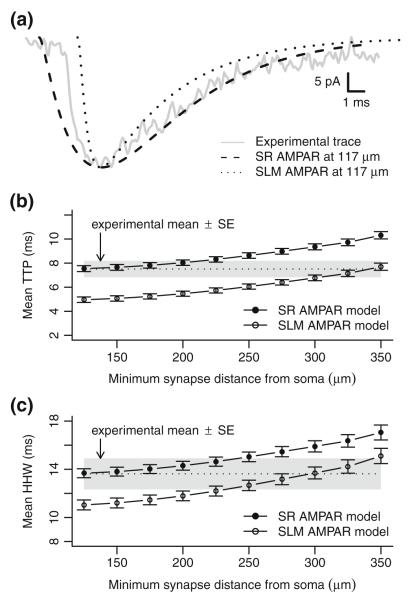
The best-fit AMPA receptor model for SR has parameter values in agreement with a prior experimental characterization of AMPA receptor responses in CA3 pyramidal cells (Williams and Johnston 1991), but seems inconsistent with other comparable characterizations of AMPA receptors in CA3 hippocampal pyramidal cells (Colquhoun et al. 1992; Jonas and Sakmann 1992; Jonas et al. 1993; Spruston et al. 1995). Such characterizations would predict more rapidly rising AMPA receptor responses with peak times generally at 1 ms or below, as found in the SLM AMPA receptor model fitted to PP responses. To explore this issue in greater depth, experimental responses were reanalyzed with a higher smoothing frequency (500 Hz) to improve detection of rapidly rising responses. Responses with the fastest TTP and smallest HHW values were identified, and from these a single exemplar response was selected for fitting. Figure 8(a) shows the raw trace of this response in conjunction with responses generated near the soma using both the SR AMPA receptor model (τ=3.3 ms) and the faster SLM AMPA receptor model (τ₁=0.4 ms, τ₂=4.1 ms). Overall, the SR and SLM AMPA receptor models provide qualitatively similar fits of the experimental trace with the SR model being somewhat better in the decaying portion of the response. Even so, small differences in fit might not be material given that the exemplar response has much more rapid kinetics than typical responses.

Fig. 8.

Faster SLM AMPAR model fits a rapid experimental trace but not overall mean TTP and HHW. (a) An experimental data trace for one of the three most rapidly rising AMPA receptor synaptic responses is shown in comparison with model responses created from a synapse 117 μm from the soma of model cell c62563 using different AMPA receptor models. The slower SR AMPAR model has time constants τ₁=τ₂=3.3 ms. The faster SLM AMPAR model has time constants τ₁=0.4 ms and τ₂=4.1 ms. Responses were scaled to align peak response values and shifted to match peak times. (b) Mean time-to-peak of model responses for all cells when synapses are constrained to a region in layer SR with different minimum distances from the soma. Error bars indicate means ± SE (c): Mean half-height width of model responses for all cells when synapses are constrained as above

A question arises as to whether matching one fast response would be sufficient for the overall model of A/C AMPA receptor responses. Even though the slower model AMPA receptor responses match the experimental mean TTP and HHW values when averaged over all cells, it could be possible that synapses measured experimentally are not distributed throughout the whole extent of SR. Such non-uniformity might then permit the faster AMPA receptor model to accurately match the experimentally determined mean TTP and HHW values. Figure 8(b) and (c) show the effect on mean TTP and HHW across all model cells when synapses are limited to a region more distal than a given minimum path distance from the soma. In this case, a minimum distance of 300–350 μm from the soma is required for the faster AMPA receptor model to match mean TTP and HHW values from experimental data, on average excluding 69%–75% of the total dendritic length in SR. Overall, it seems unlikely that such a large portion of the dendritic tree would be void of active synaptic contacts.

It should be noted that the means-fitted model of SLM AMPA receptors has a time-to-peak synaptic conductance of 1 ms, generally in agreement with prior characterizations of AMPA receptors. Even when reanalyzed as described above, no experimentally measured synaptic responses with TTP values less than 2.4 ms were found, suggesting that the faster AMPA receptor model used for SLM synapses would be a poor model for A/C AMPA receptor responses.

3.6 Passive model predictions

Currently, dendrites in CA3 pyramidal cells can only be patched within a limited region near the cell body. This precludes direct measurements of the depolarization of the dendrite at locations near the site of a unitary synaptic activation. The present model offers predictions of the local dendritic depolarization resulting from unitary synaptic activations under ideal circumstances. Figure 9 panels (a–c) show the effect of unitary activations of AMPA and NMDA receptors at different locations in the dendritic arbor. This prediction indicates that more distal dendrites could be significantly depolarized, even for individual synaptic activations. In a non-passive case, such a depolarization may be sufficient to open voltage-gated ion channels near the site of the synapse, though the details and consequences of this possibility are beyond the scope of this report.

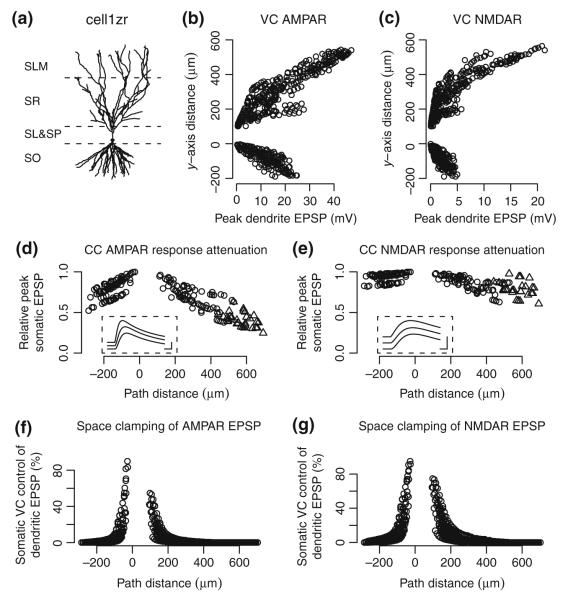
Fig. 9.

Predicted dendritic and somatic EPSPs by location. (a) Morphology of cell1zr, the cell used in these simulations. Dotted lines indicate boundaries between SO, SP & SL, SR, and SLM. (b, c) Predicted peak local depolarization from rest potential, i.e. local EPSP, for unitary AMPA and NMDA receptor responses generated along the apical-basal axis of the simulated cell. In VC, membrane potential at the soma is clamped at −80 mV. Resulting equilibrium potential is approximately −75 mV in distal dendrites. (d, e) Peak somatic EPSP in CC for AMPA and NMDA receptor synaptic responses relative to the maximum peak EPSP. Current is injected to make the initial soma potential −60 mV. Responses are shown for synapses located in SO and SR (open circles) and SLM (triangles). Locations in SO are indicated as negative path distance. Insets show sample traces along a common path at 180, 240, and 371 μm (top to bottom) from the soma. Scale bars indicate 10 ms and 0.2 mV. (f, g) Effectiveness of somatic VC control over local dendritic EPSP at different synapse locations for AMPA and NMDA receptor activations, respectively. Effectiveness is measured as the difference between peak CC and VC dendritic EPSP at a given location divided by the peak CC EPSP at the location. In this comparison, soma potential is initially −80 mV for both VC and CC modes. A randomly selected set of synapses was sampled for plotting in panels (b–e)

Model parameters were fit using experimental measurements made under voltage clamp. While the companion experimental investigation did not include current clamp (CC) measurements in the passive cell preparations (Perez-Rosello et al. in press), the present model offers predictions as to the mean EPSP response properties expected for unitary synaptic activations in passive cells when the soma is initially at a potential near rest (Table 4). Additional sources of synaptic variability were not considered in these predictions. CA3 pyramidal cells are generally electrotonically compact and, as predicted by earlier passive models (Henze et al. 1996; Jaffe and Carnevale 1999), EPSP peak value is affected by synaptic receptor kinetics and cell passive properties. Figure 9 panels (d) and (e) show the attenuation predicted by the current model for AMPA and NMDA receptor synaptic responses as a function of the path distance from the soma. For AMPA receptor synaptic responses in SO and SR, the attenuation of peak response is limited to approximately 60% of the peak response near the soma. Even though the model assumes a different AMPA receptor model for SLM synapses, the overall attenuation gradually increases with distance without apparent discontinuity. NMDA receptor synaptic responses have slower rising and falling time constants and, as may be expected, show less distance-dependent attenuation than the comparatively faster AMPA receptor responses.

Table 4.

Predicted mean response properties in passive current clamp

Response type	I (cells)	N (synapses)	Mean PV (mV) (mean ± SE)	Mean TTP (ms) (mean ± SE)	Mean HHW (ms) (mean ± SE)
AMPA receptor mediated responses
Associational/   Commissural	17	8334	0.56±0.05	17.22±0.37	47.37±0.44
Perforant Path	17	3984	0.34±0.03	23.85±1.20	54.98±1.59
NMDA receptor mediated responses
Associational/   Commissural	17	8334	0.30±0.03	34.09±0.32	71.02±0.23
Perforant Path	17	3984	0.27±0.03	41.18±0.58	75.53±1.42

Voltage clamp techniques have been used to minimize the effect of active channels on synaptic responses with the understanding that the clamp may be effective over only a limited spatial extent. Even though the passive cell model does not include voltage-gated channels, it can be used to examine the difference in local depolarization caused by unitary synaptic activations in voltage clamp as opposed to current clamp modes. Figure 9 panels (f) and (g) show the effectiveness of somatic VC control over peak local EPSPs at different dendritic path distances from the soma. The predicted relative effectiveness of voltage clamp is maximal near the soma but degrades rapidly with increasing distance from the soma. In the example cell, the effect of voltage clamp decreases by a factor of two at an apical distance of 117 μm from the soma (corresponding to 17% of the maximum path distance along the dendritic tree) for AMPA receptor activations and at 146 μm (21%) from NMDA receptor activations. Corresponding distances in the basal direction are 47 and 73 μm (16% and 26%, respectively). With a somatic holding potential of −80 mV, the peak local response to unitary AMPA receptor activations at a typical mid-SLM location would be a local depolarization of 33.68 mV in current clamp and 33.64 mV in voltage clamp, a difference of only 0.04 mV or 0.1% of the response. Somatic voltage clamp can suppress the local depolarization for a synapse adjacent to the soma, but throughout SR and SO, voltage clamp would have less than a 5% effect on the peak local depolarization for 83% of the AMPA receptor synapses in the example cell. In terms of changes in membrane potential sufficient to activate voltage-gated ion channels, any differences between somatic voltage and current clamp appear to be minimal compared with the depolarization resulting from synaptic activation.

In addition to current clamp responses, the model also predicts responses when neither AMPA nor NMDA receptors are blocked. In this case, AMPA and NMDA receptors would both contribute to the EPSC response provided that there was sufficient depolarization near the NMDA receptors. The pattern of local depolarization in Fig. 9 suggests that in some distal synapses, even unitary synaptic activations may be sufficient to depolarize the dendrite sufficiently enough to release the Mg²⁺-dependent block of the NMDA receptor (Jahr and Stevens 1990), resulting in an increased EPSC and possibly even sufficient calcium influx to induce synaptic plasticity. Table 5 shows the predicted mean response properties when both AMPA and NMDA receptors contribute as well as the difference when only NMDA receptors are blocked. For these simulations, external Mg²⁺ is assumed to be 1 mM rather than the lower concentration used for measuring isolated NMDA receptor responses. As above, additional sources of synaptic variability were not considered in these predictions Under the simulated conditions, NMDA receptors have minimal effect on either peak EPSC or response kinetics. This result arises from late opening of the NMDA receptor compared to the decay time of the local membrane potential, even when there is initially sufficient local depolarization to relieve the Mg²⁺ pore block of the NMDA receptor. Late opening of the NMDA receptor has previously been noted as a factor influencing spike-time dependent synaptic plasticity in CA3 pyramidal cells (Debanne et al. 1998). Of course, the prediction of essentially no NMDA receptor contribution to somatic EPSC is limited to unitary synaptic activations and does not apply to a more complex spike train where multiple nearby synapses could be activated concurrently.

Table 5.

Predicted AMPA and NMDA receptor response properties in passive voltage clamp

Response type	I (cells)	N (synapses)	Mean PV (pA) (mean ± SE)	Mean TTP (ms) (mean ± SE)	Mean HHW (ms) (mean ± SE)
Combined AMPA receptor and NMDA receptor responses
Associational/   Commissural	17	8334	18.21±0.71	7.60±0.25	13.84±0.39
Perforant Path	17	3984	9.42±0.88	11.32±0.77	19.42±1.26
NMDA receptor associated change
Associational/   Commissural	17	8334	0.30±0.01	0.09±0.01	0.22±0.02
Perforant Path	17	3984	0.29±0.01	0.35±0.05	0.84±0.12

3.7 Active cell models

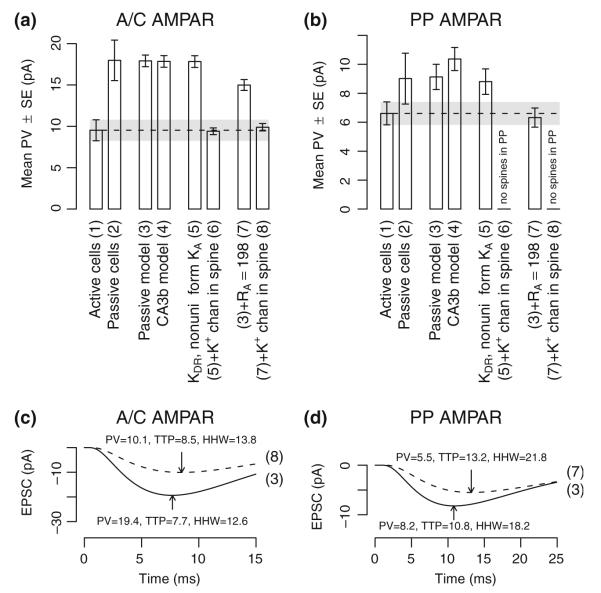
Currently available experimental findings are insufficient to form a well-constrained model of synaptic responses in active CA3 pyramidal cells. Nevertheless, the passive model can be generalized in several different ways to attempt replication of some of the active cell results from the companion experimental study (Perez-Rosello et al. 2010). Of particular interest are unitary responses generated by AMPA receptors as they could induce sufficient dendritic depolarization to activate voltage-gated ion channels (Fig. 9), thereby differentiating between active and passive cells.

In the experimental data, the passive cell mean unitary AMPA receptor response properties in voltage clamp (Table 3) display only a few notable exceptions from comparable experimentally measured mean response properties in active cells (A/C means: PV = 9.5 ± 1.3pA, TTP = 7.6 ± 0.7ms, HHW = 17.3 ± 1.9ms; PP means: PV = 6.6 ± 0.8pA, TTP = 13.2 ± 0.8ms, HHW = 24.3 ± 1.7ms). Compared with passive cells, active cell responses show a similar mean TTP but a longer mean HHW. PP response mean peak values are somewhat reduced in active cells (27%, unpaired samples) while A/C response mean peak values are reduced to a larger extent (47%, unpaired samples). Models explaining active cell experimental results should show a quantitatively similar pattern in peak response values.

Various different approaches were considered in modeling synaptic responses in active cells, each with different hypotheses with regard to the effects of voltage-gated ion channels (Fig. 10). The initial attempt involved adopting one of the most recently developed among the available active models of CA3 pyramidal cells (Hemond et al. 2008). The wide variety of ion channels of this model was incorporated into our cell morphologies to test synaptic responses (Fig. 10 (a) and (b) item (4)). Mean AMPA receptor peak values were not materially reduced in this configuration; 8% of PP unitary synaptic activations resulted in dendritic spikes, accounting for the increase in mean PP AMPA receptor peak value.

Fig. 10.

Alternative model results for non-passive AMPA receptor responses. (a) Experimental and model mean peak EPSC for A/C AMPA receptor responses. Alternative items are: (1) experimental results from active cells, i.e. where ion channels are not blocked, (2) experimental results from passive cells, i.e. where voltage-gated ion channels are blocked, (3) passive model of synaptic responses, (4) active model with ion channels from a prior study (Hemond et al. 2008), (5) passive model with K_DR (g_max=10 mS cm⁻²) and K_A (somatic g_max=20 mS cm⁻²) channels added such that K_A conductivity scales linearly with distance from the soma, (6) previous model with an unspecified K⁺ channel in synaptically activated spines (g_max=1 nS), (7) passive model with R_a changed to 198 Ωcm, and (8) the previous model with an unspecified K⁺ channel in synaptically activated spines (g_max=0.5 nS). (b) Experimental and model mean peak EPSC for PP AMPA receptor responses. Individual items are as in panel A. Synapses in SLM are modeled without spines and items (f) and (h) are omitted for PP responses. (c) Representative EPSC traces from a single A/C AMPA receptor synapse as derived from models (3) and (8). Response peaks are indicated with arrows. (d) Representative EPSC traces from a single PP AMPA receptor synapse as derived from models (3) and (7). Response peaks are indicated with arrows

Next, we tested the hypothesis that the reduced peak values in active cells could be accounted for by the activation of K⁺ channels, and in particular K_A channels, by dendritic depolarization due to synaptic activation (Fig. 10, item (5)). Although some reduction in PP peak value was found, dendritic depolarization from A/C synaptic activations was insufficient to produce a meaningful reduction in peak EPSCs. However, inclusion of a synaptically activated K⁺ conductance of 1 nS (120 mS cm⁻²) in dendritic spines approximated experimental mean peak values for active cells (Fig. 10(a) item (6)).

The pattern of increased HHW with a smaller increase in TTP is also seen in the plot of model sensitivity to axial resistivity (Fig. 7). Thus we hypothesized that ion channel blockage, resulting in different ionic concentrations within active cells, could yield different axial resistivity. An alternative hypothesis would be that dilution effects from the whole-cell patch techniques used for active and passive cells lead to different intracellular concentrations and thereby different axial resistivity. For R_a=198 Ωcm, mean AMPA receptor TTP and HHW were, respectively, 8.3±0.3 ms and 15.0±0.4 ms for A/C responses and 13.3±0.9 ms and 22.2±1.4 ms for PP responses, comparable with experimental results from active cells. A synaptically activated K⁺ conductance of 0.5 nS (55 mS cm⁻²) was needed within dendritic spines in SR to approximate the experimental mean PV value for A/C responses (Fig. 10(a) item (8)). For synapses in SLM, no spines were included in the model and the reduction in PV was attributable to the increased axial resistivity alone (Fig. 10(b) item (7)). A comparison is shown in Fig. 10 panels (a) and (d) between responses from the passive model and from one with these relatively simple modifications.

4 Discussion

A computational model involving a sample of CA3b cell morphologies was fit with the mean response values from experimental measurements of unitary synaptic stimulations of CA3b pyramidal cells from mature animals (Table 3). The experimental preparations included both internal and external ion channel blockers to render the cells electrically passive, permitting computational modeling without the level of uncertainty typically associated with assumptions regarding ion channels whose properties are not directly measureable in the thinner dendrites found in CA3b pyramidal cells. Even when using minimal stimulation protocols, experimental measurements of elicited responses do not provide direct access to synaptic properties for synapses located at a distance from the cell soma. This model leverages the experimental responses to estimate the most likely synaptic properties (Table 2), and unlike prior models of synaptic responses in CA3 pyramidal cells, was constrained by experimental measurements of evoked unitary synaptic responses. In addition, the model predicts results that have either not yet been tested experimentally or else are not obtainable using currently available experimental methods (Tables 4 and 5, Fig. 9). Alternative methods were considered for extending the current model to encompass results from cells that were not rendered passive (Fig. 10), but a well-constrained biophysically realistic model accounting for the differences between passive and non-passive cells is beyond the current scope.

Fitting model parameters based on associational/commissural or perforant pathway stimulation experiments suggests that AMPA receptors in CA3b pyramidal cells either: 1) have a composition that differs by location within the cell, 2) are modulated in ways that lead to different receptor kinetics, or 3) are affected by presynaptic differences between pathways. Differences in the glutamate concentration at the site of the AMPA receptor could lead to different rates of ligand binding and thus different kinetics in receptor activation, a phenomenon previously observed in hippocampal pyramidal cells (Jonas and Sakmann 1992; Andrásfalvy and Magee 2001), suggesting a role for presynaptic differences. Our model does not rule out previously suggested alternatives, including superposition of unitary EPSCs (Jonas et al. 1993) or other experimental artifacts. Similarities in predicted A/C and PP EPSP response kinetics (Table 4) suggest a possible functional rationalization for the difference in AMPA receptor kinetics in terms of equalizing the effects of different afferent information sources on pyramidal cell firing. Unlike the situation thought to exist in CA1 pyramidal cells (Golding et al. 2005; Nicholson et al. 2006), perforant path synapses appear capable of generating significant somatic depolarization in CA3 pyramidal cells even without recourse to dendritic spikes.

As predicted in prior models (Henze et al. 1996), NMDA receptor responses were less affected by synapse location than were AMPA receptor responses, at least for the passive cell (Fig. 9). Best-fit parameters for NMDA receptors in our model suggest relatively uniform properties throughout the cell that are generally consistent with characterizations of receptors containing NR2A subunits (Vicini et al. 1998; Erreger et al. 2005). The complex kinetics and response variability of NMDA receptors are not completely understood (Vicini et al. 1998), and no attempt was made to fully reproduce such details in the model. Contribution of the NMDA receptor to synaptic response EPSC (or EPSP) appear to be minimal in the case of unitary synaptic activations under physiological conditions, even in distal synapses where AMPA receptor co-activation could induce a relatively large depolarization of the local membrane (Fig. 9, Table 5). Although not simulated here, dendrite depolarization by multiple concurrent activations of nearby synapses or by backpropagating action potentials is a likely prerequisite for functionally significant activation of synaptic NMDA receptors in CA3b pyramidal cells.

Distance-dependent scaling of AMPA receptor conductance has been demonstrated in CA1 pyramidal cells (Magee and Cook 2000; Andrásfalvy and Magee 2001; Smith et al 2003). Experimental measurements at the site of synapses in SR and SO are not currently possible in CA3b pyramidal cells. Here we took advantage of the expected effect of synaptic location to devise an indirect test (Fig. 5). Synaptic scaling implies a lower variability of somatic responses than otherwise predicted in passive conditions (Magee and Cook 2000). In contrast, our analysis shows that the experimentally recorded somatic responses are more variable than those generated by the model using a constant synaptic conductance. These simulations account for AMPA receptor responses resulting from A/C stimulations without recourse to distance-dependent scaling by allowing a distance-independent diversity of synaptic conductance. Such a result suggests that for A/C synapses, the peak conductance of AMPA receptors in CA3 pyramidal cells does not scale with distance as observed in CA1 and, at the same time, provides an estimate of the extent of the possible conductance diversity among synapses in the same cell. However, the power of the statistical result is insufficient to rule out all possibilities of distant-dependent scaling, necessitating the use of experimental methods for measuring the response closer to the dendritic location of the synapse for a definitive determination of any distant-dependent effects.

Variability of A/C AMPA receptor response peak values not accounted for by cell morphology is estimated here to be approximately 40%–45% of the mean (Figs. 4 and 5), consistent with an intrinsic diversity of the receptor conductance in the same range. Estimates for PP AMPA receptor responses suggest much lower intrinsic peak value variability, below the level of uncertainty attributable to differences in cell morphology (Fig. 4). In CA3, long-term synaptic plasticity has been shown both in A/C synapses (Debanne et al. 1998; Debanne et al. 1999) and in PP synapses (Do et al. 2002; McMahon and Barrionuevo 2002). If diversity in AMPA receptor synaptic conductance is primarily associated with synaptic plasticity, a difference in the variability of unitary peak values may be indicative of different forms of long-term plasticity in A/C and PP synapses.

Synaptic response properties have previously been used to estimate axial resistivity (Bekkers and Stevens 1996), but more typically, estimates of axial resistivity in CA3 pyramidal cells have been made from somatic current injections (Major et al. 1994; Hemond et al. 2009). The current model uses synaptic responses to estimate axial resistivity (Fig. 7) and provides an upper bound for this value that is below earlier experimental estimates. Differences between the current estimate and others remain unexplained although “the unpleasant possibility of nonuniform electrical parameters” (Major et al. 1994, p. 4636) may need to be considered.

Some of the results from non-passive cells are well accounted for by assuming a larger axial resistivity than estimated for passive cells, suggesting that the passive cell preparation may have affected internal ion concentrations differently than the more typical non-passive cell preparations. In non-passive cells, synaptically induced dendritic depolarization in combination with voltage-gated potassium channels can account for a decreased mean peak EPSC for the more distal perforant path synapses but not for more proximal A/C synapses. Decreased mean peak EPSC were obtained in the model by assuming that potassium currents are activated in the spine immediately following activation of the AMPA receptor response itself. While this is superficially similar to effects observed experimentally (Bloodgood and Sabatini 2007), biophysical mechanisms are unclear in this case. In addition, the magnitude of the predicted potassium conductance required is larger than generally assumed for voltage- or calcium-gated channels found in synaptic spines. Active models considered here do not explain why NMDA receptor mediated responses are similar in active and passive cells. Potassium channels in spines would presumably be activated for both AMPA and NMDA receptor mediated responses leading to a reduction in NMDA receptor mediated response peak value that was not observed experimentally. The approaches used here for exploring the mechanisms underlying the experimental observations from active conditions should be taken as indicative of alternative possibilities but not as complete models in their own right.

The phenomenological model presented here relates properties of synaptic receptor types (AMPA and NMDA), realistic cell morphologies, and measurable synaptic responses in ideal passive cells. Fitting of the model uses only the sufficient statistics provided by mean values of experimentally determined peak value, time-to-peak, and half-height width. Thus, unlike in complementary approaches combining morphology and physiology from the same cells to constrain the model (e.g. Roth and Häusser 2001; Holmes et al. 2006), fitting to individual data traces was not required in this case. Within the limits of complexity considered here, the model is well constrained by these experimental results. As in any model, there are assumptions, such as the uniformity of key properties within and across cells, which may yet prove to be over simplifications. Further experimentation with both passive and non-passive cell preparations would be useful in extending the current work and a prerequisite to forming a complete and accurate biophysical model of CA3 pyramidal cells.