Detection of Modulated Tones in Modulated Noise by Non-human Primates

Abstract

In natural environments, many sounds are amplitude-modulated. Amplitude modulation is thought to be a signal that aids auditory object formation. A previous study of the detection of signals in noise found that when tones or noise were amplitude-modulated, the noise was a less effective masker, and detection thresholds for tones in noise were lowered. These results suggest that the detection of modulated signals in modulated noise would be enhanced. This paper describes the results of experiments investigating how detection is modified when both signal and noise were amplitude-modulated. Two monkeys (Macaca mulatta) were trained to detect amplitude-modulated tones in continuous, amplitude-modulated broadband noise. When the phase difference of otherwise similarly amplitude-modulated tones and noise were varied, detection thresholds were highest when the modulations were in phase and lowest when the modulations were anti-phase. When the depth of the modulation of tones or noise was varied, detection thresholds decreased if the modulations were anti-phase. When the modulations were in phase, increasing the depth of tone modulation caused an increase in tone detection thresholds, but increasing depth of noise modulations did not affect tone detection thresholds. Changing the modulation frequency of tone or noise caused changes in threshold that saturated at modulation frequencies higher than 20 Hz; thresholds decreased when the tone and noise modulations were in phase and decreased when they were anti-phase. The relationship between reaction times and tone level were not modified by manipulations to the nature of temporal variations in the signal or noise. The changes in behavioral threshold were consistent with a model where the brain subtracted noise from signal. These results suggest that the parameters of the modulation of signals and maskers heavily influence detection in very predictable ways. These results are consistent with some results in humans and avians and form the baseline for neurophysiological studies of mechanisms of detection in noise.

INTRODUCTION

The amplitudes of natural sounds fluctuate with time. Due to the prevalence of temporally modulated sounds, the auditory system may be specially adapted to encode and even take advantage of these features (Gans 1992). Studies of physiological responses of auditory-responsive neurons have shown that one such adaptation, phase locking, could lead to an up to 20 dB enhancement in sensitivity to sounds (Joris et al. 1994). However, natural environments are composed of multitudes of sounds, and the amplitude of any or all of them could vary with time. Thus, behaviorally relevant target sounds and behaviorally irrelevant distractors could both tap into the auditory sensitivity for modulations. This represents part of the complexity of auditory scene analysis problem that highlights the difficulty in auditory processing in complex, noisy environments that characterize the natural environment. Research in visual systems suggests that visual scene analysis, specifically scene segmentation, depends on feature borders and contrasts between local stimulus properties and global stimulus properties (e.g., Julesz 1986; reviewed in Nothdurft 1994).

While many studies of auditory scene analysis highlight pattern discrimination and identification, some studies deal with the processing of contrast between local signals and global signals. Amplitude modulation is one way to integrate multiple stimuli into a single auditory object (Yost and Sheft 1989). Consistent with such a hypothesis, detection thresholds of a steady-state signal in a modulated masker were lower relative to when the signal and the masker were not temporally modulated or when the modulation of the masker is uncorrelated across different spectral regions (e.g. Hall et al. 1984; Schooneveldt and Moore 1989; Fantini 1991; Langemann and Klump 2001; Dylla et al. 2013). When both signals (local stimulus to an auditory filter) and masker (global stimulus) were temporally modulated, behavioral performance was highly dependent on temporal correlations between the signal and the masker: detection thresholds were lower when the modulation of the signal and the masker were different relative to when the signal and the masker were modulated similarly (e.g., McFadden 1987; Cohen and Schubert 1987; Fantini and Moore 1994). Since animals also live in environments where signals and maskers are both modulated, potentially similar results and rules could apply to animals as well (Bee and Micheyl 2008). And, consistent with that hypothesis, experiments in avians have found that correlations between signal and masker resulted in higher thresholds for the detection of signal relative to when the signal and masker were not correlated with each other (corvids: Jensen 2007; passarines: Langemann and Klump 2007).

With the recent popularity of the macaque as a model for hearing, it is an open question to ask if some of the properties of scene analysis and auditory object processing that have been described in humans apply to macaques as well. Studies have found that macaques have U-shaped audiograms, similar to humans (e.g., Stebbins et al. 1966; Pfingst et al. 1975, 1978), and the modification of the audiograms by noise are similar to humans (compare results from Dylla et al. (2013) with Hawkins and Stevens (1950)). An early indication of modulation-based release in masking in macaques was observed when tone detection thresholds were lower when either the signal or the noise was modulated (Dylla et al. 2013), consistent with findings in humans and other species (e.g., Gustafsson and Arlinger 1994; Bacon et al. 1998; Langemann and Klump 2001; Velez and Bee 2010). In this paper, we extend the findings of our previous behavioral study to further investigate how detection is modified when both tones and noise were time-varying (temporal variation was created by amplitude modulation) and suggest a model for the computation underlying the detection. If amplitude modulation helps auditory object formation, then thresholds to detect an amplitude-modulated signal in a similarly amplitude-modulated noise would be higher than when the signal and noise were modulated differently. Theories of dip listening would suggest that detection thresholds would increase as the energy in the dip of the masker decreased. The behavioral performance of the monkeys is consistent with both predictions, and an energetic masking model where the nervous system effectively subtracts noise from the signal can account for the results. The results of these experiments form the baseline for neurophysiological experiments exploring the mechanisms underlying auditory scene analysis, auditory object formation, and the detection of signals in noise.

METHODS

Experiments were conducted on two male rhesus macaque monkeys (Macaca mulatta) that were both 5 years of age at the beginning of these experiments (monkeys C and D). The monkeys were prepared for chronic experiments using standard techniques used in primate research (e.g., Ramachandran and Lisberger 2005; Dylla et al. 2013), and their audiograms as well as the effects of noise on their audiograms were consistent with previous reports on non-human primates, including studies from our laboratory (Stebbins et al. 1966; Pfingst et al. 1975, 1978; Dylla et al. 2013). All procedures were approved by the Institutional Animal Care and Use Committee at Vanderbilt University and were in strict compliance with the guidelines for animal research established by the National Institutes of Health.

The surgical and experimental procedures have been described in detail earlier (Dylla et al. 2013). Briefly, monkeys were prepared for this study with a surgical procedure conducted using isoflurane anesthesia and performed under sterile conditions. During this surgical procedure, bone cement and screws were used to secure a head holder to the skull. The monkey was allowed to recover with a regimen of analgesics and antibiotics (if necessary) and was under careful observation by both laboratory staff and veterinary personnel. The head holder was used to position the monkey’s head in a constant location in the chair (via a head-post) relative to the speakers during experiments.

All experiments were conducted in a double-walled pseudo-anechoic sound booth (model 1200A, Industrial Acoustics Corp., NY). The monkeys were seated comfortably in an acrylic primate chair that was custom-designed for their comfort and to leave the area around the ears clear. The monkeys’ heads were fixed to the chair by means of the implanted head holder such that the head was level with the center of speakers positioned directly in front at a distance of 90.1 cm from the ears. The speakers (Rhyme Acoustics speakers, Madisound, WI) could deliver sounds between 50 and 40 kHz and were driven by linear amplifiers such that the output of the speakers varied by ±3 dB over the entire frequency range. The efficacy of the sound system was frequently tested by calibrating the output with a ½″ probe microphone system (PS 9200, ACO Pacific, Belmont, CA). All calibrations were performed with the probe microphone being placed at the location of one of the ears of the monkey with its head fixed. The same speaker was used to deliver tones and noise, so that there was no spatial separation between the two stimuli. Tones were calibrated by presenting the stimuli, measuring the signal with the probe microphone placed at the location of the monkey ears and using the known sensitivity of the microphone. Noise was calibrated by filtering the noise into 1-Hz bands using custom software written in Matlab, calibrating the sound pressure level over the entire frequency range of the noise (thus measuring dB spectrum level, see below) and then calculating the overall level based on the known relationship between decibel overall level and decibel spectrum level (see below for details).

Behavioral Task

The experiments were controlled by a computer running OpenEx software (System 3, TDT Inc., Alachua, FL). Signals (tones and noise) were generated with a sampling rate of 97.6 kHz. Lever state was sampled at a rate of 24.4 kHz, with a temporal resolution of about 40 μs on the lever release. The details of the task, basic stimulus, and experimental conditions have been described elsewhere (Dylla et al. 2013). Briefly, the monkeys initiated trials by holding down a lever (Model 829 Single Axis Hall Effect Joystick, P3America, San Diego, CA). When signals (duration = 200 ms, 10 ms rise and fall times) were presented (∼80 % of the trials, tones/amplitude-modulated tones), monkeys were required to release the lever within a 600 ms response window beginning at tone onset. A correct release resulted in fluid reward, incorrect non-releases were not penalized, and early release was treated as a false alarm. On catch trials (∼20 % of the trials, when no signals were presented), monkeys were required to hold through the response window. Correct rejects were not rewarded, but incorrect releases (false alarms) resulted in a variable duration (6–10 s) time-out period during which no new trials could be initiated. Broadband noise (bandwidth 5 Hz–40 kHz) was used and was presented continuously, beginning 10 s before the first trial could be initiated so that the monkey was adapted to the noise. On signal trials, monkeys were required to detect signal (tone/modulated tone) in noise (broadband noise/amplitude-modulated broadband noise), and on catch trials, monkeys were required to reject the noise.

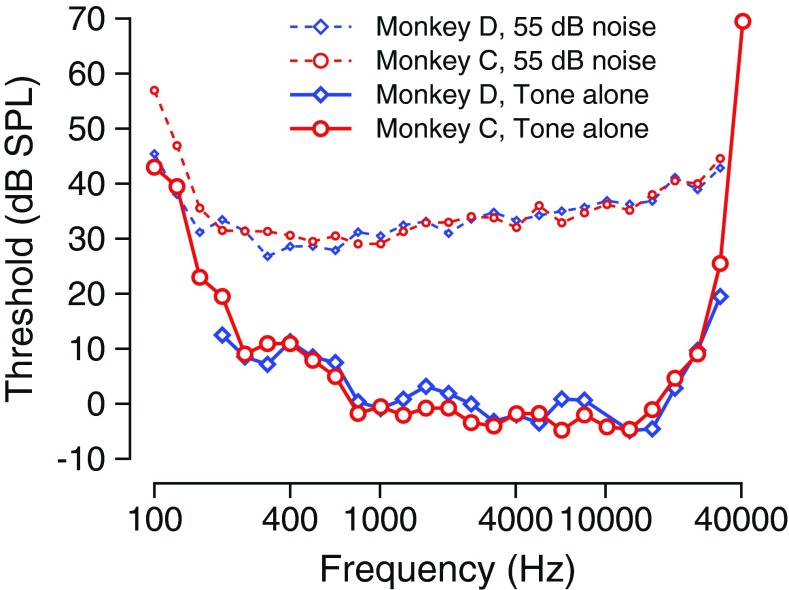
Tones were generated using the formula S(t) = A sin(2πf_ct + ϕ_c), where S(t) represents the tone signal, A represents the amplitude in volts, f_c represents the carrier (tone) frequency, and ϕ_c represents the carrier phase. Usually, the carrier phase was set to be 0 (zero) in all of the experiments described below. Broadband noise (N(t)) was generated using the “Random” function in OpenEx, which generated flat-spectrum noise with roughly equal amplitude at all frequencies and was further band-limited to 40 kHz. The amplitude of the broadband noise is always given as the total level, in decibel (dB). Usually, the mean noise amplitude was set at a 55-dB overall level. The amplitude in dB SPL spectrum level may be computed by subtracting from that overall level an amount equal to 10*log₁₀(bandwidth), 46 dB. The measure of signal level used was power (the signal duration was not taken into account for the calculation of signal level). In these experiments, the sound pressure level of the tone could vary over a 90-dB range, going from −16 to 74 dB SPL. Tone levels were usually presented in steps of 3 or 5 dB, and sound pressure levels were randomly interleaved within a block. Under the conditions of the experiments, broadband noise at 55 dB caused a roughly 30 dB change in tone thresholds across many frequencies, consistent with previous results in our laboratory (Dylla et al. 2013). Figure 1 shows the audiograms of the two monkeys to tones presented alone (large symbols and solid lines) and in continuous broadband noise at the noise level used in this study (55-dB overall level; small symbols and dashed lines). The noise level used caused significant threshold shifts that showed frequency specific trends that were consistent with and matched previous data in macaques (Dylla et al. 2013) and with data from humans (Hawkins and Stevens 1950). Note that the use of higher noise levels (>9 dB SPL spectrum level) would result in higher masked thresholds (e.g. Dylla et al. 2013) and may cause different amounts of masking release as a result of parametric variations in the signal or noise modulations.

FIG. 1.

Thresholds to tones alone and to tones in noise. Threshold to a 200-ms tone is plotted against the tone frequency for monkeys C (red circles and lines) and D (blue diamonds and lines). Thresholds are shown when tones were presented alone (large symbols, solid lines) and when tones were presented embedded in continuous broadband noise at a 55-dB overall level.

Temporal variations of signals were created via sinusoidal amplitude modulation. For any signal S(t), sinusoidal amplitude modulation was produced according to

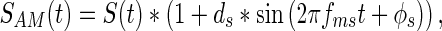where S_AM(t) is the amplitude-modulated signal, d_s is the depth of signal modulation, and f_ms and ϕ_s represent the modulation frequency and modulation phase of the signal, respectively. Amplitude-modulated noises were created similarly according to

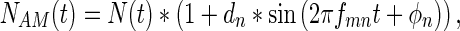where N_AM(t) is the amplitude-modulated noise, d_n is the depth of noise modulation, and f_mn and ϕ_n represent the modulation frequency and modulation phase of the noise, respectively. In both of these cases, the mean sound pressure level will be provided in the data, so the signal and the noise had peaks that were 6 dB higher than the reported mean level when the modulation depth was set at 1. The parameterization shown above allowed us the opportunity to vary d_s, d_n, f_ms, f_mn, ϕ_s, and ϕ_n independently. The experiments were performed in a block design so that all modulation parameters were constant within a block, except for A; this way, the threshold and reaction time metrics could be determined using the method of constant stimuli. Across blocks, modulation parameters could be systematically varied and their effects on behavior measured.

Data Analysis

The analytical techniques have been described previously (Dylla et al. 2013). All analyses were based on signal detection theoretic methods (Green and Swets 1966; Macmillan and Creelman 2005) and implemented using MATLAB (Mathworks, Matick, MA). Briefly, the hit rate (H) and false alarm rate (FA) were calculated based on the number of releases at tone sound pressure level (A) for each block. Signal detection theory dictates that the behavioral sensitivity for a Go/No-Go task can be analyzed in the following way:

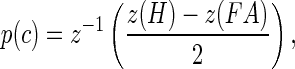where z converts hit rate and false alarm rate into units of standard deviation of a standard normal distribution (z-score, norminv in MATLAB) (Macmillan and Creelman 2005). The inverse z (z⁻¹) then converts a unique number of standard deviations of a standard normal distribution into a probability correct (p(c), normcdf in MATLAB). Care was taken to adjust for cases when hit rates and false alarm rates were 1 and 0, respectively, using methods described previously (Dylla et al. 2013; Macmillan and Creelman 2005). The probability correct values were calculated for all signal amplitudes to create the psychometric function.

The false alarms (10 % or less in all the blocks) and sometimes less than perfect performance at higher sound pressure levels cause the psychometric functions to be non-ideal. To account for that, psychometric functions were fit with a modified Weibull cumulative distribution function (cdf) using the following equation:

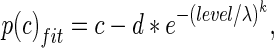where level represents the tone sound pressure level in dB SPL, and is related to A by a logarithmic function, λ and k represent the threshold and slope parameters, respectively, and c and d represent the probability correct at higher sound levels, and the estimates of chance performance at sound levels below threshold, respectively. To account for the sound pressure levels below 0 dB SPL, sound levels were translated by up to 16 dB, fit with a Weibull function, and then sound levels and thresholds were translated back by the same amount as the original translation. From the Weibull cdf, threshold was calculated as that tone sound pressure level that would cause a probability correct value of 0.76. These analyses were performed under the various conditions used in this study.

In all cases, reaction time was also computed, based on the time of the lever release. Reaction time was computed as follows:

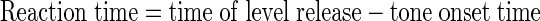Reaction time was computed on all correct Go responses. We performed statistical analyses on the reaction times to explore the variation of reaction time with signal strength and with noise level and with the modulation of noise or signal.

Statistical Analysis

All statistical analyses were implemented using MATLAB and were either coded by one of the authors based on a theory described in Zar (1984) or was implemented using a built-in function.

In many cases, the variability in the data was only able to be estimated using bootstrap methods (Efron and Tishirani 1993). Briefly, each trial was resampled using random draws with replacement, while taking care to maintain the substructure of the block (e.g., number of trials at each sound level). For example, the variability in threshold measurements would be estimated by resampling each block of behavioral responses 1,000 times. The responses at each tone level (including catch trials) were drawn with replacement from the original dataset at that particular tone level, taking care that the number of bootstrapped trials at that tone level matched the number obtained behaviorally. This was repeated at all tone levels to generate one estimate of the bootstrapped behavioral data to generate one bootstrapped threshold estimate. The same procedure was repeated 1,000 times to generate 1,000 estimates of bootstrapped threshold. This procedure permitted the calculation of the variability of the threshold measured. In all cases, the number of iterations was restricted to be the lowest number such that the parameters converged. In most cases, the distributions converged by 1,000 iterations.

RESULTS

Effect of Phase Difference

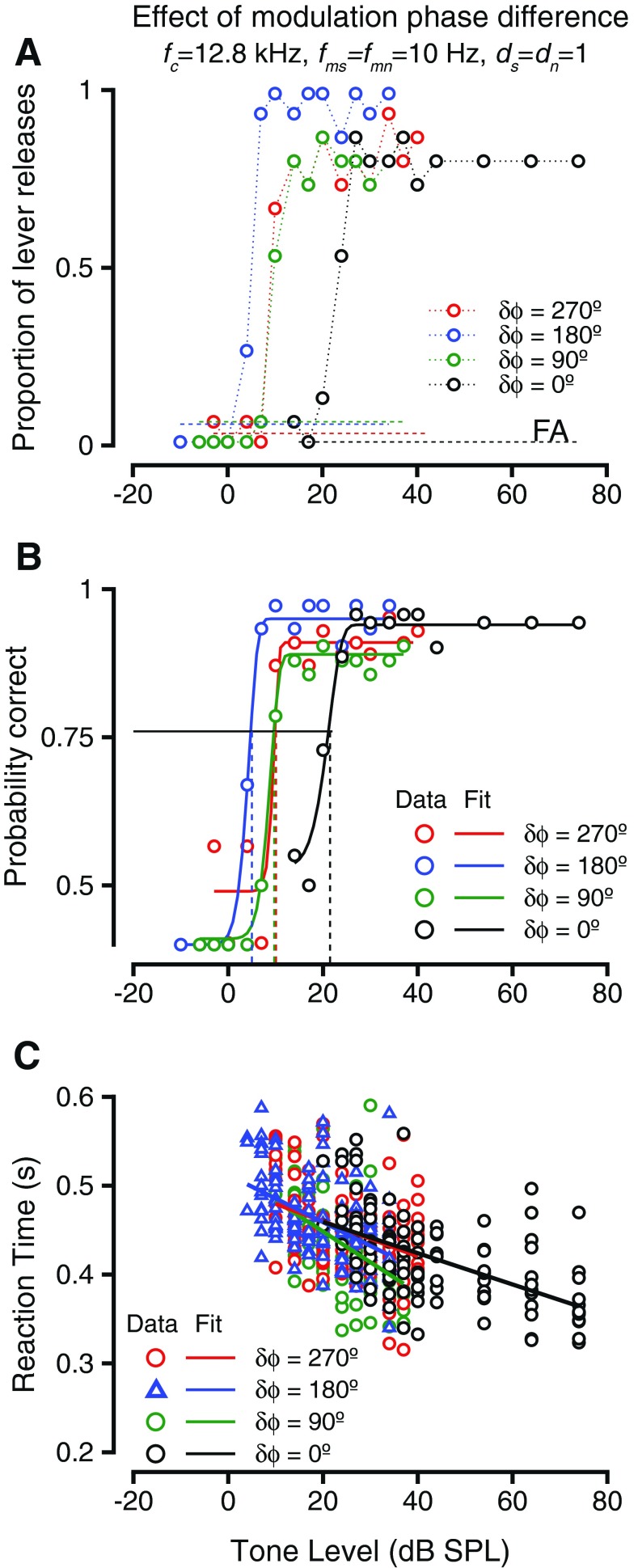
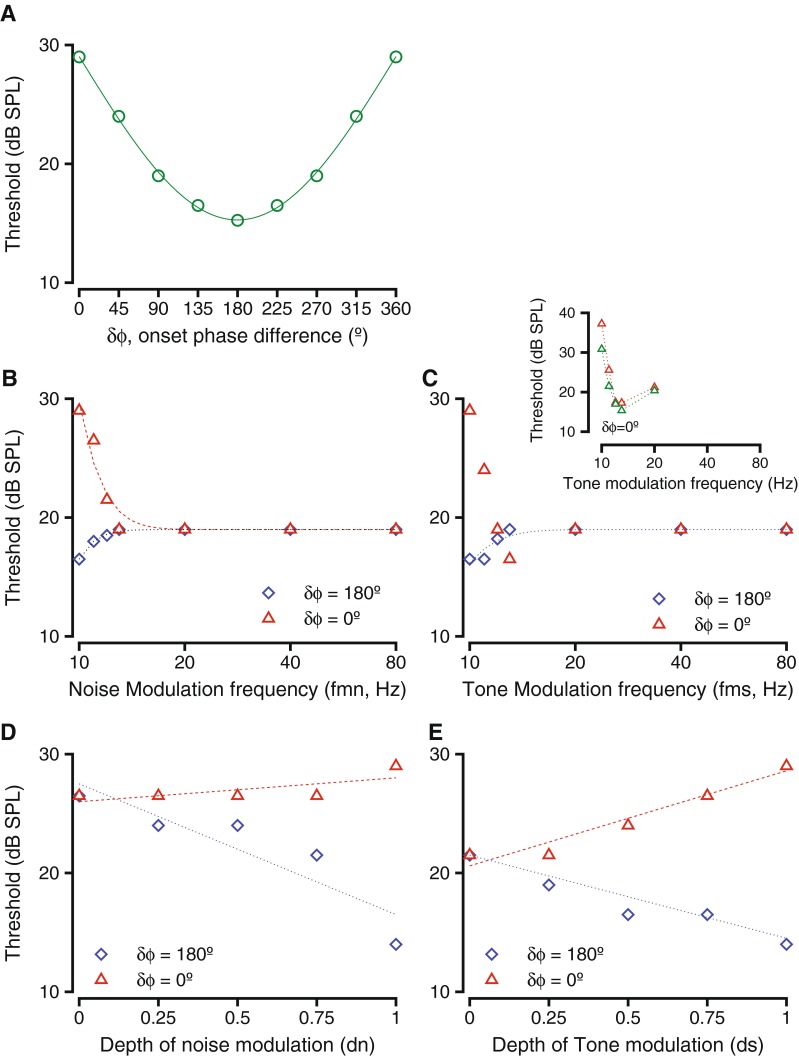
One way of varying the temporal relationship between two modulated sounds is to impose a phase difference between the modulations. The effect of phase difference between the modulations of tone and noise (δϕ = ϕ_s−ϕ_n) were investigated in two macaques. Dip listening theories predict that as more of the signal (modulated tone) occurred in the dips of the noise, thresholds would be reduced; (i.e.), the thresholds would be lowered when phase differences approached 180 ° and would be systematically higher as the phase differences deviated from 180 °. Figure 2 shows the results of such a manipulation in one monkey during the detection of a 12.8 kHz tone in broadband noise. Both the tone and the noise were amplitude-modulated at 10 Hz, and both tone and noise were modulated to a depth of 1. Figure 2A shows the hit rates (colored circles) and false alarm rates (colored dashed lines, labeled FA) as a function of the tone sound pressure level during the detection task for four different phase differences. The different colors represent different phase differences between the tone and the noise modulations (see legend). The hit rates diverged from false alarm rates at very different sound pressure levels depending on the phase difference of the modulations. This implies that the monkey could reliably release the lever at lower sound levels when the tone and noise modulations were in anti-phase at tone onset (δϕ = 180 °) relative to when the tone and noise modulations were in phase at tone onset (δϕ = 0 °). The tone levels required for a reliable lever release for the phase differences intermediate to those (δϕ = 90° and δϕ = 270°) were intermediate to those for the other two δϕ values and appeared similar to each other. The behavioral accuracy in the task at each sound pressure level was calculated by taking hit rate and false alarm rate into consideration (as in the “METHODS” section) and plotted as psychometric functions relating probability correct (p(c)) and tone sound pressure level in Figure 1B. The psychometric functions were fit with Weibull cdfs to generate smooth estimates of behavioral accuracy and to estimate behavioral thresholds. The psychometric functions varied with the modulation phase difference in a manner similar to the hit rates. The detection thresholds were lowest for δϕ = 180 °, intermediate for δϕ = 90 ° and δϕ = 270 °, and highest when δϕ = 0 °. These results are consistent with theories of dip listening that suggest decreases in threshold as more of the signal falls into the dip of the masker.

FIG. 2.

The effect of changing the phase difference between the amplitude modulation of the signal and noise waveform during a detection task. A Hit rate (probability of lever release) vs. tone level during detection of a 12.8-kHz tone embedded in broadband noise. Tone and noise were both amplitude-modulated at 10 Hz and a depth of 1. Noise level was 55-dB overall level. Performance during phase differences of 0 ° (black), 90 ° (green), 180 ° (blue), and 270 ° (red) are shown. Dashed horizontal lines represent false alarm rate (FA) during the blocks of the phase differences shown and are color-coded. B Behavioral accuracy (probability correct, see the “METHODS” section for calculation) vs. tone level for the exemplar conditions shown in A. The symbols are color-coded as in A. Weibull cumulative distribution function (cdf) fits are shown and are color-coded by phase. The horizontal line shows p(c) = 0.76; the vertical dashed lines show the behavioral thresholds under the phase difference conditions shown. C Reaction time vs. sound level for during the detection of the amplitude-modulated tone. The reaction times are color-coded based on the phase difference between tone and noise modulation as in A and B. The reaction time vs. level relationship was captured by a linear fit (shown color-coded).

Figure 2C shows how response times changed with sound pressure level. The color scheme is the same as in Figure 2B. In all cases, the reaction times decreased as the tone levels increased, similar to the trend for steady state tones, and steady state tones masked by noise. The slopes of the reaction time vs. tone level relationship were not significantly different with modulation phase difference (ANOVA after bootstrapping, F(7,993) = 1.58, p = 0.137).

Figure 3 shows how the phase differences between the signal and noise modulations (δϕ = ϕ_s-ϕ_n) influenced detection thresholds and reaction times. Figure 3A shows the relationship between the thresholds and δϕ for the exemplar case shown in Figure 2. The thresholds decreased as the phase difference increased from 0 to 180 °, but then increased as phase difference wrapped back to 360 °. The thresholds appeared to be sinusoidally modulated by phase difference and were best fit with a sinusoidal function related to half the phase difference and amplitude of 16.4 dB. The sinusoidal shape of the curve fit was consistent with a subtraction model, where the noise amplitude was subtracted from the signal amplitude or one where the modulation waveform of the noise was subtracted from the modulation waveform of the tone. Figure 3B shows the trend over all other frequencies tested, ranging between 0.4 and 25.6 kHz (shown in different colors). The offset in the curves was highly correlated with and was most likely related to the audiometric thresholds at those frequencies. The trend in threshold changes as a function of modulation phase difference was similar across f_c values, and the magnitude of the threshold change as a function of δϕ was not significantly different as a function of frequency (Kruskal Wallis test, df = 5, H = 8.57, p = 0.127). These results did not vary depending on the onset phase of the tone or noise modulation, as long as δϕ was maintained constant. These results are consistent with listening in the “dips” of the noise; as the phase difference between the signal and noise modulations was varied, the mount of signal in the dips of the noise increased, which could result in improved thresholds.

FIG. 3.

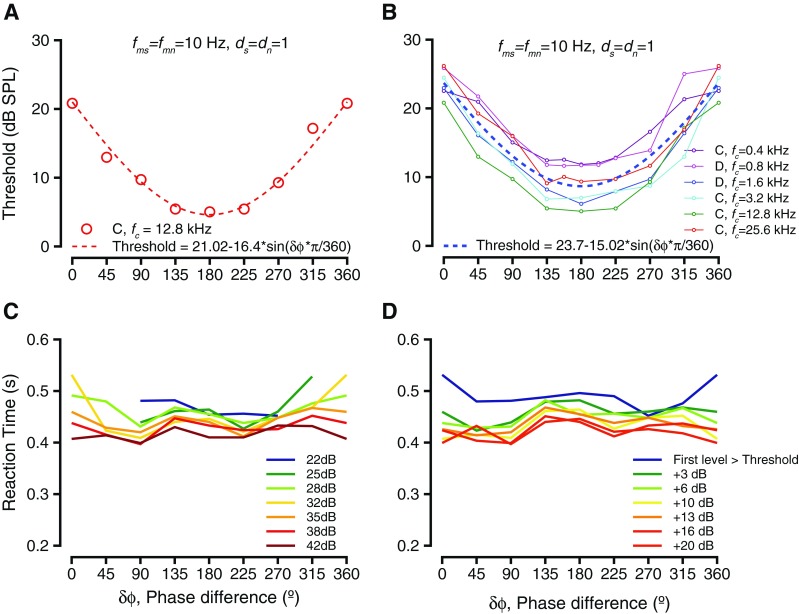
Behavioral performance as a result of varying phase difference between tone and noise modulations. A Threshold as a function of modulation phase difference for the exemplar frequency shown in Figure 1. The circles represent thresholds at the various modulation phase differences, and the dashed red line represents the best fit (sinusoid) to the threshold variations. B Threshold as a function of modulation phase difference for multiple tone frequencies tested. The individual frequencies are color-coded. Fits to individual f _c values are not shown. The dashed line is the best fit to the entire data. C Trends of reaction time as a result of modulation phase difference. The lines connect median thresholds at specific sound levels. Different colors show different sound levels. D Similar to C, but levels are considered relative to threshold.

Figure 3C and shows the effect of δϕ on reaction times at the exemplar f_c (12.8 kHz) condition shown in Figure 1. The slope of the linear fit to reaction time vs. sound level did not differ significantly as a function of phase difference for any frequency studied (see Fig. 2 for an example). We investigated the reaction times at each sound level as a function of the modulation phase difference δϕ. The reaction times at each sound pressure level did not vary significantly with δϕ (individual reaction times are not shown for clarity, line joining medians are shown in Fig. 3C). When we examined the reaction times at sound levels relative to threshold, the reaction times did not vary significantly as a function of δϕ (Fig. 3D, line joining medians shown for clarity). This lack of significant modulation held for both monkey subjects and all tone frequency conditions were studied.

Effect of Modulation Depth

The depth of modulation should have a large effect on detection thresholds. Our previous study found that modulation of signal or noise caused a masking release (lower thresholds) relative to thresholds for unmodulated tones in unmodulated noise (Dylla et al. 2013). Thus, as the depth of the tone or the noise modulation was parametrically increased from 0 to 1, thresholds would be expected to parametrically decrease. When modulation depth is changed, the depth of the trough (or dip) changes by a much larger amount than the height of the peak. The reduction in behavioral thresholds could be expected due to the dramatic increase in the depth of the dip when the noise modulation depth was increased (thus resulting in a much larger signal to noise ratio around the dip). Figure 4 shows an exemplar case describing the effects of changing modulation depth during detection of modulated tones in modulated noise. Figure 4A shows the hit rate during the detection of a 8 kHz tone modulated at 10 Hz at various tone modulation depths (d_s); the masker was broadband noise-modulated at 10 Hz at a depth of unity and was presented at a 55 dB overall level (9 dB SPL spectrum level). Increasing tone modulation depths causes small increases in the peak amplitude of the signal (up to 6 dB for d_s = 1). The noise modulation was in phase with the tone modulation at tone onset (δϕ = 0 °). The different colored symbols show hit rates at two different tone modulation depths (d_s = 0.25, and d_s = 1), and the hit rate vs. sound level function shows that as the modulation depth increased, tone levels required to produce hit rates above the false alarm rates increased. Figure 4B shows the behavioral accuracy (p(c)) for the same case. The psychometric functions (circles) and the associated Weibull fits (lines) detailing the behavioral performance at the two depths of tone modulation show that the tone detection thresholds increased as the tone modulation depth increased. The reaction times under these conditions are shown in Figure 4C. In all cases, reaction times decreased as the tone levels increased. Comparing reaction times across the depths of modulations, the slopes were not significantly different across the different modulation depths (ANOVA after bootstrapping, F(3,997) = 1.47, p = 0.22).

FIG. 4.

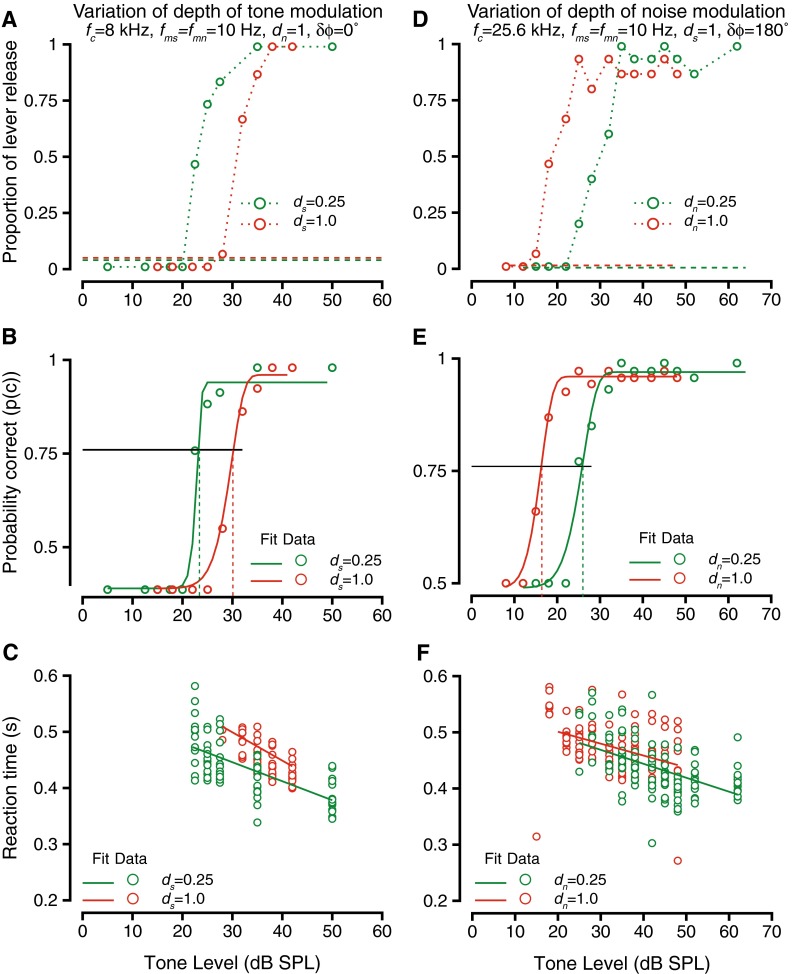
The effect of varying depth of modulation of tones (A–C) or noise (D–F) on the detection of modulated tones in modulated noise. Format is similar to Figure 2. A Hit rate vs. tone level during detection of a 8-kHz tone in broadband noise at a 55-dB overall level for two depths of tone modulation: 0.25 (green) and 1.0 (red). Tone and noise were amplitude-modulated at 10 Hz, and the modulations had a phase difference of 0 °. The depth of noise modulation was held at 1. Dashed lines show false alarm rates. B Probability correct vs. tone level for the two depths of tone modulation in A. The psychometric functions (circles) were fit with a Weibull cdf (solid lines). The horizontal line represents the threshold criterion (p(c) = 0.76), and the vertical lines represent threshold under the two conditions. C Reaction time vs. tone level during detection at the two depths of tone modulation. The reaction times (circles) relation to sound level was captured by a linear fit (solid lines). D–F Same as A–C, but hit rates (D), probability correct and thresholds (F) and reaction times (F) vs. tone level when the depth of noise modulation was manipulated. Tone frequency was 25.6 kHz, tone and noise modulation frequencies were set at 10 Hz, and noise level was 55 dB. The depth of tone modulation was held at 1.0, and the modulations had a phase difference of 180 °.

Figure 4D–F shows similar data for a case in which the depth of noise modulation (d_n) was varied. Increase of the depth of noise modulations caused a small increase in the peak amplitude and large decreases in amplitude at the trough (e.g., Malone et al. 2010). Figure 4D shows hit rates for two different d_n values when a 25.6-kHz tone was being detected; tone modulation frequency and depth were held constant at 10 Hz and 1, respectively, the noise modulation frequency was 10 Hz, and the modulation phase difference δϕ was 180 °. The mean noise level was held constant at a 55 dB overall level across the different modulation depth conditions. The tone level required to produce hit rates higher than the false alarm rate was lower for d_n = 1 compared with d_n = 0.25. This is in contrast to the experiments with tone modulation where the tone and noise modulation were in phase (see Fig. 4A). The resulting psychometric function and their Weibull fits (Fig. 4E) shows that the behavioral accuracy increased and thresholds decreased as the noise modulation depths increased. As in previous cases, there were no significant changes in the relationship between reaction time and tone level as a function of the noise modulation depth (ANOVA after bootstrapping, F(3,997) = 1.14, p = 0.33).

The exemplar data and data from some other tone frequencies (f_c) are summarized in Figure 5. For all examples and data shown, the tone and noise modulation frequencies were held constant and equal at 10 Hz. As expected from Figure 4A, the effect of varying depth of tone modulation resulted in increased tone detection thresholds when tone and noise modulations were in phase (δϕ = 0 °) (Fig. 5A). The exemplar case of Figure 4A–C is shown in blue colors. The threshold changes as a function of d_s were significantly different from zero for each case (ANOVA after bootstrapping, p < 0.01) and were fit with a line. The slopes of the linear fits at the different tone frequencies were all significantly different from zero (t test for slopes, p < 0.01 in all cases) and were not significantly different from each other (ANOVA after bootstrapping, F(2,997) = 1.48, p = 0.228). This result could be because (1) the noise and the tone modulations became more similar as the depth of tone modulation increased or (2) the signal energy in the dips of the masker decreased with increased depth of tone modulation. When the tone and noise modulations were 180 ° out of phase at tone onset (δϕ = 180 °), dip listening theories would predict that the trend would be reversed relative to the in-phase condition, due to increase in the amplitude of the peak during the dips of the masker. The experimental test of the hypothesis showed that the trend between threshold and tone modulation depth when the tone and noise modulations were anti-phase at tone onset was reversed relative to when the modulations were in phase (Fig. 5B). Increasing the depth of modulation of the tone caused a decrease in the tone detection thresholds. The threshold changes were significantly different from zero (t test for slopes, p < 0.008 in all cases). The relationship between threshold and d_s was best captured by a linear fit. This trend that held across all tone carrier frequencies was tested. The slopes of the linear fit were not significantly different from each other for the various frequencies tested (ANOVA after resampling, F(2,997) = 1.79, p = 0.1675). Note that the threshold difference between the highest and lowest modulation depth conditions were smaller when δϕ = 180 ° (modulations were anti-phase) compared to when δϕ = 0° (modulations were in phase). This result is consistent with smaller increases in the peak of the modulated signal with increases in modulation depth (important for δϕ = 180°) as opposed to large decreases in trough depth with increases in modulation depth (important for δϕ = 0 °) (e.g., Malone et al. 2010).

FIG. 5.

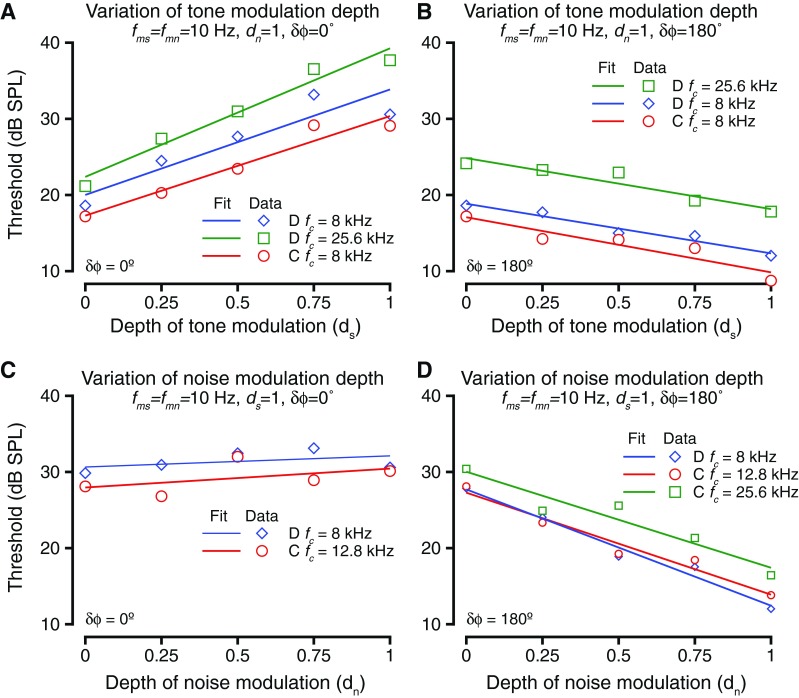
The effects of varying depths of tone and noise modulations. A Threshold as a function of change in the depth of tone modulation. Thresholds are shown for three different tone frequencies (different colors) at various depths of tone modulation. The relationship was best captured by a linear fit (solid lines). The tone and noise modulations were in phase during these blocks. B Similar to A, but for these blocks, the tone and noise modulations were anti-phase (phase difference = 180 °). C Threshold as a function of depth of noise modulation. Format is the same as in A and B. For these blocks, the tone and noise modulations were in phase. D Similar to C, but for these blocks, tone and noise modulations were anti-phase.

The effect of varying noise modulation depth on tone detection thresholds is shown in Figure 5C and D. Changing the noise modulation depth changes the depth of the dip in the masker; thus, lower noise modulation depths were expected to be correlated with tone detection at higher thresholds when the tone and noise modulations are anti-phase, and vice versa. As shown in Figure 4E, changing the depth of modulation of noise (d_n) caused a decrease in tone detection thresholds when the tone and noise modulations were 180 ° out of phase. This trend is summarized for the exemplar frequency (shown in blue) and for some other frequencies (other colors) in Figure 5D. The thresholds varied significantly as a result of changing d_n (t test for slopes, p < 0.01 in all cases), and the relationship between them was captured by a linear fit. The slopes of the linear fit were not significantly different across frequency (ANOVA after resampling, F(2,997) = 2.013, p = 0.15). The threshold changes as a result of changing d_n when δϕ = 180 ° were comparable to the threshold differences after changing d_s when δϕ = 0 ° (compare Fig. 5A and D).

Surprisingly, changing d_n while keeping δϕ = 0 ° did not result in a significant change in tone thresholds (Kruskal Wallis test, p > 0.3 in each case). Figure 5C shows the summary of two examples of changing d_n (using two different tone frequencies). In these cases, the tone and noise were modulated at 10 Hz, and the modulations were in phase. The slope of the relationship between modulation depth and tone threshold was not significantly different from 0 for either of the two examples or the several other tone carrier frequencies tested (t test for slopes, p > 0.24 in each case).

Effect of Modulation Frequency

If the tone and noise were modulated at the same frequency (f_ms = f_mn), one would expect that the tone detection threshold would be high; when the modulation frequencies are different, detection thresholds would be expected to be lower than the equal modulation frequency case (Bregman 1994). We tested that prediction by varying the tone modulation frequency or the noise modulation frequency by blocking modulation frequency. The results of two experiments are shown in Figure 6. Figure 6A–C shows the results of an experiment in which the tone modulation frequency was changed between blocks (varying f_ms), and Figure 6D–F show the results of an experiment in which noise modulation frequency (f_mn) was varied. In both cases, the modulations of tone and noise were in phase at the onset of the tone (onset phase difference, δϕ = 0 °). Figure 6A shows the hit rates as the tone modulation frequency was changed between 10 (blue), 20 (green), and 40 Hz (red). The false alarm rates were zero in all cases and are shown as separated dashed lines for clarity. As expected, for each modulation frequency, the hit rates matched false alarm rates for low sound levels and then increased rapidly until they reached high values close to unity for higher sound levels (Fig. 6A). The effect of changing modulation frequency of the tone was that the tone level at which the hit rates diverged from false alarm rates were lower as f_ms changed from 10 to 20 Hz and differed more from the modulation frequency of noise (Fig. 6A). But at a higher f_ms, the threshold did not change much. This was true at a higher f_ms value tested (80 Hz, data not shown). The behavioral accuracy was computed from the hit rates, and the psychometric functions and Weibull fits in Figure 6B show that the detection thresholds decreased as the tone modulation frequency increased from 10 to 20 Hz (compare blue and green symbols and lines), but did not show a large change going from f_ms = 20 Hz to f_ms = 40 Hz. The reaction times as a result of changing the tone modulation frequency are shown in Figure 6C. As in previous cases, while reaction times decreased as tone level increased under each of the tone modulation frequency conditions. The relationship between reaction time and tone level was best captured by a linear fit (shown by the blue, green, and red lines). There was not a change in the relationship between reaction time and tone level as a result of changing the tone modulation frequency (slopes were not different, intercepts were not different). Reaction times examined in greater detail as a function of modulation frequency (similar to Fig. 3C and D) did not show a trend when examined with absolute sound level or with sound level re: threshold (data not shown).

FIG. 6.

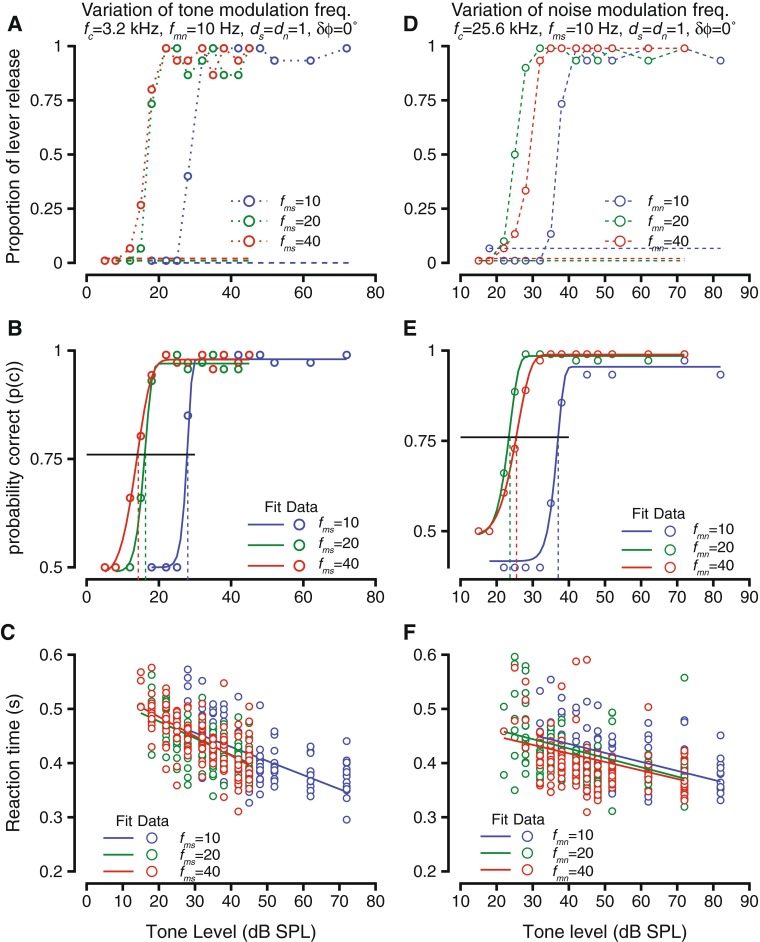
The effects of varying modulation frequency of tones (A–C) or noise (D–F) on detection of modulated tone in modulated noise. Format of the figures are same as in Figure 4. A–C Hit rate vs. tone level (A), psychometric functions, Weibull cdf fits and detection thresholds (B), and reaction times vs. tone level (C) during detection of modulated tone in modulated noise. Tone frequency was 3.2 kHz; noise level was 55 dB, noise modulation frequency was 10 Hz, tone and noise modulation depths were 1.0 each, and the modulations were in phase at tone onset. Data is shown for three tone modulation frequencies—10 Hz (blue), 20 Hz (green), and 40 Hz (red). D–F Similar to A–C, but as noise modulation frequencies were changed. Tone frequency was 25.6 kHz, noise level 55 dB, frequency of tone modulation was10 Hz, depth of modulation of tone and noise 1.0, and the tone and noise modulations were in phase at tone onset.

Figure 6D–F shows an example of when the f_mn was varied over different blocks. As mentioned above, the phase difference between the modulations was zero at tone onset. Figure 6D shows the hit rates, using the same format as Figure 6A. False alarm rates were ∼6 % for the f_mn = 10 Hz condition (blue dashed lines), but were zero for the other two conditions (green and red dashed lines). As with Figure 6A, the false alarm rates are shown staggered for the two cases when they were zero. The effect of changing f_mn was different from the effect of changing f_ms. At f_mn = 20 Hz, the tone levels required to change the hit rate from the false alarm rate to higher levels was reduced relative to f_mn = 10 Hz (compare blue and green symbols, Fig. 6D). When the noise modulation frequency was changed to 40 Hz, then the tone levels required to change the hit rate to levels above false arm rate increased above those for the 20-Hz conditions, but were still lower than the 10-Hz condition. This trend was reflected in the psychometric functions and their Weibull fits (Fig. 6E). Psychometric functions for f_mn = 20 Hz were shifted to lower levels relative to those for f_mn = 10 Hz, as well as those for f_mn = 40 Hz; the psychometric functions for fmn = 40 Hz were shifted to lower levels relative to f_mn = 10 Hz (Fig. 6E). As in previous cases, reaction times decreased as the tone levels increased and were best related to tone level by a linear fit. The linear fit was not significantly impacted by changes in f_mn. A closer examination revealed that reaction times were not impacted by f_mn, whether one examined the relationship based on absolute tone sound pressure level or tone sound pressure level re: threshold (data not shown).

Figure 7 summarizes the results of effects on threshold at various f_c values as a result of changing f_mn or f_ms. Figure 7A shows the effect of varying f_ms while keeping δϕ = 0°. Theories of dip listening predict that the detection thresholds would be lower when tone modulation frequencies increased, due to more signal energy in the dip of the masker. Each color and symbol represents a different tone frequency (f_c) tested (see legend in Fig. 7B for details). For all of these cases, f_mn = 10 Hz and noise level was 55 dB overall level. The detection threshold was largest at f_ms = 10 Hz and was lower for higher values of f_ms. The thresholds for f_ms > 10 Hz were not different from each other (ANOVA after resampling for each frequency, p > 0.2). A similar trend held when the noise modulation frequency (f_mn) was changed for the same f_c values tested (Fig. 7B). When noise modulation frequencies varied, previous studies have found that the thresholds increased due to a reduction in the duration of the masker dip, and thus smaller integration time (e.g., Velez and Bee 2010). In these experiments, tone detection thresholds were highest when f_mn = 10 Hz and were lower for the other values of f_mn. However, thresholds at f_mn = 20 Hz were lower than those for higher f_mn values, a trend that held for all f_c values (ANOVA after resampling, p > 0.17).

FIG. 7.

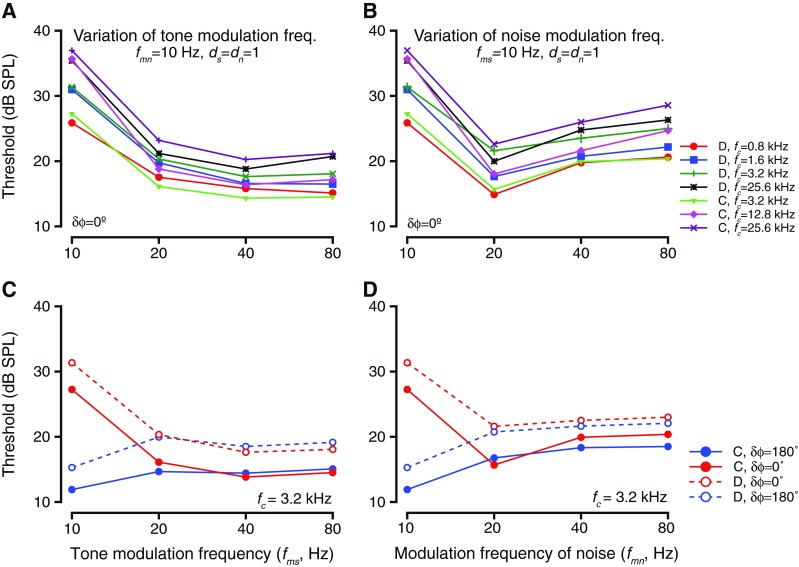
The effects of varying the frequency of tone or noise modulations. A Threshold as a function of tone modulation frequency. Thresholds for detection of tones of varying carrier frequencies (fc, different colors and symbols; legend with panel B) in modulated noise, when tone modulation frequencies were changed. The tone and noise modulation frequencies were in phase during these blocks. B Similar to A, but shows detection thresholds for tones having same fc values as in A (different colors) in modulated noise when the noise modulation frequencies were varied. C Threshold as a function of tone modulation frequency when the tone and noise modulations were in phase (red) or anti-phase (blue) at tone onset for two subjects (solid and dashed lines, respectively). The tone frequency was 3.2 kHz. D Similar to C, but for variations in frequency of noise modulation.

One concern is that when the modulation frequency was changed, then the instantaneous phase of the tone modulation waveform and the noise modulation waveform changed as a function of time. If a subject had multiple looks at the stimuli during the tone presentation (i.e., the subject were to sample instantaneous signal and noise waveforms multiple times) and based the response on instantaneous phase difference, then there would be no effects of phase difference at tone onset on the effect of modulation frequency on detection thresholds. This was tested by testing the effect of modulation frequency with δϕ = 180 °. As a result of this manipulation, the relationship between thresholds and modulation frequency had an inverted shape relative to δϕ = 0 °. One example is shown for changes in f_ms and one for changes in f_mn. Both δϕ = 0 ° and δϕ = 180 ° cases are shown for both modulation frequency variations. When δϕ = 0 ° and f_ms was varied, thresholds at 10 Hz were highest, and thresholds at higher f_ms values were not different from each other (Fig. 7C, see red symbols). When δϕ = 180°, the thresholds at 10 Hz were lower than thresholds at higher f_ms values, and the thresholds at higher f_ms values were not different from each other (blue symbols and lines, Fig. 7C). Note that the thresholds at f_ms ≥ 20 Hz did not differ as a function of δϕ (Kruskal Wallis test after resampling, p > 0.11 at every f_c value tested). This trend was true for other tone frequencies tested (data not shown). Similarly, changing the δϕ values while varying f_mn caused the relationship between f_mn and threshold to be inverted relative to δϕ = 0 °. When δϕ = 0 °, thresholds were highest at f_mn = 10 Hz, lowest at f_mn = 20 Hz, and had values intermediate between the above two at higher f_mn values (red symbols and lines, Fig. 7D). When δϕ = 180 °, thresholds at 10 Hz were lowest, and other thresholds were higher at the other f_mn values. Similar to when f_ms was varied, the thresholds for f_mn ≥ 20 Hz in the δϕ = 180 ° and the δϕ = 0 ° conditions were not significantly different from each other (Kruskal Wallis test after resampling, p > 0.2 for every f_c value). The same trend was observed at all f_c values tested (data not shown).

Predictions of a Model Based on Stimulus Structure

In situations such as this, it is instructive to look at a simple model to fit the behavioral data to attempt to infer the computations taking place underlying this behavior. Our goal is to compare the best model with empirical results and models of processing at each various stages of the pathway to localize transformations in signal processing. The sinusoidal change in threshold with the variation of modulation phase differences suggests that a difference model would fit the threshold changes as a result of the manipulation of tone and noise parameters, reminiscent of the equalization-cancellation (EC) model proposed for binaural processing (Durlach 1963). Note that a secondary formulation of the model would involve just subtraction of the envelopes, similar to models proposed by Hall et al. (1988); the trend in the predicted results of a model that computed envelope differences matched those observed by the proposed model, but getting threshold equivalents proved problematic since the envelope subtraction model was independent of stimulus or noise levels. An alternate formulation of the model computed signal to noise ratio at the dips of the masker (dips were designated as the time intervals when the instantaneous masker levels fell below steady state levels, after Velez and Bee (2010)). The results of this model showed trends that did not match the behavioral results for the effect of manipulating tone modulation frequency and δϕ = 0 ° (see below). To formalize the difference model in our analysis, we computed the difference between the amplitude-modulated signal waveform and the amplitude-modulated noise waveform (S_AM(t) − N_AM(t)) as a function of time for each tone level. The amplitudes of the tone and noise waveform were logarithmically transformed so as to match sensitivity to perceptually related parameters. If the log-transformed noise amplitude for t = t₀ was larger than the log-transformed signal amplitude at t = t₀, the signal would be masked; in those cases, we set the difference equal to zero. When the log-transformed signal amplitude exceeded the log-transformed noise amplitude (either positive or negative), the absolute value of the difference was calculated. The total energy of this difference function was calculated by integrating the difference waveform numerically over time, consistent with the finding that for short duration (<1 s) signals, signal to noise ratio is best expressed as a dimensionless quantity of signal energy to noise spectrum level (e.g., Green et al. 1959). The area under this accumulated difference curve was calculated using the trapezoidal rule and should be directly related to the behavioral performance at that tone level. That is, if the area under the difference curve increased with the parametric variation, it is expected that the hit rate would increase. The area was calculated at all tone levels that were used in the experiment. We then made an assumption that the criterion for behavioral threshold was the same across all conditions and used a criterion to define the threshold for a specific set of parameters. We set the criterion such that the threshold to tones alone matched audiometric thresholds. The criterion was varied in the simulation; the specific value of the criterion changed the absolute threshold level, but did not affect the change in threshold as a result of the parametric manipulation. Figure 8 provides the results of such a model calculation.

FIG. 8.

Results of a simple energy difference model that predicts variation in behavioral threshold as a result of the parameter manipulations for the studies presented here. Parameters match those used in the experiments. A Effect of varying phase difference between tone and noise modulations. Circles show thresholds, solid line represents best fit to the data. B Effect of varying frequency of noise amplitude modulation. Thresholds are shown when tone and noise modulation were in phase (red triangles) and anti-phase (blue diamonds) at tone onset. Dashed and dotted lines show best fit to the symbols (exponential functions). C Similar to B, but for variations in tone amplitude modulation frequency. Inset. The results of behavioral experiments in two monkeys testing the effects of frequency of tone modulation between 10 and 20 Hz shows an undershoot in threshold to match model predictions when tone and noise modulations were in phase at tone onset. D Effects of varying depth of noise modulation. Format is similar to C. E Similar to D, but parameter varied was depth of tone modulation.

The results shown in Figure 8 were obtained using a tone frequency of 1 kHz. The results did not change with the use of other frequencies, so the results shown could represent any frequency within the audible range of the primate. The simulation was such that the model predicted a threshold of 1.5 dB SPL when a 1-kHz tone was presented alone, and the predicted threshold in 55 dB noise was 29 dB SPL. These values were similar to the actual threshold values measured for the two monkeys used as subjects in this study (tone alone: monkey C: −0.5 dB; D: −0.8 dB; tone in 55 dB noise: C: 29.5 dB; D: 30.5 dB; see Fig. 1). The criterion area value used to define threshold for all future simulations was maintained identical to that for the unmodulated tone presented alone and in noise. The noise and the tone were amplitude-modulated, and the model run as described. The effects of manipulating the modulation phase difference on the model thresholds are shown in Figure 8A. The thresholds were highest at δϕ = 0 °; as the values of δϕ increased from 0 to 180 °, thresholds decreased and then increased as δϕ wrapped back around to 360 ° (green circles, Fig. 8A). This trend in model thresholds is just identical to the data shown in Figure 3A and B. The relationship between the threshold and δϕ was best fit with a sinusoidal function with an amplitude of 13.9 dB (green line, Fig. 8A), much like the behavioral data was fit by a sinusoid (Fig. 3A and B). The magnitude of the effect of phase difference on model thresholds was very similar to its effect on the behavioral thresholds (compare Fig. 3A and B with Fig. 8A). This suggests that a difference model is sufficient to capture the effects of changing δϕ.

Figure 8B and C shows the effect of varying the frequency of amplitude modulation of the tone or the noise on the model thresholds. Figure 8B shows the effects of varying the frequency of noise modulation (f_mn) while keeping the frequency of tone modulation (f_ms) constant at 10 Hz. With δϕ = 0 °, and as f_mn differed from f_ms, the thresholds decreased rapidly and then saturated for f_mn ≥ 20 Hz (red triangles, Fig. 8B). The range of model threshold values and their trend are similar to the behavioral data shown in Figure 6B. This relationship was best captured by an exponential function of (f_mn − f_ms) (red dashed line, Fig. 8B). With δϕ = 180 °, the thresholds increased from a smaller value when f_mn = 10 and saturated at f_mn ≥ 20 Hz (blue diamonds, Fig. 8B). It is noteworthy that the model thresholds matched for the two δϕ values, in a manner similar to the behavioral data (Fig. 7D). This result is consistent with behavioral thresholds for δϕ = 180 ° that increased as f_mn increased and saturated at f_mn values larger than 20 Hz (consistent with Fig. 7D). An exponential function of f_mn − f_ms best fit the model. Note also that the model predicts that the threshold changes in the δϕ = 0 ° condition to be larger than those in the δϕ = 180 ° condition. This is, in fact, consistent with the behavioral data from both subjects in this study (see Fig. 7D).

The effect of changing f_ms while maintaining constant f_mn on threshold are shown in Figure 8C. As f_ms differed from f_mn, and with δϕ = 180 °, the model predicts thresholds that increased and then saturated as f_ms ≥ 20 Hz (blue diamonds, Fig. 8C), similar to the effect of changing f_mn. The behavioral results were similar to this function (see Fig. 7C). However, when δϕ = 0 °, the area increased as f_ms increased, attained a peak value at f_ms = 13 Hz, and then decreased to saturate for f_ms ≥ 20 Hz. Because of the low resolution of the sampling of f_ms values in the data reported in Figure 7, the correlation with the behavioral values is not clear. To clarify the match of this model result with behavior, we tested the monkeys at f_ms = 11, 12, 13 Hz, and the behavioral results are shown inset. The behavioral results (see Fig. 8C, inset) show that the thresholds initially decrease, attained a minimum at f_ms = 13 Hz, and then increased when f_ms = 20 Hz. This trend, which was observed for both monkeys (different colors, Fig. 7C, inset), matched the model prediction. Further analyses with the model indicated that the dip in threshold is matched with the frequency at which the lowest cross-correlation was obtained with a 10-Hz sine wave (representing the noise modulation) for a 200-ms duration signal, and the frequency at which the modulation envelope of the signal and the noise were most different cumulatively. The range of threshold values and their trend matched behavioral values. As with f_mn values, the model predicted similar thresholds in the δϕ = 0 ° and δϕ = 180 ° conditions for f_ms ≥ 20 Hz and predicted smaller threshold changes in the δϕ = 180 ° condition relative to the δϕ = 0 ° condition. Both of these were also consistent with behavioral results (Fig. 7).

The model predictions for the effects of modulation depth are shown in Figure 8D and E. For these calculations, f_ms and f_mn were held constant at 10 Hz. When the depth of tone modulation (d_s) increased from 0 to 1, and δϕ = 0 °, the predicted thresholds increased (red triangles, Fig. 8E) and was fit with a straight line. This trend and its magnitude are both consistent with the behavioral data (compare with Fig. 5). When d_s increased from 0 to 1, and δϕ = 180°, the predicted thresholds decreased (blue diamonds, Fig. 8E) and was best fit with a straight line. This trend and the range of thresholds predicted were also consistent with the behavioral data (Fig. 5). Note that the model is consistent with larger threshold differences in the δϕ = 180 ° condition relative to the δϕ = 0 ° condition. When the depth of noise modulation (d_n) increased from 0 to 1, and δϕ = 180°, the thresholds decreased (blue diamonds, Fig. 8D) and were fit with a straight line. This is consistent with behavioral thresholds decreasing under the same conditions (Fig. 5). When d_n increased from 0 to 1, and δϕ = 0 °, the model thresholds stayed identical for modulation depths of 0 to 0.75, and then increased by 2 dB for a noise modulation depth of 1 (red triangles, Fig. 8D). The model thresholds were fit with a straight line, the slope of which was not different from zero (t test for slopes, p = 0.473). This result is also similar to the behavioral data, which suggests that varying d_n does not significantly change amplitude-modulated tone detection thresholds (Fig. 5). This may be related to increased sensitivity to tone modulation relative to noise modulation as a result of two-tone suppression at the level of the auditory nerve. Note also that the model is consistent with larger threshold differences in the δϕ = 180 ° condition relative to the δϕ = 0 ° condition. Thus, a single energy difference accumulation model can account for all the results.

DISCUSSION

The results of this study show the effects of varying the temporal relationship between time varying signal and time varying noise. By systematically varying the various parameters that characterize the relationship between signal and noise modulations, the results of this study show that the computations underlying the detection of signal in noise are consistent with a differencing operation.

Comparison with Previous Results

The power spectrum model of hearing suggests that during the masked detection of a sine-wave signal, the subject utilizes information from the auditory filter that is centered on the sinusoid to be detected (Moore 2003). While there is evidence that the system is able to utilize across-frequency cues in certain circumstances, a test of within vs. across-frequency band cues requires manipulating the bandwidth of the noise, which was not done in this study. The results of this study are generally consistent with the findings that when the modulation properties of the signal and the noise are different, signal detection thresholds were lower; when modulation properties between signal and noise were similar, signal detection thresholds were higher. These results are consistent with previous findings in humans (e.g., McFadden 1987; Cohen and Schubert 1987; Fantini and Moore 1994), passarines (Langemann and Klump 2007), and corvids (Jensen 2007).

Recent studies have suggested that dip listening (listening selectively during the trough of the masker) is sufficient to explain changes in detection thresholds or recognition thresholds (e.g., Velez and Bee 2010, 2011). Some of the results of this study are generally consistent with dip listening mechanisms that account for trends in threshold changes. For example, changing δϕ changes the amount of signal energy in the dip of the masker; the least signal energy was at δϕ = 0 °, and the most energy was at δϕ = 180 ° and would result in threshold changes consistent with trends observed in Figure 3B. However, dip listening theories predict that as the modulation frequency of the masker increased, detection thresholds would increase due to reduced duration of dips (e.g., Gustafsson and Arlinger 1994; Bacon et al. 1998; Velez and Bee 2010, 2011). Those results are not consistent with the findings after the manipulation of noise modulation frequency (Fig. 7). In fact, the only model that explains the data across all conditions is the energy difference model (see Fig. 8).

In general, detection experiments involving modulated sounds have been done in the context of comodulation. In comodulation masking ratio (CMR) experiments, the detectability of static signals of various sorts was determined in the presence of multiple narrow bands of noise having either the same or different modulations or in the presence of bandpass noise that was amplitude-modulated (e.g., Hall et al. 1984; Cohen and Schubert 1987; Hall 1986; McFadden 1986). These studies cannot be directly compared with CMR studies because both signal and noise were modulated in this study. A better comparison would be studies of comodulation detection differences (CDDs), in which subjects were asked to detect a modulated band of noise that was simultaneously masked by one or more spectrally non-overlapping noisebands (called cue or flanking bands) that were also modulated. When the modulation of the signal band is different from that of the flanking band(s), detection thresholds can be 10–12 dB better than when all of the flanking band envelopes were the same (councorrelated condition) relative to when all the flanking band modulations were different (all random condition, Cohen and Schubert 1987; McFadden 1987; Wright 1990; Fantini and Moore 1994). Experiments in corvids and paasarenes showed similar threshold changes under CDD measurements in birds (Langemann and Klump 2007; Jensen 2007), suggesting that the CDD is not specific to humans, but maybe a general processing mode used to segregate sounds in complex environments (Cohen and Schubert 1987; Bee and Micheyl 2008). The experimental conditions in this paper are similar to the “all correlated” condition in CDD studies (when the signal and the masker had similar modulations) or the all uncorrelated condition (when the signal and masker had different modulations). While the experiments in the current study did not really test CMR or CDD explicitly by using bands of noise as signal or noise, the results are consistent with large threshold changes as a result of changes in the correlation between the signal and noise in the above studies.

The parameters manipulated in this paper have also been manipulated, but mainly in studies of the CMR, when signals were unmodulated and maskers were modulated (e.g., Hall et al. 1988; Schooneveldt and Moore 1989; Grose and Hall 1989; Fantini 1991). Many studies have documented that human subjects were able to discriminate the modulation parameters manipulated here (e.g., Wakefield and Edwards 1987; Yost and Sheft 1989; Wakefield and Viemeister 1990). Most of the experiments in which the signal and masker were both modulated involved manipulation of correlation between the different noisebands (noisebands generated with different amplitude and phase parameters; McFadden and Wright 1990; Wright 1990; Borrill and Moore 2002) rather than the depth of modulation, the modulation phase, or the modulation frequency. The threshold changes in the current study were roughly comparable to than those seen for human behavior caused by changed noiseband correlations (e.g., ∼10 dB, McFadden and Wright 1990); however, maskers in previous studies had no spectral overlap with the signal (e.g. Cohen and Schubert 1987; Langemann and Klump 2007). Perhaps, the lack of uncertainty of the signal or noiseband modulations contributed to the large effects in the current study (see ∼15-dB threshold change for modulating phase difference in Fig. 3, and ∼10–20-dB threshold change while manipulating depth of modulation, Fig. 5).

In general, the detection or discrimination of target sounds among distractors is facilitated under conditions that promote the perceptual segregation of targets from interferers, especially if targets and interferers share some common features (Gockel et al. 1999; Micheyl and Carlyon 1998; Micheyl et al. 2005) or when they vary rapidly and unpredictably over time (Kidd et al. 1994, 1995, 2002; Micheyl et al. 2007). This suggests that (1) changing the modulation phase difference between signal and noise increases the segregation between signal and noise (Fig. 3); (2) changing depth of modulation of the tone to values closer to the depth of noise modulation when the tone and noise modulations were in phase decreased the segregation of signal and noise (Fig. 5); (3) when tone and noise modulations were anti-phase, changing the depth of noise modulation to values closer to the tone modulation depth improved the segregation of tone and noise (Fig. 5B and D; probably as a result of enhanced dip listening arising from deeper dips in noise modulation); (4) changing the difference between tone and noise modulation frequency increased segregation when the tone and noise modulations were in phase, whereas the same stimulus manipulation when the modulations were anti-phase at tone onset decreased segregation (Fig. 7). All of these are consistent with theories of auditory scene analysis, which suggest that when modulation parameters are different, stream segregation is enhanced (Bregman 1994). This is also consistent with the idea that amplitude modulation is an important contributor to object formation (Yost and Sheft 1989) and that the monkeys had lower thresholds detecting signal from noise when the properties of the signal and noise modulations were larger (implying signal and noise were treated as two different objects). An addition to the theories of scene analysis here is that the various factors causing stream segregation are not independent; rather, they interact in predictable ways (e.g., modulation phase and depth of modulation).

Alternatively, all the data in this study could be explained by selectively listening in the dips of the masker. Dip listening caused enhanced behavioral performance when the masker modulation frequencies were low (Gustafsson and Arlinger 1994; Bacon et al. 1998; Velez and Bee 2010). However, these data show that the relationship between the modulation frequencies of signal and masker form an important determinant of behavioral performance.

Previous studies have suggested either perceptual segregation of signal and noise, or dip listening, or suppression in the auditory pathways as a mechanism to explain effects such as those seen in this paper (e.g. Borrill and Moore 2002; Moore and Borrill 2002; see Moore 2003 for a review). The perceptual performance in such stream segregation or dip listening tasks can be explained by comparing the different segregated streams (effectively a subtraction operation, similar to Durlach’s EC model (1963)). So, this would suggest that the signal and the noise in this study could be segregated when the parameters of the signal and noise were different (e.g., when δϕ ≠ 0, or when the f_ms ≠ f_mn, or when d_s ≠ d_n). Consistent with such a suggestion, the threshold changes as a result of the manipulations in this study were consistent with a differencing or comparator operation being performed by the auditory system (compare Fig. 8 with Figs. 3, 5, and 7). This is consistent with previous suggestions that subtraction mechanisms may be in play in a detection task (e.g., Hall et al. 1988). However, the dip listening may also apply for the current study that could not apply to the Hall et al. study; the thresholds were lower when the tone and the noise modulations were anti-phase at the onset of the signal relative to when the tone and noise modulations were in phase. In the cases where modulation frequency was changed, having higher tone modulation frequency meant that even if the signal and noise modulations were in phase at signal onset, there was some signal during the dip of the noise; when signals and noise modulations were anti-phase at signal onset, the energy at the dip decreased as a result of changing the tone modulation frequency, so thresholds increased as the tone modulation frequency increased (Fig. 7). However, even in those conditions where dip listening could explain the behavioral performance, a signal to noise difference or comparison best explained the threshold changes. Some previous studies have found that perceptual streaming and dip listening did not apply under certain conditions, and the only mechanisms that could explain detection based on correlations would be neural suppression (Borrill and Moore 2002).

An interesting finding is that the δϕ values that are equally separated from 180 ° produced roughly equal thresholds (i.e., thresholds for 45 ° and 315 ° phase shifts were very similar as were thresholds for 90 ° and 270 °, etc.; Figs. 1 and 2). This suggests that the exact timing of the peaks and troughs of the signal and noise did not matter, just that the peaks were coincident or not. This suggests that the behavioral strategy used by the monkeys did not involve the relative timing of the features of the tone and noise stimulus and was possibly related to simply the stimulus energy.

The one parameter that did not affect behavioral thresholds (or simulated thresholds) was when the depth of noise modulation was varied while the tone and noise modulations were in phase at the onset of the signal (data: Fig. 5C; model: Fig. 8D). Previous results in macaques (Dylla et al. 2013) and in humans (e.g., Hall et al. 1984) suggest that detection thresholds in modulated maskers were much lower than those in steady-state (unmodulated) maskers. These two results together suggest that the system is highly tuned to the salience of the tone modulation, and any potential advantage provided by noise modulation was potentially minimal when the tone and noise were in phase.

An unusual prediction of the model was that the detection threshold for modulated tones would decrease from its high values at f_ms = 10 Hz, be lowest at f_ms = 13 Hz, and then saturate at a higher value for f_ms ≥ 20 Hz (see Fig. 8C). Thus, the 13 Hz represents the tone modulation frequency at which an observer would notice the greatest dissimilarity between the tone and the noise modulation waveforms. This finding lends some credence to the idea that correlations could play a role in the generation of perceptual streams. Such sensitivity might require modulation shape discrimination, such as those observed in the auditory cortex in macaques (Malone et al. 2007).

Potential Neurophysiological Mechanisms

While the neurophysiological responses under these exact conditions have not been studied, some studies have examined neuronal responses when signals are masked by modulated noise. Studies in songbirds have shown that changes in correlation in the envelope between signal and noisebands cause changes in the response thresholds of neurons in the analog of the primary auditory cortex (Bee et al. 2007). The range of changes in these forebrain neuronal thresholds matches, roughly, those observed behaviorally in the same species (Langemann and Klump 2007). Similarly, other studies in mammalian species have also shown that cortical neurons modulate their responses in a manner similar to behavior in response to stimuli in the presence of modulated maskers (Fishman et al. 2001, 2012). One possible mechanism of signal detection in the presence of time varying masker—the masker causes a synchronization of the responses of a population of neurons, and the presentation of a signal (modulated or otherwise) desynchronizes the responses of neurons tuned to the signal parameters from the rest of the neurons (Nelken et al. 1999). Recent studies have found that neurons in auditory cortex are very sensitive to changes in amplitude (both increases and decreases) and function as envelope shape discriminators with a wide range of response characteristics (Malone et al. 2007, 2010). This suggests that the responses of cortical neurons would be able to respond differentially to the parameters of the modulations of tones and noise. This is consistent with results from Sutter’s laboratory that show that cortical neurons change their responses depending on the modulation parameters as well as the behavioral state of the animal and the variations in behavioral performance (Yin et al. 2011; Niwa et al. 2012a, b; Johnson et al. 2012). While those results suggest enough information in the responses of forebrain neurons to account for behavior, it was not clear if such information represented by auditory objects was present in the earlier parts of the brain or what exact computations or mechanisms were involved in the generation of the responses.

Studies in the visual system have implicated early structures like the primary visual cortex and even the retina in some species in the processing of local vs. global stimulus properties to account fro scene segmentation (e.g., Olveczky et al. 2003; Baccus et al. 2008; Nothdurft 1994). Very few studies of the auditory system have looked at neuronal responses in relation to scene segmentation, and they have been mainly in the auditory cortex (e.g. Fishman et al. 2001, 2012; Fishman and Steinschneider 2010; Gutschalk et al. 2005; Nelken and Bar-Yosef 2008). Modulations clearly are a major signal for segregating or integrating sounds. Modulated sounds change responses in multiple parts of the auditory system. The manipulations in this study (the onset phase difference, modulation frequency, and modulation depth) cause changes of activity in many parts of the auditory system such as the cochlear nucleus (CN; e.g. Rhode and Greenberg 1994; Joris et al. 1994; Moller 1976) and the inferior colliculus (e.g., Nelson and Carney 2007; Krishna and Semple 2000; Langner and Schreiner 1988; Muller-Preuss et al. 1994; Rees and Moller 1983). However, very few studies have directly tested the neuronal correlates of signal detection when the masker is temporally modulated (CN: Pressnitzer et al. 2001; Neuert et al. 2004). The studies in the cochlear nucleus found that very few neurons in the ventral CN showed neuronal correlates of enhanced thresholds such as those seen in behavior (Pressnitzer et al. 2001). However, a majority of neurons in the dorsal CN showed such neuronal correlates (Neuert et al. 2004), and these threshold enhancements were postulated to result due to wideband inhibition. However, magnitude of neuronal threshold changes in the dorsal CN could not account for behavioral threshold changes. A study in the inferior colliculus of cats has shown that a majority of inferior colliculus (IC) neurons show responses that are associated with wideband inhibition beyond that observed in the CN (Davis et al. 2003). This suggests that neurons in the IC should show detection thresholds that are larger than those seen in CN and may be more in line with behavioral observations. These responses may be further modified at the level of thalamus and cortex to represent the behaviorally similar changes in neuronal responses seen in the forebrain during such tasks (e.g., Bee et al. 2007; Fishman et al. 2012).