Skip to main content
PMC home page
BMC Ecology logoLink to BMC Ecology
. 2004 May 7;4:6. doi: 10.1186/1472-6785-4-6

Intrinsic and climatic factors in North-American animal population dynamics

Nicolas Loeuille 1,✉, Michael Ghil 2
PMCID: PMC416486  PMID: 15132754

Abstract

Background

Extensive work has been done to identify and explain multi-year cycles in animal populations. Several attempts have been made to relate these to climatic cycles. We use advanced time series analysis methods to attribute cyclicities in several North-American mammal species to abiotic vs. biotic factors.

Results

We study eleven century-long time series of fur-counts and three climatic records – the North Atlantic Oscillation (NAO), the El-Niño-Southern Oscillation (ENSO), and Northern Hemisphere (NH) temperatures – that extend over the same time interval. Several complementary methods of spectral analysis are applied to these 14 times series, singly or jointly. These spectral analyses were applied to the leading principal components (PCs) of the data sets. The use of both PC analysis and spectral analysis helps distinguish external from intrinsic factors that influence the dynamics of the mammal populations.

Conclusions

Our results show that all three climatic indices influence the animal-population dynamics: they explain a substantial part of the variance in the fur-counts and share characteristic periods with the fur-count data set. In addition to the climate-related periods, the fur-count time series also contain a significant 3-year period that is, in all likelihood, caused by biological interactions.

Keywords: population dynamics, climatic effects, principal component analysis, spectral analysis, multi-annual periodicities.

Background

The dynamics of animal populations are driven by both biotic and abiotic factors. Following the seminal work of Volterra [1], many models assume that direct interactions between species, such as predation, competition or mutualism, play a dominant role in population dynamics. The key role of such biotic factors need not exclude other potentially important processes. Abiotic factors that are likely to play a significant role in the dynamics of an animal community include the climatic, physical and chemical conditions in which the different populations live.

The present work aims at separating the influence of biotic and climatic factors in the dynamics of eleven North-American mammal populations. The animal species we study are bear, beaver, fisher, fox, lynx, marten, mink, muskrat, otter, wolf and wolverine. The variations in these populations are determined by using the Hudson Bay Company's database of annual fur-counts [2]. The basic assumption is that the number of animals captured is directly proportional to the animal populations. This assumption is clearly an approximation but more complete animal-population counts of comparable length do not seem to exist. The lengths of these time series almost equal one century and they allow us to assess the relative role of the different factors that affect these eleven populations, even those that vary on an interdecadal time-scale.

The application of both principal component (PC) analysis and spectral analysis helps separate the different factors that influence the dynamics of the animal community under study. Using a fairly large set of long population records makes the application of PC analysis necessary: it allows us to distinguish between climatic factors that affect all the populations and those that do not. Advanced spectral methods permit us, on the other hand, to detect subtle but systematic variations in one or more of the mammalian populations under study. The results of this combined data analysis approach allow us to conclude that both climatic and intrinsic factors affect this community and to quantify, at least approximately, their relative role.

Results

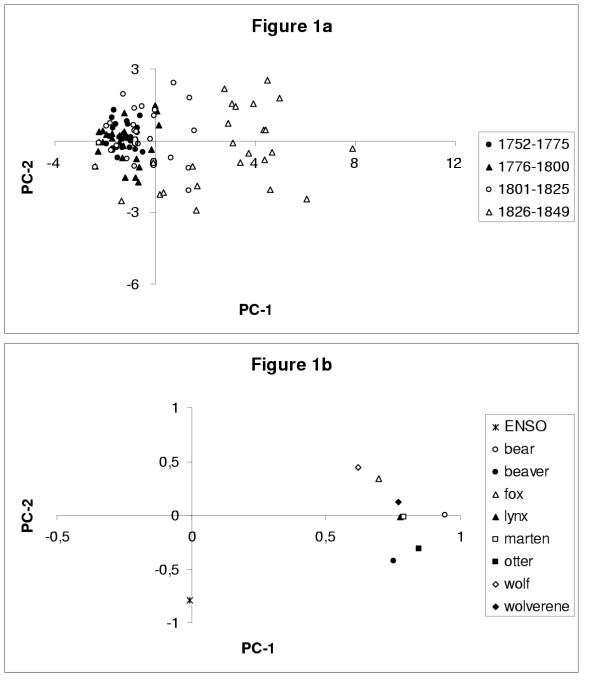
We analyzed four different data sets: one contains the fur-counts alone, the other three contain in addition one climatic index each (see Methods section). Using PC analysis, the individual years that constitute each data set may be separated into two groups. In the plane spanned by the first two PCs (Figure 1a), the first half of the data set that contains the eight longest fur-counts and the ENSO index is concentrated in a small area, whereas the other years are much more dispersed. This separation holds for all the data sets studied (not shown). It reflects the fact that the amplitude of the variations of the fur-counts is fairly low for the first half of the data, and much higher thereafter.

Figure 1.

Figure 1

Open in a new tab

Principal component (PC) analysis of the data set composed of the eight longest fur-counts and the Niño-3 sea surface temperatures (SSTs). EOF-k is the eigenvector corresponding to the kth largest eigenvalue of the covariance matrix of the data set. Each time series, whether fur count or climatic index, is centered and normalized (i.e., it has zero mean and unit variance), and the EOFs so obtained have length one. (a) Distribution of the annual values of the two leading PCs with respect to time; points are grouped by quarter-century intervals (see legend inside the figure). Note that the first half of the record (1752–1800) lies entirely within a small area in the left half-plane, and that the amplitude of the variations from one year to the next increases significantly later in the record. The results are similar when using just the eight longest fur-count records or the combination of these with either one of the other two climatic indices (not shown). (b) Correlation circle corresponding to the same PC analysis as in panel (a). The abscissa (PC-1) captures 54% of the total variance and is highly correlated with each animal-population index. The animal populations included here are bear, beaver, fox, lynx, marten, otter, wolf and wolverine. The ordinate (PC-2) captures 14% of the variance and is very well correlated (r = 0.76) with the Niño-3 SSTs; see legend in the figure for symbols.

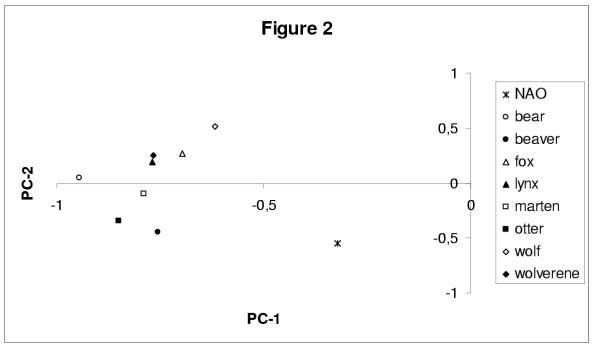
The variance captured by each component is given by the corresponding eigenvalue. The eigenvalues of the PC analysis for all four data sets are collected in Table 1. The meaning of the leading principal axes is given by the correlation circles. The one presented in Figure 1b corresponds to the data set of {(fur-counts) + ENSO}. The first axis is clearly correlated to all the animal populations, whereas the second axis is correlated to the ENSO index. The correlation coefficient r between PC-1 and each animal population in Figure 1b ranges between r = 0.94 (for the bears) and r = 0.63 (for the wolves). The same plot for the other three data sets (shown only, in Figure 2, for the {(fur-counts) + NAO}) indicates that the first component is always by far the largest, since it embodies at least 54% of the total variance (see Table 1); PC-1 correlates, most clearly and exclusively, with the animal populations, in all four data sets. The animal populations are thus most strongly correlated to each other.

Table 1.

Eigenvalues of the principal component (PC) analysis for the four data sets, given as percent of the total variance (rounded off to the nearest whole percentage point). Note that the first component captures the lion's share of the variance, and that the second component is also quite sizable.

Data set Egv 1 Egv 2 Egv 3 Egv4 Egv5 Egv6 Egv7 Egv8 Egv9
Furs 61% 13% 9% 6% 5% 4% 1% 1% --
Furs + NAO 55% 12% 10% 7% 5% 5% 3% 2% 1%
Furs + ENSO 54% 14% 9% 7% 5% 5% 3% 2% 1%
Furs + temp 56% 12% 11% 7% 5% 4% 3% 2% 1%
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

Correlation circle corresponding to the PC analysis of the data set that includes the same eight fur-counts as in Figure 1, but replaces the ENSO climate index there with the NAO index here. The abscissa (PC-1) captures 55% of the total variance and is highly correlated with each one of the animal populations; same notation as in Figure 1b. The ordinate (PC-2) captures 12% of the variance and is correlated fairly well (r = 0.52) with the NAO index, but not as highly as for ENSO in Fig. 1b.

When a climatic index is added to the data set of fur-counts, it is strongly correlated, in all three cases, with the second axis. This correlation is shown for the data set of {(fur-counts) + ENSO} in Figure 1b and the {(fur-counts) + NAO} in Figure 2; it is also true for the NH temperature (NHT) index (not shown). The different animal species are thus affected to various degrees by climatic factors, but apparently less so than by biotic interactions among species.

The PC analysis also allows one to separate the signal from the noise in the data sets. As already mentioned, the first component contains the lion's share of the variance (54% to 61%) and PC-2 is quite important, too (12% to 14%; see Table 1). We studied PC-5 as well, because its variance is very close to that of PC-6 and so this pair may jointly capture a single mode of, possibly oscillatory, behavior; if this were the case, the combined mode would also represent 9%–10% of the variance. Consequently, spectral analysis was performed on all four of these components, PC-1, PC-2, PC-5 and PC-6. The results for PC-5 and PC-6, however, turned out to be less interesting and are thus omitted here.

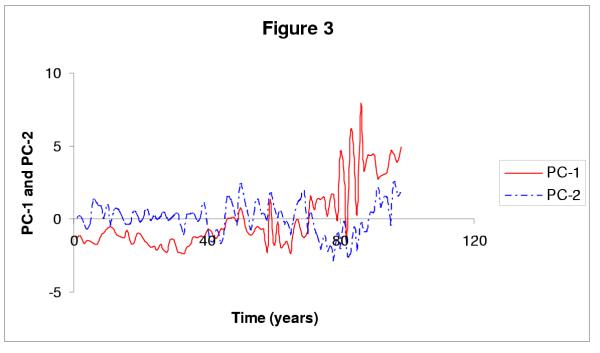
Figure 3 displays the projection of the {(fur-counts) + ENSO} data set on the two leading components. The projection on PC-1 (Figure 3) is quite similar in the other three data sets, given that it stands essentially for the animal populations, which are the same in all four sets. Projection on the other components (shown for this particular data set and PC-2 in Figure 3), on the other hand, does depend on the climatic index chosen, or its absence (not shown for the other PCs and other data sets).

Figure 3.

Figure 3

Open in a new tab

Projection of the {(fur-counts) + ENSO} data set on axes 1 and 2 of the PC analysis; see legend inside the figure. Each of these two projections is then analyzed, using the SSA-MTM Toolkit, for all four data sets, to give the spectral results shown in Table 2.

The results of spectrally analyzing PC-1 and PC-2 in all four data sets are shown in Table 2. We cross-checked the spectral peaks obtained by the median-filter version [3] of the multi-taper method (MTM), as listed in the Table, with those given by the Monte Carlo version [4] of Singular Spectrum Analysis (SSA; not shown). The two sets of results agree overall very well for all species. Occasionally, slight differences arise for minor peaks that are statistically significant at the 90% level in one of the analyses but not the other. The main periods are all significant at the 99% level when tested against a red-noise null hypothesis [5], whereas the significance threshold for secondary periods is 95%.

Table 2.

Spectral analysis of the two leading components of the four data sets; the periods are given in years. The first column for each PC gives the dominant periodicities, the second one gives the less pronounced peaks; for economy of presentation, the 160–170-year nonlinear trend [5] is also included in the first column for PC-1. The analysis reported in this Table was performed using the median-filter MTM [3,5] with the bandwidth parameter p = 2 and K = 3 tapers. These parameter values give a spectral resolution of 0.04 cycles/year, i.e., they allow us to discriminate between peaks at 2, 2.5, 3 and 3.5 years. The results were checked using Monte Carlo SSA [4,5] with a window width of M = 9 year. The significance level of the main periods is at least 99% against a null hypothesis of red noise; for the secondary periods, the threshold is 95%. Periods in bold are significant in both the MTM and SSA analyses; periods in italics are strongly significant in one of the two methods and marginally significant in the other, while other periods are only significant in one of the two analyses.

PC-1 PC-2
Main periods Secondary periods Main periods Secondary periods
Furs 170 3 2.5 2.5 40
Furs+NAO 160 3 2.5 3.5 40 2
Furs +ENSO 160 3 2.5 4 2.5 2 30
Furs+temp 170 3 2.5 44 2.5 3.5
Open in a new tab

In order to verify the interpretation of the results in Table 2, we also carried out a spectral analysis of each climatic index by itself (Table 3). For the ENSO index, the main period is of 4 years and the secondary period is 2-year long, in agreement with known results ([6,7], and references therein). The NAO results are much less clear cut: two periods are emerging, 3.5 and 3 years, but their level of significance is quite low (90%). For the NHT index, the main modes of variation are a 170-year trend [8,9] and a 2.5-year period; a secondary 2-year period also arises in this signal. A 160–170-year trend is present in the ENSO and the NAO indices as well, but is less significant than in the NHT index.

Table 3.

Spectral analysis of the individual climatic indices and fur-count records. As in Table 2, the main periods are significant at the 99% level and secondary periods at the 95% level in MTM. The analysis after removing the trend yields the same periods, except 170 years, in the fur-count records and the NHT index.

Time series Main periods Secondary periods
NAO 3, 3.5
ENSO 4 2
NHT 170, 2.5 2
Bear 170, 3, 2.5
Beaver 170, 3, 2.5
Fisher 170, 3, 2.5
Fox 170 3, 2.5
Lynx 170, 10, 2.5 3
Marten 170, 3 10, 2.5
Mink 170, 3, 2.5
Muskrat 170, 3 2
Otter 170, 3, 2.5
Wolf 170, 2.5
Wolverene 170, 3, 2.5
Open in a new tab

The spectral analysis results for the first component are independent of the data set, because PC-1 always embodies the animal populations' behavior. The main modes are a 160–170 year trend and a 3-year periodicity; a secondary, 2.5-year peak is also highly significant (see Table 2). The main periods of PC-2 correspond to the characteristic periods of the corresponding climatic index: 3.5 years for the {(fur-counts) + NAO} data set, 4 years and 2 years for the {(fur-counts) + ENSO}, and 2.5 years for the {(fur-counts) + NHT}. Other periods appear for this second component, especially a 30–45-year peak. The pair (PC-5) + (PC-6) also contains an 8.5-year peak, as a main or secondary period (not shown), for all three data sets that do include a climatic index.

Discussion

A striking result of our data analysis is the large and fairly sudden increase in the amplitude of the oscillations in the animal populations, around 1810. This could be seen directly in the raw fur-counts plotted against time (not shown, but please see the appendices), and it explains why the first half of the century-long records is tightly grouped along the negative PC-1 axis (Figure 1a). We know that the hunting pressure on the fur-yielding mammals increased during the time interval under study (1752–1849), mainly because fur clothing became more fashionable and the market for it increased.

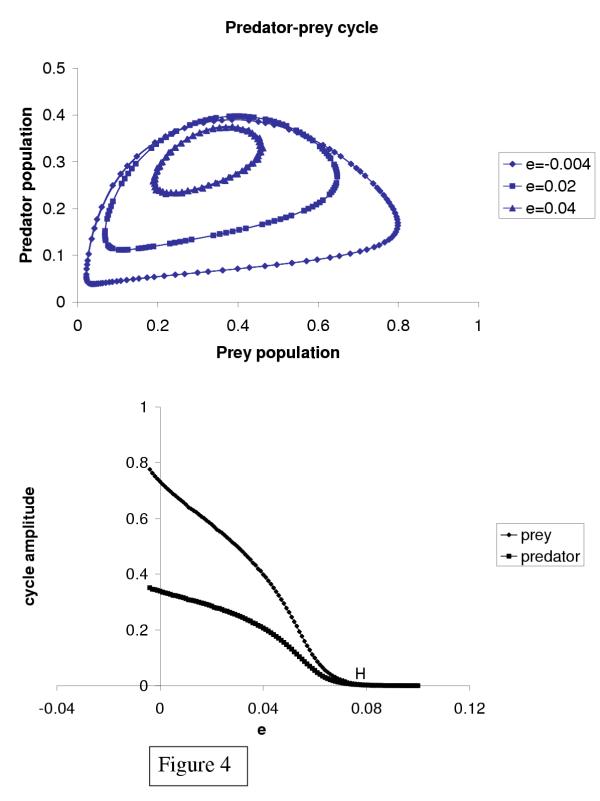
A very simple predator-prey model of Lotka–Volterra type, in which the prey population is harvested, leads to an increase in the oscillation amplitude of this population when the harvesting parameter increases; our model is described in the Methods section and the results are shown in Figure 4. References [10,11] also discussed how harvesting may destabilize population dynamics, using a somewhat different, discrete-time model [10] and a single predator population [11].

Figure 4.

Figure 4

Open in a new tab

Changes in the solution behavior of a predator–prey model subject to environmental pressures and given by system (2). (a) Phase plane showing the limit cycles exhibited by the populations of prey and predator species for different values of the environmental pressure parameter e. Note that the amplitude of the oscillations increases as e decreases, i.e. when environmental effects are less favorable. This may be the case when the prey population is submitted to intense hunting. (b) Amplitude of the limit cycle as a function of the parameter e.

The meaning of the mode that we refer to as "the 160–170-year trend" is the following. Both SSA [8,9,12] and MTM [3] permit the reliable extraction of trends that are more robust than the usual linear ones, which are obtained by least-square fitting. Such a nonlinear trend may take at times the shape of an incomplete sine function. If the curve in question is close to or exceeds about one-half the period of a sine function, both Monte Carlo SSA and MTM can determine the period of the sine function of closest fit. In our case, this period equals 160–170 years for the leading PCs of all four data sets we consider, as well as for the NHT time series, taken separately. We cannot, therefore, attach a true statistical significance to this period, but believe that longer data sets might support its presence in both NH temperatures and North American mammal populations.

This interpretation would suggest that long-term variations of the animal populations are linked to long-term variations of temperature and that the high-latitude animals we study have benefited from the temperature increase associated with the NH recovery from the "Little Ice Age" [9]. Note that the presence of the 160–170-year trend in the ENSO and NAO indices, too, reflects large-scale climatic interactions and has, obviously, nothing to do with the fur-counts we concentrate on here.

The 2.5-year period is also common to the spectral analysis of the NHT index and of the fur-counts. The role of temperature in population dynamics has been documented for many species (e.g., [13]); it may be due to the sensitivity of reproduction, survival, or intra- and inter-specific interactions to temperature.

The well-known ENSO periods of 4 and 2 years do not arise unambiguously from the spectral analysis of the leading PCs of the fur data alone (Table 2). Still, PC analysis of the {(fur-counts) + ENSO} data set clearly underlines the contribution of ENSO to the variance of the fur-counts (Figure 1b).

To clarify the reason for this apparent discrepancy, we carried out the spectral analysis of each of the climatic indices and fur-count records by itself (Table 3). Indeed, the ENSO periods are seldom highly significant in the individual population records; only in the muskrat time series is the 2-year peak significant at the 95% level. Furthermore, a well known 10-year period [14,15] does appear at the 99% level in our lynx record and at the 95% level in the marten population, but it does not show up in the leading PCs of Table 2.

These two discrepancies between the spectral results for individual time series and for the leading PCs of the whole population arise because of the nonlinearity present in combining PC analysis and spectral analysis. Each of these analyses separately involves a linear operator; for a finite record, finitely sampled, this operator takes the form of a matrix. The combination of the two analyses, however, is not a linear operator, i.e., a matrix product, acting between the individual records and the spectra of the PCs (or the PCs of the spectra). The PC analysis renders more significant the collective impact of ENSO on all mammalian populations combined, while it renders less significant the 10-year mode of variability that seems to be restricted to the lynx and the marten populations.

The second component of the {(fur-counts) + ENSO} data set is highly correlated with ENSO, as shown by the ordering of the different species along the second axis of Figure 1b. Although the role of ENSO in the dynamics of North American mammals had not been documented so far, its impact on Canadian climate is well-known by now [16,17].

The second component of the {(fur-counts) + NAO} data set is correlated to NAO (Figure 2), even though the relation is somewhat less pronounced than in the ENSO case. Consequently NAO effects help explain part of the differences in the variability observed between the different animal species. The presence of a 40–44-year period in PC-2 for furs alone, as well as in the {(fur-counts) + NAO} and {(fur-counts) + NHT} data sets, may be related to a similar period being present in variations of the North Atlantic Ocean's thermohaline circulation [18,19]. Post et al. [20] underscored the correlation between NAO and several parameters that describe animal behavior and their interactions. For example, they explain how NAO may influence wolf-pack sizes and the risk of predation exerted on moose. Stenseth et al. [21] discuss more specifically how NAO may influence the dynamics of lynx populations in three distinct climatic regions of Canada. Fur-counts of both lynx and wolf are among our eight longest data sets.

The exact mechanism by which the NAO and ENSO have an impact on the group of mammal populations we studied remains to be determined. We know that these two climatic indices are both linked to diverse features of North American climate, such as seasonal temperature means, liquid precipitation, freezing and snowfall. All these climatic variables may influence the individual fitness of the animal species used in the present work.

Having discussed the influence of external factors on the population dynamics of North American mammals, it is time to turn to the effect of intrinsic factors. In each PC analysis we carried out here, climatic indices are correlated to the second axis (Figures 1b and 2), while the leading component, which captures at least 54% of the variance (Table 1), is representative of the animal populations themselves: the correlation between the fur-counts of each species and PC-1 of the furs-only data set ranges between 0.63 (for the wolf) and 0.94 (for the bear). The spectral analysis of PC-1 displays, in all four data sets, two dominant components that are significant at the 99% level: a 160–170-year trend (significant at this level only in the MTM analysis) and a 3-year oscillation (highly significant in both the MTM and SSA analyses).

The 160–170-year trend is probably linked to long-term variations in temperature, while the 3-year period does not appear as a significant peak in any of the climatic indices. As explained in the caption of Table 2, our spectral resolution distinguishes clearly between this 3-year period and the climate-related ones of 2.5 and 3.5 years. The 3-year period in the fur-counts must therefore be linked either to the intrinsic population dynamics of the mammal species under consideration or to an external factor that acts on all the populations but has entirely escaped our attention. It may also arise from density-dependent ecological interactions, whether intra- or interspecific, and their interplay with seasonality. More detailed spectral analyses of individual species (not shown) have indicated that this 3-year period is strongest in those North-American mammals that are linked by predation, especially beaver, mink, muskrat and wolf. This seems to confirm the role of interspecific mechanisms in giving rise to the 3-year peak in our data.

Seldal et al. [22] related the 3-year period observed for lemmings populations to plant palatability and herbivory tolerance, while Turchin et al. [23] also based their explanation of the 3-year lemming cycles on two inter-specific interactions: predation and herbivory. The present analysis of North American fur-count data extends the range of interspecific dynamics that leads to a 3-year cycle to species other than lemmings. Indeed, we find this dominant period for data sets that include as many as eleven mammal species.

The results of the present study may also be linked to the issues of synchroneity among variations in spatially separated populations. The Moran [24] effect refers to a population that is subject to a density-independent process, while being fragmented into subpopulations within which density dependence is important. Synchroneity between the subpopulations may be due to the density-independent process (Moran effect) or to dispersal of individuals between the subpopulations. Several studies have described such synchronization, based either on natural data or on models [15,24-27]. Our results clearly show that climatic phenomena, which are clearly independent of mammalian populations, do have an influence on these populations, and that synchroneity between the variations of the latter may then be expected. Since we do not possess geographical details on the mammalian populations concerned, it is not possible at present to discuss the relative role of dispersal vs the Moran effect in the population variations we find. Nonetheless, we feel that our methodological framework, in general, and particularly the advanced spectral methods used, in particular, may be of great help in future synchroneity studies.

Conclusions

Our two-step methodology led us to distinguish between intrinsic and external factors in the dynamics of over ten North American mammal populations. PC analysis shows that internal dynamics is most important but also captures the role of ENSO, NAO and NH temperatures in the animal population dynamics. The striking change in the amplitude of the oscillations present in our fur-count data is probably linked to an increase of hunting pressure over the century-long interval of study.

Our spectral analysis determines the key periods of the three climatic indices we use. They are 170 years and 2.5 years for the mean NH temperatures, and 4 years and 2 years for the Niño-3 SSTs, while the NAO has only spectral peaks that are both weaker and marginally significant. The key periods of all four data sets that comprise the animal fur-counts are 170 years and 3 years. The latter has to be attributed to biological interactions.

Methods

Data sets

Four different data sets were analyzed. The first set includes fur-counts of the eleven animal populations within a given year. The three other sets were obtained by augmenting the fur records by one climatic record in each case. The three records we use are the North Atlantic Oscillation (NAO) index, as defined in [28], the cold-season Niño-3 sea-surface temperatures (SSTs), and the mean surface-air temperature of the Northern Hemisphere.

The time series of eight animal populations (bear, beaver, fox, lynx, marten, otter, wolf and wolverine) are 98-year long, extending from 1752 to 1849; those of fisher, mink and muskrat start in 1767 and are thus only 83-year long. All the fur-counts are provided in Appendices 1 through 11. The main results reported in this paper were obtained using the eight species with 98-year long records. When adding the three species with shorter records to the previous eight, the results are very similar (not shown). All the climatic data were available throughout the 1752–1849 time interval.

The NAO index represents a suitably normalized difference in sea-level pressure between the Açores High and the Icelandic Low; it determines the strength of the westerly winds over the North Atlantic Ocean and is correlated with several climatic patterns over the adjacent land masses [28]. We calculated the NAO index by using 3-month averages of the monthly sea-level pressure data provided by [29] for Iceland and Gibraltar, from December 1658 on; the monthly data are available in ref. [30] and our 3-month box-car averages, as used in the present study, appear in Appendix 12. This data set is well correlated with other paleoclimatic proxy indicators of NAO [31], as well as with modern instrumental records, when available.

The cold-season Niño-3 SSTs are a reliable index of the phase of the El Niño-Southern Oscillation (ENSO); ENSO dominates interannual climate variability in the Tropical Pacific [32] and has important effects on other parts of the world, including North America [16,17]. The Niño-3 SSTs and the Northern Hemisphere temperature (NHT) index are taken from [33]; the values used in this study are provided in Appendices 13 and 14, respectively.

Principal component analysis

Our data analysis includes two steps: principal component (PC) analysis and spectral analysis. PC analysis has been extensively used in the biomedical sciences [34,35], as well as in climate dynamics [36]. Its main purpose here is twofold: (i) data reduction, i.e., separating the signal from the noise in each data set; and (ii) the identification of significant correlations among the time series. We refer to the previously cited publications [34-36] for technical details.

Advanced spectral methods

Once the population-count or climatic signal was isolated, we used a battery of spectral analysis tools to determine the main periods it contains. Singular-spectrum analysis (SSA) is based on eigenvalue-eigenvector decomposition of a time series' lag-covariance matrix [37,38]. Given a series of length N, and a maximum lag M, the eigenvectors are data-adaptive basis functions for the representation of the series and are called empirical orthogonal functions (EOFs), by analogy with the PC analysis of meteorological fields. The eigenvalues are the associated variances λk, ordered from largest to smallest. When two eigenvalues are nearly equal, and the corresponding pair of (odd and even) EOFs are in phase quadrature, they may capture, subject to statistical significance tests, an anharmonic (i.e., not sinusoidal) oscillation of possibly nonlinear origin [8,12].

SSA can decompose a short, noisy time series into a (variable) trend, periodic oscillations, other statistically significant components that are aperiodic, and noise. The projection of the time series onto an EOF yields the corresponding principal component (PC) of length N-M+1. Reconstructed components (RCs) are series of length N that are obtained by the least-square fitting of their lagged copies, at lag 0, 1, ..., M-1 to the projection of the original series and its copies onto a given EOF or a set of EOFs [5,12]. In the life sciences, SSA has already been applied to the analysis of continuous zooplankton records and their environment [39], the possible connections between ENSO and cholera [40], biophysical [41] and neurophysiological problems [42], among others.

The multi-taper method (MTM) is designed to reduce the variance of spectral estimates by using a small set of tapers rather than the unique data taper or spectral window used by Blackman-Tukey methods [43]. MTM has the additional advantage of being nonparametric, in that it does not prescribe an a priori (e.g., autoregressive) model for the process generating the time series under analysis. A set of independent estimates of the power spectrum is computed, by pre-multiplying the data by orthogonal tapers which are constructed to minimize the spectral leakage due to the finite length of the data set. The optimal tapers or "eigentapers" belong to a family of functions known as discrete prolate spheroidal sequences (DPSS) and defined as the eigenvectors of a suitable Rayleigh-Ritz minimization problem [44]. Averaging over this set of spectra yields a better and stabler estimate – i.e., one with lower variance – than do single-taper methods.

Mann & Lees [4] and Ghil et al. [5] show that the spectral resolution of the MTM method equals Δf = min {fN/4, 2pfR}, where fN is the Nyquist frequency, fR is the Rayleigh frequency, and p is a bandwidth parameter; in the present case fN = 0.5 cycles.year-1, fR = 0.02 cycles.year-1, and we used p = 2. This means that Δf = 0.04 cycles.year-1, and so all the periods listed in Table 2 are well separated by the MTM method. The Monte Carlo SSA method only yields a spectral resolution of 1/M = 0.11 cycles.year-1, which is marginally useful for separating the shortest periodicities in the Table, but the fact that the peaks coincide in both methods lends further credence to their independent existence.

The SSA-MTM Toolkit was developed by the Theoretical Climate Dynamics group at the University of California, Los Angeles (UCLA) [45] and further improved in collaboration with researchers in Europe and North America [5,46]. It supports four different spectral methodologies: classical Fourier analysis, SSA, MTM, and the maximum entropy method (MEM). The toolkit provides a battery of statistical significance tests for each method, as well as visualisation tools that help compare results between the methods. More complete descriptions of all four methods, as well as comparisons of their features and practical performance can be found in [5]. For the data sets under examination, we found SSA and MTM to be the most useful. The entire SSA-MTM Toolkit, along with the User Guide, is available as freeware [46]; further references on advanced spectral methods and their various applications are also listed there.

Heuristic population model

We propose here to link the striking and fairly sudden increase in variance of all the fur-count records to a slight variation of environmental conditions. To do so, consider the very simple model:

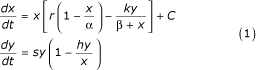
graphic file with name 1472-6785-4-6-i1.gif

of the interaction of a prey population x with its predator population y. The parameters r and s represent the birth rate of prey and predator respectively, while α stands for the carrying capacity. The predation function is of Holling type II, h is the rate of mortality of the predator, and k is the rate of predation exerted on the prey.

All parameters are strictly positive, except C, which stands for the effects, negative or positive, of external pressures on the prey population; C is zero if x = 0 but is otherwise assumed to be independent of x. Our model (1) is close to harvesting models used in fisheries management [47-49]. If the hunting pressures imposed on the prey population are too large, then C may be small or negative, even if other abiotic parameters are favorable.

Non-dimensionalizing the model (1) gives:

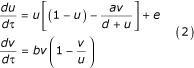
graphic file with name 1472-6785-4-6-i2.gif

where 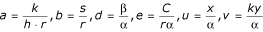Inline graphic and τ = rt.

The equilibrium associated with system (2) was studied using the CONTENT software [50]. Let us suppose that hunting pressures increased, as it is likely that they did during the period 1752–1848, and so the parameter e decreased. To examine the effects of such a decrease, we performed a bifurcation analysis with respect to the parameter e. An oscillatory instability occurs at e = eH: if e >eh, a single equilibrium, with finite and nonzero u and v, is stable; for e ≤ eh, this equilibrium becomes unstable and gives rise to a stable limit cycle. The larger the difference e - eh, the larger the amplitude of the oscillations (see Figure 4). The amplitude is roughly proportional to the square root of the difference eh - e, as expected in the vicinity of a Hopf bifurcation.

This very simple model, with only one prey and one predator species, shows that, as the external conditions deteriorate even slightly, the amplitude of both the predator's and the prey's population cycles increases. The large change in the oscillations' amplitude for all the population records studied here could therefore be linked to a deterioration in Canada's environmental conditions in the early 1800s. This deterioration might also be linked to increased hunting pressures.

Other results show that harvesting pressure may have a destabilizing effect. Basson & Fogarty [10] have demonstrated that harvesting of adults in an age-structured model may have a destabilizing effect in the sense that complex dynamics may then emerge. They also explained the potential role of predation links in the destabilization; this role is in accordance, at least intuitively, with the presence of multiple prey and predator populations in our records. Gamarra & Sole [11] showed that lynx trapping may be the reason for a switch between a stable regime, with low-amplitude fluctuations of the population, to a less stable regime, with larger fluctuations and more complex dynamics. Our model, while simpler than theirs, still seems to capture the key aspect of this effect.

Acknowledgments

Acknowledgement

This work was initiated as part of a collaboration between the Ecole Normale Supérieure and UCLA. We thank both institutions for their respective support and mutual hospitality. We also thank Régis Ferrière at the ENS for helpful advice on ecological modeling, Pascal Yiou of the Laboratoire des Sciences du Climat et de l'Environnement for advice on and help with the acquisition of paleoclimatic data, and Andrew W. Robertson for constructive comments on an earlier version of the manuscript. The SSA-MTM Toolkit is available as freeware at http://www.atmos.ucla.edu/tcd and is maintained by UCLA's Theoretical Climate Dynamics group. Our research was partially supported by a U.S. National Science Foundation grant to Michael Ghil.

Contributor Information

Nicolas Loeuille, Email: loeuille@biologie.ens.fr.

Michael Ghil, Email: ghil@lmd.ens.fr.

References

  1. Volterra V. Variazioni e fluttuazioni del numero d'individui in specie animali conviventi. Mem Acad Lincei. 1926;2:31–11. [Google Scholar]
  2. Jones JW. Fur-Farming in Canada. Ottawa: Commission of Conservation; 1914. [Google Scholar]
  3. Mann ME, Lees JM. Robust estimation of background noise and signal detection in climatic time series. Clim Change. 1996;33:409–445. [Google Scholar]
  4. Allen M, Smith LA. Monte Carlo SSA: Detecting irregular oscillations in the presence of coloured noise. J Climate. 1996;9:3373–3404. doi: 10.1175/1520-0442(1996)009<3373:MCSDIO>2.0.CO;2. [DOI] [Google Scholar]
  5. Ghil M, Allen RM, Dettinger MD, Kondrashov D, Mann ME, Robertson A, Saunders A, Tian Y, Varadi F, Yiou P. Advanced spectral methods for climatic time series. Rev Geophys. 2002;40:3.1–3.41. doi: 10.1029/2000RG000092. 10.1029/2000GR000092. [DOI] [Google Scholar]
  6. Rasmusson EM, Wang X, Ropelewsky CF. The biennial component of ENSO variability. J Mar Syst. 1990;1:71–96. [Google Scholar]
  7. Ghil M, Jiang N. Recent forecast skill for the El Niño/Southern Oscillation. Geophys Res Lett. 1998;25:171–174. doi: 10.1029/97GL03635. [DOI] [Google Scholar]
  8. Ghil M, Vautard R. Interdecadal oscillations and the warming trend in global temperature time series. Nature. 1991;350:324–327. doi: 10.1038/350324a0. [DOI] [Google Scholar]
  9. Plaut G, Ghil M, Vautard R. Interannual and interdecadal variability in 335 years of central England temperatures. Science. 1995;268:710–713. doi: 10.1126/science.268.5211.710. [DOI] [PubMed] [Google Scholar]
  10. Basson M, Fogarty MJ. Harvesting in discrete time predator-prey systems. Math Biosciences. 1997;141:41–74. doi: 10.1016/S0025-5564(96)00173-3. [DOI] [PubMed] [Google Scholar]
  11. Gamarra JGP, Solé RV. Bifurcation and chaos in ecology: lynx returns revisited. Ecol Lett. 2000;3:114–122. doi: 10.1046/j.1461-0248.2000.00128.x. [DOI] [Google Scholar]
  12. Vautard R, Yiou P, Ghil M. Singular-spectrum analysis: a toolkit for short, noisy, chaos signals. Physica D. 1992;58:95–126. doi: 10.1016/0167-2789(92)90103-T. [DOI] [Google Scholar]
  13. Sanford E. Regulation of keystone predation by small changes in ocean temperature. Science. 1999;283:2095–2097. doi: 10.1126/science.283.5410.2095. [DOI] [PubMed] [Google Scholar]
  14. Elton C, Nicholson M. The ten-year cycle in numbers of the lynx in Canada. J Anim Ecol. 1942;11:215–244. [Google Scholar]
  15. Blasius B, Huppert A, Stone L. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature. 1999;399:354–359. doi: 10.1038/20676. [DOI] [PubMed] [Google Scholar]
  16. Ropelewski CF, Halpert MS. Precipitation patterns associated with the high-index phase of the Southern Oscillation. J Climate. 1989;2:268–284. doi: 10.1175/1520-0442(1989)002<0268:PPAWTH>2.0.CO;2. [DOI] [Google Scholar]
  17. Halpert MS, Ropelewski CF. Surface temperature patterns associated with the Southern Oscillation. J Climate. 1992;5:577–593. doi: 10.1175/1520-0442(1992)005<0577:STPAWT>2.0.CO;2. [DOI] [Google Scholar]
  18. Delworth TL, Manabe S, Stouffer RJ. Interdecadal variations of the thermohaline circulation in a coupled ocean-atmosphere model. J Climate. 1993;8:172–190. [Google Scholar]
  19. Chen F, Ghil M. Interdecadal variability of the thermohaline circulation and high-lattitude surface fluxes. J Phys Oceanogr. 1995;25:2547–2568. doi: 10.1175/1520-0485(1995)025<2547:IVOTTC>2.0.CO;2. [DOI] [Google Scholar]
  20. Post E, Peterson RO, Stenseth NC, Mac Laren BE. Ecosystem consequences of wolf behavioral response to climate. Nature. 1999;401:905–907. doi: 10.1038/44814. [DOI] [Google Scholar]
  21. Stenseth NC, Chang KS, Tong H, Boonstra R, Boutin S, Krebs CJ, Post E, O'Donoghue M, Yoccoz NG, Forchhammer MC, Hurrell JW. Common dynamic structure of Canada lynx populations within three climatic regions. Science. 1999;285:1071–1073. doi: 10.1126/science.285.5430.1071. [DOI] [PubMed] [Google Scholar]
  22. Seldal T, Andersen KJ, Högstedt G. Grazing-induced proteinase inhibitors: a possible cause for lemmings population cycles. Oïkos. 1994;70:3–11. [Google Scholar]
  23. Turchin P, Oksanen L, Ekerholm P, Oksanen T, Hentonnen H. Are lemmings preys or predators? Nature. 2000;405:562–565. doi: 10.1038/35014595. [DOI] [PubMed] [Google Scholar]
  24. Moran PAP. The statistical analysis of the Canadian lynx cycle. II Synchronization and meteorology. Australian J Zoology. 1953;1:291–298. [Google Scholar]
  25. Ranta E, Kaitala V. Travelling waves in vole population dynamics. Nature. 1997;390:456. doi: 10.1038/37261. [DOI] [Google Scholar]
  26. Ranta E, Kaitala V, Lundberg P. The spatial dimension in population fluctuations. Science. 1997;278:1621–1623. doi: 10.1126/science.278.5343.1621. [DOI] [PubMed] [Google Scholar]
  27. Lindstrom J, Ranta E, Linden H. Large scale synchroneity in the dynamics of capercaillie, black grouse and hazel grouse populations in Finland. Oikos. 1996;76:221–227. [Google Scholar]
  28. Hurrell JW. Decadal trends in the North Atlantic Oscillation regional temperatures and precipitation. Science. 1995;269:446–449. doi: 10.1126/science.269.5224.676. [DOI] [PubMed] [Google Scholar]
  29. Luterbacher J, Xoplaki E, Dietrich D, Rickli R, Jacobeit J, Beck C, Gyalistras D, Schmutz C, Wanner H. Reconstruction of sea level pressure fields over the Easter North Atlantic and Europe back to AD 1500. Clim Dyn. 2002;18:545–561. [Google Scholar]
  30. Monthly NAO data http://www.ngdc.noaa.gov/paleo/pubs/luterbacher2002/luterbacher2002.html
  31. Souriau A, Yiou P. Grape harvest dates for checking NAO paleoreconstructions. Geophys Res Lett. 2001;28:3895–3898. doi: 10.1029/2001GL012870. [DOI] [Google Scholar]
  32. Philander SGH. El Niño, La Niña, and the Southern Oscillation. San Diego: Academic Press; 1990. [DOI] [PubMed] [Google Scholar]
  33. Mann ME, Gille E, Bradley RS, Hugues MK, Overpeck J, Keimig FT, Gross W. Global temperature patterns in past centuries: an interactive presentation. Earth Interactions. 2000;4–4:1–29. doi: 10.1175/1087-3562(2000)004<0001:GTPIPC>2.3.CO;2. http://www.ngdc.noaa.gov/paleo/ei/ei_cover.html [DOI] [Google Scholar]
  34. Fisher LD, Van Belle G. Biostatistics. New York: John Wiley & Sons; 1993. [Google Scholar]
  35. Agarwal A, Sharma RK, Nelson DR. New semen quality scores developed by principal component analysis of semen characteristics. J Androl. 2003;24:343–352. doi: 10.1002/j.1939-4640.2003.tb02681.x. [DOI] [PubMed] [Google Scholar]
  36. Preisendorfer RW. Principal Component Analysis in Meteorology and Oceanography. New York: Elsevier Science; 1988. [Google Scholar]
  37. Broomhead DS, King G. Extracting qualitative dynamics from experimental data. Physica D. 1986;20:217–236. doi: 10.1016/0167-2789(86)90031-X. [DOI] [Google Scholar]
  38. Fraedrich K. Estimating the dimension of weather and climate attractors. J Atm Sci. 1986;43:419–432. doi: 10.1175/1520-0469(1986)043<0419:ETDOWA>2.0.CO;2. [DOI] [Google Scholar]
  39. Colebrook JM. Continuous plankton records – zooplankton and environment, Northeast Atlantic and North Sea, 1948–1975. Oceanol Acta. 1978;1:9–23. [Google Scholar]
  40. Rodo X, Pascual M, Fuchs G, Faruque ASG. ENSO and cholera: A nonstationary link related to climate change? Proc Nat Acad Sci USA. 2002;99:12901–12906. doi: 10.1073/pnas.182203999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Brawanski A, Faltermeier R, Rothoerl RD, Woertgen C. Comparison of near-infrared spectroscopy and tissue PO2 time series in patients after severe head injury and aneurysmal subarachnoid hemorrhage. J Cerebr Blood F Met. 2002;22:605–611. doi: 10.1097/00004647-200205000-00012. [DOI] [PubMed] [Google Scholar]
  42. Mineva A, Popivanov D. Method of singletrial readiness potential identification, based on singular spectrum analysis. J Neurosci Methods. 1996;68:91–99. doi: 10.1016/S0165-0270(96)00012-X. [DOI] [PubMed] [Google Scholar]
  43. Thompson JD. Spectrum estimation and harmonic analysis. Proc IEEE. 1982;70:1055–1096. [Google Scholar]
  44. Slepian D. Prolate spheroidal wave-functions, Fourier-analysis and uncertainty. 5. Discrete case. Bell System Tech J. 1978;57:1371–1430. [Google Scholar]
  45. Dettinger MD, Ghil M, Strong CM, Weibel W, Yiou P. Software expedites singular-spectrum analysis of noisy time series. Eos Trans Amer Geophys U. 1995;76:12–21. [Google Scholar]
  46. SSA-MTM Toolkit User's Guide http://www.atmos.ucla.edu/tcd/ssa
  47. Bassan M, Fogarty MJ. Harvesting in discrete time predator-prey systems. Math Biosciences. 1997;141:41–74. doi: 10.1016/S0025-5564(96)00173-3. [DOI] [PubMed] [Google Scholar]
  48. Bhattacharya DK, Begum S. Bionomic equilibrium of two-species systems. Math Biosciences. 1996;135:111–127. doi: 10.1016/0025-5564(95)00170-0. [DOI] [PubMed] [Google Scholar]
  49. Cooke KL, Nusse HE. Analysis of the complicated dynamics of some harvesting models. J Math Biol. 1987;25:521–542. doi: 10.1007/BF00276197. [DOI] [PubMed] [Google Scholar]
  50. Kuznetsov YA, Levitin VV. CONTENT a multiplatform for continuation and bifurcation analysis of dynamical systems Centrum Voor Wiskunde en Informatica, Kruislaan 413, 1098 SI Amsterdam, The Netherlands. 1997. http://www.can.nl/Systems_and_Packages/Per_Purpose/Special/DiffEqns/Content/GCbody.html

Articles from BMC Ecology are provided here courtesy of BMC

RESOURCES