Abstract
For automatic segmentation of optic disc and cup from color fundus photograph, we describe a fairly general energy function that can naturally fit into a global optimization framework with graph cut. Distinguished from most previous work, our energy function includes priors on the shape & location of disc & cup, the rim thickness and the geometric interaction of “disc contains cup”. These priors together with the effective optimization of graph cut enable our algorithm to generate reliable and robust solutions. Our approach is able to outperform several state-of-the-art segmentation methods, as shown by a set of experimental comparisons with manual delineations and a series of results of correlations with the assessments of a merchant-provided software from Optical Coherence Tomography (OCT) regarding several cup and disc parameters.
1 Introduction
As the second leading cause of blindness in the United States, glaucoma is characterized by progressive optic nerve damage and defects in retinal sensitivity leading to loss of visual function. Early diagnosis and optimal treatment have been shown to minimize the risk of visual loss due to glaucoma. The hallmark of glaucomatous progression is optic disc cupping, a phenomenon of enlargement of cup which is a small crater-like depression seen at the front of the optic nerve head (ONH), as shown in Fig. 1. Cupping is caused by little nerve fibers wiped out along the rim of the optic nerve in glaucoma.
Fig. 1.
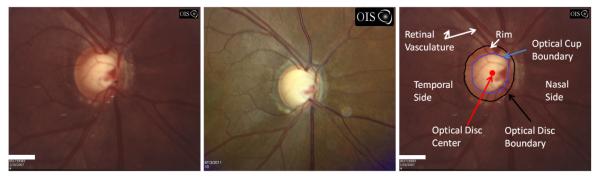
A glaucomatous patient with progressed optic nerve cupping as shown by the color fundus images of optic nerve head (ONH) taken at an early time (left picture) and a late time (middle picture) after about 53 months. The right picture shows the annotation of main ONH landmarks. Neuroretinal rim, defined as the region between optic disc and cup boundaries, manifest as a “lantern ring” around the optic disc center.
Ocular imaging instruments provide clinically useful quantitative assessment of optic disc cupping. However, fully automated ONH quantification techniques are still lacking and it is still a clinical standard to perform subjective optic disc assessment using disc photographs. Conventional ONH evaluations include subjective assessment by observing the pair of stereo fundus photographs and computerized planimetry which allows for generating several disc parameters based on manual labeling of disc and cup margins [1]. However, these conventional methods are time consuming, labor intensive and prone to high intra/inter-observer variabilities.
Automatic segmentation of optic disc and cup can help to eliminate the disadvantages of the conventional ONH evaluation methods; nevertheless, it is surprisingly difficult. There have been efforts to automatically segment optic disc and cup from color fundus photographs, which can be classified as techniques based on template matching [2], machine learning [3], active contour model [4], level sets [5, 6] and Hough transform [7]. Our experiments showed that most of these existing techniques are incapable of generating accuracy and robustness enough for evaluating ONH in clinical practice. The deteriorations of these algorithms first come from the challenges of the involved task, caused by the blurry and faint boundaries of optic disc and cup, large inter-subject variability in ONH appearance, interference of blood vessel and confounding bright pathologies, as shown in Fig. 1. Moreover, most of these existing techniques segment optic disc and cup independently and the strong shape and location priors of neuroretinal rim (as shown in Fig. 1) cannot be fully used. Finally, most of them try to eliminate the interference of blood vessel with an image preprocess of vessel removal which turned out to be a very hard task in practice.
To deal with the above-mentioned challenges of automatic segmentation of optic disc and cup, we propose to address this task by introducing graph cut which is an effective combinatorial optimization technique [8] and incorporating priors not only on shape, location and geometric interactions of optic disc and cup, but also on rim thickness. Our algorithm is reliable and robust not only because graph cut offers a globally optimal solution but also due to the incorporated priors which can effectively reduce the search space of feasible segmentations. Different from previous work, the interference of blood vessel can be accounted for in the segmentation process by modeling the vessel intensity information instead of removing vessels with a preprocess.
We describe a fairly general energy function which integrates a set of model-specific visual cues, contextual information and topological constraints to include a wide range of priors. First, boundaries of both “cup” and “disc” are nearly circular around optic disc center and their radii can be a prior approximated. Second, “cup” is contained in “disc”. Third, the minimum rim thickness can also be a prior estimated for the given data set. Our energy function is submodular and can therefore be formulated as a s-t cut problem and minimized efficiently via graph cut (min-cut/max-flow algorithm) [8].
We evaluate the performance of our algorithm not only by comparing with manual delineations of optic disc and cup on a rigorous pixel-by-pixel basis, but also by comparing the algorithm’s assessments on a set of ONH parameters from color fundus photograph against the corresponding evaluations generated by the merchant-provided software in the Optical Coherence Tomography (OCT) machine. Our results show that the proposed algorithm outperforms two state-of-the-art segmentation methods and demonstrates strong correlations with the merchant-provided software in OCT imaging.
2 Method
Upon the location of optic disc center is known, our segmentation task amounts to searching regions of optic disc and cup which boundaries are circle-like, around the optic center and with radii that can be a priori approximated.
2.1 Simultaneous Segmentation of Optic Disc and Cup
Our optic disc and cup segmentation framework divides a rectangle region around the optic disc center into parts of cup, disc and background. It relies on the powerful graph cut algorithm [8] and allows for spatial interaction of those segmented parts and the incorporation of priors on location and shape of and distance between disc and cup boundaries. Our framework results in a submodular energy minimization problem and can therefore generate a global optimization.
Let be the set of pixel indices and be the set of region indices. We set where the set elements denote “cup” and “disc”, respectively. We then define binary variables where and index x, and xp is a binary vector of all variables corresponding to p. Obviously, xp is in length of where ∣·∣ denotes the number of elements in a set. If pixel p is in region l, then we have . If xp = 0, pixel p is in the region of “background”.
The proposed energy function to be minimized via graph cut is defined as
| (1) |
where the three ∑ components contain data terms, smoothness terms and region interaction terms [9], respectively, and are to be defined in the following.
2.2 Data Terms
The data term Dp(xp) in Eq. (1) is constructed from the probability of each pixel p belonging to any of the regions r ∈ {“cup”, “disc”, “background”}. For each region, we train a Gaussian Mixture Model (GMM) and use it to decide a posterior probability with the following equation
| (2) |
In Eq. (2), P(Ip∣Θr) is the probability density function of each region r, P(Θr) is the prior probability, and P(Ip) is merely a scaling signatures factor and can be neglected.
Ip is the fundus color vector of pixel . Region r is assumed to contain K (empirically set to 4) components and is the Gaussian probability function with mean value and covariance matrix . αk are positive weights of the component k and . The parameter list Θr = {α1, μ1, ∑1, ⋯ , αK, μK, ∑K} defines a particular GMM probability function. The parameters in Θr are estimated with the Expectation Maximization (EM) algorithm (an iterative method for calculating maximum likelihood distribution parameters) and a set of manually labeled color fundus ONH photographs.
With the posterior probability of Eq. (2), Dp(xp) in Eq. (1) is defined in Table. 1, which is apparently submodular [8] considering the fact that
More importantly, the ∞ value in Table. 1 is specified in order to prohibit the corresponding configuration (i.e. a “cup” pixel is not in “disc” region) of xp. In other words, this defination can help to guarantee the truth that “cup” region is contained in the “disc” region.
Table 1.
Definition of data term Dp(xp) and region interaction term in Eq. (1).
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | |
| Dp(xp) | –log P(“background”|Ip) | –log P(“disc”|Ip) | ∞ | –log P(“cup”|Ip) |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | ∞ | 0 |
2.3 Smoothness Terms
The smoothness terms in Eq. (1) are enforced only on neighboring pixels which are defined on a nearest neighbor grid connectivity (e.g. 4-connectivity in a 2D space). Specifically, for each , this pairwise term is defined as a Pott’s-like model:
| (3) |
where
| (4) |
is a Kronecker delta function and Bp,q comprises the “boundary” properties of “cup” and “disc”. We define Bp,q as
| (5) |
where σ is an adjusting parameter (empirically set to 4), Rp,q denotes the average value of distances of pixels p and q to the optical center, Rl represents a radius value a priori approximated based on our knowledge of ONH anatomy and the photograph resolution (we empirically set Rc = 210 pixels and Rd = 345 pixels), and ∊ is an adjusting parameter (empirically set to 0.4). In Eq. (5), the left term is large when the pixels p and q are similar in their color and close to zero when the two are very different, resulting in a lot penalization for label discontinuities between pixels of similar colors. The right term encourages the detected boundary to appear in the vicinity of a circle with an a priori known radius of “cup” or “disc”. Parameter ∊ controls how far the detected boundary can appear away from the a priori known boundary.
2.4 Region Interaction Terms
The region interaction terms in Eq. (1) are employed on all pairs (denoted by ) of pixels between which the distance is below a a priori known value. This value is assigned to the thinnest rim thickness (empirically set to 15 pixels) in our experiments. As defined in Table. 1, these region interaction terms can help to enforce two constraints that the “disc” region contains the “cup” region and that the rim thickness is above the a priori known value. Inclusion of this region containment and a hard uniform margin (between “cup” and “disc” boundaries) into graph cut are also explained in [9].
2.5 Optimization
As defined in Table. 1 and Eq. (3), the energy function E(x) in Eq. (1) is obviously submodular [8] and therefore can be formulated as a s-t cut problem and minimized efficiently via graph cut (min-cut/max-flow algorithm) [8]. A local minimum lying within a multiplicative factor of the global minimum can be obtained with the α-expansion algorithm [8].
2.6 Detection of Optic Disc Center
Detection of optic disc center is necessary because the shape and location priors applied to our segmentation scheme require the location of optic disc center. We employ an automatic method based on template matching followed by a false positive removal with a directional matched filtering similar to [6], which are based on the fact that optic disc appears in the fundus image as a brighter circular area and that the main vessels originate from the optic disc center, respectively. Technical details are omitted for economy. In our experiments, manual adjustments were applied to the obviously wrong detections.
3 Results
3.1 Data
Stereoscopic ONH photographs, taken by a simultaneous stereo fundus camera (Zeiss 30°), of bilateral eyes of 30 progressed glaucoma subjects and 32 control subjects were used (totally 248 color fundus photographs), with size of 239× 2042 pixels and resolution of 2.6 × 2.6μm2. HD-OCT (Cirrus; Carl Zeiss Meditec. Inc.,) scans were also acquired with the ONH parameters of disc area, rim area, cup area and cup-to-disc (C/D) area ratio generated by the Cirrus HD-OCT software (version 5.0). Optic cup and disc margins were manually delineated by a trained rater with the stereo disc photographs of randomly chosen 15 glaucoma subjects and 16 control subjects.
3.2 Experiments
We first compared the optic disc and cup segmentation of our algorithm with the active contour model [4] and the original graph cut algorithm [8]. For the original graph cut algorithm, we removed all location and shape priors of optic cup and disc and only kept its original smoothness term. Mean±STD values of the average distance between the automatically detected cup and disc margins and the subjective assessed margins (of the 15 glaucoma subjects and 16 control subjects) were computed and listed in Table 2. We also put the segmentation results for two example images in Fig. 2.
Table 2.
Statistics of average distance between the subjectively assessed optic cup and disc margins and the automatically detected margins by our algorithm (OUR), the active contour model (ACM) [4] and graph cut (GC) [8] from photos of 16 normal controls and 15 glaucoma subjects.
| Mean±STD | Normal | Glaucoma | ||||
|---|---|---|---|---|---|---|
| OUR | ACM | GC | OUR | ACM | GC | |
| Cup | *8.2 ± 6.1 | 42.9 ± 28.5 | 31.3 ± 22.9 | *10.5 ± 7.7 | 55.6 ± 34.4 | 48.1 ± 29.6 |
| Disc | *14.5 ± 12.4 | 46.2 ± 20.0 | 50.7 ± 28.3 | *16.9 ± 12.8 | 60.8 ± 44.0 | 59.2 ± 30.7 |
indicates the best performance value.
Fig. 2.
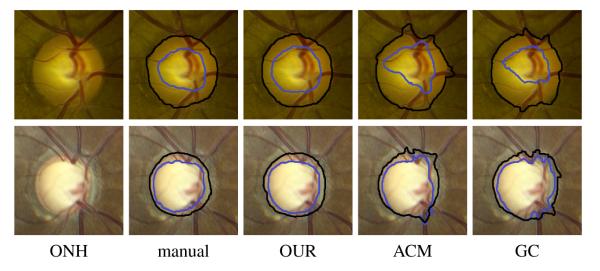
ONH images (only a rectangle region around optic disc is shown) and margins of cup (blue) and disc (black) manually assessed and automatically detected by our algorithm (OUR), the active contour model (ACM) [4] and graph cut (GC) [8].
From the results in Table 2 and Fig. 2, we had several findings. First, our algorithm outperformed the active contour model and the original graph cut for segmentation of both optic cup and disc. Second, all automatic algorithms performed better on normal controls than glaucoma subjects. Third, graph cut was comparable with the active contour model regarding optic disc segmentation but superior in sense of optic cup segmentation.
Failure of the automatic algorithms to detect the cup and disc margins properly was defined as when the average distance between the automatically detected margin and the subjective assessed margin was larger than 34 pixels (5% of the average disc diameter). We found that our algorithm failed only for one glaucoma subject, and in contrast, the active contour model failed for 10 glaucoma subjects and 9 normal controls while graph cut failed for 8 glaucoma subjects and 6 normal controls.
The results of the ONH parameters (including the subject defined as failure) generated by our algorithm were compared with the results produced by the merchant-provided software of the OCT machine. The corresponding Mean ± STD values of each parameter and the correlation coefficient (r) and p-value (p) of Pearson correlation between our algorithm and the OCT machine were listed in Table. 3. We can see that all ONH measurements based on OCT machine-defined margins showed a high correlation with our algorithm which uses fundus photographs. For each eye, the average of our algorithm’s evaluations on the stereoscopic pair was used as the final result.
Table 3.
Comparison of ONH measurements generated by the merchant-provided software of the OCT machine and our algorithm regarding area (mm2) of disc, rim and cup and C/D ratio.
| Parameter | Normal | Glaucoma | ||||||
|---|---|---|---|---|---|---|---|---|
| OCT* | Algorithm* | r† | p† | OCT* | Algorithm* | r† | p† | |
| Disc area (mm2) | 2.50 ± 0.54 | 2.41 ± 0.39 | 0.88 | 0 | 2.97 ± 0.88 | 2.94 ± 0.86 | 0.86 | 4e-13 |
| Rim area (mm2) | 1.71 ± 0.69 | 1.64 ± 0.67 | 0.86 | 2e-12 | 1.45 ± 0.75 | 1.46 ± 0.78 | 0.82 | 7e-8 |
| Cup area (mm2) | 0.78 ± 0.51 | 0.77 ± 0.63 | 0.85 | 3e-19 | 1.52 ± 0.82 | 1.48 ± 0.79 | 0.80 | 9e-5 |
| C/D Ratio | 0.31 ± 0.14 | 0.32 ± 0.23 | 0.85 | 5e-17 | 0.51 ± 0.20 | 0.50 ± 0.34 | 0.81 | 3e-6 |
Mean ± STD;
Pearson correlation
4 Conclusion and Future Work
Inspired by recent image segmentation methods that can combine certain shape priors or region/boundary interactions [9], we propose a fairly general energy function that can naturally fit into a global optimization framework with graph cut for the automatic segmentation of optic cup and disc from color fundus photographs. Our main contribution lies in the introduction of a set of priors obtained from the fundus anatomical characteristics of optic nerve head, which include the location and shape priors of optic cup and disc, the thinnest thickness of rim and the fact that “disc” contains “cup”. These priors can help to greatly reduce the search space of feasible solutions, and together with the effective optimization of graph cut, generate reliable and robust segmentation results.
Our approach incorporates shape priors in a different fashion from several existing techniques which are based on shape statistics (e.g. the deformable segmentation [10, 11] and the Active Shape Model [12]). Shape statistics are mostly obtained from a set of training images. In contrast, our approach encodes the prior knowledge (on contextual information or geometric interactions) in the algorithm directly and is free from any training process.
Our future work would include tests on a larger data set and more evaluations on the automatic detection of optic disc center.
ACKNOWLEDGEMENT
This work was made possible by support from National Institute of Health (NIH) via grant P30-EY001583.
References
- 1.Greaney MJ, Hoffman DC, Garway-Heath DF, Nakla M, Coleman AL, Caprioli J. Comparison of optic nerve imaging methods to distinguish normal eyes from those with glaucoma. Invest Ophthalmol Vis Sci. 2002;43:140–145. [PubMed] [Google Scholar]
- 2.Lalonde M, Beaulieu M, Gagnon L. Fast and robust optic disc detection using pyramidal decomposition and hausdorff-based template matching. Medical Imaging, IEEE Transactions on. 2001;20(11):1193–1200. doi: 10.1109/42.963823. [DOI] [PubMed] [Google Scholar]
- 3.Abràmoff MD, Alward WL, Greenlee EC, Shuba L, Kim CY, Fingert JH, Kwon YH. Automated segmentation of the optic disc from stereo color photographs using physiologically plausible features. Investigative ophthalmology & visual science. 2007;48(4):1665–1673. doi: 10.1167/iovs.06-1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Joshi GD, Sivaswamy J, Krishnadas S. Optic disk and cup segmentation from monocular color retinal images for glaucoma assessment. Medical Imaging, IEEE Transactions on. 2011;30(6):1192–1205. doi: 10.1109/TMI.2011.2106509. [DOI] [PubMed] [Google Scholar]
- 5.Liu J, Wong D, Lim J, Li H, Tan N, Zhang Z, Wong T, Lavanya R. Argali: an automatic cup-to-disc ratio measurement system for glaucoma analysis using level-set image processing. 13th International Conference on Biomedical Engineering; Springer; 2009. pp. 559–562. [Google Scholar]
- 6.Yu H, Barriga E, Agurto C, Echegaray S, Pattichis M, Bauman W, Soliz P. Fast localization and segmentation of optic disk in retinal images using directional matched filtering and level sets. Information Technology in Biomedicine, IEEE Transactions on. 2012;16(4):644–657. doi: 10.1109/TITB.2012.2198668. [DOI] [PubMed] [Google Scholar]
- 7.Aquino A, Gegundez-Arias ME, Marín D. Detecting the optic disc boundary in digital fundus images using morphological, edge detection, and feature extraction techniques. Medical Imaging, IEEE Transactions on. 2010;29(11):1860–1869. doi: 10.1109/TMI.2010.2053042. [DOI] [PubMed] [Google Scholar]
- 8.Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2001;23(11):1222–1239. [Google Scholar]
- 9.Ulen J, Strandmark P, Kahl F. An efficient optimization framework for multi-region segmentation based on lagrangian duality. Medical Imaging, IEEE Transactions on. 2013;32(2):178–188. doi: 10.1109/TMI.2012.2218117. [DOI] [PubMed] [Google Scholar]
- 10.Zhang S, Zhan Y, Metaxas DN. Deformable segmentation via sparse representation and dictionary learning. Medical Image Analysis. 2012;16(7):1385–1396. doi: 10.1016/j.media.2012.07.007. [DOI] [PubMed] [Google Scholar]
- 11.Zhang S, Zhan Y, Dewan M, Huang J, Metaxas DN, Zhou XS. Towards robust and effective shape modeling: Sparse shape composition. Medical Image Analysis. 2012;16(1):265–277. doi: 10.1016/j.media.2011.08.004. [DOI] [PubMed] [Google Scholar]
- 12.Cootes TF, Taylor CJ, Cooper DH, Graham J, et al. Active shape models-their training and application. Computer vision and image understanding. 1995;61(1):38–59. [Google Scholar]


